理论力学模拟题1

一、判断题（10分）1、某平面任意力系向A、B两点简化主矩皆为零，则此力系简化的最终结果不可能为一个力偶。

（）2、当作用于物体上的主动力系的合力作用线与接触面法线间的夹角小于物体与接触面间的摩擦角时，不论该合力的大小如何，物体总是处于平衡状态。

（）3、平面图形上各点的速度大小与该点到速度瞬心的距离成正比；各点加速度的大小也与该点到速度瞬心的距离成正比。

（）4、已知平面图形中基点A的速度为υA，平面图形相对于A点的角速度ωA≠0若选另一点B为基点，则有υB≠υA，ωA=ωB。

（）5、两个运动着质量完全相同的质点，初速度大小、方向也完全相同，以后任一瞬时的速度大小都相同，则任何瞬时，这两个质点受力大小一定相同。

（）6、圆盘在粗糙的地面上作纯滚动，地面对圆盘的静滑动摩擦力为F，由于摩擦力F作用点是圆盘速度瞬心，因此摩擦力不作功。

（）7、刚体瞬时平动时，其上任意两点的速度相同，因此，加速度也一定相等。

（）8、利用虚位移原理只能求解主动力，而不能求解约束反力。

（）9、质点系中各质点都处于静止时，质点系的动量为零。

于是可知如果质点系的动量为零，则质点系中各质点必都静止。

（）10、平面图形绕基点转动的角速度和角加速度与基点的选择有关。

（）二、（42分）简要计算与回答下列各题1、如图所示结构中，各杆的自重略去不计，在构件BC上作用一力偶矩为M的力偶，其它尺寸如图所示，求支座A的约束力。

2、如图所示，正方体的边长为a，求图示力F对三个坐标轴的矩。

3、刚体在图示平面内绕O轴转动，在平面内有A，B两点。

已知OA=2OB，某一瞬时a A=10m/s，方向如图所示。

求此时B点加速度的大小，并在图上绘出B点加速度的方向。

R2 2G=2qL，力偶矩m=q2L。

求：插入端A的约束反力和CD两端的约束反力。

四、计算题（18分）平面机构的曲柄OA的长度为2L，以匀角速度ω0绕O轴转动，在图示位置时，AB=BO，并且∠OAD=90°。

理论力学试题库及答案(通用篇)一、理论力学试题库（通用篇）试题一：已知一质点在平面直角坐标系中的运动方程为 x = 2t² + 3，y = 4t² - t + 1。

求该质点在t = 2s 时的速度和加速度。

试题二：一质点沿圆周运动，其半径为 r，角速度为ω，角加速度为α。

求质点在任意时刻 t 的速度和加速度。

试题三：一质点从静止开始沿直线运动，受到恒力F 的作用。

求质点在任意时刻 t 的速度和位移。

试题四：一质点在平面内做匀速圆周运动，半径为r，角速度为ω。

求质点在任意时刻 t 的速度和加速度。

试题五：一质点在平面内做匀速运动，速度大小为v，方向与水平方向成θ 角。

求质点在任意时刻 t 的位移。

试题六：一质点在重力作用下做自由落体运动，求质点在任意时刻 t 的速度和位移。

试题七：一质点在水平地面上受到一斜向上的拉力F，拉力与水平方向的夹角为θ。

求质点在任意时刻 t 的速度和加速度。

试题八：一质点在平面内做匀速圆周运动，半径为r，角速度为ω。

求质点在任意时刻 t 的切向加速度和法向加速度。

试题九：一质点在平面内做匀速运动，速度大小为v，方向与水平方向成θ 角。

求质点在任意时刻 t 的位移和速度。

试题十：一质点在水平地面上受到一恒力 F 的作用，力与水平方向的夹角为θ。

求质点在任意时刻 t 的速度和位移。

二、答案答案一：t = 2s 时，速度 v = (4t, 8t - 1) = (8, 15) m/s；加速度 a = (8, 8) m/s²。

答案二：质点在任意时刻 t 的速度v = (rω, 0)，加速度a = (0, rα)。

答案三：质点在任意时刻 t 的速度 v = (F/m)t，位移 s = (F/m)t²/2。

答案四：质点在任意时刻 t 的速度 v =(rωcos(ωt), rωsin(ωt))，加速度 a = (-rω²sin(ωt), rω²cos(ωt))。

理论力学xia模拟试题及答案理论力学模拟试题及答案一、选择题（每题2分，共20分）1. 在经典力学中，牛顿第一定律描述的是：A. 物体的加速度与作用力成正比B. 物体的加速度与作用力成反比C. 物体在没有外力作用下保持静止或匀速直线运动D. 物体在任何情况下都有惯性2. 根据牛顿第二定律，力的量度是：A. 质量B. 加速度C. 动量D. 质量与加速度的乘积3. 以下哪一项不是牛顿第三定律的内容：A. 作用力与反作用力大小相等B. 作用力与反作用力方向相反C. 作用力与反作用力同时产生D. 作用力与反作用力作用在不同物体上4. 在圆周运动中，角速度的大小是：A. 线速度与半径的比值B. 线速度与时间的比值C. 弧长与时间的比值D. 半径与时间的比值5. 动量守恒定律适用于：A. 只有重力作用的系统B. 只有摩擦力作用的系统C. 只有外力作用的系统D. 系统所受外力之和为零的系统二、填空题（每题2分，共20分）6. 牛顿第一定律也被称为______定律。

7. 牛顿第二定律的数学表达式是______。

8. 当物体受到多个力作用时，合力的作用效果与______力的效果相同。

9. 角动量守恒定律适用于______。

10. 一个物体的动能与其______的平方成正比。

三、简答题（每题10分，共30分）11. 简述牛顿运动定律的基本内容。

12. 解释什么是角动量守恒，并给出一个实际应用的例子。

13. 描述动量守恒定律在碰撞问题中的应用。

四、计算题（每题15分，共30分）14. 一个质量为2kg的物体在水平面上以5m/s的速度匀速运动，受到一个10N的水平拉力作用。

求物体的动量变化率。

15. 一个质量为3kg的物体从静止开始，在竖直方向上受到一个恒定的力作用，力的大小为50N。

如果物体在2秒内上升了10米，请计算物体的最终速度。

参考答案：一、选择题1. C2. D3. D4. A5. D二、填空题6. 惯性7. F = ma8. 一个等效9. 系统所受外力之和为零10. 速度三、简答题11. 牛顿运动定律包括：第一定律（惯性定律），第二定律（动力定律），第三定律（作用与反作用定律）。

注册岩土工程师（基础考试-上午-理论力学）模拟试卷1单项选择题共120题，每题1分。

每题的备选项中只有一个最符合题意。

1．如图所示，斜梁AB的中部承受铅垂荷载F=20kN，则A、B两端的支座反力为( )。

A．FA=13．2kN，FB=13．2kNB．FA=13．2kN，FB=8．66kNC．FA=8．66kN，FB=8．66kND．FA=8．66kN，FB=13．2kN2．如图所示，一均质球重W=100kN，放在两个相交的光滑斜面之间。

斜面AB的倾角为α=45。

，斜面BC的倾角为β=60。

，则两斜面的反力FD 和FE为( )。

A．FD=85．6kN，FE=74．2kNDFE=75．2kNC．FD=90．6kN，FE=73．2kND．FD=89．6kN，FE=73．2kN3．如图所示，四个力F1、F2、F3和F4同时作用于同一物体上的A、B、C、D四个点(A、B、C、D共面)。

已知F1=F3，F2=F4，该力系向D点简化，则合力为( )。

A．F4B．F1C．D．一F44．如图所示，梁的支座反力为( )。

A．FA=190kN，FB=290kNB．FA=192kN，FB=288kNC．FA=196kN，FB=284kNA FB=280kN5．如图所示，已知挡土墙重W1=75kN，铅垂土压力W2=120kN，水平土压力F=90kN，则这三个力对前趾点A的矩为( )。

A．179kN.mB．170kN.mC．189kN.mD．169kN.m6．如图所示，刚架的支座反力为( )。

A．FAx =0，FAy=17kN，MA=33kN.mB．FAx =5kN，FAy=12kN，MA=15kN.mC．FAx =5kN，FAy=12kN，MA=17kN.mD．FAx =0，FAy=17kN，MA=16kN.m7．如图所示，梁的支座反力为( )。

A．FAx =一1．41kN，FAy=一1．08kN，FB=2．49kNB．FAx =一1．08kN，FAy=一1．41kN，FB=2．49kNC．FAx =一1．41kN，FAy=一1．41kN，FB=2．49kND．FAx =一1．08kN，FAy=一1．08kN，FB=2．49kN8．如图所示，物体重W=1000kN，放在倾角α=30。

理论力学模拟题计算题1、图示梁，已知m＝20 kN.m，q＝ 10 kN／m , l＝1m，求固定端支座A的约束力。

2、如图所示三铰刚架，已知P=20kN，m=10kN.m，q=10kN/m不计自重，计算A、B、C的束力。

3、多跨梁在C点用铰链连接。

已知均布荷载集度q =10 kN／m，CD上作用一力偶，力偶矩为M=40kN·m，l＝2m。

试求A、B、 D处约束力。

4、平面曲柄摆杆机构如图所示，曲柄OA的一端与滑块A用铰链连接。

当曲柄OA以匀角速度ω绕固定轴O转动时，滑块在摇杆O1B上滑动，并带动摇杆O1B绕固定轴O1摆动。

设曲柄长OA= r，两轴间距离OO1=l。

求当曲柄OA在水平位置时摇杆的角速度和角加速度。

5、图示四连杆机构，O1B＝l, AB=1.5 l 且C点是AB 中点，OA 以角速度ω转动，在图示瞬时，求B、C 两点的速度和加速度，刚体AB 的角速度ABω6、在图示四连杆机构中，已知：曲柄OA= r =0.5 m ，以匀角速度rad/s 40=ω转动，r AB 2=，r BC 2=；图示瞬时OA 水平，AB 铅直， 45=ϕ。

试求（1）该瞬时点B 的速度；（2）连杆AB 的角速度。

7、图示摇杆机构，折杆AB 以等速度υ向右运动。

摇杆长度OC ＝a ，用点的合成运动知识求当︒=45ϕ（距离l OA =）时C 点的速度、加速度。

8、刨床的急回机构如图所示。

曲柄OA 以匀角速度ω绕O 作定轴转动，滑块在摇杆B O 1上滑动，并带动杆B O 1绕定轴1O 摆动。

设曲柄长为r OA =，在图示位置时OA 水平，1OO 铅垂，30=ϕ。

求：该瞬时摇杆B O 1角速度和角加速度。

9、质量为m 1和m 2的两重物，分别挂在两条绳子上，绳又分别绕在半径为1r和2r 并装在同一轴的两鼓轮上，已知两鼓轮对于转轴O 的转动惯量为I ，系统在重力作用下发生运动，求鼓轮的角加速度。

（m 1＜m 2）10、已知均质圆轮绕轴O 转动，轮的重量为P ，半径为R ，其上作用一主动力偶M ，重物的质量为m ，计算重物上升的加速度a 。

《理论力学》考试试卷（答案）1.如图3所示，a图中B端的反支力为M/2L , b图中B端的反支力为M/L 。

2.某桁架如图2所示，其中零杆数目为—o3.如图3所示，刚架受到一对力偶和一对共线的力作用，且知m=5kN.m以及P = 41kN , A处支座反力分别为X.= 0 ,Y A= 0 ,此= （逆时针为正）。

5.如图4所示，刚体作平面运动，其平面图形（未画出）内两点A、B相距L = 3m, 两点的加速度均垂直于AB连线，方向相反，大小分别为5m/s和10m/s。

则该瞬时图形的角速度的大小为5 rad/s 。

6.如图5所示，均质直杆0A质量为m,长为L,以角速度3绕固定轴0顺时针转动（逆时针为正）。

在图示位置直杆水平，其动量的大小为mLco/2 ；直杆对0轴动量矩的大小为ml? 3/3 ,杆动能大小为ml； 3 76。

二、计算题（共60分）。

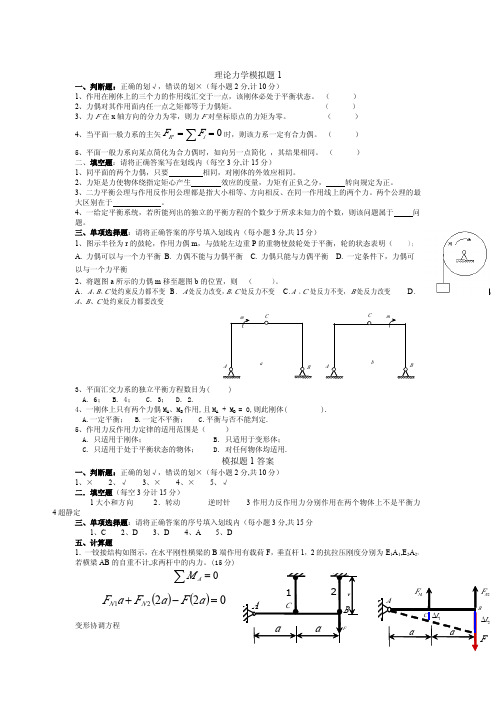
1.如图所示，梁AC用三根链杆支承，梁受集中力P和均布荷载作用，已知P=40kN, q=5kN/m,试求各链杆的内力。

（本题15分）解：受力分析如图所示:2.桁架如图所示，试求杆件CD, CE和EF的内力。

（本题15分）解：由图分析可知CD杆为0杆。

……（1分）1）先取整体分析，如图所示分别对A点和B点取矩：Am尸)=o-2x10-4x10-6x10-8x5 + 8x7? = 0D2>*)=°2x10 + 4x10 + 6x10 + 8x5-8x7?^ =0解得：R A =20kN, R B =20kN如图取I - I截面左半部分对A点取矩，取II-11截面右部分对B点取矩£ 〃很了）= 0-2xl0-2x S CE sin（cif）-lx S CE cos（o） = 0£ 〃七（了）= o8X7?A +8X5+6X10+4X10+6X S CE sin（。

）-lx S CE cos（。

）+ 4x S FE = 0上式解得：S^=—11.18KN, S FF = 1QKNCc r Zi3,图示机构中，曲柄04长为r,绕。

《理论力学》期末考试卷模拟试卷01一．判断题（认为正确的请在每题括号内打√，否则打×；每小题3分，共15分）（√）1.几何约束必定是完整约束，但完整约束未必是几何约束。

（×）2.刚体做偏心定轴匀速转动时，惯性力为零。

（×）3.当圆轮沿固定面做纯滚动时，滑动摩擦力和动滑动摩擦力均做功。

（√）4.质点系动量对时间的导数等于作用在质点系上所有外力的矢量和。

（√）5.平面运动随基点平动的运动规律与基点的选择有关，而绕基点转动的规律与基点选取无关。

二．选择题（把正确答案的序号填入括号内，每小题3分，共30分）1.如图1所示，楔形块A，B自重不计，并在光滑的mm，nn 平面相接触。

若其上分别作用有大小相等，方向相反，作用线相同的二力P,P’，则此二刚体的平衡情况是（ A ）（A）二物体都不平衡（B）二物体都能平衡（C）A平衡，B不平衡（D）B平衡，A不平衡2.如图2所示，力F作用线在OABC平面内，则力F对空间直角坐标Ox，Oy，Oz轴之距，正确的是（ C ）（A）m x(F)=0，其余不为零（B）m y(F)=0，其余不为零（C）m z(F)=0，其余不为零（D）m x(F)=0, m y(F)=0, m z(F)=03.图3所示的圆半径为R，绕过点O的中心轴作定轴转动，其角速度为ω，角加速度为ε。

记同一半径上的两点A，B的加速度分别为a A,a B（OA=R，OB=R/2），它们与半径的夹角分别为α,β。

则a A,a B的大小关系，α,β的大小关系，正确的是（B ）（A）BAaa2=, α=2β（B）BAaa2=, α=β（C）BAaa=, α=2β（D）BAaa=, α=βy图14.直管AB 以匀角速度ω绕过点O 且垂直于管子轴线的定轴转动，小球M 在管子内相对于管子以匀速度v r 运动。

在图4所示瞬时，小球M 正好经过轴O 点，则在此瞬时小球M 的绝对速度v ，绝对加速度a 是（D ）（A ）v=0,a =0 （B ）v=v r, a =0 （C ）v=0,r v a ω2=,← （D ）v=v r , r v a ω2=,← 5. 图5所示匀质圆盘质量为m ，半径为R ，可绕轮缘上垂直于盘面的轴转动，转动角速度为ω，则圆盘在图示瞬时的动量是（ B ） （A ）K=0 （B ）K=mR ω，↓ （C ）K=2mR ω ，↓ （D ）K=mR ω2 ，←6. 条件同前题（5），则圆盘的动能是（D ）（A ）2221ωmR T = （B ）2241ωmR T =（C ）22ωmR T = （D ）2243ωmR T =7. 匀质半圆盘质量为m ，半径为R ，绕过圆心O 并垂直于盘面的定轴转动（图6），其角速度为ω，则半圆盘对点O 的动量矩的大小L 0 是（ C ）。

考试题型：一、根据力学公理作受力图。

[2×5分=10分] 二、求约束反力。

[2×10分=20分]三、轴向拉压杆强度、变形、超静定问题。

[20分] 四、扭转强度、刚度。

[20分] 五、作弯曲内力图。

[10分]六、弯曲正应力强度问题。

[20分]一、作受力图。

（a ）（b ） （c ）（d ）（e ）（f ）（g ） （h ）二、求约束反力。

1，AB 梁受如图所示约束和荷载，已知40F kN =,10/q kN m =,20.M kN m =1a m =。

求两端所受的约束反力。

（15分）2，求约束反力大小。

（i ）题1图 题1图题2图题2图三、轴向拉压杆强度、变形、超静定问题。

1，如题3.1图所示圆截面直杆，已知直径10d mm =，1000a mm =，材料的弹性模量200E GPa =，[]80MPa σ=。

（1）作直杆的轴力图；（2）对AC 杆进行强度校核；（3）求杆AC 的总变形。

（15分）题3.1图题3.2图2、如题3.2图所示杆系结构，已知BD 杆为圆截面钢板，直径20d mm =，长度1l m =，200E GPa =；BC 杆为方截面木杆，边长100a mm =，12E GPa =；荷载50F kN =。

(a)求各杆的内力；（b ）求B 点的位移。

(15分)3,图示结构中。

若1、2两杆的EA 相同，则节点A 的竖向位移∆Ay ＝ ，水平位移为∆Ax ＝ 。

4,正方形结构受力如图，P ＝50 kN ，各杆横截面积A ＝2000 mm 2，求各杆的正应力。

5,图示木制桁架受水平力P 作用，已知P ＝80 kN ，许用拉、压应力分别为：[ σ t ]＝8 MPa ，[ σc ]＝10 MPa ，设计AB 杆和CD 杆的横截面面积。

6,钢质圆杆的直径d ＝10 mm ，P ＝5 kN ，弹性模量E ＝210 GPa 。

求杆内最大应变和杆的总伸长。

7,如图所示，杆ABC 为刚杆，①、②、③各杆E 、A 、l 均相同，求各杆内力值。

一、判断题 (正确打“√”，错误打“×”，每小题2分，共10分)1、平面任意力系，只要主矢0≠'RF，最后必可简化为一合力。

( √ )2、刚体在3个力的作用下平衡，这3个力不一定在同一个平面内。

( × )3、某刚体作平面运动时，若A 和B 是其平面图形上的任意两点，则速度投影定理[][]AB B AB A v v=恒成立。

( √ )4、作瞬时平移的刚体，该瞬时其惯性力系向质心简化，主矩为零。

( × )5、当牵连运动为定轴转动时一定有科氏加速度。

( × )二、选择题（每一小题只有一个正确答案，多选不给分。

请将正确答案的序号填入括号内。

每题3分，共15分）1、已知杆AB 和CD 的自重不计，且在C 处光滑接触。

若作用在AB 杆上的力偶矩为1m ，欲使系统保持平衡，需在CD 杆上施加力偶矩2m ，其大小为( A )。

A 、 12m m =；B 、 1234m m =；C 、 122m m =；D 、 1221m m =。

2、平面一般力系的二力矩式平衡方程为,0)(,0==∑∑i A y F M F 0)(=∑i B F M ，其适用条件是 ( D )。

A 、 A 、B 两点均在y 轴上； B 、 y 轴垂直于 A 、B 连线；C 、 x 轴垂直于A 、B 连线；D 、 y 轴不垂直于A 、B 连线。

3、圆盘作定轴转动，若某瞬时其边缘上A 、B 、C 、D 四点的速度、加速度如图所示，则（ D ）的运动是可能的。

（A ）点A 、B ； （B ）点A 、C ； （C ）点C 、B ；Am 1BCD m 260ºAD C B V 1V 2V 3V 4a 2a 1a 4a 3O（D ）点C 、D 。

4、平面图形上任意两点A 、B 的加速度A a 、B a 与A 、B 连线垂直，且B A a a ≠，则该瞬时平面图形的角速度ω和角加速度α为 ( C )。