立体几何垂直证明(基础)
- 格式:doc
- 大小:374.80 KB
- 文档页数:6

立体几何基础平行与垂直的性质与判定立体几何基础——平行与垂直的性质与判定立体几何是数学中的一个重要分支,它研究的对象是在三维空间内的图形和物体。
在立体几何中,平行和垂直是两个基本概念,它们在判断和解决几何问题时起着重要的作用。
本文将介绍平行与垂直的性质和判定方法,帮助读者更好地理解立体几何的基础知识。
一、平行的性质与判定平行是指在同一平面内,两条直线永不相交的性质。
在立体几何中,我们常用平行性质来推导和证明定理。
以下是一些与平行相关的性质和判定方法。
1. 平行线性质:(1)平行线上的对应角相等:如果两条平行线被一条横截线所交,那么对应的角都是相等的。
(2)平行线上的内错角互补:如果两条平行线被一条横截线所交,那么内错角互补,即相互补充的角和为180度。
(3)平行线上的同旁内角相等:如果两条平行线被一条横截线所交,那么同旁内角相等,即相邻的内角相等。
2. 判定平行线的方法:(1)两条线段平行的充要条件是斜率相等:如果两条线段的斜率相等,那么它们是平行的。
(2)两个向量平行的充要条件是比值相等:如果两个向量的坐标分量比值相等,那么它们是平行的。
(3)两条直线互相垂直的充要条件是斜率乘积为-1:如果两条直线的斜率乘积为-1,那么它们互相垂直。
二、垂直的性质与判定垂直是指两条直线或线段在交点处互相成直角的性质。
垂直的性质在几何证明中经常被用到,下面是关于垂直的一些性质和判定方法。
1. 垂直线性质:(1)垂直线上的对应角互补:如果两条垂直线被一条横截线所交,那么对应的角互补,即相互补充的角和为90度。
(2)垂直线上的内角相等:如果两条垂直线被一条横截线所交,那么内角相等,即相邻的内角相等。
2. 判定垂直线的方法:(1)两条线段垂直的充要条件是斜率乘积为-1:如果两条线段的斜率乘积为-1,那么它们是垂直的。
(2)两个向量垂直的充要条件是内积为0:如果两个向量的内积为0,那么它们是垂直的。
三、平行和垂直在实际中的应用平行和垂直的性质在日常生活和工程实践中有广泛的应用。

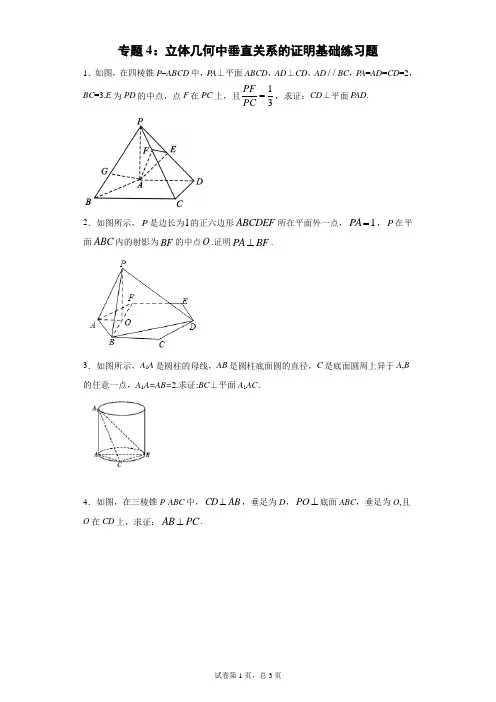
立体几何垂直证明题常见模型及方法垂直转化:线线垂直线面垂直面面垂直;基础篇类型一:线线垂直证明(共面垂直、异面垂直)(1) 共面垂直:实际上是平面内的两条直线的垂直 (只需要同学们掌握以下几种模型)○1 等腰(等边)三角形中的中线○2 菱形(正方形)的对角线互相垂直 ○3勾股定理中的三角形 ○4 1:1:2 的直角梯形中 ○5 利用相似或全等证明直角。
例:在正方体1111ABCD A BC D -中,O 为底面ABCD 的中心,E 为1CC ,求证:1AO OE ⊥(2) 异面垂直 (利用线面垂直来证明,高考中的意图) 例1 在正四面体ABCD 中,求证AC BD ⊥变式 1 如图,在四棱锥ABCD P -中,底面A B C D 是矩形,已知60,22,2,2,3=∠====PAB PD PA AD AB .证明:AD PB ⊥;变式2 如图,在边长为2的正方形ABCD 中,点E 是AB 的中点,点F 是BC 的中点,将△AED,△DCF 分别沿,DE DF 折起,使,A C 两点重合于'A. 求证:'A D EF ⊥;类型二:线面垂直证明BE 'ADFG方法○1 利用线面垂直的判断定理例2:在正方体1111ABCD A BC D -中,O 为底面ABCD 的中心,E 为1CC ,求证:1AO BDE ⊥平面变式1:在正方体1111ABCD A BC D -中,,求证:11AC BDC ⊥平面 变式2:如图:直三棱柱ABC -A 1B 1C 1中, AC =BC =AA 1=2,∠ACB =90︒.E 为BB 1的中点,D 点在AB 上且DE = 3 .求证:CD ⊥平面A 1ABB 1;变式3:如图,在四面体ABCD 中,O 、E 分别是BD 、BC 的中点,AD BC ∥,90ABC ∠=°,PA ⊥平面ABCD .3PA =,2AD =,AB =,6BC =C○2 利用面面垂直的性质定理 例3:在三棱锥P-ABC 中,PA ABC ⊥底面,PAC PBC ⊥面面,BC PAC ⊥求证:面。


立体几何(垂直平面交线的证明)
简介
本文将证明在立体几何中,两个垂直平面交线垂直。
垂直平面交线是指两个平面的交线。
证明过程
设两个垂直平面为平面A和平面B,它们的交线为线段CD。
步骤一:确定垂直平面
首先,我们需要确定平面A和平面B垂直。
根据立体几何的性质,两个平面垂直的充要条件是它们的法向量垂直。
设平面A的法向量为向量a,平面B的法向量为向量b。
如果向量a与向量b垂直,则平面A和平面B垂直。
步骤二:确定交线
在确定平面A和平面B垂直后,我们需要证明线段CD垂直。
设线段CD在平面A上的一个点为点C,在平面B上的一个点为点D。
我们需要证明向量CD与向量a和向量b均垂直。
如果向量CD与向量a垂直,则线段CD垂直平面A;如果向量CD与向量b垂直,则线段CD垂直平面B。
步骤三:证明
根据向量的垂直性质,我们知道两个向量垂直的充要条件是它们的点积为零。
首先,我们证明向量CD与向量a垂直。
设向量CD为向量c,向量a为向量d。
如果向量c与向量d的点积为零,则向量CD与向量a垂直。
同样地,我们证明向量CD与向量b垂直。
设向量CD为向量c,向量b为向量e。
如果向量c与向量e的点积为零,则向量CD与向量b垂直。
结论
通过以上证明,我们可以得出结论:在立体几何中,两个垂直平面交线垂直。
参考文献
- 立体几何教材,作者A,出版社B,年份C。

立体几何中的向量方法(一)——证明平行与垂直1.直线的方向向量与平面的法向量确实定(1)直线的方向向量:在直线上任取一非零向量作为它的方向向量.(2)平面的法向量可利用方程组求出:设a ,b 是平面α两不共线向量,n 为平面α的法向量,则求法向量的方程组为⎩⎨⎧n ·a =0,n ·b =0.2.用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ,与平面α共面的两个不共线向量v 1和v 2,则l ∥α或l ⊂α⇔存在两个实数*,y ,使v =*v 1+y v 2.(3)设直线l 的方向向量为v ,平面α的法向量为u ,则l ∥α或l ⊂α⇔v ⊥u .(4)设平面α和β的法向量分别为u 1,u 2,则α∥β⇔u 1∥u 2.3.用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2=0.(2)设直线l 的方向向量为v ,平面α的法向量为u ,则l ⊥α⇔v ∥u .(3)设平面α和β的法向量分别为u 1和u 2,则α⊥β⇔u 1⊥u 2⇔u 1·u 2=0.【思考辨析】判断下面结论是否正确(请在括号中打"√〞或"×〞)(1)直线的方向向量是唯一确定的.()(2)平面的单位法向量是唯一确定的.()(3)假设两平面的法向量平行,则两平面平行.()(4)假设两直线的方向向量不平行,则两直线不平行.()(5)假设a ∥b ,则a 所在直线与b 所在直线平行.()(6)假设空间向量a 平行于平面α,则a 所在直线与平面α平行.()1.以下各组向量中不平行的是()A .a =(1,2,-2),b =(-2,-4,4)B .c =(1,0,0),d =(-3,0,0)C .e =(2,3,0),f =(0,0,0)D .g =(-2,3,5),h =(16,24,40)2.平面α有一点M (1,-1,2),平面α的一个法向量为n =(6,-3,6),则以下点P 中,在平面α的是()A .P (2,3,3)B .P (-2,0,1)C .P (-4,4,0)D .P (3,-3,4)3.AB →=(1,5,-2),BC →=(3,1,z ),假设AB →⊥BC →,BP →=(*-1,y ,-3),且BP ⊥平面ABC ,则实数*,y ,z 分别为______________.4.假设A (0,2,198),B (1,-1,58),C (-2,1,58)是平面α的三点,设平面α的法向量n =(*,y ,z ),则*∶y ∶z =________.题型一 证明平行问题例1(2013·改编)如图,在四面体A -BCD 中,AD ⊥平面BCD ,BC ⊥CD ,AD =2,BD =22,M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且AQ =3QC .证明:PQ ∥平面BCD .如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F ,M ,N 分别是棱AB ,AD ,A 1B 1,A 1D 1的中点,点P ,Q 分别在棱DD 1,BB 1上移动,且DP =BQ =λ(0<λ<2).(1)当λ=1时,证明:直线BC 1∥平面EFPQ ;(2)是否存在λ,使平面EFPQ 与平面PQMN 所成的二面角为直二面角?假设存在,求出λ的值;假设不存在,说明理由.题型二 证明垂直问题例2 如下图,正三棱柱(底面为正三角形的直三棱柱)ABC —A 1B 1C 1的所有棱长都为2,D 为CC 1的中点.求证:AB 1⊥平面A 1BD .如下图,在四棱锥P -ABCD 中,PC ⊥平面ABCD ,PC =2,在四边形ABCD 中,∠B =∠C =90°,AB =4,CD =1,点M 在PB 上,PB =4PM ,PB 与平面ABCD 成30°角.(1)求证:CM ∥平面PAD ;(2)求证:平面PAB ⊥平面PAD .题型三 解决探索性问题例3 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1AC均为60°,平面AA1C1C⊥平面ABCD.(1)求证:BD⊥AA1;(2)求二面角D-A1A-C的余弦值;(3)在直线CC1上是否存在点P,使BP∥平面DA1C1,假设存在,求出点P的位置,假设不存在,请说明理由.如下图,四棱锥S—ABCD的底面是正方形,每条侧棱的长都是底面边长的2倍,P为侧棱SD上的点.(1)求证:AC⊥SD.(2)假设SD⊥平面PAC,则侧棱SC上是否存在一点E,使得BE∥平面PAC.假设存在,求SE∶EC的值;假设不存在,试说明理由.利用向量法解决立体几何问题典例:如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设二面角D-AE-C为60°,AP=1,AD=3,求三棱锥E-ACD的体积.A组专项根底训练1.假设直线l的方向向量为a=(1,0,2),平面α的法向量为n=(-2,0,-4),则()A.l∥αB.l⊥αC.l⊂αD.l与α相交2.假设AB→=λCD→+μCE→,则直线AB与平面CDE的位置关系是()A.相交B.平行C.在平面D.平行或在平面3.A(4,1,3),B(2,-5,1),C(3,7,-5),则平行四边形ABCD的顶点D的坐标是() A.(2,4,-1) B.(2,3,1)C.(-3,1,5) D.(5,13,-3)4.a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),假设a,b,c三向量共面,则实数λ等于()A.627B.637C.607D.6575.如图,在长方体ABCD —A 1B 1C 1D 1中,AB =2,AA 1=3,AD =22,P 为C 1D 1的中点,M 为BC 的中点.则AM 与PM 所成的角为()A .60°B .45°C .90°D .以上都不正确6.平面α的三点A (0,0,1),B (0,1,0),C (1,0,0),平面β的一个法向量n =(-1,-1,-1),则不重合的两个平面α与β的位置关系是________.7.设点C (2a +1,a +1,2)在点P (2,0,0)、A (1,-3,2)、B (8,-1,4)确定的平面上,则a =________.8.如图,在正方体ABCD —A 1B 1C 1D 1中,棱长为a ,M 、N 分别为A 1B 和AC 上的点,A 1M =AN =2a 3,则MN 与平面BB 1C 1C 的位置关系是________. 9.如图,四边形ABCD 为正方形,PD ⊥平面ABCD ,PD ∥QA ,QA =AB=12PD .证明:平面PQC ⊥平面DCQ . 10.如图,在底面是矩形的四棱锥P -ABCD 中,PA ⊥底面ABCD ,E ,F 分别是PC ,PD 的中点,PA =AB =1,BC =2.(1)求证:EF ∥平面PAB ;(2)求证:平面PAD ⊥平面PDC .B 组 专项能力提升11.如图,正方形ABCD 与矩形ACEF 所在平面互相垂直,AB =2,AF =1,M 在EF 上,且AM ∥平面BDE ,则M 点的坐标为()A .(1,1,1)B .(23,23,1) C .(22,22,1) D .(24,24,1)12.设u =(-2,2,t ),v =(6,-4,4)分别是平面α,β的法向量,假设α⊥β,则t 等于()A .3B .4C .5D .613.在正方体ABCD —A 1B 1C 1D 1中,P 为正方形A 1B 1C 1D 1四边上的动点,O 为底面正方形ABCD 的中心,M ,N 分别为AB ,BC 的中点,点Q 为平面ABCD 一点,线段D 1Q 与OP 互相平分,则满足MQ →=λMN→的实数λ有________个.14.如下图,直三棱柱ABC —A 1B 1C 1中,△ABC 为等腰直角三角形,∠BAC =90°,且AB =AA 1,D 、E 、F 分别为B 1A 、C 1C 、BC 的中点.求证:(1)DE ∥平面ABC ;(2)B 1F ⊥平面AEF .15.在四棱锥P —ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD =DC ,E 、F 分别是AB 、PB 的中点.(1)求证:EF ⊥CD ;(2)在平面PAD 求一点G ,使GF ⊥平面PCB ,并证明你的结论.。

立体几何线线垂直的证明方法在立体几何中,线线垂直是一种非常重要的关系,它在很多问题中都有着重要的应用。
本文将介绍几种线线垂直的证明方法,希望能够帮助读者更好地理解和运用这一关系。
一、垂线段的垂线段垂直首先介绍的是垂线段的垂线段垂直的证明方法。
具体来说,如果有两个垂直于同一个平面的线段AB和CD,且它们之间有一条垂线段EF,则EF和CD垂直。
证明如下:1、连接AE和CF,得到平面ACEF。
2、由于AB和CD垂直于平面ACEF,所以它们的交点O在平面ACEF 内。
3、由于EF垂直于平面ACEF,所以它与平面ACEF的任意一条交线都垂直,特别地,它与CF垂直。
4、因此,EF和CD垂直。
二、平面的法线和平面内的任意直线垂直接下来介绍的是平面的法线和平面内的任意直线垂直的证明方法。
具体来说,如果有一个平面P和一条直线L在平面P内,且L与P垂直,则L与P的法线垂直。
证明如下:1、连接L和P的交点O。
2、在平面P内任意取一点A,连接OA。
3、由于L与P垂直,所以OA与L垂直,即OA和L在点O处垂直。
4、由于P的法线垂直于P,所以它与P内任意一条直线都垂直,特别地,它与OA垂直。
5、因此,L与P的法线垂直。
三、垂线段和平面的法线垂直最后介绍的是垂线段和平面的法线垂直的证明方法。
具体来说,如果有一条垂直于平面P的直线L,且L与平面P上的一条线段AB相交于点O,则OA和OB的中垂线与P的法线垂直。
证明如下:1、连接OA和OB,得到线段AB的中垂线CD。
2、连接CO和DO,得到平面COD。
3、由于L垂直于平面P,所以L和P的法线在平面P内的交点O 处垂直。
4、由于OA和OB在点O处相交,所以它们的中垂线CD也经过点O。
5、因此,CD与P的法线垂直。
以上就是三种线线垂直的证明方法,它们都非常简单易懂,但是能够解决很多实际问题。
在实际应用中,我们可以根据具体情况选择不同的证明方法,以便更好地解决问题。


立体几何垂直证明题常见模型及方法证明空间线面垂直需注意以下几点:①由已知想性质,由求证想判定,即分析法与综合法相结合寻找证题思路。
②立体几何论证题的解答中,利用题设条件的性质适当添加辅助线(或面)是解题的常用方法之一。
③明确何时应用判定定理,何时应用性质定理,用定理时要先申明条件再由定理得出相应结论。
垂直转化:线线垂直 线面垂直 面面垂直;基础篇类型一:线线垂直证明(共面垂直、异面垂直)(1) 共面垂直:实际上是平面内的两条直线的垂直 (只需要同学们掌握以下几种模型)○1 等腰(等边)三角形中的中线○2 菱形(正方形)的对角线互相垂直 ○3勾股定理中的三角形 ○4 1:1:2 的直角梯形中 ○5 利用相似或全等证明直角。
例:在正方体1111ABCD A B C D -中,O 为底面ABCD 的中心,E 为1CC ,求证:1A O OE ⊥(2) 异面垂直 (利用线面垂直来证明,高考中的意图) 例1 在正四面体ABCD 中,求证AC BD ⊥变式 1 如图,在四棱锥ABCD P -中,底面ABCD 是矩形,已知60,22,2,2,3=∠====PAB PD PA AD AB .证明:AD PB ⊥;变式2 如图,在边长为2的正方形ABCD 中,点E 是AB 的中点,点F 是BC 的中点,将△AED,△DCF 分别沿,DE DF 折起,使,A C 两点重合于'A . 求证:'A D EF ⊥;变式3如图,在三棱锥P ABC -中,⊿PAB 是等边三角形,∠P AC =∠PBC =90 º证明:AB ⊥PC类型二:线面垂直证明方法○1 利用线面垂直的判断定理例2:在正方体1111ABCD A B C D -中,O 为底面ABCD 的中心,E 为1CC ,求证:1A O BDE ⊥平面变式1:在正方体1111ABCD A B C D -中,,求证:11AC BDC ⊥平面 变式2:如图:直三棱柱ABC -A 1B 1C 1中, AC =BC =AA 1=2,∠ACB =90︒.E 为BB 1的中点,D 点在AB 上且DE = 3 . 求证:CD ⊥平面A 1ABB 1;BE'ADFG变式3:如图,在四面体ABCD 中,O 、E 分别是BD 、BC 的中点,变式4 如图,在底面为直角梯形的四棱锥P ABCD -中,AD BC ∥,90ABC ∠=°,PA ⊥平面ABCD .3PA =,2AD =,AB =6BC =C类型3:面面垂直的证明。

空间点、线、面的位置关系:垂直【背一背基础知识】1.判定两直线垂直,可供选用的定理有:①若a ∥b ,b ⊥c ,则a ⊥c .②若a ⊥α,b ⊂α,则a ⊥b .2.线面垂直的定义:一直线与一平面垂直⇔这条直线与平面内任意直线都垂直;3.线面垂直的判定定理,可选用的定理有:①若a ⊥b ,a ⊥c ,b ,c ⊂α,且b 与c 相交,则a ⊥α.②若a ∥b ,b ⊥α,则a ⊥α.③若α⊥β,α∩β=b ,a ⊂α,a ⊥b ,则a ⊥β.4.判定两平面垂直,可供选用的定理有:若a ⊥α,a ⊂β,则α⊥β.线面垂直1.如图,在三棱台ABC-DEF 中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=F C=1,BC=2,AC=3.(I)求证:BF⊥平面ACFD;2.如图,在四棱锥P ABCD -中,底面ABCD 是︒=∠60DAB 且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD ⊥底面ABCD ,G 为AD 的中点.求证:BG ⊥平面PAD .线线垂直1、如图,在三棱锥P ABC -中,90PAC BAC ∠=∠=︒,PA PB =,点D ,F 分别为BC ,AB 的中点.(1)求证:PF ⊥AD .2、如图,在三棱柱111ABC A B C -中,面11ABB A 为矩形,11,2,AB BC AA D ===为1AA 的中点,BD与1AB 交于点1,O BC AB ⊥.(Ⅰ)证明:1CD AB ⊥3、下图为一简单组合体,其底面ABCD 为正方形,PD ⊥平面ABCD ,//EC PD ,且22PD AD EC ===,N 为线段PB 的中点.(Ⅰ)证明:NE PD ⊥;4、如图所示,在三棱柱111ABC A B C -中,11AA B B 为正方形,11BB C C 为菱形,1160BB C Ð=°,平面11AA B B ^平面11BB C C 。
立体几何(垂直关系的证明)1. 什么是垂直关系垂直关系是指两条线、两个平面或者一条线和一个平面之间的互相垂直的关系。
在立体几何中,垂直关系是非常重要的,它涉及到角度、边长和面积等概念。
2. 垂直关系的证明方法证明两条线或者一个线和一个平面垂直可以采用不同的方法,以下是一些常见的证明方法:2.1. 利用垂直的性质证明当两个线段的斜率乘积为-1时,这两个线段就互相垂直。
这是一个常用的方法来证明两条直线的垂直关系。
例如,如果两条直线的斜率分别为m1和m2,并且m1 * m2 = -1,则可以证明这两条直线是垂直的。
2.2. 利用垂直线段的性质证明对于一个平面内的几条垂直线段来说,其平分线是相交于一个点,并且平分线与原始线段之间的夹角为90度。
这可以用来证明两条线段是垂直的。
2.3. 利用垂直平分线的性质证明对于一个多边形来说,如果一条线段能够将另外两条线段的中点连接起来并且垂直于它们,那么这条线段就是垂直于这两条线段的平分线。
这个原理可以用来证明线段和平面的垂直关系。
2.4. 利用垂直距离的性质证明如果一个点到一直线的距离为0,并且这个点在另外一条直线上,那么这两条直线是垂直的。
这个方法可以用来证明直线和平面的垂直关系。
3. 如何选择合适的证明方法在选择合适的证明方法时,需要根据具体问题的要求和条件进行判断。
通常来说,可以根据已知的条件和所需证明的结论来选择并结合不同的证明方法。
4. 总结在立体几何中,垂直关系的证明是一个重要的内容。
通过掌握不同的证明方法,我们可以更好地理解和应用垂直关系,进一步深入研究立体几何的问题。
立体几何垂直判定定理立体几何垂直判定定理一、前言在立体几何中,垂直是一个非常重要的概念。
垂直关系不仅存在于平面内,也存在于空间中。
本文将介绍立体几何中的垂直判定定理。
二、定义在三维空间中,两条直线或两个平面互相垂直,当且仅当它们的方向向量互相垂直。
三、证明1. 两条直线的垂直判定对于两条不共面的直线l1和l2,它们互相垂直当且仅当它们的方向向量l1和l2满足以下条件:l1·l2=0(点乘为0)其中,“·”表示向量点乘运算。
证明如下:设l1的方向向量为a=(x1,y1,z1),l2的方向向量为b=(x2,y2,z2)。
则有:a·b=x1x2+y1y2+z1z2若a·b=0,则有x1x2+y1y2+z1z2=0。
这说明a与b互相垂直。
反之,若a与b互相垂直,则有a·b=0。
因此,两条不共面的直线互相垂直当且仅当它们的方向向量满足上述条件。
对于两条共面的直线,它们互相垂直当且仅当它们的方向向量l1和l2满足以下条件:l1·l2=0(点乘为0),且l1和l2不共线其中,“·”表示向量点乘运算。
证明如下:设l1的方向向量为a=(x1,y1,z1),l2的方向向量为b=(x2,y2,z2)。
则有:a·b=x1x2+y1y2+z1z2若a·b=0,则有x1x2+y1y2+z1z2=0。
这说明a与b互相垂直。
但是,如果a和b共线,则它们不可能互相垂直。
因此,我们需要加上一个限制条件:l1和l2不共线。
反之,若a与b互相垂直,且l1和l2不共线,则有a·b=0。
因此,两条共面的直线互相垂直当且仅当它们的方向向量满足上述条件。
综上所述,两条直线互相垂直当且仅当它们的方向向量满足上述条件。
2. 两个平面的垂直判定对于两个平面P1和P2,它们互相垂直当且仅当它们的法向量n1和n2满足以下条件:n1·n2=0(点乘为0)其中,“·”表示向量点乘运算。
摇生"攵浬化知识篇科学备考新指向高考数学2021年2月立"#何%&行直问题的证明■江苏省华罗庚中学李普红平行与垂直关系的证明是高考考查立体几何的高频考点,大部分问题都可以用传统的几何方法解决,有一部分问题需要建立空间直角坐标系利用空间向量解决。
用传统法解题时,应注重线线平行、线线垂直、线面平行、线面垂直、面面平行、面面垂直等问题的性质定理和判定定理的灵活应用。
用向量法解题时,应建立恰当的空间直角坐标系,准确表示各点与相关向量的坐标。
考向一:证明线面平行!!如图1,已知空间几何体BACDE中,&BCD与&CDE均是边长为2的等边三角形,&ABC是腰长为3,底边为BC的等腰三角形,平面CDE丄平面BCD,平面ABC丄平面BCD"(1)试在平面BCD内作一条直线,使得直线上任意一点F与E的连线EF均与平面ABC平行,并给出证明;(2)求三棱锥E-ABC的体积。
解析:(1)如图2所示,取DC的中点为N,BD的中点为/,连接MN,则MN即为所求。
连接EM,EN,取BC的中点4,连接AH"因为&ABC是腰长为3的等腰三角形,H为BC的中点,所以AH丄BC。
又平面ABC丄平面BCD,平面ABC'平面BCD$BC,AH U平面ABC,所以AH 丄平面BCD"同理可证EN丄平面BCD"所以EN/AH"因为EN1平面ABC,AH U平面ABC,所以EN/平面ABC"又M,N分别为BD,DC的中点,所以MN/BC"因为MN1平面ABC,BC U平面ABC,所以MN/平面ABC"又MN'EN$N,MN U平面EMN,EN U平面EMN,所以平面EMN/平面ABC"又EF U平面EMN,所以EF/平面ABC,即直线MN上任意一点F与E的连线EF均与平面ABC平行°(2)连接DH,取CH的中点为G,连接NG,则NG/DH"由(1)可知EN/平面ABC,所以点E到平面ABC的距离与点N到平面ABC的距离相等°又&BCD是边长为2的等边三角形,所以DH丄BC。
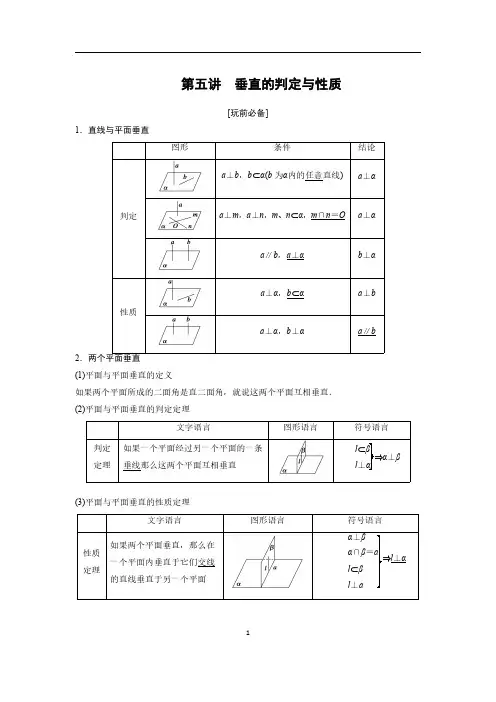
立体几何证明【知识梳理】1.直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行⇒线面平行”)相交,那么这条直线和交线平行.(“线面平行⇒线线平行”)2..直线与平面垂直判定定理一如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直⇒线面垂直”)判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.性质1.如果一条直线垂直于一个平面,那么这条直线垂直于这个平面内的所有直线。
(线面垂直⇒线线垂直)性质2:如果两条直线同垂直于一个平面,那么这两条直线平行.三。
平面与平面空间两个平面的位置关系:相交、平行.1.平面与平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(“线面平行⇒面面平行”)2. 两个平面垂直判定定理:如果一条直线与一个平面垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直⇒面面垂直”)性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.(面面垂直⇒线面垂直)知识点一 【例题精讲】1.在棱长为2的正方体1111D C B A ABCD -中,E 、F 分别为1DD 、DB 的中点。
(1)求证:EF//平面11D ABC ;(2)求证: 平面B 11D C C B 1⊥ EF C B 1⊥; (3)求三棱锥EFC B -1的体积V.2.如图所示, 四棱锥P -ABCD 底面是直角梯形,,,2,BA AD CD AD CD AB PA ⊥⊥=⊥底面ABCD , E 为PC 的中点, PA =AD =AB =1. (1)证明: //EB PAD 平面; (2)证明: BE PDC ⊥平面; (3)求三棱锥B -PDC 的体积V .3、如图所示,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点,证明:(1)AE⊥CD(2)PD⊥平面ABE.4、.如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°(Ⅰ)证明:AB⊥A1C;练习1、如图,菱形ABCD与等边△PAD所在的平面相互垂直,AD=2,∠DAB=60°.(Ⅰ)证明:AD⊥PB;(Ⅱ)求三棱锥C﹣PAB的高.2.如图14所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.求证:EF⊥平面BCG;3.如图11所示,三棱柱ABCA1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.(1)证明:AC1⊥A1B;4、如图,在三棱台ABC﹣DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.(Ⅰ)求证:BF⊥平面ACFD;(Ⅱ)求直线BD与平面ACFD所成角的余弦值.5、三棱锥P﹣ABC中,∠BAC=90°,PA=PB=PC=BC=2AB=2,(1)求证:面PBC⊥面ABC6.已知四棱锥P-ABCD中,底面四边形为正方形,侧面PDC为正三角形,且平面PDC⊥底面ABCD,E为PC的中点.(1)求证:PA∥平面EDB;(2)求证:平面EDB⊥平面PBC;7、如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.(1)求证:AP∥平面BDE;2.求证BE 垂直平面PAC8、将如图一的矩形ABMD沿CD翻折后构成一四棱锥M﹣ABCD(如图二),若在四棱锥M﹣ABCD中有MA=.(1)求证:AC⊥MD;(2)求四棱锥M﹣ABCD的体积.作业1、如图1,菱形ABCD的边长为12,∠BAD=60°,AC交BD于点O.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M,N分别是棱BC,AD 的中点,且DM=6.(Ⅰ)求证:OD⊥平面ABC;2、如图,在斜三棱柱ABC﹣A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.(Ⅰ)求证:A1B⊥AC1;3、如图所示,四棱锥P﹣ABCD的侧面PAD是边长为2的正三角形,底面ABCD 是∠ABC=60°的菱形,M为PC的中点,PC=.(Ⅰ)求证:PC⊥AD;AD,E,4、如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=12F分别为线段AD,PC的中点.(Ⅰ)求证:AP∥平面BEF;(Ⅱ)求证:BE⊥平面PAC.5、如图,四棱锥S﹣ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=1,SD=.(1)证明:CD⊥SD;6.如图,四棱锥S ﹣ABCD 中,△ABD 是正三角形,CB=CD ,SC ⊥BD .(Ⅰ)求证:SB=SD ;(Ⅱ)若∠BCD=120°,M 为棱SA 的中点,求证:DM ∥平面SBC .7、如图,在矩形ABCD 中,点E 为边AD 上的点,点F 为边CD 的中点,234A E D B A A ===,现将ABE ∆沿BE 边折至PBE ∆位置,且平面PBE ⊥平面BCDE .(1)求证:平面PBE ⊥平面PEF ;8、如图5.在椎体P-ABCD 中,ABCD 是边长为1的棱形, 且∠DAB=60︒,2PA PD ==,PB=2,E,F 分别是BC,PC 的中点.(1) 证明:AD ⊥平面DEF;AB CDEBCDEFP9、在如图所示的多面体ABCDEF 中,ABCD 为直角梯形,//AB CD ,90DAB ∠=︒,四边形ADEF 为等腰梯形,//EF AD ,已知AE EC ⊥,2AB AF EF ===,4AD CD ==.(Ⅰ)求证:平面ABCD ⊥平面ADEF10.如图,在底面为平行四边形的四棱锥P ABCD -中,AB AC ⊥,PA ⊥平面ABCD ,且PA AB =,点E 是PD 的中点. (Ⅱ)求证://PB 平面AEC ;11.棱长为2的正方体ABCD﹣A1B1C1D1中,M是棱AA1的中点,过C、M、D1作正方体的截面,则截面的面积是。
立体几何垂直证明方法技巧类型一:线线垂直证明(共面垂直、异面垂直)(1) 共面垂直:掌握几种模型①等腰(等边)三角形中的中线 ②菱形(正方形)的对角线互相垂直 ③勾股定理中的三角形 ④ 直角梯形⑤利用相似或全等证明直角。
例:在正方体1111ABCD A B C D -中,O 为底面ABCD 的中心, E 为1CC 中点,求证: (1) 1A O OE ⊥ (2) 1A O BDE ⊥平面(2) 异面垂直(利用线面垂直来证明)例1 在正四面体ABCD 中, 求证:AC BD ⊥变式1 如图,在四棱锥ABCD P -中,底面ABCD 是矩形,已知ο60,22,2,2,3=∠====PAB PD PA AD AB .证明:AD PB ⊥;变式2 如图,在边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点,将△AED,△DCF分别沿,DE DF折起,使,A C两点重合于'A.求证:'A D EF⊥;变式3如图,在三棱锥P ABC-中,⊿PAB是等边三角形,∠P AC=∠PBC=90 º证明:AB⊥PC类型二:直线与平面垂直证明BE'ADFG方法○1利用线面垂直的判断定理例:在正方体1111ABCD A B C D -中,,求证:11AC BDC ⊥平面变式1:如图:直三棱柱ABC -A 1B 1C 1中, AC =BC =AA 1=2,∠ACB =90︒.E 为BB 1的中点,D 点在AB 上且DE = 3 . 求证:CD ⊥平面A 1ABB 1;变式2:如图,在四面体ABCD 中,O 、E 分别是BD 、BC 的P中点,2,CA CB CD BD AB AD ====== 求证:AO ⊥平面BCD ;变式3 如图,在底面为直角梯形的四棱锥P ABCD -中,(1) 求证://AF 平面BCE ;(2) 求证:平面BCE ⊥平面CDE ;例2 如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,60AB AD AC CD ABC ⊥⊥∠=,,°,PA AB BC ==,FADPEE是PC的中点.⊥;(2)证明PD⊥平面ABE;(1)证明CD AE变式1已知直四棱柱ABCD—A′B′C′D′的底面是菱形,∠60ABC,E、F分别是棱CC′与BB′上的点,=︒且EC=BC=2FB=2.(1)求证:平面AEF⊥平面AA′C′C;类型三:平面与平面垂直证明1.AB是圆O的直径,PA垂直于圆O所在的平面,M是圆周上任意一点,AN⊥PM,点N为垂足,求证:平面PAM⊥平面PBM2.如图,在空间四边形ABCD中,AB=BC,CD=DA,E,F,G分别为CD,DA和对角线AC的中点。
证明两线互相垂直的常用方法我们学习了平面与直线垂直的定义、判定定理和性质定理,大家可以体会线线垂直在证明线面垂直时的重要性,将“三维”问题转化为“二维”解决是一种重要的立体几何数学思想方法.在处理实际问题过程中,可以先从题设条件入手,分析已有的垂直关系,再从结论入手分析所要证明的重要垂直关系,从而架起已知与未知的“桥梁”,同学们下面欣赏常见的线面垂直证明方法.一、利用定义垂直的定义:如果两条直线相交成直角,那么这两条直线互相垂直。
从定义可以看出,只要说明两条直线相交的角是直角,就可以说明两条直线互相垂直。
例1:如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.求证:PC是⊙O的切线;分析:因为点C在圆上,只要说明OC⊥CP即可。
解:∵OA=OC,∴∠A=∠ACO∵∠COB=2∠ A ,∠COB=2∠PCB∴∠A=∠ACO=∠PCB∵AB是⊙O的直径∴∠ACO+∠OCB=90°∴∠PCB+∠OCB=90°,即OC⊥CP∵OC是⊙O的半径∴PC是⊙O的切线例2:(1)把两个含有45°角的直角三角板如图1放置,点D在BC上,连结BE,AD,AD的延长线交BE于点F.求证:AF⊥BE.分析:线段之间的垂直,只要说明∠BFD=90°,直接计算不出来,通过三角形全等,间接证明角度为90°。
证明:在△ACD和△BCE中,AC=BC,∠DCA=∠ECB=90°,DC=EC,∴ △ACD≌△BCE(SAS)∴ ∠DAC=∠EBC.∵ ∠ADC=∠BDF,∴ ∠EBC+∠BDF=∠DAC+∠ADC=90°.∴ ∠BFD=90°∴ AF⊥BE.(2)把两个含有30°角的直角三角板如图2放置,点D在BC上,连结BE,AD,AD的延长线交BE于点F.问AF与BE是否垂直?并说明理由.分析:题目同(1)类似,类比(1)思路,这里△ACD和△BCE,显然不全等,考虑相似即可。
立体几何垂直的证明
类型一:线线垂直证明(共面垂直、异面垂直)
(1)共面垂直:掌握几种模型
①等腰(等边)三角形中的中线 ②菱形(正方形)的对角线互相垂直 ③勾股定理中的三角形 ④ 直角梯形
⑤利用相似或全等证明直角。
【例1】在正方体1111ABCD A B C D -中,O 为底面ABCD 的中心, E 为1CC 中点,求证: (1) 1A O OE ⊥ (2) 1A O BDE ⊥平面
(2)异面垂直(利用线面垂直来证明) 【例2】在正四面体ABCD 中, 求证:AC BD ⊥
【变式1】如图,在四棱锥ABCD P -中,底面ABCD 是矩形,已知
ο60,22,2,2,3=∠====PAB PD PA AD AB .
证明:AD PB ⊥;
【变式2】如图,在边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点,
将△AED,△DCF分别沿,
DE DF折起,使,A C两点重合于'A.
求证:'A D EF
⊥;
【变式3】如图,在三棱锥P ABC
-中,⊿PAB是等边三角形,∠P AC=∠PBC=90 º。
证明:AB⊥PC
类型二:直线与平面垂直证明
方法○1利用线面垂直的判断定理
【例3】在正方体
1111
ABCD A B C D
-中,,求证:
11
AC BDC
⊥平面
【变式1】如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90︒.E为BB1的中点,D点在AB上且DE= 3 .
求证:CD⊥平面A1ABB1;
B
E
'
A
D
F
G
P
C
B
A
D
E
【变式2】如图,在四面体ABCD 中,O 、E 分别是BD 、BC 的 中点,2, 2.CA CB CD BD AB AD ======
求证:AO ⊥平面BCD ;
【变式3】如图,在底面为直角梯形的四棱锥P ABCD -中,AD BC ∥,90ABC ∠=°,PA ⊥平面ABCD .3PA =,2AD =,23AB =6BC =
()1求证:BD ⊥平面PAC
○
2利用面面垂直的性质定理 【例4】在三棱锥P-ABC 中,PA ABC ⊥底面,PAC PBC ⊥面面,BC PAC ⊥求证:面。
【变式1】在四棱锥P ABCD -,底面ABCD 是正方形,侧面PAB 是等腰三角形,且
PAB ABCD ⊥面底面,求证:BC PAB ⊥面
类型3:面面垂直的证明。
(本质上是证明线面垂直)
【例5】如图,已知AB ⊥平面ACD ,DE ⊥平面ACD ,△ACD 为等边三角形,
2AD DE AB ==,F 为CD 的中点.
(1) 求证://AF 平面BCE ; (2) 求证:平面BCE ⊥平面CDE ;
【例6】如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,
60AB AD AC CD ABC ⊥⊥∠=,,°,PA AB BC ==,E 是PC 的中点.
(1)证明CD AE ⊥; (2)证明PD ⊥平面ABE ;
【变式1】已知直四棱柱ABCD —A ′B ′C ′D ′的底面是菱形,︒=∠60ABC ,E 、F 分别是棱CC ′与BB ′上的点,且EC=BC =2FB =2. (1)求证:平面AEF ⊥平面AA ′C ′C ;
A B
C
D E
F
A
C
D
P
E
类型三:平面与平面垂直证明
1.AB是圆O的直径,PA垂直于圆O所在的平面,M是圆周上任意一点,AN⊥PM,点
N为垂足,
求证:平面PAM⊥平面PBM
2.如图,在空间四边形ABCD中,AB=BC,CD=DA,E,F,G分别为CD,DA和对角线AC的中点。
求证:平面BEF⊥平面BGD
.
3.在直平行六面体AC1中,四边形ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.
(1)求证:C1O∥平面AB1D1;
(2)求证:平面AB1D1⊥平面ACC1A1.
4. 如下图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
(1)求证:BM∥平面ADEF;
(2)求证:平面BDE⊥平面BEC.。