1、渐开线的形成

课题渐开线齿廓课型新授授课日期10.25 授课时数1总课时数38教具使用多媒体课件教学目标①掌了解渐开线的形成过程；②掌握渐开线的性质。

教学重点和难点重点：渐开线的形成及性质；难点：渐开线的性质。

学情分析本节课内容比较重要，学生应课前做好预习工作，这样便于上课接受。

板书设计一、渐开线的形成；二、基本概念：1、基圆；2、发生线；3、渐开线；3、曲率半径、曲率、向径；4、齿形角。

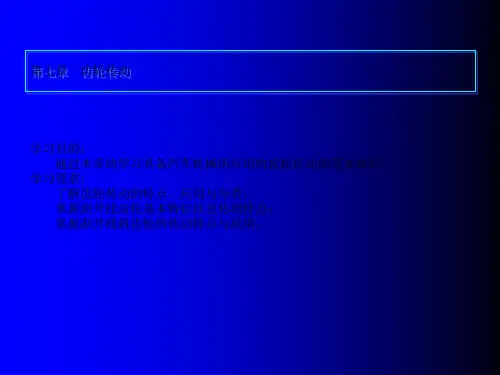
三、渐开线的性质；教学后记【复习旧知】1、齿轮传动的应用场合？2、齿轮机构的类型有哪些？【讲授新课】一、渐开线的形成1、渐开线的形成：当一条动直线（发生线），沿着一个固定的圆（基圆）作纯滚动时，动直线上任意一点K的轨迹称为该圆的渐开线。

2、基本概念：基圆：形成渐开线的固定的圆；发生线：形成渐开线的动直线；纯滚动：是指无相对滑动的滚动。

二、渐开线的性质1、渐开线的性质：由渐开线的形成过程可知：（1）发生线在基圆上滚过的线段KB，等于基圆上被滚过的圆弧长AB；（2）渐开线上的任意一点K的法线必与基圆相切；（3）渐开线上的各点的曲率半径不相等；点离基圆越远，其曲率半径越大，渐开线越平直。

反之亦然。

（4）渐开线的形状决定与基圆的大小；基圆相同，渐开线的形状完全相同。

基圆半径无穷大时，渐开线将变成直线，齿轮就变成齿条。

（5）渐开线上各点的齿形角不相等；（6）基圆内无渐开线。

2、基本概念曲率半径:渐开线上的任一点到基圆上切点之间的长度。

向径：渐开线上的任一点到基圆圆心的径向距离；齿形角：过渐开线上的任一点的切线与改点径向线之间所夹的锐角。

【问题探究】1、渐开线是如何形成的？2、渐开线形成后具有哪些基本性质？3、什么是渐开线的曲率半径？它对渐开线的形状有何影响？4、什么是渐开线上点的齿形角？它对渐开线的形状有何影响？【检测训练】一、填空题：1.从____________和______________两个方面来考虑，齿轮传动应满足传动要平稳和承载能力强的两个基本要求。

渐开线的名词解释渐开线（Involute）是一种几何曲线，具有许多有趣的属性和应用。

渐开线的形状特点让它在工程、数学、生物学以及其他领域中得到广泛的应用。

本文将对渐开线进行详细的解释，并展示一些常见的应用案例。

一、渐开线的定义和基本性质渐开线是指一个固定点在另一个曲线上滚动时，滚动过程中的路径。

具体来说，当一个线段一端的端点（定点）开始绕着一个固定圆滚动时，线段另一端的端点所形成的轨迹就是渐开线。

渐开线常见的特点是，其切线始终垂直于被滚动的圆的切线。

这意味着渐开线可以用来描述一些特殊的旋转和曲线形状。

二、渐开线的数学表达和参数方程渐开线可以通过数学方程来表示，其中最常见的是参数方程。

一般来说，渐开线由以下参数方程描述：x = a(t - sin(t))y = a(1 - cos(t))其中x和y分别表示渐开线上的点的坐标，a是一个常数，t是一个参数，其取值范围通常是0到2π。

三、渐开线的几何性质和应用1. 渐开线的切线性质渐开线的切线垂直于被滚动的圆的切线，这一性质使得渐开线在机械工程和设计中得到了广泛的应用。

例如，在制造齿轮时，齿轮齿槽的形状常常使用渐开线，这样可以保证齿轮的正常齿轮传动。

2. 渐开线的包络性质渐开线的滚动过程中，点P（x，y）的运动轨迹被称为包络线，它能够完全覆盖被滚动的圆。

渐开线的包络性质使得它在制造和设计中的应用十分广泛。

例如，在织布机械中，渐开线被用来控制织布的运动，确保布料的平整而没有褶皱。

3. 渐开线的应用案例除了齿轮和织布机械之外，渐开线在其他领域也有很多应用。

例如在机械工程中，渐开线被用来设计曲柄轴、滚动轮、螺丝等。

在建筑和航天工程中，渐开线可以用来设计支撑结构和杆件。

此外，渐开线还有用于神经和肺部成像中的图像重建，以及流体力学中的边界层控制等。

四、渐开线的历史和进一步的研究渐开线作为一种几何曲线，早在古希腊时期就被人们发现并开始研究。

然而，对于渐开线的深入研究和应用是在近代工程和数学领域的发展中逐渐出现的。

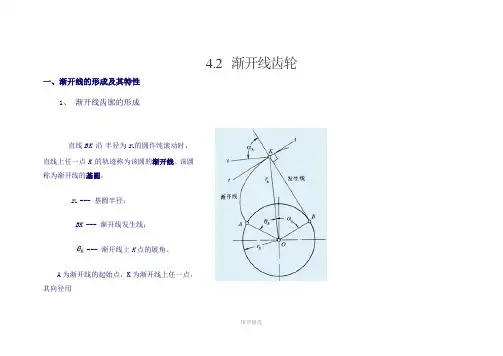
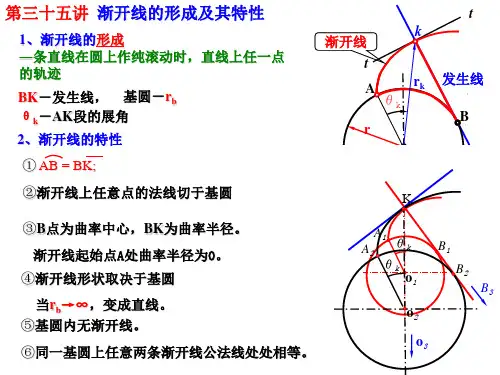
4.2 渐开线齿轮一、渐开线的形成及其特性1、渐开线齿廓的形成直线BK沿半径为r b的圆作纯滚动时，直线上任一点K 的轨迹称为该圆的渐开线。

该圆称为渐开线的基圆。

r b--- 基圆半径；BK --- 渐开线发生线；--- 渐开线上K点的展角。

A为渐开线的起始点，K为渐开线上任一点，其向径用r k表示。

渐开线齿轮的齿廓曲线是渐开线。

2、渐开线的特性1）发生线沿基圆滚过的长度，等于基圆上被滚过的圆弧长度。

由于发生线BK在基圆上作纯滚动，故2）渐开线上任一点的法线恒与基圆相切。

发生线BK沿基圆作纯滚动，它与基圆的切点B即为其速度瞬心，所以发生线BK即为渐开线在K点的法线。

又由于发生线恒切于基圆，故渐开线上任一点的法线恒与基圆相切。

3）渐开线上离基圆愈远的部分，其曲率半径愈大，渐开线愈平直。

发生线BK与基圆的切点B是渐开线在点K 的曲率中心，而线段KB是相应的曲率半径，故渐开线上离基圆愈远的部分，其曲率半径愈大，渐开线愈平直；渐开线初始点A处的曲率半径为零。

4）基圆内无渐开线。

5）渐开线的形状取决于基圆的大小。

基圆愈小，渐开线愈弯曲；基圆愈大，渐开线愈平直。

当基圆半径为无穷大时，其渐开线将成为一条直线。

二、渐开线齿廓的啮合特点一对齿轮传动，是依靠主动轮的齿廓依次推动从动轮的齿廓来实现的。

因此，要能实现预定的传动比，一个齿轮最关键的部位是轮齿的齿廓曲线。

图示为一对分别属于齿轮1和齿轮2的两条齿廓曲线G1、G2在点K 啮合接触的情况。

齿廓曲线G1绕O1点转动,G2绕O2 转动。

过K点所作的两齿廓的公法线nn与连心线 O1O2 相交于点C。

由三心定理知，点C是两齿廓的相对速度瞬心,齿廓曲线G1和齿廓曲线G2在该点有相同的速度：由此可得我们称点C为两齿廓的啮合节点，简称节点。

齿廓啮合基本定律：两齿廓在任一位置啮合接触时，过接触点所作的两齿廓的公法线必通过节点C，它们的传动比等于连心线O1O2被节点C 所分成的两条线段的反比。

章节名称渐开线齿廓授课形式讲授课时1班级电气、机电教学目的①掌握渐开线的形成及性质，②了解齿轮啮合基本定律，掌握渐开线齿廓的啮合的特点教学重点渐开线的形成，齿轮啮合的基本定律教学难点渐开线的形成辅助手段齿轮，渐开线的形成的模型课外作业习题册教学进程及说明★教具演示并导入新课：（讲解相关理论知识）一、渐开线的形成、性质1、渐开线的形成当一条动直线（发生线），沿着一个固定的圆（基圆）作纯滚动时，动直线上任意一点K的轨迹称为该圆的渐开线。

2、渐开线的性质由渐开线的形成可知：（1）发生线在基圆上滚过的线段KB，等于基圆上被滚过的圆弧长AB。

（2）渐开线上的任意一点K的法线必与基圆相切。

（3）渐开线上的各点的曲率半径不相等。

点离基圆越远，其曲率半径越大，渐开线越平直。

反之亦然。

（4）渐开线的形状决定与基圆的大小。

基圆相同，渐开线的形状完全相同。

基圆半径无穷大时，渐开线将变成直线，齿轮就变成齿条。

（5）基圆内无渐开线。

二、渐开线齿廓啮合基本定律齿轮传动要满足瞬时传动比保持不变，则两轮的齿廓不论在何处接触，过接触点的公法线必须与两轮的连心线交于固定的一点。

三、渐开线齿廓的啮合特点1、传动比恒定两齿轮的传动比为：i＝ω1／ω2＝O2P／O1P＝rb2／rb1＝r2′／r1′＝常数2、传动的可分性当两轮的中心距稍有变化时，其瞬时传动比仍将保持不变，这个特点称为渐开线齿轮传动的可分性。

由于齿轮制造和安装误差等原因，常使渐开线齿轮的实际中心距与设计中心距之间产生一定误差，但因有可分性的特点，其传动比仍能保持不变。

3、啮合角为定值cosα′＝rb1／r1′＝rb2／r2′＝常数说明渐开线齿廓在啮合时啮合角α′为定值。

由于啮合角不变，则齿廓间的压力方向不会改变，这对齿轮传动的平稳性很有利。

四、本次课小结本次课重点掌握①渐开线的形成及性质，②了解齿轮啮合基本定律，掌握渐开线齿廓的啮合的特点。

五、布置作业练习册对应内容六、[教学反思]本节的名词、概念多，图多，而且有些图的线条相当多。

第一章常用机构一、零件、构件、部件零件，是指机器中每一个最基本的制造单元体。

在机器中，由一个或几个零件所构成的运动单元体，称为构件。

部件，指机器中由若干零件所组成的装配单元体。

二、机器、机构、机械机器具有以下特征：（一）它是由许多构件经人工组合而成的；（二）构件之间具有确定的相对运动；（三）用来代替人的劳动去转换产生机械能或完成有用的机械功。

具有机器前两个特征的多构件组合体，称为机构。

机器和机构一般总称为机械。

三、运动副使两构件直接接触而又能产生一定相对运动的联接称为运动副。

四、铰链四杆机构由四个构件相互用铰销联接而成的机构，这种机构称为铰链四杆机构。

四杆机构的基本型式有以下三种：（一）曲柄摇杆机构两个特点：具有急回特性，存在死点位置。

（二）双曲柄机构（三）双摇杆机构曲柄滑块机构是由曲柄、连杆、滑块及机架组成的另一种平面连杆机构。

六、凸轮机构（一）按凸轮的形状分：盘形凸轮机构，移动凸轮机构，圆柱凸轮机构。

（二）按从动杆的型式分：尖顶从动杆凸轮机构，滚子从动杆凸轮机构，平底从动杆凸轮机构。

七、螺旋机构螺旋机构的基本工作特性是将回转运动变为直线移动。

螺纹的导程和升角：螺纹的导程L与螺距P及线数n的关系是L = n P根据从动件运动状况的不同，螺旋机构有单速式、差速式和增速式三种基本型式。

第二章常用机械传动装置机械传动装置的主要功用是将一根轴的旋转运动和动力传给另一根轴，并且可以改变转速的大小和转动的方向。

常用的机械传动装置有带传动、链传动、齿轮传动和蜗杆传动等。

一、带传动带传动的工作原理：带传动是用挠性传动带做中间体而靠摩擦力工作的一种传动。

带传动的速比计算公式为：i = n1/n2 = D2/D1主要失效形式为打滑和疲劳断裂。

在进行V带传动计算和选用时，可先按下列公式计算基准长度Ld的近似值Ld':Ld ' = 2 a + p（D1 + D2）/2 + （D1-D2）/ 4 a式中a为主、从二带轮的中心距；D1、D2为主、从二带轮的基准直径。

渐开线原理渐开线是一种特殊的曲线，它具有许多独特的性质和应用。

渐开线的研究与应用领域涵盖了数学、物理、工程等多个学科，具有重要的理论和实际意义。

渐开线是一种由一点沿着一条直线不断运动形成的曲线。

当这点沿着直线移动时，它同时绕着另一点旋转，形成了渐开线的轨迹。

这个旋转点被称为渐开线的极点，而直线被称为渐开线的直线母线。

渐开线具有许多独特的性质。

首先，渐开线上的任意一点到极点的距离与该点到直线母线的垂直距离之积是一个常数，这个常数被称为渐开线的参数。

其次，渐开线上的切线与直线母线垂直，这是由渐开线的定义可推导出的结论。

最后，渐开线还具有对称性，即以直线母线为轴进行对称时，渐开线的曲线形状完全相同。

渐开线的研究与应用广泛存在于数学领域。

在纯数学中，渐开线是曲线的一种特殊形式，它的研究与其他曲线的性质和方程密切相关。

在几何学中，渐开线的对称性和切线性质被广泛应用于曲线的研究和构造。

在微积分中，渐开线的参数方程可以用来描述物体的运动轨迹，如行星、卫星的运动等。

除了数学领域，渐开线还在物理和工程领域有着重要的应用。

在物理学中，渐开线的对称性和切线性质被广泛应用于描述光学和声学中的波的传播和反射。

在工程学中，渐开线的特性被应用于机械设计和结构工程中的齿轮、蜗杆等零件的设计和制造。

渐开线的应用不仅限于理论研究和工程设计，还可以在日常生活中找到许多实际应用。

例如，渐开线的形状可以用于设计摆线钟表的齿轮，使其运行更加平稳和精确。

此外，渐开线的曲线形状也可以用于设计音箱的扬声器，以实现更好的声音分布和扩散效果。

渐开线是一种具有独特性质和广泛应用的曲线。

它的研究与应用涉及多个学科领域，具有重要的理论和实际意义。

通过深入研究和应用渐开线的原理，我们可以更好地理解和利用这一特殊曲线的性质，推动科学技术的发展和创新。

双啮齿轮知识汇总在汽车变速器齿轮加工过程中(热处理前和热后)，为了保证齿轮啮合质量完全达到产品图样要求，目前我公司通常是在双啮仪采用标准齿轮与加工零件进行啮合，检查齿轮磕碰伤及控制中心距。

渐开线圆柱齿轮的综合检验一般可分为单面啮合、双面啮合和噪声综合检验三种。

其中双面啮合综合检验(简称双啮检验)广泛应用于大批量生产的齿轮检验。

双啮检验所用综合检查仪结构简单，操作和调整方便，测量元件容易获得，从双啮检验得到的中心距变动量曲线可快速获得加工机床、刀具、夹具和齿坯安装造成检验项目超差的信息。

虽然双啮检验只反映了齿轮的径向误差部分，但辅以切向误差方面的单向检验，仍可全面地评定齿轮的质量。

双啮检验时需根据被测齿轮和测量齿轮的法向变位系数计算双啮中心距。

我们可以从分析和实践应用出发，导出齿轮啮合条件及设计计算公式。

一、渐开线齿轮齿廓及传动比1.渐开线的形成(见图1)2.渐开线的性质1)发生线在基圆上滚过的长度等于基圆上被滚过的弧长，即;2)发生线与基圆的切点B 就是渐开线上K 点的瞬时速度中心，发生线BK就是渐开线在K点的法线，同时它也是基圆在B点的切线;3)切点B是渐开线上K点的曲率中心，BK是渐开线上K点的曲率半径。

离基圆越近，曲率半径越小;4)渐开线的形状取决于基圆的大小;5)基圆内无渐开线。

3.渐开线方程4.渐开线齿廓的啮合特点1)四线合一：啮合线、过啮合点的公法线、基圆的内公切线和正压力作用线四合一;2)中心距可分性：;3)啮合角不变;4)齿面的滑动，如图2所示。

二、双面啮合的啮合条件在传动过程中，各对齿轮的接触点，一定是落在两基圆的内公切线上。

这条线称之为啮合线，同时从渐开线的形成可知，这条线又是这些接触点的公法线。

双啮检验时的齿轮啮合状况与齿轮传动设计时一样，如图3所示。

被测齿轮1和测量齿轮2的两节圆相切并做无滑动的纯滚动。

所以两节圆齿距应相等，即。

被测齿轮的节圆齿厚应等于测量齿轮的节圆齿槽宽，或被测齿轮的节圆齿槽宽等于测量齿轮的节圆齿厚，。

螺旋锥齿轮球面渐开线齿面形成原理及推论
螺旋锥齿轮是一种常见的传动装置。

其齿面形状为球面渐开线，具有良好的传动性能和稳定性。

在制造过程中，球面渐开线齿轮齿面形成原理主要有以下两点：
一、渐开线生成原理
渐开线是啮合曲线（沿齿面滚动方向每个点对应的啮合面）在弦向的投影线。

在生成螺旋锥齿轮齿面时，应按照渐开线生成原理来设计齿形。

具体而言，根据齿数、啮合角、压力角等参数计算出基本啮合曲线，然后根据渐开线的生成方法，通过多个步骤计算出最终的齿形曲线。

二、球面成形原理
球面齿轮的齿面形状是由球面曲率半径变化而形成的。

在球面齿轮加工中，首先确定齿轮的基准球面，然后通过切削的方式将基准球面加工成为齿面。

具体的加工方法包括滚切、插刀等。

根据球面渐开线齿面形成原理，可以得出以下推论：
一、螺旋锥齿轮具有高精度和高可靠性的特点，可以应用于精密机械和高速传动系统中。

二、在设计和加工过程中，需要密切注意齿面的角度、啮合角度、轴向偏差等因素，以保证齿轮的性能和寿命。

三、球面渐开线齿轮制造难度较大，需要借助高精度的加工设备和技术，以保证齿轮的精度和稳定性。

总之，球面渐开线齿轮具有广泛的应用前景，但在制造和设计过程中需要注意各种因素，以确保齿轮的性能和可靠性。