22-2第二型曲面积分
- 格式:ppt
- 大小:2.08 MB
- 文档页数:32









二型曲面积分的对称性
曲面积分是指对于实数函数f(x, y)求其在某一范围内的定
积分,即求出该函数在所给区域内的积分值。
曲面积分有多种类型,其中二型曲面积分是最常用的一种,其定义为:给定二元函数f(x,y),设定曲面S上的两个参数变量u,v,当P(u,v)是
S上的点时,f(x,y)在参数空间上的积分可以定义为二型曲面
积分的对称性是指其能够满足一定的对称性。
常用的两种对称性有:
1、关于曲面原点的对称性:若曲面S上的原点为P
0,任意点P(u,v)都有P0(u',v')=P(u,v),则有f(x,y)满足关
于P0的对称性;
2、关于曲面的轴的对称性:若曲面S上的轴为L,任意
点P(u,v)都有P(u,v)=P(u',v'),则有f(x,y)满足关于L的对称性。
二型曲面积分的对称性不仅仅可以满足上述的两种形式,它还可以满足更多的形式,比如满足曲面上的点组合的对称性,以及曲面上的点之间的对称性等等。
二型曲面积分的对称性在科学研究中有着非常重要的作用,比如在物理学中,它可以用来研究物体的动力学状态、在天文学中用来研究星系的结构、在化学中可以用来研究分子的结构等。
借助于二型曲面积分的对称性,科学家们可以更加深入地研究宇宙中各种现象,从而更好地理解这个宇宙。
总之,二型曲面积分的对称性对科学研究有着重要的作用,也是研究宇宙现象的基础。
因此,理解和研究这种对称性是非常必要的,以便更好地理解宇宙的奥秘。

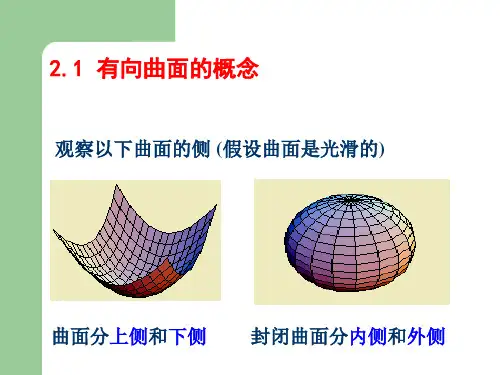
第二十二章 曲面积分§2 第二型曲面积分一 曲面的侧为了给曲面确定方向,先要阐明曲面的侧的概念。
设连通曲面S 上到处都有连续变动的切平面(或法线),M 为曲面S 上的一点,曲面在M 处的法线有两个方向:当取定其中一个指向为正方向时,则另一个指向就是负方向。
设0M 为S 上任一点,L 为S 上任一经过点0M ,且不超出S 边界的闭曲线。
又设M 为动点,它在0M 处与0M 有相同的法线方向,且有如下特性:当M 从0M 出发沿L 连续移动,这时作为曲面上的点M ,它的法线方向也连续地变动。
最后当M 沿L 回到0M 时,若这时M 的法线方向仍与0M 的法线方向一致,则说这曲面S 是双侧曲面①;若与0M 的法线方向相反,则说S 是单侧曲面。
我们通常碰到的曲面大多是双侧曲面。
单侧曲面的一个典型例子是默比乌斯(M öbius)带。
它的构造方法如下:取一矩形长纸带ABCD(如图22-3(a)),将其一端扭转1800后与另一端粘合在一起(即让A 与C 重合,B 与D 重合。
如图22-3(b)所示)。
读者可以考察这个带状曲面是单侧的。
事实上,可在曲面上任取一条与其边界相平行的闭曲线L ,动点M 从L 上的点0M 出发,其法线方向与① 事实上,可以证明,只需对S 中某一点...0M 且又不超出S 的边界的任何闭曲线L 上 具有上述特性,则S 是双侧曲面。
0M 的法线方向相一致,当M 沿L 连续变动一周回到0M 时,由图22-3(b)看到,这时M 的法线方向却与0M 的法线方向相反。
对默比乌斯带还可更简单地 说明它的单侧特性,即沿这个带子上任一处出发涂以一种颜色,则可以不越过边 界而将它全部涂遍(即把原纸带的两面都涂上同样的颜色)。
通常由()y x z z ,=所表示的曲面都是双侧曲面,当以其法线正方向与z 正向的夹角成锐角的一侧(也称为上侧)为正侧时,则另一侧(也称下侧)为负侧。
当S 为封闭曲面时,通常规定曲面的外侧为正侧,内侧为负侧。
第二十二章曲面积分2 第二型曲面积分一、曲面的侧概念:设连通曲面S上到处都有连续变动的切平面(或法线),M为曲面S上的一点,曲面在M处的法线有两个方向:当取定其中一个指向为正方向时,则另一个指向是负方向。
设M0为S上任一点,L为S上任一经过点M0,且不超出S边界的闭曲线。
动点M在M0处与M0有相同的法线方向,且有:当M从M0出发沿L连续移动时,它的法线方向连续地变动,最后当M沿L回到M0时,若这时M的法线方向仍与M0的法线方向相一致,则称曲面S是双侧曲面;若与M0的法线方向相反,则称S是单侧曲面.默比乌斯带:这是一个典型的单侧曲面例子。
取一矩形长纸带ABCD,将其一端扭转180°后与另一端黏合在一起(即让A与C重合,B与D 重合(如图).注:通常由z=z(x,y)所表示的曲面都是双侧曲面,当以其法线正方向与z轴的正向的夹角成锐角的一侧为正侧(也称为上侧)时,另一侧为负侧(也称为下侧). 当S为封闭曲面时,通常规定曲面的外侧为正侧,内侧为负侧.二、第二型曲面积分的概念引例:设流体以一定的流速v=(P(x,y,z),Q(x,y,z),R(x,y,z))从给定的曲面S 的负侧流向正侧,其中P ,Q,R 为所讨论范围上的连续函数,求单位时间内流经曲面S 的总流量E.分析:设在曲面S 的正侧上任一点(x,y,z)处的单位法向量为 n=(cos α,cos β,cos γ). 这里α,β,γ是x,y,z 的函数,则 单位时间内流经小曲面S i 的流量近似地等于v(ξi ,ηi ,ζi )·n(ξi ,ηi ,ζi )△S i =[P(ξi ,ηi ,ζi )cos αi ,Q(ξi ,ηi ,ζi )cos βi ,R(ξi ,ηi ,ζi )cos γi ]△S i , 其中(ξi ,ηi ,ζi )是S i 上任意取定的一点,cos αi ,cos βi ,cos γi 分别是S i 正侧上法线的方向余弦, 又△S i cos αi ,△S i cos βi ,△S i cos γi 分别是S i 正侧在坐标面yz, zx 和xy 上 投影区域的面积的近似值, 并分别记作△S iyz ,△S izx ,△S ixy , 于是 单位时间内由小曲面S i 的负侧流向正侧的流量也近似地等于 P(ξi ,ηi ,ζi )△S iyz +Q(ξi ,ηi ,ζi )△S izx +R(ξi ,ηi ,ζi )△S ixy ,∴单位时间内由曲面S 的负侧流向正侧的总流量为: E=}),,(),,(),,({lim 10ixy i i i ni izx i i i iyz i i i T S R S Q S P ∆+∆+∆∑=→ζηξζηξζηξ.定义1:设P , Q, R 为定义在双侧曲面S 上的函数,在S 所指定的一侧作分割T ,它把S 分成n 个小曲面S 1,S 2,…,S n 组,分割T 的细度T =ni ≤≤1max {S i 的直径}, 以△S iyz ,△S izx ,△S ixy 分别表示S i 在三个坐标面上的投影区域的面积, 它们的符号由S i 的方向来确定.若S i 的法线正向与z 轴正向成锐角时, S i 在xy 平面的投影区域的面积 △S ixy 为正. 反之,若S i 的法线正向与z 轴正向成钝角时, △S ixy 为负. 在各小曲面S i 上任取一点(ξi ,ηi ,ζi ). 若存在以下极限∑∑∑=→=→=→∆+∆+∆ni ixy iiiT ni izx iiiT ni iyz iiiT S R S Q S P 111),,(lim),,(lim),,(limζηξζηξζηξ,且与曲面S 的分割T 和(ξi ,ηi ,ζi )在S i 上的取法无关,则称此极限为 函数P , Q, R 在曲面S 所指定的一侧上的第二型曲面积分,记作:⎰⎰++Sdxdy z y x R dzdx z y x Q dydz z y x P ),,(),,(),,(, 或⎰⎰⎰⎰⎰⎰++SSSdxdy z y x R dzdx z y x Q dydz z y x P ),,(),,(),,(.注:1、流体以v=(P ,Q,R)在单位时间内从曲面S 的负侧流向正侧的总流量E=⎰⎰++Sdxdy z y x R dzdx z y x Q dydz z y x P ),,(),,(),,(.2、若空间磁场强度为(P(x,y,z),Q(x,y,z),R(x,y,z),), 则通过曲面S 的磁通量(磁力线总数) H=⎰⎰++Sdxdy z y x R dzdx z y x Q dydz z y x P ),,(),,(),,(.性质:1、若⎰⎰++S i i i dxdy R dzdx Q dydz P(i=1,2,…,k)存在,则有dxdy R c dzdx Q c dydz P c k i i i k i i i S k i i i ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛∑∑⎰⎰∑===111=dxdy R dzdx Q dydz P c i i S i ki i ++⎰⎰∑=1,其中c i(i=1,2,…,k)是常数.2、若曲面S 是由两两无公共内点的曲面块S 1,S 2,…,S k 所组成,且⎰⎰++iS RdxdyQdzdx Pdydz(i=1,2,…,k)存在,则有⎰⎰++SRdxdy Qdzdx Pdydz =∑⎰⎰=++ki S Rdxdy Qdzdx Pdydz i1.三、第二型曲面积分的计算定理22.2:设连续函数R 定义在光滑曲面S :z=z(x,y), (x,y)∈D xy 上, 以S 的上侧为正侧(即S 的法线方向与z 轴正向成锐角),则有⎰⎰Sdxdy z y x R ),,(=⎰⎰xyD dxdy y x z y x R )),(,,(.证:由第二型曲面积分定义得⎰⎰Sdxdy z y x R ),,(=ixy ni iiiT S R ∆∑=→1),,(lim ζηξ=ixy ni i i i i d S z R ∆∑=→1)),(,,(lim ηξηξ,其中d=max{S ixy 的直径}. ∴由T =ni ≤≤1max {S i 的直径}→0, 可推得d →0, 又R 在S 上连续,z 在D xy 上连续(即曲面光滑),根据复合函数的连续性, R(x,y,z(x,y))在D xy 上也连续. 由二重积分的定义,有⎰⎰xyD dxdy y x z y x R )),(,,(=ixyni iiiid Sz R ∆∑=→1)),(,,(lim ηξηξ,∴⎰⎰Sdxdy z y x R ),,(=⎰⎰xyD dxdy y x z y x R )),(,,(.注:同理可得,当P 在光滑曲面S :x=x(y,z), (y,z)∈D yz 上连续时, 有 则有⎰⎰Sdydz z y x P ),,(=⎰⎰yzD dydz z y z y x P ),),,((.这里S 是以S 的法线方向与x 轴正向成锐角的那一侧为正侧. 当Q 在光滑曲面S :y=y(z,x), (z,x)∈D zx 上连续时, 有 则有⎰⎰Sdzdx z y x Q ),,(=⎰⎰zxD dzdx z x z y x Q )),,(,(.这里S 是以S 的法线方向与y 轴正向成锐角的那一侧为正侧.例1:计算⎰⎰Sxyzdxdy ,其中S 是球面x 2+y 2+z 2=1在x ≥0, y ≥0部分并取球面外侧.解:S 在第一、五卦限部分分别为:S 1:z 1=221y x --; S 2:z 2=-221y x --; D xy ={(x,y)|x 2+y 2≤1, x ≥0, y ≥0}, 依题意积分沿S 1上侧和S 2下侧进行, ∴⎰⎰Sxyzdxdy =⎰⎰1S xyzdxdy +⎰⎰2S xyzdxdy=⎰⎰--xyD dxdy y x xy 221-⎰⎰---xyD dxdy y x xy 221=2⎰⎰-201023cos sin 1πθθθdr r r d =⎰2022sin 151πθθd =152.注:如果光滑曲面S 由参量方程给出:S: ⎪⎩⎪⎨⎧===),(),(),(v u z z v u y y v u x x , (u,v)∈D.若在D 上各点的函数行列式),(),(v u y x ∂∂,),(),(v u z y ∂∂,),(),(v u x z ∂∂不同时为0,则有 ⎰⎰SPdydz =⎰⎰∂∂±Ddudv v u z y v u z v u y v u x P ),(),()),(),,(),,((, ⎰⎰SQdzdx =⎰⎰∂∂±Ddudv v u x z v u z v u y v u x Q ),(),()),(),,(),,((, ⎰⎰SRdxdy =⎰⎰∂∂±Ddudv v u y x v u z v u y v u x R ),(),()),(),,(),,((, 其中正负号分别对应S 的两个侧,特别当uv 平面的正方向对应于曲面S 的所选定的正向一侧时,取正号,否则取负号.例2:计算⎰⎰Sdydz x 3,其中S 为椭球面222222cz b y a x ++=1的上半部并选取外侧.解:把曲面表示为参数方程:x=asin φcos θ, y=bsin φsin θ, z=ccos φ, 0≤φ≤2π, 0≤θ≤2π. 则),(),(θϕ∂∂z y =sin cos sin sin cos ϕθϕθϕc b b -=bcsin 2φcos θ, 又积分在S 的正侧,∴⎰⎰Sdydz x 3=⎰⎰⋅20202333cos sin cos sin ππθθϕθϕϕd bc a d=⎰⎰2020453cos sin ππθθϕϕd d bc a =52πa 3bc.四、两类曲面积分的联系定理22.3:设S 为光滑曲面,正侧法向量为(cos α,cos β,cos γ), P(x,y,z), Q(x,y,z), R(x,y,z)在S 上连续,则⎰⎰++SRdxdy Qdzdx Pdydz =⎰⎰++SdS R Q P )cos cos cos (γβα.证:⎰⎰Sdxdy z y x R ),,(=ixy ni i i i T S R ∆∑=→1),,(lim ζηξ, 又△S i =dxdy ixyS ⎰⎰γcos 1. 由S 光滑知cos γ在区域S ixy 上连续. 应用中值定理,在S ixy 内必存在一点,使这点的法线方向与z 轴正向的夹角γi °满足 △S i =ixy i S ∆°cos 1γ,即△S ixy =cos γi °△S i .∴R(ξi ,ηi ,ζi )△S ixy =R(ξi ,ηi ,ζi )cos γi °△S i . 于是ixy ni i i i S R ∆∑=1),,(ζηξ=i ni i i i i S R ∆∑=1°cos ),,(γζηξ. 以cos γi 表示曲面S i 在点(x i ,y i ,z i )的法线方向与z 轴正向夹角的余弦,由cos γ的连续性,知当T →0时,i ni i i i i S R ∆∑=1°cos ),,(γζηξ的极限存在, ∴⎰⎰Sdxdy z y x R ),,(=⎰⎰SdS z y x R γcos ),,(. 同理可证:⎰⎰Sdydz z y x P ),,(=⎰⎰SdS z y x P αcos ),,(; ⎰⎰S dzdx z y x Q ),,(=⎰⎰SdS z y x Q βcos ),,(.∴⎰⎰++SRdxdy Qdzdx Pdydz =⎰⎰++SdS R Q P )cos cos cos (γβα.注:当改变曲面的侧时,左边积分改变符号,右边积分中的角要加减π以改变余弦的符号.定理22.4:设P , Q, R 是定义在光滑曲面S: z=z(x,y), (x,y)∈D 上的连续函数,以S 的上侧为正侧,则⎰⎰++Sdxdyz y x R dzdx z y x Q dydz z y x P ),,(),,(),,(=⎰⎰+-+-Dy x dxdy y x z y x R z y x z y x Q z y x z y x P ))),(,,()))(,(,,()))(,(,,(.证:cos α=221yx x z z z ++-, cos β=221yx y z z z ++-, cos γ=1, dS=221y x z z ++dxdy.∴⎰⎰++Sdxdyz y x R dzdx z y x Q dydz z y x P ),,(),,(),,(=⎰⎰++SdS z y x R z y x Q z y x P )cos ),,(cos ),,(cos ),,((γβα=⎰⎰+-+-Dy x dxdy y x z y x R z y x z y x Q z y x z y x P ))),(,,()))(,(,,()))(,(,,(.例3:计算⎰⎰++Szdxdy dydz z x )2(,其中S={(x,y,z)|z=x 2+y 2, z ∈[0,1]},取上侧.解:∵z x =2x, z y =2y,∴⎰⎰++Szdxdy dydz z x )2(=⎰⎰++++-Ddxdyy x y x x x )]()2(2[2222=⎰⎰++-+-Ddxdy y x x x )])(12(4[222=⎰⎰+-+-πθθθ2010323])1cos 2(cos 4[drr r r d=⎰+--πθθθ202)41cos 52cos (d =2π-.注:由于x(x 2+y 2)是奇函数,∴⎰⎰+Ddxdy y x x )(22=0,又由对称性有⎰⎰Ddxdy x 2=⎰⎰Ddxdy y 2,∴例3中也可化简⎰⎰++Szdxdy dydz z x )2(=⎰⎰++++-Ddxdyy x y xx x )]()2(2[2222=⎰⎰-Ddxdy x y )3(22=-⎰⎰Ddxdy x 22=-⎰⎰πθθ20123cos 2dr r d =-⎰πθθ202cos 21d =2π-. 习题1、计算下列第二型曲面积分:(1)⎰⎰+++-Sdxdy xz y dzdx x dydz z x y )()(22,其中S 为由x=y=z=0, x=y=z=a 六个平面围成的立方体表面并取外侧为正向; (2)⎰⎰+++++Sdxdy x z dzdx z y dydz y x )()()(,其中S 为以原点为中心,边长为2的立方体表面并取外侧为正向; (3)⎰⎰++Szxdxdy yzdzdx xydydz ,其中S 为由x=y=z=0, x+y+z=1所围的四面体表面并取外侧为正向; (4)⎰⎰Syzdzdx ,其中S 为球面x 2+y 2+z 2=1的上半部分并取外侧为正向;(5)⎰⎰++Sdxdy z dzdx y dydz x 222,其中S 为球面(x-a)2+(y-b)2+(z-c)2=R 2并取外侧为正向. 解:(1)∵⎰⎰-Sdydz z x y )(=⎰⎰⎰⎰+-aaaazdz ydy dz z a ydy 0000)(=24a ;⎰⎰Sdzdx x 2=⎰⎰⎰⎰-a aa a dx x dz dx x dz 002002=0;⎰⎰+Sdxdy xz y)(2=⎰⎰⎰⎰-+a aa a dy y dx dy ax y dx 022)(=24a .∴⎰⎰+++-S dxdy xz y dzdx x dydz z x y )()(22=24a +24a =a 4.(2)∵⎰⎰+Sdydz y x )(=⎰⎰⎰⎰----+--+11111111)1()1(dz dy y dz dy y =8,⎰⎰+Sdzdx z y )(=⎰⎰+Sdxdy x z )(=8,∴⎰⎰+++++Sdxdy x z dzdx z y dydz y x )()()(=24.(3)∵⎰⎰Sxydydz =⎰⎰---yydz z y dy 1010)1(=241,⎰⎰S yzdzdx =⎰⎰Szxdxdy =241. ∴⎰⎰++Szxdxdy yzdzdx xydydz =81.(4)令x=sin φcos θ, y=sin φsin θ, z=cos φ, 0≤φ≤2π, 0≤θ≤2π, 则),(),(θϕ∂∂x z =θϕθϕϕsin sin cos cos 0sin -=sin 2φsin θ, 又积分在S 的正侧,∴⎰⎰Syzdzdx =⎰⎰ππθθϕϕϕ202320sin sin cos d d =4π.(5)令x=Rsin φcos θ+a, y=Rsin φsin θ+b, z=Rcos φ+c, 0≤φ≤π, 0≤θ≤2π, 则),(),(θϕ∂∂z y =sin cos sin sin cos ϕθϕθϕR R R -=R 2sin 2φcos θ, 又积分在S 的正侧,∴⎰⎰Sdydz x 2=⎰⎰+ππθθϕθϕϕ202220cos sin )cos sin (d R a R d=⎰⎰++ππθθϕθϕθϕϕ202222333440)cos sin cos sin 2cos sin (d R a aR R d=⎰πϕϕπ033sin 2d aR=338aR π. 根据变换的对称性,可得:⎰⎰++Sdxdy z dzdx y dydz x 222=)(383c b a R ++π. 解法二:令x=rcos θ+a, y=rsin θ+b, 则⎰⎰Sdxdy z 2=rdr r R c d R ⎰⎰-+022220)(πθ-rdr r R c d R⎰⎰--022220)(πθ=4c dr r R r d R⎰⎰-02220πθ=338cR π. 根据变换的对称性,可得:⎰⎰++Sdxdy z dzdx y dydz x 222=)(383c b a R ++π.2、设某流体的流速为v=(k,y,0), 求单位时间内从球面x 2+y 2+z 2=4的内部流过球面的流量.解:E=⎰⎰+Sydzdx kdydz , 又⎰⎰S kdydz =⎰⎰S dydz k -⎰⎰Sdydz k =0(注:球前+球后).∴E=⎰⎰Sydzdx =⎰⎰ππθθϕϕ20230sin sin 8d d =π332.3、计算第二型曲面积分I=⎰⎰++Sdxdy z h dzdx y g dydz x f )()()(, 其中S 是平行六面体0≤x ≤a, 0≤y ≤b, 0≤z ≤c 的表面并取外侧为正向, f(x),g(y),h(z)为S 上的连续函数.解:⎰⎰Sdydz x f )(=⎰⎰-cbdz f a f dy 00)]0()([=bc[f(a)-f(0)],同理有:⎰⎰Sdzdx y g )(=ac[g(b)-g(0)],⎰⎰Sdxdy z h )(=ab[h(c)-h(0)],∴I=bc[f(a)-f(0)]+ac[g(b)-g(0)]+ab[h(c)-h(0)].4、设磁场强度为E(x,y,z)=(x 2,y 2,z 2), 求从球内出发通过上半球面x 2+y 2+z 2=a 2, z ≥0的磁通量.解:设磁通量为φ, 则φ=⎰⎰++Szdxdy ydzdx xdydz .利用球坐标变换有⎰⎰Szdxdy =⎰⎰ππθϕϕϕ202320sin cos d a d =323a π.又由变换后的对称性,有φ=3zdxdy=2πa3.S。