复利现值系数表(P F)

复利现值系数表完整版介绍复利现值系数表是一个用于计算复利投资的工具。

在金融领域中，复利是指在一段时间内将利息再投资以增加本金，并在下个计息期继续获得利息的过程。

通过使用复利现值系数表，投资者可以根据不同的投资期限和利率，计算出未来的现值，帮助他们做出更明智的投资决策。

表格示例下面是一个复利现值系数表的示例，用于计算不同投资期限和利率的复利现值：投资期限（年）利率（%）复利现值系数1 2 0.98041 5 0.95241 10 0.90912 2 0.96122 5 0.90702 10 0.82645 2 0.90535 5 0.78405 10 0.620910 2 0.819410 5 0.614510 10 0.3869从上述表格可以看出，投资期限和利率对于复利现值系数的计算有很大影响。

当投资期限较短或利率较高时，复利现值系数较小，说明投资者能够在较短的时间内获得较高的现值。

反之，当投资期限较长或利率较低时，复利现值系数较大，说明投资者需要更长的时间才能获得相同的现值。

使用方法要使用复利现值系数表进行计算，首先需要确定投资期限和利率。

然后在表格中找到对应的投资期限和利率的行和列，查找对应的复利现值系数。

例如，假设我们有一笔投资期限为5年，利率为2%的投资，我们可以在表格中找到投资期限为5年、利率为2%的行和列。

从表格中可以看出，复利现值系数为0.9053。

现在，我们需要将投资金额乘以复利现值系数，就可以计算出未来的现值。

假设我们的投资金额为10000元，那么未来5年后的现值将为：10000 *0.9053 = 9053元。

结论复利现值系数表是一个有用的工具，可以帮助投资者在进行复利投资时做出更明智的决策。

通过使用复利现值系数表，投资者可以计算出未来的现值，并根据不同的投资期限和利率做出相应的投资安排。

这样，投资者可以更好地利用复利的优势，获得更多的利润。

当然，复利现值系数表只是一个工具，投资决策还需要考虑其他因素，如风险偏好、市场走势等。

复利现值系数表图（复利现值系数表）如果年金是每年年底收到的1万元，那就是年金。

年金现值是指在发生期间收到的年金利息，按照利率折算成价值的总和。

年金现值系数公式：PVA/a[1]=1/I-1/[复利现值系数表怎么看问题一：复利现值系数表怎么看？当然有关系了。

所谓插值法么。

就是把根据表中的利率计算出来的业绩和你实际的未来现金流进行比较，正好在两个利率之间，然后算出一个实际利率。

插值法也叫试值法，就是不断的换数儿来确定一个利率范围。

问题二：复利现值系数怎么计算？复利现值的计算公式为：P=F*1/(1+i)^n其中的1/(1+i)^n就是复利现值系数。

，记作（P/F，i,n）.其中i是利率（折现率），n是年数。

根据这两个条件就可以查到具体对应的复利现值系数了。

问题三：求解财务管理中，什么时候用复利现值系数表、什么时候用年金现值系数表？计算期末现金流量或各期现金流量不相等时的现值，使用复利现值系数表；在几期现金流已知，各期现金流相等的情况下计算现值，使用年金现值系数表。

问题四：当期为2.5年的复利现值系数如何计算？（系数表查不到）=(1+年利率）*-2.5年次方问题五：注册会计师考试，财务成本管理科目，复利现值系数、年金现值系数表怎么看？财务成本管理科目，复利现值系数、年金现值系数表怎么看？综合考虑这个似乎比较麻烦，就只说你这个问题吧。

复利现值是相对于单利现值而言的。

比如我们把钱存在银行，就按照单利计算利息。

如果借高利贷，除了利息高，他们一般会按照复利计算利息，也就是所谓的复利，就是利息也会产生利息。

复利现值的计算公式是P＝F（1＋i）-n＝F/（1＋i）n其中（1＋i）-n称为复利现值系数，其数值可查阅按不同利率和时期编成的复利现值系数表。

p就是现值，F是终值，i是利率，按照这个公式就可以在已知终值的情况下计算出现值。

例如：某人5年后需要现金20万元，若银行存款利率为5%，如按复利计息，问此人现在应存入现金多少？计算过程如下：P（1+5％）5＝20万元P＝20（1+5％）-5查复利现值系数表可知，i＝5％，n＝5对应的数值为0.7835。

附表一复利终值系数表计算公式：复利终值系数二6+i)1,S=P G+i需P—现值或初始值；i—报酬率或利率；n—计息期数；S—终值或本利和附表一复利终值系数表续表注：*〉99999计算公式：复利终值系数二G+i)1,S=P G+i, P—现值或初始值i—报酬率或利率n—计息期数S—终值或本利和附表二复利现值系数表注：计算公式：复利现值系数二G+i)-n,P==SG+i)-n(1+l)nP—现值或初始值；i—报酬率或利率；n—计息期数；S—终值或本利和附表二复利现值系数表续表注：*<0.0001计算公式：复利现值系数二G+i)-n,P==S G+i)-nQ+i)iP—现值或初始值；i—报酬率或利率；n—计息期数；S—终值或本利和附表三年金终值系数表注：计算公式：年金终值系数=_*£±@二1,S=A心二1iiA—每期等额支付（或收入）的金额；i—报酬率或利率；n—计息期数；S—年金终值或本利和附表三年金终值系数表续表注：*>999999.99计算公式：年金终值系数=_*£±@二1,S=A心二1iiA—每期等额支付（或收入）的金额；i—报酬率或利率；n—计息期数；S—年金终值或本利和附表四年金现值系数表1-(1+i)-n1-(1+i)-n计算公式：年金现值系数=,P=A—iiA—每期等额支付（或收入）的金额；i—报酬率或利率；n—计息期数；P—年金现值或本利和附表四年金现值系数表续表注：1-(1+i)-n1-(1+i)-n计算公式：年金现值系数=,P=A—iiA—每期等额支付(或收入)的金额；i—报酬率或利率；n—计息期数；P—年金现值或本利和。

复利现值系数表(PVIF表)
复利现值系数表，英文名称为Present Value Interest Factor (PVIF) Table，是一个帮助计算现值的工具，广泛应用于财务分析、投资评估和财务规划等领域。

该表格列出了不同利率和期限下的各种复利因素，以帮助人们计算投资的现值。

以下是PVIF表的相关参考内容：
1. PVIF表格通常由两个变量组成：利率和期限。

2. 列出了各种利率和期限下的复利因子，这些复利因子表示每个单位货币在未来某个时间点的现值。

3. PVIF表格可以帮助计算出未来现金流的现值，并且可以用于评估不同投资选项之间的相对价值。

4. PVIF表格通常按照利率和期限的递增顺序排列，以便查找和比较不同的复利因子。

5. PVIF表格适用于所有类型的复利计算，包括简单利息、复利和累积利息等。

6. PVIF表格是一种标准工具，可以在不同的软件和计算机程序中使用，以减轻手动计算的负担并提高计算的精度。

7. PVIF表格是财务规划和投资决策的重要工具，可以帮助投资者做出有根据的决策并避免潜在的风险。

复利现值系数表1、现值和终值的计算(1)单期中的终值。

计算公式为：FV=PV×(1+r)(2)单期中的现值。

计算公式为：PV=FV/(1+r)(3)多期中的终值。

计算公式为：FV=PV×(1+r)t(4)多期中的现值。

计算公式为：PV=FV/(1+r)t2、72法则金融学上的72法则是用作估计一定投资额倍增或减半所需要的时间的方法，即用72除以收益率或通胀率就可以得到固定一笔投资(钱)翻番或减半所需时间。

这个法则只适用于利率(或通货膨胀率)在一个合适的区间内的情况下，若利率太高则不适用。

3、有效利率的计算(1)复利期间与复利期间数量。

复利期间数量是指一年内计算复利的次数。

(2)有效年利率。

名义年利率r与有效年利率EAR之间的换算为：(3)连续复利。

当复利期间变得无限小的时候，相当于连续计算复利。

连续复利情况下，计算终值的一般公式是：FV=PV×ert 其中，PV为现值，r为年利率，t为按年计算的投资期间，e 为自然对数的底数，约等于2.7182。

4、复利现值复利现值一般指当要实现期末投资价值时，在给定的投资报酬率和投资期限的情况下，以复利计算出投资者在期初应投入的金额。

是复利终值的逆运算。

理论上，复利现值计算公式为：PV=FV/(1+r)n=FV×(1+r)-n其中，PV代表现值(期初投资金额);FV代表终值(期末获得投资价值);r 代表折现率、投资报酬率或通货膨胀率;n代表期数;(1+r)-n以上参数中，n与r为查表时对照的变量，复利现值系数表中已假定终值(FV)为1，现值(PV)就是复利现值系数。

5、普通年金终值普通年金终值是通过货币时间价值，在给定的回报率下，计算年金现金流的终值之和，以计算期期末为基准。

普通年金现金流一般都具备待客与连续这两个特征：每期的现金流入与流出的金额必须固定且出入方向一致，并保证在计算期内各期现金流量不能中断。

没有满足以上两个特征都不算是普通年金。

复利现值系数表PVIF表复利现值系数表（PVIF 表）在金融领域，复利现值系数表（PVIF 表）是一个非常重要的工具。

它虽然看似复杂，但实际上对于我们进行财务规划、投资决策以及评估各种金融方案的价值都有着不可或缺的作用。

首先，让我们来理解一下什么是复利现值。

简单来说，复利现值就是未来的一笔钱在当前时刻的价值。

比如说，你知道一年后会收到1000 元，但考虑到时间价值和可能的利率影响，这 1000 元在现在到底值多少钱？这就是复利现值要解决的问题。

而复利现值系数，就是为了计算复利现值而设定的一个系数。

通过这个系数，我们可以快速地将未来的金额折算为现在的价值。

那么，复利现值系数表是怎么来的呢？它是基于复利计算的原理和特定的利率水平生成的。

在不同的利率下，对应着不同的复利现值系数。

比如说，假设年利率是 5%，期限为 1 年，那么复利现值系数就是1÷（1 ＋ 5%）＝ 09524。

这意味着一年后收到的 1 元，在当前只相当于 09524 元。

如果期限是 2 年，复利现值系数就是 1÷（1 ＋ 5%）² ≈ 09070。

为什么我们需要复利现值系数表呢？想象一下，如果你要评估一个长期的投资项目，比如一个 5 年期的债券，每年支付利息 100 元，最后本金 1000 元在 5 年后归还。

如果不借助复利现值系数表，要手动计算每一笔现金流在当前的价值，那将是非常繁琐的。

但有了复利现值系数表，我们可以快速找到对应利率和期限的系数，然后轻松地计算出总的现值。

在实际应用中，复利现值系数表有着广泛的用途。

对于企业来说，在进行项目评估和投资决策时，需要考虑资金的时间价值。

通过使用复利现值系数表，能够更准确地评估项目的真实收益和成本。

比如，一个项目预计在未来 5 年内每年产生 200 万元的净现金流，如果企业的资金成本是 8%，那么可以通过复利现值系数表将这些未来的现金流折算为现值，从而判断这个项目是否值得投资。

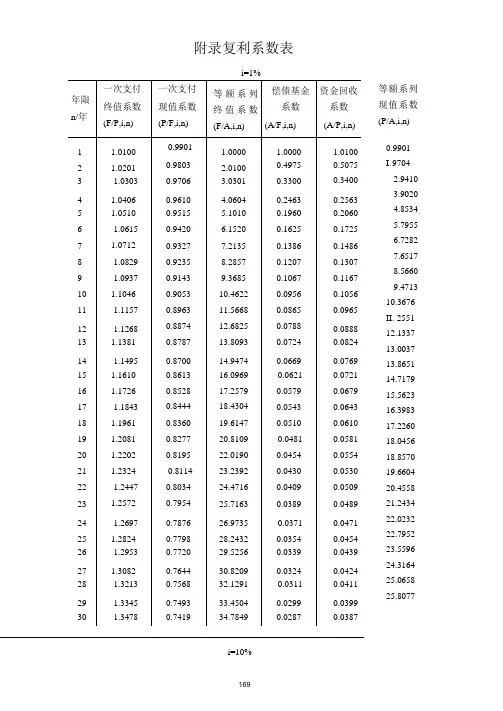
复利系数表通常用于计算利息或投资在不同时间周期下的增长。

复利系数（F/P, P/F, F/A, P/A）是基于复利计算公式得出的，它们分别代表终值系数、现值系数、等额系列终值系数和等额系列现值系数。

这些系数可以用来计算在特定利率和时间周期下的单笔投资或一系列定期投资的未来价值或现值。

：
n 年后的价值，现值系数(P/F, i, n) 表示为了在n 年后获得一定的金额，现在需要投资的金额。

请注意，上述表格只是一个简化的示例，实际的复利系数表可能会根据具体的计息方式和利率有所不同。

在实际应用中，通常使用财务计算器或电子表格软件来计算复利系数。