- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2) 利用多项式逼近函数 , 例如 sin x
(3) 其他应用
求极限 , 证明不等式 等.
例如 目录 上页 下页 返回 结束
单调性
1. 可导函数单调性判别
f (x) 0, x I f (x) 0, x I
2.曲线凹凸与拐点的判别
f (x) 0, x I
在 I 上单调递增 在 I 上单调递减
x 0表示 x 从右侧以任意方式趋于 0 .
机动 目录 上页 下页 返回 结束
泰勒展开
1. 泰勒公式
f (x0 )
f (x0 )(x x0 )
f
( x0 2!
)
(
x
x0
)2
f
(n) (x0 ) (x n!
x0 )n Rn (x)
其中余项
Rn (x)
f (n1) ( )
(n 1) !
(
x
x0
)n1
o((x x0 )n )
( 在 x0 与x 之间)
当 x0 0 时为麦克劳林公式 .
机动 目录 上页 下页 返回 结束
2. 常用函数的麦克劳林公式 ( P140 ~ P142 )
ex , ln(1 x), sin x, cos x, (1 x)
3. 泰勒公式的应用 (1) 近似计算
+
f (x) 0, x I
–
拐点 — 连续曲线上有切线的凹凸分界点
机动 目录 上页 下页 返回 结束
思考与练习
1. 设在[0,1] 上 f (x) 0, 则 f (0), f (1), f (1) f (0) 或 f (0) f (1) 的大小顺序是 ( B )
(A) f (1) f (0) f (1) f (0) (B) f (1) f (1) f (0) f (0) (C) f (1) f (0) f (1) f (0) (D) f (1) f (0) f (1) f (0) 提示: 利用 f (x) 单调增加 , 及
最值点应在极值点和边界点上找 ; 应用题可根据问题的实际意义判别 .
思考与练习
1.
设
lim
xa
f
(x) f (a) (x a)2
1,
则在点
a
处(
B
).
(A) f (x) 的导数存在 , 且 f (a) 0;
(B) f (x) 取得极大值 ; (C) f (x) 取得极小值;
(D) f (x)的导数不存在. (L. P500 题4)
f (x0) 4 f (x0) 0
机动 目录 上页 下页 返回 结束
图形
1. 曲线渐近线的求法
机动 目录 上页 下页 返回 结束
3. 设 y f (x) 是方程 y 2 y 4 y 0 的一个解,
A 若 f (x0) 0, 且 f (x0) 0, 则 f (x) 在 x0 ( )
(A) 取得极大值 ; (B) 取得极小值 ; (C) 在某邻域内单调增加 ; (D) 在某邻域内单调减少 . 提示:
思考与练习
1. 填空题 1) 函数
在区间 [1, 2] 上满足拉格朗日定理
条件, 则中值 _3__145__ .
2) 设
方程
有 3 个根 , 它们分别在区间 (1, 2), (2, 3), (3, 4) 上.
机动 目录 上页 下页 返回 结束
2. 设 f (x) C[0, ], 且在 (0, )内可导, 证明至少存 在一点 (0, ), 使 f ( ) f ( )cot .
欲证: ( x1 , x2),使 f ( ) f ( ) 0 只要证 e f ( ) e f ( ) 0
亦即
[ ex f (x ) ] x 0
作辅助函数 F (x) ex f (x ) , 验证 F (x )在 [ x1 , x2 ]上满足
罗尔定理条件.
机动 目录 上页 下页 返回 结束
f (1) f (0) f ( ) (0 1)
机动 目录 上页 下页 返回 结束
2. 曲线
y 1 ex2 的凹区间是
(
1 2
,
1 2
)
;
凸区间是
( ,
1 2
)
及
(
1 2
,
)
;
拐点为
(
1 2
,
1
e
1 2
)
.
提示: y 2ex2 (1 2 x2 )
作业
P151 3 (1),(7) ; 4 (2), (4) ; 8 (3), (6) ; 9 (3) ; 10 ; 12 ; 13 ; 14
4. 思考: 在
上对函数
应用拉格朗日中值定理得
f (x) f (0) f ( )(x 0), (0, x)
即
x
2
sin
1 x
(
2
sin
1
cos
1
)
x,
(0, x)
cos
1
2
sin
1
x
sin
1 x
当
x
0
时
0 ,
因此由上式得
cos
1
0.
问是否可由此得出
lim
x0
cos
1 x
0
?
不能 ! 因为 (x) 是依赖于 x 的一个特殊的函数.
中值定理
1. 微分中值定理的条件、结论及关系
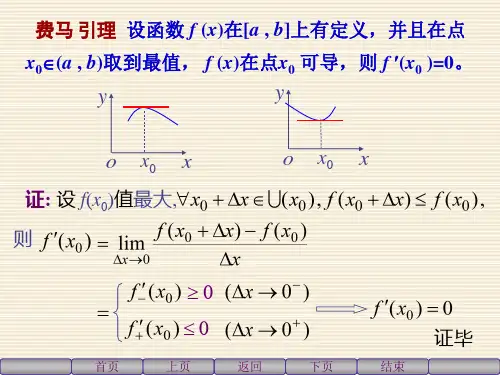
费马引理 f (b) f (a)
拉格朗日中值定理
F(x) x
罗尔定理
f (b) f (a)
F(x) x
2. 微分中值定理的应用
(1) 证明恒等式
(2) 证明不等式
(3) 证明有关中值问题的结论
柯西中值定理
关键: 利用逆向思维 设辅助函数
机动 目录 上页 下页 返回 结束
提示: 利用极限的保号性 .
机动 目录 上页 下页 返回 结束
2. 设 f (x) 在 x 0 的某邻域内连续, 且 f (0) 0,
lim f (x) 2, 则在点 x 0 处 f (x) ( D ).
x01 cos x
(A) 不可导 ;
(B) 可导, 且 f (0) 0;
(C) 取得极大值 ; (D) 取得极小值 . 提示: 利用极限的保号性 .
第五节 目录 上页 下页 返回 结束
极值与最值
1. 连续函数的极值
(1) 极值可疑点 : 使导数为0 或不存在的点
(2) 第一充分条件
过 由正变负
为极大值
过 由负变正
为极小值
(3) 第二充分条件
为极大值
为极小值
(4) 判别法的推广 ( Th.3)
定理3 目录 上页 下页 返回 结束
2. 连续函数的最值
提示: 由结论可知, 只需证
即
f (x )sin x x 0
设
F(x) f (x)sin x
验证 F (x ) 在 [0, ] 上满足罗尔定理条件.
机动 目录 上页 下页 返回 结束
3. 若 f (x )可导, 试证在其两个零点间一定有
f (x ) f (x ) 的零点.
提示: 设 f (x1) f (x2 ) 0, x1 x2 ,