三角形中位线

三角形的中位线与中心三角形是初中数学学习的重要内容之一，中位线是三角形的一个重要性质。

本文将介绍三角形的中位线以及与之相关的中心。

一、中位线的概念在三角形ABC中，连接线段AD、BE和CF的三条线段称为三角形ABC的中位线。

其中，D、E和F分别是AB、BC和AC的中点。

二、中位线的性质1. 三角形中位线的长度相等在三角形ABC中，有AD=BE=CF。

这是因为D、E和F分别是AB、BC和AC的中点，所以三角形ADB、BEC和AFC都是等边三角形，因此AD=BE=CF。

2. 三角形的中位线互相平行在三角形ABC中，有AD∥BC，BE∥AC和CF∥AB。

这是因为D、E和F分别是AB、BC和AC的中点，所以由平行线性质可知，AD∥BC，BE∥AC和CF∥AB。

三、三角形的中心三角形的中位线交于一点，这个点称为三角形的中心。

在三角形ABC中，三条中位线AD、BE和CF的交点是三角形的重心G。

四、重心的性质1. 重心到各顶点的距离比例为2:1在三角形ABC中，设重心为G，连接AG、BG和CG，有AG:GD=BG:GE=CG:GF=2:1。

这是由于重心是三角形的中位线交点，根据中位线的性质可知，AD=2DG，BE=2GE，CF=2GF。

2. 重心将三角形分成六个小三角形，且这些小三角形的面积相等以重心G为顶点，将三角形ABC分成了六个小三角形：△BAG、△CBG、△ACG、△AGD、△BGE和△CGF。

这六个小三角形的面积相等。

这是因为重心等分了中位线，并且中位线等分了三角形的面积。

3. 重心是重心轴的对称中心重心轴是连接重心和对边中点的线段，对于三角形ABC，重心轴是DE。

重心是重心轴的对称中心，即以重心G为中心，DE为轴进行对称，对应的点分别为A和C。

五、应用三角形的中位线和重心在数学中有广泛的应用。

例如：1. 在几何证明题中，可以利用重心的性质推导出其他结论。

2. 在力学中，可以利用重心的概念计算物体的重心位置。

三角形中位线的推论三角形有三条中位线，分别连接每个顶点与对面的中点。

在以下内容中，我们将讨论中位线的一些推论以及它们在几何学中的应用。

1. 三角形中位线相等最基本的推论是，三角形中的三条中位线相等。

我们可以通过使用向量的方法来证明这一点。

通过连接一对顶点并标记对角线上的中点，我们可以将三角形分成两个相等的三角形。

根据向量加法的定义，我们知道中位线的两端点的向量和等于顶点向量的和的一半。

因为我们拥有两个相等的三角形，它们的顶点向量之和相等，并且它们的中位线向量之和也相等。

因此，三角形中的三条中位线相等。

2. 中位线的交点是重心三条中位线的交点形成一个点，叫做三角形的重心。

重心是三条中位线的交点，并且它到三角形的每个顶点的距离相等。

重心也被定义为三角形质心的一种形式。

重心在几何学中扮演着重要的角色，因为它是很多求解问题的关键点。

3. 重心黄金分割我们可以进一步推导出一个有趣的结论，即：重心将每个中位线分成两个部分，其中一个部分的长度是另一个部分长度的2倍。

这种比例被称为“重心黄金分割”，并且在某些证明和设计问题中非常有用。

4. 中位线长度的应用中位线的另一个应用是在解决三角形面积问题时。

根据中位线长度的定义，我们可以将三角形分成4个形似的三角形。

其中的3个三角形是等边三角形，并且它们的边长是中位线的长度。

因此，我们可以使用等边三角形的公式（底边乘以高的1/2）来计算它们的面积。

通过将3个面积相加，我们得到三角形的面积。

5. 完美一致性最后，我们需要注意的是，在三角形中位线的推论中，它们之间存在完美的一致性。

这意味着，如果我们知道了中位线的长度，我们就可以推导出其他与之相关的所有值，如重心位置、面积等。

同时，如果我们知道了三角形某些属性，比如重心或者面积，我们也可以计算出相应的中位线长度。

这种完美一致性使得中位线在解决三角形问题时非常方便。

综上所述，中位线在解决三角形几何问题时非常有用。

它们的长度相等，交于重心，将三角形分成形似的三角形并且满足完美一致性。

三角形的中线与中位线在几何学中，三角形是最基本的图形之一，而其中线和中位线则是与三角形密切相关的概念。

本文将重点探讨三角形的中线与中位线，并阐述它们在三角形属性研究和实际应用中的重要性。

一、中线的概念首先，我们来介绍三角形的中线。

中线是连接三角形的一个顶点与对边中点的直线段。

对于任意三角形ABC，连接顶点A与对边BC的中点M的线段AM就是该三角形的中线。

中线有以下两个重要性质：1. 中线的长度相等：在任意三角形中，连接一个顶点与对边中点的线段的长度相等。

即AM = BM = CM。

2. 中线互相平分：在任意三角形中，中线互相平分。

即AM与BM 的长度相等，BM与CM的长度相等，CM与AM的长度相等。

二、中位线的概念接下来，我们来介绍三角形的中位线。

中位线是连接三角形的两个顶点的中点与对边中点的直线段。

对于任意三角形ABC，连接顶点A 与对边BC中点M以及连接顶点B与对边AC中点N的线段AM和BN就是该三角形的中位线。

中位线有以下两个重要性质：1. 中位线长度：在任意三角形中，连接一个顶点与对边中点的线段的长度等于对边的一半。

即AM = 0.5 BC，BN = 0.5 AC。

2. 中位线交点：在任意三角形中，三条中位线的交点被称为三角形的重心G，也就是三角形的质心。

重心G将每条中位线都平分成两段，其中一段的长度是另一段的两倍。

三、中线和中位线的应用中线和中位线是研究三角形属性时经常使用的重要工具。

它们有多种应用，如下所示：1. 确定三角形的重心：通过连接三角形的顶点和对边中点，可以确定三角形的重心G。

重心G在三角形内部，对于一些三角形问题的解决具有重要作用。

2. 判断三角形的形状：根据中线和中位线互相平分的性质，可以判断三角形的形状。

例如，如果三角形的三条中位线相等，则该三角形是等边三角形；如果三角形的中线相等，则该三角形是等腰三角形。

3. 解决三角形的证明问题：在三角形的证明中，利用中线和中位线的性质可以简化问题的证明过程。

三角形的中位线三角形的中位线是指连接一个三角形的一个顶点与对边中点的线段。

每个三角形都有三条中位线，它们相交于三角形的质心。

中位线在三角形的性质和应用中起着重要作用，下面将详细介绍三角形的中位线及其相关内容。

一、中位线的定义和性质1. 定义：三角形ABC的中位线是连接顶点A与对边BC的中点M的线段AM，也包括连接顶点B与对边AC的中点N的线段BN，以及连接顶点C与对边AB的中点P的线段CP。

2. 性质：a) 三角形的每条中位线都与其他两条中位线相交于同一点，这个点被称为三角形的质心。

b) 质心是三角形内部离顶点最近的点，也是三角形内部的一个重心。

c) 三角形的每条中位线都等于对边的一半，即AM = MB = BN = NC = CP = PA。

d) 三角形的三条中位线等于质心到对边中点的距离之和，即AM+ BN + CP = BM + CN + AP。

二、中位线的作用与应用1. 分割三角形：中位线将三角形分割成6个小三角形，这些小三角形具有相似性质，使得对三角形的研究和证明更加便于进行。

2. 构造平行四边形：连接三角形的质心和顶点可以构造出平行四边形。

将质心作为平行四边形的一个顶点，顶点和质心连线则为该顶点对应边的中位线。

3. 计算面积与判断形状：通过中位线可以计算三角形的面积。

当三角形的中位线相等时，三角形是等腰三角形；当三角形的中位线相交于一点时，三角形是等边三角形。

4. 解决几何问题：中位线具有调和性质，可以解决各类几何问题，如证明线段平分、证明角平分以及证明两条线段平行等。

5. 几何嵌套：中位线与其他几何图形可以嵌套在一起，如嵌套的正方形和圆。

三、实例分析与证明1. 证明质心存在：通过中位线的性质，可以证明三角形的质心存在且唯一。

2. 证明中位线与三角形边的关系：通过研究中位线与三角形边的长度关系，可以证明中位线等于对边的一半。

3. 证明中位线相交于一点：利用向量法、相似三角形等方法，可以证明三条中位线交于同一点，即三角形的质心。

三角形的中线与中位线在解析几何中，三角形是一个基础而重要的概念，而其中线和中位线则是三角形中的两个重要线段。

本文将介绍三角形的中线和中位线，并探讨它们的性质和应用。

一、中线的定义和性质中线是连接三角形两个顶点与对应边中点的线段。

在任意三角形ABC中，连结A与BC的中点D，B与AC的中点E，C与AB的中点F，则线段DE称为三角形ABC的中线。

中线有以下几个重要性质：1. 中线长度相等在任意三角形中，三条中线的长度是相等的。

这一性质可以用中位线定理进行证明。

假设DE为中线，在三角形ABC中，连接EF和FD，由中位线定理可知，EF和FD分别是AC和AB的中位线，所以EF=FD=1/2AC=1/2AB，因此DE与EF长度相等。

2. 中线互相平分在任意三角形中，三条中线相互平分。

换句话说，三条中线的交点是三角形的重心。

设三条中线相交于点G，则可以证明GD:GA=GE:GB=GF:GC=1:2。

3. 中线与对应边平行在任意三角形中，中线与对应边是平行的。

即DE∥AB，EF∥BC，FD∥AC。

这一性质可以通过向量法进行证明，利用向量的平行性质和中点的定义可以推导出这一结论。

二、中位线的定义和性质中位线是连接三角形的两个边中点的线段。

在任意三角形ABC中，连结AB的中点D，AC的中点E，BC的中点F，则线段DE称为三角形ABC的中位线。

中位线有以下几个重要性质：1. 中位线长度相等在任意三角形中，三条中位线的长度是相等的。

由于中位线连接对边的中点，而对边的长度相等，所以中位线的长度也相等。

2. 中位线与对边平行在任意三角形中，中位线与对边是平行的。

即DE∥BC，DF∥AC，EF∥AB。

这一性质同样可以通过利用向量法进行证明。

3. 中位线与中线交点在任意三角形中，三条中位线的交点是三角形的重心。

与中线类似，重心是三角形内部的一个特殊点，可以用中位线的交点来确定。

重心具有平分中线和平分面积的性质，是三角形的一个重要参考点。

三角形的中位线与中心线一、三角形的中位线1.定义：三角形的中位线是从三角形的一个顶点出发，在对面的边上找到中点，然后连接这个中点和顶点的线段。

(1)三角形的中位线平行于第三边。

(2)三角形的中位线等于第三边的一半。

(3)三角形的中位线将对边的夹角平分。

二、三角形的中心线1.定义：三角形的中心线是从三角形的某个顶点出发，延长到对边上的点，使得这个点到三角形其他两个顶点的距离相等。

(1)三角形的中心线将对边的夹角平分。

(2)三角形的中心线将对边的中点连接起来，形成的线段是三角形的中位线。

(3)三角形的三条中心线相交于一点，称为三角形的心。

1.在等边三角形中，中位线和中心线重合，都是三角形的角平分线、中线和高线。

2.在一般三角形中，中位线是中心线的一部分，中心线是延长的中位线。

四、三角形的中位线与中心线在实际应用中的意义1.在建筑设计中，通过测量三角形的中位线和中心线，可以判断建筑物的结构是否稳定。

2.在工程测量中，利用三角形的中位线和中心线可以简化计算，提高测量精度。

3.在解决几何问题时，运用三角形的中位线和中心线可以简化问题，找到解决问题的突破口。

习题及方法：1.习题：在三角形ABC中，D、E、F分别是边AB、BC、AC上的中点，求证：DE平行于BC，且DE等于BC的一半。

答案：根据三角形的中位线性质，D、E分别是边AB、BC的中点，所以DE平行于BC，且DE等于BC的一半。

2.习题：在三角形ABC中，M是边AC上的中点，求证：BM平行于AC。

答案：延长BM到N，使得MN=BM。

由于M是AC的中点，所以AN=NC。

根据等腰三角形的性质，AN平行于BC，且AN=BC。

又因为DE平行于BC，所以DE平行于AN。

又因为DE=BC，所以MN平行于AC，且MN=AC。

根据平行线的性质，BM平行于AC。

3.习题：在等边三角形DEF中，G是边DE的中点，求证：FG平行于DE。

答案：由于DEF是等边三角形，所以DE平行于DF。

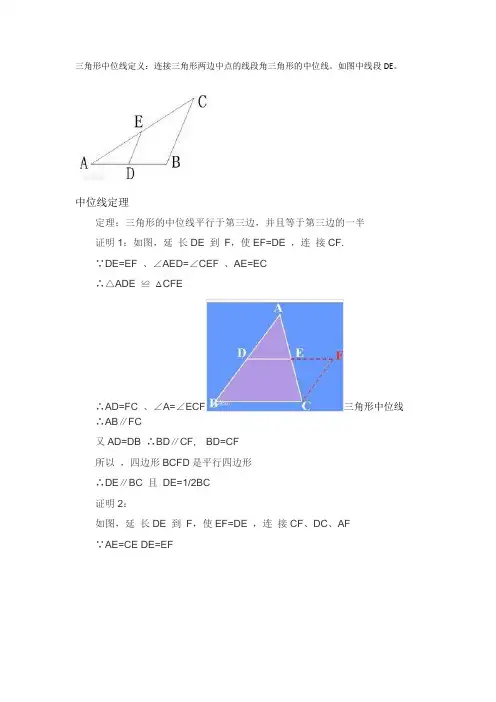
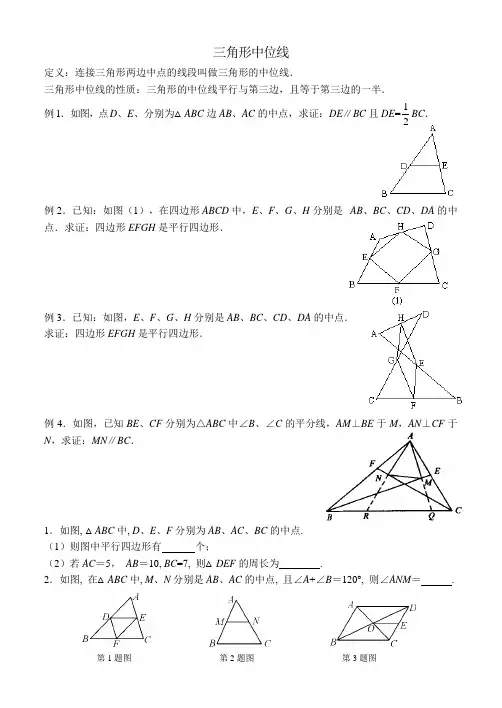
三角形中位线定义：连接三角形两边中点的线段叫做三角形的中位线．三角形中位线的性质：三角形的中位线平行与第三边，且等于第三边的一半． 例1．如图，点D 、E 、分别为△ABC 边AB 、AC 的中点，求证：DE ∥BC 且DE =21BC ．例2．已知：如图（1），在四边形ABCD 中，E 、F 、G 、H 分别是 AB 、BC 、CD 、DA 的中点．求证：四边形EFGH 是平行四边形．例3．已知：如图，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点．求证：四边形EFGH 是平行四边形．例4．如图，已知BE 、CF 分别为△ABC 中∠B 、∠C 的平分线，AM ⊥BE 于M ，AN ⊥CF 于N ，求证：MN ∥BC ．1．如图, △ABC 中, D 、E 、F 分别为AB 、AC 、BC 的中点.（1）则图中平行四边形有 个；（2）若AC ＝5， AB ＝10, BC =7, 则△DEF 的周长为 .2．如图, 在△ABC 中, M 、N 分别是AB 、AC 的中点, 且∠A +∠B ＝120°, 则∠ANM ＝ .3．如图, 在ABCD中, 对角线AC, BD相交于O点, E为CD的中点, 若OE＝3cm, 则AD＝( ).A．3cm B．6cm C．9cm D．12cm4．顺次连结任意四边形四边中点所得到的四边形为.5．已知等腰三角形两条中位线的长分别为3和5，则此三角形的周长为.6．已知△ABC中，AB：BC：CA=3：2：4且AB=9cm，D、E、F分别是AB、BC、AC的中点，则△DEF的周长是________．7．已知△ABC中，D、E分别是AB、AC的中点，F为BC上一点，EF=BC，∠EFC=35°，•则∠EDF=________．8．如图，四边形ABCD中，E、F、M、N分别为AB、CD、BD、AC的中点，求证：四边形EMFN为平行四边形.9．如图，△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CF交AD于F，点E是AB的中点，求证：EF∥BC.10．如图, △ABC中, M为BC的中点, AD为∠BAC的平分线, BD⊥AD于D，（1）求证：1()2DM AC AB=-；（2）若AD=6，BD=8，DM=2，求AC的长. 1 211．如图，△ABC中，点M为BC的中点，AD为△ABC的外角平分线，且BD⊥AD，若AB = 12，AC = 18，求MD的长．12．如图, 四边形ABCD中，M、N分别为AD、BC的中点, 连BD,若AB=10，CD=8，求MN 的取值范围；13．如图，在ABCD中，E、F是对角线AC的两个三等分点，•求证：四边形BFDE是平行四边形．14．已知五边形ABCDE中，AC∥ED，交BE于点P，AD∥BC，•交BE于点Q，BE∥CD，求证：△BCP≌△QDE．15．如图所示，在△ABC中，∠BAC=120°，以AB、AC为边向形外作等边三角形ABD和等边三角形ACE，M为AD中点，N为AE中点，P为BC中点，试求∠MPN的度数.F EDC B A16．如图, △ACB , △CDE 都为等腰直角三角形. ∠ACB ＝∠DCE ＝90°, 连AE , P 、M 、N 分别为AE 、AB 、DE 的中点.(1)如图1, 为D 、E 分别在AC 、BC 上时, PM 、PN 之间有何数量关系和位置关系？(2)如图2, 将△CDE 绕点C 逆时旋转一个锐角时, 上述结论是否仍成立？请证明.17．如图，点B 为AC 上一点，分别以AB 、BC 为边在AC 同侧作等边△ABD 和等边△BCE ， 点P 、M 、N 分别为AC 、AD 、CE 的中点．（1）求证：PM = PN ．（2）求∠MPN 的度数．18．已知△ACB , △ADE 都为等腰直角三角形, 以CE 、BC 为边作平行四边形CEFB .如图, 求CFCD 的值；图1。

如图1，连接三角形两边中点的线段叫做三角形的中位线。

ED C B A图12. 三角形中位线定理三角形的中位线平行于第三边，并且等于第三边的一半。

如图1，△ABC 中，DE 是中位线，则有DE ∥BC ，12DE BC 。

3. 三角形中位线定理的证明教材上的证明方法如图2所示，延长DE 到点F ，使EF=DE ， FE D C B A图2连接CF ，进一步证明四边形DBCF 是平行四边形。

请写出定理的证明过程。

（1）三角形中位线的定义是判定的主要方法。

（2）如图5，运用定理“过三角形一边的中点与另一边平行的直线平分第三边”来判定线段是三角形的中位线. ED C B A图5已知，△ABC 中，点D 是AB 的中点，DE ∥BC ，试说明线段DE 是△ABC 的中位线。

5.三角形中位线定理的逆定理三角形的中位线定理“三角形的中位线平行于第三边，并且等于第三边的一半。

”那么它的逆命题为______________________________________________________________________。

这个逆命题是真命题还是假命题？请作图并证明。

6.关于运用三角形中位线定理的题目特点：含有“中点”、“中线”之类的字眼，或者通过线段相等、平行四边形、等腰三角形三线合一等方式间接说明是中点，并且“中点”的数量一般不止一个。

方法：根据题目中的“中点”寻找或构造中位线模型，如下图。

ED A7.中点四边形：依次连接四边形各边的中点所得的四边形称为中点四边形。

1.画一个四边形ABCD，依次连接四边的中点M、N、P、Q，判定四边形MNPQ的形状。

2.画一个对角线相等的四边形ABCD，依次连接四边的中点M、N、P、Q，判定四边形MNPQ的形状。

3.画一个对角线互相垂直的四边形ABCD，依次连接四边的中点M、N、P、Q，判定四边形MNPQ的形状。

4.画一个对角线互相垂直且相等的四边形ABCD，依次连接四边的中点M、N、P、Q，判定四边形MNPQ的形状。

三角形的中位线与中心三角形是几何学中最基本的图形之一，它有很多重要的性质和特点。

本文将着重讨论三角形的中位线及其与三角形中心的关系。

一、中位线的定义所谓中位线，是指三角形内任意两个顶点之间的连线中点所组成的线段。

对于任意三角形ABC，连接顶点A和B的中点M₁，连接顶点B和C的中点M₂，连接顶点C和A的中点M₃所组成的线段M₁M₂M₃即为三角形的中位线。

二、中位线的性质1. 中位线互相平行在任意三角形中，三条中位线互相平行，即M₁M₂ // M₂M₃ //M₃M₁。

2. 中位线长度相等三角形三条中位线的长度相等，即M₁M₂ = M₂M₃ = M₃M₁。

3. 中位线交于一点三条中位线交于同一点G，这个交点G被称为三角形的重心。

重心是三角形的内心，也是重心到三角形三个顶点的距离之和最小的点。

三、三角形中位线与重心的关系重心是三角形的中位线的交点，也是三角形的一个特殊点。

1. 重心到顶点的距离重心到三角形三个顶点的距离之比为2:1。

即AG = 2GM₁，BG =2GM₂，CG = 2GM₃。

2. 重心的位置重心将每条中位线分成两个部分，即AG = GM₁，BG = GM₂，CG = GM₃。

3. 重心的作用重心是三角形内部重要的几何中心之一，具有以下作用：- 重心所在的中位线可以将三角形分成面积相等的两部分。

- 当三角形悬挂在任意一条中位线上时，重心处于该中位线的中点。

- 重心是三角形内切圆的圆心。

四、应用实例1. 设计建筑在建筑设计中，重心的概念被广泛运用。

由于重心的位置对于建筑物的平衡性和稳定性具有重要影响，建筑师需要在设计过程中考虑到重心的位置，以确保建筑物能够安全地承受外部的压力和重力。

2. 交通规划在交通规划中，重心也是一个重要的考虑因素。

交通规划师通过分析城市不同区域的人口、就业机会和基础设施等因素，可以确定城市的重心位置，从而优化交通网络的设计，提高交通效率。

3. 科学研究三角形的中位线和重心不仅仅在几何学中有重要的应用，它们在其他学科中也扮演着重要的角色。

【考点精讲】1. 三角形中位线的定义：连接三角形两边中点的线段叫做三角形的中位线。

A BCA BCD DE E F2. 三角形的中位线定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半。

3. 三角形的中位线的作用：一是位置关系，可用来证明线段平行； 二是数量关系，可用来证明线段相等或倍分。

【典例精析】例题1 如图，M 是△ABC 的边BC 的中点，AN 平分∠BAC ，BN ⊥AN 于点N ，延长BN 交AC 于点D ，已知AB ＝10，BC ＝15，MN ＝3。

（1）求证：BN ＝DN ； （2）求△ABC 的周长。

A BCDN12思路导航：（1）证明△ABN ≌△ADN ，即可得出结论；（2）先判断MN 是△BDC 的中位线，从而求出CD 的长，再计算△ABC 的周长即可。

答案：（1）证明：∵BN ⊥AN ，∴∠ANB ＝∠AND ＝90°，在△ABN 和△ADN 中，∵⎩⎪⎨⎪⎧∠1＝∠2AN ＝AN ∠ANB ＝∠AND ，∴△ABN ≌△ADN ，∴BN ＝DN ； （2）解：∵△ABN ≌△ADN ，∴AD ＝AB ＝10，由（1）知DN ＝BN ，又∵点M 是BC 中点，∴MN 是△BDC 的中位线， ∴CD ＝2MN ＝2×3＝6，故△ABC 的周长＝AB ＋BC ＋CD ＋AD ＝10＋15＋6＋10＝41。

点评：本题考查了三角形的中位线定理及等腰三角形的判定，注意培养数学灵感，一般出现高、角平分线重合的情况，都需要找等腰三角形；出现三角形某边的中点，常常构造三角形的中位线。

例题2 如图，在△ABC 中，AB ＝AC ，M ，N 分别是AB ，AC 的中点，D 、E 为BC 上的点，连接DN ，EM 。

若AB ＝13cm ，BC ＝10cm ，DE ＝5cm ，求图中阴影部分的面积。

A思路导航：连接MN ，根据中位线定理，可得出MN ＝DE ＝5cm ；图中阴影部分的面积就是图中三个三角形的面积，由图可知，这三个三角形的底相等都是5cm ，这三个三角形的高之和是从A 点到BC 的垂线段的长，利用勾股定理可求得高的值，据此可求出图中阴影部分的面积。

三角形中位线(华师大版)1. 引言三角形是几何学中的基本概念，而其中位线是研究三角形特性的重要工具之一。

本文将介绍华师大版教材中关于三角形中位线的相关知识。

2. 三角形中位线的定义在三角形中，连接每个顶点与对应边的中点的线段被称为中位线。

具体地说，一个三角形的中位线共存在三条，分别连接三个顶点，并同时通过三个对边的中点。

3. 三角形中位线的特性3.1 中位线的长度比定理1：连接三角形两个顶点的中位线与第三个顶点所在边的比为1:2。

具体地说，如果一个三角形的三个顶点分别为A、B、C，其中M是边AB的中点，那么AM和BC的长度比为1:2。

3.2 中位线的交点定理2：三角形中的三条中位线交于一点，该点称为三角形的重心。

三角形的重心是三角形内部到三条中位线距离之和最短的点，通常用字母G表示。

3.3 重心和中位线的关系定理3：三角形的重心将每一条中位线分为两个部分，其中一部分的长度为另一部分的两倍。

具体地说，如果一个三角形的重心为G，连接重心G和任意顶点A的中位线交于点D，那么GD的长度是AD长度的两倍。

4. 三角形中位线的应用三角形中位线在解决三角形问题时起到重要的作用。

下面介绍两个与三角形中位线有关的应用例子。

4.1 判断三角形类型已知一个三角形的三边长度，可以通过判断三个中位线的交点是否与三角形的重心重合来确定三角形类型。

•如果三个中位线的交点与重心重合，说明该三角形是等边三角形。

•如果三个中位线的交点在重心的同一侧，说明该三角形是等腰三角形。

•如果三个中位线的交点在重心的不同侧，说明该三角形是普通三角形。

4.2 计算三角形面积已知一个三角形的两个顶点坐标，可以通过计算中位线长度来求解三角形的面积。

具体的计算方法是：首先求出三个中位线的长度，根据定理1中的比例关系，可以求得任意一条中位线的长度。

然后使用海伦公式或其他方法求解由中位线构成的三角形的面积。

5. 总结本文介绍了华师大版教材中关于三角形中位线的相关知识。

3角形中位线定理三角形中位线定理，是在三角形中，与三条相邻边的中点相连的线段，它们构成的三个交点都在同一点上。

本文将从定理的证明、推广应用、例题等三个方面进行阐述。

一、定理的证明证明思路：设三角形ABC的三边分别为a、b、c，D为BC的中点，E为AC的中点，F 为AB的中点，则连接AD、BE、CF的交点为G。

则需证明AD、BE、CF三条线段的交点G是一个固定点。

证明：由于D、E、F都是各边中点，可得：∵ D是BC的中点，∴ BD = DC；又∵ G是AD与BE的交点，故可以得出：∵ D、E分别为BC和AC的中点，∴ DE // AC，同时AE = EC，∴ △AED与△CEB 相似。

$\frac{GA}{BD}=\frac{GC}{CE}$又 $\because BD=DC$ ， $\therefore GA=GC$同理可得：于是，我们得到了两个相等的值：GA=GC，GB=GC。

由此，可知三角形GAC是一个等腰三角形，且AG与CF之间的线段垂直于CF，同理可得：因为三角形GAC、GBA、CBG均拥有最长边CG，所以它们就构成了一个共同的圆，而这个圆的中心就是点G。

因此可以得知：三角形ABC的三边中位线的交点G是一个固定点。

二、推广应用利用中位线定理，我们可以推导容易证明的三条定理和一个相关问题：中位线长定值定理、七分线长定值定理、以及在四边形中应用中位线定理、解决中位线问题。

1. 中位线长定值定理在三角形中，如果其中一条中位线相等，那么这个三角形就是等边三角形。

设△ABC为等边三角形，则BD、AE、CF三条中位线的长度均为$\frac{1}{2}$边长，又 $\because BD=AE=CF$ ，所以可以得到：BD=AE=CF=$\frac{1}{2}$a=a，同理可得：b=c=a。

在三角形中，三条中位线可将它们所在线段的长分为1:2:3的比例。

首先，由于三角形的三角形内部对角线互不交于同一点，那么三角形内部的线段AB、AC、BC是不会共线的。