精馏例题讲解

精馏习题课例题1.一分离苯、甲苯的常压精馏塔，按以下三种方式冷凝(图1，图2，图3)，塔顶第一板上升蒸汽浓度为含苯0.8(摩尔分率)，回流比均为2。

(1)采用全凝器冷凝，在塔顶及回流处插二支温度计，测得温度分别为0t 、1t ，问0t 、1t 是否相等?为什么?并求0t 、1t 的值。

(2)在图1，图2，图3三种冷凝情况下，第一板浓度为1y 含苯0.8(摩尔分率)。

①比较温度1t 、2t 、3t 的大小；②比较回流液浓度1L x 、2L x 、3L x 的大小；③比较塔顶产品浓度1D x 、2D x 、3D x 的大小。

将以上参数分别按顺序排列，并说明理由。

(3)三种情况下精馏段操作线是否相同?在同一x y -图上表示出来，并将三种情况下D x 、L x 、V x 的值在x y -图上表示出来。

已知阿托因常数如下(阿托因方程为)/(lg 0T C B A p +-=，其中P 单位为mmHg ，T 单位为℃)：例题2.用一连续精馏塔分离苯—甲苯混合液。

进料为含苯0.4(质量分率，下同)的饱和液体，质量流率为1000kg/h 。

要求苯在塔顶产品中的回收率为98%，塔底产品中含苯不超过0.014。

若塔顶采用全凝器，饱和液体回流，回流比取为最小回流比的1.25倍，塔底采用再沸器。

全塔操作条件下，苯对甲苯的平均相对挥发度为2.46，塔板的液相莫弗里(Murphree)板效率为70%,并假设塔内恒摩尔溢流和恒摩尔汽化成立。

试求：①塔顶、塔底产品的流率D 、W 及塔顶产品的组成x D ； ②从塔顶数起第二块板上汽、液相的摩尔流率各为多少； ③精馏段及提馏段的操作线方程；④从塔顶数起第二块实际板上升气相的组成为多少？例题3.如图所示，对某双组分混合液，分别采用简单蒸馏和平衡蒸馏方法进行分离，操作压力、原料液的量F 、组成x F 均相同。

①若气相馏出物浓度（或平均浓度）相同，即平D 简D ＝x x ,,，试比较残液（或液相产品）浓度x W ，简、x W ，平，气相馏出物量V 简、V 平；②若气相馏出物量相同，即V 简=V 平，试比较残液（或液相产品）浓度x W ，简、x W ，平，气相馏出物浓度（或平均浓度）平D 简D 、xx ,,及残液（或液相产品）量。

精馏[例1] 当分离要求和回流比一定时，进料的q值最小，此时分离所需的理论板数。

[解题思路] 5种进料状况中的q值是依过冷液体、饱和液体、气—液混合和蒸气和过热蒸气顺序由大变小的，这是由热状况参数q的定义确定的。

由定义可见，在Iv、I L为定值的情况下，原料的原状态焓值越低，q值越大。

q值的改变使提馏段操作线与平衡曲线间的距离发生变化。

当q值减小时，两线靠近，故所需理论板数增多。

[答案] 过热蒸气，最多[例2]精馏操作的依据是。

精馏操作得以实现的必要条件包括和。

[解题思路]精馏操作的依据只能是各组分间挥发度的差异或者说相对挥发度不等于1，而不可认为是各组分间沸点的不同。

对于纯组分，当压力一定时，沸点低者挥发性大。

但对于混合溶液，由于一个组分的挥发性受其他组分的影响，故不能仅从沸点或蒸气压大小来判断其挥发性能，为此，组分的挥发度是用蒸气压与液相摩尔分数的比值来表示的。

而在有些物系中，各组分沸点虽存在差异，但在恒沸组成处，相对挥发度为1，不能用普通的精馏方法分离。

塔内始终有逆向流动的液、气两股物流是实现精馏的必要条件，但并不意味塔顶必须有液相回流，塔底必须有产生回流蒸气的再沸器。

例如：将液态原料自塔顶加入，将气态原料自塔底加入或将饱和蒸气直接加入塔底等情况，均可替代回流作用。

[答案] 混合液中各组分的挥发度的差异；自塔顶向下的液流；自塔底向上的气流[例3]若精馏塔塔顶某块理论板上气相露点为t1，液相泡点为t2；塔底某块理论板上气相露点为t3，液相泡点为t4。

将4个温度间的关系用“＞〞、“＝〞、“＜〞表示为。

[解题思路] 精馏塔内塔底压力大于塔顶压力．故塔底温度高于塔顶温度；同一块理论板上，当气、液两相达成平衡时，温度一致。

[答案][例4] 当增大操作压力时，精馏过程中物系的相对挥发度度，塔顶温度，塔釜温度。

[解题思路] 同一物系，总压越高，物系中各组分的沸点与混合物的泡点越高。

物系中各组分的饱和蒸气压也随总压升高而升高，由于轻组分的饱和蒸气压上升的速率低于重组分的饱和蒸气压上升的速率，故各组分的挥发度差异变小。

1. 用一精馏塔分离二元理想混合物，塔顶为全凝器冷凝，泡点温度下回流，原料液中含轻组分0.5(摩尔分数，下同)，操作回流比取最小回流比的１.４倍，所得塔顶产品组成为０．９５，釜液组成为０．０５．料液的处理量为１００kmol/．料液的平均相对挥发度为３，若进料时蒸气量占h一半，试求：（1）提馏段上升蒸气量；（86.1kmol/h）（2）自塔顶第2层板上升的蒸气组成。

0.88分析：欲解提馏段的蒸气量v'，须先知与之有关的精馏段的蒸气量V。

而V又须通过D=才可确定。

可见，先(+V)1R确定最小回流比R，进而确定R是解题的思路。

min理想体系以最小回流比操作时，两操作线与进料方程的交点恰好落在平衡线上，所以只须用任一操作线方程或进料方程与相平衡方程联立求解即可。

某二元混合液的精馏操作过程如图4—9。

已知组成为52.0的原料液在泡点温度下直接加入塔釜，工艺要求塔顶产品的组成为0.75，（以上均为轻组分A 的摩尔分数），塔顶产品采出率D/F 为1:2，塔顶设全凝器，泡点回流。

若操作条件下，该物系的a 为2.5，回流比R 为2.5，求完成上述分离要求所需的理论板数（操作满足恒摩尔流假设）。

包括塔釜在共需3块理论塔板。

分析：因题中未给平衡相图，只可考虑逐板计算法求理论板数。

当料液直接加入塔釜时，应将塔釜视作提馏段，然后分段利用不同的操作线方程与相平衡方程交替使用计算各板的气液相组成，直至W x x 时止。

图4-94在一连续精馏塔中分离二元理想混合液。

原料液为饱和液体，其组成为0.5，要求塔顶馏出液组成不小于0.95,釜残液组成不大于0.05(以上均为轻组分A 的摩尔分数)。

塔顶蒸汽先进入一分凝器，所得冷凝液全部作为塔顶回流,而未凝的蒸气进入全凝器，全部冷凝后作为塔顶产品。

全塔平均相对挥发度为2.5,操作回流比min 5.1R R 。

当馏出液流量为100h kmol /时，试求：（1） 塔顶第1块理论板上升的蒸汽组成；0.909（2） 提馏段上升的气体量。

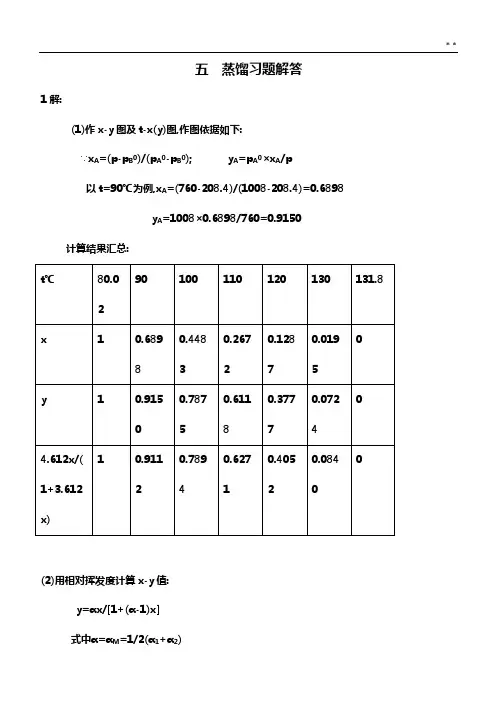
五蒸馏习题解答1解:(1)作x-y图及t-x(y)图,作图依据如下:∵x A=(p-p B0)/(p A0-p B0); y A=p A0×x A/p以t=90℃为例,x A=(760-208.4)/(1008-208.4)=0.6898y A=1008×0.6898/760=0.9150 计算结果汇总:(2)用相对挥发度计算x-y值:y=αx/[1+(α-1)x]式中α=αM=1/2(α1+α2)∵α=p A0/p B0α1=760/144.8=5.249 ;α2=3020/760=3.974∴αM=1/2(α1+α2)=1/2(5.249+3.974)=4.612y=4.612x/(1+3.612x)由此计算x-y值亦列于计算表中,y-x图,t-x(y) 图如下:1 题附图2解:(1)求泡点:在泡点下两组分的蒸汽分压之和等于总压P,即:p A+p B=p A0x A+x B0x B=p求泡点要用试差法,先设泡点为87℃lgp A0=6.89740-1206.350/(87+220.237)=2.971p A0=102.971=935.41[mmHg]lgp B0=6.95334-1343.943/(87+219.337)=2.566p B0=102.566=368.13[mmHg]935.41×0.4+368.13×0.6=595≈600mmHg∴泡点为87℃,气相平衡组成为y=p A/p=p A0x A/P=935.41×0.4/600=0.624(2)求露点:露点时,液滴中参与甲苯组成应符合下列关系: x A+x B=1或p A/p A0+p B/p B0=1 式中p A=0.4×760=304[mmHg]; p B=0.6×760=456[mmHg]求露点亦要用试差法,先设露点为103℃,则:lgp A0=6.8974-120.635/(103+220.237)=3.165∴p A0=1462.2[mmHg]lgp B0=6.95334-1343.943/(103+219.337)=2.784∴p B0=608.14[mmHg]于是:304/1462.2+456/608.14=0.96<1再设露点为102℃,同时求得p A0=1380.4; p B0=588.84304/1380.4+456/588.84=0.995≈1故露点为102℃,平衡液相组成为x A=p A/p A0=304/1380.4=0.223解:(1)x A=(p总-p B0)/(p A0-p B0)0.4=(p总-40)/(106.7-40)∴p总=66.7KPay A=x A·p A0/p=0.4×106.7/66.7=0.64 (2)α=p A0/p B0=106.7/40=2.674解:(1) y D=?αD =(y/x)A/(y/x)B=(y D /0.95)/((1-y D )/0.05)=2y D =0.974(2) L/V D =?∵V=V D +L(V/V D )=1+(L/V D )V0.96=V D 0.974+L0.95(V/V D )0.96=0.974+(L/V D )0.95(1+L/V D )0.96=0.974+(L/V D )0.95(L/V D )=1.45解:简单蒸馏计算: lnW 1/W 2=⎰-12x x xy dxW 2=(1-1/3)W 1=2/3W 1;y=0.46x+0.549,x 1=0.6,代入上式积分解得: 釜液组成:x 2=0.498,馏出液组成:W D x D =W 1x 1 -W 2x 2(1/3W 1)x D =W 1×0.6-(2/3W 1)×0.498 ∴x D =0.804 6解:Fx F =Vy+Lx ∴0.4=0.5y+0.5x --------(1) y=αx/(1+(α-1)x)=3x/(1+2x) --------(2) (1),(2)联立求解,得y=0.528,x=0.272回收率=(V ·y)/(Fx F )=0.5×0.528/0.4=66% 7.解:F=D+W Fx F =Dx D +Wx W已知x F =0.24,x D =0.95,x W =0.03,解得:D/F=(x F -x W )/(x D -x W )=(0.24-0.03)/(0.95-0.03)=0.228 回收率 Dx D /Fx F =0.228×0.95/0.24=90.4%残液量求取:W/D=F/D-1=1/0.228-1=3.38∴W=3.38D=3.38(V-L)=3.38(850-670)=608.6[kmol/h]8解:(1) 求D及W,全凝量VF=D+WFx F =Dx D +Wx Wx F =0.1,x D =0.95,x W =0.01(均为质量分率)F=100[Kg/h],代入上两式解得:D=9.57[Kg/h]; W=90.43[Kg/h]由恒摩尔流得知:F(0.1/78+0.9/92)=V(0.95/78+0.05/92)[注意:如用质量百分数表示组成,平均分子量M m=1/(a A/M A+a B/M B)] 解得V=87[Kg/h] 由于塔顶为全凝器,故上升蒸汽量V即为冷凝量,(2) 求回流比RV=D+L ∴L=V-D=87-9.57=77.43[Kg/h]R=L/D=77.43/9.57=8.09(因为L与D的组成相同,故8.09亦即为摩尔比)(3) 操作线方程.因塔只有精馏段,故精馏段操作线方程为y n+1 =Rx n /(R+1)+x D /(R+1)式中x D应为摩尔分率x D =( x D /M A)/[x D /M A+(1-x D )/M B]=(0.95/78)/(0.95/78+0.05/92)=0.961∴y n+1=8.09x n/9.09+0.961/9.09=0.89x n +0.106操作线方程为:y n+1 =0.89x n +0.1069解:y=[R/(R+1)]x+x D /(R+1)(1) R/(R+1)=0.75 R=0.75R+0.75 R=0.75/0.25=3(2) x D /(R+1)=0.2075 x D /(3+1)=0.2079 x D =0.83(3) q/(q-1)=-0.5 q=-0.5q+0.5 q=0.5/1.5=0.333(4) 0.75x+0.2075=-0.5x+1.5x F0.75x q'+0.2075=-0.5x q '+1.5×0.441.25x q '=1.5×0.44-0.2075=0.4425 x q '=0.362(5)0<q<1 原料为汽液混合物10解:(1) 求精馏段上升蒸汽量V和下降的液体量L,提馏段上升蒸汽量V'和下降的液体量L'. 进料平均分子量: Mm=0.4×78+0.6×92=86.4F=1000/86.4=11.6[Kmol/h]Fx F =Dx D +Wx WF=D+W11.6×0.4=D×0.97+(11.6-D)0.02∴D=4.64[Kmol/h]W=6.96[Kmol/h]R=L/D, ∴L=3.7×4.64=17.17[Kmol/h]V=(R+1)D=4.7×4.64=21.8[Kmol/h]平均气化潜热r=30807×0.4+33320×0.6=32313.6[KJ/Kmol]从手册中查得x F =0.4时泡点为95℃,则:q=[r+cp(95-20)]/r=(32313.6+159.2×75)/32313.6=1.37 ∴L'=L+qF=17.17+1.37×11.6=33.1[Kmol/h]V'=V-(1-q)F=21.8+0.37×11.6=26.1[Kmol/h](2) 求塔顶全凝器热负荷及每小时耗水量.Qc=Vr∴r=0.97×30804+33320×0.03=30879.5[KJ/Kmol]∴Qc=21.8×30879.5=673172.7[KJ/h]耗水量Gc=673172.7/4.18(50-20)=5368.2[Kg/h](3) 求再沸器热负荷及蒸汽耗量.塔的热量衡算Q B+Q F +Q R=Q v+Q W +Q LQ B=Q v+Q W +Q L-Q F -Q R该式右边第一项是主要的,其它四项之总和通常只占很小比例,故通常有: Q B≈Q V=V·I vIv=(r+Cpt)=30879.5+159.2×8.2=43933.9[KJ/Kmol]∴Q B=21.8×43933.9=957759.02[KJ/h]2.5[KgF/cm2]下蒸汽潜热r=522Kcal/Kg=522×4.18×18=39275.3[KJ/Kmol]∴蒸汽需量为G vG v =Q B/r=957759.02/39275.3=24.4Kmol/h=24.4×18=39.04[Kg/h](4) 提馏段方程y=L'x/(L'-W)-Wx W /(L'-W)=1.26x-0.00511解:提馏段: y m+1’=1.25x M’-0.0187---------(1)=L'x M'/V'-Wx W /V',L'=L+qF=RD+FV'=(R+1)DW=F-D,精馏段: y n+1 =Rx n /(R+1)+x D /(R+1)=0.75x n +0.25x D --------(2)q线:x F =0.50 --------------(3)将(3)代入(1)得出:y m+1=1.25×0.5-0.0187=0.606,代入(2)0.606=0.75×0.5+0.25x D ,x D =0.92412解:(1) y1=x D =0.84,0.84=0.45x1+0.55x1=0.64,y W =3×0.64/(3+1)+0.84/(3+1)=0.69,0.69=0.45×x W +0.55,x W =0.311,(2) D=100(0.4-0.311)/(0.84-0.311)=16.8(Kmol/h),W=100-16.8=83.2(Kmol/h)13解:(1) 求R,x D,x W精馏段操作线斜率为R/(R+1)=0.723 ∴R=2.61提馏段方程y=L'x/(L'-W)-Wx W/(L'-W)=1.25x-0.0187精馏段操作线截距为x D/(R+1)=0.263 ∴x D =0.95提馏段操作线与对角线交点坐标为y=x=x W x W =1.25 x W -0.0187 ∴x W =0.0748(2)饱和蒸汽进料时,求取进料组成将y=0.723x+0.263y=1.25x-0.0187联立求解,得x=0.535,y=0.65* * 因饱和蒸汽进料,q线为水平线,可得原料组成y=x F=0.6514解:(1) y1=x D =0.9,x1=0.9/(4-3×0.9)=0.692,(2) y2=1×0.692/(1+1)+0.9/2=0.796(3) x D =x F =0.5, y D =0.5/2+0.9/2=0.715解:(1) Fx F=Vy q+Lx q0.45=(1/3)y q+(2/3)x qy q =2.5x q /(1+1.5x q)∴x q=0.375 y q=0.6(2) Rmin=(x D-y q)/(y q-x q)=(0.95-0.6)/(0.6-0.375)=1.56R=1.5Rmin=2.34D=0.95×0.45/0.95=0.45 W=1-0.45=0.55x W=(Fx F-Dx D)/W=(0.45-0.45×0.95)/0.55=0.041L=RD=2.34×0.45=1.053; V=(R+1)D=1.503L'=L+qF=1.053+(2/3)×1=1.72; V'=V-(1-q)F=1.503-1/3=1.17y'=(L'/V')x'-Wx W/V'=1.72/1.17x'-0.55×0.041/1.17=1.47x'-0.019316解:* * 精馏段操作线方程y n+1 =3/4x n +0.24平衡线方程y=αx/[1+(α-1)x]=2.5x/(1+1.5x)提馏段操作线方程y=1.256x-0.01278其计算结果如下:N0x y1 0.906 0.962 0.821 0.923 0.707 0.864 0.573 0.775 0.462 0.706 0.344 0.5677 0.224 0.4198 0.128 0.2689 0.065 0.14810 0.029 0.069由计算结果得知:理论板为10块(包括釜), 加料板位置在第五块；17解:D/F=(x F -x W )/(x D -x W )=(0.52-x W )/(0.8-x W )=0.5解得:x W =0.24精馏段操作线方程:y n+1 =(R/(R+1))x n +x D /(R+1)=0.75x n +0.2 --------(1) 平衡线方程:y=αx/(1+(α-1)x)=3x/(1+2x)或:x=y/(α-(α-1)y)=y/(3-2y) --------(2)交替运用式(1),(2)逐板计算:x D =y1=0.8 .x1=0.571;y2=0.628,x2=0.360;y3=0.470,x3=0.228<x W=0.24∴共需N T=3块(包括釜).18解:q=0,x D =0.9,x F =0.5,x W =0.1,R=5,精馏段操作线方程:y n+1=Rx n/(R+1)+x D/(R+1)=5x n/(5+1)+0.9/(5+1)=0.833x n+0.15图解:得理论板数为11块(不包括釜),包括釜为12块18题附图19解:(1) F=D+WFx F =Dx D +Wx WD=F(x F -x W )/(x D -x W )=100(0.3-0.015)/(0.95-0.015)=30.48 Kmol/h=30.5 Kmol/hW=F-D=69.50 Kmol/h(2) N T及N F =?x D =0.95、x W =0.015、q=1、R=1.5；x D /(R+1)=0.38作图得:N T =9-1=8(不含釜)进料位置: N F =6(3)L’,V’,y W及x W-1 19题附图∵q=1,V'=V=(R+1)DV'=30.5(1.5+1)=76.25Kmol/hL'=L+qF=RD+F=1.5×30.5+100=145.8Kmol/h由图读得:y W =0.06, x W-1=0.0320解:(1) 原料为汽液混合物,成平衡的汽液相组成为x ,y平衡线方程y=αx/[1+(α-1)x]=4.6x/(1+3.6x) --------- (1)q线方程(q=2/(1+2)=2/3)则y=[q/(q-1)]x-x F /(q-1)=-2x+1.35 ---------- (2)联解(1),(2)两式,经整理得:-2x+1.35=4.6x/(1+3.6x)7.2x2 +1.740x-1.35=0解知,x=0.329y=0.693(2) Rmin=(x D -y e)/(y e-x e)=(0.95-0.693)/(0.693-0.329)=0.70621解:因为饱和液体进料,q=1y e=αx e/[1+(α-1)x e]=2.47×0.6/(1+1.47×0.6)=0.788R min=(x D -y e)/(ye-x e)=(0.98-0.788)/(0.788-0.6)=1.02R=1.5×R min=1.53N min=lg[(x D /(1-x D ))((1-x W )/x W )]/lgα=lg[(0.98/0.02)(0. 95/0. 05)]/lg2.47= 7.56x=(R-R min)/(R+1)=(1.53-1.02)/(1.53+1)=0.202Y=(N-N min)/(N+1) Y=0.75(1-x0.567)∴(N-7.56)/(N+1)=0.75(1-0.2020.567) 解得N=14.5 取15块理论板(包括釜)实际板数: N=(15-1)/0.7+1=21(包括釜)求加料板位置,先求最小精馏板数(N min)精=lg[x D /(1-x D )×(1-x F )/x F ]/lgα=lg[0.98/0.02·0.4/0.6]/lg2.47=3.85N精/N=(N min)精/N min∴N精=N(N min)精/N min=14.5×3.85/7.56=7.4则精馏段实际板数为7.4/0.7=10.6取11块故实际加料板位置为第12块板上.22解:(1) 由y=αx/[1+(α-1)x]=2.4x/(1+1.4x) 作y-x图由于精馏段有侧线产品抽出,故精馏段被分为上,下两段, 抽出侧线以上的操作线方程式: y n+1 =Rx n /(R+1)+x D /(R+1)=2/3x n +0.3 ----------- (1)侧线下操作线方程推导如下:以虚线范围作物料衡算V=L+D1+D2Vy s+1=Lx s+D1x D1+D2x D2 ;y s+1=Lx s/V +(D1x D1+D2x D2)/V=Lxs/(L+D1+D2)+(D1x D1+D2x D2)/(L+D1+D2);L=L0-D2, 则:y s+1=(L0-D2)x s/(L0-D2+D1+D2)+(D1x D1+D2x D)/(L0-D2+D1+D2)2=(R-D2/D1)x s/(R+1)+(x D1+D2x D2/D1)/(R+1)(R=L0/D1)将已知条件代入上式,得到:y S+1=0.5x+0.416(2) 用图解法,求得理论塔板数为（5-1）块,见附图.22题附图23解:根据所给平衡数据作x-y图.精馏段操作线y n+1 =Rx n /(R+1)+x D /(R+1)=1.5x n /(1.5+1)+0.95/(1.5+1)=0.6x n +0.38q线方程与q线:料液平均分子量:M m=0.35×+0.65×18=22.9甲醇分子汽化潜热:r=252×32×4.2=33868.8[KJ/Kmol]水的分子汽化潜热:r=552×18×4.2=41731.2[KL/Kmol] 23题附图料液的平均分子汽化潜热:r=0.35×33868.8+0.65×41731.2=38979.4[KL/Kmol]料液的平均分子比热Cp=0.88×22.9×4.2=84.6[KL/Kmol·℃]q=[r+Cp(ts-t F )]/r=[38979.4+84.6(78-20)]/38979.4=1.13q线斜率q/(q-1)=1/13/0.13=8.7提馏段操作线方程与操作线：由于塔釜用直接蒸汽加热,故提馏段操作线过横轴上(x W ,0)一点,于是在x-y图上,作出三条线,用图解法所得理论板数为7.6块,可取8块(包括釜).24解:对全塔进行物料衡算:F1+F2=D+W ----------(1)F1x F1+F2x F2=Dx D +Wx W100×0.6+200×0.2=D×0.8+W×0.02100=0.8D+0.02W -----------(2)由式(1) W=F1+F2-D=100+200-D=300-D代入式(2)得:D=120.5Kmol/hL=RD=2×120.5=241kmol/hV=L+D=241+120.5=361.5Kmol/h在两进料间和塔顶进行物料衡算,并设其间液汽流率为L",V",塔板序号为s.V''+F1=D+L''V''y s+1"+F1x F1=L''xs''+Dx Dy s+1=(L''/V'')xs''+(Dx D -F1x F1)/V''L''=L+q1F1=241+1×100=341Kmol/hV''=V=361.5y s+1"=(341/361.5)x s''+(120.5×0.8-100×0.6)/361.5y s+1"=0.943x s''+0.125解:对于给定的最大V',V=(R+1)D,回流比R愈小,塔顶产品量D愈大,但R 需满足产品的质量要求x D》0.98, 故此题的关键是求得回流比R.由题已知加料板为第14层,故精馏段实际板数为13层,精馏段板数为:13×0.5=6.5取苯-甲苯溶液相对挥发度为α=2.54用捷算法求精馏段最小理论板数(N min)精=ln[0.98/0.02-0.5/0.5]/ln2.54=4.175y=[N精馏段-(N min)精]/(N精馏段+1)=(6.5-4.175)/(6.5+1)=1.31由y=0.75(1-x0.567)x=(1-Y/0.75)(1/0.567)=0.392=(R-R min)/(R+1)∴R=(0.392+R min)/(1-0.392)R min=(x D -y e)/(y e-x e)对泡点进料x e=x F =0.5y e=αx/[1+(α-1)x]=2.54×0.5/(1+1.54×0.5)=1.27/1.77=0.72∴R min=(0.98-0.72)/(0.72-0.5)=0.26/0.22=1.18∴R=(0.392+1.18)/(1-0.392)=1.572/0.608=2.59∴D=V/(R+L)=2.5/(2.59+1)=0.696[Kmol/h]故最大馏出量为0.696[Kmol/h]26解:求n板效率: Emv =(y n -y n+1 )/(y n*-y n+1 ),因全回流操作,故有y n+1 =x n ,y n =x n-1与x n成平衡的y n*=αx n /[1+(α-1)x n ]=2.43×0.285/(1+1.43×0.285)=0.492 于是: Emv=(x n-1 -x n )/(y n*-x n )=(0.43-0.285)/(0.492-0.285)=0.7求n+1板板效率:Emv=(y n+1-y n+2)/(y n+1*-y n+2)=(x n-x n+)/(y n+1*-x n+1 )y’n+1 =2.43×0.173/(1+1.43×0.173)=0.337∴Emv=(0.285-0.173)/(0.337-0.173)=0.68327解:由图可知:该板的板效率为Emv=(y1-y )/(y1*-y W)从图中看出,y1=x D =0.28,关键要求y1*与y W .由已知条件Dx D /Fx F =0.8∴D/F=0.8×0.2/0.28=0.57作系统的物料衡算: Fx F =Dx D +Wx WF=D+W联立求解: x F =Dx D /F+(1-D/F)x W0.2=0.57×0.28+(1-0.57)x W解得x W =0.093 习题27附图因塔釜溶液处于平衡状态,故y W =αx W /[1+(α-1)x W ]=2.5×0.093/(1+1.5×0.093)=0.204y W与x1是操作线关系.y n+1 =L'x n /V'-Wx W /V'=Fx n /D-Wx W/D =Fx n /D-(F-D)x W /D=Fx n /D-(F/D-1)x W∴y n+1 =x n /0.57-(1/0.57-1)0.093=1.75x n -0.07当y n+1 =y W时,x n =x1∴x1=(y W +0.07)/1.75=(0.204+0.07)/1.75=0.157与x1成平衡气相组成为y1*y1*=αx1/[1+(α-1)x1]=2.5×0.157/(1+1.5×0.157)=0.318 ∴Emv=(0.28-0.204)/(0.318-0.204)=66.8%28解:(1)精馏段有两层理论板,x D=0.85,x F=0.5,用试差法得精馏段操作线ac,与x=x F=0.5线交于d.提馏段有两层理论板,从点d开始再用试差法作图,得提馏段操作线bd，得：x W =0.17x D/(R+1)=0.103R=0.85/0.103-1=7.25F=D+W Fx F =Dx D +Wx W100=D+W100×0.5=D×0.85+W×0.17得D=48.5Kmol/hV'=V=(R+1)D=8.25×48.5=400Kmol/h 28题附图(2)此时加入的料液全被气化而从塔顶排出,其组成与原料组成相同,相当于一个提馏塔. 29解:(1)D=η,Fx F /x D =0.9×100×0.4/0.92=39.13Kmol/h,W=60.9Kmol/hx W =0.1Fx F /W=0.1×100×0.4/60.9=0.0656∵q=1 ∴x q =0.4 查图得y q =0.61R min=(x D -y q )/(y q -x q )=(0.92-0.61)/(0.61-0.4)=1.48R=1.5×1.48=2.2 x D /(R+1)=0.92/3.2=0.29在y-x图中绘图得N T =15-1=14块(未包括釜),N加料=第6块理论板N p=14/0.7=20块(不包括釜) N p精=5/0.7=7.14,取8块,∴第九块为实际加料板(2) 可用措施:(1)加大回流比,x D↑,x W↓,η=↑(2)改为冷液进料,N T <N T' q=1, N T =const ∴x D↑q约为const,下移加料点,x D↑.29题附图30解:(1)Dx D /Fx F =0.922; Dx D =0.922×150×0.4=55.32Dx D =Fx F -Wx W =Fx F -(F-D)x W =55.32150×0.4-(150-D)×0.05=55.32D=56.4Kmol/h W=F-D=93.6Kmol/hx D =55.32/56.4=0.981(2) N T及N F (进料位置)x D =0.981,x W =0.05,q=1,x D /(R+1)=0.981/(2.43+1)=0.286a(0.981,0.981), b(0.05,0.05)q线: x F=0.4、q=1, q线为垂线。

一、判断题1.进行蒸馏分离，混合溶液中易挥发组分在气相中的含量较液相中低。

（）2.回流液的作用，是使蒸汽部分冷凝的冷却剂，并使精馏稳定进行。

（）3.通过提馏段物料衡算得出的方程是提馏段操作线方程。

（）4.精馏塔釜的作用，是向最下面一块塔板供应蒸汽。

（）5.精馏（或蒸馏）的基本原理为：易挥发组分在气相中的含量大于它在液相中的含量。

（）6.普通精馏操作可分离所有的液体混合物。

（）7.全回流时，精馏所用理论板层数最多。

（）8.精馏是一种既符合传质规律，又符合传热规律的单元操作。

（）9.蒸馏是分离均相液的一种单元操作。

（）10.精馏操作线方程是指相邻两块塔板之间蒸气组成与液体组成之间的关系。

（）11.简单蒸馏属于间歇性操作。

( )12.精馏塔的进料板属于精馏段。

( )13.饱和蒸汽进料的进料线是一条与x轴垂直的直线。

( )14.浮阀塔板的特点是造价较高，操作弹性小，传质性差。

（）15.液泛不能通过压强降来判断。

（）16.筛板精馏塔的操作弹性大于泡罩精馏塔的操作弹性。

（）17.精馏过程中，平衡线随回流比的改变而改变。

（）18.蒸馏的原理是利用液体混合物中各组分溶解度的不同来分离各组分的。

（）19.精馏塔发生液泛现象可能是由于气相速度过大，也可能是液相速度过大。

（）20.蒸馏塔总是塔顶作为产品，塔底作为残液排放。

（）21.浮阀塔板结构简单，造价也不高，操作弹性大，是一种优良的塔板。

（）22.精馏操作的回流比减小至最小回流时，所需理论板数为最小。

（）23.精馏是传热和传质同时发生的单元操作过程。

（）24.正常操作的精馏塔从上到下，液体中轻相组分的浓度逐渐增大。

（）25.精馏操作中，回流比越大越好。

（）26.灵敏板温度上升，塔顶产品浓度将提高。

（）27.筛板塔板结构简单，造价低，但分离效率较泡罩低，因此已逐步淘汰。

（）28.精馏塔板的作用主要是为了支承液体。

（）29.连续精馏停车时，先停再沸器，后停进料。

（）30.回流是精馏稳定连续进行的必要条件。

第9章 精馏 典型例题例1：逐板法求理论板的基本思想有一常压连续操作的精馏塔用来分离苯-甲苯混合液，塔顶设有一平衡分凝器，自塔顶逸出的蒸汽经分凝器后，液相摩尔数为汽相摩尔数的二倍，所得液相全部在泡点下回流于塔，所得汽相经全凝器冷凝后作为产品。

已知产品中含苯0.95（摩尔分率），苯对甲苯的相对挥发度可取为2.5 。

试计算从塔顶向下数第二块理论板的上升蒸汽组成。

解: 884.095.05.15.295.05.115.20000=⨯-=→=+=x x x x y DR=L/D=2905.03/95.0884.0323/95.032:11=+⨯=+=+y x y n n 精馏段方程845.03/95.0793.032793.0905.05.15.2905.05.15.22111=+⨯==⨯-=-=y y y x例2：板数较少塔的操作型计算拟用一 3 块理论板的（含塔釜）的精馏塔分离含苯50%（摩尔分率，下同）的苯-氯苯混合物。

处理量F=100 Kmol/h ，要求 D=45 Kmol/h 且 x D >84%。

若精馏条件为：回流比R=1 ，泡点进料，加料位置在第二块理论板，α=4.10 ，问能否完成上述分离任务？ 解：W=55kmol/h精馏段操作线方程：y n+1=0.5x n +0.42提馏段的操作线方程：Fq D R Wx x F q D R qFRD y w )1()1()1()1(--+---++=将相关数据代入得提馏段操作线方程：134.061.1-=x y 逐板计算：y 1=x D =0.84y 2=0.5×0.56+0.42=0.7057.0134.036.061.13=-⨯=y.22.05584.04550=⨯-=-=WDx Fx x Df w ()56.084.01.31.484.01111=⨯-=--=y y x αα36.07.01.31.470.02=⨯-=x22.024.057.01.31.457.03≥=⨯-=x所以不能完成任务。

精馏典型计算例题1. 某连续精馏操作中，已知精馏段操作线方程为：y =0.723x +0.263,提馏段操作线方程为：y =1.25x -0.0187,若原料液于露点温度下进入精馏塔中，求原料液、馏出液和釜残液的组成及回流比。

解：由精馏段操作线方程 1111n n D Ry x x R R +=+++0.7231RR =+，得 R = 2.61；10.2631D x R =+，得 x D = 0.95 将提馏段操作线方程与对角线方程 y = x 联立1.250.0187y x y x =-⎧⎨=⎩解得 x = 0.07，即 x w = 0.07将两操作线方程联立0.7230.2631.250.0187y x y x =+⎧⎨=-⎩解得 x = 0.535，y = 0.65因是露点进料，q = 0，q 线水平，两操作线交点的纵坐标即是进料浓度， ∴ x F = 0.652. 有苯和甲苯混合物，含苯0.4，流量1000 kmol/h ，在一常压精馏塔内进行分离，要求塔顶馏出液中含苯0.9（以上均为摩尔分率），苯的回收率不低于90%，泡点进料，泡点回流，取回流比为最小回流比的1.5倍，已知相对挥发度α=2.5。

试求。

（1）塔顶产品量D ；塔底残液量W 及组成x W ； （2）回流比R 及精馏段操作线方程；（3）由第二块理论板（从上往下数）上升蒸汽的组成。

解：（1）kmol/h 600kmol/h 400%904.010009.0===⨯W D D10000.44000.910000.44000.96000.0667600W W x x ⨯-⨯⨯=⨯+==（2）111F x qq y x q q ==---q 线方程：0.4F x =平衡线方程：()x xy x x y 5.115.2115.2+=-+==ααα 联立求得：625.04.0==e e y x8333.15.1222.14.0625.0625.09.0min min ===--=--=R R x y y x R dd D精馏段操作线：317.0647.011+=+++=x R x x R R y D（3）9.01==D x y 由平衡线方程可得：7826.05.115.29.0111=+=x x x由精馏段操作线：8234.0317.0647.012=+=x y3. 一连续精馏塔分离二元理想混合溶液，已知精馏段某塔板的气、液相组成分别为0.83和0.70，相邻上层塔板的液相组成为0.77，而相邻下层塔板的汽相组成为0.78（以上均为轻组分A 的摩尔分数，下同）。