人教版九年级数学上《圆周角》拔高练习

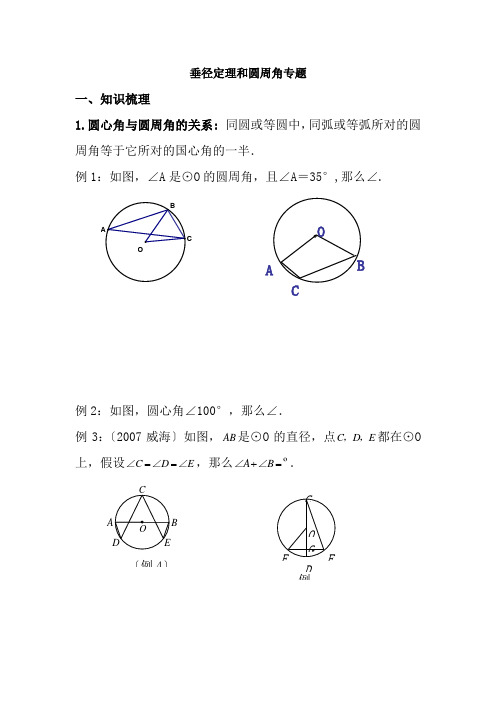
垂径定理和圆周角专题一、知识梳理1.圆心角与圆周角的关系: 同圆或等圆中，同弧或等弧所对的圆周角等于它所对的国心角的一半．例1：如图，∠A 是⊙O 的圆周角，且∠A ＝35°,那么∠.例2：如图，圆心角∠100°，那么∠．例3：〔2007威海〕如图，AB 是⊙O 的直径，点C D E ，，都在⊙O 上，假设C D E ==∠∠∠，那么A B +=∠∠º．OABC〔例4〕BE F CDG O例例4：〔2007常德〕如图2，⊙O 的直径CD 过弦EF 的中点G ，40EOD ∠=，那么DCF ∠=．2.圆周角定理：直径所对的圆周角是直角，反过来，90°的圆周角所对的弦是直径。

例5：：如图，•是⊙O•的直径，∠•30•°，那么∠．例6：〔2007南京〕⊙O 中，30C ∠=，2cm AB =，那么⊙O 的半径为cm ．例7：〔2006青岛〕某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，以下图是水平放置的破裂管道有水局部的截面. (1)请你补全这个输水管道的圆形截面；_. ..C(2)假设这个输水管道有水局部的水面宽＝16，水面最深地方的高度为4，求这个圆形截面的半径.二、稳固练习1.〔2007浙江温州〕如图，ACB ∠是⊙O 的圆周角，50ACB ∠=︒，那么圆心角AOB ∠是〔 〕A ．40︒ B. 50︒C. 80︒D. 100︒2.(2007四川宜宾)：如图，四边形是⊙O 的内接正方形，点P 是劣弧上不同于点C 的任意一点，那么∠的度数是〔 〕A ．45°B ．60°C ．75°D ．90°3.〔2006·陕西省〕△中，∠A ＝30°，∠B ＝60°，＝6，那么△外接圆的半径为〔 〕 A ．32B ．33C ．3D ．34.圆的弦长与它的半径相等，那么这条弦所对的圆周角的度数是〔 〕OD CB AA ．30°B ．150°C ．30°或150°D ．60° 5.(2007上海)小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图5所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是〔 〕A ．第①块B ．第②块C ．第③块D ．第④块6.〔2021山东德州〕如下图，是⊙O 的直径，＝，与交于点C ，那么图中与∠相等的角有〔 〕A ．2个B ．3个C ．4个D ．5个7.〔2021浙江台州〕以下命题中，正确的选项是〔 〕 ①顶点在圆周上的角是圆周角；②圆周角的度数等于圆心角度数的一半；③90的圆周角所对的弦是直径；④不在同一条直线上的三个点确定一个圆；⑤同弧所对的圆周角相等A ．①②③B ．③④⑤C ．①②⑤D ．②④⑤8.〔2021南京〕如图，⊙O 是等边三角形ABC 的外接圆，⊙O 的半径为2，那么等边三角形ABC 的边长为〔 〕BEDACO〔第8A BCOA ．3B ．5C ．23D ．259.〔2006·盐城市〕四边形内接于⊙O ，且∠A ：∠C ＝1∶2，那么∠＝ .10.〔2007山东枣庄〕如图，△内接于⊙O ，∠120°，，为 ⊙O 的直径，6，那么＝。

答案先由AB是的直径得出,再根据勾股定理求出AB的长,连接AD,则,再由CD平分可以知道,故,所以,是等腰直角三角形,由勾股定理即可求出BD的长.5．⊙O 的半径10cm ，根据下列点P 到圆心O 的距离，判断点P 和圆O 的位置关系．（1）PO ＝8cm （2）PO ＝10cm （3）PO ＝12cm解：（1）∵8cm＜10cm，∴点P在圆内；（2）∵10cm=10cm，∴点P在圆上；（3）∵12cm＞10cm，∴点P在圆外.6．在矩形ABCD 中，AB ＝3，AD ＝4，以A 为圆心，使B 、C 、D 三点中至少有一点在圆内，至少有一点在圆外，求此圆的半径R 的范围．答案：3＜r＜5，连接AC，∵AB=3cm，AD=4cm，∴AC=5cm，以点A为圆心作⊙A，使B，C，D三点中至少有一个点在圆内，且至少有一点在圆外，∴⊙A的半径r的取值范围是：3＜r＜5．7．如图，⊙O 是△ABC 的外接圆，D 是弧AB 上一点，连结BD ，并延长至E ，连结AD 若AB ＝AC ，∠ADE ＝65°，试求∠BOC 的度数．答案，1000由题意 ABCD四点共圆，圆内接四边形对角互补角ACB+角ADB=180度角ADE+角ADB=180度角ADE=角ACB=65度角BAC=180度-角ABC-角ACB=50度8．如图，通过防治“非典”，人们增强了卫生意识，大街随地乱扔生活垃圾的人少了，人们自觉地将生活垃圾倒入垃圾桶中，如图所示，A 、B 、C•为市内的三个住宅小区，环保公司要建一垃圾回收站，为方便起见，要使得回收站建在三个小区都相等的某处，请问如果你是工程师，你将如何选址．答案为：选在∆ABC的外心处.若想把垃圾回收站建在三个小区都相等的某处只需连接AC、BC及AC，分别作出两边的垂直平分线，两边垂直平分线的交点即为所求点．即三角形的外心。

9、在数轴上，点A 所表示的实数为3，点B 所表示的实数为a ，⊙A 的半径为2．下列说法中不正确的是（）A ．当a ＜5时，点B 在⊙A 内B ．当1＜a ＜5时，点B 在⊙A 内C ．当a ＜1时，点B 在⊙A 外D ．当a ＞5时，点B 在⊙A 外答案A由于圆心A在数轴上的坐标为3,圆的半径为2,∴当d=r时,⊙A与数轴交于两点：1、5,故当a=1、5时点B在⊙O上；当d＜r即当1＜a＜5时,点B在⊙O内；当d＞r即当a＜1或a＞5时,点B在⊙O外．由以上结论可知选项B、C、D正确,选项A错误．故选A．10、如图，点A 、D 、M 在半圆O 上，四边形ABOC 、DEOF 、HMNO 均为矩形，设BC ＝a ，EF ＝b ，NH ＝c ，则下列各式正确的是（）A 、a ＞b ＞c ；B 、a ＝b ＝c ；C 、c ＞a ＞b ；D 、b ＞c ＞a ．答案连接OM、OD、OA、根据矩形的对角线相等，得BC=OA，EF=OD，NH=OM．再根据同圆的半径相等，得a=b=c．故选B．11、如果点A 到⊙O 的最短举例是3cm ，最长距离是6cm ，则⊙O 的半径是 cm ．答案当这个点在圆外面的的时候直径为6cm-3cm半径为1.5cm当这个点在园内时直径为3cm+6cm半径为4.5cm12、已知Rt △ABC 中，∠C ＝90°，AC ＝3cm ，BC ＝4cm ，则它的外心与顶点C 的距离为 cm ．答案：Rt△ABC中，∠C=90°，AC=3cm，BC=4cm；由勾股定理，得：AB==5cm，斜边上的中线是AB=2.5cm．因而外心到直角顶点的距离即斜边的长为2.5cm．故选B．13、已知⊙O 的半径为1，点P 与圆心O 的距离为为d ，且方程x2-2 x+ d=0没有实数根，则点P 与⊙O 的位置关系是．（填园内，圆上或圆外）答案：利用由已知条件方程有实数根,可得出一元二次方程根的判别式,,求出d的取值范围,结合圆的半径是1,得出d与r大小关系,当,点P在上;当,点P在的内部,根据点与圆的位置关系得出p与圆的位置关系.14、棱形ABCD 的对角线AC 与BD 相交于点O ，E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点．求证：E 、F 、G 、H 四点在以O 为圆心的同一个圆上．答案连结OH、OE、OF、本题考查梯形的中位线性质，梯形中位线平行于上下底且等于上下底和的一半，同时考查点和圆的位置关系：点在圆外，点和圆心的连线大于半径；点在圆上，它们之间的连线等于半径；点在圆内，它们之间的连线小于半径.(1)若点M在⊙则,,,, ,则可以列方程为,(,;所以能将其完全覆盖的圆的最小半径2，.。

提技能·题组训练圆周角定理及其推论1.( 滨州中考 ) 如图 , 在☉ O中, 圆心角∠ BOC=78°, 则圆周角∠ BAC的大小为 ()A.156°B.78 °C.39°【解析】选C.∠BOC是所对的圆心角D.12°, ∠ BAC是所对的圆周角,∴∠ BAC=∠ BOC=39°.2.( 海南中考 ) 如图 , 在☉ O中 , 弦 BC=1,点 A 是圆上一点 , 且∠ BAC=30°, 则☉ O的半径是 ()A.1B.2C.D.【解析】选A. 方法一 : 连接OB,OC.∵∠ BAC=30°, ∴∠ BOC=2∠ BAC=60° ,∵OB=OC,∴△ OBC是等边三角形 ,∴OB=OC=BC =1.方法二 : 作直径 CD,连接 BD.则∠ CBD=90°, ∵∠ BDC=∠ BAC=30°, ∴CD=2BC=2,∴OC=CD=1.3.( 长春中考 ) 如图 , △ABC内接于☉ O,∠ABC=71° , ∠ CAB=53° , 点 D 在上,则∠ ADB的大小为()A.45°B.53 °C.56 °D.71 °【解析】选 C.在△ ABC中, ∵∠ ABC=71° , ∠ CAB=53°,∴∠ C=180°-71 °-53 °=56° , ∴∠ ADB=∠C=56°.D,则∠ BOD=. 4.( 佛山中考 ) 图中圆心角∠ AOB=30° , 弦 CA∥ OB,延长CO与圆交于点【解析】因为圆心角∠ AOB=30°, 弦 CA∥OB,所以∠ AOB=∠CAO=30°,又 OA=OC,所以∠ CAO=∠ ACO=30° , 所以∠ AOD=∠ CAO+∠ ACO=60° =∠ AOB+∠ BOD,所以∠BOD=30°.答案 : 30°5.( 贵阳中考 ) 如图 ,AD,AC 分别为☉ O的直径和弦 , ∠CAD=30°,B 是 AC上一点 ,BO⊥AD,垂足为【解析】在Rt△AOB中 , ∠A=30° ,BO=5cm,∴AO=5cm,∵AD是直径 ,∴AD=10cm,∠C=90°, 在 Rt△ ADC中,∠A=30°,AD=10cm,∴CD=5cm.答案: 56. 如图 , 正方形ABCD的顶点都在☉O上 ,P是弧DC上的一点 , 则∠ BPC=.【解析】连接 BD,则 BD是直径 ,∴△ BCD是等腰直角三角形 ,∴∠ BDC=45°, ∴∠ BPC=∠ BDC=45°.答案 : 45°【知识归纳】圆周角与直径1.当题目中出现了直径时 , 常作辅助线 , 利用直径所对的圆周角是直角解决问题 .2.当出现 90°的圆周角时 , 常连接该圆周角所对的弦 , 则该弦为直径 .7. 如图 , 在☉ O中, 直径 AB与弦 CD相交于点 P, ∠CAB=40°, ∠APD=65° .(1)求∠B 的大小 .(2)已知 AD=6,求圆心 O到 BD的距离 .【解析】 (1) ∵∠ APD=∠C+∠CAB,∴∠ C=65°-40 °=25° .∴∠ B=∠C=25° .(2) 过点 O作 OE⊥ BD于 E, 则 DE=BE.又∵ AO=BO,∴OE= AD= ×6=3.∴圆心 O到 BD的距离为 3.圆内接四边形1. 如图 , 四边形 ABCD内接于☉ O,如果∠ BOD=130°, 则∠ BCD的度数是 ()A.115°B.130°C.65°D.50°【解析】选 A. ∵∠ BOD=130°, ∴∠ A= ∠BOD=65°, ∵∠2.( 莱芜中考 ) 如图 , 在☉ O中 , 已知∠ OAB=22.5°, 则∠C 的度数为 ()A. 135 °B.122.5 °C.115.5°D.112.5 °【解析】选 D.如图, 作所对的圆周角 .∵OA=OB,∴∠ OBA=∠ OAB=22.5° . ∴∠ AOB=180 ° - ∠ OAB-∠ OBA =180° -22.5 ° -22.5 °=135° .∴∠ D= ∠ AOB=×135°=67.5 °.∵四边形 ACBD是圆内接四边形 ,∴∠ C+∠D=180° .∴∠ C=112.5 °.【方法技巧】1. 在圆中 , 求角的度数时 , 常利用圆周角定理和圆内接四边形的对角互补来完成.2.有时需要自己作出与已知角互补的圆周角 , 才能运用圆内接四边形的性质 .3. 四边形 ABCD内接于☉ O,AD∥BC,∠ B=75° , 则∠ C=.【解析】∵AD∥ BC,∴∠ A+∠B=180° ,∴∠ A=180°-75 °=105°,答案 : 75°【变式训练】已知 , 四边形 ABCD内接于☉ O, 且∠ A∶∠ C=1∶2, 则∠ BOD= ° .【解析】∵四边形 ABCD内接于☉ O,∴∠ A+∠C=180°.又∠ A∶∠ C=1∶ 2, 得∠ A=60° .∴∠ BOD=2∠A=120°.答案 : 1204.如图 , △ ABC内接于☉ O,AD为△ ABC的外角平分线 , 交☉ O 于点 D, 连接 BD,CD,判断△DBC的形状 , 并说明理由 .【解析】△DBC为等腰三角形 . 理由如下 :∵四边形 ABCD为☉ O的内接四边形 ,∴∠ DCB+∠DAB=180°,又∠ EAD+∠DAB=180°,∴∠ EAD=∠DCB.又∠ DAC=∠DBC,∠EAD=∠DAC,∴∠ DBC=∠DCB,∴DB=DC,即△ DBC为等腰三角形 .【错在哪？】作业错例课堂实拍A,B 为☉ O上的两点 , ∠ AOB=100° , 若点 C 也在☉ O上, 且点 C不与 A,B 重合 , 求∠ACB的度数 .(1)错因 :____________________________________.(2)纠错 :____________________________________________________________ _________________________________.答案： (1) 点 C也可能在劣弧AB上，需要分情况讨论(2)当 C在优弧AB上时，∠ ACB=1∠AOB=50°，当 C 在劣弧AB上时，∠ ACB=2 180°-50 °=130°。

九年级数学上册《圆周角》练习题及答案解析学校:___________姓名：___________班级：______________一、单选题1．如图，在⊙O中，AB＝AC，⊙AOB＝40°，则⊙ADC的度数是（）A．40°B．30°C．20°D．15°2．下列说法正确的是（）A．劣弧一定比优弧短B．面积相等的圆是等圆C．长度相等的弧是等弧D．如果两个圆心角相等，那么它们所对的弧也相等3．如图，⊙O的两条弦AB⊙CD，已知⊙ADC＝35°，则⊙BAD的度数为（）A．55°B．70°C．110°D．130°4．如图，在⊙O中，点A是BC的中点，⊙ADC＝24°，则⊙AOB的度数是（）A．24°B．26°C．48°D．66°5．如图，正五边形ABCDE 和正三角形AMN 都是O 的内接多边形，则BOM ∠的度数是（ ）A ．36︒B ．45︒C ．48︒D ．60︒6．如图，AB 是⊙O 的直径，P A 与⊙O 相切于点A ，⊙ABC ＝25°，OC 的延长线交P A 于点P ，则⊙P 的度数是( )A ．25°B ．35°C ．40°D ．50°7．如图，AB 是O 的直径，C ，D 是O 上的两点，若54ABD ∠=︒，则BCD ∠的度数是（ ）A ．36°B ．40°C ．46°D ．65°8．下列说法正确的是（ ）A ．顶点在圆上的角是圆周角B ．两边都和圆相交的角是圆周角C ．圆心角是圆周角的2倍D ．圆周角度数等于它所对圆心角度数的一半9．下列命题是真命题的是（ ）A ．相等的两个角是对顶角B ．相等的圆周角所对的弧相等C ．若a b <，则22ac bc <D ．在一个不透明的箱子里放有1个白球和2个红球，它们除颜色外其余都相同，从箱子里任意摸出1个球，摸到白球的概率是1310．如图，⊙O 是ABC 的外接圆，AC 是⊙O 的直径，点P 在⊙O 上，若40ACB ∠=︒，则BPC ∠的度数是（ ）A ．40︒B ．45︒C ．50︒D ．55︒11．如图，O 的半径OD ⊥弦AB 于点C ，连接AO 并延长交O 于点E ，连接EB ．若4AB =，1CD =，则EB 的长为（ ）A ．5B ．4C ．3D ．2.512．如图，点A ，B ，C 是O 上的点，连接,,AB AC BC ，且15ACB ∠=︒，过点O 作OD AB ∥交O 于点D ．连接,AD BD ，已知O 半径为2，则图中阴影面积为( )A ．2πB ．3πC ．4πD ．23π 13．如图，ABC ∆中，AB 是O 的直径，AC 交O 于点E ，BC 交O 于点D ，点D 是BC 中点，O 的切线DF 交AC 于点F ，则下列结论中⊙A ABE ∠=∠；⊙BD DE =；⊙AB AC =；⊙F 是EC 中点，正确的个数是（ ）A ．1B ．2C ．3D ．4二、填空题14．如图，点A 、B 、C 、D 、E 在O 上，且弧AB 为50︒，则E C ∠+∠=________．15．如图，A 、B 、C 是⊙O 上的三点，AB ＝2，∠ACB ＝30°，那么⊙O 的半径等于_____．16．如图，AB 是⊙O 的直径，CD 为弦，AB ⊙CD ，若CD =CB ＝2，则阴影部分的面积是______．17．如图，在半径为1的O 上顺次取点A ，B ，C ，D ，E ，连接AB ，AE ，OB ，OC ，OD ，OE ．若65BAE ∠=︒，70COD ∠=︒，则BC 与DE 的长度之和为__________．（结果保留π）．18．如图，ABC内接于⊙O，AB＝BC，⊙BAC＝30°，AD为⊙O的直径，AD＝2，则BD＝________．19．如图，OE、OF分别为⊙O的弦AB、CD的弦心距，如果OE=OF，那么________（只需写一个正确的结论）．20．如图，AB是⊙O的直径，C、D是⊙O上的两点，⊙AOC＝120°，则⊙CDB＝_____°．三、解答题21．如图．AB是⊙O的直径，点C，D在⊙O上，C是BD的中点，连接BD交AC于点E，延长AC至F，使CE＝CF．(1)求证：BF 是⊙O 的切线．(2)若BF ＝3，1sin 3A =，求BD 的长． 22．如图，在⊙AOB 和⊙COD 中，OA ＝OB ，OC ＝OD ，若⊙AOB ＝⊙COD ＝60°．(1)求证：AC ＝BD ．(2)求⊙APB 的度数．23．如图，已知ABCD 是某圆的内接四边形，AB BD =，BM AC ⊥于M ，求证：AM DC CM =+．24．已知AB 是⊙O 的直径，点C 在AB 的延长线上，AB ＝4，BC ＝2，P 是⊙O 上半部分的一个动点，连接OP ，CP ．(1)如图⊙，⊙OPC 的最大面积是________；(2)如图⊙，延长PO 交⊙O 于点D ，连接DB ，当CP ＝DB 时，求证：CP 是⊙O 的切线．25．如图，,,//,//AD DB AE EC FG AB AG BC ==．利用平移或旋转的方法研究图中的线段,,DE BF FC 之间的位置关系和数量关系．参考答案及解析：1．C【详解】先由圆心角、弧、弦的关系求出⊙AOC=⊙AOB=50°，再由圆周角定理即可得出结论．解：⊙在⊙O 中，= ，⊙⊙AOC=⊙AOB ，⊙⊙AOB=40°，⊙⊙AOC=40°， ⊙⊙ADC=12⊙AOC=20°， 故选C ．2．B【分析】根据圆的相关概念、圆周角定理及其推论进行逐一分析判断即可．【详解】解：A.在同圆或等圆中，劣弧一定比优弧短，故本选项说法错误，不符合题意；B.面积相等的圆是等圆，故本选项说法正确，符合题意；C.能完全重合的弧才是等弧，故本选项说法错误，不符合题意；D.必须在同圆或等圆中，相等的圆心角所对的弧相等，故本选项说法错误，不符合题意．故选：B ．【点睛】本题主要考查了圆周角定理及其推论、等弧、等圆、以及优弧和劣弧等知识，解题关键是理解各定义的前提条件是在同圆或等圆中．3．A【分析】根据垂直定义和三角形的两锐角互余进行解答即可．【详解】解：⊙AB ⊙CD ，⊙⊙ADC +⊙BAD =90°，⊙⊙ADC =35°，⊙⊙BAD =90°﹣35°=55°，故选：A ．【点睛】本题考查垂直定义、直角三角形的两锐角互余，熟练掌握直角三角形的两锐角互余是解答的关键．4．C【分析】直接利用圆周角求解．【详解】解：⊙点A 是BC 的中点，⊙AC AB =，⊙⊙AOB =2⊙ADC =2×24°=48°．故选：C ．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．5．C【分析】如图，连接AO ．利用正多边形的性质求出AOM ∠，AOB ∠，可得结论．【详解】解：如图，连接AO ．AMN △是等边三角形，60ANM ∠∴=︒，2120AOM ANM ∠∠∴==︒， ABCDE 是正五边形，360725AOB ∠︒∴==︒，1207248BOM ∠∴=︒-︒=︒．故选：C ．【点睛】本题考查正多边形与圆，等边三角形的性质，圆周角定理等知识，解题的关键是熟练掌握正多边形的性质，属于中考常考题型．6．C【分析】根据圆周角定理可得50AOC ∠=︒，根据切线的性质可得90PAO ∠=︒，根据直角三角形两个锐角互余即可求解．【详解】AC AC =，⊙ABC ＝25°，250AOC ABC ∴∠=∠=︒，AB 是⊙O 的直径，∴90PAO ∠=︒，9040P AOC ∴∠=︒-∠=︒．故选C ．【点睛】本题考查了圆周角定理，切线的性质，掌握圆周角定理与切线的性质是解题的关键．7．A【分析】连接AD ，如图，根据圆周角定理得到⊙ADB =90°，⊙C =⊙A ，然后利用余角的性质计算出⊙A ，从而得到⊙C 的度数．【详解】解：如图，连接AD ，⊙AB 为⊙O 的直径，⊙⊙ADB =90°，⊙⊙A =90°−⊙ABD =90°−54°=36°，⊙⊙C =⊙A =36°．故选：A ．【点睛】本题主要考查了同弦所对的圆周角相等，直径所对的圆周角是直角，解题的关键在于能够熟练掌握相关知识进行求解．8．D【详解】解：顶点在圆上，且与圆有相交的角是圆周角，则A 和B 是错误的；同弧所对的圆周角的度数等于圆心角度数的一半，故选D ．9．D【分析】分别根据对顶角的定义，圆周角定理，不等式的基本性质及概率公式进行判断即可得到答案．【详解】有公共顶点且两条边互为反向延长线的两个角是对顶角，故A 选项错误，不符合题意； 在同圆或等圆中，相等的圆周角所对的弧相等，故B 选项错误，不符合题意；若a b <，则22ac bc ≤，故C 选项错误，不符合题意；在一个不透明的箱子里放有1个白球和2个红球，它们除颜色外其余都相同，从箱子里任意摸出1个球，摸到白球的概率是13，故D 选项正确，符合题意； 故选：D ．【点睛】本题考查了命题的真假，涉及对顶角的定义，圆周角定理，不等式的基本性质及概率公式，熟练掌握知识点是解题的关键．10．C【分析】根据圆周角定理得到90ABC ∠=︒，BPC A ∠=∠，然后利用互余计算出⊙A 的度数，从而得到BPC ∠的度数．【详解】解：⊙AB 是⊙O 的直径，⊙90ABC ∠=︒，⊙90904050A ACB ∠=︒-∠=︒-︒=︒，⊙50BPC A ∠=∠=︒，故选：C ．【点睛】本题考查了圆周角定理，解题的关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半；半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．11．C【分析】设圆O 的半径为r ，则OC =OD -CD =r -1，AE =2OA =2r ，先利用垂径定理得到AC =2，即可利用勾股定理求出半径，从而求出AE 的长，再利用勾股定理即可求出BE ．【详解】解：设圆O 的半径为r ，则OC =OD -CD =r -1，AE =2OA =2r ， 由垂径定理得122AC BC AB ===，在Rt ⊙OAC 中，222OA OC AC =+，⊙()22221r r =+-， ⊙52r =， ⊙AE =5，⊙AE 是圆O 的直径，⊙⊙B =90°，⊙在Rt ⊙ABE 中，3BE ，故选：C ．【点睛】本题主要考查了垂径定理，勾股定理，直径所对的圆周角是直角等等，熟知垂径定理是解题的关键．12．B【分析】根据圆周角定理可得⊙AOB =30°，再由OD AB ∥，可得AOB ADB SS =，从而得到阴影面积等于扇形AOB 的面积，即可求解．【详解】解：⊙15ACB ∠=︒，⊙⊙AOB =30°， ⊙23023603AOB S ππ⨯==扇形， ⊙OD AB ∥，⊙AOB ADB S S =，⊙阴影面积等于扇形AOB 的面积，⊙阴影面积等于3π． 故选：B【点睛】本题考查了圆周角定理、扇形面积公式和同底等高的两个三角形的面积相等等知识，属于常考题型，熟练掌握上述基本知识是解题的关键．13．C【分析】连接连接OD ，AD 、DE ，根据直径所对的圆周角是直角以及等腰三角形的性质可判断结论⊙；根据同圆或等圆中，同弧所对的弦相等可得结论⊙；根据切线的性质以及三角形中位线定理可得结论⊙；因为只有ABE △是等腰直角三角形时，才能满足结论⊙．【详解】解：连接OD，AD、DE．AB是O的直径，∴∠=︒（直径所对的圆周角是直角），ADB90∴⊥，AD BC点D是BC中点，=，故⊙正确；∴∠=∠，AB ACBAD CAD∴BD DE=，∴=，故⊙正确；BD DEDF是O的切线，∴⊥，OD DF=，BD DCAO BO=，∴，OD AC//∴⊥，DF AF∴，DF BE//⊙点D是BC的中点，∴点F是EC的中点，故⊙正确；只有当ABE△是等腰直角三角形时，45∠=∠=︒，BAC ABE故⊙错误，正确的有⊙⊙⊙共3个，故选：C．【点睛】本题考查了圆周角定理，圆切线的性质，等腰三角形的性质，三角形中位线定理的应用，题目难度适中，熟练掌握相关图形的性质定理是解本题的关键．14．155︒【分析】先根据弧的度数与它所对应的圆心角的度数的关系，求得弧AB对应的圆心角的度数，再根据圆周角与圆心角的关系，则可求得E C ∠+∠.【详解】弧的度数等于它所对应的圆心角的度数，由于弧AB 为50︒，所以3=50∠︒ .顶点在圆上且两边都和圆相交的角叫做圆周角，而一条弧所对的圆周角等于它所对的圆心角的一半，所以：112E ∠=∠ ,122C ∠=∠ ， ()()()11112360336050155222E C ∠+∠=∠+∠=︒-∠=︒-︒=︒.【点睛】本题考查弧、圆周角、圆心角的概念，及它们之间的关系.15．2【分析】根据题意和圆周角定理得∠O ＝60°，则△OAB 是等边三角形，根据AB ＝2即可得．【详解】解：∵OA ＝OB ，∠ACB ＝30°，OA =OB ，∴∠O ＝60°，∴△OAB 是等边三角形，∵AB ＝2，∴OA ＝AB ＝2，故答案为：2．【点睛】本题考查了等边三角形的判定与性质，圆周角定理，解题的关键是掌握这些知识点．16．23π【分析】连接OC ，设CD 与AB 的交点为E ，利用垂径定理、勾股定理判定△OBC 是等边三角形，运用扇形的面积减去△OBC 的面积即可．【详解】连接OC ，设CD 与AB 的交点为E ，⊙AB 是⊙O 的直径，AB ⊙CD ，CD =CB ＝2，⊙CE 1BE ==，⊙⊙ECB =30°，⊙CBE =60°，⊙CO =BO ，⊙△OBC 是等边三角形，⊙⊙BOC =60°，OC =OB =2，⊙2602123602S =π⨯⨯-⨯阴影=23π故答案为：23π 【点睛】本题考查了垂径定理，勾股定理，扇形的面积公式，等边三角形的判定和性质，熟练掌握垂径定理，扇形的面积公式是解题的关键．17．13π##3π 【分析】由圆周角定理得2130BOE BAE ∠=∠=︒，根据弧长公式分别计算出BE 与DC 的长度，相减即可得到答案．【详解】解：⊙65BAE ∠=︒，⊙2130BOE BAE ∠=∠=︒又O 的半径为1，BE 的长度=130113=18018ππ⨯，又70COD ∠=︒，⊙DC 的长度=7017=18018ππ⨯， ⊙BC 与DE 的长度之和=13761-==1818183ππππ，故答案为：13π． 【点睛】本题主要考查了计算弧长，圆周角定理，熟练掌握弧长计算公式是解答本题的关键．18【分析】根据AB ＝BC ，可得⊙C =⊙BAC =30°，再由圆周角定理，可得⊙D =30°，然后利用锐角三角函数，即可求解．【详解】解：⊙AB ＝BC ，⊙⊙C =⊙BAC =30°，⊙⊙C =⊙D ，⊙⊙D =30°，⊙AD 为⊙O 的直径，⊙⊙ABD =90°，在Rt ABD △ 中，AD ＝2，⊙D =30°，⊙cos302BD AD =⋅︒==．【点睛】本题主要考查了圆周角定理，锐角三角函数等知识，熟练掌握相关知识点是解题的关键．19．AB =CD （答案不唯一）【分析】根据圆心角、弧、弦、弦心距之间的关系定理的推论可以直接得到所求的结论．【详解】解：⊙OE =OF ，OE 、OF 分别为⊙O 的弦AB 、CD 的弦心距，⊙AB =CD ．故答案为：AB =CD （答案不唯一）【点睛】本题主要考查了圆心角、弧、弦的关系．熟练掌握在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等是解题的关键． 20．30．【分析】先利用邻补角计算出BOC ∠，然后根据圆心周角定理得到CDB ∠的度数．【详解】⊙⊙BOC ＝180°﹣⊙AOC ＝180°﹣120°＝60°，⊙⊙CDB ＝12⊙BOC ＝30°． 故答案为30．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．21．(1)见详解(2)BD=16 3【分析】（1）根据直径所对圆周角得出⊙ACB=90°，根据C是BD的中点，得出DC BC=，利用等弧所对圆周角得出⊙CAB=⊙CBD即可（2）连结OC，交BD于G，根据垂径定理得出OC⊙BD，DG=BG=12BD，由三角函数求出AF=9，利用勾股定理求出ABAB BFBCAF⋅===（1）证明：⊙AB是⊙O的直径，⊙⊙ACB=90°，⊙C是BD的中点，⊙DC BC=，⊙⊙CAB=⊙CBD，⊙CE=CF，BC⊙EF，⊙BE=BF，⊙⊙FBC=⊙CBE，⊙⊙FBC=⊙CBE=⊙CAB，⊙⊙CAB+⊙CBA=90°，⊙⊙FBC+⊙CBA=90°，⊙FB⊙AB，AB为直径，⊙BF为⊙O的切线；，（2）解：连结OC，交BD于G，⊙DC BC=，OC为半径，⊙OC⊙BD，DG=BG=12 BD，⊙BF＝3，1 sin3A=，⊙31sin 3BF A AF AF ===， ⊙AF =9，在Rt △ABF 中AB⊙S △ABF =12BC ·AF =12AB ·BF ，⊙AB BF BC AF ⋅=== ⊙sin A =sin⊙CBG =13CG BC ==，⊙3CG =，在Rt ⊙BCG 中83BG ==， ⊙BD =2BG =163．【点睛】本题考查圆的切线判定，等弧所对圆周角性质，线段线段垂直平分线性质，等腰三角形等腰三角形三线合一性质，勾股定理锐角三角函数，面积等积式，本题难度不大，是中考常考试题，掌握好相关知识是解题关键．22．(1)见解析(2)60°【分析】（1）通过证明⊙AOC ⊙⊙BOD ，即可求证；（2）由（1）可得⊙OAC ＝⊙OBD ，从而得到⊙P AB +⊙PBA ＝⊙OAB +⊙OBA ，利用三角形内角和的性质即可求解．（1）证明：⊙⊙AOB ＝⊙COD ，⊙AOB BOC COD BOC ∠+∠∠+∠＝，即⊙AOC ＝⊙BOD ，在⊙AOC 和⊙BOD 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，⊙⊙AOC ⊙⊙BOD （SAS ），⊙AC ＝BD ．（2）解：⊙⊙AOC ⊙⊙BOD ，⊙⊙OAC ＝⊙OBD ，⊙⊙PBA ＝⊙ABO +⊙OBD ，⊙OAB =⊙P AB +⊙OAC ，⊙⊙P AB +⊙PBA ＝⊙P AB +⊙ABO +⊙OBD =⊙P AB +⊙OAC +⊙ABO =⊙OAB +⊙OBA ，⊙OA ＝OB ，⊙AOB ＝60°，⊙⊙AOB 是等边三角形，⊙⊙OAB +⊙OBA ＝120°⊙⊙P AB +⊙PBA ＝120°，⊙()180********APB PAB PBA ∠︒-∠+∠︒-︒︒＝＝＝． 【点睛】此题考查了全等三角形的判定与性质，三角形内角和定理，等边三角形的判定和性质，解题的关键是熟练掌握全等三角形的判定和性质．23．见解析【分析】在MA 上截取ME MC =，连接BE ，利用圆周角定理易得()ABE DBC AAS ≅，利用三角形的性质得到AE CD =即可求解．【详解】证明：在MA 上截取ME MC =，连接BE ，BM AC ⊥，BE BC ∴=，BEC BCE ∴∠=∠．AB BD =，∴AB BD =，ADB BAD ∴∠=∠，而ADB BCE ∠=∠，BCE BAD ∴∠=∠．又180BCD BAD ∠+∠=︒，180BEA BCE ∠+∠=︒，BEA BCD ∴∠=∠．BAE BDC ∠=∠，()ABE DBC AAS ∴∆≅∆，AE CD ∴=，AM AE EM DC CM ∴=+=+．【点睛】本题主要考查了圆周角定理，全等三角形的判定和性质，作出辅助线构建三角形全等是解答关键．24．(1)4(2)见解析【分析】（1）因为OC 长度确定，所以当点P 到OC 的距离最大时⊙OPC 的面积最大，当OP ⊙OC 时，当点P 到OC 的距离最大，等于圆O 的半径，求出此时的⊙OPC 的面积即可；（2）连接AP ，BP ，利用同圆中，相等的圆心角所对的弦相等，可得AP =DB ，因为CP ＝DB ，所以AP =CP ，可证⊙APB ⊙⊙CPO （SAS ），得到⊙OPC ＝90°，即可证明CP 是切线．（1）解：⊙AB ＝4，⊙OB ＝2，OC ＝OB +BC ＝4．在⊙OPC 中，设OC 边上的高为h ，⊙S △OPC 12=OC •h ＝2h ， ⊙当h 最大时，S △OPC 取得最大值．作PH ⊙OC ，如图⊙，则PO PH >，当OP ⊙OC 时，PO PH =，此时h 最大，如答图1所示：此时h ＝半径＝2，14242OPC S ⨯⨯＝＝．⊙⊙OPC 的最大面积为4， 故答案为：4．（2）证明：如答图⊙，连接AP ，BP ．⊙⊙AOP ＝⊙BOD ，⊙AP ＝BD ，⊙CP ＝DB ，⊙AP ＝CP ，⊙⊙A ＝⊙C ，在⊙APB 与⊙CPO 中， AP CPA C AB CO=⎧⎪∠=∠⎨⎪=⎩，⊙⊙APB ⊙⊙CPO （SAS ）， ⊙⊙APB ＝⊙OPC ，⊙AB 是直径，⊙⊙APB ＝90°，⊙⊙OPC＝90°，⊙DP⊙PC，⊙DP经过圆心，⊙PC是⊙O的切线．【点睛】本题考查了圆，熟练掌握圆的半径、切线、弦与圆心角的关系等知识是解题的关键．25．DE与BF平行且相等，DE与FC平行且相等，BF与FC相等且在一条直线上【分析】易知DE是△ABC的中位线，则DE∥BC∥AG；由此可知四边形ADEG和四边形DBFE都是平行四边形，故AG＝DE＝BF；由全等三角形可得AG＝FC，故DE＝BF＝FC．【详解】解：线段DE，BF，FC之间的位置关系是DE∥BF，DE∥FC，数量关系是DE＝BF＝FC，∵AG∥BC（已知）∴∠G＝∠EFC（两直线平行，内错角相等）∵∠AEG＝∠FEC（对顶角相等），又AE＝EC（已知）∴△AGE≌△CFE（AAS）；∴AG＝FC，FE＝EG（全等三角形的对应边相等），可以看做△AGE绕点E旋转180°得到△CFE，又∵AD＝DB（已知）∴DE为三角形ABC的中位线，BC，∴DE∥BC，DE=12即DE∥BF，DE∥FC，∵FG∥AB，AG∥BC（已知）∴四边形ABFG是平行四边形∴AG＝BF，BC，∴BF＝FC＝12∴DE＝BF＝FC，可以看做⊙ADE沿直线AE平移得到△EFC，故线段DE，BF，FC之间的位置关系是DE∥BF，DE∥FC，BF与FC在一条直线上，数量关系是DE＝BF＝FC．【点睛】题考查的是三角形中位线定理、平行四边形及全等三角形的判定和性质．三角形的中位线的性质定理，为证明线段相等和平行提供了依据．第21页共21页。

人教版数学九年级上册第二十四章圆24.1.4圆周角同步测试一、选择题1. 下列图形中的角是圆周角的是()A B C D2. 下列说法中正确的是()A. 顶点在圆周上的角叫圆周角B. 圆周角等于圆心角的一半C. 同弦所对的所有圆周角相等D. 弦所对的圆周角有无数个3. 如图，⊙O的直径AB垂直于弦CD，垂足是E，∠A＝22.5°，OC＝4，CD的长为()A. 22B. 4C. 42D. 8第3题第4题4. 如图，△ABC的顶点A，B，C均在⊙O中，若∠ABC＋∠AOC＝90°，则∠AOC的大小是()A. 30°B. 45°C. 60°D. 70°5. 如图，四边形ABCD是圆内接四边形，E是线段BC延长线上的一点，若∠BAD＝105°，则∠DCE 的大小是()A. 115°B. 105°C. 75°D. 85°6. ⊙O的半径为1，AB是⊙O的一条弦，且AB＝3，则弦AB所对的圆周角为()A. 30°B. 60°C. 30°或150°D. 60°或120°7. 如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ADC的大小为()A. 45°B. 50°C. 60°D. 75°第7题 第8题8. 如图，AB 是⊙O 的直径，CD 是⊙O 的弦，∠ABD ＝59°，则∠C 等于( ) A. 29° B. 31° C. 59° D. 62°9. 如图，在⊙O 中，∠AOB 的度数为m ，C 是ACB ︵上一点，D ，E 是AB ︵上不同的两点(不与A ，B 两点重合)，则∠D ＋∠E 的度数为( )A. mB. 180°－m 2C. 90°＋m 2D. m2第9题 第10题10. 如图，BA 是半圆O 的直径，点C 在⊙O 上，若∠ABC ＝50°，则∠CAB ＝ .11. 如图所示，A ，B ，C ，D 是⊙O 上顺次四点，若∠AOC ＝160°，则∠D ＝ ，∠B ＝ .第11题 第12题12. 如图，AB 是⊙O 的直径，C 是圆上一点，连接BC ，AC ，∠BAC ＝60°，弦AD 平分∠BAC ，若AD ＝6，那么AC ＝ .13. 如图所示，AB 是⊙O 的直径，AB ＝AC ，D ，E 在⊙O 上，说明：BD ＝DE .14. 如图，已知A ，B ，C ，D 是⊙O 上的四点，延长DC ，AB 相交于点E ，若BC ＝BE . 求证：△ADE 是等腰三角形.15. 如图，在⊙O 中，AB 是直径，CD 是弦，AB ⊥CD . (1)P 是CAD ︵上一点(不与C ，D 重合)，求证：∠CPD ＝∠COB ；(2)点P ′在CD ︵上(不与C ，D 重合)时，∠CP ′D 与∠COB 有什么数量关系？请证明你的结论.16. 如图，正方形ABCD 内接于⊙O ，M 为AD ︵中点，连接BM ，CM . (1)求证：BM ＝CM ；(2)当⊙O 的半径为2时，求BM ︵的长.17. 如图，已知AB 是⊙O 的弦，OB ＝2，∠B ＝30°，C 是弦AB 上任意一点(不与点A ，B 重合)，连接CO 并延长CO 交⊙O 于点D ，连接AD .(1)弦长AB ＝ (结果保留根号)； (2)当∠D ＝20°时，求∠BOD 的度数.18. 在⊙O 中，AB 为直径，点C 为圆上一点，将劣弧AC 沿弦AC 翻折交AB 于点D ，连接CD . (1)如图①，若点D 与圆心O 重合，AC ＝2，求⊙O 的半径r ； (2)如图②，若点D 与圆心O 不重合，∠BAC ＝25°，求∠DCA 的度数.答案1. B2. D3. C4. C5. B6. D7. C8. B9. B 10. 40° 11. 80° 100° 12. 213. 解：连接AD .∵AB 为⊙O 的直径，∴∠ADB ＝90°，即AD ⊥BC .又∵AB ＝AC ，∴∠BAD ＝∠EAD ，∴︵BD ＝︵DE，∴BD ＝DE .14. 证明：∵BC ＝BE ，∴∠E ＝∠BCE .∵四边形ABCD 是圆内接四边形，∴∠A ＋∠DCB ＝180°.∵∠BCE ＋∠DCB ＝180°，∴∠A ＝∠BCE .∴∠A ＝∠E .∴AD ＝DE .∴△ADE 是等腰三角形.15. (1)证明：连接OD ，∵AB 是直径，AB ⊥CD ，∴︵BC ＝︵BD ，∴∠COB ＝∠BOD ＝21∠COD .又∵∠CPD ＝21∠COD ，∴∠CPD ＝∠COB .(2)解：∠CP ′D ＋∠COB ＝180°.证明：∵四边形PCP ′D 是圆内接四边形，∴∠CPD ＋∠CP ′D ＝180°.∴∠CP ′D ＋∠COB ＝180°.16. (1)证明：∵四边形ABCD 是正方形，∴AB ＝CD ，∴︵AB ＝︵CD ，∵M 为︵AD 中点，∴︵AM ＝︵DM ，∴︵AB ＋︵AM ＝︵CD ＋︵DM ，即︵BM ＝︵CM.∴BM ＝CM .(2)解：∵⊙O 的半径为2，∴⊙O 的周长为4π，∴︵BM 的长＝83×4π＝23π. 17. 解：(1)2(2)∵∠BOD 是△BOC 的外角，∠BCO 是△ACD 的外角，∴∠BOD ＝∠B ＋∠BCO ，∠BCO ＝∠A ＋∠D .∴∠BOD ＝∠B ＋∠A ＋∠D .又∵∠BOD ＝2∠A ，∠B ＝30°，∠D ＝20°，∴2∠A ＝∠B ＋∠A ＋∠D ＝∠A ＋50°，∴∠A ＝50°，∴∠BOD ＝2∠A ＝100°.18. 解：(1)如图①，过点O 作OE ⊥AC 于点E ，则AE ＝21AC ＝21×2＝1.∵翻折后点D 与圆心O 重合，∴OE ＝21r .在Rt △AOE 中，AO 2＝AE 2＋OE 2，即r 2＝12＋(21r )2，解得r ＝33.(2)连接BC .∵AB 是直径，∴∠ACB ＝90°，∵∠BAC ＝25°，∴∠B ＝90°－∠BAC ＝65°.根据翻折的性质，︵AC 所对的圆周角为∠B ，︵ABC所对的圆周角为∠ADC ，∴∠ADC ＋∠B ＝180°，∴∠B ＝∠CDB ＝65°，∴∠DCA ＝∠CDB －∠A ＝65°－25°＝40°.。

24.1.4 圆周角第1课时 圆周角定理及其推论01 基础题知识点1 圆周角的概念1．下列图形中的角是圆周角的是(B)知识点2 圆周角定理2．(茂名中考)如图，A ，B ，C 是⊙O 上的三点，∠B ＝75°，则∠AOC 的度数是(A)A ．150°B ．140°C ．130°D ．120°3．(滨州中考)如图，在⊙O 中，圆心角∠BOC ＝78°，则圆周角∠BAC 的大小为(C)A ．156°B ．78°C ．39°D ．12°4．(山西模拟)如图，直径为AB 的⊙O 中，BC ︵＝2AC ︵，连接BC ，则∠B 的度数为(B)A ．35°B ．30°C ．20°D ．15° 知识点3 圆周角定理的推论5．如图，已知AB 是⊙O 的直径，点C 在⊙O 上，∠A ＝35°，则∠B 的度数是(C)A ．35°B ．45°C ．55°D ．65°6．(绍兴中考)如图，BD 是⊙O 的直径，点A ，C 在⊙O 上，AB ︵＝BC ︵，∠AOB ＝60°，则∠BDC 的度数是(D)A ．60°B ．45°C ．35°D ．30°7．(黔西南中考)如图，在⊙O 中，AB ︵＝AC ︵，∠BAC ＝50°，则∠AEC 的度数为(A)A ．65°B ．75°C ．50°D ．55°8．(太原二模)如图，BD 是圆O 的直径，∠CBD ＝30°，则∠A 的度数为(C)A ．30°B ．45°C ．60°D ．75°9．(常州中考)如图，把直角三角板的直角顶点O 放在破损玻璃镜的圆周上，两直角边与圆弧分别交于点M ，N ，量得OM ＝8 cm ，ON ＝6 cm ，则该圆玻璃镜的半径是(B)A.10 cm B ．5 cm C ．6 cm D ．10 cm10．(朝阳中考)如图是一个圆形人工湖的平面图，弦AB 是湖上的一座桥，已知桥长100 m ，测得圆周角∠ACB ＝30°，则这个人工湖的直径为200m.11．如图，已知A ，B ，C ，D 是⊙O 上的四个点，AB ＝BC ，BD 交AC 于点E ，连接CD ，AD.求证：DB 平分∠ADC.证明：∵AB ＝BC ， ∴AB ︵＝BC ︵. ∴∠ADB ＝∠BDC. ∴DB 平分∠ADC.易错点 忽略弦所对的圆周角不唯一而致错12．已知⊙O 的弦AB 的长等于⊙O 的半径，则此弦AB 所对的圆周角的度数为30°或150°． 02 中档题13．(海南中考)如图，点A 、B 、C 在⊙O 上，AC ∥OB ，∠BAO ＝25°，则∠BOC 的度数为(B)A ．25°B ．50°C ．60°D ．80°14．(吕梁孝义市期中)如图，AB 是⊙O 的直径，点C ，D ，E 在⊙O 上，若∠AED ＝20°，则∠BCD 的度数为(B)A ．100°B ．110°C ．115°D ．120°15．(广州中考)如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为E，连接CO，AD，∠BAD＝20°，则下列说法中正确的是(D)A．AD＝2OB B．CE＝EOC．∠OCE＝40°D．∠BOC＝2∠BAD16．如图，⊙C经过原点，并与两坐标轴分别交于A，D两点，已知∠OBA＝30°，点A的坐标为(2，0)，则点D17．如图，⊙O的直径AB的长为10，弦AC的长为5，∠ACB的平分线交⊙O于点D.(1)求BC的长；(2)求BD的长．解：(1)∵AB为⊙O的直径，∴∠ACB＝∠ADB＝90°.∴在Rt△ABC中，BC＝AB2－AC2＝102－52＝5 3.(2)∵CD平分∠ACB，∴∠ACD＝∠BCD＝45°.∴∠BAD＝∠ABD＝45°.∴AD＝BD.设BD＝AD＝x，在Rt△ABD中，由勾股定理，得AD2＋BD2＝AB2.∴x2＋x2＝102.解得x＝5 2.∴BD＝5 2.18．如图，在△ABC中，AB＝BC＝2，以AB为直径的⊙O分别交BC，AC于点D，E，且点D为边BC的中点．(1)求证：△ABC为等边三角形；(2)求DE的长．解：(1)证明：连接AD.∵AB是⊙O的直径，∴∠ADB＝90°.∵点D是BC的中点，∴AD是BC的垂直平分线．∴AB＝AC.又∵AB＝BC，∴AB＝AC＝BC.∴△ABC为等边三角形．(2)连接BE.∵AB是⊙O的直径，∴∠AEB＝90°.∴BE⊥AC.∵△ABC是等边三角形，∴AE＝EC，即E为AC的中点．又∵D是BC的中点，∴DE是△ABC的中位线．∴DE ＝12AB ＝12×2＝1.03 综合题19．(东营中考)如图，在⊙O 中，AB 是⊙O 的直径，AB ＝8 cm ，AC ︵＝CD ︵＝BD ︵，M 是AB 上一动点，CM ＋DM 的最小值为8__cm ．第2课时 圆内接四边形01 基础题知识点 圆内接四边形的性质1．(湘潭中考)如图，四边形ABCD 是⊙O 的内接四边形，若∠DAB ＝60°，则∠BCD 的度数是(D)A ．60°B ．90°C ．100°D ．120°2．如图，四边形ABCD 是圆内接四边形，E 是BC 延长线上一点．若∠BAD ＝105°，则∠DCE 的大小是(B)A ．115°B ．105°C ．100°D ．95°3．(娄底中考)如图，四边形ABCD 为⊙O 的内接四边形，已知∠C ＝∠D ，则AB 与CD 的位置关系是AB ∥CD ．4．如图，AB 是半圆O 的直径，∠BAC ＝30°，D 是AC ︵的中点，则∠DAC 的度数是30°．5．如图所示，已知圆心角∠AOB ＝100°，求∠ACD 的度数．解：在优弧AMB ︵上任取一点N ，连接AN ，BN ， 由圆周角定理，得∠N ＝12∠AOB ＝12×100°＝50°.∴∠ACB ＝180°－∠N ＝180°－50°＝130°. ∴∠ACD ＝180°－∠ACB ＝180°－130°＝50°.6．已知圆内接四边形相邻三个内角度数的比为2∶1∶7，求这个四边形各内角的度数． 解：根据圆内接四边形的对角互补可知，其对角和相等，所以四个内角的度数的比为2∶1∶7∶8.设这四个内角的度数分别为2x°、x°、7x°、8x°，则 2x ＋x ＋7x ＋8x ＝360.解得x ＝20. 则2x ＝40，7x ＝140，8x ＝160.答：这个四边形各内角的度数分别为40°、20°、140°、160°.7．(T4的变式)如图，四边形ABCD 内接于⊙O ，∠B ＝50°，∠ACD ＝25°，∠BAD ＝65°.求证： (1)AD ＝CD ；(2)AB 是⊙O 的直径．证明：(1)∵四边形ABCD 内接于⊙O ， ∴∠D ＝180°－∠B ＝130°. ∵∠ACD ＝25°，∴∠DAC ＝180°－∠D －∠ACD ＝180°－130°－25°＝25°. ∴∠DAC ＝∠ACD. ∴AD ＝CD.(2)∵∠BAC ＝∠BAD －∠DAC ＝65°－25°＝40°，∠B ＝50°， ∴∠ACB ＝180°－∠B －∠BAC ＝180°－50°－40°＝90°. ∴AB 是⊙O 的直径．易错点 对圆内接四边形的概念理解不清导致错误8．(来宾中考)如图，在⊙O 中，点A ，B ，C 在⊙O 上，且∠ACB ＝110°，则∠α＝140°．02 中档题9．(山西中考模拟百校联考)如图，点A ，B ，C ，D 为⊙O 上的点，四边形AOBC 是菱形，则∠ADB 的度数是(C)A ．30°B ．45°C ．60°D ．75°10．(聊城中考)如图，四边形ABCD 内接于⊙O ，F 是CD ︵上一点，且DF ︵＝BC ︵，连接CF 并延长交AD 的延长线于点E ，连接AC.若∠ABC ＝105°，∠BAC ＝25°，则∠E 的度数为(B)A ．45°B ．50°C ．55°D ．60°11．(南京中考)如图，在⊙O的内接五边形ABCDE中，∠CAD＝35°，则∠B＋∠E＝215°．12．(吉林中考)如图，四边形ABCD内接于⊙O，∠DAB＝130°，连接OC，点P是半径OC 上任意一点，连接DP，BP，则∠BPD可能为80(50°≤∠BPD≤100°)(写出一个即可)．13．如图，⊙C经过坐标原点，且与两坐标轴分别交于点A与点B，点A的坐标为(0，4)，M是圆上一点，∠BMO＝120°.求⊙C的半径．解：∵四边形ABMO内接于⊙C，∴∠BAO＋∠BMO＝180°.∵∠BMO＝120°，∴∠BAO＝60°.在Rt△ABO中，AO＝4，∠BAO＝60°，∴AB＝8.∵∠AOB＝90°，∴AB为⊙C的直径．∴⊙C的半径为4.14．(苏州中考)如图，AB是圆O的直径，D，E为圆O上位于AB异侧的两点，连接BD并延长至点C，使得CD＝BD.连接AC交圆O于点F，连接AE，DE，DF.(1)求证：∠E＝∠C；(2)若∠E＝55°，求∠BDF的度数．解：(1)证明：连接AD.∵AB是⊙O的直径，∴∠ADB＝90°，即AD⊥BC.∵CD＝BD，∴AD垂直平分BC.∴AB＝AC.∴∠B＝∠C.又∵∠B＝∠E，∴∠E＝∠C.(2)∵四边形AEDF是⊙O的内接四边形，∴∠AFD＝180°－∠E.又∵∠CFD＝180°－∠AFD，∴∠CFD＝∠E＝55°.∵∠E＝∠C＝55°，∴∠BDF＝∠C＋∠CFD＝110°.03综合题15．(佛山中考)如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E，F.(1)若∠E＝∠F，求证：∠ADC＝∠ABC；(2)若∠E＝∠F＝42°，求∠A的度数；(3)若∠E＝α，∠F＝β，且α≠β.请你用含有α，β的代数式表示∠A的大小．解：(1)证明：∵∠DCE＝∠BCF，∠E＝∠F，又∵∠ADC＝∠E＋∠DCE，∠ABC＝∠F＋∠BCF，∴∠ADC＝∠ABC.(2)由(1)知∠ADC＝∠ABC，∵四边形ABCD内接于⊙O，∴∠ADC＋∠ABC＝180°.∴∠ADC＝90°.在Rt△ADF中，∠A＝90°－∠F＝90°－42°＝48°.(3)连接EF.∵四边形ABCD为⊙O的内接四边形，∴∠ECD＝∠A.∵∠ECD＝∠CEF＋∠CFE，∴∠A＝∠CEF＋∠CFE.∵∠A＋∠CEF＋∠CFE＋∠DEC＋∠BFC＝180°，∴2∠A＋α＋β＝180°.∴∠A＝90°－α＋β2.。

《圆》拔高练习一、选择题（本大题共5小题，共25.0分）1．（5分）已知点C在线段AB上（点C与点A、B不重合），过点A、B的圆记作为圆O1，过点B、C的圆记作为圆O2，过点C、A的圆记作为圆O3，则下列说法中正确的是（）A．圆O1可以经过点C B．点C可以在圆O1的内部C．点A可以在圆O2的内部D．点B可以在圆O3的内部2．（5分）下列说法：①直径是弦；②长度相等的两条弧是等弧；③任何一条直径所在的直线都是圆的对称轴；④任何一条直径都是圆的对称轴，其中正确的有（）A．1个B．2个C．3个D．4个3．（5分）下列说法中，不正确的是（）A．圆既是轴对称图形又是中心对称图形B．圆有无数条对称轴C．圆的每一条直径都是它的对称轴D．圆的对称中心是它的圆心4．（5分）下列说法错误的是（）A．长度相等的两条弧是等弧B．直径是圆中最长的弦C．面积相等的两个圆是等圆D．半径相等的两个半圆是等弧5．（5分）下列语句中正确的有几个（）①关于一条直线对称的两个图形一定能重合；②两个能重合的图形一定关于某条直线对称；③两个轴对称图形的对应点一定在对称轴的两侧；④一个圆有无数条对称轴．A．1B．2C．3D．4二、填空题（本大题共5小题，共25.0分）6．（5分）如图，OA、OB是⊙O的半径，C是⊙O上一点，∠AOB＝40°，∠OBC＝50°，则∠OAC＝°．7．（5分）点A、B在⊙O上，若∠AOB＝40°，则∠OAB＝．8．（5分）线段AB＝10cm，在以AB为直径的圆上，到点A的距离为5cm的点有个．9．（5分）如图，小量角器的0°刻度线在大量角器的0°刻度线上，且小量角器的中心在大量角器的外缘边上．如果它们外缘边上的公共点P在大量角器上对应的度数为40°，那么在小量角器上对应的度数为．（只考虑小于90°的角度）10．（5分）如图，C是以点O为圆心，AB为直径的半圆上一点，且CO⊥AB，在OC两侧分别作矩形OGHI和正方形ODEF，且点I，F在OC上，点H，E在半圆上，可证：IG ＝FD．小云发现连接图中已知点得到两条线段，便可证明IG＝FD．请回答：小云所作的两条线段分别是和；证明IG＝FD的依据是矩形的对角线相等，和等量代换．三、解答题（本大题共5小题，共50.0分）11．（10分）如图，AB是半圆O的直径，D是半圆上的一点，∠DOB＝75°，DC交BA的延长线于E，交半圆于C，且CE＝AO，求∠E的度数．12．（10分）如图AB＝3cm，用图形表示：到点A的距离小于2cm，且到点B的距离不小于2cm的所有点的集合（用阴影表示，注意边界上的点是否在集合中，如果在，用实线表示，如果不在，则用虚线表示）．13．（10分）如图，已知AB是⊙O的直径，C是⊙O上的一点，CD⊥AB于D，AD＜BD，若CD＝2cm，AB＝5cm，求AD、AC的长．14．（10分）已知：如图，AB是⊙O的直径，点C、D在⊙O上，CE⊥AB于E，DF⊥AB 于F，且AE＝BF，AC与BD相等吗？为什么？15．（10分）已知：如图，AB是⊙O的直径，AC是⊙O的弦，AB＝2，∠BAC＝30°．在图中作弦AD，使AD＝1，并求∠CAD的度数．《圆》拔高练习参考答案与试题解析一、选择题（本大题共5小题，共25.0分）1．（5分）已知点C在线段AB上（点C与点A、B不重合），过点A、B的圆记作为圆O1，过点B、C的圆记作为圆O2，过点C、A的圆记作为圆O3，则下列说法中正确的是（）A．圆O1可以经过点C B．点C可以在圆O1的内部C．点A可以在圆O2的内部D．点B可以在圆O3的内部【分析】根据已知条件对个选项进行判断即可．【解答】解：∵点C在线段AB上（点C与点A、B不重合），过点A、B的圆记作为圆O1，∴点C可以在圆O1的内部，故A错误，B正确；∵过点B、C的圆记作为圆O2，∴点A可以在圆O2的外部，故C错误；∵过点C、A的圆记作为圆O3，∴点B可以在圆O3的外部，故D错误．故选：B．【点评】本题考查了圆的认识，根据已知条件正确的作出判断是解题的关键．2．（5分）下列说法：①直径是弦；②长度相等的两条弧是等弧；③任何一条直径所在的直线都是圆的对称轴；④任何一条直径都是圆的对称轴，其中正确的有（）A．1个B．2个C．3个D．4个【分析】根据弧的分类、圆的性质对各小题进行逐一分析即可．【解答】解：①直径是最长的弦，故本小题正确；②在等圆或同圆中，长度相等的两条弧是等弧，故本小题错误；③经过圆心的每一条直线都是圆的对称轴，故本小题正确；④经过圆心的每一条直线都是圆的对称轴，故本小题错误．故选：B．【点评】本题考查的是圆的认识，熟知圆周角定理、等弧的概念以及弦的定义．注意熟记定理与公式是关键．3．（5分）下列说法中，不正确的是（）A．圆既是轴对称图形又是中心对称图形B．圆有无数条对称轴C．圆的每一条直径都是它的对称轴D．圆的对称中心是它的圆心【分析】利用圆的对称性质逐一求解可得．【解答】解：A．圆既是轴对称图形又是中心对称图形，正确；B．圆有无数条对称轴，正确；C．圆的每一条直径所在直线都是它的对称轴，此选项错误；D．圆的对称中心是它的圆心，正确；故选：C．【点评】本题主要考查圆的认识，解题的关键是掌握圆的对称性．4．（5分）下列说法错误的是（）A．长度相等的两条弧是等弧B．直径是圆中最长的弦C．面积相等的两个圆是等圆D．半径相等的两个半圆是等弧【分析】利用等弧的定义、等圆的定义及弦的定义分别判断后即可确定正确的选项．【解答】解：A、长度相等的弧的度数不一定相等，故错误；B、直径是圆中最长的弦，正确；C、面积相等的两个圆是等圆，正确；D、半径相等的两个半圆是等弧，正确，故选：A．【点评】本题考查了圆的认识的知识，了解圆的有关定义是解答本题的关键，难度不大．5．（5分）下列语句中正确的有几个（）①关于一条直线对称的两个图形一定能重合；②两个能重合的图形一定关于某条直线对称；③两个轴对称图形的对应点一定在对称轴的两侧；④一个圆有无数条对称轴．A．1B．2C．3D．4【分析】根据轴对称图形的性质、全等图形的性质即可一一判断；【解答】解：①关于一条直线对称的两个图形一定能重合；正确．②两个能重合的图形一定关于某条直线对称；错误．③两个轴对称图形的对应点一定在对称轴的两侧；错误，也可以在对称轴上．④一个圆有无数条对称轴．正确．故选：B．【点评】本题考查圆的认识、轴对称图形等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．二、填空题（本大题共5小题，共25.0分）6．（5分）如图，OA、OB是⊙O的半径，C是⊙O上一点，∠AOB＝40°，∠OBC＝50°，则∠OAC＝30°．【分析】连接OC，根据等腰三角形的性质和三角形内角和定理得到∠BOC＝80°，求出∠AOC，根据等腰三角形的性质计算．【解答】解：连接OC，∵OC＝OB，∴∠OCB＝∠OBC＝50°，∴∠BOC＝180°﹣50°×2＝80°，∴∠AOC＝80°+40°＝120°，∵OC＝OA，∴∠OAC＝∠OCA＝30°，故答案为：30．【点评】本题考查的是等腰三角形的性质，三角形内角和定理，掌握三角形内角和等于180°是解题的关键．7．（5分）点A、B在⊙O上，若∠AOB＝40°，则∠OAB＝70°．【分析】由∠AOB＝40°，OA＝OB知∠OAB＝∠OBA＝，代入计算可得．【解答】解：如图，∵∠AOB＝40°，OA＝OB，∴∠OAB＝∠OBA＝＝70°，故答案为：70°．【点评】本题主要考查圆的基本性质，解题的关键是掌握圆的所有半径都相等及等腰三角形的性质．8．（5分）线段AB＝10cm，在以AB为直径的圆上，到点A的距离为5cm的点有2个．【分析】以A为圆心，5cm长为半径作圆，与以AB为直径的圆交于2点，依此即可求解．【解答】解：如图所示：到点A的距离为5cm的点有2个．故答案为：2．【点评】此题考查了圆的认识，关键是熟悉圆可以看做是所有到定点O的距离等于定长r的点的集合的知识点．9．（5分）如图，小量角器的0°刻度线在大量角器的0°刻度线上，且小量角器的中心在大量角器的外缘边上．如果它们外缘边上的公共点P在大量角器上对应的度数为40°，那么在小量角器上对应的度数为70°．（只考虑小于90°的角度）【分析】设大量角器的左端点为A，小量角器的圆心为B．利用三角形的内角和定理求出∠PBA的度数．然后根据圆的知识可求出小量角器上对应的度数．【解答】解：设大量角器的左端点是A，小量角器的圆心是B，连接AP，BP，则∠APB ＝90°，∠P AB＝20°，因而∠PBA＝90°﹣20°＝70°，在小量角器中弧PB所对的圆心角是70°，因而P在小量角器上对应的度数为70°．故答案为：70°；【点评】本题主要考查了直径所对的圆周角是90度．能把实际问题转化为数学问题是解决本题的关键．10．（5分）如图，C是以点O为圆心，AB为直径的半圆上一点，且CO⊥AB，在OC两侧分别作矩形OGHI和正方形ODEF，且点I，F在OC上，点H，E在半圆上，可证：IG ＝FD．小云发现连接图中已知点得到两条线段，便可证明IG＝FD．请回答：小云所作的两条线段分别是OH和OE；证明IG＝FD的依据是矩形的对角线相等，同圆的半径相等和等量代换．【分析】连接OH、OE，由矩形OGHI和正方形ODEF的性质得出IG＝OH，OE＝FD，由OH＝OE，即可得出结论．【解答】解：连接OH、OE，如图所示：∵在矩形OGHI和正方形ODEF中，IG＝OH，OE＝FD，∵OH＝OE，∴IG＝FD；故答案为：OH、OE，同圆的半径相等．【点评】本题考查了矩形的性质、正方形的性质、同圆的半径相等的性质；熟练掌握矩形和正方形的性质是解决问题的关键．三、解答题（本大题共5小题，共50.0分）11．（10分）如图，AB是半圆O的直径，D是半圆上的一点，∠DOB＝75°，DC交BA的延长线于E，交半圆于C，且CE＝AO，求∠E的度数．【分析】连结OC，如图，由CE＝AO，OA＝OC得到OC＝EC，则根据等腰三角形的性质得∠E＝∠1，再利用三角形外角性质得∠2＝∠E+∠1＝2∠E，加上∠D＝∠2＝2∠E，所以∠BOD＝∠E+∠D，即∠E+2∠E＝75°，然后解方程即可．【解答】解：连结OC，如图，∵CE＝AO，而OA＝OC，∴OC＝EC，∴∠E＝∠1，∴∠2＝∠E+∠1＝2∠E，∵OC＝OD，∴∠D＝∠2＝2∠E，∵∠BOD＝∠E+∠D，∴∠E+2∠E＝75°，∴∠E＝25°．【点评】本题考查了圆的认识：掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．也考查了等腰三角形的性质．12．（10分）如图AB＝3cm，用图形表示：到点A的距离小于2cm，且到点B的距离不小于2cm的所有点的集合（用阴影表示，注意边界上的点是否在集合中，如果在，用实线表示，如果不在，则用虚线表示）．【分析】根据圆的定义解答即可．【解答】解：到点A的距离小于2cm，且到点B的距离不小于2cm的所有点的集合如图所示：【点评】本题考查了圆的认识，关键是了解圆的定义，灵活运用所学知识解决问题．13．（10分）如图，已知AB是⊙O的直径，C是⊙O上的一点，CD⊥AB于D，AD＜BD，若CD＝2cm，AB＝5cm，求AD、AC的长．【分析】由直径AB＝5cm，可得半径OC＝OA＝AB＝cm，分别利用勾股定理计算AD、AC的长．【解答】解：连接OC，∵AB＝5cm，∴OC＝OA＝AB＝cm，Rt△CDO中，由勾股定理得：DO＝＝cm，∴AD＝﹣＝1cm，由勾股定理得：AC＝＝，则AD的长为1cm，AC的长为cm．【点评】本题考查了同圆的半径相等、勾股定理，在圆中常利用勾股定理计算边的长，本题熟练掌握勾股定理是关键．14．（10分）已知：如图，AB是⊙O的直径，点C、D在⊙O上，CE⊥AB于E，DF⊥AB 于F，且AE＝BF，AC与BD相等吗？为什么？【分析】连结OC、OD，由OA＝OB，AE＝BF，得到OE＝OF，由CE⊥AB，DF⊥AB 得到∠OEC＝∠OFD＝90°，再根据“HL”可判断Rt△OEC≌Rt△OFD，则∠COE＝∠DOF，所以AC弧＝BD弧，AC＝BD．【解答】解：AC与BD相等．理由如下：连结OC、OD，如图，∵OA＝OB，AE＝BF，∴OE＝OF，∵CE⊥AB，DF⊥AB，∴∠OEC＝∠OFD＝90°，在Rt△OEC和Rt△OFD中，，∴Rt△OEC≌Rt△OFD（HL），∴∠COE＝∠DOF，∴AC弧＝BD弧，∴AC＝BD．【点评】本题考查了圆的认识：掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．也考查了直角三角形全等的判定与性质．15．（10分）已知：如图，AB是⊙O的直径，AC是⊙O的弦，AB＝2，∠BAC＝30°．在图中作弦AD，使AD＝1，并求∠CAD的度数．【分析】利用圆周角定理、圆弧、弧所对的弦的关系，进而得出∠DAB＝∠B＝60°，进而得出答案．【解答】解：连接BC，∵AB是⊙O的直径，∴∠ACB＝90°，∵∠BAC＝30°，∴BC＝AB＝1，∠B＝60°，以A圆心BC长为半径画弧可得点D，再连接AD即可；∵AD＝BC，∴＝，∴∠DAB＝∠B＝60°，∴∠DAC＝60°﹣30°＝30°；同理可得：∠D′AC＝60°+30°＝90°；综上所述：∠CAD的度数为30°或90°．【点评】此题主要考查了圆周角定理以及圆有关的概念，得出∠DAB＝∠B＝60°是解题关键．。

九年级数学24.1.4《圆周角》同步练习一、选择题：1、如图，已知AB 是⊙O 的直径，∠D ＝40°，则∠CAB 的度数为( )A. 40°B.50°C. 45°D. 60°2、如图，AD 是⊙O 的弦，AB ∥CD ，∠AOC ＝76°，则∠BAD ＝( )A. 48°B.60°C. 38°D.26°3、如图，弦AB 把圆周分成1：2的两部分，已知⊙O 半径为1，则弦长AB 为（ ）．A. 3B.2C. 2.5D. √34、如图，A.B.C 是⊙O 上三点，42ACB ∠，则ABO ∠等于( )A. 48°B.50°C. 45°D. 64°5、如图，△ABC 的三个顶点都在⊙O 上，且AB 是⊙O 的直径，∠A ＝20°，则∠B ＝ ()A. 40°B.50°C. 45°D. 70°6、若⊙O 的弦AB 的长等于⊙O 的半径，则弦AB 所对的圆周角的度数为( )A. 60°B.50°C. 45°或150°D. 30°或150°7、如图，⊙O的弦AB、CD的延长线相交于点P，且DA＝DP．若BC＝5，则BP=（）．A. 5B.10C. 2.5D. 5√28、如图，A、B、C、D四个点均在⊙O上，∠AOD＝70°，AO∥DC，则∠B的度数为（）A. 45°B.70°C. 55°D. 35°9、如图，点A、B、C、D在⊙O上，AC为直径，若∠D＝22°，则∠ACB＝( )A. 68°B.44°C. 45°D. 64°10、如图，AB是⊙O的直径，C、D是圆上的两点（不与A、B重合），已知BC＝6，∠ADC ＝30°，则AB＝( )A. 4√3B.6C. 7.5D. 5√211、如图，四边形ABCD为⊙O的内接四边形，E是BC延长线上的一点，已知∠BOD＝100°，则∠DCE的度数为( )A ．40°B ．50°C ．60°D ．80°12、如图，AB 为⊙O 的直径，AB ＝AC ，BC 交⊙O 于点D ，AC 交⊙O 于点E ，∠BAC ＝45°.则∠EBC 的度数为（ ）A ．40°B ．22.5°C ．30°D ．17.5°二、填空题：13、如图，已知点A B C ，，在⊙O 上，若50ACB ∠=°，则AOB ∠= °．14、如图，点A 、B 、C 在⊙O 上，∠AOB ＝72°，则∠ACB 等于 .15、在直径为10cm 的⊙O 中，弦AB ＝5cm ，则弦AB 所对的圆周角= .16、如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，OC=5cm ，CD=8cm ，则AE= 。

24.1.4圆周角知识点1 圆周角定理例1．如图，«Skip Record If...»是«Skip Record If...»的直径，«Skip Record If...»为圆内一点，则下列说法中正确的是（）A．«Skip Record If...»是«Skip Record If...»的弦B．«Skip Record If...»是圆心角C．«Skip Record If...»是圆周角D．«Skip Record If...»变式2．如图，在«Skip Record If...»中，点«Skip Record If...»是«Skip Record If...»上一点，若«Skip Record If...»，则«Skip Record If...»的度数是（）A．80°B．100°C．120°D．130°3．AB是⊙O的直径，C.D是圆上两点，∠BDC＝32°，则∠AOC的度数为（）A．32°B．64°C．116°D．128°知识点2 同弧或等弧所对的圆周角相等例4．如图，«Skip Record If...»、«Skip Record If...»是«Skip Record If...»的直径，«Skip Record If...»，«Skip Record If...»交«Skip Record If...»于点«Skip Record If...»，«Skip Record If...»，则«Skip Record If...»的度数为（）A．20°B．40°C．60°D．70°变式5．如图，«Skip Record If...»是«Skip Record If...»的直径，点«Skip Record If...»，«Skip Record If...»在圆上，«Skip Record If...»，则«Skip Record If...»等于（）A．«Skip Record If...»B．«Skip Record If...»C．«Skip Record If...»D．«Skip Record If...»6．如图CD是⊙O的直径，CD=10，点A在⊙O上，∠ACD=30°，B为«Skip Record If...»的中点，P是直径CD上一动点，则PA+PB的最小值为（）A．5«Skip Record If...»B．«Skip Record If...»C．5D．«Skip Record If...»知识点3 直径所对的圆周角例7．如图，半径为5的«Skip Record If...»经过点C和点O，点B是y轴右侧«Skip Record If...»的优弧上一点，«Skip Record If...»，则点C的坐标为（）A．«Skip Record If...»B．«Skip Record If...»C．«Skip Record If...»D．«Skip Record If...»变式8．如图，在圆内接五边形ABCDE中，∠EAB∠+∠C+∠CDE+∠E＝430°，则∠CDA ＝_____度．9．如图，扇形OAB的圆心角为124°，C是弧«Skip Record If...»上一点，则∠ACB＝_______．课堂练习10．如图，在⊙O 中，AC =«Skip Record If...»AB ， 直径BC =2«Skip Record If...»， «Skip Record If...»， 则AD =___．11．如下是小华设计的“作«Skip Record If...»的角平分线”的尺规作图过程，请帮助小华完成尺规作图并填空（保留作图痕迹）．步骤作法推断第一步在«Skip Record If...»上任取一点C ，以点C 为圆心，«Skip Record If...»为半径作半圆，分别交射线«Skip Record If...»于点P ，点Q ，连接«Skip Record If...»«Skip Record If...» ①«Skip Record If...»，理由是② 第二步过点C 作«Skip Record If...»的垂线，交«SkipRecord If...»于点D ，交«Skip Record If...»于点E«Skip Record If...»，«Skip Record If...» ③ 第三步作射线«Skip Record If...»射线«Skip Record If...»平分«Skip Record If...»射线«Skip Record If...»为所求作．12．如图，△ABC 是⊙O 的内接三角形，点C 是优弧AB 上一点（点C 不与A ，B 重合），设∠OAB ＝α，∠C ＝β，（1）当α＝35°时，求β的度数；（2）猜想α与β之间的关系，并给以证明．13．如图所示，已知AB为圆O的直径，CD是弦，且AB⊥CD于点E，连接AC.OC.BC．（1）求证：∠ACO＝∠BCD；（2）若EB＝2cm，CD＝8cm，求圆O的直径．14．如图，⊙O是△ABD的外接圆，AB为直径，点C是弧AD的中点，连接OC，BC 分别交AD于点F，E．（1）求证：∠ABD＝2∠C．（2）若AB＝10，BC＝8，求BD的长．参考答案1．B【分析】根据弦、圆心角、圆周角的概念可直接进行排除选项．【详解】解：A.点C不在«Skip Record If...»上，所以AC不是«Skip Record If...»的弦，故错误，不符合题意；B.因为点O是圆心，所以∠BOC是圆心角，故正确，符合题意；C.点C不在«Skip Record If...»上，所以∠C不是圆周角，故错误，故不符合题意；D.当点C在圆上时，则OC=OA=OB，若«Skip Record If...»成立，则AC+OC＜OA+OB，∴AC＜OA，与题干矛盾，∴D选项错误，不符合题意；故选B．【点拨】本题主要考查弦、圆心角、圆周角的概念，熟练掌握弦、圆心角、圆周角的概念是解题的关键．2．D【分析】在优弧AC上取点D，连接AD.CD，由∠AOC= 100° 求出∠ADC= «Skip Record If...»∠AOC，根据四边形ABCD是圆内接四边形，得到∠ADC+∠ABC= 180° ，即可求出∠ABC的度数．【详解】在优弧AC上取点D，连接AD.CD，∵∠AOC= 100° ，∴∠ADC= «Skip Record If...»∠AOC=50° ，∵四边形ABCD是圆内接四边形，∴∠ADC+∠ABC= 180° ，∴∠ABC= 180° -50° =130° ，故选：D．【点拨】此题考查圆周角定理：同弧所对的圆周角等于圆心角的一半，圆内接四边形的性质：圆内接四边形的对角互补．3．C【分析】根据圆周角定理可求∠AOC，根据邻补角定义可求∠AOC的度数．【详解】∵AB是⊙O的直径，C.D是圆上两点，∠BDC＝32°∴∠BOC=2∠D=2×32°=64°∴∠AOC=180°-∠BOC=116°故选：C【点拨】考核知识点：圆周角定理．理解圆周角定理是关键．4．C【分析】先根据圆周角定理可得∠EOD＝2∠A＝40°，再根据平行线的性质可得∠ADB＝∠A ＝20°，由三角形外角定理即可得出答案．【详解】解：∵∠A＝20°，∴∠EOD＝2∠A＝40°，又∵«Skip Record If...»，∴∠ADB＝∠A＝20°，∴∠AFC＝∠EOD＋∠ADB＝40°＋20°＝60°．故选：C．【点拨】本题主要考查了圆周角定理，熟练应用圆周角定理进行求解是解决本题的关键．5．B【分析】由圆周角定理得出∠ACB＝90°，由直角三角形的性质求出∠B＝55°，再由圆周角定理得出∠ADC＝∠B＝55°即可．【详解】解：∵AB是⊙O的直径，∴∠ACB＝90°，∵∠BAC＝35°，∴∠B＝90°﹣35°＝55°，∴∠ADC＝∠B＝55°．故选：B．【点拨】此题主要考查了三角形的外接圆、圆周角定理以及直角三角形的性质；熟练掌握圆周角定理是解题的关键．6．A【分析】首先作A关于CD的对称点Q，连接BQ，然后根据圆周角定理、圆的对称性质和勾股定理解答．本题考查的是轴对称-最短路线问题，解答此题的关键是找到点A的对称点，把题目的问题转化为两点之间线段最短解答．【详解】解：作A关于MN的对称点Q，连接CQ，BQ，BQ交CD于P，此时AP+PB=QP+PB=QB，根据两点之间线段最短，PA+PB的最小值为QB的长度，连接OQ，OB，∵B为«Skip Record If...»的中点，∴∠BOD=∠ACD=30°，∴∠QOD=2∠QCD=2×30°=60°，∴∠BOQ=30°+60°=90°．∵直径CD=10，∴OB=«Skip Record If...»CD=«Skip Record If...»×10=5，∴BQ=«Skip Record If...»=«Skip Record If...»=5«Skip Record If...»，即PA+PB的最小值为5«Skip Record If...» ．故选A．【点拨】此题主要考查圆周角定理的应用，解题的关键是熟知圆周角定理、圆的对称性质应用．7．A【分析】先根据«Skip Record If...»可得CD是«Skip Record If...»的直径，进而求得«Skip Record If...»，再利用圆周角定理得出∠CDO的度数，进而利用含30°的直角三角形的性质得出答案．【详解】解：如图，设«Skip Record If...»与x轴的交点为D，连接CD．«Skip Record If...»∴CD是«Skip Record If...»的直径，∵«Skip Record If...»的半径为5，«Skip Record If...»，«Skip Record If...»，«Skip Record If...»，∴点C的坐标为«Skip Record If...»，故选：A．【点拨】此题主要考查了圆周角定理及其推论以及含30°的直角三角形的性质，作出正确的辅助线是解决本题的关键．8．70【分析】先利用多边的内角和得到∠EAB+∠B+∠C+∠CDE+∠E=540°，则可计算出∠B=110°，然后根据圆内接四边形的性质求∠CDA的度数．【详解】解：∵五边形ABCDE的内角和为（5-2）×180°=540°，∴∠EAB+∠B+∠C+∠CDE+∠E=540°，∵∠EAB+∠C+∠CDE+∠E=430°，∴∠B=540°-430°=110°，∵四边形ABCD为⊙O的内接四边形，∴∠B+∠CDA=180°，∴∠CDA=180°-110°=70°．故答案为70．【点拨】本题考查了多边形的内角和与圆内接四边形的性质，运用圆内接四边形的性质是解决问题的关键．9．118°【分析】在⊙O上取点D，连接AD，BD，根据圆周角定理求出∠D的度数，由圆内接四边形的性质即可得出结论．【详解】解：如图所示，在⊙O上取点D，连接AD，BD，∵∠AOB＝124°，∴∠ADB＝«Skip Record If...»∠AOB＝«Skip Record If...»×124°＝62°．∵四边形ADBC是圆内接四边形，∴∠ACB＝180°﹣62°＝118°．故答案为：118°．【点拨】本题主要考查了圆内接四边形的性质，圆心角与它的圆周角的关系，解题的关键在于能够熟练掌握相关知识进行求解.10．«Skip Record If...»【分析】过D点作DE⊥AB交AB于E，连接BD，DC，根据«Skip Record If...»和BC是直径可以得到，∠DAB=∠DAC=45°=∠DBC=∠DCB，即可得到AE=DE，利用勾股定理先求出AB，BD再求出AE，即可求出AD.【详解】解：如图所示，过D点作DE⊥AB交AB于E，连接BD，CD∵BC是圆的直径∴∠BAC=90°=∠BDC∵«Skip Record If...»∴∠DAB=∠DAC=45°=∠DBC=∠DCB∴BD=DC∵DE⊥AB∴∠AED=90°∴∠EDA=∠DAB=45°∴AE=DE在Rt△ABC中，AC=«Skip Record If...»AB，BC=2«Skip Record If...»，«Skip Record If...»∴«Skip Record If...»∴«Skip Record If...»同理«Skip Record If...»∴«Skip Record If...»∴«Skip Record If...»设AE=DE=x，则BE=4-x在Rt△DEB中，«Skip Record If...»∴«Skip Record If...»解得«Skip Record If...»或«Skip Record If...»∵«Skip Record If...»，«Skip Record If...»∴«Skip Record If...»∴«Skip Record If...»∴«Skip Record If...»∴«Skip Record If...»∴AE=DE=3∴«Skip Record If...»故答案为：«Skip Record If...».【点拨】本题主要考查了圆周角定理，直径所对的圆周角是90°，勾股定理，等腰三角形的判定等等，大角对大边，解题的关键在于能够熟练掌握相关知识进行求解.11．见解析；①90；②直径所对的圆周角是直角；③«Skip Record If...»【分析】根据直径所对的圆周角是直角，和同弧所对的圆周角相等即可得出结论【详解】解：补全的图形如图1所示．①∵OQ是直径∴∠OPQ=90°故答案为：90；②故答案为：直径所对的圆周角是直角；③∵CE⊥PQ∴由垂径定理得：«Skip Record If...»«Skip Record If...»．故答案为：«Skip Record If...»【点拨】本题考查圆周角定理的推论，垂径定理，熟练掌握圆周角定理及推论是关键12．（1）55°；（2）α+β=90°，证明见解析．【分析】（1）连接OB，根据等腰三角形的性质得到∠OBA=35°，根据三角形内角和定理求出∠AOB，根据圆周角定理计算即可；（2）根据三角形内角和定理和圆周角定理计算．【详解】解：（1）连接OB，∵∠OAB=α=35°，∴∠OBA=35°，∴∠AOB=110°，∴β=«Skip Record If...»∠AOB=55°；（2）结论：α+β=90°．证明：∵∠AOB=180°-2α，β=«Skip Record If...»∠AOB∴β=90°-α，∴α+β=90°．【点拨】本题考查的是三角形的外接圆与外心，掌握圆周角定理、三角形内角和定理是解题的关键．13．（1）翙解析；（2）圆O的直径为10cm．【分析】（1）由AB为⊙O的直径，AB⊥CD，根据垂径定理即可得«Skip Record If...»，然后由圆周角定理可得∠BCD=∠BAC，又由OA=OC，根据等边对等角，可得∠BAC=∠ACO，继而证得结论；（2）根据勾股定理，求出各边之间的关系，即可确定半径．【详解】（1）证明：∵AB为⊙O的直径，AB⊥CD，∴«Skip Record If...»，∴∠BCD=∠BAC，∵OA=OC，∴∠BAC=∠ACO，∴∠ACO=∠BCD；（2）设⊙O的半径为R cm，则OE=OB-EB=（R-2）cm，CE=«Skip Record If...»CD=«Skip Record If...»×8=4（cm）．在Rt△CEO中，由勾股定理可得OC2=OE2+CE2，即R2=（R-2）2+42，解得R=5，∴OB=5 cm．故圆O的直径为10 cm．【点拨】本题考查圆周角定理、垂径定理、勾股定理等知识，解题的关键是学会利用参数构建方程解决问题．14．（1）见解析；（2）BD＝2.8【分析】（1）利用弧的中点，等腰三角形的性质计算即可．（2）利用勾股定理，三角形中位线定理，垂径定理的推论计算即可．【详解】（1）证明：∵C是«Skip Record If...»的中点，∴«Skip Record If...»，∴∠ABC＝∠CBD，∵OB＝OC，∴∠ABC＝∠C，∴∠ABC＝∠CBD＝∠C，∴∠ABD＝∠ABC+∠CBD＝2∠C；（2）解：连接AC，∵AB为⊙O的直径，∴∠ACB＝90°，∴AC＝«Skip Record If...»＝6，∵C是«Skip Record If...»的中点，∴OC⊥AD，∴«Skip Record If...»，∴«Skip Record If...»，∴OF＝1.4，又∵O是AB的中点，F是AD的中点，∴OF是△ABD的中位线，∴BD＝2OF＝2.8．【点拨】本题考查了垂径定理及其推论，直径所对的圆周角是直角，勾股定理，三角形中位线定理，熟练掌握垂径定理，灵活运用勾股定理和三角形中位线定理是解题的关键．。