2017初三八校联考数学答案

2017 年全国初中数学联合竞赛（初二决赛）试题参考答案及评分标准明：卷，依据本分准. 和填空只 7 分和 0 分两档；解答，格按照本分准定的分档次分,不要再增加其他中档次. 如果考生的解答方法和本解答不同 , 只要思路合理 , 步正确 ,在卷参照本分准划分的档次, 予相的分数 .一、 (本分 42 分，每小7 分 )1、 C2、D3、 A4、 B5、 C6、 B二、填空（本分28 分，每小7 分）7、 238、 75°9、13或填）10、 1625(0.52三、（本共三小，第11 20分，第12、 13 各 25 分，分 70分）11. 已知关于x的方程x21 a 有且有两个解，求数 a 的取范.解：由已知必有 a0 ，由原方程得：x21a（ 1）；⋯⋯⋯⋯⋯⋯⋯⋯ 5 分若 a1， x 21 a ，此方程（1）有两解，原方程也有两解；⋯⋯10 分若 0a1，此方程（1）的解： x 3 a ， x3a ， x 1 a ， x 1 a ，要使原方程只有两解，四个解中必有两个解相等 . 若x 3 a 3 a ，得 a0 ，此x 1a1 a ，故原方程有两解；若 x3a1a，得 a1（舍去），若 x 3a1a ，得 a1，此方程有三个解，不符合要求；然3a1a， 3 a 1 a 。

故此 a0原方程有两解 .上， a 0 或 a 1原方程有两解.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯20 分12. 如 , 已知等腰直角三角形ABC中， B 90 ,D BC的中点， E 段 AC上一点，且EDC ADB .求BE ED的.BD解：点 C 作 BC 的垂交 DE 的延于点F， AF. 易△ ABD ≌△ FCD.∴AD=FD. ⋯⋯⋯⋯⋯⋯⋯⋯ 5 分易四形 ABCF 是正方形，∴ AB=AF.⋯⋯⋯⋯⋯ 10 分易△ ABE ≌△ AFE ，∴ FE=BE. ⋯⋯⋯⋯⋯⋯⋯⋯ 15 分-1-∴ AD=FD=DE+EF= BE +ED.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯20 分∴ BE ED AD 5. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯25 分BD BD13.从的自然数1， 2，⋯， 2017 中可以取出n个不同的数，使所取出的n 个不同的数中任意三个数之和都能被21 整除．求n的最大．解： a 、b、 c 、d是所取出的任意四个数．由意有a b c21m ，a b d21n ，其中，m、n正整数．所以，c d 21( m n) ．上式表明，所取出的数中任意两数之差是21的倍数，即所取的每个数除以21 所得的余数相同．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分个余数 k ，于是，a21a1 k ， b21b1k ， c 21c1 k ，其中， a1、 b1、c1是整数，0k2110 分．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯a b c21(a1b1c1 ) 3k ．因a b c 能被21整除，所以，3k能被 21整除，即 k能被 7 整除．因此，k =0，7或14．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯15 分当 k0 ，可取21， 42， 63，⋯， 2016 共 96 个数，符合意；当 k7 ，可取7，28， 49，⋯， 2002 共 96 个数，符合意；当 k14 ，可取14， 35， 56，⋯， 2009 共 96 个数，符合意⋯⋯⋯⋯⋯20 分上所述， n 的最大是96．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯25 分-2-。

福建省2017年初中毕业和高中阶段学校招生考试数学答案解析第Ⅰ卷一、选择题1.【答案】A【解析】3的相反数是-3，故选A 。

【提示】相反数的定义：如果两个数只有符号不同，我们称其中一个数为另一个数的相反数，特别地，0的相反数还是0。

【考点】相反数。

2.【答案】B【解析】从左边看几何体得到的图形是左视图，该几何体的左视图是两个竖直排列的正方形，故选B 。

【考点】简单组合体的三视图。

3.【答案】B【解析】5136000 1.3610=⨯，故选B 。

【提示】科学记数法的表示形式为10⨯n a 的形式，其中110≤<a ，n 为整数，其关键要正确确定a 的值以及n 的值。

【考点】科学计数法。

4.【答案】C【解析】2222(2)24=⨯=x x x ，故选C 。

【提示】积的乘方等于各因式乘方的积。

【考点】积的乘方。

5.【答案】A【解析】圆、线段和菱形既是轴对称图形，又是中心对称图形；正三角形是轴对称图形，但不是中心对称图形，故选A 。

【提示】轴对称图形和中心对称图形的概念是解题的关鍵。

【考点】图形的对称性。

6.【答案】A【解析】解不等式20-≤x 得2≤x ，解不等式30+>x 得3>-x ，所以不等式组的解集为32-<≤x ，故选A 。

【提示】解不等式组时，正确求出每一个不等式解集，利用“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则求解不等式组的解集。

【考点】解一元一次不等式组。

7.【答案】D【解析】由统计图可知正确答题数为15的有两个，个数最多，故众数是15。

将正确答题数按从小到大的顺序排列为10，13，15，15，20，位于最中间位置的数是15，故中位数为15。

综上所述，故选D 。

【提示】熟悉中位数和众数的概念是觯题的关键。

【考点】中位数和众数。

8.【答案】D【解析】∵AB 是e O 的直径，∴90∠=︒ADB ，∴90∠+∠=︒ABD BAD ，∵∠=∠ABD ACD ，∴90∠+∠=︒ACD BAD ，∴∠BAD —定与∠ACD 互余，故选D 。

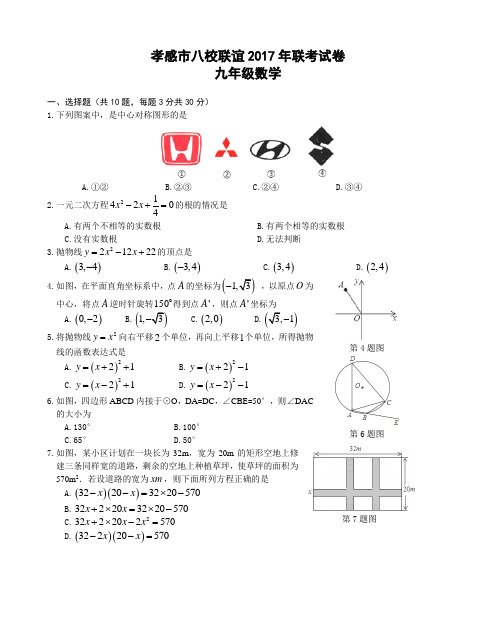
孝感市八校联谊2017年联考试卷九年级数学一、选择题（共10题，每题3分共30分） 1.下列图案中，是中心对称图形的是A.①②B.②③C.②④D.③④2.一元二次方程214204x x -+=的根的情况是 A.有两个不相等的实数根 B.有两个相等的实数根 C.没有实数根 D.无法判断 3.抛物线221222y x x =-+的顶点是A.()3,4-B.()3,4-C.()3,4D.()2,4 4.如图，在平面直角坐标系中，点A的坐标为(- ，以原点O 为中心，将点A 逆时针旋转150得到点'A ，则点'A 坐标为 A.()0,2-B.(1,C.()2,0D.)1-5.将抛物线2y x =向右平移2个单位，再向上平移1个单位，所得抛物线的函数表达式是A.()221y x =++ B.()221y x =+- C.()221y x =-+ D.()221y x =--6.如图，四边形ABCD 内接于⊙O ，DA =DC ，∠CBE =50°，则∠DAC 的大小为A.130°B.100°C.65°D.50°第4题图第6题图7.如图，某小区计划在一块长为32m ，宽为20m 的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m 2．若设道路的宽为xm ，则下面所列方程正确的是A.()()32203220570x x --=⨯-B.322203220570x x +⨯=⨯-C.2322202570x x x +⨯-= D.()()32220570x x --=第7题图8.如图，在Rt ABC ∆中，90,A BC ∠=︒=BC 的中点O 为圆心分别与AB ，AC 相切于D ，E 两点，则⌒ED 的长为A.4π B.2πC.πD.2π 9.已知m 整数，且满足210521m m -⎧⎨--⎩＞＞，则关于x 的一元二次方程第8题图()22242234m x x m x x --=+++的解为A.1232,2x x =-=-或67x =-B.1232,2x x ==C.67x =-D.1232,2x x =-=-10.二次函数()20y ax bx c a =++≠的图象如图，给出下列四个结论：①240ac b -＜； ②320b c +＜；③42a c b +＜； ④()()1m am b b a m ++≠-＜，其中正确结论的个数是A.4B.3C.2D.1第10题图二、填空题（共6题，每题3分共18分）11.已知关于x 的方程20x x a +-=的一个根为2，则另一个根是 . 12.若21,x x 是方程01222=--+-m m mx x 的两个实数根，且21211x x x x -=+，则m 的值为 .13.一个圆锥的侧面积是底面积的3倍，则圆锥侧面展开图的扇形的圆心角是 .14.如图，将△AOB 绕点O 按逆时针方向旋转45°后，得到△COD ，如果∠AOB=15°，则∠AOD 的度数是 . 15.如图，AB 是⊙O 的弦，AB=5，点C 是⊙O 上的一个动点，且∠ACB=45°，若点M 、N 分别是AB 、AC 的中点，则MN 长的最大值是 . 16.对称轴与y 轴平行且经过原点O 的抛物线也经过()()2,,4,A m B m ，若AOB ∆的面积为4，则抛物线的解析式为 .第14题图第15题图三、解答题（共8题，72分）17.（本题满分6分，各3分）解下列方程：⑴ 2221x x x -=+ ⑵ ()()2232x x x -=-18.（本题满分8分）如图所示，在Rt △ABC 中，∠ACB=90°，点D 、F 分别在AB 、AC 上，CF=CB ，连接CD ，将线段CD 绕点C 按顺时针方向旋转90°后得CE ，连接EF ． ⑴求证：△BCD ≌△FCE ；⑵若EF ∥CD ，求∠BDC 的度数．19.（本题满分8分）如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，ABC ∆ 的三个顶点的坐标分别为(3,4)A -，(5,2)B -，(2,1)C -．⑴画出ABC ∆关于y 轴的对称图形111A B C ∆；⑵画出将ABC ∆绕原点O 逆时针方向旋转90︒ 得到的222A B C ∆； ⑶求⑵中线段OA 扫过的图形面积．20.（本题满分8分）如图，已知在△ABC 中，∠A=90°⑴请用圆规和直尺作出⊙P ，使圆心P 在AC 边上，且与AB ，BC 两边都相切（保留作图痕迹，不写作法和证明）．⑵若∠B=60°，AB=3，求⊙P 的面积．21.（本题满分10分）甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点上正方1m 的P 处发出一球，羽毛球飞行的高度()y m 与水平距离()x m 之间满足函数表达式()24y a x h =-+．已知点O 与球网的水平距离为5m ，球网的高度为1.55m ．⑴当124a =-时，①求h 的值； ②通过计算判断此球能否过网；⑵若甲发球过网后，羽毛球飞行到Q 处时,乙扣球成功。

2017年初三年级八校联考数学参考答案第一部分 选择题一、（本大题共12题，每小题3分，共36分）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案ACBCAACBDDBD11。

解:如下图,分别过点A 、B 作x 轴的垂线AC 、BD ，垂足分别为C 、D ，则△OAC ∽△OBD ,根据“相似三角形面积的比等于相似比的平方”及反比例函数图象性质可知OBDOACS S OBOA∆∆==6。

12。

解：如上图,抛物线352+-=ax ax y 的对称轴为：直线25=x ，所以,AB =5,易得OA =3，因为ABC ∆≌ABD ∆,所以，只需考虑点C 位于对称轴左侧的情形.当0<a 时,只能BC 为底边，此时AC =5，则C 点坐标为（-4,0）,代入解析式可求得=a 121-；当0>a 时, ① 当AB 为底边时，此时点C 与点D 重合，则由042=-ac b ， 可得 =a 2512， ② 当AB 为腰时，因点C 位于对称轴左侧，所以,AC <5，只能AB =BC =5,则C 点坐标为(1，0)，代入解析式可求得=a 43.所以选D.（说明：本题虽有点复杂，但考察重点在于学生分类讨论，学生只需正确分类，不用计算，也能得到正确答案.）第二部分 非选择题二、填空题：（本大题共4题，每小题3分，共12分）题号 131415 16答案)2)(2(-+a a a21 20αcos 2R16.解：21122C O APB ∠=∠=∠,则可知C PBC ∠=∠,于是PB =PC ，所以，AP +BP = AC ,由垂径定理AC =2cos R α。

三、解答题（本题共7小题，其中第17小题5分,第18小题8分，第19小题6分，第20小题7分，第21小题8分，第22小题9分，第23小题9分，共52分） 17．解: 原式＝133333--⋅+ ——---—----—-—————----1+1+1+1分 ＝1313--+ —---———--——————-—-———4分 ＝0 -—-———————-—-—-——-—--5分(注：只写后两步也给满分。

2017年下联考九年级期中考试数学试卷（总分：120分 时量：120分钟 ）学校 姓名 班级一、精心选一选：（每小题3分，共计36分）1A ． 3 B ．π C ．32 D ．1 2、下列运算中，正确的是（ ）A.34x x x ÷= B.236()x x =C.321x x -=D.()222a b a b -=-3．在下列图形中，既是轴对称图形，又是中心对称图形的是（ ）4、物线4)3(22+-=x y 的顶点坐标是（ ）A ．)4,3(B ．)4,3(-C ．)4,3(-D ．)4,2(5、抛物线23x y =先向上平移2个单位，再向右平移3个单位，所得抛物线的函数表达式为（）A 、2)3(32++=x yB 、2)3(32-+=x y C 、2)3(32--=x y D 、2)3(32+-=x y 6、某次商品交易会上，所有参加会议的商家之间都签订了一份合同，共签订28份，则参加了交易会的商家共有( )个。

A.7B. 8C. 9 D 10 7、学校准备修建一个面积为220m 的矩形花圃，它的长比宽多m 10，设花圃的宽为xm ，则可列方程为（）A. 20)10(=-x xB. 20)10(22=-+x xC. 20)10(=+x x8、一元二次方程220x x m ++= A ．1m ≤- B ．1m ≤ C ．9、某市近年来大力发展芦笋产业，某芦笋生产企业在两年内的销售额从20万元增加到80万元．设这两年的销售额的年平均增长率为x ，根据题意可列方程为 A ．20(1+2x ) =80 B ．2×20(1+x ) =8010．在同一坐标系内，一次函数y=ax+b 与二次函数y=ax 2+8x+b 的图象可能是（ ）A B C D11、一个等腰三角形的两边长分别是方程x 2－7x ＋10＝0的两根，则该等腰三角形的周长为( )A ．12B ．9C ．13D ．12或912．二次函数y =ax 2+bx +c (a ≠0)的图象如图所示，下列说法①2a +b =0；②当﹣1≤x ≤3时，y ＜0；③若当(x 1，y 1)，(x 2，y 2)在函数图象上， 当x 1＜x 2时，y 1＜y 2；④9a +3b +c =0，其中正确的是 （ ） A.①②④ B.①④ C.①②③ D.③④二、填空题（每小题3分，共18分．） 13．一元二次方程20x x -=的解是 .14、已知关于x 的方程240x kx -+=的一个根是2，则实数k 的值为_________. 15、函数24y x =-的最小值为16、已知点P 的坐标为（-1，4），则点P 关于原点的对称点P ，坐标为 。

2015-2016 学年第二学期初三质量检测数学试题答案一、选择题（每小题3分，共36分） 二 填空题（本题共4小题，每小题3分，共12分）__,三解答题（本题共7个小题，共52分，17题5分 18题6分 19题7分 20题8分 21题8分 22题8分 23题10分 解答时应写出必要的文字说明，证明过程或演算步骤） 17 解原式=+ 1﹣2×+ 4 ……………………………………4分 每对一个给1分原式=5 ……………………………………5分 18解答：解：由①得：x≥2， ……………………………………2分 由②得：x ＜4， ……………………………………4分 所以这个不等式组的解集为：2≤x ＜4． ……………………………………5分 不等式组的整数为：2 、 3 ……………………………………6分19解解：（1）解：（1）∵参加“读书社”的学生有15人，且在扇形统计图中，所占比例为：25%，∴该班的学生共有：15÷25%=60（人）； ……………………………………1分 故答案为：60；该班参加“爱心社”的人数为12名……………………………………2分 参加“吉他社”的学生在全班学生中所占比为=10%，所以，“吉他社”对应扇形的圆心角的度数为：360°×10%=36°；…………………………3分 [ 不需要写出过程] （3）画树状图如下：， ……………………………………5分由树状图可知，共有6种可能的情况，其中恰好选中甲和乙的情况有2种，故P （选中甲和乙）==． ……………………………………7分EDB OCA20证明：（1） ∵DE ∥AC ，CE ∥BD ， ∴DE ∥OC ，CE ∥OD∴四边形OCED 是平行四边形， ……………………………………2分 又∵四边形ABCD 是菱形，∴AC ⊥BD ，∴∠COD=90°， ……………………………………3分 ∴四边形OCED 是矩形． ……………………………………4分 （2）∵∠ADB =60°，AD=∴ OD= AO=3 ……………………………………6分 ∴CE=AC =6∴SIN ∠AED =SIN ∠C AE=13=……………………………………8分 21 解 1）由题意可知∠ABC=45° ，AB=20 AC ：CD=1：2∵∠ABC=45° AB=20∴AC=BC=20 ……………………………………1分 ∵AC ：CD=1：2∴CD=40，BD=20 ……………………………………2分△ABD 的面积=200 ……………………………………3分② 堤坝的土石方总量=100x200=20000 ……………………………………4分 设原计划每天完成的土方为x 立方，则实际每天完成的土石方为（1+25%）x 由题意可得()200002000010125%xx-=+ ……………………………………6分解得 x=400 ……………………………………7分 经检验x=400是原方程的解答 原计划每天完成的土方为400立方米 ……………………………………8分22（1）证明：∵⊙O 切BC 于D ，∴OD ⊥BC ， ……………………………………1分 ∵AC ⊥BC ，∴AC ∥OD ， ……………………………………2分 ∴∠CAD=∠ADO ， ∵OA=OD ，∴∠OAD=∠ADO ， ……………………………………3分 ∴∠CAD=∠OAD即AD 平分∠CAB ； ……………………………………4分（2）方法一：连接OE ，ED .∵∠BAC =60°，OE =OA ， ∴△OAE 为等边三角形， ∴∠AOE =60°， ∴∠ADE =30°.又∵1302OAD BAC ∠=∠=，∴∠ADE =∠OAD ，∴ED ∥AO ， …………………………………… 6分 ∴S △AED ＝S △OED ，∴阴影部分的面积 = S 扇形ODE = 60423603ππ⨯⨯=.……………………………………8分方法二：同方法一，得ED ∥AO ， …………………………………… 6分 ∴四边形AODE 为平行四边形，∴1S S 22AED OAD ==⨯=V V又S 扇形ODE －S △O ED=60423603ππ⨯⨯=- ∴阴影部分的面积 = (S 扇形ODE －S △O ED ) + S △A E D=2233ππ. ···························· 8分BCA23 （1）b=2、c=3 ……………………………………2分（2） 作DN//CF 交CB 于N ，∴DE DNEF CF=…………………………3分 直线BC 的表达式为 3y x =-+设D 2(,23)m mm -++，则N 坐标为(,3)m m -+N DN=23m m -+，CF=2 ……………4分∴DE DN EF CF ==232m m -+DN=23m m -+的最大值为94 DE EF 的最大值为98……………6分 3）∵P 点的坐标为（1，4），PM 的解析式为x=1，直线BC 的解析式为y=﹣x+3，∴M 的坐标为（1，2）， 设PM 与x 轴交于点G ， ∵PM=GM=2，∴过点G 与BC 平行的直线为y=﹣x+1， …………………………8分由得或，∴点Q 的坐标为（，﹣），（，﹣）， ………………10分∴使得△QMB 与△PMB 的面积相等的点Q 的坐标为（，﹣），（，﹣）．G备注：此题也可过Q 作X 轴的垂线来求解，同样给分。

第8题图2017年初三第二次联考数学试卷（考生注意：本试题共25小题，满分120分，考试时间120分钟）一、选择题：（本大题共10个小题，每小题3分，共30分）在每个小题的下面，都给出了代号为A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将正确答案的代号在答题卡中对应的方框涂黑．1．在14，1-，0， 3.2-这四个数中，属于负分数的是（ ）． A ．14B ．1-C ．0D ． 3.2-2．下列4个图形中，是中心对称图形但不是．．轴对称的图形是（）．A ．B ．C ．D ． 3．下列计算正确的是（ ）．A ．523m m -=B ．236a a a ⋅=C ．326()ab ab = D ．322()2m n mn m ÷= 4．下列说法中，正确的是（ ）．A ．不可能事件发生的概率是0B ．打开电视机正在播放动画片，是必然事件C ．随机事件发生的概率是21D ．对“梦想的声音”节目收视率的调查，宜采用普查 5．如图，AB ∥CD ，CB 平分∠ABD ，若∠C=40°，则∠D 的度数为（ ）． A ．90° B ． 100° C ． 110° D ． 120°6．在函数2y x=中，自变量x 的取值范围是（ ）． A ．3x -≥且0x ≠B ．3x ≤且0x ≠C ．0x ≠D ．3x -≥7．如图，在□ABCD 中，E 为CD 上一点，连接AE 、BD ，且AE 、BD 交于点F ，25:4:=∆∆ABF DEF S S ，则DE ：EC =（ ）． A ．2：5 B ．2：3 C ．3：5 D ．3：2 8．如图，⊙O 的直径AB 垂直于弦CD ，垂足是E ，22.5A ∠=︒，4OC =，CD 的长为（ ）．A ．22B ．4C ．24D ．8B第5题图BC9.如果关于x 的分式方程1311a x x x --=++有负分数解，且关于x 的不等式组()24,3412a x x x x -≥--⎧⎪⎨+<+⎪⎩的解集为2x <-，那么符合条件的所有整数a 的积是（ ） A 、3- B 、0C 、3D 、910．如图，平面直角坐标系中，矩形OABC 的顶点B 在第一象限，点C 在x 轴上，点A 在y 轴上，D 、E 分别是AB ，OA 中点．过点D 的双曲线(,)00ky x k x=>>与BC 交于点G ．连接DC ，F 在DC 上，且DF ：FC =3:1,连接DE ，EF ．若△DEF 的面积为6，则k 的值为（ ）． A ．163 B ．323C ．6D ．10二、填空题：（本大题共6小题，每小题3分，共18分）请把下列各题的正确答案填写在答题卡中对应的横线上． 11．经过十多年的成长，中国城市观众到影院观影的习惯已经逐渐养成：2010年，某影院观众人次总量才23400，但到2016年已经暴涨至13.5万．其中13。

2017年全国初中数学联合竞赛试题 初二卷第一试一、选择题：（本题满分 42 分，每小题 7 分） 1.已知实数a,b,c 满足2a+13b+3c=90，3a+9b+c=72，则32b ca b++的值为（ ）. A.2 B.1 C.0 D.-1 2.已知实数a,b,c 满足a+b+c=1，1110135a b c ++=+++，则(a+1)2+(b+3)2+(c+5)2的值为（ ）. A.125 B.120 C.100 D.813.若正整数a,b,c 满足a ≤b ≤c 且abc=2(a+b+c)，则称(a,b,c)为好数组.那么好数组的个数为（ ）. A.4 B.3 C.2 D.14.已知正整数a,b,c 满足a 2-6b-3c+9=0，-6a+b 2+c=0，则a 2+b 2+c 2的值为（ ）. A.424 B.430 C.441 D.4605.梯形ABCD 中，AD ∥BC ，AB=3，BC=4，CD=2，AD=1，则梯形的面积为（ ）. A.1023 B.1033C.32D.33 6.如图，梯形ABCD 中，AD ∥BC ，∠A=90°，点E 在AB 上，若AE=42，BE=28，BC=70，∠DCE=45°，则DE 的值为（ ）.A.56B.58C.60D.62二、填空题：（本题满分 28 分，每小题 7 分）7.311a a ++=a 的值为________.8.已知△ABC 的三个内角满足A ＜B ＜C ＜100°.用θ表示100°-C,C-B,B-A 中的最小者，则θ的最大值为________.9.设a,b 是两个互质的正整数，且38ab p a b=+为质数.则p 的值为________.10.20个都不等于7的正整数排成一行，若其中任意连续若干个数之和都不等于7，则这20个数之和的最小值为________.第二试一、（本题满分20分）设A,B是两个不同的两位数，且B是由A交换个位数字和十位数字所得，如果A2-B2是完全平方数，求A的值.二、（本题满分25分）如图，△ABC中，D为BC的中点，DE平分∠ADB，DF平分∠ADC，BE⊥DE，CF⊥DF，P为AD与EF的交点.证明：EF=2PD.三、（本题满分25分）已知a,b,c 55a bb c++为有理数，求222a b ca b c++++的最小值.2017年全国初中数学联合竞赛试题初二卷参考答案第一试一、选择题：（本题满分42 分，每小题7 分）1.已知实数a,b,c满足2a+13b+3c=90，3a+9b+c=72，则32b ca b++的值为（）.A.2B.1C.0D.-1答案：B对应讲次：所属知识点：方程思路：因为所求分式的特点可以想到把a+2b，3b+c看成一个整体变量求解方程.解析：已知等式可变形为2(a+2b)+3(3b+c)=90，3(a+2b)+(3b+c)=72，解得a+2b=18，3b+c=18，所以312b ca b+=+.2.已知实数a,b,c满足a+b+c=1，111135a b c++=+++，则(a+1)2+(b+3)2+(c+5)2的值为（）.A.125B.120C.100D.81答案：C对应讲次：所属知识点：方程思路：可以想到换元法.解析：设x=a+1，y=b+3，z=c+5，则x+y+z=10，111x y z++=，∴xy+xz+yz=0，由x2+y2+z2=(x+y+z)2-2(xy+xz+yz)=100.则(a+1)2+(b+3)2+(c+5)2 =100.3. 若正整数a,b,c满足a≤b≤c且abc=2(a+b+c)，则称(a,b,c)为好数组.那么好数组的个数为（）.A.4B.3C.2D.1答案：B对应讲次：所属知识点：数论思路：先通过a≤b≤c且abc=2(a+b+c)的限定关系确定可能的种类，再通过枚举法一一验证. 解析：若(a,b,c)为好数组，则abc=2(a+b+c)≤6c，即ab≤6，显然a=1或2.若a=1，则bc=2(1+b+c)，即(b-2)(c-2)=6，可得(a,b,c)=(1,3,8)或(1,4,5)，共2个好数组.若a=2，则b=2或3，可得b=2,c=4；b=3,c=52，不是整数舍去，共1个好数组.共3个好数组(a,b,c)=(1,3,8) (1,4,5) (2,2,4).4. 已知正整数a,b,c满足a2-6b-3c+9=0，-6a+b2+c=0，则a2+b2+c2的值为（）.A.424B.430C.441D.460答案：C对应讲次：所属知识点：方程思路：由已知等式消去c整理后，通过a,b是正整数的限制，枚举出所有可能，并一一代入原方程验证，最终确定结果.解析：联立方程可得(a-9)2+3(b-1)2=75，则3(b-1)2≤75，即1≤b≤6.当b=1,2,3,4,5时，均无与之对应的正整数a；当b=6时，a=9，符合要求，此时c=18，代入验证满足原方程.因此，a=9，b=6，c=18，则a2+b2+c2=441.5. 梯形ABCD中，AD∥BC，AB=3，BC=4，CD=2，AD=1，则梯形的面积为（）.A.1023B.1033C.32D.33答案：A对应讲次：所属知识点：平面几何思路：通过作平行四边形把边长关系转化到一个三角形中来.解析：作AE∥DC，AH⊥BC，则ADCE是平行四边形，则BE=BC-CE=BC-AD=3=AB，则△ABE 是等腰三角形，BE=AB=3，AE=2，经计算可得423AH =. 所以梯形ABCD 的面积为()14210214233⨯+⨯=.6. 如图，梯形ABCD 中，AD ∥BC ，∠A=90°，点E 在AB 上，若AE=42，BE=28，BC=70，∠DCE=45°，则DE 的值为（ ）.A.56B.58C.60D.62 答案：B 对应讲次：所属知识点：平面几何思路：补形法，把直角梯形先补成正方形，再利用旋转把边长关系转化到同一个三角形Rt △EAD 中去，利用勾股定理求解.解析：作CF ⊥AD ，交AD 的延长线于点F ，将△CDF 绕点C 逆时针旋转90°至△CGB ，则ABCF 为正方形，可得△ECG ≌△ECD ，∴EG=ED. 设DE=x ，则DF=BG=x-28，AD=98-x.在Rt △EAD 中，有422+(98-x)2=x 2，解得x=58.二、填空题：（本题满分 28 分，每小题 7 分）7.311a a ++=a 的值为________.答案：8 对应讲次： 所属知识点：方程思路：通过等式两边都6次方可以去掉最外面根式，再用换元法化简等式，最后要验证结果是否满足最初的等式.解析：易得(321a =.令x ，则x ≥0，代入整理可得x(x-3)(x+1)2=0，解得x 1=0, x 2=3, x 3=-1，舍负，即a=-1或8，验证可得a=8.8. 已知△ABC 的三个内角满足A ＜B ＜C ＜100°.用θ表示100°-C,C-B,B-A 中的最小者，则θ的最大值为________. 答案：20° 对应讲次： 所属知识点：代数思路：一般来说，求几个中最小者的最大值时，就是考虑这几个都相等的情况. 解析：∵θ≤100°-C ，θ≤C-B ，θ≤B-A ∴θ≤16［3（100°-C ）+2(C-B)+(B-A)］=20°又当A=40°,B=60°,C=80°时，θ=20°可以取到. 则θ的最大值为20°.9. 设a,b 是两个互质的正整数，且38ab p a b=+为质数.则p 的值为________.答案：7 对应讲次： 所属知识点：数论思路：因为p 是质数，只能拆成1和p ，另一方面通过a+b 、a 、b 两两互质来拆分38ab a b+的可能种类，最后分类讨论，要么与条件矛盾，要么得出结果.解析：因为a,b 互质，所以a+b 、a 、b 两两互质，因为38ab a b +质数，所以318ab p a b⎧=⎪⎨=⎪+⎩可得a=b=1，p=4，不是质数舍；381ab p a b⎧=⎪⎨=⎪+⎩可得a=7，b=1，p=7，符合题意.则p=7.10.20个都不等于7的正整数排成一行，若其中任意连续若干个数之和都不等于7，则这20个数之和的最小值为________. 答案：34 对应讲次： 所属知识点：数论思路：考虑1,1,1,1,1,1,8,1,1,1,1,1,1,8,1,1,1,1,1,1满足题设要求，其和为34，接下来只需要考虑该数列是否为和最小的数列.解析：设该正整数列为()20,*n a n n N ≤∈，考虑()16,,,14,*k k k i i i k i ka a a k k N ++==≤∈∑∑，依抽屉原理必然有两项模7的余数相同，则该两项的差是7的倍数，于是任意连续7项之中必有连续子列之和为7的倍数，又不能为7，则最小为14.于是20个数中至少有2组这样的子列其总和不小于28，剩下6个数之和不小于6，于是该数列之和不小于34.由1,1,1,1,1,1,8,1,1,1,1,1,1,8,1,1,1,1,1,1可知，存在数列和为34的情况.第二试一、（本题满分 20 分）设A,B 是两个不同的两位数，且B 是由A 交换个位数字和十位数字所得，如果A 2-B 2是完全平方数，求A 的值. 答案：65 对应讲次： 所属知识点：数论思路：对于需要考虑不同位数上数字的情况，可以把一个两位数ab 设为10a+b ，转为为代数问题，再利用完全平方数的质因数分解式也是以完全平方数对的形式出现，综合分析所有限定下可能性，最终确定结果. 解析：设A=10a+b(1≤a,b ≤9,a,b ∈N)，则B=10b+a ，由A,B 不同得a ≠b ，A 2-B 2=（10a+b ）2-(10b+a)2=9×11×（a+b ）(a-b).………5分由A 2-B 2是完全平方数，则a ＞b ，()()11|a b a b +-，可得a+b=11， ………10分 a-b 也是完全平方数，所以a-b=1或4.………15分若a-b=1，则a=6，b=5； 若a-b=4，则没有正整数解. 因此a=6，b=5，A=65.………20分二、（本题满分 25 分）如图，△ABC 中，D 为BC 的中点，DE 平分∠ADB ，DF 平分∠ADC ，BE ⊥DE ，CF ⊥DF ，P 为AD 与EF 的交点.证明：EF=2PD.对应讲次：所属知识点：平面几何思路：因为EF 、PD 都在△DEF 中，所以想办法推出其性质，比较容易得出∠EDF=90°，此时若能得出EF=PD ，则自然可以得到结论.解析：由DE 平分∠ADB ，DF 平分∠ADC ，可得∠EDF=90°.………5分由BE ⊥DE 得BE ∥DF ，则∠EBD=∠FDC. ………10分又BD=DC ，∠BED=∠DFC=90°，则△BED ≌△DFC ，BE=DF . ………15分 得四边形BDFE 是平行四边形，∠PED=∠EDB=∠EDP ，EP=PD. ………20分 又△EDF 是直角三角形，∴EF=2PD.………25分三、（本题满分 25 分）已知a,b,c 为有理数，求222a b c a b c ++++的最小值.答案：3 对应讲次： 所属知识点：数论思路：通过a,b,c 是正整数，可以把有理部分和无理部分分离考虑.0c -≠，可以通过分母有理化来实现分离，再利用a,b,c 互不相等，从最小正整数开始讨论即可得出最小值.0c -≠)()22222555bcab bc bac b cb c +--+-==--b 2=ac. …10分()()22222a c ba b c a c b a b c a c b +-++==+-++++.………15分不妨设a ＜c ，若a=1，c=b 2，因为a ≠b ，则a+c-b=1+b(b-1)≥3，取等号当且仅当b=2时. ………20分 若a ≥2，因为c ≠b ≠1，则a+c-b=a+b(b-1)≥a+2≥4＞3.所以222a b c a b c++++的最小值为3，当a=1，b=2，c=4时.………25分。

2017年福建省漳州市八校联考高考数学模拟试卷（3月份）一、选择题：（每小题5分，共60分）1．已知集合M={0，1，2}，N={x|﹣1≤x≤1，x∈Z}，则M∩N为（）A．（0，1） B．[0，1]C．{0，1}D．∅2．已知复数的实部和虚部相等，则|z|=（）A．2 B．3 C．D．3．命题p：x∈R且满足sin2x=1．命题q：x∈R且满足tanx=1．则p是q的（）A．充分非必要条件 B．必要非充分条件C．充要条件D．既不充分也不必要条件4．已知点P的坐标（x，y）满足，过点P的直线l与圆C：x2+y2=16相交于A，B两点，则|AB|的最小值为（）A．B．C．D．5．“微信抢红包”自2015年以来异常火爆，在某个微信群某次进行的抢红包活动中，若所发红包的总金额为9元，被随机分配为1.49元，1.31元，2.19元，3.40元，0.61元，共5份，供甲、乙等5人抢，每人只能抢一次，则甲、乙二人抢到的金额之和不低于4元的概率是（）A．B．C．D．6．设方程2x|lnx|=1有两个不等的实根x1和x2，则（）A．x1x2＜0 B．x1x2=1 C．x1x2＞1 D．0＜x1x2＜17．某程序框图如图所示，其中，若输出的，则判断框内应填入的条件为（）A．n＜2017 B．n≤2017 C．n＞2017 D．n≥20178．某几何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．9．为得到函数y=2cos2x﹣sin2x的图象，只需将函数y=2sin2x+1的图象（）A．向左平移个长度单位B．向右平移个长度单位C．向左平移个长度单位D．向右平移个长度单位10．已知M是抛物线C：y2=2px（p＞0）上一点，F是抛物线C的焦点，若|MF|=p，K是抛物线C的准线与x轴的交点，则∠MKF=（）A．45°B．30°C．15°D．60°11．我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”，设△ABC三个内角A、B、C所对的边分别为a、b、c，面积为S，则“三斜求积”公式为．若a2sinC=4sinA，（a+c）2=12+b2，则用“三斜求积”公式求得△ABC的面积为（）A．B．2 C．3 D．12．若函数在上单调递增，则实数a的取值范围为（）A． B．C．D．[1，+∞）二、填空题（每题5分，满分20分）13．函数f（x）=lnx的图象在点x=1处的切线方程是．14．||=1，||=2，，且，则与的夹角为．15．在锐角△ABC中，内角A，B，C的对边分别为a，b，c，且2asinB=b．（1）求角A的大小；（2）若a=2，b+c=4，求△ABC的面积．16．已知双曲线x2﹣=1的左右焦点分别为F1、F2，过点F2的直线交双曲线右支于A，B两点，若△ABF1是以A为直角顶点的等腰三角形，则△AF1F2的面积为．三、解答题（本大题共5小题，共70分.）=2a n﹣1．17．已知数列{a n}满足a1=2，a n+1（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设b n=n•（a n﹣1），求数列{b n}的前n项和S n．18．某学校高三年级有学生500人，其中男生300人，女生200人，为了研究学生的数学成绩是否与性别有关，现采用分层抽样的方法，从中抽取了100名学生，先统计了他们期中考试的数学分数，然后按性别分为男、女两组，再将两组学生的分数分成5组：[100，110），[110，120），[120，130），[130，140），[140，150]分别加以统计，得到如图所示的频率分布直方图．（1）从样本中分数小于110分的学生中随机抽取2人，求两人恰好为一男一女的概率；（2）若规定分数不小于130分的学生为“数学尖子生”，请你根据已知条件完成2×2列联表，并判断是否有90%的把握认为“数学尖子生与性别有关”？附：K 2=．19．如图所示，四棱锥P﹣ABCD的底面为直角梯形，AB ⊥AD ，CD ⊥AD ，CD=2AB ．点E 是PC 的中点．（Ⅰ）求证：BE ∥平面PAD ；（Ⅱ）已知平面PCD ⊥底面ABCD ，且PC=DC ．在棱PD 上是否存在点F ，使CF ⊥PA ？请说明理由．20．已知圆O ：x 2+y 2=1过椭圆C ：（a ＞b ＞0）的短轴端点，P ，Q 分别是圆O 与椭圆C 上任意两点，且线段PQ 长度的最大值为3．（Ⅰ）求椭圆C的方程；（Ⅱ）过点（0，t）作圆O的一条切线交椭圆C于M，N两点，求△OMN的面积的最大值．21．设函数f（x）=lnx﹣ax2+ax，a为正实数．（1）当a=2时，求曲线y=f（x）在点（1，f（1））处的切线方程；（2）求证：f（）≤0；（3）若函数f（x）有且只有1个零点，求a的值．[选修4-4：坐标系与参数方程]22．已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线L的参数方程是（t为参数）．（1）求曲线C的直角坐标方程和直线L的普通方程；（2）设点P（m，0），若直线L与曲线C交于A，B两点，且|PA|•|PB|=1，求实数m的值．[选修4-5：不等式选讲]23．已知函数f（x）=2|x+1|+|x﹣2|的最小值为m．（Ⅰ）求实数m的值；（Ⅱ）若a，b，c均为正实数，且满足a+b+c=m，求证： ++≥3．2017年福建省漳州市八校联考高考数学模拟试卷（3月份）参考答案与试题解析一、选择题：（每小题5分，共60分）1．已知集合M={0，1，2}，N={x|﹣1≤x≤1，x∈Z}，则M∩N为（）A．（0，1） B．[0，1]C．{0，1}D．∅【考点】交集及其运算．【分析】化简集合N，根据交集的定义写出M∩N即可．【解答】解：集合M={0，1，2}，N={x|﹣1≤x≤1，x∈Z}={﹣1，0，1}，则M∩N={0，1}．故选：C．2．已知复数的实部和虚部相等，则|z|=（）A．2 B．3 C． D．【考点】复数代数形式的乘除运算．【分析】直接由复数代数形式的乘除运算化简复数z，再结合已知条件求出b的值，根据复数求模公式计算得答案．【解答】解：，∵复数的实部和虚部相等，∴﹣b=﹣3，即b=3．∴．故选：D．3．命题p：x∈R且满足sin2x=1．命题q：x∈R且满足tanx=1．则p是q的（）A．充分非必要条件 B．必要非充分条件C．充要条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据三角函数的性质以及充分条件和必要条件的定义进行判断．【解答】解：由sin2x=1得2x=+2kπ，k∈Z，即x=，k∈Z，由tanx=1，得x=，k∈Z，∴p是q的充要条件．故选：C．4．已知点P的坐标（x，y）满足，过点P的直线l与圆C：x2+y2=16相交于A，B两点，则|AB|的最小值为（）A．B． C． D．【考点】简单线性规划．【分析】作出不等式组对应的平面区域，画出以原点为圆心，半径是4的圆，利用数形结合即可得到在哪一个点的直线与圆相交的弦最短．【解答】解：作出不等式组对应的平面区域如图由图象可知，当P点在直线x=1与x+y=4的交点时，与圆心距离最远，作出直线与圆相交的弦短．P的坐标为（1，3），圆心到P点距离为d=，根据公式|AB|=2，可得：|AB|=2．故选：A．5．“微信抢红包”自2015年以来异常火爆，在某个微信群某次进行的抢红包活动中，若所发红包的总金额为9元，被随机分配为1.49元，1.31元，2.19元，3.40元，0.61元，共5份，供甲、乙等5人抢，每人只能抢一次，则甲、乙二人抢到的金额之和不低于4元的概率是（）A．B．C．D．【考点】列举法计算基本事件数及事件发生的概率．【分析】基本事件总数n==10，再利用列举法求出其中甲、乙二人抢到的金额之和不低于4元的情况种数，帖经能求出甲、乙二人抢到的金额之和不低于4元的概率．【解答】解：所发红包的总金额为10元，被随机分配为1.49元，1.81元，2.19元，3.41元，0.62元，0.48元，共6份，供甲、乙等6人抢，每人只能抢一次，基本事件总数n==10，其中甲、乙二人抢到的金额之和不低于4元的情况有：（0.61，3.40），（1.49，3.40），（1.31，3.40），（2.19，3.40），共有4种，∴甲、乙二人抢到的金额之和不低于4元的概率p==．故选：A．6．设方程2x|lnx|=1有两个不等的实根x1和x2，则（）A．x1x2＜0 B．x1x2=1 C．x1x2＞1 D．0＜x1x2＜1【考点】根的存在性及根的个数判断．【分析】由题意可得y=|lnx|和y=（）x的图象有两个交点，如图可得设0＜x1＜1，x2＞1，求得ln（x1x2）的范围，即可得到所求范围．【解答】解：方程2x|lnx|=1有两个不等的实根x1和x2，即为y=|lnx|和y=（）x的图象有两个交点，如图可得设0＜x1＜1，x2＞1，由ln（x1x2）=lnx1+lnx2=﹣+=，由0＜x1＜1，x2＞1，可得2x1﹣2x2＜0，2x1+x2＞0，即为ln（x1x2）＜0，即有0＜x1x2＜1．故选：D．7．某程序框图如图所示，其中，若输出的，则判断框内应填入的条件为（）A ．n ＜2017B ．n ≤2017C ．n ＞2017D ．n ≥2017 【考点】程序框图．【分析】由输出的S 的值，可得n 的值为2016时，满足判断框内的条件，当n 的值为2017时，不满足判断框内的条件，退出循环，从而得解．【解答】解：由S=++…+=（1﹣）+（）+…（﹣）=1﹣==，解得：n=2016，可得n 的值为2016时，满足判断框内的条件，当n 的值为2017时，不满足判断框内的条件，退出循环，输出S 的值． 故判断框内应填入的条件为n ＜2017？ 故选：A ．8．某几何体的三视图如图所示，则该几何体的体积为（ ）A ．B ．C ．D ． 【考点】由三视图求面积、体积．【分析】几何体为同底的三棱柱和三棱锥的组合体，代入体积公式计算即可求出体积．【解答】解：由三视图可知几何体为直三棱柱和三棱锥的组合体，直棱柱的底面为直角三角形，直角边为1，2，棱柱的高为1，三棱锥的底面与棱柱的底面相同，棱锥的高为1．∴几何体的体积V=+=1+=．故选B．9．为得到函数y=2cos2x﹣sin2x的图象，只需将函数y=2sin2x+1的图象（）A．向左平移个长度单位B．向右平移个长度单位C．向左平移个长度单位D．向右平移个长度单位【考点】函数y=Asin（ωx+φ）的图象变换．【分析】利用三角函数的恒等变换化简函数的解析式，再利用函数y=Asin（ωx+φ）的图象变换规律，得出结论．【解答】解：∵y=2cos2x﹣sin2x=cos2x﹣sin2x+1=2sin（﹣2x）+1=﹣2sin（2x﹣）+1=2sin（2x+）+1，将函数y=2sin2x+1的图象向左平移个长度单位，可得得到函数y=2sin （2x+）+1的图象，故选：C．10．已知M是抛物线C：y2=2px（p＞0）上一点，F是抛物线C的焦点，若|MF|=p，K是抛物线C的准线与x轴的交点，则∠MKF=（）A．45°B．30°C．15°D．60°【考点】抛物线的简单性质．【分析】设点M（，p），K（﹣，0），则直线KM的斜率k=1，即可求得∠MKF=45°．【解答】解：由题意，|MF|=p，则设点M（，p），∵K（﹣，0），∴∠MKF=45°，故选A．11．我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”，设△ABC三个内角A、B、C所对的边分别为a、b、c，面积为S，则“三斜求积”公式为．若a2sinC=4sinA，（a+c）2=12+b2，则用“三斜求积”公式求得△ABC的面积为（）A．B．2 C．3 D．【考点】类比推理．【分析】根据正弦定理：由a2sinC=4sinA得ac=4，则由（a+c）2=12+b2得a2+c2﹣b2=4，利用公式可得结论．【解答】解：根据正弦定理：由a2sinC=4sinA得ac=4，则由（a+c）2=12+b2得a2+c2﹣b2=4，则．故选A．12．若函数在上单调递增，则实数a的取值范围为（）A． B．C．D．[1，+∞）【考点】三角函数的化简求值．【分析】利用导函数的性质研究原函的单调性即可得答案．【解答】解：函数，则f′（x）=﹣sin2x+3a（cosx+sinx）+4a﹣1．∵函数f（x）在上单调递增，可得f′（）≥0，且f′（0）≥0，即，解得：a≥1．∴得实数a的取值范围为[1，+∞）．二、填空题（每题5分，满分20分）13．函数f（x）=lnx的图象在点x=1处的切线方程是y=x﹣1．【考点】利用导数研究曲线上某点切线方程．【分析】先x=1代入解析式求出切点的坐标，再求出函数的导数后代入求出f′（1），即为所求的切线斜率，再代入点斜式进行整理即可．【解答】解：把x=1代入f（x）=lnx得，f（1）=ln1=0，∴切点的坐标为：（1，0），由f′（x）=（lnx）′=，得在点x=1处的切线斜率k=f′（1）=1，∴在点x=1处的切线方程为：y=x﹣1，故答案为：y=x﹣1．14．||=1，||=2，，且，则与的夹角为π．【考点】数量积表示两个向量的夹角．【分析】根据，且可得进而求出=﹣1然后再代入向量的夹角公式cos＜＞=再结合＜＞∈[0，π]即可求出＜＞．【解答】解：∵，且∴∴（）•=0∵||=1∴=﹣1∵||=2∴cos＜＞==﹣∵＜＞∈[0，π]∴＜＞=π；故答案为π15．在锐角△ABC中，内角A，B，C的对边分别为a，b，c，且2asinB=b．（1）求角A的大小；（2）若a=2，b+c=4，求△ABC的面积．【考点】余弦定理；正弦定理．【分析】（1）已知等式利用正弦定理化简，根据sinB不为0求出sinA的值，即可确定出A的度数；（2）利用余弦定理列出关系式，把a，cosA的值代入，并利用完全平方公式变形，把b+c=4代入求出bc=2，联立求出b与c的值，再由sinA的值，利用三角形面积公式即可求出三角形ABC面积．【解答】解：（1）由正弦定理及2asinB=b得：2sinAsinB=sinB，∵sinB≠0，∴sinA=，又A是锐角，∴A=；（2）由a=2，b+c=4，cosA=及余弦定理可得：cosA=，即=，整理得：b2+c2﹣4=bc，即（b+c）2﹣4=3bc，化简得：bc=2，解得：b=c=2，则△ABC面积S=bcsinA=．16．已知双曲线x2﹣=1的左右焦点分别为F1、F2，过点F2的直线交双曲线右支于A，B两点，若△ABF1是以A为直角顶点的等腰三角形，则△AF1F2的面积为4﹣2．【考点】双曲线的简单性质．【分析】由题意可知丨AF2丨=m，丨AF1丨=2+丨AF2丨=2+m，由等腰三角形的性质即可求得4=（2+m），丨AF2丨=m=2（﹣1），丨AF1丨=2，由三角的面积公式，即可求得△AF1F2的面积．【解答】解：双曲线x2﹣=1焦点在x轴上，a=1，2a=2，设丨AF2丨=m，由丨AF1丨﹣丨AF2丨=2a=2，∴丨AF1丨=2+丨AF2丨=2+m，又丨AF1丨=丨AB丨=丨AF2丨+丨BF2丨=m+丨BF2丨，∴丨BF2丨=2，又丨BF1丨﹣丨BF2丨=2，丨BF1丨=4，根据题意丨BF1丨=丨AF1丨，即4=（2+m），m=2（﹣1），丨AF1丨=2，△AF1F2的面积S=•丨AF2丨•丨AF1丨=×2（﹣1）×2=4﹣2，△AF1F2的面积4﹣2，故答案为：4﹣2．三、解答题（本大题共5小题，共70分.）=2a n﹣1．17．已知数列{a n}满足a1=2，a n+1（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设b n=n•（a n﹣1），求数列{b n}的前n项和S n．【考点】数列递推式；数列的求和．【分析】（I）数列{a n}满足a1=2，a n+1=2a n﹣1．变形为：a n+1﹣1=2（a n﹣1）．利用等比数列的通项公式即可得出．（II）b n=n•（a n﹣1）=n•2n﹣1，利用“错位相减法”与等比数列的求和公式即可得出．【解答】解：（I）数列{a n}满足a1=2，a n+1=2a n﹣1．变形为：a n+1﹣1=2（a n﹣1）．a1﹣1=1．∴数列{a n﹣1}是等比数列，∴a n﹣1=2n﹣1，解得a n=1+2n﹣1．（II）b n=n•（a n﹣1）=n•2n﹣1，∴数列{b n}的前n项和S n=1+2×2+3×22+…+n•2n﹣1，∴2S n=2+2×22+…+（n﹣1）•2n﹣1+n•2n，∴﹣S n =1+2+22+…+2n ﹣1﹣n•2n =﹣n•2n =（1﹣n ）•2n ﹣1，可得S n =（n ﹣1）•2n +1．18．某学校高三年级有学生500人，其中男生300人，女生200人，为了研究学生的数学成绩是否与性别有关，现采用分层抽样的方法，从中抽取了100名学生，先统计了他们期中考试的数学分数，然后按性别分为男、女两组，再将两组学生的分数分成5组：[100，110），[110，120），[120，130），[130，140），[140，150]分别加以统计，得到如图所示的频率分布直方图．（1）从样本中分数小于110分的学生中随机抽取2人，求两人恰好为一男一女的概率；（2）若规定分数不小于130分的学生为“数学尖子生”，请你根据已知条件完成2×2列联表，并判断是否有90%的把握认为“数学尖子生与性别有关”？附：K 2=．【考点】独立性检验；频率分布直方图．【分析】（1）根据分层抽样原理计算抽取的男、女生人数，利用列举法计算基本事件数，求出对应的概率值；（2）由频率分布直方图计算对应的数据，填写列联表，计算K 2值，对照数表即可得出概率结论．【解答】解：（1）由已知得，抽取的100名学生中，男生60名，女生40名，分数小于等于110分的学生中，男生人有60×0.05=3（人），记为A1，A2，A3；女生有40×0.05=2（人），记为B1，B2；…从中随机抽取2名学生，所有的可能结果共有10种，它们是：（A1，A2），（A1，A3），（A2，A3），（A1，B1），（A1，B2），（A2，B1），（A2，B2），（A3，B1），（A3，B2），（B1，B2）；其中，两名学生恰好为一男一女的可能结果共有6种，它们是：（A1，B1），（A1，B2），（A2，B1），（A2，B2），（A3，B1），（A3，B2）；…故所求的概率为P==…（2）由频率分布直方图可知，在抽取的100名学生中，男生60×0.25=15（人），女生40×0.375=15（人）；…据此可得2×2列联表如下：所以得K2==≈1.79；…因为1.79＜2.706，所以没有90%的把握认为“数学尖子生与性别有关”…19．如图所示，四棱锥P﹣ABCD的底面为直角梯形，AB⊥AD，CD⊥AD，CD=2AB．点E是PC的中点．（Ⅰ）求证：BE∥平面PAD；（Ⅱ）已知平面PCD⊥底面ABCD，且PC=DC．在棱PD上是否存在点F，使CF ⊥PA？请说明理由．【考点】直线与平面平行的判定；平面与平面垂直的判定．【分析】（1）根据线面平行的判定定理即可证明：BE∥平面PAD；（2）棱PD上存在点F为PD的中点，使CF⊥PA，利用三垂线定理可得结论．【解答】（1）证明：取PD中点Q，连结AQ、EQ．…∵E为PC的中点，∴EQ∥CD且EQ=CD．…又∵AB∥CD且AB=CD，∴EQ∥AB且EQ=AB．…∴四边形ABED是平行四边形，∴BE∥AQ．…又∵BE⊄平面PAD，AQ⊂平面PAD，∴BE∥平面PAD．…（2）解：棱PD上存在点F为PD的中点，使CF⊥PA，∵平面PCD⊥底面ABCD，平面PCD∩底面ABCD=CD，AD⊥CD，∴AD⊥平面PCD，∴DP是PA在平面PCD中的射影，∴PC=DC，PF=DF，∴CF⊥DP，∴CF⊥PA．20．已知圆O：x2+y2=1过椭圆C：（a＞b＞0）的短轴端点，P，Q分别是圆O与椭圆C上任意两点，且线段PQ长度的最大值为3．（Ⅰ）求椭圆C的方程；（Ⅱ）过点（0，t）作圆O的一条切线交椭圆C于M，N两点，求△OMN的面积的最大值．【考点】椭圆的简单性质．（Ⅰ）由圆O过椭圆C的短轴端点b=1，线段PQ长度的最大值为3，a+1=3，【分析】a=2，即可求得椭圆方程；（Ⅱ）设直线MN的方程，由点到直线的距离公式，求得k2=t2﹣1，代入椭圆方程，由韦达定理及弦长公式求得丨MN丨，利用三角形的面积公式及基本不等式的性质，即可求得△OMN的面积的最大值．【解答】解：（Ⅰ）∵圆O过椭圆C的短轴端点，∴b=1，又∵线段PQ长度的最大值为3，∴a+1=3，即a=2，∴椭圆C的标准方程为．（Ⅱ）由题意可设切线MN的方程为y=kx+t，即kx﹣y+t=0，则，得k2=t2﹣1．①联立得方程组，消去y整理得（k2+4）x2+2ktx+t2﹣4=0．其中△=（2kt）2﹣4（k2+4）（t2﹣4）=﹣16t2+16k2+64=48＞0，设M（x1，y1），N（x2，y2），则，，则．②将①代入②得，∴，而，等号成立当且仅当，即．）max=1．综上可知：（S△OMN21．设函数f（x）=lnx﹣ax2+ax，a为正实数．（1）当a=2时，求曲线y=f（x）在点（1，f（1））处的切线方程；（2）求证：f（）≤0；（3）若函数f（x）有且只有1个零点，求a的值．【考点】利用导数研究曲线上某点切线方程；利用导数求闭区间上函数的最值．【分析】（1）求导数，确定切线的斜率，切点坐标，可得切线方程；（2）构造函数，确定函数的单调性与最值，即可证明结论；（3）由题意可知，函数f（x）有且只有1个零点为（1，0），则f′（1）=0，即可得出结论．【解答】（1）解：当a=2时，f（x）=lnx﹣2x2+2x，f′（x）=﹣2x+2，∴f′（1）=1，∵f（1）=0，∴曲线y=f（x）在点（1，f（1））处的切线方程是y=x；（2）证明：f（）=﹣lna﹣+1（a＞0），令g（x）=﹣lnx﹣+1（x＞0），则g′（x）=，∴0＜x＜1时，g′（x）＞0，函数单调递增；x＞1时，g′（x）＜0，函数单调递减，∴x=1时，函数取得极大值，即最大值，∴g（x）≤g（1）=0，∴f（）≤0；（3）解：由题意可知，函数f（x）有且只有1个零点为（1，0），则f′（1）=0，即1﹣2a+a=0∴a=1．[选修4-4：坐标系与参数方程]22．已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线L的参数方程是（t为参数）．（1）求曲线C的直角坐标方程和直线L的普通方程；（2）设点P（m，0），若直线L与曲线C交于A，B两点，且|PA|•|PB|=1，求实数m的值．【考点】参数方程化成普通方程；简单曲线的极坐标方程．【分析】（1）曲线C的极坐标方程是ρ=2cosθ，化为ρ2=2ρcosθ，利用可得直角坐标方程．直线L的参数方程是（t为参数），把t=2y代入+m消去参数t即可得出．（2）把（t为参数），代入方程：x2+y2=2x化为： +m2﹣2m=0，由△＞0，得﹣1＜m＜3．利用|PA|•|PB|=t1t2，即可得出．【解答】解：（1）曲线C的极坐标方程是ρ=2cosθ，化为ρ2=2ρcosθ，可得直角坐标方程：x2+y2=2x．直线L的参数方程是（t为参数），消去参数t可得．（2）把（t为参数），代入方程：x2+y2=2x化为： +m2﹣2m=0，由△＞0，解得﹣1＜m＜3．∴t1t2=m2﹣2m．∵|PA|•|PB|=1=|t1t2|，∴m2﹣2m=±1，解得，1．又满足△＞0．∴实数m=1，1．[选修4-5：不等式选讲]23．已知函数f（x）=2|x+1|+|x﹣2|的最小值为m．（Ⅰ）求实数m的值；（Ⅱ）若a，b，c均为正实数，且满足a+b+c=m，求证： ++≥3．【考点】不等式的证明．【分析】（Ⅰ）分类讨论，即可求实数m的值；（Ⅱ）a+b+c=3，由柯西不等式可得（a+b+c）（++）≥（a+b+c）2，即可证明结论．【解答】（Ⅰ）解：x≤﹣1，f（x）=﹣2x﹣2﹣x+2=﹣3x≥3，﹣1＜x＜2，f（x）=2x+2﹣x+2=x+4∈（3，6），x≥2，f（x）=2x+2+x﹣2=3x≥6，∴m=3；（Ⅱ）证明：a+b+c=3，由柯西不等式可得（a+b+c）（++）≥（a+b+c）2，∴++≥3．2017年4月9日。