模糊综合评判在中学生综合素质评价体系中的应用

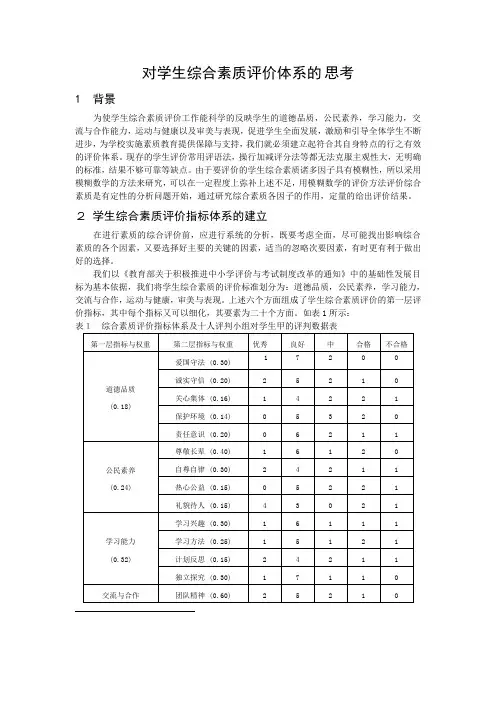
对学生综合素质评价体系的 思考1 背景为使学生综合素质评价工作能科学的反映学生的道德品质，公民素养，学习能力，交流与合作能力，运动与健康以及审美与表现，促进学生全面发展，激励和引导全体学生不断进步，为学校实施素质教育提供保障与支持，我们就必须建立起符合其自身特点的行之有效的评价体系。

现存的学生评价常用评语法，操行加减评分法等都无法克服主观性大，无明确的标准，结果不够可靠等缺点。

由于要评价的学生综合素质诸多因子具有模糊性，所以采用模糊数学的方法来研究，可以在一定程度上弥补上述不足，用模糊数学的评价方法评价综合素质是有定性的分析问题开始，通过研究综合素质各因子的作用，定量的给出评价结果。

２学生综合素质评价指标体系的建立在进行素质的综合评价前，应进行系统的分析，既要考虑全面，尽可能找出影响综合素质的各个因素，又要选择好主要的关键的因素，适当的忽略次要因素，有时更有利于做出好的选择。

我们以《教育部关于积极推进中小学评价与考试制度改革的通知》中的基础性发展目标为基本依据，我们将学生综合素质的评价标准划分为：道德品质，公民素养，学习能力，交流与合作，运动与健康，审美与表现。

上述六个方面组成了学生综合素质评价的第一层评价指标，其中每个指标又可以细化，其要素为二十个方面。

如表1所示：表１综合素质评价指标体系及十人评判小组对学生甲的评判数据表３ 模糊综合评判的数学模型综合评判，又称多元决策，即按一定的标准，对某系统的相关因素进行综合考虑，按一定意义进行排序，以期得到最佳的决策。

对于比较简单的问题，利用一级综合评判就能够得出合理的结果，而在复杂的应用实例中，需要考虑的因素往往很多，每一因素所分得的权重常常很小，因而在作模糊运算时，信息容易丢失，常常出现模型失效的情况，而这时可以采用多层次综合评判模型和广义模糊算子加以改进。

它的一般的数学模型如下： 3.1确定评价对象的因素论域si i U U 1== 其中},,,{21i ip i i i u u u U = ),,2,1(s i =},,,{21S U U U U =称i U 为第一因素集，其元素ij u 为第二层因素集。

模糊综合评价在学生思想品德评判中的应用
曾赤洁
【期刊名称】《甘肃联合大学学报（自然科学版）》
【年(卷),期】2011(025)004
【摘要】在对大学生进行综合素质测评时,思想品德评判是其中很重要的一项内容.本文应用模糊数学的综合评价法对学生的思想品德进行了评价,给出了一种有效的量化评估方法,为进一步进行综合素质测评打下基础.
【总页数】2页(P35-36)
【作者】曾赤洁
【作者单位】临沧师范高等专科学校数理系,云南临沧677000
【正文语种】中文
【中图分类】C934
【相关文献】
1.模糊综合评价在学生管理中的应用 [J], 徐欣
2.模糊综合评价在学生综合素质测评中的应用 [J], 赵华龙
3.模糊综合评价法在学生评教中的应用——以厦门华天涉外职业技术学院为例 [J], 林水生
4.模糊综合评判在学生成绩评价中的应用 [J], 吴延红;丛银凤;闫佩玉;于倩
5.二级模糊综合评判在学生思想品德测评中的应用 [J], 王爱英;许加风;齐山华
因版权原因，仅展示原文概要，查看原文内容请购买。

模糊综合评价方法及其应用研究一、本文概述本文旨在探讨模糊综合评价方法及其应用研究。

我们将对模糊综合评价方法进行概述，阐述其基本原理和特点。

接着，我们将深入探讨模糊综合评价方法在各种领域中的应用，包括但不限于企业管理、环境评估、医疗卫生等。

通过对实际案例的分析，我们将展示模糊综合评价方法在解决实际问题中的有效性和实用性。

我们还将对模糊综合评价方法的未来发展进行展望，以期为其在更多领域的应用提供参考和借鉴。

通过本文的研究，我们希望能够为相关领域的研究者和实践者提供有益的启示和帮助。

二、模糊综合评价方法理论基础模糊综合评价方法（Fuzzy Comprehensive Evaluation，简称FCE）是一种基于模糊数学理论的评价方法，旨在解决那些难以用精确数学语言描述的问题。

这种方法最早由我国学者汪培庄于1983年提出，现已在多个领域得到了广泛应用。

模糊综合评价方法理论基础主要包括模糊集合理论、模糊运算规则和模糊关系矩阵。

其中，模糊集合理论是该方法的核心。

它允许在元素对集合的隶属程度不唯不精确的情况下进行定量描述，从而突破了传统集合理论中元素对集合的隶属关系必须明确的限制。

在模糊综合评价中，评价对象通常被视为一个模糊集合，而评价因素则构成该集合的多个子集。

每个子集都有一个隶属函数，该函数描述了评价对象在不同因素下的隶属程度。

通过对隶属函数进行计算和分析，可以得出评价对象在各个因素上的综合评价结果。

模糊运算规则是模糊综合评价方法的另一个重要组成部分。

它定义了模糊集合之间的运算方式，如并、交、补、差等，使得我们能够根据实际需求进行模糊集合的组合和转换。

模糊关系矩阵则用于描述评价对象与评价因素之间的模糊关系。

该矩阵中的元素表示评价对象在不同因素上的隶属度，是进行模糊综合评价的重要依据。

模糊综合评价方法理论基础包括模糊集合理论、模糊运算规则和模糊关系矩阵。

这些理论和方法为我们在复杂系统中进行综合评价提供了有效的工具。

模糊综合评价法1 模糊综合评价的方法、步骤1）模糊综合评价模糊综合评价法是一种基于模糊数学的综合方法。

该综合评价法根据模糊数学的理论把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。

它具有结果清晰，系统性强的特点，能较好地解决模糊的难以、量化的问题，适合各种非确定性问题的解决。

2）模糊综合评价法分析步骤对某事物的评价往往涉及多个因素，甚至多个级别，需根据诸多因素作出综合评价。

当某些具体问题的评价因素或级别具有模糊性时，所作的综合评价称为模糊综合评价，或综合模糊评判。

模糊综合评价是应用模糊变换原理和最大隶属原则，考虑与被评价事物相关的各个因素，对其所作的综合评价。

模糊综合评价具有计算简捷、实用性强的优点，其分析步骤如下[13]。

(1)建立风险等级评价指标体系。

确定因素集{}n u u u U ,,,21Λ=,将因素集按照属性的类型划分为s 个子集,记作1U ，2U ，…，i U ，其中：{}i in i i i u u u U ,,,21Λ=，nn si i =∑=1；并且应满足UUsi i==Y 1，()s j i j i U U j i ,,2,1,;ΛI =≠=≅。

(2)建立评语集{}m v v v V ,,,21Λ=及确定不同风险等级相应各分级指标的值域，并根据某一具体工况给出各分级指标的数值及所属值域。

其中，m 为风险划分等级个数。

(3)构造隶属函数，确定单因素评价矩阵[]mn iji i r R ⨯=。

(4)专家经验评分法计算各分级指标权重U 的权重集为{}s a a a A ,,,21Λ=，i U 的权重集为{}iin i i i a a a A ,,,21Λ=。

(5)初级评价。

由i U 的单因素评价矩阵i R ，及i U 上的权重集i A ，得第一级综合决策向量：[]im i i i i i b b b R A B Λ21=︒= (1)其中，“°”为模糊关系合成算子。

模糊数学综合评判原理在高中生选专业评价中的应用模糊数学综合评判原理是指将评价对象的各种属性用模糊数学中的隶属函数表示出来，然后通过模糊综合评价方法求出综合评价值的过程。

在高中生选专业评价中，可以将感兴趣程度、学科基础、职业前景等多种属性用模糊数学表示，并通过模糊综合评价方法得出高中生对各专业的综合评价值，从而为其选择专业提供参考依据。

具体而言，高中生选专业评价中的模糊数学综合评判原理应用可分为以下三个步骤：
1. 建立评价指标体系。

确定影响选专业的因素，例如感兴趣程度、学科基础、职业前景等，将其转化为模糊度量。

2. 确定隶属函数。

通过询问高中生或专家意见，设计每个指标的隶属函数，即将该指标的取值范围和评价值之间的对应关系定义为一个隶属函数。

3. 进行模糊综合评价。

将考虑到的指标的隶属函数进行数据处理，即将各指标的隶属函数进行加权平均或其他运算得到专业的评价值，可将综合评价值转换成固有的序数或等级判断。

应用模糊数学综合评判原理在高中生选专业评价中，能够较好地解决评价对象中存在模糊不确定性的问题，提高评价的准确程度，为高中生提供科学可靠的选专
业建议。

模糊综合评价法在中职数学实验教学质量评价中的应用模糊综合评价法（Fuzzy Comprehensive Evaluation）是一种综合评价方法，它将模糊数学理论引入到评价中，能够更全面地考虑评价对象的各种特征和因素，对于中职数学实验教学质量的评价具有重要的意义。

本文将以中职数学实验教学质量评价为背景，探讨模糊综合评价法在其中的应用。

一、中职数学实验教学的特点和挑战中职数学实验教学是中等职业学校数学教学中的重要组成部分，与传统的理论教学相比，实验教学更加贴近学生的生活和实际应用，能够培养学生的动手能力、实验能力和创新能力。

中职数学实验教学也面临着一些挑战：实验设备条件不足、学生动手能力弱、实验教学资源缺乏等，这些问题对于提高实验教学的质量提出了新的要求。

1. 考虑多个因素模糊综合评价法能够考虑多个因素对于实验教学质量的影响，比如实验内容的设计、实验设备的完好程度、学生的动手能力和实验报告的撰写质量等。

这些因素都对实验教学的质量产生影响，而且这些因素之间往往存在相互关联和影响，模糊综合评价法能够很好地处理这种关联。

2. 获取模糊评价值模糊综合评价法不仅仅能够考虑到多个因素，还能够将这些因素的影响程度通过模糊数学的方式转化为模糊评价值，将评价问题的模糊性和不确定性纳入到了评价中。

这样一来，评价结果更加客观和真实。

3. 构建模糊综合评价模型通过构建合理的模糊综合评价模型，采用合适的评价指标和评价方法，可以实现对实验教学质量的全面评价。

模糊综合评价模型能够将各个方面的评价信息进行整合，给出一个综合的评价结果。

1. 设计合理的评价指标在进行中职数学实验教学质量评价时，需要首先确定评价的指标体系。

评价指标需要区分主客观指标，如实验设计的科学性和学生的实验报告撰写规范性属于客观指标，而学生动手能力和实验设备的完好程度属于主观指标。

2. 收集评价数据收集中职数学实验教学质量评价数据是评价的基础，包括学生的实验报告、教师的实验设计方案、实验设备的完好程度等。