当前位置：文档之家 › 大学物理圆周运动

大学物理圆周运动

  • 格式：ppt
  • 大小：753.50 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

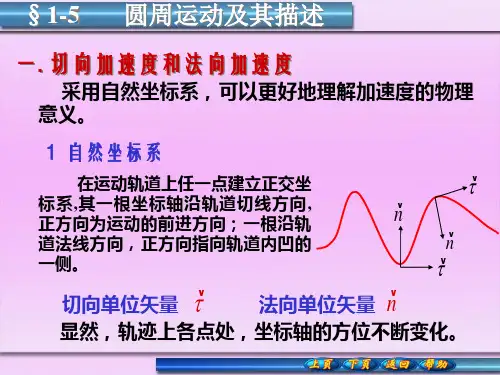
大学物理 圆周运动及其描述

大学物理 圆周运动及其描述
dv dnv
即，
dv d nv d(R ) nv 1 ds nv v nv
dt dt Rdt R dt R
因此
a

dv dt
v
v2 R
nv
e t
oe n
d
ds
e t
P
v
dv
d v
P
切向加速度和法向加速度
即圆周运动的加速度可分解为两个正交 分量：
2R cos
(7.27 105 )2 6.73106 cos
3.37 102 cos (m/s 2 )
P点加速度的方向在运动平面上由P指向地轴。
线量与角量之间的关系
例如:已知北京、上海和广州三地的纬度分别 是北纬3957、3112和 2300，则三地的v 和 an 分别为：
如图所示 一质点作圆周运动：
在t 时间内，质点的角位移为，则 A、B间的有向线段与弧将满足下面的
关系
t+t B 0+

lim AB lim AB
t 0
t 0
R
A t0
+
O
x
两边同除以t，得到速度与角速度之间的关系：
v R
线量与角量之间的关系
上式两端对时间求导，得到切向加速度与角加 速度之间的关系：
显然，轨迹上各点处，坐标轴的方位不断变化。
切向加速度和法向加速度
2 自然坐标系下的加速度
由于质点速度的方向一定沿着轨迹的切向，因
此，自然坐标系中可将速度表示为：
vr

vv
ds v
dt
由加速度的定义有
a
ddvt
dv vv
dt

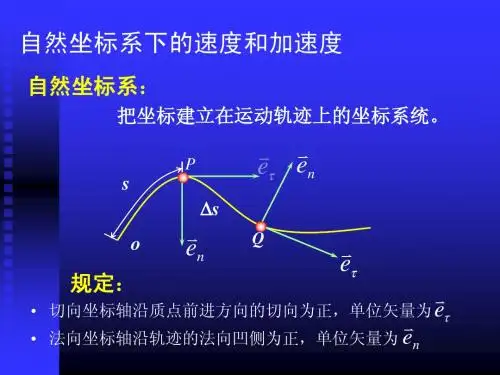
大学物理01_2圆周运动

大学物理01_2圆周运动

2
讨论
det dt
O
Δ
et et (t t ) - et (t )
当： t 0 , 0 有 e t e t 方向
et t t
s
P 1
P2
et t
et et
et
et t t
自然坐标系下的速度和加速度
自然坐标系：
把坐标建立在运动轨迹上的坐标系统。 s o
P
e en
s
Q
en
•
•
切向坐标轴沿质点前进方向的切向为正，单位矢量为 e 法向坐标轴沿轨迹的法向凹侧为正，单位矢量为 en
规定：
e
s
P
s en
e
Q
o
e
v
质点位置： s st 路程：
（2 ）
at an
解得
b R t c c
at r (2) 0.2 0.4 m s 2
1
v
an r 2 0.2(2 1 4) 2 0.8 m s 2
2 a at2 an 0.89 m s 2
1 an 1 0.8 tan tan 63.4 at 0.4
2 n
2 t
速度的方向（以与切线方向的夹角表示）：
an arctan a
例：抛体运动
an

at
g
2 v d a = et + v e n = at + a n R dt
讨论:
v d et 的产生是由于 1. 切向加速度 at = dt 速度 v 大小的变化。 2 v 法向加速度 a n = e n 的产生是由于 R 速度 v 方向的变化。 只有速度方向的改变，所以加速度为 v 2 R

大学物理102 第一章第二节 圆周运动

大学物理102 第一章第二节 圆周运动

• 速度与角速度的矢量关系式
dr dθ r dθ v dt dt dt 大小 v r (标量式) 方向
k r ω r ω r (由右手法则确定)
• 加速度与角加速度的矢量关系式
dr dv d(ω r ) dω a r ω β r ω v dt dt dt dt ω 第一项 r aτ 大小 a r
解：
本题涉及：
风、地、车上人
V风对人 V风对地 V地对人
西
★人感到风是从西北方向吹来
北
y
东
x
V风对人
南
例3 一个带篷子的卡车，篷高为h=2 m ，当它停在马路边时， 雨滴可落入车内达 d=1 m ，而当它以15 km/h 的速率运动 时，雨滴恰好不能落入车中。 求 雨滴的速度矢量。
v K 2 2 4 s 3 t Rt
2

当t 0.5s v R 4 Rt
2
4t
2
dv 2 a 8 Rt 8 . 0 ( m/s ) v 4 Rt 2.0(m/s) τ dt v2 2 2 2 2 an 2.0(m/s ) a an a 8.25(m/s ) R an arctan( ) 13.6 a
解 根据速度变换定理
va vr ve
ve
h
d
va
画出矢量图
h arctan 63.4 d
ve 15 va 33.5km/h 9.3 m/s cos α cos
2. 适当画出矢量图，有助于分析问题。

大学物理圆周运动

大学物理圆周运动

引言：大学物理中，圆周运动是一个重要的概念和题目，是建立在基础的运动学知识上的一个重要应用。

本文将详细介绍大学物理中的圆周运动（二），包括角速度、角加速度、牛顿定律在圆周运动中的应用以及相关的数学推导和实践应用。

概述：圆周运动是指物体在一个固定圆轨道上运动的情况。

在这种运动中，物体以一个恒定的速度绕着圆心旋转。

圆周运动是一种重要的运动形式，广泛应用于物理学、工程学和天文学等领域。

本文将着重介绍圆周运动中的角速度、角加速度以及相关的应用和推导。

正文：1.角速度的定义和计算1.1角速度的定义1.2圆周运动中的角速度计算方法1.3角速度与线速度的关系2.角加速度的定义和计算2.1角加速度的定义2.2圆周运动中的角加速度计算方法2.3角加速度与线加速度的关系3.牛顿定律在圆周运动中的应用3.1牛顿第一定律在圆周运动中的应用3.2牛顿第二定律在圆周运动中的应用3.3牛顿第三定律在圆周运动中的应用4.圆周运动相关的数学推导4.1圆周运动中的位移、速度和加速度的关系4.2圆周运动中的周期和频率的关系4.3圆周运动中的力学能量守恒定律5.圆周运动的实践应用5.1汽车在转弯时的圆周运动5.2行星围绕太阳的圆周运动5.3粒子加速器中的圆周运动总结：圆周运动是大学物理中一个重要的概念和题目，掌握相关的知识和应用对于深入理解物体的运动学特性和动力学规律具有重要意义。

本文通过对角速度、角加速度、牛顿定律在圆周运动中的应用以及相关的数学推导和实践应用的详细阐述，希望能够对读者加深对圆周运动的认识和理解，提高解题能力和应用能力。

在实践应用中，圆周运动的概念和方法也被广泛应用于各个领域，为相关领域的发展和进步做出了重要贡献。

大学物理-圆周运动

大学物理-圆周运动
§1-6 圆周运动
圆周运动是曲线运动的一个重要特例 圆周运动中质点的速度的大小和方向都在改变
存在两个加速度
法向加速度（速度方向变化引起） 用 an 表示 切向加速度（速度大小变化引起） 用 at 表示
一．匀速率圆周运动
质点作匀速率圆周运动时，速
度大小不变，方向改变，只有 法向加速度用 an
a
a
lim v lim sv
解：v dS / dt b ct
a dv / dt c t
a b ct2 / R n
根据题意： at= an
c b ct2 / R
t Rb cc
三、一般曲线运动
总加速度
a
a
n
a
t
v2 R
e
n
dv
dt
e
t
用曲率半径 代替R
在曲线上某一点找到一个 和它内切的半径最大的圆， 这个圆的半径就定义为曲 率半径。
v vn vt
lim
vn
lim
v t
t t 0
t t 0
a a
n
t
法向加速度
an
v2 RΒιβλιοθήκη v2 v1or
v vt v2vn v1
切向加速度
at
lim vt t vt
t 0
t
dv dt
a t 大小
at
dv dt
a t 方向
v 当 v2 v1 时, a t 与 方向一致
v2 v1
o
r
v 当 v2 v1 时, a t 与 方向相反
总加速度
aa a
n
t
v2
e
dv
e
R n dt t

物理必修二圆周运动知识点总结

物理必修二圆周运动知识点总结

物理必修二圆周运动知识点总结一、圆周运动的基本概念定义：质点以某点为圆心，半径为r在圆周上运动，其轨迹是圆周或圆弧的运动称为圆周运动。

圆周运动是曲线运动的一种，因此它一定是变速运动。

分类：圆周运动可分为匀速圆周运动和变速圆周运动。

匀速圆周运动指的是线速度大小处处相等的圆周运动，尽管线速度大小不变，但由于方向时刻改变，因此匀速圆周运动仍然是变速运动。

二、描述圆周运动的物理量线速度：描述质点沿圆周运动的快慢的物理量，其方向是质点在圆周上某点的切线方向。

在匀速圆周运动中，线速度大小不变，但方向时刻改变。

角速度：描述质点绕圆心转动的快慢的物理量，是矢量，其方向用右手螺旋定则确定。

在匀速圆周运动中，角速度大小和方向都不变。

周期和频率：周期是质点完成一次圆周运动所需的时间，频率是周期的倒数，表示单位时间内完成圆周运动的次数。

在匀速圆周运动中，周期和频率都不变。

向心力：使质点沿圆周运动的力，方向始终指向圆心。

向心力的大小与线速度、角速度和半径有关，其作用是改变质点的速度方向，使质点能够持续沿圆周运动。

三、圆周运动的规律和应用牛顿第二定律在圆周运动中的应用：通过向心力表达式，可以推导出圆周运动的线速度、角速度、周期等物理量之间的关系。

圆周运动在日常生活和科技领域中的应用：例如电动机转子、车轮、皮带轮等的运动都是圆周运动。

此外，人造卫星、行星运动等天体运动也可以视为圆周运动。

四、离心运动做圆周运动的物体，由于惯性，总有沿着切线方向飞去的倾向。

一旦受力突然消失或合力不足以提供所需的向心力时，物体就会做离心运动。

以上是物理必修二中关于圆周运动的主要知识点总结。

这些知识点是理解和分析圆周运动的基础，对于后续学习物理的其他部分以及应用物理知识解决实际问题具有重要意义。

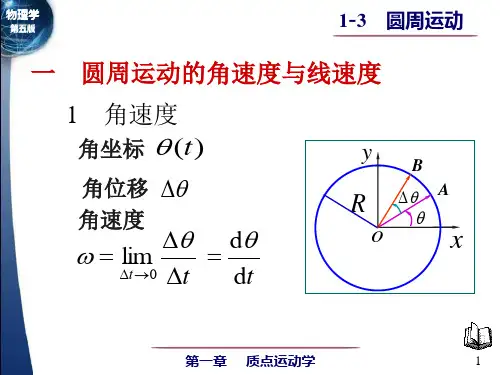
大学物理之 圆周运动

大学物理之 圆周运动
第一章 质点运动学
13
物理学
第五版
1-3
v 0 R 0 0 . 50 18 . 8 9 . 42 m / s
圆周运动
解：（1）吊扇翼尖P原来的转动角速度为
v
则翼尖的线速度为
0 2 n
2 180 60 18 .8 rad / s
P at an aθ ω
R
2
方向
tan
1 a t an
tan
1
0 . 105 2 . 16
2 . 78

第一章
质点运动学
15
物理学
第五版
作业
1-3
圆周运动
• P36-38
1.6 1.12 1.16
结束
第一章
质点运动学
16
物理学
第五版
1-3
圆周运动
例 一歼击机在高空 A vA 点A时的水平速率为1 940 B km·-1 ,沿近似圆弧曲线俯 r h 冲到点B，其速率为2 192 -1 , 经历时间为3 s , km· h vB o 设 AB 的半径约为 3.5 km , 飞机从A到B过程视为匀变速率圆周运动，不 计重力加速度的影响，求：(1) 飞机在点B的 加速度；(2)飞机由点A到点B所经历的路程.
4
物理学
第五版
1-3
圆周运动
• 所以，
法向加速度
v
det dt
v e n
2
那么，
a n v R dv v a e v e 2
dt
t n
v
(v )n
at an
第一章 质点运动学
(v )t

大学物理圆周运动教案

大学物理圆周运动教案

课时：2课时教学目标：1. 理解圆周运动的概念，掌握匀速圆周运动和变速圆周运动的特点。

2. 掌握线速度、角速度、周期、频率等物理量的定义和计算方法。

3. 理解向心力的概念，掌握向心力公式及其应用。

4. 能够运用圆周运动的知识解决实际问题。

教学重点：1. 线速度、角速度、周期、频率等物理量的定义和计算方法。

2. 向心力的概念及其应用。

教学难点：1. 向心力的来源和作用。

2. 圆周运动中的能量守恒。

教学过程：第一课时一、导入1. 回顾物体运动的基本形式，引入圆周运动的概念。

2. 提出问题：什么是圆周运动？圆周运动有哪些特点？二、新课讲授1. 圆周运动的概念：物体沿圆周轨迹运动的现象。

2. 匀速圆周运动的特点：线速度大小不变，方向时刻改变；角速度大小不变，方向始终指向圆心。

3. 线速度、角速度、周期、频率的定义和计算方法。

- 线速度：物体在单位时间内沿圆周轨迹所通过的弧长。

- 角速度：物体在单位时间内绕圆心转过的角度。

- 周期：物体完成一周圆周运动所需的时间。

- 频率：单位时间内物体完成的圆周运动次数。

4. 线速度、角速度、周期、频率之间的关系：v = ωr，T = 1/f，n = 1/T。

三、课堂练习1. 计算匀速圆周运动中物体在某一时刻的线速度和角速度。

2. 根据线速度和角速度的关系，计算匀速圆周运动中物体的半径。

第二课时一、复习导入1. 回顾匀速圆周运动的特点和物理量的计算方法。

2. 提出问题：匀速圆周运动中物体受到的向心力是什么？二、新课讲授1. 向心力的概念：使物体沿圆周轨迹运动的力。

2. 向心力公式：F = mω²r，其中m为物体质量，ω为角速度，r为半径。

3. 向心力的来源：物体受到的合外力。

4. 向心力的应用：- 计算向心力的大小。

- 分析向心力对物体运动的影响。

三、课堂练习1. 计算匀速圆周运动中物体所受的向心力。

2. 分析向心力对物体运动的影响。

四、总结1. 回顾圆周运动的特点和物理量的计算方法。

大学物理12圆周运动

大学物理12圆周运动
S系 (Oxyz)
基本参考系
S'系(O' x' y' z')
运动参考系
u是S’系相对S系
运动的速度
1-3 相对运动
yy'
P P'
*
oo'
xx'
t0
y
o
P
y'
D
r
P'
uQ
r'
xx'
ut o' t t
第一章 质点运动学
22
物理学
第五版
位移关系
r r'D 或 r r'ut
速度变换
r r' u t t v v'u
理解伽利略速度变换式, 并会用它求简 单的质点相对运动问题．
第一章 质点运动学
2
物理学
第五版
质点运动的自然坐标描述
自然坐标系 —— 坐标原点固接 于质点, 坐标轴沿质点运动轨道
1-2 圆周ev运t 动 evt B
的切向和法向的坐标系，叫做自
然坐标系。切向以质点前进方向 A
为 侧正方，向记 为做 正，ev记t ，做法ev向n以。曲线凹
y
A
r
二 圆周运动的角速度
❖ 角坐标 (t)
o
❖角位移
y
xx
B
❖ 角速度
lim
d
t0 t dt
r A
o
x
单位：rad·s-1
第一章 质点运动学
4
物理学
第五版
1-2 圆周运动
❖ 速率 v lim Δs r lim Δθ
Δt0 Δt
Δt0 Δt

力学中的圆周运动

力学中的圆周运动

力学中的圆周运动圆周运动（Circular Motion）是力学中一种重要的运动形式，广泛应用于各个领域，与人们的日常生活息息相关。

本文将从基本概念、运动规律以及实际应用等方面介绍力学中的圆周运动。

一、基本概念圆周运动是物体在半径为r的圆周轨道上运动的过程。

在圆周运动中，物体保持一定的速度，并不断改变运动方向。

根据力学定律，物体沿圆周运动所受的向心力可以计算为Fc = mv²/r，其中Fc为向心力，m为物体的质量，v为物体的速度，r为圆周半径。

二、运动规律在圆周运动中，可以根据运动规律来计算与描述物体的运动状态。

1. 圆周运动的速度物体在圆周运动中的速度可以通过v = ωr来计算，其中v为线速度，ω为角速度，r为圆周半径。

角速度可以表示物体单位时间内绕圆周运动的角度变化量。

2. 圆周运动的加速度物体在圆周运动中的加速度可以通过a = αr来计算，其中a为加速度，α为角加速度，r为圆周半径。

角加速度可以表示物体单位时间内角速度的变化量。

3. 圆周运动的周期与频率圆周运动的周期T是一个物体绕圆周一周所需的时间，可以通过T = 2π/ω来计算，其中π为圆周率。

频率f是圆周运动单位时间内的循环次数，可以通过f = 1/T来计算。

三、实际应用圆周运动在生活中有着广泛的应用，以下是一些实际场景的例子：1. 环形公路上的车辆行驶当车辆在环形公路上行驶时，车辆会保持一定的速度并沿着圆周轨道行驶，这就是圆周运动的一个实际应用。

向心力将车辆约束在圆周轨道上，保证了行驶的稳定性。

2. 标注行进半径的扭转开关在很多扭转开关上，设计师会标注行进半径，这是因为该开关需要旋转一定角度才能开启或关闭电路。

这个旋转的过程就是一个圆周运动，通过设定行进半径可以控制旋转的灵敏度。

3. 悬挂球体的运动当有一个绳子固定在某一点，下面悬挂着一个球体时，球体做圆周运动。

绳子提供了向心力，使球体沿着圆周轨道运动。

总结：力学中的圆周运动是一种重要的运动形式，涉及到很多基本概念和运动规律。

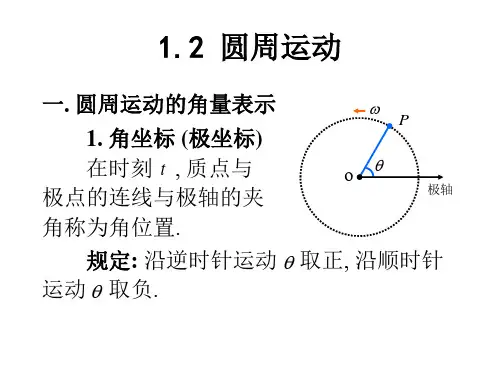
大学物理第1章第2节-圆周运动

大学物理第1章第2节-圆周运动
2 v v lim P Q an r t 0 t r
v2 an an n n r
称为法向加速度.
(2) at lim(vt t )
方向: 当 t 0 时,
0 vt v1 vt v at 沿平行于 v
lim | OA || v1 |
n v | v |
v
O
v2
| OA || v1 |
A
vt
Q
称为切向加速度
v 2 dv a an at n r dt
加速度的大小
a a a
2 n 2 t
P
an
O
v2
A
v2
作| OA || v1 | , 记 PA vn , AQ vt , v vn vt
v a lim t 0 t vn vt v v v lim lim t 0 t t 0 t
例1.6 某发动机工作时, 主轴边缘一点 做圆周运动的方程为 t 3 4t 3 (SI). 求: (1) t 2s 时, 该点的角速度和角加速度 为多大? (2) 若主轴直径 D 40cm , 则时 t 1s , 该 点的速率和加速度. 解 (1) 已知运动方程求角速度和角加速 度是微分问题.
t 0
v1
P
O
| OA || v1 |
vn
v
vt
Q
A
v2
(即 v1 ) 的方向.
大小:
| vv | t1 | at | lim t 0 t O
| vt | v2 v1 t 0

圆周运动的基本概念与公式推导

圆周运动的基本概念与公式推导

圆周运动的基本概念与公式推导一、圆周运动的基本概念1.圆周运动：物体沿着圆周轨道运动的现象称为圆周运动。

2.圆心：圆周运动的中心点，通常用O表示。

3.半径：从圆心到圆周上任意一点的线段，用r表示。

4.角速度：描述圆周运动快慢的物理量，表示单位时间内物体绕圆心转过的角度，用ω表示。

5.周期：圆周运动一次完整往返所需要的时间，用T表示。

6.频率：单位时间内圆周运动的次数，与周期互为倒数，用f表示。

二、圆周运动的公式推导1.线速度公式：线速度（v）= 半径（r）× 角速度（ω）2.角速度与周期的关系：角速度（ω）= 2π / 周期（T）即ω = 2π / T3.向心加速度公式：向心加速度（a）= 半径（r）× 角速度的平方（ω²）即a = rω²4.向心力公式：向心力（F）= 质量（m）× 向心加速度（a）即F = ma = mrω²三、圆周运动的分类1.匀速圆周运动：角速度恒定的圆周运动。

2.非匀速圆周运动：角速度变化的圆周运动。

四、圆周运动的应用1.匀速圆周运动的应用：2.非匀速圆周运动的应用：–匀速圆周运动的加速器五、注意事项1.在研究圆周运动时，要区分角速度、线速度、向心加速度和向心力等概念，并理解它们之间的关系。

2.注意圆周运动的分类，掌握匀速圆周运动和非匀速圆周运动的特点及应用。

3.在实际问题中，要根据题目条件选择合适的公式进行分析。

习题及方法：1.习题：一个物体在半径为2m的圆形轨道上做匀速圆周运动，角速度为2rad/s，求物体的线速度和向心加速度。

根据线速度公式v = rω，将给定的半径 r = 2m 和角速度ω = 2rad/s 代入公式，得到物体的线速度：v = 2m × 2rad/s = 4m/s根据向心加速度公式a = rω²，将给定的半径 r = 2m 和角速度ω = 2rad/s 代入公式，得到物体的向心加速度：a = 2m × (2rad/s)² = 8m/s²答案：物体的线速度为4m/s，向心加速度为8m/s²。

圆周运动的规律及其应用课件

圆周运动的规律及其应用课件
合理选择转动半径
选择合适的转动半径，以减小离 心力对圆周运动的影响。
增加质量
增加运动物体的质量，可以降低离 心力对圆周运动的影响。
增加约束力
通过增加约束力，如使用弹性绳或 弹簧，可以减小离心运动的影响。
如何利用圆周运动进行工作？
旋转机械
利用圆周运动设计旋转机械，如 电动机、发电机和泵等，以实现
能量的转换和传输。
旋转木马的速度和旋转半径可以根据需要进行调整，为游客提供安全、舒适的旋 转体验。
洗衣机脱水原理
洗衣机脱水原理基于离心力作用，通过高速旋转将衣物中的 水分甩出。
脱水时，洗衣机内桶高速旋转，使衣物受到离心力作用紧贴 内桶壁，同时衣物中的水分被甩出，从而达到脱水的目的。
05 圆周运动的挑战与解决方 案
离心力
当物体做圆周运动时，会受到一个始 终指向圆外的力，称为离心力。离心 力的大小与速度的大小和半径有关， 速度越大，半径越小，离心力越大。
匀速圆周运动
01
匀速圆周运动是指物体做圆周运 动时，速度大小保持不变。匀速 圆周运动中，向心加速度的大小 不变，方向始终指向圆心。
02
匀速圆周运动中，物体所受的合 外力提供向心力，即合外力等于 向心力。
如何保持稳定的圆周运动？
确定合适的转动半径
01
根据物体质量和运动速度，选择合适的转动半径，以确保圆周
运动稳定。
保持恒定的角速度
02
在圆周运动过程中，应尽量保持恒定的角速度，以减少不稳定
性。
减小摩擦力
03
减小运动过程中的摩擦力，如使用润滑油或改进轴承设计，有
助于提高圆周运动的稳定性。
如何减小离心运动的影响？
圆周运动的周期和频率

大学物理-圆周运动

大学物理-圆周运动

o r
v1
et1
A
et2et et1
法向加速度,方向沿半径指向圆心,反映速度方向变化.
物第综理五版学上所述：
(1) 一般圆周运动加速度
a at an
a ddvt et ven
切向加速度 法向加速度
1-2 圆周运动
y
a
vaet t
o an
en A
第五版
1-2 圆周运动
a at2 an2 109m s2 A
vA
B
arctan at 12.4o
an
r an
a
o
at
vB
（2）矢径 r所转过的角度

At

1t 2
2
s

r

v At

1 2
att 2
1722m
第一章 质点运动学
18
如 t 0 时, 0 ， 0
可得：
0 t θ θ0 0t
1 t 2
2

2

2 0

2 (
0)
第一章 质点运动学
14
物理学
第五版
1-2 圆周运动
匀变速率圆周运动与匀变速率直线运动类比
0 t θ θ0 0t

1 t
2
2
2
一.平面极坐标
质点在A点的位置由
（r,θ）来确定．
平面极坐标与平面直 角坐标系之间的变换
x r cos
y
y

o
A
r
x x 极轴
角位置
y r sin
强调 1. 平面极坐标只用于平面描述。

《大学物理》圆周运动

《大学物理》圆周运动

得切向加速度与角加速度的关系为a r
dt
而法向加速度an
v2 r
dt r 2
质点作匀变速圆周运动时的角速度、角位移与角加速度的关系式
为：
ω ω0 t
θ θ0 ω0t t 2 / 2
ω2 ω02 2 (θ θ0 )
v v0 at
x
x0
v0t
at2 / 2
v2
v02
2a( x
(R
sin
ti
R
c
ostj )
a(t)
dv(dtt)
2 (R
costi
R 2
sin tj)
dt
速度、加速度也可以用其在x、y方向上的分量来表示
二、自然坐标系下的描述
自然坐标系：以动点为坐标原点，以动点所在轨道处的切线和 法线为坐标轴（切向指向前进方向，法向指向曲率中心），、n 为切、法向的单位矢量。
1-16.飞轮作匀减速转动 , 在 5 秒内角速度由 40πrad/s 减到 10πrad/s , 则飞轮在这 5秒内总共转过了多少圈?飞轮再经过多 少时间才能停止转动?
课后习题 1-8 1-9 1-10
（2）如
匀变速直线运动
（3）如 a 0,a；则0 质点作
n
t
匀速直线运动
（4）如
a n
0,
a t
0；, 质 点 c作
一般曲线运动
（5）如 a 0, a 0；, 质点c作
n
t
变速圆周运动
（6）如
a n
0,
a t
c；, 质点c作
匀变速圆周运动
（7）如 a 0, a 0；, 质点c作
dt dt
dt dt

大学物理圆周运动ppt讲解

大学物理圆周运动ppt讲解
1 – 3 圆周运动
物理学教程 （第二版）
平面极坐标
设一质点在 Oxy 平面内
运径动r，与某时x刻轴它之位间于的点夹A角.矢
为 . 于是质点在点 A 的位
置可由 A(r, ) 来确定 .
y

o
A
r
x
以 (r, ) 为坐标的参考系为平面极坐标系 .
它与直角坐标系之间的变换关系为
x r cos y r sin
第一章 质点运动学
1 – 3 圆周运动
一 圆周运动的角速度和角加速度
角坐标 (t)
角速度 (t) d (t)
dt
速率
vltim0st rltim0t
v

ds dt
v(t) r(t)
角加速度 d
dt
第一章 质点运动学
物理学教程 （第二版）
y
B
r A
v2
en
et
v1
o r
v2vt v vv1n

1 – 3 圆周运动
a atet anen
物理学教程
a 与 et 夹角
（第二版）


tan1
an at
an 0 0 π
切向加速度
at

dv dt

r
0, 0 π2, v 增大

o
x
1 – 3 圆周运动
二 匀速率圆周运动
v
v


ddstret
vr
加速度大小 a


vet
v t
lim
ret
v r r t
v v2
t0 t r

大学物理 第一章 第二节圆周运动与一般平面曲线运动

大学物理 第一章 第二节圆周运动与一般平面曲线运动

2、角加速度
lim
t 0 t
d
dt
d 2
dt 2
方向？
四、 圆周运动中线量和角量的关系 1、线速度与角速度 v R
角速度 的方向:
按“右旋规则”确定 角加速度 的方向: 加速时与方向相同 减速时与方向相反
y
R
o
x
2、切向加速度与角加速度 3、 法向加速度与角速度
a R
an
v2 R
v
R 2
4、速度分量式
（1）可将抛体运动分解为 沿x和y 两个方向的独立运动。
立进行的运动迭加而成。
※
抛体运动方程的矢量形式
v
(v0cos )i
(v0
sin
gt)
j
v0t
r
1
gt
2
2
v dr dt
r
t vdt
0
t 0
(vxi
vy
j )dt
(v0t
cos
)i
(v0t
sin
1 2
gt2 )
j
（2）也可将抛体运动分解为沿初速度方向的匀速直线运动和
t
a a
ax2
a
2 y
R 2
7
五、匀变速率圆周运动
常量， 故 at r，an r 2
dω 常量，
dt
又
dω dt d dt，
如 t 0 时, 0 ， 0
可得：
0 t θ θ0 0t
1 2
t
2
2
2 0
2 (
0)
匀变速率圆周运动
0 t
θ
θ0
0t
1 2
t

大学物理圆周运动

大学物理圆周运动

圆周运动的分类
总结词
圆周运动可以根据不同的分类标准进行分类，如匀速圆周运动和变速圆周运动。
详细描述
匀速圆周运动是指物体在转动过程中角速度保持不变的运动，其特点是线速度的 大小不变，只有方向改变。变速圆周运动是指物体在转动过程中角速度发生变化 的运动，其特点是线速度的大小和方向都可能改变。
02
匀速圆周运动
ቤተ መጻሕፍቲ ባይዱ 匀速圆周运动的定义
总结词
匀速圆周运动是指物体沿着圆周路径做等速运动，即线速度大小恒定，方向时刻改变。
详细描述
匀速圆周运动是圆周运动的一种特殊形式，其特点是线速度的大小恒定，方向始终沿着圆周的切线方 向。匀速圆周运动中，物体的加速度大小恒定，方向始终指向圆心，即向心加速度的大小恒定，方向 始终与线速度垂直并指向圆心。
圆周运动的描述
总结词
圆周运动可以通过角速度、角加速度、转速等物理量进行描述。
详细描述
角速度是描述圆周运动快慢的物理量，单位为弧度/秒，其值等于物体转动一周所需的时间。角加速度是描述圆 周运动加速度的物理量，单位为弧度/秒²，表示物体转动过程中角速度的变化率。转速是描述圆周运动频率的物 理量，单位为转/分，表示物体每分钟转动的圈数。
03
非匀速圆周运动
非匀速圆周运动的定义
特点
加速度不指向圆心，存在 切向加速度和法向加速度 。
非匀速圆周运动
与匀速圆周运动相对，速 度大小或方向发生变化的 圆周运动。
切向加速度
改变速度大小，不改变速 度方向。
法向加速度
改变速度方向，不改变速 度大小。
非匀速圆周运动的描述
描述参数
线速度、角速度、周期、频率、向心加速 度等。
离心力的计算

大学物理§1.2 圆周运动

大学物理§1.2 圆周运动

a dv dt
gt v0 sin v0 g t 2v0 gt sin
2 2 2
g
o
P
(t )
☻ a an a
2 v ) 2 ( dv ) 2 dv 大小: a a a ( (对曲线运动) dt r dt 2 n 2
方向: arctg (
an a
)
Chapter 1. 质点运动学 主编：杨茂田
§1. 2 圆周运动
P. 14 / 21 .
如何直观反映加速度 a 是怎样随着速度的大小和方
向变化而变化
Chapter 1. 质点运动学 主编：杨茂田
§1. 2 圆周运动
P. 6 / 21 .
自然坐标系是建立在物体运动的轨迹上的，有两个坐
标轴，切向坐标轴和法向坐标轴。
☻切向坐标轴沿轨迹的切线
ˆ en
ˆ e
ˆ en
(运动)方向； 法向坐标轴
Chapter 1. 质点运动学 主编：杨茂田
§1. 2 圆周运动
P. 1 / 21 .
§1.2
圆周运动
Chapter 1. 质点运动学 主编：杨茂田
§1. 2 圆周运动
P. 2 / 21 .
一、圆周运动的角量描述
在极坐标系中可用一组角量描述：
☻角位置：极角 θ (rad)
☻角位置变动：角位移 △θ ( rad ) ☻角位置变动快慢：角速度 ω
2

x v0t cos
y v0t sin 1 gt 2 v x dx v0 cos dt dy v0 sin gt vy dt
2
y
v0
an
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第一章 质点运动学
1 – 3 圆周运动
物理学教程 （第二版）
三 变速圆周运动 切向加速度和法向加速度
a liv m v v tt l iv m nv n l tla ti i m 0 m 0 t d d v v v t0 ttn t tav d d tre 2 v tt e e t n ta 0 n a a e ntn te e nt
B
ran at
o
a vB
第一章 质点运动学
aa 与 法向a之t2 间a 夹n 2角1 为0 m s9 2
arctaatn12.4
an
1 – 3 圆周运动
物理学教程 （第二版）
已知： vA19k4m h0 1vB21k9m h2 1
（2）在时t间3ts内矢径A r所B 转3.5过k的m 角度 为
a a x
0, π 2π, v减小
第一章 质点运动学
1 – 3 圆周运动
物理学教程 （第二版）
➢ 对于一般的曲线运动
vddstet addvt et v2en
其中
ds
d
曲率半径 .
利用自然坐标, 一切运动可以
an
根据切向、法向加速度来分类：
a
at
an= 0 at= 0
an= 0 at 0 an 0 at = 0 an 0 at 0
1 – 3 圆周运动
物理学教程 （第二版）
平面极坐标
设一质点在 Oxy 平面内
运径动r ，与某时x刻轴它之位间于的点夹A 角.矢
为 . 于是质点在点 A 的位
置可由 A(r,)来确定 .
y
A
r
o
x
以 (r
x r cos y r sin
d
dt
atddvtr
➢ 若 = 常量，t = 0 时， ＝ 0， ＝ 0 ,可求
匀变角加速圆周运动公式.
＝ 0＋ t
00t12t2
20 22(0)
注意：仅 适用于角加速 度为恒量情况.
第一章 质点运动学
1 – 3 圆周运动
物理学教程 （第二版）
例2 如图一超音速歼击机在高空 A 时的水平速率
第一章 质点运动学
1 – 3 圆周运动
一 圆周运动的角速度和角加速度
角坐标 (t )
角速度 (t) d(t)
dt
速v 率 lt i0 m s t r lt i0 m t
vd d s t v(t)r(t)
角加速度 d
dt
第一章 质点运动学
物理学教程 （第二版）
y
B
r A
o
x
1 – 3 圆周运动
为 1940 km/h , 沿近似于圆弧的曲线俯冲到点 B ,其速率
为 2192 km/h , 所经历的时间为 3s , 设圆弧 AB的半径
约为 3.5km , 且飞机从 A 到 B 的俯冲过程可视为匀变
速率圆周运动 , 若不计重力加速度的影响, 求 (1) 飞机
在点 B 的加速度; (2)飞机由点A 到点B 所经历的路程 .
物理学教程 （第二版）
二 匀速率圆周运动
加v速vv 度大d d 小rstre at v lei vttm v vrre rtvt2
vB
oren rvetA
a t d dv t 0 , v r2e n t 0 0, 2 rtv e n rv 法位向矢单量 vB v vA
第一章 质点运动学
匀速直线运动 变速直线运动 匀速曲线运动 变速曲线运动
a与 at的夹角
tan an
at
1 – 3 圆周运动
物理学教程 （第二版）
讨论
对于作曲线运动的物体，以下几种说法中哪一种 是正确的：
（A）切向加速度必不为零；
（B）法向加速度必不为零（拐点处除外）；
（C）由于速度沿切线方向，法向分速度必为零， 因此法向加速度必为零；
v2
en
et
v1
o r
v2vt v vv1n
第一章 质点运动学
1 – 3 圆周运动
物理学教程 （第二版）
切向加速度（速度大小变化引起）
atd dv trd d2 t2 s
法向加速度（速度方向变化引起）
v2
en
et
v1
an
v2rv2
r
o r
➢
圆周运动加速度
a a ddvtt e et t a vrn 2e en n v2vt
At
1t2
2
A
vA
飞机经过的路程为
B
ran at
srvAt1 2att2
o
a
vB
代入数据得
s17m 22
第一章 质点运动学
1 – 3 圆周运动
物理学教程 （第二版）
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
第一章 质点运动学
dt
（2）
at
dv dt
b
dt
2
an
v2 r
(bt)2 r
（3） a tan (a t2 aata n 2)(1b2 r2 2 t4b (1 b)r2 2 t1421)12
第一章 质点运动学
1 – 3 圆周运动
物理学教程 （第二版）
四 角加速度 匀变角加速圆周运动公式
➢ 角加速度 ➢ 切向加速度
第一章 质点运动学
1 – 3 圆周运动
物理学教程 （第二版）
例1 设有一个质点作半径为 r 的圆周运动. 质点沿
圆周运动所经历的路程与时间的关系为 s = bt2/2, 并设
b 为一常量, 求（1）此质点在某一时刻的速率;
（2）法向加速度和切向加速度的大小;（3）总加速度.
解：（1） vdsd(1b2t)bt
A
vA
ran
B
at
o
a vB
解（1）因飞机作匀变速率
运动所以 a t 和 为常量 .
at
dv dt
分离变量有
vB dv
vA
t
0atdt
第一章 质点运动学
1 – 3 圆周运动
物理学教程 （第二版）
已知：vA19k4m h0 1vB21k9m h2 1
t3s AB 3.5km
Av在vAB点dvBv的A0法ta向td加t 速度在at点aBvnB 的 t加vv r速B 2A度120.3 m 6m ss 22
（D）若物体作匀速率运动，其总加速度必为零；
a （E）若物体的加速度 为恒矢量，它一定作
匀变速率运动 .
第一章 质点运动学
1 – 3 圆周运动
物理学教程 （第二版）
讨论
例 质点作半径为R的变速圆周运动的加 速度大小为：
（1） d v dt
（3） d v v 2 dt R
（2） v 2 R
（4） (dv)2 (v2)2 dt R
v vv1n
a at2an 2
第一章 质点运动学
1 – 3 圆周运动
物理学教程 （第二版）
a a te t a n e n a与 et 夹角 ta n1aant
➢
a
a n 0 0 π
切向加速度
y
atddvt r
a
0 , 0π 2, v增大
o
t 0, π 2, v常量
v
en et