下载文档原格式
第二章衍射公式及衍射是指波在通过一个孔或绕过一个障碍物时发生的偏折现象。
在物理学中，衍射是一种常见的现象，可以解释光、声波等的传播和干涉。
衍射公式是用来计算衍射现象的数学表达式，它描述了波通过一个狭缝或孔时偏折的规律。
根据衍射公式，我们可以计算出特定条件下的衍射图样和衍射角度。
由于衍射公式的推导较复杂，下面我们将通过一个简单的例子来说明衍射的基本原理和公式的应用。
假设有一束单色光通过一个宽度为a的狭缝，我们希望计算出衍射图样中间的主极大（也叫零级衍射极大）的角度。
根据衍射公式，主极大的角度为：sinθ = λ/a其中，θ为主极大的角度，λ为波长，a为狭缝的宽度。
这个公式可以用来计算单缝衍射的主极大角度，也可以应用于其他衍射实验中。
衍射公式的推导涉及到波的数学描述和波动方程的求解过程，需要通过波动光学等课程进行学习。
在推导过程中，我们需要使用亥姆霍兹方程和惠更斯原理等基本假设来求解解析解。
除了单缝衍射，衍射公式还可以应用于其他形状和结构的衍射实验。
例如，在光的衍射实验中，当光通过一个孔径很小的圆形屏幕时，会产生中央强度最强的中央最大光斑，以及周围逐渐减弱的一系列光斑。
这种现象被称为菲涅耳圆形屏幕衍射。
对于不同形状和结构的衍射实验，衍射公式的具体形式和应用方法可能不同。
但是，衍射公式的核心思想是一样的，即通过计算波的传播和干涉，来确定衍射图样和衍射角度。
总结起来，衍射公式是用来计算衍射现象的数学表达式，它描述了波在通过狭缝或孔时的偏折规律。
通过衍射公式，我们可以计算出衍射图样和衍射角度，从而深入理解波的传播和干涉现象。
衍射公式的具体形式和应用方法会根据不同的衍射实验而有所不同，需要通过学习相关课程来掌握。
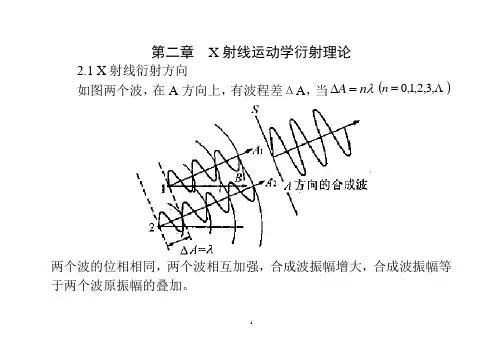
第二章 X 射线运动学衍射理论2.1 X 射线衍射方向如图两个波，在A 方向上，有波程差ΔA ，当λn A =∆() ,3,2,1,0=n两个波的位相相同，两个波相互加强，合成波振幅增大，合成波振幅等于两个波原振幅的叠加。
在B 方向上，波程差λ)2/1(+=∆n B () ,3,2,1,0=n ，两波的位相不同，一个波的波峰与另一个的波谷重叠，合成波振幅为零。
如下图b 。
两波的波程差随方向不同而不同，位相差也有变化。
在A 方向和B 方向之间的方向上，合成波振幅介于前两者之间。
如上图c 。
因此，两个波的波程不同就会产生位相差，随着位相差的变化，其合成波振幅也有变化。
下图是平行的单色X射线以θ角入射到晶面上，在与入射线成2θ角的方向上的散射波。
对于波1和1a，它们在1′和1a′方向上的散射波位相相同，波程差为零。
两波互相加强。
A晶面上该方向的所有散射线均互相加强。
对于波1和2分别被K和L原子散射时，1′和2′的波程差为ML＋NL＝2d′sinθ，如果波程差2d′sinθ为波长的整数倍，即满足：时，散射波1′和2′的位相相同，两波相互加强。
上式就是布拉格定律。
它是X射线衍射的最基本的定律。
式中n为整数，称为反射级数。
因sinθ≤1，n的大小有一定限制。
n =1时称为第一级反射。
对于一定的λ和d′，存在可以产生衍射的若干个角θ1,θ2,θ3,…，分别对应于n =1，2，3，…。
在满足布拉格定律的方向上，各晶面的散射波位相都相同，其振幅互相加强，散射强度增加，这样，在与入射线成2θ角的方向上就会出现衍射线。
而其他方向上的散射波位相不同，振幅互相抵消，散射强度减弱或完全消除。
X射线衍射和可见光反射有相似的现象，如：入射束、反射面法线、反射束三者处于同一平面，且入射角和反射角相等，但衍射和反射有如下本质的区别：a. X射线不仅被晶体表面的原子散射，而且被晶体内层原子散射，衍射线是晶体中X射线路径上所有原子散射波干涉的结果。
