5 P
3 60
E
B
0
a
A
例 • 已知在一个60°的二面角的棱上有两点A、
B,AC、BD分别是在这个二面角度两个面 内,且垂直于AB的线段,又知AB=4cm, AC=6cm,BD=8cm,求CD的长。
C A D B
能力·思维·方法
例.如图,已知A1B1C1—ABC是正三棱柱,D是AC的中点. (1)证明AB1∥平面DBC1. (2)假设AB1⊥BC1,求以BC1为棱,DBC1与CBC1为面的二 面角α的度数. A A1
∠A O B
B1 B
?
l
O1
∠A1O1B1 平面角是直角的二面角 叫做直二面角
A A1
O
9
⑵二面角的平面角的取 值范围是 [0 ,180 ]
以二面角的棱上任意一点为端点,在 两个面内分别作垂直于棱的两条射线,这 两条射线所成的角叫做二面角的平面角。 二面角的平面角必须满足:
注意:
A
1)角的顶点在棱上 2)角的两边分别在两个面内 3)角的边都要垂直于二面角的棱
。
C
B
D
E
即AB⊥BE ∴AB⊥ β .
又∵CD∩BE=B,
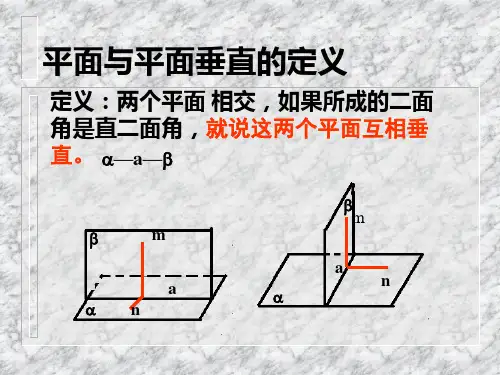
性质定理:
如果两个平面相互垂直,那么在一个平面内垂 直于它们交线的直线垂直于另一个平面.
已知 : , P , P a, a .求证 : a .
例2.求证:如果两个平面互相垂直,那么经过第 一个平面内的一点垂直于第二个平面的直线必 在第一个平面内.
P
b a b
a
P
c
c
本课小结:
定义:如果两个平面相交所成的二面角是直二面角,那么我们称这两个平面相 互垂直.