实验2螺线管电磁阀静磁场分析(综合性)实验指导书

霍尔效应测量螺线管磁场实验报告一、实验目的1、了解霍尔效应的基本原理。

2、掌握用霍尔效应测量螺线管磁场的方法。

3、学会使用霍尔效应实验仪，并对实验数据进行处理和分析。

二、实验原理1、霍尔效应当电流 I 沿垂直于磁场 B 的方向通过导体时，在导体垂直于电流和磁场的方向上会产生一个横向电位差 UH，这种现象称为霍尔效应。

霍尔电压 UH 与电流 I、磁感应强度 B 以及导体的厚度 d 等因素有关，其关系式为：UH ＝ KHIB/d，其中 KH 为霍尔元件的灵敏度。

2、螺线管磁场对于一个长直螺线管，其内部的磁场近似为均匀磁场，磁场强度 B 与电流 I、螺线管的匝数 N 和长度 L 有关，其关系式为：B ＝μ0nI，其中μ0 为真空磁导率，n ＝ N/L 为单位长度上的匝数。

三、实验仪器霍尔效应实验仪、螺线管、直流电源、数字电压表、毫安表等。

四、实验步骤按照实验电路图，将霍尔效应实验仪、螺线管、直流电源、数字电压表、毫安表等仪器正确连接。

2、调整仪器（1）将霍尔元件置于螺线管的中间位置，确保霍尔元件与螺线管的轴线平行。

（2）调节直流电源的输出电压，使通过螺线管的电流逐渐增大，观察数字电压表的读数变化，确保仪器正常工作。

3、测量霍尔电压（1）保持通过螺线管的电流不变，改变磁场方向（即改变电流方向），分别测量正、反向磁场下的霍尔电压 UH1 和 UH2，计算平均值UH ＝（UH1 ＋ UH2)／2，以消除副效应的影响。

（2）改变通过螺线管的电流 I，每次改变一定的值，测量对应的霍尔电压 UH，记录数据。

4、数据处理（1）根据测量数据，绘制 UH I 曲线。

（2）利用曲线的斜率和已知的霍尔元件灵敏度 KH，计算出螺线管内部的磁感应强度 B。

五、实验数据记录与处理｜通过螺线管的电流 I （mA) ｜霍尔电压 UH1 （mV) ｜霍尔电压UH2 （mV) ｜平均霍尔电压 UH （mV) ｜｜｜｜｜｜｜ 10 ｜ 125 ｜－120 ｜ 1225 ｜｜ 20 ｜ 250 ｜－245 ｜ 2475 ｜｜ 30 ｜ 370 ｜－365 ｜ 3675 ｜｜ 40 ｜ 490 ｜－485 ｜ 4875 ｜｜ 50 ｜ 610 ｜－605 ｜ 6075 ｜2、绘制 UH I 曲线以通过螺线管的电流 I 为横坐标，平均霍尔电压 UH 为纵坐标，绘制 UH I 曲线。

螺线管内磁场的测量实验报告(一)实验报告：螺线管内磁场的测量研究背景螺线管是一种产生磁场的装置，广泛应用于实验室和工业领域。

为了深入了解螺线管内部的磁场分布情况，需要进行测量实验。

实验目的本次实验的目的是测量螺线管内磁场的分布情况，掌握螺线管的基本特性，提高实验操作能力。

实验原理螺线管内部的磁场分布可以通过霍尔元件进行测量。

将霍尔元件放置在螺线管内部，测量不同位置的磁场强度并进行数据处理。

实验步骤1.准备实验装置，将螺线管和霍尔元件连接好。

2.打开电源，调整电流大小，使磁场强度达到预定值。

3.按照实验布置图，在不同位置上放置霍尔元件，记录磁场强度值和坐标位置。

4.对实验数据进行处理，得出螺线管内部磁场的分布情况。

实验结果通过实验，我们得到了螺线管内部磁场的分布情况数据，绘制出了磁场分布曲线图。

实验结果符合理论值，表明实验操作正确，数据可靠。

实验结论本次实验成功测量了螺线管内部的磁场分布情况，掌握了螺线管的基本特性，提高了实验操作能力。

实验注意事项1.实验时需保持安全，注意电源等设备的正确使用。

2.实验前需仔细阅读实验原理，了解实验操作流程。

3.实验过程中需要仔细记录实验数据，确保数据的准确性。

4.实验后要及时整理实验数据和材料，保持实验区的整洁。

实验难点及解决方法实验中主要难点在于对螺线管和霍尔元件的连接以及实验数据的处理。

连接不良会导致数据不准确，数据处理错误会导致结果偏差。

为了解决这些问题，我们在实验前进行设备调试，确保设备连接正常，且能够正常工作。

在实验过程中，我们仔细记录实验过程和数据，防止数据处理错误。

同时，我们也进行了多次实验，对实验结果进行检验和验证，保证数据的可靠性和准确性。

实验拓展为了进一步深入了解螺线管的特性和应用，可以进行以下拓展实验：1.对不同尺寸的螺线管进行磁场分布测量，比较不同尺寸螺线管的磁场分布情况。

2.探究螺线管的电流-磁场关系，测量不同电流下螺线管的磁场强度，绘制出电流-磁场关系曲线。

霍尔效应测量螺线管磁场实验报告霍尔效应测量螺线管磁场实验报告引言：霍尔效应是一种基于电磁学原理的重要现象，它在工业和科学研究中有着广泛的应用。

本实验旨在通过测量霍尔效应来研究螺线管磁场的特性。

实验步骤：1. 实验器材准备：螺线管、直流电源、霍尔元件、电流表、电压表和万用表。

2. 搭建实验电路：将螺线管连接到直流电源，通过电流表测量电流大小。

将霍尔元件连接到电压表和万用表，以测量霍尔电压和磁场强度。

3. 测量电流：调节直流电源，使电流通过螺线管，记录电流值。

4. 测量霍尔电压：将万用表调至电压测量档，将霍尔元件放置在螺线管附近，记录霍尔电压值。

5. 改变电流方向：改变直流电源的极性，重复步骤3和4，记录数据。

6. 分析数据：根据测得的电流和霍尔电压数据，计算磁场强度。

实验结果：通过实验测得的数据，我们可以得出以下结论：1. 霍尔电压与电流成正比：根据实验数据，霍尔电压与电流之间存在线性关系。

当电流增大时，霍尔电压也随之增大。

2. 霍尔电压与磁场强度成正比：实验结果表明，霍尔电压与磁场强度之间存在线性关系。

当磁场强度增大时，霍尔电压也随之增大。

3. 霍尔电压的正负与电流方向有关：当电流方向改变时，霍尔电压的正负也会随之改变。

讨论与分析：霍尔效应的测量原理是基于洛伦兹力的作用。

当电流通过螺线管时，螺线管周围会产生一个磁场。

霍尔元件中的电荷受到磁场的作用力，导致电荷在元件两侧产生电势差，即霍尔电压。

根据霍尔电压的大小可以推算出磁场的强度。

实验中我们观察到了霍尔电压与电流、磁场强度之间的关系。

这与霍尔效应的理论预测相符。

实验结果的线性关系表明，霍尔效应是一个可靠且精确的测量手段。

然而，在实际应用中，霍尔效应的测量也存在一些局限性。

例如，霍尔元件的位置和方向对测量结果有影响，因此需要仔细调整实验装置。

此外，霍尔元件的灵敏度也会影响测量的准确性，因此需要选择合适的霍尔元件。

结论：本实验通过测量霍尔效应，研究了螺线管磁场的特性。

电磁场与电磁波项目训练报告螺线管磁场特性班级：姓名：学号：指导教师：成绩：电子与信息工程学院信息与通信工程系实验三 螺线管中不同介质分界磁场特性1 实验目的1.掌握安培环路定理的使用条件；2.熟悉边界条件的推导；3.了解磁介质磁化电流对边界的影响；4.复习Maxwell 软件的使用方法。

2 实验原理利用不同介质表面的边界条件和安培环路定律可推导出： 在两种介质边界上有：B1n =B2n ， 由于边界上磁场是垂直于边界的，得：B1=B2；再由B1=1μH1以及 B2=2μH2，而1μ≠2μ，可以得到H1≠H2。

在两种介质内部有：由安培环路定律 ⎰=∙NI dl H ，由于两种介质内部的单位长度所包含的电流相同，可以得到H1=H2。

但是这与上面推出的H1≠H2相互矛盾。

3 进行分推导整个推理过程分为两部分，分别得出相互矛盾的结论H1=H2、H1≠H2。

一、对于H1=H2： 在两种介质内部有：由安培环⎰=∙cNI dl H 路定律，由于两种介质内部的单位长度 所包含的电流相同，可以得到H1=H2。

作如图所示的闭合回路，由安培环路定律⎰⎰⎰⎰=+++∙∙∙∙bccdrda rcd rbc ABrab NI dl H dl H dl H dl Hda1111 (1)磁场与管轴线平行，即 01,0rab 1==rcd H H 管外磁场为零，即 01=rda H从而 ⎰⎰⎰==ab1110,,0cddard rcd rab adl H dl H dl H⎰=bc1dl NI H bc同理 ⎰=fg1NI dl H bc所以 ⎰⎰=cfgfg bc dl H dl H b 21又 2211,H H H H fg bc == 得出H1=H2 检验讨论过程的每一步，发现几个问题： （一）01,0rab 1==rcd H H 的条件是否正确这一条件的得出是基于以下推理：均匀无限长圆柱形密绕螺线管，螺距为零，视为一系列平行圆电流紧密排列，磁感应线不泄漏。

霍尔效应测量螺线管磁场实验报告一、实验目的。

本实验旨在通过霍尔效应测量螺线管中的磁场强度，进一步了解霍尔效应在磁场测量中的应用，加深对磁场的理解。

二、实验仪器和设备。

1. 螺线管。

2. 直流电源。

3. 示波器。

4. 霍尔元件。

5. 电阻箱。

6. 万用表。

三、实验原理。

当螺线管通以电流时，产生的磁场会使螺线管内的载流子受到洛伦兹力的作用，从而在螺线管的两端产生电势差。

这种现象被称为霍尔效应。

利用霍尔效应，我们可以测量螺线管中的磁场强度。

四、实验步骤。

1. 将螺线管连接至直流电源，并调节电流强度为一定数值。

2. 将霍尔元件连接至示波器，观察示波器的显示情况。

3. 调节电流强度，使示波器显示出最大的霍尔电压信号。

4. 利用万用表测量霍尔电压和电流的数值。

5. 调节电流强度，重复步骤3和步骤4，记录不同电流强度下的霍尔电压和电流数值。

五、实验数据处理。

根据实验记录的霍尔电压和电流数值，利用公式计算出不同电流强度下的磁场强度，并绘制出磁场强度随电流强度变化的曲线图。

六、实验结果分析。

根据实验数据处理得到的曲线图，我们可以清晰地观察到螺线管中磁场强度随电流强度的变化规律。

通过分析曲线图，我们可以得出螺线管中磁场强度与电流强度之间的定量关系，进一步验证了霍尔效应在磁场测量中的应用。

七、实验结论。

本实验通过霍尔效应成功测量了螺线管中的磁场强度，得出了磁场强度与电流强度之间的定量关系。

实验结果符合霍尔效应的理论预期，验证了霍尔效应在磁场测量中的应用。

八、实验总结。

通过本次实验，我们进一步了解了霍尔效应在磁场测量中的应用，掌握了利用霍尔效应测量螺线管磁场的方法。

同时，实验中我们也发现了一些操作上的注意事项，对于今后的实验操作有了更加深入的认识。

九、参考文献。

1. 《霍尔效应在磁场测量中的应用》，物理学报，2008年。

2. 《霍尔效应测量螺线管磁场实验指导书》，XX大学物理实验室，2019年。

十、致谢。

感谢实验指导老师对本次实验的指导与帮助，让我们更加深入地了解了霍尔效应在磁场测量中的应用。

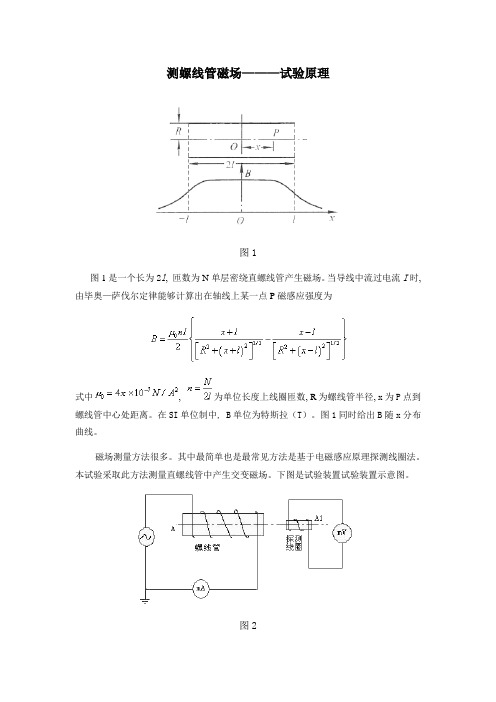
测螺线管磁场———试验原理图1图1是一个长为2l, 匝数为N单层密绕直螺线管产生磁场。

当导线中流过电流I时, 由毕奥—萨伐尔定律能够计算出在轴线上某一点P磁感应强度为式中, 为单位长度上线圈匝数, R为螺线管半径, x为P点到螺线管中心处距离。

在SI单位制中, B单位为特斯拉（T）。

图1同时给出B随x分布曲线。

磁场测量方法很多。

其中最简单也是最常见方法是基于电磁感应原理探测线圈法。

本试验采取此方法测量直螺线管中产生交变磁场。

下图是试验装置试验装置示意图。

图2当螺线管A中经过一个低频交流电流i(t) = I0sinωt时, 在螺线管内产生一个与电流成正比交变磁场B(t) = C p i(t) = B0sinωt其中C p是百分比常数, 把探测线圈A1放到螺线管内部或周围, 在A1中将产生感生电动势, 其大小取决于线圈所在处磁场大小、线圈结构和线圈相对于磁场取向。

探测线圈尺寸比较小, 匝数比较多。

若其截面积为S1, 匝数为N1, 线圈平面法向平面与磁场方向夹角为θ, 则穿过线圈磁通链数为:Ψ = N1S1B(t)cosθ依据法拉第定律, 线圈中感生电动势为:通常测量是电压有效值, 设E(t)有效值为V, B(t)有效值为B, 则有, 由此得出磁感应强度:其中r1是探测线圈半径, f是交变电源频率。

在测量过程中如一直保持A和A1在同一轴线上, 此时, 则螺线管中磁感应强度为在试验装置中, 在待测螺线管回路中串接毫安计用于测量螺线管导线中交变电流有效值。

在探测线圈A1两端连接数字毫伏计用于测量A1中感应电动势有效值。

使用探测线圈法测量直流磁场时, 能够使用冲击电流计作为探测仪器, 同学们能够参考冲击电流计原理设计出测量方法。

测螺线管磁场———试验内容1．研究螺线管中磁感应强度B与电流I和感生电动势V之间关系, 测量螺线管中磁感应强度。

2．测量螺线管轴线上磁场分布。

测螺线管磁场———试验仪器图 1 : 测量螺线管内磁场试验装置全貌测量螺线管内磁场试验仪器包含: 铜导线螺线管、霍尔元件（轴向磁场探针）、（毫）特斯拉计、电流源。

实验题目：测量螺线管的磁场实验目的：学习测量交变磁场的一种方法,加深理解磁场的一些特性及电磁感应定律.实验原理：1、有限长载流直螺线管的磁场长为2l,匝数为N的单层密绕的直螺线管产生的磁场.当导线中流过电流I时,由毕奥-萨伐尔定律可以计算出在轴线上某一点P的磁感应强度为(1式中为单位长度上的线圈匝数,R为螺线管半径,x为P点到螺线管中心处的距离.由曲线显示,在螺线管内部磁场近于均匀,只在端点附近磁感应强度才显著下降.当l>>R时,与场点的坐标x无关,而在螺线管两端为内部B值的一半.无限长密绕直螺线管是实验室中经常使用到的产生均匀磁场的理想装置.2、测线圈法测量磁场本实验采用探测线圈法测量直螺线管中产生的交变磁场.图6.3.2-2是实验装置的示意图.当螺线管A中通过一个低频的交流电流时,在螺线管内产生一个与电流成正比的交变磁场(2其中CP是比例常数.把探测圈A1放在螺线管线圈内部或附近,在A1中将产生感生电动势.探测线圈的尺寸比1较小,匝数比较少.若其截面积为S,匝数为N1,线圈平面的发线与磁场方向的夹角为θ,则穿过线圈的磁通链数为(3根据法拉第定律,线圈中的感生电动势为(4通常测量的是电压的有效值.设E(t有效值为V,B(t有效值为B,则有(5由此得出磁感应强度(6其中r1是探测线圈的半径,f是交变电源的频率.在测量过程中如始终保持A和A1在同一轴线上,此时,则螺线管中的磁感应强度为(7在实验装置中,在待测螺线管回路中串接毫安计用于测量螺线管导线中交变电流的有效值.在探测线圈A1两端连接数字毫安计用于测量A1种感生电动势的有效值.实验数据:2R=32.5mm 2L=30.00cm N=3893匝2r=21.00mm N1=335匝探测线圈的感生电动势与螺线管电流的V-I曲线I /mA1520253035404550 V /mV (f=1500Hz289382485581680779875970 V /mV (f=750Hz130175220270318363410458 V /mV (f=375Hz5078101124150173197220 x=0.0cmf /Hz I /mA I*f V /mV1500 12.5 18750 103750 25.0 18750 105375 50.0 18750 105x=L=15.0cm测量值螺线管上的磁场分布x /cm0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 V /mV10011004100210011000999990988986x /cm9.0 10.0 11.0 12.0 12.5 13.0 13.5 14.0 14.5 V /mV987980971948930902856783663x /cm15.0 15.5 16.0 16.5 17.0 17.5 18.0 f=1500HzV /mV5103582501751289880观察互感现象f /Hz x /cm I /mA V /mVA接信号发生器1000 7.5 45 549A1接信号发生器1000 7.5 45 510数据分析及处理:1探测线圈的感生电动势与螺线管中的磁感应强度B与电流I的关系:(2改装后的电路图(3做出实验数据的V-I曲线,得:容易发现,上面的图像可以高度拟合为一条过原点的直线,顾客认为U正比于I,即U=kI,且其斜率同样与频率f存在正比关系(k1500=19.55=2.08k750=4.05k375,k750=1.95k375,故可认为U正比于I与f的乘积,即(4观察第二组数据,其中V和f*I均可认为是不变量,这一结果更验证了上述结论.(5(1(7以B1表示有(1式算出的理论值,B7表示由(7式算出的实验值.(1 x=0,f=750Hz,I=25.0mA, V=220mV:B1=0.000405TB7=0.000402T(2 x=l5cm,f=750Hz, I=25.0mA, V=105mV:B1=0.000204TB7=0.000192T(3 结果分析：由上述结果可以看到理论值B1之与实验值B7的差别不大,且,符合理论的预言,但在x=15cm时B1与B7的差别稍大,这主要是因为实验中的各种误差,如探测线圈与螺线管的互感,探测线圈略为偏离了螺线管的中心轴等因素造成的.2 测量值螺线管上的磁场分布(3有实验数据做出V(x - x曲线:L该曲线的形状与螺线管中的磁场分布理论图形基本一致,且在公式中,V与B成正比关系,故可认为该曲线既是在纵轴拉伸过的B(x – x曲线.可以由图形看出:曲线在一定误差内可以认为是单调递减的,即距离螺线管中心越远,磁场越弱.在x<10时,曲线基本保持水平,即是说明在螺线管内部,靠近中心的部分磁场基本均匀.在10 时 , 曲线呈凸形下降 , 并在 x=L 处基本降至 x=0 处的 1 半 . 这说明在螺线管的边缘部分 , 磁场的空间分布不再均匀 .在x>L=15时,曲线呈凹形下降,并在无穷远处趋于零.即,在螺线管外部依然存在不均匀的磁场,且其强度随距离递减.(4,原因在于,且,该值在误差范围内符合理论预言.3 观察互感现象取x=7.5cm,f=1000Hz,I=45.0mA ,V=549mV,反接后V=510mV.两次测量的V值基本相同.由电磁感应定律,在互感现象中,电压比等于匝数比,电流比等于匝数的反比,从而两次测量的电压相等.思考题：用探测线圈法测量磁场时,为何产生磁场的导体中必须通过低频交流电而不能通过高频交流电？答：螺线管可以看成是一个电感,如果用高频的交流电,会使得感抗很大,影响电流及电压的测量.。

实验九 螺线管内磁场的测量在工业、国防和科学研究中经常要对磁场进行测量，例如在粒子回旋加速器、受控热核反应、同位素分离、地球资源探测、地震预测和磁性材料研究等方面。

测量磁场的方法较多，从测量原理上大体可以分为五类：力和力矩法、电磁感应法、磁传输效应法、能量损耗法、基于量子状态变化的磁共振法。

常用的测量方法主要有冲击电流计法，霍尔元件法、核磁共振法和天平法。

练习一 用冲击电流计法测量螺线管内磁场【实验目的】1．学习用冲击法测量磁感应强度的原理和方法； 2．学会使用冲击电流计；3．研究长直螺线管内轴线上的磁场分布；4．对比螺线管轴线上磁场的测量值与理论值，加深对毕奥－萨伐尔定律的理解。

【实验仪器】冲击电流计、螺线管磁场测量仪、直流电源、直流电流表、电阻箱、滑线变阻器。

【实验原理】1. 长直螺线管轴线上的磁场如图5.9.1所示，设螺线管长为L ，半径为r 0，表面均匀地绕有N 匝线圈，放在磁导率为μ的磁介质中，并通以电流I 。

如果在螺线管上取一小段线圈dL ，则可看作是通过电流为INdL/L 的圆形载流线圈。

由毕奥－萨伐尔定律得到在螺线管轴线上距离中心O 为x 的P 点产生的磁感应强度dB x 为322rr L INdL dB x μ⎪⎭⎫ ⎝⎛= (5.9.1)由图5.9.1可知，0sin r r β=，ββ=sin rd dL ，代入式（5.9.1）得到 图5.9.1长直螺线管轴的结构图ββd LμINdB x sin 2=(5.9.2) 因为螺线管的各小段在P 点的磁感应强度方向均沿轴线向左，故整个螺线管在P 点产生的磁感应强度()21cos cos 2sin 22121ββμββμββββ-===⎰⎰LNId LNIdB B x (5.9.3)由图5.9.1可知，（5.9.3）式还可以表示为⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛+++⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛--=212022*********r x L x Lr x L x L L NI B x μ (5.9.4) 令x =0，得到螺线管中点O 的磁感应强度()2120204rLNIB +μ=(5.9.5)令x =L /2，得到螺线管两端面中心点的感应强度()2122202L NIB L rμ=+ (5.9.6)当L ≥r 0时，由式（5.9.5）和式（5.9.6）可知，B L /2≈B 0/2。

实验一静电场电力线与等位线绘制一、实验目的1.掌握电场中电厂线的测量方法；2.掌握电场中等位线的描绘方法。

二、实验设备1.DZ-2型电场扫描仪器 1台2.双层探针 1个3.两点电荷水槽电极 1个4.同轴柱面水槽电极 1块5.聚焦电场水槽电极 1块三、实验原理在一些电子器件和设备中，有时需知道其中的电场分布，一般都通过实验的方法来确定。

直接测量电场有很大的困难，所以实验时常采用一种物理实验的方法－模拟法，即仿造一个电场 ( 模拟场 ) 与原电场完全一样。

当用探针去测模拟场时，也不受干扰，因此可间接地测出被模拟的电场中各点的电位，连接各等电位点作出等位线。

根据电力线与等位线的垂直关系，描绘出电力线，即可形象地了解电场情况，加深电场强度、电位和电位差概念的理解。

1. 两点电荷的电场分布由图1.1所示，两点电荷A、B各带等量异号电荷，其上分别为+V和-V，由于对称性，等电位面也是对称分布的，电场分布图见图1。

图1.1 两点电荷的电场分布图1.2 同轴柱面的电场分布做实验时，是以导电率很好的自来水，填充在水槽电极的两极之间。

若在两电极上加一定的电压，可以测出自来水中两点电荷的电场分布。

与长平行导线的电场分布相同。

2. 同轴柱面的电场分布由图1.2所示，因环B 的中心放一点电荷A ，分别加+V 和-V ，由于对称性，等位面都是同心园，电场分布的图形见图1.2。

如图 1.2 所示，设小圆的电位为Va 半径为a ，大圆的电位为Vb ，半径为b ，则电场中距离轴心为r 处的电位Vr 可表示为：⎰⋅-=raa r dr E V V （1）又根据高斯定理，则圆柱内r 点的场强E=K/r （当a < r < b 时） （2）式中K 由圆柱的线电荷密度决定。

将（2）式代入（1）式arK V dr r K V V a ra a r ln -=-=⎰ （3） 在r=b 处应有：a b K V V a b /⋅-= 所以ab V V K ba /ln -=（4）如果取0V V a =，0=b V ，将（4）式代入（3）式，得到：ab rb V V r /ln /ln 0= （5）为了计算方便，上式也可写作：ab rb V V r /log /log 0= （6）3. 聚焦电极的电场分布示波管的聚焦电场是由第一聚焦电极A2和第二加速电极A2组成，A2的电位比A1的电位高。