参数方程练习题

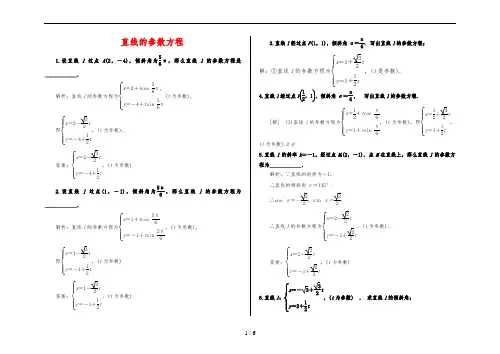
直线的参数方程1.设直线l 过点A (2，－4)，倾斜角为56π，那么直线l 的参数方程是____________．解析：直线l 的参数方程为⎩⎪⎨⎪⎧x ＝2＋t cos 56π，y ＝－4＋t sin 56π(t 为参数)，即⎩⎪⎨⎪⎧x ＝2－32t y ＝－4＋12t ，(t 为参数)．答案：⎩⎪⎨⎪⎧x ＝2－32t y ＝－4＋12t ，(t 为参数)2.设直线l 过点(1，－1)，倾斜角为5π6，那么直线l 的参数方程为____________．解析：直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋t cos5π6y ＝－1＋t sin 5π6，(t 为参数)，即⎩⎪⎨⎪⎧x ＝1－32t y ＝－1＋12t ，(t 为参数)答案：⎩⎪⎨⎪⎧x ＝1－32t y ＝－1＋12t ，(t 为参数)3.直线l 经过点P (1，1)，倾斜角α＝π6. 写出直线l 的参数方程；解：①直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋32t y ＝1＋12t ，(t 是参数)．4.直线l 经过点P ⎝ ⎛⎭⎪⎫12，1，倾斜角α＝π6， 写出直线l 的参数方程.[解] (1)直线l 的参数方程为⎩⎪⎨⎪⎧x ＝12＋t cos π6y ＝1＋t sin π6，(t 为参数)，即⎩⎪⎨⎪⎧x ＝12＋32t y ＝1＋12t ，(t 为参数).2分5.直线l 的斜率k ＝－1，经过点M 0(2，－1)．点M 在直线上，那么直线l 的参数方程为____________．解析：∵直线的斜率为－1， ∴直线的倾斜角α＝135°. ∴cos α＝－22，sin α＝22. ∴直线l 的参数方程为⎩⎪⎨⎪⎧x ＝2－22t y ＝－1＋22t ，(t 为参数)．答案：⎩⎪⎨⎪⎧x ＝2－22t y ＝－1＋22t ，(t 为参数)6.直线l ：⎩⎪⎨⎪⎧x ＝－3＋32t y ＝2＋12t ，(t 为参数) , 求直线l 的倾斜角；解：(1)由于直线l ：⎩⎪⎨⎪⎧x ＝－3＋t cos π6，y ＝2＋t sin π6(t 为参数)表示过点M 0(－3，2)且斜率为tan π6的直线，故直线l 的倾斜角α＝π6.7.假设直线的参数方程为⎩⎪⎨⎪⎧x ＝3＋12t y ＝3－32t ，(t 为参数)，那么此直线的斜率为( )A. 3 B ．－ 3 C.33D ．－33解析：选B.直线的参数方程⎩⎪⎨⎪⎧x ＝3＋12t y ＝3－32t，(t为参数)可化为标准形式⎩⎪⎨⎪⎧x ＝3＋⎝ ⎛⎭⎪⎫－12〔－t 〕y ＝3＋32〔－t 〕，(－t 为参数)．∴直线的斜率为－ 3.8.化直线l 的参数方程⎩⎨⎧x ＝1＋3t ，y ＝3＋6t(t 为参数)为参数方程的标准形式．解：由⎩⎨⎧x ＝1＋3t ，y ＝3＋6t ，得⎩⎪⎨⎪⎧x ＝1＋332＋〔6〕2〔32＋〔6〕2t 〕，y ＝3＋632＋〔6〕2〔32＋〔6〕2t 〕.令t ′＝32＋〔6〕2t ，得到直线l 的参数方程的标准形式为⎩⎪⎨⎪⎧x ＝1＋155t ′y ＝3＋105t ′，(t ′为参数)． 9.化直线l 的参数方程⎩⎪⎨⎪⎧x ＝2－3t y ＝1＋t(t 为参数)为参数方程的标准形式．解：10.直线l 经过点P (1，1)，倾斜角α＝π6.①写出直线l 的参数方程；②设l 与圆x 2＋y 2＝4相交于A ，B 两点，求点P 到A ，B 两点的距离之积． 解：①直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋32t y ＝1＋12t ，(t 是参数)．②把直线l 的参数方程⎩⎪⎨⎪⎧x ＝1＋32t ，y ＝1＋12t 代入圆x 2＋y 2＝4，整理得t 2＋(3＋1)t －2＝0，t 1，t 2是方程的根，t 1·t 2＝－2.∵A ，B 都在直线l 上，设它们对应的参数分别为t 1和t 2，∴|PA |·|PB |＝|t 1|·|t 2|＝|t 1t 2|＝2.11.在直角坐标系xOy 中，曲线C的参数方程为⎩⎪⎨⎪⎧x ＝1＋4cos θy ＝2＋4sin θ，(θ为参数)，直线l 经过定点P (3，5)，倾斜角为π3.(1)写出直线l 的参数方程和曲线C 的标准方程；(2)设直线l 与曲线C 相交于A ，B 两点，求|PA |·|PB |的值． 解：(1)曲线 C ：(x －1)2＋(y －2)2＝16， 直线l ：⎩⎪⎨⎪⎧x ＝3＋12t y ＝5＋32t，(t 为参数)．(2)将直线l 的参数方程代入圆C 的方程可得t 2＋(2＋33)t －3＝0，设t 1，t 2是方程的两个根，那么t 1t 2＝－3，所以|PA ||PB |＝|t 1||t 2|＝|t 1t 2|＝3.12.曲线C 的极坐标方程为ρ＝1，以极点为平面直角坐标系原点，极轴为x 轴正半轴，建立平面直角坐标系，直线l的参数方程是⎩⎪⎨⎪⎧x ＝－1＋4ty ＝3t ，(t 为参数)，那么直线l 与曲线C 相交所截得的弦长为________．解析：曲线C 的直角坐标方程为x 2＋y 2＝1，将⎩⎪⎨⎪⎧x ＝－1＋4ty ＝3t ，代入x 2＋y 2＝1中得25t 2－8t ＝0，解得t 1＝0，t 2＝825.故直线l 与曲线C 相交所截得的弦长l ＝42＋32·|t 2－t 1|＝5×825＝85.答案：8513.斜率为1的直线l 过椭圆x 24＋y 2＝1的右焦点，交椭圆于A ，B 两点，求弦AB 的长度．解：因为直线l 的斜率为1，所以直线l 的倾斜角为π4.椭圆x 24＋y 2＝1的右焦点为(3，0)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝3＋22t y ＝22t ，(t 为参数)，代入椭圆方程x 24＋y 2＝1，得⎝⎛⎭⎪⎫3＋22t 24＋⎝ ⎛⎭⎪⎫22t 2＝1，整理，得5t 2＋26t －2＝0. 设方程的两实根分别为t 1，t 2， 那么t 1＋t 2＝－265，t 1·t 2＝－25，|t 1－t 2|＝〔t 1＋t 2〕2－4t 1t 2 ＝⎝ ⎛⎭⎪⎫－2652＋85＝85， 所以弦长AB 的长为85.14.直线l 经过点P ⎝ ⎛⎭⎪⎫12，1，倾斜角α＝π6，圆C 的极坐标方程为ρ＝2·cos ⎝⎛⎭⎪⎫θ－π4. (1)写出直线l 的参数方程，并把圆C 的方程化为直角坐标方程； (2)设l 与圆C 相交于A ，B 两点，求点P 到A ，B 两点的距离之积．[解] (1)直线l 的参数方程为⎩⎪⎨⎪⎧x ＝12＋t cos π6y ＝1＋t sin π6，(t 为参数)，即⎩⎪⎨⎪⎧x ＝12＋32t y ＝1＋12t ，(t 为参数).2分由ρ＝2cos ⎝ ⎛⎭⎪⎫θ－π4得ρ＝cos θ＋sin θ， 所以ρ2＝ρcos θ＋ρsin θ， 得x 2＋y 2＝x ＋y ，即圆C 的直角坐标方程为⎝ ⎛⎭⎪⎫x －122＋⎝ ⎛⎭⎪⎫y －122＝12.5分(2)把⎩⎪⎨⎪⎧x ＝12＋32t ，y ＝1＋12t 代入⎝ ⎛⎭⎪⎫x －122＋⎝ ⎛⎭⎪⎫y －122＝12，得t 2＋12t －14＝0，7分设A 、B 两点对应的参数分别为t 1、t 2，那么t 1t 2＝－14，所以|PA |·|PB |＝|t 1·t 2|＝14.10分15.(2016·高考卷)在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝32t (t为参数)，椭圆C的参数方程为⎩⎪⎨⎪⎧x ＝cos θy ＝2sin θ(θ为参数)．设直线l 与椭圆C 相交于A ，B 两点，求线段AB 的长．[解] 椭圆C 的普通方程为x 2＋y 24＝1.将直线l的参数方程⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝32t代入x 2＋y 24＝1，得(1＋12t )2＋⎝ ⎛⎭⎪⎫32t 24＝1，即7t 2＋16t ＝0，解得t 1＝0，t 2＝－167.所以AB ＝|t 1－t 2|＝167.16.直线⎩⎪⎨⎪⎧x ＝2＋3ty ＝－1＋t ，(t 为参数)上对应t ＝0，t ＝1两点间的距离是( )A ．1B.10 C ．10D ．2 2解析：选B.将t ＝0，t ＝1代入参数方程可得两点坐标为(2，－1)和(5，0) ∴d ＝〔2－5〕2＋〔－1－0〕2＝10.17.在直角坐标系中，以原点为极点，x 轴的正半轴建立极坐标系，曲线C ：ρsin 2θ＝2a cos θ(a >0)，过点P (－2，－4)的直线l 的参数方程为：⎩⎪⎨⎪⎧x ＝－2＋22t y ＝－4＋22t ，(t 为参数)，直线l 与曲线C 分别交于M ，N 两点．(1)写出曲线C 的直角坐标方程和直线l 的普通方程； (2)假设|PM |，|MN |，|PN |成等比数列，求a 的值．解：(1)曲线的极坐标方程变为ρ2sin 2θ＝2aρcos θ，化为直角坐标方程为y 2＝2ax ，直线⎩⎪⎨⎪⎧x ＝－2＋22t y ＝－4＋22t ，(t 为参数)化为普通方程为y ＝x －2.(2)将⎩⎪⎨⎪⎧x ＝－2＋22ty ＝－4＋22t ，代入y 2＝2ax 得t 2－22(4＋a )t ＋8(4＋a )＝0.那么有t 1＋t 2＝22(4＋a )，t 1t 2＝8(4＋a )， 因为|MN |2＝|PM |·|PN |， 所以(t 1－t 2)2＝t 1·t 2，即(t 1＋t 2)2－4t 1t 2＝t 1t 2，(t 1＋t 2)2－5t 1t 2＝0， 故8(4＋a )2－40(4＋a )＝0， 解得a ＝1或a ＝－4(舍去)． 故所求a 的值为1. 18.直线l 1：⎩⎪⎨⎪⎧x ＝1＋3t y ＝2－4t，(t 为参数)与直线l 2：2x －4y ＝5相交于点B ，且点A (1，2)，那么|AB |＝________．解析：将⎩⎪⎨⎪⎧x ＝1＋3t y ＝2－4t，代入2x －4y ＝5，得t ＝12，那么B ⎝ ⎛⎭⎪⎫52，0.而A (1，2)，得|AB |＝52.答案：5219.如下图，直线l 过点P (2，0)，斜率为43，直线l 和抛物线y 2＝2x 相交于A ，B 两点，设线段AB 的中点为M ，求：①P ，M 间的距离|PM |；②点M 的坐标解：①由题意，知直线l 过点P (2，0)，斜率为43，设直线l 的倾斜角为α，那么tan α＝43，cos α＝35，sin α＝45，∴直线l 的参数方程的标准形式为 ⎩⎪⎨⎪⎧x ＝2＋35t y ＝45t，(t 为参数)．(*) ∵直线l 和抛物线相交，∴将直线l 的参数方程代入抛物线方程y 2＝2x 中， 整理得8t 2－15t －50＝0，Δ＝152＋4×8×50>0.设这个二次方程的两个根为t 1，t 2，由根与系数的关系得t 1＋t 2＝158，t 1t 2＝－254.由M 为线段AB 的中点， 根据t 的几何意义，得|PM |＝⎪⎪⎪⎪⎪⎪t 1＋t 22＝1516.②因为中点M 所对应的参数为t M ＝1516，将此值代入直线l 的参数方程的标准形式(*)，得⎩⎪⎨⎪⎧x ＝2＋35×1516＝4116，y ＝45×1516＝34，即M ⎝ ⎛⎭⎪⎫4116，34. 20.以直角坐标系原点O 为极点，x 轴正半轴为极轴，并在两种坐标系中取一样的长度单位，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝12＋t cos αy ＝t sin α，(t 为参数，0<α<π)，曲线C 的极坐标方程ρ＝2cos θsin 2θ. (1)求曲线C 的直角坐标方程；(2)设直线l 与曲线C 相交于A ，B 两点，当α变化时，求|AB |的最小值． 解：(1)由ρ＝2cos θsin 2θ得ρ2sin 2θ＝2ρcos θ，所以曲线C 的直角坐标方程为y 2＝2x .(2)将直线l 的参数方程代入y 2＝2x ，得t 2sin 2α－2t cos α－1＝0， 设A ，B 两点对应的参数分别为t 1，t 2， 那么t 1＋t 2＝2cos αsin 2α，t 1·t 2＝－1sin 2α， 所以|AB |＝|t 1－t 2| ＝〔t 1＋t 2〕2－4t 1t 2 ＝4cos 2αsin 4α＋4sin 2α＝2sin 2α， 当α＝π2时，|AB |取得最小值2。

圆锥曲线的参数方程练习题1、若点()3,P m 在以点F 为焦点的抛物线24{4x t y t == (t 为参数)上,则PF 等于( )A.2B.3C.4D.5答案：C解析：抛物线为24y x =,准线为1x =-, PF 为()3,P m 到准线1x =-的距离,即为4.故选C.2、参数方程sin cos ,{1sin 2x y θθθ=+=+ (θ为参数)所表示的曲线为( )A.圆的一部分B.抛物线的一部分C.双曲线的一部分D.椭圆的一部分答案：B解析：参数方程sin cos ,{1sin 2x y θθθ=+=+ (θ为参数),化为普通方程为2(02)x y y =≤≤,表示抛物线的一部分.3、椭圆5cos ,{3sin x y ϕϕ== (ϕ为参数)的焦点坐标为( ) A.(5,0)± B.(4,0)± C.(3,0)± D.(0,4)±答案：B解析：椭圆5cos ,{3sin x y ϕϕ== (ϕ为参数)的普通方程为221259x y +=,故4c ==. 又椭圆焦点在x 轴上,故焦点坐标为(4,0)±.4、已知过曲线3cos ,{4sin x y θθ== (θ为参数,0θπ≤≤)上一点P 和原点O 的连线PO 的倾斜角为4π,则P 点的坐标是( ) A.(3,4) B.1212,55⎛⎫- ⎪⎝⎭C.2⎛ ⎝D.1212,55⎛⎫ ⎪⎝⎭ 答案：D解析：直线PO 的方程是y x =,又点P 为曲线3cos ,{4sin x y θθ==上一点,故3cos 4sin θθ=,即3tan 4θ=,因为倾斜角为4π,0θπ≤≤,所以曲线与直线的交点在第一象限,故3sin 5θ=,4cos 5θ=,所以125x y ==. 5、已知O 为原点,P为椭圆4cos ,{x y αα== (α为参数)上第一象限内一点,OP 的倾斜角为3π,则点P 坐标为( ) A.()2,3 B.()4,3C.(D.(,55答案：D解析：椭圆4cos ,{x y αα== (α为参数)化为普通方程,得2211612x y +=.由题意可得直线OP的方程为y = (0x >).由22(0),{11612y x x y =>+=解得x y ==. ∴点P的坐标为.故选D. 6、参数方程cos 2sin x y θθ=⎧⎨=⎩(θ为参数)化为普通方程为( ) A.2214y x += B.2212y x += C.2214x y += D.2212x y +=答案：A 解析：易知,2y cos x sin θθ==,∴2214y x +=,故选A. 7、方程cos cos x a y b θθ=⎧⎨=⎩(θ为参数,0ab ≠)表示的曲线是( ) A.圆 B.椭圆 C.双曲线 D.双曲线的一部分 答案：D解析：由xcos a θ=,∴a cos xθ=,代入y bcos θ=,得xy ab =,又由y bcos θ=知,||,y b b ∈-⎡⎤⎣⎦,∴曲线应为双曲线的一部分.8、若曲线2sin cos 1x y θθ⎧=⎨=-⎩ (θ为参数)与直线x m =相交于不同两点,则m 的取值范围是( )A.RB.()0,+∞C.()0,1D.[)0,1答案：D解析：将曲线2sin cos 1x y θθ⎧=⎨=-⎩化为普通方程得()()()21101y x x +=--≤≤.它是抛物线的一部分,如图所示,由数形结合知01m ≤<.8、过椭圆5cos ,{3sin x y ϕϕ== (为参数)的右焦点,斜率为12的直线方程为__________ 答案：x-2y-4=0解析：椭圆的普通方程为221259x y+=,故5,3,a b==所以4c==,故右焦点的坐标为(4,0),又直线的斜率为12,故直线的方程为1(4)2y x=-,即240x y--=.9、已知实数0p>,曲线212:{2x ptCy pt==(t为参数)上的点(2,)A m,曲线26cos :{26sinpxCyθθ=+ = (θ为参数)的圆心为点B,A,B两点间的距离等于圆2C的半径,则p=__________.答案：8解析：曲线212:{2x ptCy pt==(t为参数)化为普通方程为22y px=,代入2x=得m=±则点(2,A±.曲线26cos:{26sinpxCyθθ=+=的圆心为(,0)2p,半径为6.10、设点O为坐标原点,直线l:4,{2xy t=+=(参数t R∈)与曲线24,:{4x uCy u==(参数u R∈)交于A、B两点.（1）求直线l与曲线C的普通方程;（2）求证:OA OB⊥.答案：1.直线l:4y x=-.曲线C:24y x=.2.证明:设1122(,),(,),A x yB x y由24{4y xy x==-消去y,得212160x x-+=.∴121212,16,x x x x+==∴12121212121212(4)(4)4()161OA OBy y x x x x x xk kx x x x x x---+⋅====-.∴OA OB⊥.11、在直角坐标系 xOy 中,直线l 的方程为40x y -+=,曲线 C的参数方程为,{sin ,x y θθ== (θ为参数).1.已知在极坐标系(与直角坐标系 xOy 取相同的长度单位,且以原点 O 为极点,以 x 轴正半轴为极轴)中,点P 的极坐标为4,2π⎛⎫ ⎪⎝⎭,判断点P 与直线l 的位置关系; 2.设点 Q 是曲线 C 上的一个动点,求它到直线l 的距离的最小值.答案：1. 点P 的极坐标为4,2π⎛⎫ ⎪⎝⎭,则直角坐标为(0,4), 把()0,4P 代入直线l 的方程40x y -+=, 因为0?4? 4? 0-+=,所以点P 在直线l 上.2.因为点 Q 是曲线 C 上的一个动点,则点 Q的坐标可设为),sin Q αα. 点 Q 到直线l 的距离为2cos 4d πα⎛⎫++ ⎪==6πα⎛⎫=++ ⎪⎝⎭所以当cos 16πα⎛⎫+=- ⎪⎝⎭时,d.。

圆的参数方程1.已知曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θy ＝3sin θ，(θ为参数，0≤θ<2π)判断点A (2，0)，B ⎝⎛⎭⎫－3，32是否在曲线C 上？若在曲线上，求出点对应的参数的值． 解：将点A (2，0)的坐标代入⎩⎪⎨⎪⎧x ＝2cos θy ＝3sin θ，得⎩⎪⎨⎪⎧cos θ＝1，sin θ＝0.由于0≤θ<2π，解得θ＝0，所以点A (2，0)在曲线C 上，对应θ＝0.将点B ⎝⎛⎭⎫－3，32的坐标代入⎩⎪⎨⎪⎧x ＝2cos θy ＝3sin θ，得⎩⎪⎨⎪⎧－3＝2cos θ，32＝3sin θ，即⎩⎨⎧cos θ＝－32，sin θ＝12.由于0≤θ<2π， 解得θ＝5π6，所以点B ⎝⎛⎭⎫－3，32在曲线C 上，对应θ＝5π6. 2.已知曲线C 的参数方程是⎩⎪⎨⎪⎧x ＝2ty ＝3t 2－1，(t 为参数)．(1)判断点M 1(0，－1)和M 2(4，10)与曲线C 的位置关系； (2)已知点M (2，a )在曲线C 上，求a 的值．[思路点拨] (1)将点的坐标代入参数方程，判断参数是否存在． (2)将点的坐标代入参数方程，解方程组．[解] (1)把点M 1(0，－1)的坐标代入参数方程⎩⎪⎨⎪⎧x ＝2t ，y ＝3t 2－1，得⎩⎪⎨⎪⎧0＝2t－1＝3t 2－1，∴t ＝0.即点M 1(0，－1)在曲线C 上．把点M 2(4，10)的坐标代入参数方程⎩⎪⎨⎪⎧x ＝2t ，y ＝3t 2－1，得⎩⎪⎨⎪⎧4＝2t10＝3t 2－1，方程组无解． 即点M 2(4，10)不在曲线C 上． (2)∵点M (2，a )在曲线C 上，∴⎩⎪⎨⎪⎧2＝2t ，a ＝3t 2－1. ∴t ＝1，a ＝3×12－1＝2. 即a 的值为2.3.已知曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝t 2＋1y ＝2t ，(t 为参数)．①判断点A (1，0)，B (5，4)，E (3，2)与曲线C 的位置关系； ②若点F (10，a )在曲线C 上，求实数a 的值． 解：①把点A (1，0)的坐标代入方程组，解得t ＝0， 所以点A (1，0)在曲线上．把点B (5，4)的坐标代入方程组，解得t ＝2， 所以点B (5，4)也在曲线上．把点E (3，2)的坐标代入方程组，得到⎩⎪⎨⎪⎧3＝t 2＋1，2＝2t ，即⎩⎨⎧t ＝±2，t ＝1.故t 不存在，所以点E 不在曲线上． ②令10＝t 2＋1，解得t ＝±3，故a ＝2t ＝±6.4.(1)曲线C ：⎩⎪⎨⎪⎧x ＝ty ＝t －2，(t 为参数)与y 轴的交点坐标是____________．解析：令x ＝0，即t ＝0得y ＝－2，∴曲线C 与y 轴交点坐标是(0，－2)． 答案：(0，－2)(2)在直角坐标系xOy 中，已知曲线C 1：⎩⎪⎨⎪⎧x ＝t ＋1y ＝1－2t ，(t 为参数)与曲线C 2：⎩⎪⎨⎪⎧x ＝a sin θy ＝3cos θ，(θ为参数，a >0)有一个公共点在x 轴，则a ＝________． 解析：由y ＝0知1－2t ＝0，t ＝12，所以x ＝t ＋1＝12＋1＝32.令3cos θ＝0，则θ＝π2＋k π(k ∈Z )，sin θ＝±1，所以32＝±a .又a >0，所以a ＝32.答案：325.已知某条曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋2ty ＝at 2，(其中t 为参数，a ∈R)．点M (5，4)在该曲线上，则常数a ＝________．解析：∵点M (5，4)在曲线C 上，∴⎩⎪⎨⎪⎧5＝1＋2t 4＝at 2，解得⎩⎪⎨⎪⎧t ＝2，a ＝1.∴a 的值为1. 答案：16.圆(x ＋1)2＋(y －1)2＝4的一个参数方程为____________．解析：令x ＋12＝cos θ，y －12＝sin θ得⎩⎪⎨⎪⎧x ＝－1＋2cos θy ＝1＋2sin θ(θ为参数)．答案：⎩⎪⎨⎪⎧x ＝－1＋2cos θy ＝1＋2sin θ(θ为参数)(注本题答案不唯一)7.已知圆的普通方程x 2＋y 2＋2x －6y ＋9＝0，则它的参数方程为____________．解析：由x 2＋y 2＋2x －6y ＋9＝0，得(x ＋1)2＋(y －3)2＝1.令x ＋1＝cos θ，y －3＝sin θ，所以参数方程为⎩⎪⎨⎪⎧x ＝－1＋cos θy ＝3＋sin θ，(θ为参数)．答案：⎩⎪⎨⎪⎧x ＝－1＋cos θy ＝3＋sin θ，(θ为参数)(注答案不唯一)8.圆(x ＋2)2＋(y －3)2＝16的参数方程为( )A.⎩⎪⎨⎪⎧x ＝2＋4cos θy ＝－3＋4sin θ，(θ为参数) B.⎩⎪⎨⎪⎧x ＝－2＋4cos θy ＝3＋4sin θ，(θ为参数) C.⎩⎪⎨⎪⎧x ＝2－4cos θy ＝3－4sin θ，(θ为参数) D.⎩⎪⎨⎪⎧x ＝－2－4cos θy ＝3－4sin θ，(θ为参数) 解析：选B.∵圆(x －a )2＋(y －b )2＝r 2的参数方程为⎩⎪⎨⎪⎧x ＝a ＋r cos θy ＝b ＋r sin θ，(θ为参数)∴圆(x ＋2)2＋(y －3)2＝16的参数方程为⎩⎪⎨⎪⎧x ＝－2＋4cos θy ＝3＋4sin θ，(θ为参数)9.已知圆的方程为x 2＋y 2＝2x ，则它的一个参数方程是____________．解析：将x 2＋y 2＝2x 化为(x －1)2＋y 2＝1知圆心坐标为(1，0)，半径r ＝1，∴它的一个参数方程为⎩⎪⎨⎪⎧x ＝1＋cos θy ＝sin θ(θ为参数)．答案：⎩⎪⎨⎪⎧x ＝1＋cos θy ＝sin θ(θ为参数)10.已知圆P ：⎩⎨⎧x ＝1＋10cos θy ＝－3＋10sin θ，(θ为参数)，则圆心P 及半径r 分别是( )A ．P (1，3)，r ＝10B ．P (1，3)，r ＝10C ．P (1，－3)，r ＝10D ．P (1，－3)，r ＝10解析：选C.由圆P 的参数方程可知圆心P (1，－3)，半径r ＝10.11.圆的参数方程为⎩⎪⎨⎪⎧x ＝2＋2cos θy ＝2sin θ，(θ为参数)，则圆的圆心坐标为( )A ．(0，2)B ．(0，－2)C ．(－2，0)D ．(2，0) 解析：选D.由⎩⎪⎨⎪⎧x ＝2＋2cos θy ＝2sin θ得(x －2)2＋y 2＝4，其圆心为(2，0)，半径r ＝2.12.直线：3x －4y －9＝0与圆：⎩⎪⎨⎪⎧x ＝2cos θy ＝2sin θ(θ为参数)的位置关系是( )A ．相切B ．相离C ．直线过圆心D ．相交但直线不过圆心解析：选 D.圆心坐标为(0，0)，半径为2，显然直线不过圆心，又圆心到直线距离d ＝95<2，故选 D.13.已知圆C ：⎩⎪⎨⎪⎧x ＝－3＋2sin θy ＝2cos θ，(θ∈[0，2π)，θ为参数)与x 轴交于A ，B 两点，则|AB |＝________．解析：令y ＝2cos θ＝0，则cos θ＝0，因为θ∈[0，2π)，故θ＝π2或3π2，当θ＝π2时，x ＝－3＋2sin π2＝－1，当θ＝3π2时，x ＝－3＋2sin 3π2＝－5，故|AB |＝|－1＋5|＝4.答案：414.已知动圆x 2＋y 2－2x cos θ－2y sin θ＝0.求圆心的轨迹方程．解：设P (x ，y )为所求轨迹上任一点． 由x 2＋y 2－2x cos θ－2y sin θ＝0得： (x －cos θ)2＋(y －sin θ)2＝cos 2θ＋sin 2θ，∴⎩⎪⎨⎪⎧x ＝cos θy ＝sin θ这就是所求的轨迹方程．15.P 是以原点为圆心，r ＝2的圆上的任意一点，Q (6，0)，M 是PQ 中点， (1)画图并写出⊙O 的参数方程；(2)当点P 在圆上运动时，求点M 的轨迹的参数方程． 解：(1)如图所示，⊙O 的参数方程⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2sin θ.(2)设M (x ，y )，P (2cos θ，2sin θ)，因Q (6，0)， ∴M 的参数方程为⎩⎨⎧x ＝6＋2cos θ2，y ＝2sin θ2，即⎩⎪⎨⎪⎧x ＝3＋cos θ，y ＝sin θ. 16.已知点P (2，0)，点Q 是圆⎩⎪⎨⎪⎧x ＝cos θy ＝sin θ上一动点，求PQ 中点的轨迹方程，并说明轨迹是什么曲线．解：设Q (cos θ，sin θ)，PQ 中点M (x ，y )，则由中点坐标公式得x ＝2＋cos θ2＝12cos θ＋1，y ＝0＋sin θ2＝12sin θ.∴所求轨迹的参数方程为⎩⎨⎧x ＝12cos θ＋1y ＝12sin θ(θ为参数)消去θ可化为普通方程为(x －1)2＋y 2＝14，它表示以(1，0)为圆心、半径为12的圆．17.设Q (x 1，y 1)是单位圆x 2＋y 2＝1上一个动点，则动点P (x 21－y 21，x 1y 1)的轨迹方程是____________．解析：设x 1＝cos θ，y 1＝sin θ，P (x ，y )．则⎩⎪⎨⎪⎧x ＝x 21－y 21＝cos 2θ，y ＝x 1y 1＝12sin 2θ.即⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝12sin 2θ，为所求． 答案：⎩⎪⎨⎪⎧x ＝cos 2θy ＝12sin 2θ18.已知P 是曲线⎩⎪⎨⎪⎧x ＝2＋cos αy ＝sin α，(α为参数)上任意一点，则(x －1)2＋(y ＋1)2的最大值为________．解析：将⎩⎪⎨⎪⎧x ＝2＋cos αy ＝sin α代入(x －1)2＋(y ＋1)2得(1＋cos α)2＋(1＋sin α)2＝2sin α＋2cos α＋3＝22sin ⎝⎛⎭⎫α＋π4＋3， ∴当sin ⎝⎛⎭⎫α＋π4＝1时有最大值为3＋2 2. 答案：3＋2219.已知点P (x ，y )在曲线C ：⎩⎪⎨⎪⎧x ＝1＋cos θy ＝sin θ，(θ为参数)上，则x －2y 的最大值为( )A ．2B ．－2C ．1＋ 5D ．1－ 5解析：选C.由题意，得⎩⎪⎨⎪⎧x ＝1＋cos θ，y ＝sin θ，所以x －2y ＝1＋cos θ－2sin θ＝1－(2sin θ－cos θ) ＝1－5⎝⎛⎭⎫25sin θ－15cos θ＝1－5sin ()θ－φ⎝⎛⎭⎫其中tan φ＝12， 所以x －2y 的最大值为1＋ 5.20.已知曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋cos θy ＝sin θ，(θ为参数)，求曲线C 上的点到直线l ：x－y ＋1＝0的距离的最大值．解：点C (1＋cos θ，sin θ)到直线l 的距离 d ＝|1＋cos θ－sin θ＋1|12＋12＝|2＋cos θ－sin θ|2＝⎪⎪⎪⎪2＋2cos ⎝⎛⎭⎫θ＋π42≤2＋22＝2＋1，即曲线C 上的点到直线l 的最大距离为2＋1.21.(2016·高考全国卷Ⅰ)在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝a cos t ，y ＝1＋a sin t ，(t为参数，a ＞0)．在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ＝4cos θ.(1)说明C 1是哪一种曲线，并将C 1的方程化为极坐标方程；(2)直线C 3的极坐标方程为θ＝α0，其中α0满足tan α0＝2，若曲线C 1与C 2的公共点都在C 3上，求a .[解] (1)消去参数t 得到C 1的普通方程x 2＋(y －1)2＝a 2.C 1是以(0，1)为圆心，a 为半径的圆．将x ＝ρcos θ，y ＝ρsin θ代入C 1的普通方程中，得到C 1的极坐标方程为ρ2－2ρsin θ＋1－a 2＝0.(2)曲线C 1，C 2的公共点的极坐标满足方程组⎩⎪⎨⎪⎧ρ2－2ρsin θ＋1－a 2＝0，ρ＝4cos θ. 若ρ≠0，由方程组得16cos 2θ－8sin θcos θ＋1－a 2＝0，由已知tan θ＝2，可得16cos 2θ－8sin θcos θ＝0，从而1－a 2＝0，解得a ＝－1(舍去)或a ＝1.a ＝1时，极点也为C 1，C 2的公共点，在C 3上． 所以a ＝1.22.若P (x ，y )是曲线⎩⎪⎨⎪⎧x ＝2＋cos αy ＝sin α，(α为参数)上任意一点，则(x －5)2＋(y ＋4)2的最大值为( )A ．36B ．6C ．26D ．25解析：选A.依题意P (2＋cos α，sin α)，∴(x －5)2＋(y ＋4)2＝(cos α－3)2＋(sin α＋4)2＝26－6cos α＋8sin α＝26＋10sin(α－φ)(其中cos φ＝45，sin φ＝35)∴当sin(α－φ)＝1，即α＝2k π＋π2＋φ(k ∈Z )时，有最大值为36.23.已知点P ⎝⎛⎭⎫12，32，Q 是圆⎩⎪⎨⎪⎧x ＝cos θy ＝sin θ，(θ为参数)上的动点，则|PQ |的最大值是________．解析：由题意，设点Q (cos θ，sin θ)， 则|PQ |＝⎝⎛⎭⎫cos θ－122＋⎝⎛⎭⎫sin θ－322＝2－3sin θ－cos θ ＝2－2sin ⎝⎛⎭⎫θ＋π6 故|PQ |max ＝2＋2＝2. 答案：224.已知曲线方程⎩⎪⎨⎪⎧x ＝1＋cos θy ＝sin θ，(θ为参数)，则该曲线上的点与定点(－1，－2)的距离的最小值为________．解析：设曲线上动点为P (x ，y )，定点为A ，则|P A |＝（1＋cos θ＋1）2＋（sin θ＋2）2 ＝9＋42sin ⎝⎛⎭⎫θ＋π4， 故|P A |min ＝9－42＝22－1. 答案：22－125.已知圆C ⎩⎪⎨⎪⎧x ＝cos θy ＝－1＋sin θ，与直线x ＋y ＋a ＝0有公共点，求实数a 的取值范围．解：法一：∵⎩⎪⎨⎪⎧x ＝cos θ，y ＝－1＋sin θ消去θ，得x 2＋(y ＋1)2＝1.∴圆C 的圆心为(0，－1)，半径为1. ∴圆心到直线的距离d ＝|0－1＋a |2≤1.解得1－2≤a ≤1＋ 2.法二：将圆C 的方程代入直线方程， 得cos θ－1＋sin θ＋a ＝0，即a ＝1－(sin θ＋cos θ)＝1－2sin ⎝⎛⎭⎫θ＋π4. ∵－1≤sin ⎝⎛⎭⎫θ＋π4≤1，∴1－2≤a ≤1＋ 2.26.设P (x ，y )是圆x 2＋y 2＝2y 上的动点．①求2x ＋y 的取值范围；②若x ＋y ＋c ≥0恒成立，求实数c 的取值范围．解：圆的参数方程为⎩⎪⎨⎪⎧x ＝cos θy ＝1＋sin θ，(θ为参数)．①2x ＋y ＝2cos θ＋sin θ＋1＝5sin(θ＋φ)＋1(φ由tan φ＝2确定)，∴1－5≤2x ＋y ≤1＋ 5.②若x ＋y ＋c ≥0恒成立，即c ≥－(cos θ＋sin θ＋1)对一切θ∈R 成立．且－(cos θ＋sin θ＋1)＝－2sin ⎝⎛⎭⎫θ＋π4－1的最大值是2－1，则当c ≥2－1时，x ＋y ＋c ≥0恒成立．27.已知圆的极坐标方程为ρ2－42ρcos ⎝⎛⎭⎫θ－π4＋6＝0. (1)将极坐标方程化为普通方程，并选择恰当的参数写出它的参数方程； (2)若点P (x ，y )在该圆上，求x ＋y 的最大值和最小值． [解] (1)由ρ2－42ρcos ⎝⎛⎭⎫θ－π4＋6＝0， 得ρ2－4ρcos θ－4ρsin θ＋6＝0， 即x 2＋y 2－4x －4y ＋6＝0，∴圆的标准方程(x －2)2＋(y －2)2＝2，3分 令x －2＝2cos α，y －2＝2sin α，得圆的参数方程为⎩⎨⎧x ＝2＋2cos αy ＝2＋2sin α，(α为参数)6分(2)由(1)知x ＋y ＝4＋2(cos α＋sin α) ＝4＋2sin ⎝⎛⎭⎫α＋π4，9分 又－1≤sin ⎝⎛⎭⎫α＋π4≤1， 故x ＋y 的最大值为6，最小值为2.12分28.圆的直径AB 上有两点C ，D ，且|AB |＝10，|AC |＝|BD |＝4，P 为圆上一点，求|PC |＋|PD |的最大值．解：如图所示，以AB 所在直线为x 轴，线段AB 的中点为坐标原点建立平面直角坐标系．圆的参数方程为⎩⎪⎨⎪⎧x ＝5cos θ，y ＝5sin θ(θ为参数)．易知点C (－1，0)，D (1，0)．因为点P 在圆上，所以可设P (5cos θ，5sin θ)． 所以|PC |＋|PD |＝（5cos θ＋1）2＋（5sin θ）2＋（5cos θ－1）2＋（5sin θ）2 ＝26＋10cos θ＋26－10cos θ ＝（26＋10cos θ＋26－10cos θ）2 ＝52＋2262－100cos 2θ.当cos θ＝0时，|PC |＋|PD |有最大值为226.29.(2014·高考课标全国卷Ⅱ)在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，半圆C 的极坐标方程为ρ＝2cos θ，θ∈⎣⎡⎦⎤0，π2. (1)求C 的参数方程；(2)设点D 在C 上，C 在D 处的切线与直线l ：y ＝3x ＋2垂直，根据(1)中你得到的参数方程，确定D 的坐标．解：(1)C 的普通方程为(x －1)2＋y 2＝1(0≤y ≤1)．可得C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋cos t ，y ＝sin t (t 为参数，0≤t ≤π)．(2)设D (1＋cos t ，sin t )，由(1)知C 是以G (1，0)为圆心，1为半径的上半圆．因为C 在点D 处的切线与l 垂直，所以直线GD 与l 的斜率相同，tan t ＝3，t ＝π3.故D 的直角坐标为⎝⎛⎭⎫1＋cos π3，sin π3，即⎝⎛⎭⎫32，32.。

高中数学选修参数方程练习题学校：_____姓名：___班级：___考号：___一．填空题1．直线l：（t为参数）的倾斜角为______．2．若P（m，n）为椭圆（θ为参数）上的点，则m+n的取值范围是______．3．在平面直角坐标系xoy中，直线l的参数方程是（其中t为参数），以Ox为极值的极坐标系中，圆C的极坐标方程为ρ=4cosθ，则圆心到直线的距离为______．4．在直角坐标系xOy中，M是曲线C1：（t为参数）上任意一点，N是曲线C2：（θ为参数）上任意一点，则|MN|的最小值为______．5．（坐标系与参数方程选做题）过点A（2，3）的直线的参数方程（t为参数），若此直线与直线x-y+3=0相交于点B，则|AB|=______．6．已知曲线C的参数方程为（t为参数），若点P（m，2）在曲线C上，则m=______．7、A．将参数方程（e为参数）化为普通方程是______．B．不等式|x-1|+|2x+3|＞5的解集是______．C．如图，在△ABC中，AD是高线，CE是中线，|DC|=|BE|，DG⊥CE于G，且|EC|=8，则|EG|=______．8．椭圆的离心率是______．三．简答题9．已知直线的极坐标方程为，圆M的参数方程为（其中θ为参数）．（Ⅰ）将直线的极坐标方程化为直角坐标方程；（Ⅱ）求圆M上的点到直线的距离的最小值．10．已知曲线C1：（t为参数，C2：（θ为参数）．（Ⅰ）C1、C2的方程为普通方程，并说明它们分别表示什么曲线；（Ⅱ）若C1上的点P对应的参数t=，Q为C2上的动点，求PQ中点M到直线C3：（t为参数）距离的最小值．11．在平面直角坐标系xOy中，圆C的参数方程为为参数）．直线l经过点P（2，2），倾斜角．（1）写出圆的标准方程和直线l的参数方程．（2）设l与圆C相交于A、B两点，求|PA|•|PB|的值．12．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C：（α为参数）与极坐标下的点．（1）求点M与曲线C的位置关系；（2）在极坐标系下，将M绕极点逆时针旋转θ（θ∈[0，π]），得到点M‘，若点M'在曲线C上，求θ的值．13．选修4-4：坐标系与参数方程以直角坐标系的原点O为极点，x轴正半轴为极轴，并在两种坐标系中取相同的长度单位．已知直线l的参数方程为（t为参数，0＜α＜π），曲线C的极坐标方程为，（Ⅰ）求曲线C的直角坐标方程：（Ⅱ）设直线l与曲线C相交于A、B两点，当a变化时，求|AB|的最小值．14．设平面直角坐标系原点与极坐标极点重合，x轴正半轴与极轴重合，若已知曲线C的极坐标方程为ρ2=，点F1、F2为其左、右焦点，直线l的参数方程为（t为参数，t∈R）．（Ⅰ）求曲线C的标准方程和直线l的普通方程；（Ⅱ）若点P为曲线C上的动点，求点P到直线l的最大距离．15．过点P（-3，0）且倾斜角为30°的直线和曲线（t为参数）相交于A，B两点．求线段AB的长．参考答案一．填空题（共__小题）1．直线l：（t为参数）的倾斜角为。

高考数学专题复习：参数方程知识与习题一．常见直曲线的参数方程1、直线参数方程的标准式是2、圆心在点(a,b)，半径为r 的圆的参数方程是3、 4、双曲线12222=-b y a x 的参数方程是5、抛物线y 2=2px 的参数方程是备注：参数t 的几何意义：Tips:判断参数方程表示的是什么曲线题中，关键是“消参”.常用方法：平方法——三角函数、t t 1+型.注意观察是否规定参数的范围练习1：将参数方程化为普通方程 （1） （2）练习2：已知椭圆16410022=+y x 有一内接矩形ABCD ，求矩形ABCD 的最大面积.练习3：如图，已知点P 是圆x 2+y 2=16上的一个懂点，点A 坐标为(12,0).当点P 在圆上运动时，线段PA 中点M 的轨迹是什么？一、直线参数方程中的参数的几何意义1、已知直线l 经过点(1,1)P ,倾斜角6πα=，①写出直线l 的参数方程;②设l 与圆422=+y x 相交与两点,A B ，求点P 到,A B 两点的距离之积.2、已知直线).3cos(2.32),2,1(πθρπ+=-圆方程的直线倾斜角为是过点P l（I ）求直线l 的参数方程；（II ）设直线l 与圆相交于M 、N 两点，求|PM|·|PN|的值.二、巧用参数方程解最值题1、在椭圆2211612x y+=上找一点，使这一点到直线2120x y--=的距离的最小值.2、已知点(,)P x y是圆222x y y+=上的动点，（1）求2x y+的取值范围；（2）若0x y a++≥恒成立，求实数a的取值范围.3、在平面直角坐标系xOy中，动圆2228cos6sin7cos80x y x yθθθ+--++=的圆心为(,)P x y，求2x y-的取值范围高考数学专题复习：参数方程知识与习题专题：参数方程练习1：(1) y=1-x 2 (x ∈[-1,1]) (2) 12222=-b y a x练习2：设椭圆的参数方程为 θθsin 8cos 10==y x ，设点A 坐标为(10cos θ,8sin θ)，θ∈[0,2π] 则由椭圆的对称性知：B(10cos θ, - 8sin θ)，D(-10cos θ,8sin θ)|AB|=16sin θ ， |AD|= 20cos θS 矩形ABCD=|AB|·|AD|=320 sin θ cos θ=160sin2θ∵θ∈[0,2π]， sin 2θ∈[-1,1]∴当2θ=π/2时sin2θ取得最大值1，此时矩形面积最大值为S max =160练习3设圆的参数方程为θθsin 4cos 4==y x ，设点P 坐标为(4cos θ,4sin θ)，θ∈[0,2π]则PA 中点M(2cos θ+6,2sin θ)，即θθsin 26cos 2=+=y x (移项、平方、相加)得(x-6)2+y 2=4∴M 轨迹为圆巩固练习一、1解 （1）直线的参数方程为，31112x t y t ⎧=+⎪⎪⎨⎪=+⎪⎩ 运用 快速写出（2）则点P 到,A B 两点的距离之积为22解：（Ⅰ）l的参数方程为，11,2()2.x t t y ⎧=--⎪⎪⎨⎪=⎪⎩为参数（Ⅱ）12||||||6PM PN t t ==+g)3/cos(π+θ∈[-1,1]当cos()13πθ+=时，min 5d =，此时所求点为(2,3)-.2圆的参数方程为1sin cos +==θθy x ，则P(cos θ, sin θ) (1)2x+y=2cos θ+ sin θ+1=5sin(αθ+)+1 (tan α=2) -1≤sin(αθ+)≤1121x y ≤+≤∴2x+y ∈[-5+1, 5+1](2) x+y+a= cos θ+ sin θ+1+a=2 sin(4/π+θ)+1+a ≥0恒成立，即a ≥-2 sin(4/π+θ)-1 恒成立，所以a ≥[-2 sin(4/π+θ)-1]max ，即a ≥2-13圆的标准方程为1)sin 3()4cos -(x 22=-+θθy ，即P(4cos θ, 3sin θ)。

参数方程直线、圆专题练习.。

评卷人得分一．选择题（共9小题）1．曲线C的参数方程为（θ为参数），直线l的方程为x﹣y﹣2=0，P、M分别为曲线C和直线l上的点，则|PM｜的最小值为（）A．0 B．C． D．22．直线l的参数方程为(t为参数)，则l的倾斜角大小为（）A． B． C．D．3．直线(t为参数)与曲线（θ为参数）相交的弦长为（）A．1 B．2 C．3 D．44．已知曲线的参数方程为（0≤t≤5），则曲线为( )A．线段B．双曲线的一支 C．圆弧D．射线5．参数方程（t为参数,且0≤t≤3）所表示的曲线是( ）A．直线B．圆弧C．线段D．双曲线的一支6．椭圆的参数方程为（θ为参数），则它的两个焦点坐标是（)A．（±4，0） B．（0，±4） C．（±5，0） D．（0，±3）7．已知α是锐角，则直线（t为参数）的倾斜角是( )A．αB．α﹣C．α+D．α+8．已知M为曲线C：(θ为参数）上的动点．设O为原点，则｜OM｜的最大值是（）A．1 B．2 C．3 D．49．已知椭圆的参数方程(t为参数），点M在椭圆上，对应参数t=，点O为原点，则直线OM的斜率为（）A． B．﹣C．2D．﹣2评卷人得分二．填空题（共16小题）10．参数方程（α为参数）化成普通方程为．11．已知椭圆的参数方程为，则该椭圆的普通方程是．12．椭圆（θ为参数)的右焦点坐标为13．已知圆C的参数方程为（θ为参数),以原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρsinθ+ρcosθ=1，则直线l截圆C所得的弦长是．14．若直线（t为参数）与曲线（θ为参数)相切，则实数m的值为．15．设点A是曲线是参数)上的点，则点A到坐标原点的最大距离是．16．直线（t为参数）与曲线（θ为参数）的公共点个数为．17．参数方程（θ为参数）化为普通方程是．：18．直角坐标系xOy中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C1 (θ为参数）,曲线C：ρcos（θ+）=t，若两曲线有公共点，则t的取值范围2是．19．直线（t为参数）对应的普通方程是．20．直线(t为参数）的倾斜角的大小为．21．将参数方程(t为参数)化为普通方程是．22．直线（t为参数）被圆(θ为参数）所截得的弦长为．23．直线(t为参数）与曲线（θ为参数）的交点个数是．24．已知直线C1：（t为参数），C2:(θ为参数）,当α=时，则C1与C2的交点坐标为．25．若直线l的参数方程为,t∈R,则直线l在y轴上的截距是．评卷人得分三．解答题(共5小题）26．在直角坐标系xOy中，曲线C1：(t为参数)．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C2：ρ2﹣10ρcosθ﹣6ρsinθ+25=0．（Ⅰ)求C1的普通方程与曲线C2的直角坐标方程,并说明方程所表示的曲线名称；（Ⅱ）判断曲线C1与曲线C2的位置关系，若相交，求出弦长．27．已知直线l参数方程：(t为参数），曲线C1：．(1）求直线l的直角坐标方程和曲线C1的参数方程；(2）若点M在曲线C1上运动，求M到直线l距离的最小值．28．已知直线l：（t为参数），曲线C1:，（θ为参数)．（1）设l与C1相交于A，B两点，求｜AB|；（2）曲线C2为（θ为参数）,点P是曲线C2上的一个动点，求它到直线l的距离的最小值．29．在平面直角坐标系xOy中，⊙O的参数方程为，(θ为参数）,过点(0，﹣)且倾斜角为α的直线l与⊙O交于A，B两点．（1）求α的取值范围；(2）求AB中点P的轨迹的参数方程．30．在直角坐标系xOy中，曲线C的参数方程为，（θ为参数)，直线l的参数方程为，(t为参数）．（1）求C和l的直角坐标方程；（2)若曲线C截直线l所得线段的中点坐标为(1,2）,求l的斜率．参数方程直线、圆专题练习参考答案与试题解析一．选择题（共9小题）1．曲线C的参数方程为（θ为参数）,直线l的方程为x﹣y﹣2=0，P、M分别为曲线C和直线l上的点，则｜PM|的最小值为（）A．0 B．C． D．2【分析】直接利用三角函数关系式的恒等变变换和正弦型函数的性质及点到直线的距离公式的应用求出结果．【解答】解：曲线C的参数方程为（θ为参数）,设P（2c osθ，sinθ），则：点P到直线x﹣y﹣2=0的距离d==,当sin（θ+α）=1时，|PM|的最小值为．故选：B．【点评】本题考查的知识要点：点到直线的距离公式的应用,三角函数关系式的恒等变变换,正弦型函数性质的应用．2．直线l的参数方程为（t为参数）,则l的倾斜角大小为( )A． B． C．D．【分析】根据题意，将直线的参数方程变形为普通方程，由直线的方程形式分析可得答案．【解答】解：根据题意，直线l的参数方程为(t为参数），则到直线的方程为，所以直线的斜率为，倾斜角为，故选：C．【点评】本题考查直线的参数方程及倾斜角，注意将直线的参数方程变形为普通方程．3．直线(t为参数）与曲线（θ为参数）相交的弦长为（)A．1 B．2 C．3 D．4【分析】分别化直线与圆的参数方程为普通方程，再由圆心在直线上可得弦长．【解答】解：由，得x﹣，由,得（x﹣1)2+y2=1．∴圆(x﹣1)2+y2=1的圆心坐标为（1，0)，半径为1．而圆心（1，0）在直线x﹣上，∴直线与曲线相交的弦长为2．故选：B．【点评】本题考查参数方程化普通方程,考查直线与圆位置关系的应用,是基础题．4．已知曲线的参数方程为（0≤t≤5)，则曲线为（）A．线段B．双曲线的一支 C．圆弧D．射线【分析】曲线的参数方程消去参数t，得x﹣3y=5．再由0≤t≤5，得﹣1≤y≤24．从而求出该曲线是线段．【解答】解:由（0≤t≤5），消去参数t,得x﹣3y=5．又0≤t≤5，故﹣1≤y≤24．故该曲线是线段．故选：A．【点评】本题考查曲线形状的判断,考查极坐标方程、参数方程、直角坐标方程的互化等基础知识，考查推理论证能力、运算求解能力，考查函数与方程思想、化归与转化思想，是基础题．5．参数方程(t为参数，且0≤t≤3）所表示的曲线是（）A．直线B．圆弧C．线段D．双曲线的一支【分析】根据题意,由参数方程中t的范围分析可得x、y的范围,结合参数方程消去参数可得x ﹣3y=10，结合x、y的范围分析可得答案．【解答】解：根据题意，参数方程，若0≤t≤3，则有：4≤x≤31，﹣2≤y≤7,又由参数方程，则y+2=(x﹣4），即x﹣3y=10，又由4≤x≤31，﹣2≤y≤7,则参数方程表示的是线段;故选:C．【点评】本题考查参数方程与普通方程的转化，注意t的取值范围．6．椭圆的参数方程为（θ为参数），则它的两个焦点坐标是（)A．（±4，0） B．（0,±4）C．（±5,0）D．（0，±3）【分析】根据题意，将椭圆的参数方程变形为普通方程，分析a、b的值，计算可得c的值，即可得答案．【解答】解：根据题意，椭圆的参数方程为（θ为参数）,则其普通方程为+=1，其中a=5，b=3,则c==4,其它的两个焦点坐标是（±4，0）；故选：A．【点评】本题考查椭圆的参数方程，关键是将椭圆的方程变形为普通方程．7．已知α是锐角,则直线（t为参数)的倾斜角是（）A．αB．α﹣C．α+D．α+【分析】设直线的倾斜角为θ，则tanθ==，α锐角，化简即可得出．【解答】解：设直线的倾斜角为θ，则tanθ====，α锐角．∴θ=,故选：C．【点评】本题考查了直线的倾斜角与斜率之间的关系、诱导公式的应用，考查了推理能力与计算能力，属于中档题．8．已知M为曲线C：（θ为参数）上的动点．设O为原点，则|OM｜的最大值是( ) A．1 B．2 C．3 D．4【分析】直接把圆的参数方程转化为直角坐标方程，进一步利用两点间的距离公式求出结果．【解答】解：曲线C：（θ为参数）转化为：（x﹣3）2+y2=1，则：圆心（3,0）到原点（0.0）的距离为3,故点M到原点的最大值为：3+1=4．故选：D．【点评】本题考查的知识要点：参数方程和直角坐标方程的转化,两点间的距离公式的应用．9．已知椭圆的参数方程（t为参数)，点M在椭圆上,对应参数t=，点O为原点，则直线OM的斜率为（)A． B．﹣C．2D．﹣2【分析】将点对应的参数代入椭圆的参数方程得到M的坐标,再利用直线的斜率公式即可求出答案．【解答】解:当t=时，点M的坐标为（2cos，4sin），即M（1,2),∴OM的斜率为k=2．故选：C．【点评】本题主要考查了椭圆的参数方程，直线的斜率等基本知识,属于基础题．二．填空题(共16小题）10．参数方程（α为参数）化成普通方程为x2+（y﹣1)2=1 ．【分析】欲将参数方程（α为参数）化成普通方程,只须消去参数即可，利用三角函数的同角公式中的平方关系即得．【解答】解：∵（α为参数）∴x2+（y﹣1)2=cos2α+sin2α=1．即:参数方程(α为参数）化成普通方程为：x2+（y﹣1）2=1．故答案为：x2+（y﹣1）2=1．【点评】本小题主要考查参数方程的概念的应用、圆的参数方程的概念、三角函数的同角公式等基础知识，考查运算求解能力、化归与转化思想．属于基础题．11．已知椭圆的参数方程为，则该椭圆的普通方程是．【分析】根据题意，由椭圆的参数方程可得=cosα，=sinα，进而可得,即可得答案．【解答】解:根据题意，椭圆的参数方程为，则有=cosα，=sinα，则有，即该椭圆的普通方程为：，故答案为：．【点评】本题考查椭圆的参数方程，注意椭圆的参数方程的形式，属于基础题．12．椭圆（θ为参数）的右焦点坐标为（1，0)【分析】根据题意，将椭圆的参数方程变形为标准方程，分析可得a、b的值，计算可得c的值，即可得椭圆的右焦点坐标，即可得答案．【解答】解:根据题意,椭圆（θ为参数）的普通方程为+=1，其中a=2，b=,则c=1；故椭圆的右焦点坐标为（1，0）;故答案为：(1，0）【点评】本题考查椭圆的参数方程，注意将椭圆的参数方程变形为普通方程．13．已知圆C的参数方程为（θ为参数）,以原点为极点，x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρsinθ+ρcosθ=1，则直线l截圆C所得的弦长是．【分析】利用弦长=，(其中d为弦心距）公式即可计算出．【解答】解：直线l的极坐标方程为ρsinθ+ρcosθ=1，化为直角坐标系下的普通方程为y+x=1；由圆C的参数方程为（θ为参数），消去参数θ化为普通方程x2+(y﹣2）2=1，其圆心C（0，2），半径r=1．直线l截圆C所得的弦长=2=．故答案为．【点评】熟练弦长、弦心距及半径三者之间的关系是解题的关键．14．若直线（t为参数）与曲线(θ为参数）相切，则实数m的值为﹣3或7 ．【分析】把参数方程化为普通方程，根据圆心到直线的距离等于半径，求得m的值．【解答】解：直线l：(t为参数）即 2x﹣y+m﹣2=0．曲线C：曲线（θ为参数) 即 x2+y2=5，表示以(0，0）为圆心，半径等于的圆．再根据圆心到直线的距离等于半径,可得==，求得 m=﹣3或7,故答案为：﹣3或7．【点评】本题主要考查把参数方程化为普通方程的方法，点到直线的距离公式的应用,直线和圆的位置关系,属于基础题．15．设点A是曲线是参数）上的点，则点A到坐标原点的最大距离是 3 ．【分析】设A（,1+sinθ),原点O（0,0）,｜AO｜==，由此能求出点A到坐标原点取最大距离．【解答】解：∵点A是曲线是参数)上的点，∴设A（,1+sinθ）,原点O（0，0），｜AO|===,∴当sin（）=1时，点A到坐标原点取最大距离3．故答案为：3．【点评】本题考查两点间距离的最大值的求法,考查勇数方程、两点间距离公式、三角函数的性质等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．16．直线（t为参数）与曲线（θ为参数）的公共点个数为 2 ．【分析】直线消去参数t，得x﹣2y=0，曲线消去参数,得（x﹣2）2+y2=1，联立，能求出交点个数．【解答】解：直线（t为参数）消去参数t，得x﹣2y=0，曲线(θ为参数)消去参数，得（x﹣2)2+y2=1，联立，得或．∴直线(t为参数)与曲线（θ为参数）的公共点个数为2．故答案为：2．【点评】本题考查直线与曲线的交点个数的求法，考查参数方程、直角坐标方程、极坐标方程的互化等基础知识，考查运算求解能力，考查函数与方程思想,是中档题．17．参数方程（θ为参数）化为普通方程是（x﹣3）2+y2=1 ．【分析】由参数方程可得，结合sin2θ+cos2θ=1可得答案．【解答】解：由参数方程可得，两边平方作和得(x﹣3)2+y2=1．故答案为:（x﹣3）2+y2=1．【点评】本题主要考查参数方程与普通方程的相互转化,属于基础题．：18．直角坐标系xOy中，以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C1（θ为参数)，曲线C：ρcos(θ+）=t,若两曲线有公共点，则t的取值范围是2t＜﹣1或t＞3 ．【分析】分别化直线和圆的方程为普通方程，由直线和圆的位置关系可得t的不等式，解不等式可得．【解答】解：由C：可得cosθ=x﹣1，sinθ=y，1两式平方相加可得（x﹣1)2+（y)2=1，整理可得(x﹣2）2+y2=4,表示圆心为(2，0）半径为2的圆，：ρcos（θ+）=t可得ρcosθ﹣ρsinθ=t，由C2即x﹣y=t，即x﹣y﹣2t=0，表示一条直线，由两曲线有公共点可得直线与圆相离，∴圆心到直线的距离d大于半径，即＞2,解得t＜﹣1或t＞3故答案为：t＜﹣1或t＞3【点评】本题考查圆的参数方程和直线的极坐标方程，化为普通方程并利用直线和圆的位置关系是解决问题的关键，属基础题．19．直线（t为参数）对应的普通方程是x+y﹣1=0 ．【分析】利用加减消元法消去参数t，即可得到直线的普通方程．【解答】解：两个方程相加得x+y﹣1=0,故答案为：x+y﹣1=0．【点评】本题考查了参数方程与普通方程的转化，属于基础题．20．直线（t为参数）的倾斜角的大小为．【分析】化参数方程为普通方程，求出斜率，即可求得倾斜角．【解答】解:（t为参数）化参数方程为普通方程，两方程相加可得x+y=2，则直线的斜率为﹣1，故倾斜角为．故答案为：．【点评】本题考查直线的斜率与倾斜角的关系,解题的关键是化参数方程为普通方程,属于基础题．21．将参数方程（t为参数）化为普通方程是2x+y﹣3=0 ．【分析】2x=2+2，与y=1﹣2相加即可得出．【解答】解:2x=2+2，与y=1﹣2相加可得：2x+y=3．故答案为:2x﹣y﹣3=0．【点评】本题考查了参数方程化为普通方程，考查了推理能力与计算能力，属于基础题．22．直线(t为参数)被圆（θ为参数）所截得的弦长为．【分析】分别化直线与圆的参数方程为普通方程，由点到直线的距离公式求出圆心到直线的距离，再由垂径定理得答案．【解答】解：由，得x+y﹣8=0，由，得，两式平方作和得：（x﹣3）2+（y+1)2=25．∴圆心坐标为(3,﹣1），半径为5．圆心到直线的距离d=．∴直线被圆所截弦长为2．故答案为：．【点评】本题考查参数方程化普通方程，考查了直线与圆位置关系的应用,考查垂径定理的应用，是基础题．23．直线（t为参数）与曲线(θ为参数）的交点个数是 2 ．【分析】直线与曲线的参数方程，化为普通方程，联立可得13x2﹣18x﹣27=0,即可得出结论．【解答】解：直线（t为参数）与曲线(θ为参数），普通方程分别为x+y﹣1=0，=1，联立可得13x 2﹣18x ﹣27=0，△=（﹣18)2﹣4×13×（﹣27）＞0， ∴交点个数是2， 故答案为：2．【点评】本题考查直线的参数方程与普通方程的转化，考查方程思想,比较基础．24．已知直线C 1：(t 为参数），C 2：（θ为参数），当α=时，则C 1与C 2的交点坐标为 （1,0）,（，﹣） ．【分析】先消去参数将曲线C 1与C 2的参数方程化成普通方程，再联立方程组求出交点坐标即可． 【解答】解：（Ⅰ)当α=时，C 1的普通方程为y=（x ﹣1)，C 2的普通方程为x 2+y 2=1． 联立方程组，解得C 1与C 2的交点为(1，0),(，﹣）．故答案为（1，0），（，﹣）．【点评】本题主要考查直线与圆的参数方程，参数方程与普通方程的互化,比较基础．25．若直线l 的参数方程为，t ∈R ，则直线l 在y 轴上的截距是 1 ．【分析】令x=0，可得t=1，y=1，即可得出结论． 【解答】解：令x=0,可得t=1,y=1， ∴直线l 在y 轴上的截距是1． 故答案为1．【点评】本题考查参数方程的运用，考查学生的计算能力，比较基础．三．解答题（共5小题)26．在直角坐标系xOy中，曲线C1：（t为参数）．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C2：ρ2﹣10ρcosθ﹣6ρsinθ+25=0．（Ⅰ）求C1的普通方程与曲线C2的直角坐标方程，并说明方程所表示的曲线名称;（Ⅱ）判断曲线C1与曲线C2的位置关系，若相交，求出弦长．【分析】（Ⅰ）直接利用转换关系，把参数方程直角坐标方程和极坐标方程之间进行转换．(Ⅱ)利用点到直线的距离公式的应用求出结果．【解答】解:（Ⅰ）曲线C1：（t为参数）．转换为直角坐标方程为：x﹣2y﹣4=0．（x≥2）．故该曲线表示一条射线．曲线C2：ρ2﹣10ρcosθ﹣6ρsinθ+25=0．转换为直角坐标方程为:x2+y2﹣10x﹣6y+25=0，整理得：(x﹣5）2+（y﹣3）2=9,该曲线表示以（5，3）为圆心，3为半径的圆．（Ⅱ）由于该圆是以(5,3）为圆心，3为半径,所以与射线x﹣2y﹣4=0．（x≥2)有两个交点．圆心到射线的距离d=,所以弦长l=2=4．【点评】本题考查的知识要点：参数方程直角坐标方程和极坐标方程之间的转换，点到直线的距离公式的应用．27．已知直线l参数方程：（t为参数），曲线C1：．（1）求直线l的直角坐标方程和曲线C1的参数方程;（2）若点M在曲线C1上运动,求M到直线l距离的最小值．【分析】（1）直接利用转换关系式，把参数方程和极坐标方程与直角坐标方程进行转化．（2)利用三角函数关系式的恒等变换和点到直线的距离公式求出结果．【解答】解:（1)直线l参数方程：(t为参数）,转化为直角坐标方程为：x+2y﹣10=0．曲线C1：．转换为参数方程为：（θ为参数)，(2)设M(3cosθ，2sinθ）到直线l的距离d==．当sin(θ+α）=1时，．【点评】本题考查的知识要点：参数方程和极坐标方程与直角坐标方程的转化,三角函数关系式的恒等变换，点到直线的距离公式的应用．28．已知直线l:（t为参数）,曲线C1：,（θ为参数)．（1）设l与C1相交于A，B两点，求|AB|;（2）曲线C2为（θ为参数），点P是曲线C2上的一个动点，求它到直线l的距离的最小值．【分析】（1）转化hi街利用转换关系式，把参数方程和极坐标方程与直角坐标方程进行转化，进一步求出弦长．（2）利用三角函数关系式的恒等变换，进一步利用点到直线的距离公式求出结果．【解答】解：（1）直线l：(t为参数，转化为直角坐标方程为：，曲线C1：，(θ为参数)．转化为直角坐标方程为：x2+y2=1,则:，解得交点的坐标A（1，0)，B（，）．所以：｜AB｜=1．（2）曲线C2为（θ为参数），点P是曲线C2上的一个动点，则点P的坐标是（），从而点P到直线l的距离是=，当时，d取得最小值，且最小值为．【点评】本题考查的知识要点：参数方程和极坐标方程与直角坐标方程的转化，点到直线的距离公式的应用．29．在平面直角坐标系xOy中，⊙O的参数方程为，（θ为参数）,过点（0，﹣)且倾斜角为α的直线l与⊙O交于A，B两点．(1）求α的取值范围;（2）求AB中点P的轨迹的参数方程．【分析】（1)⊙O的普通方程为x2+y2=1，圆心为O（0，0），半径r=1，当α=时,直线l的方程为x=0，成立；当α≠时,过点（0，﹣）且倾斜角为α的直线l的方程为y=tanα•x+，从而圆心O（0，0)到直线l的距离d=＜1，进而求出或，由此能求出α的取值范围．（2）设直线l的方程为x=m（y+），联立，得（m2+1）y2+2+2m2﹣1=0，由此利用韦达定理、中点坐标公式能求出AB中点P的轨迹的参数方程．【解答】解：（1)∵⊙O的参数方程为（θ为参数），∴⊙O的普通方程为x2+y2=1，圆心为O（0，0），半径r=1,当α=时，过点(0，﹣）且倾斜角为α的直线l的方程为x=0，成立；当α≠时，过点（0，﹣）且倾斜角为α的直线l的方程为y=tanα•x﹣，∵倾斜角为α的直线l与⊙O交于A,B两点,∴圆心O（0，0）到直线l的距离d=＜1，∴tan2α＞1，∴tanα＞1或tanα＜﹣1,∴或，综上α的取值范围是(，）．（2）由（1）知直线l的斜率不为0，设直线l的方程为x=m（y+），设A(x1，y1），(B（x2，y2），P（x3，y3），联立，得(m2+1）y2+2+2m2﹣1=0，,=﹣+2，=，=﹣，∴AB中点P的轨迹的参数方程为,（m为参数),(﹣1＜m＜1）．【点评】本题考查直线直线的倾斜角的取值范围的求法，考查线段的中点的参数方程的求法，考查参数方程、直角坐标方和、韦达定理、中点坐标公式等基础知识，考查数形结合思想的灵活运用,考查运算求解能力，考查函数与方程思想，是中档题．30．在直角坐标系xOy中，曲线C的参数方程为，（θ为参数），直线l的参数方程为，（t为参数）．（1）求C和l的直角坐标方程;（2）若曲线C截直线l所得线段的中点坐标为（1，2），求l的斜率．【分析】(1）直接利用转换关系，把参数方程和极坐标方程与直角坐标方程进行转化．（2）利用直线和曲线的位置关系,在利用中点坐标求出结果．【解答】解：（1）曲线C的参数方程为（θ为参数），转换为直角坐标方程为：．直线l的参数方程为(t为参数）．转换为直角坐标方程为:sinαx﹣cosαy+2cosα﹣sinα=0．(2）把直线的参数方程代入椭圆的方程得到：+=1整理得:（4cos2α+sin2α）t2+(8cosα+4sinα）t﹣8=0，则：,由于（1，2）为中点坐标，①当直线的斜率不存时，x=1．②当直线的斜率存在时,利用中点坐标公式，，则：8cosα+4sinα=0，解得：tanα=﹣2，即：直线l的斜率为﹣2．【点评】本题考查的知识要点：参数方程和极坐标方程与直角坐标方程的转化,直线和曲线的位置关系的应用，中点坐标的应用．。

直线的参数方程练习题（带答案）1、若直线l 的参数方程为13{24x ty t=+=- (t 为参数),则直线l 的倾斜角的余弦值为( )A.45-B.45C.35-D.35答案：C解析：方法一:直线l 的参数方程13{24x ty t=+=- (t 为参数)可转化为31'{524'x t y t ⎛⎫=+- ⎪⎝⎭=-('5t t =-为参数),故直线l 的倾斜角的余弦值为35-.方法二:由直线l 的参数方程取得普通方程为43100x y +-=,故斜率4tan 3k α==-,所以3cos 5α=- (α为倾斜角).2、若圆的方程12cos ,{32sin x y θθ=-+=+ (θ为参数),直线的方程为21,{61x t y t =-=- (t 为参数),则直线与圆的位置关系是( )A.相交过圆心B.相交而不过圆心C.相切D.相离 答案：B解析：圆的圆心坐标是(1,3)-,半径是2,直线的普通方程是320x y -+=,圆心到25==<,故直线与圆相交而不过圆心. 3、直线11,2{2x t y =+=- (t 为参数)和圆2216x y +=交于,A B 两点,则AB 的中点坐标为( )A.(3,3)-B.()C.)3-D.(3,答案：D解析：将直线方程代入圆的方程得2211162t⎛⎫⎛⎫++-=⎪⎪ ⎪⎝⎭⎝⎭,整理得28120t t-+=,所以128t t+=,1242t t+=,依据t的几何意义可知中点坐标为114,422⎛⎫+⨯-⎪⎪⎝⎭,即(3,.4、直线21y x=+的参数方程是( )A.22{21x ty t==+(t为参数) B.21{41x ty t=-=+(t为参数)C.1{21x ty t=-=-(t为参数) D.sin{2sin1xyθθ==+(θ为参数)答案：C解析：选项A中20t≥,选项D中sin[1,1]θ∈-,因此不会是A,D.B中消掉参数得23y x=+,故只有C正确.5、已知O为原点,P为椭圆4cos,{xyαα==(α为参数)上第一象限内一点,OP的倾斜角为3π,则点P坐标为( )A.()2,3 B.()4,3C.(D.(,55答案：D解析：椭圆4cos,{xyαα==(α为参数)化为普通方程,得2211612x y+=.由题意可得直线OP的方程为y= (0x>).由22(0),{11612y xx y=>+=解得x y==.∴点P的坐标为(,55.故选D.6、直线1cos 2sin x t y t αα=+⎧⎨=-+⎩ (α为参数,0a π≤<)必过点( )A.()1,2-B.()1,2-C.()2,1-D.()2,1- 答案：A解析：直线表示过点()1,2-的直线.7、下列可以作为直线210x y -+=的参数方程的是( )A.13x t y t =+⎧⎨=+⎩ (t 为参数)B.152x t y t =-⎧⎨=-⎩(t 为参数)C.12x t y t =-⎧⎨=-⎩ (t 为参数) D.255x y t⎧=⎪⎪⎨⎪=+⎪⎩ (t 为参数) 答案：C解析：题目所给的直线的斜率为2,选项A 中直线斜率为1,选项D 中直线斜率为12,所以可排除选项A 、D.而选项B 中直线的普通方程为230x y -+=,故选C.8、极坐标方程cos ρθ=和参数方程12x ty t =--⎧⎨=+⎩ (t 为参数)所表示的图形分别是( )A.直线、直线B.直线、圆C.圆、圆D.圆、直线 答案：D解析：∵cos ρθ=,∴2cos ρρθ=,即22x y x +=,即221124x y ⎛⎫-+= ⎪⎝⎭,∴cos ρθ=所表示的图形是圆.由12x ty t =--⎧⎨=+⎩(t 为参数)消参得:1x y +=,表示直线.10、在平面直角坐标系 xOy 中,若直线:{x tl y t a==- (t 为参数)过椭圆3cos :{2sin x C y ϕϕ== (ϕ为参数)的右顶点,则常数a 的值为__________.答案：3解析：由直线l 的参数方程:{x tl y t a==- (t 为参数)消去参数t ,得直线l 的一般方程为y x a =-, 由椭圆的参数方程可知其右顶点为(3,0).因为直线l 过椭圆的右顶点,所以30a -=,即 3a =. 11、在平面直角坐标系 xOy 中,若直线121,:{x s l y s=+= ( s 为参数)和直线2,:{21x at l y t ==- (t 参数)平行,则常数a 的值为__________.答案：4解析：将直线方程化为平面直角坐标方程,得1l 的方程是210x y --=,2l 的方程是022a a x y --=.因为两直线平行,所以22a -=-,且12a-≠-,所以4a =. 12、化直线l的参数方程31x t y =-+⎧⎪⎨=⎪⎩,(t 为参数)为普通方程,并求倾斜角,说明t的几何意义.答案：由31x ty =-+⎧⎪⎨=+⎪⎩消去参数t ,得直线l10y -+=.故斜率tan k α==,由于0απ≤<,即3πα=.因此直线l 的倾斜角为3π.又31x t y +=⎧⎪⎨-=⎪⎩得()()222314x y t ++-=,∴t =故t 是t 对应点M 到定点()03,1M -的向量2M M 的模的一半.13、在直角坐标系中,参数方程为212x y t ⎧=+⎪⎪⎨⎪=⎪⎩ (t 为参数)的直线l 被以原点为极点,x 轴的正半轴为极轴,极坐标方程为2cos ρθ=的曲线C 所截,求截得的弦长.答案：参数方程为212x y t ⎧=+⎪⎪⎨⎪=⎪⎩ (t 为参数)表示的直线l 是过点()2,0A ,倾斜角为30,极坐标方程2cos ρθ=表示的曲线C 为圆2220x y x +-=. 此圆的圆心为()1,0,半径为1,且圆C 也过点()2,0A ;设直线l 与圆C 的另一个交点为B ,在Rt OAB ∆中,2cos30AB =︒=。

极坐标与参数方程单元练习1一、选择题（每小题5分，共25分）1、已知点M 的极坐标为⎪⎭⎫⎝⎛35π，，下列所给出的四个坐标中能表示点M 的坐标是（ ）。

A. 53，-⎛⎝ ⎫⎭⎪πB. 543，π⎛⎝ ⎫⎭⎪C. 523，-⎛⎝ ⎫⎭⎪πD. ⎪⎭⎫ ⎝⎛-355π， 2、直线：3x-4y-9=0与圆：⎩⎨⎧==θθsin 2cos 2y x ，(θ为参数)的位置关系是( )A.相切B.相离C.直线过圆心D.相交但直线不过圆心3、在参数方程⎩⎨⎧+=+=θθsin cos t b y t a x （t 为参数）所表示的曲线上有B 、C 两点，它们对应的参数值分别为t 1、t 2，则线段BC 的中点M 对应的参数值是（ ）4、曲线的参数方程为⎩⎨⎧-=+=12322t y t x (t 是参数)，则曲线是（ ）A 、线段B 、双曲线的一支C 、圆D 、射线 5、实数x 、y 满足3x 2＋2y 2=6x ，则x 2＋y 2的最大值为（ ）A 、27 B 、4 C 、29D 、5二、填空题（每小题5分，共30分）1、点()22-，的极坐标为 。

2、若A 33，π⎛⎝ ⎫⎭⎪，B ⎪⎭⎫ ⎝⎛-64π，，则|AB|=___________，S AOB ∆=___________。

（其中O 是极点）3、极点到直线()cos sin 3ρθθ+=的距离是________ _____。

4、极坐标方程2sin 2cos 0ρθθ-⋅=表示的曲线是_______ _____。

5、圆锥曲线()为参数θθθ⎩⎨⎧==sec 3tan 2y x 的准线方程是 。

6、直线l 过点()5,10M ，倾斜角是3π，且与直线032=--y x 交于M ，则0MM 的长为 。

三、解答题（第1题14分，第2题16分，第3题15分；共45分）1、求圆心为C 36，π⎛⎝ ⎫⎭⎪，半径为3的圆的极坐标方程。

2、已知直线l 经过点P(1,1),倾斜角6πα=，（1）写出直线l 的参数方程。

1．极坐标系与直角坐标系xoy 有相同的长度单位，以原点O 为极点，以x 轴正半轴为极轴.已知直线l 的参数程为1222x t y ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数），曲线C 的极坐标程为2sin 8cos ρθθ=.（Ⅰ）求C 的直角坐标程；（Ⅱ）设直线l 与曲线C 交于,A B 两点，求弦长||AB .2．已知直线l 经过点1(,1)2P ，倾斜角α＝6π，圆C的极坐标程为)4πρθ=-. (1)写出直线l 的参数程，并把圆C 的程化为直角坐标程；(2)设l 与圆C 相交于两点A 、B ，求点P 到A 、B 两点的距离之积．3．（本小题满分10分）选修4－4：坐标系与参数程已知直线l 的参数程是)(242222是参数t t y t x ⎪⎪⎩⎪⎪⎨⎧+==，圆C 的极坐标程为)4cos(2πθρ+=． （I ）求圆心C 的直角坐标；(Ⅱ)由直线l 上的点向圆C 引切线，求切线长的最小值．4．已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中x 轴的正半轴重合，且两坐标系有相同的长度单位，圆C 的参数程为12cos 12sin x y αα=+⎧⎨=-+⎩（α为参数），点Q的极坐标为7)4π。

（1）化圆C 的参数程为极坐标程；（2）直线l 过点Q 且与圆C 交于M ，N 两点，求当弦MN 的长度为最小时，直线l 的直角坐标程。

5．在极坐标系中，点M 坐标是)2,3(π，曲线C 的程为)4sin(22πθρ+=；以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，斜率是1-的直线l 经过点M ．（1）写出直线l 的参数程和曲线C 的直角坐标程；（2）求证直线l 和曲线C 相交于两点A 、B ，并求||||MB MA ⋅的值．6．（本小题满分10分） 选修4-4坐标系与参数程在直角坐标系中，曲线1C 的参数程为⎩⎨⎧+==ααsin 22cos 2y x ，(α为参数) M 是曲线1C 上的动点，点P 满足OM 2=，（1）求点P 的轨迹程2C ；（2）在以D 为极点，X 轴的正半轴为极轴的极坐标系中，射线3πθ=与曲线1C ，2C 交于不同于原点的点A,B 求AB7．在平面直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐V 标程为πcos =13ρθ⎛⎫- ⎪⎝⎭，M ，N 分别为曲线C 与x 轴、y 轴的交点． （1）写出曲线C 的直角坐标程，并求M ，N 的极坐标；（2）求直线OM 的极坐标程．8．在直角坐标系中，曲线C 1的参数程为：2cos x y αα=⎧⎪⎨=⎪⎩（α为参数），以原点为极点，x 轴的正半轴为极轴，并取与直角坐标系相同的长度单位，建立极坐标系，曲线C 2是极坐标程为：cos ρθ=，(1)求曲线C 2的直角坐标程；(2)若P ，Q 分别是曲线C 1和C 2上的任意一点，求PQ 的最小值.9．已知圆C 的极坐标程为2cos ρθ=，直线l的参数程为1221122x t x t ⎧=+⎪⎪⎨⎪=+⎪⎩（t 为参数），点A的极坐标为4π⎫⎪⎪⎝⎭，设直线l 与圆C 交于点P 、Q .（1）写出圆C 的直角坐标程；（2）求AP AQ ⋅的值.10．已知动点P ，Q 都在曲线C ：2cos 2sin x t y t =⎧⎨=⎩（β为参数）上，对应参数分别为t α= 与2t α=（0＜α＜2π），M 为PQ 的中点。

参数方程一、选择题1．直线34x t y t =-⎧⎨=+⎩，（t 为参数)上与点(3,4)P 的距离等于 ）A ．)3,4(B ．)5,4(-或)1,0(C ．)5,2(D ．)3,4(或)5,2(2．已知直线t ty t x (12⎩⎨⎧+=+=为参数）与曲线C ：03cos 42=+-θρρ交于B A ,两点， ）A ．1 BC 3．曲线θθθ(sin 2cos 1⎩⎨⎧+=+-=y x 为参数）的对称中心（ ）A 、在直线y=2x 上B 、在直线y=-2x 上C 、在直线y=x-1上D 、在直线y=x+1上4．曲线的参数方程为⎩⎨⎧-=+=12322t y t x (t 是参数)，则曲线是（ ） C 、圆 D 、射线二、解答题5．选修4-4：坐标系与参数方程在直角坐标系xOy 中，圆C 的参数方程1cos (sin x y ϕϕϕ=+⎧⎨=⎩为参数）．以O 为极点，x 轴的非负半轴为极轴建立极坐标系．（Ⅰ）求C 的极坐标方程；（Ⅱ）直线l 的极坐标方程是记射线OM ：与C 分别交于点O ，P ，与l 交于点Q ，求PQ 的长．6．选修4−4：坐标系与参数方程在直角坐标系xOy 中，圆C 的方程为（x+6）2+y 2=25.（Ⅰ）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求C 的极坐标方程；（Ⅱ）直线l 的参数方程是cos ,sin ,x t y t αα=⎧⎨=⎩（t 为参数），l 与C 交于A ，B 两点，∣AB ∣l 的斜率.7．选修4-4：坐标系与参数方程在直角坐标系xOy 中，曲线C 1的参数方程为cos 1sin x a ty a t =⎧⎨=+⎩（t 为参数，a ＞0）.在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ=4cos θ.（Ⅰ）说明C 1是哪种曲线，并将C 1的方程化为极坐标方程；（Ⅱ）直线C 3的极坐标方程为θ=α0，其中α0满足tan α0=2，若曲线C 1与C 2的公共点都在C 3上，求a. 8．选修4-4：坐标系与参数方程．已知直线l 的参数方程为431x t ay t =-+⎧⎨=-⎩（t 为参数），在直角坐标系xOy 中，以O 点为极点，x 轴的非负半轴为极轴，以相同的长度单位建立极坐标系，设圆M 的方程为26sin 8ρρθ-=-．（1）求圆M 的直角坐标方程；（2）若直线l 截圆M 所得弦长为，求实数a 的值． 9．（本小题满分10分）已知在直角坐标系xOy 中，圆C 的参数方程为12cos (2sin x y θθθ=+⎧⎨=⎩为参数）． （1）以原点为极点、x 轴正半轴为极轴建立极坐标系，求圆C 的极坐标方程； （2）直线l 的坐标方程是，且直线l 与圆C 交于,A B 两点，试求弦AB 的长．10．（2014•大武口区校级一模）已知直线的极坐标方程为，圆M 的参数方程为（其中θ为参数）．（Ⅰ）将直线的极坐标方程化为直角坐标方程； （Ⅱ）求圆M 上的点到直线的距离的最小值．11．以直角坐标系的原点O 为极点，x 轴的正半轴为极轴，且两个坐标系取相等的长度单位,已知直线 l 的参数方程为 1cos sin x t y t αα=+⎧⎨=⎩（t 为参数， 0απ<<），曲线C 的极坐标方程为2sin 4cos ρθθ=．（Ⅰ）求曲线C 的直角坐标方程。

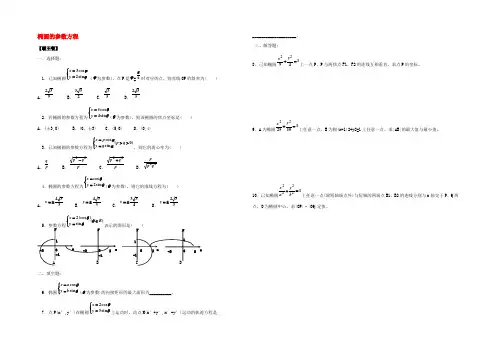
椭圆的参数方程【霸王餐】 一、选择题：1．已知椭圆⎩⎨⎧==ϕϕsin 2cos 3y x （ϕ为参数），点P 是ϕ=6π时对应的点，则直线OP 的斜率为( )A ．932B ．233C ．33D ．3322．若椭圆的参数方程为⎩⎨⎧==θθsin 4cos 5y x (θ为参数)，则该椭圆的焦点坐标是( )A ．(±3,0)B ．(0，±3)C ．(5,0)D ．(0,4)3．已知椭圆的参数方程为)0(sin cos >>⎩⎨⎧==q p q y p x αα，则它的离心率为( )A ．p qB ．pq p 22- C ．pq p 22+ D ．22q p p4．椭圆的参数方程为⎩⎨⎧==θθsin 2cos y x (θ为参数)，则它的准线方程为( )A ．334±=x B ．334±=y C ．433±=x D ．332±=y)(sin |cos |2R y x ∈⎩⎨⎧==θθθ( )二、填空题：6．椭圆⎩⎨⎧==θθsin cos b y a x (θ为参数)的内接矩形的最大面积为__________。

7．点P(x ′,y ′)在椭圆⎩⎨⎧==θθsin 3cos 2y x 上运动时，动点M(x ′+y ′,x ′-y ′)运动的轨迹方程是____________________。

三、解答题：8．已知椭圆14922=+y x 上一点P ，P 与两焦点F1、F2的连线互相垂直，求点P 的坐标。

9．A 为椭圆1102522=+y x 上任意一点，B 为圆(x-1)2+y2=1上任意一点，求|AB|的最大值与最小值。

10．已知椭圆12222=+b y ax 上任意一点(除短轴端点外)与短轴的两端点B1、B2的连线分别与x 轴交于P 、Q 两点，O 为椭圆中心，求|OP|·|OQ|定值。

高一数学参数方程练习题【例1】 曲线cos 1:sin 1x C y θθ=-⎧⎨=+⎩（θ为参数）的普通方程为（ ）A ．()()22111x y -++= B ．()()22111x y +++= C ．()()22111x y ++-=D ．()()22111x y -+-=【例2】 将参数方程12cos ,2sin ,x y θθ=+⎧⎨=⎩（θ为参数）化成普通方程为 ．【例3】 若直线112:2.x t l y kt =-⎧⎨=+⎩，（t 为参数）与直线2:12.x s l y s =⎧⎨=-⎩，（s 为参数）垂直，则k = ．【例4】 若直线1223x ty t =-⎧⎨=+⎩（t 为参数）与直线41x ky +=垂直，则常数k = ．【例5】 若直线340x y m ++=与圆1cos 2sin x y θθ=+⎧⎨=-+⎩（θ为参数）没有公共点，则实数m 的取值范围是 ．【例6】 在平面直角坐标系xOy 中，直线l 的参数方程为11x y t =⎧⎨=+⎩（参数t ∈R ），圆C 的参数方程为cos 1sin x y θθ=+⎧⎨=⎩（参数[)0,2πθ∈），则圆心到直线l 的距离是 ．【例7】 已知曲线C 的参数方程为cos ,2sin ,x y θθ=⎧⎨=-+⎩()θ为参数，则曲线C 的普通方程是 ；点A 在曲线C 上，点(,)M x y 在平面区域22020210x y x y y -+⎧⎪+-⎨⎪-⎩≥≤≥上，则AM 的最小值是 ．典例分析【例8】 已知曲线C的参数方程为13x y t t ⎧=⎪⎪⎨⎛⎫⎪=+ ⎪⎪⎝⎭⎩（t 为参数，0t >）．求曲线C 的普通方程．【例9】 在平面直角坐标系xOy 中，设()P x y ，是椭圆2213x y +=上的一个动点，求S x y =+的最大值．【例10】 已知曲线14cos :3sin x t C y t =-+⎧⎨=+⎩（t 为参数），28cos :3sin x C y θθ=⎧⎨=⎩（θ为参数）．化1C ，2C 的方程为普通方程，并说明它们分别表示什么曲线．【例11】 若1C 上的点P 对应的参数为π2t =，Q 为2C 上的动点，求PQ 中点M 到直线332,:2x t C y t =+⎧⎨=-+⎩（t为参数）距离的最小值．【例12】 已知曲线1C ：cos ()sin x y θθθ=⎧⎨=⎩为参数，曲线2C：()2x t y ⎧=-⎪⎪⎨⎪=⎪⎩为参数．⑴指出1C ，2C 各是什么曲线，并说明1C 与2C 公共点的个数；⑵若把1C ，2C 上各点的纵坐标都压缩为原来的一半，分别得到曲线1C '，2C '．写出1C '，2C '的参数方程．1C '与2C '公共点的个数和1C 与2C 公共点的个数是否相同？说明你的理由．。

直线参数方程的练习题直线参数方程是解决平面几何问题中常用的一种数学工具。

它通过引入参数来描述曲线的特性，帮助我们更好地理解与解决问题。

下面将通过几个练习题，来探讨直线参数方程的应用。

1. 问题描述：有一直线L，过点A(1, 2)，且与直线x - y = 0平行。

求直线L的参数方程。

解答思路：由题意可知，直线L与直线x - y = 0平行，所以直线L的斜率与x - y = 0的斜率相等。

因此，我们首先需要求出直线x - y = 0的斜率。

直线x - y = 0的一般式方程为y = x，所以其斜率为1。

假设直线L的斜率也为1，设直线L的参数方程为：x = t + a,y = t + b，其中t为参数，a、b为待定常数。

由题意可知，直线L过点A(1, 2)，代入参数方程可得：1 = t + a,2 = t + b.解上述方程组，可得t = -1, a = 2, b = 3。

因此，直线L的参数方程为：x = t + 2,y = t + 3.2. 问题描述：有一直线L1，它过点A(-1, 2)，斜率为2，与直线x + y = 0垂直。

求直线L1的参数方程。

解答思路：直线L1过点A(-1, 2)，且与直线x + y = 0垂直。

垂直直线的斜率乘积为-1，所以直线L1的斜率为-1/2。

设直线L1的参数方程为：x = t + a,y = -1/2t + b，其中t为参数，a、b为待定常数。

由题意可知，直线L1过点A(-1, 2)，代入参数方程可得：-1 = t + a,2 = -1/2t + b.解上述方程组，可得t = -2, a = 1, b = 3。

因此，直线L1的参数方程为：y = -1/2t + 3.3. 问题描述：有一直线L，过点A(3, 5)，且与直线x - 2y + 4 = 0垂直。

求直线L 的参数方程。

解答思路：与直线x - 2y + 4 = 0垂直的直线，可以通过求垂线的斜率来得到。

垂线的斜率是原直线斜率的负倒数。

开封高中1012届参数方程 练习题一、选择题1．将参数方程⎩⎨⎧αα cos ＝－1－ cos 2＝y x (a 为参数)化成普通方程为( )．A ．2x ＋y ＋1＝0B ．x ＋2y ＋1＝0C ．2x ＋y ＋1＝0(－3≤x ≤1)D ．x ＋2y ＋1＝0(－1≤y ≤1)2．双曲线xy ＝1的参数方程是( )．A ．⎪⎪⎩⎪⎪⎨⎧21－21＝＝t y t x B ．⎪⎩⎪⎨⎧t y t x sin 1＝ sin ＝ C ．⎪⎩⎪⎨⎧t y t x tan 1＝ tan ＝ D ．⎪⎪⎩⎪⎪⎨⎧t t t t y x －－e ＋e 2＝2＋e ＝e 3．对于参数方程和⎩⎨⎧οο30sin ＋2 ＝ 30 cos －1 ＝ t y t x ⎪⎩⎪⎨⎧οο30sin 2＝　30 cos ＋ 1 ＝ t －y t x 的曲线，正确的结论是( )． A ．是倾斜角为30º的平行线 B ．是倾斜角为30º的同一直线 C ．是倾斜角为150º的同一直线 D ．是过点(1，2)的相交直线 4．参数方程⎪⎪⎩⎪⎪⎨⎧)(θθθ sin ＋121＝2sin ＋2cos ＝y x (0≤θ≤2π)的曲线( )．A ．抛物线的一部分，且过点(－1，21)B ．抛物线的一部分，且过点(1，21) C ．双曲线的一支，且过点(－1，21) D ．双曲线的一支，且过点(1，21) 5．直线⎩⎨⎧t y tx ＋ 3＝－－ 2＝(t 为参数)上与点A (2，－3)的距离等于1的点的坐标是( )．A ．(1，－2)或(3，－4)B ．(2－2，－3＋2)或(2＋2，－3－2)C ．(2－22，－3＋22)或(2＋22，－3－22)D ．(0，－1)或(4，－5) 6．直线x cos α＋y sin α＝2与圆⎩⎨⎧θθ＝ ＝2sin 2cos y x (θ 为参数)的位置关系是( )．A ．相交不过圆心B ．相交且过圆心C ．相切D ．相离7．若点P (4，a )在曲线⎪⎩⎪⎨⎧ty tx 2＝2＝(t 为参数)上，点F (2，0)，则|PF |等于( )．A ．4B ．5C ．6D ．78． 已知点(m ，n )在曲线⎪⎩⎪⎨⎧ααsin 6＝ cos 6 ＝ y x (α为参数)上，点(x ，y )在曲线⎩⎨⎧ββsin 24＝ cos 24＝y x (β为参数)上，则mx＋ny 的最大值为( )． Ａ．12 B ．15 C ．24 D ．309．直线y ＝k x ＋2与曲线⎪⎩⎪⎨⎧ααsin 3＝ 2cos y x ＝至多一个交点的充要条件是( )．A ．k ∈[－21，21] B ．k ∈(－∞，－21]∪［21，＋∞) C ．k ∈[－22，22]D ．k ∈(－∞，－22]∪［22，＋∞) 10．过椭圆C ：⎪⎩⎪⎨⎧θθsin 3＝ 2cos y x ＝(θ 为参数)的右焦点F 作直线l 交C 于M ，N 两点，|MF |＝m ，|NF |＝n ，则nm 1＋1的值为( )．A ．32B ．34C ．38D ．不能确定二、填空题11． 弹道曲线的参数方程为⎪⎪⎩⎪⎪⎨⎧221 sin ＝ cos ＝00gt －t v y t v x αα(t 为参数，a ，v 0，g 为常数)，当炮弹达到最高点时，炮弹飞行的水平距离为 ．12．直线的参数方程为⎪⎩⎪⎨⎧οο20cos ＝－3＋20 sin ＝t y t x (t 为参数)，则直线的倾斜角为 ．13．曲线C 1：y ＝|x |，C 2：x ＝0，C 3的参数方程为⎪⎩⎪⎨⎧t y tx 1－＝＝(t 为参数)，则C 1，C 2，C 3围成的图形的面积为 ．14．直线⎩⎨⎧θθsin ＝ cos ＝t y t x 与圆⎩⎨⎧ααsin 2 ＝ cos 2＋4＝y x 相切，则该直线的倾斜角＝________．15．变量x ，y 满足⎪⎩⎪⎨⎧ty tx －1＝＝2(t 为参数)，则代数式2＋＋x y 2的取值范围是 ．16．若动点(x ，y )在曲线1＝　＋4222b y x (0＜b ≤4)上变化，则x 2＋2y 的最大值为 ． 三．解答题17．已知直线l 1过点P (2，0)，斜率为34．(1)求直线l 1的参数方程；(2)若直线l 2的方程为x ＋y ＋5＝0，且满足l 1∩l 2＝Q ，求|PQ |的值．18．已知点P (x ，y )为曲线C ：⎩⎨⎧θθθθ － 4sin ＋ 3sin 3cos 4cos y ＝x ＝(θ 为参数)上动点，若不等式x ＋y ＋m ＞0恒成立，求实数m 的取值范围．19．经过点M (2，1)作直线交曲线⎪⎪⎩⎪⎪⎨⎧t t y tt x 1－＝1＋＝ (t 是参数)于A ，B 两点，若点M 为线段AB 的中点，求直线AB 的方程．20、据气象预报，在气象台以东400千米的B 处的海面上有一个台风中心形成。

含参数整式练习题七年级一、选择题1. 若多项式3x^2 + ax 2与2x^2 3x + 1是同类项，则a的值为（）。

A. 3B. 3C. 6D. 62. 下列各式中，单项式是（）。

A. 4x^2 + 3xyB. 5a^3bC. 2x^2 3x + 1D. a + b3. 若a 2b = 0，则下列等式成立的是（）。

A. a = bB. a = 2bC. b = 2aD. a + b = 0二、填空题1. 已知单项式3xy^2的系数是______，次数是______。

2. 若5x^3 2x^2 + mx 7与3x^2 4x + 2是同类项，则m的值为______。

3. 已知多项式3x^2 4x + 1，则其首项系数是______，常数项是______。

三、计算题1. 计算：(2x 3y)(x + 4y) 5xy。

2. 计算：(3a^2 2a + 1) (a^2 + 2a 3)。

3. 计算：4x^3 2x^2 + 3x 5 + 3x^2 7x + 2。

四、应用题1. 某同学用代数式表示一块长方形菜地，长为a米，宽为b米，求这块菜地的面积。

2. 小明买了x千克苹果，每千克y元，请用代数式表示小明买苹果的总费用。

3. 一辆汽车行驶的速度是v千米/小时，行驶了t小时，请用代数式表示汽车行驶的路程。

五、简答题1. 请问什么是单项式？单项式的系数和次数分别指什么？2. 什么是多项式？多项式的项和次数是如何定义的？3. 请举例说明同类项的概念，并说明同类项可以如何进行合并。

六、作图题1. 画出多项式3x^2 2x + 1的图像，并标出其顶点坐标。

2. 在同一坐标系中画出单项式2x和3x的图像，并说明它们的图像特点。

七、解答题1. 已知多项式A = 4x^2 3x + 2，多项式B = 2x^2 + x 1，求A + B的值。

2. 若a b = 5，且a + b = 7，求a^2 b^2的值。

3. 已知多项式C = 5x^3 2x^2 + 3x 4，求C中x的系数和常数项。

初一数学上册综合算式专项练习题综合运用参数方程在初一数学上册中，我们学习了综合算式的相关知识和应用。

其中，参数方程是一种特殊的方程形式，为我们解决一些复杂的数学问题提供了便利。

接下来，我们将通过几道综合算式专项练习题，综合运用参数方程的知识，进一步巩固我们的学习成果。

练习题一：已知一条直线的参数方程为:x = 2 - ty = 3 + 2t请问该直线与x轴和y轴的交点分别是什么？解析：当直线与x轴相交时，直线上的点的纵坐标为0，代入参数方程中即可求得交点的横坐标：0 = 3 + 2tt = -1.5将t的值代入参数方程中，可以求得交点的坐标为：x = 2 - (-1.5) = 3.5y = 3 + 2(-1.5) = 0同理，当直线与y轴相交时，直线上的点的横坐标为0，代入参数方程中即可求得交点的纵坐标：x = 2 - t0 = 3 + 2tt = -1.5将t的值代入参数方程中，可以求得交点的坐标为：x = 2 - (-1.5) = 3.5y = 3 + 2(-1.5) = 0综上所述，该直线与x轴和y轴的交点分别为(3.5, 0)和(0, 0)。

练习题二：已知一条抛物线的参数方程为:x = t^2y = -3t + 4请问该抛物线的焦点坐标是什么？解析：为了确定抛物线的焦点坐标，我们需要先将参数方程形式转换为普通的函数形式。

通过将参数方程中的t表示为x的函数，然后代入y的表达式，我们可以得到以下函数方程：y = -3 * (x^(1/2)) + 4由于抛物线的对称性，焦点坐标的横坐标应该为0。

因此，我们只需要找到对应于横坐标为0的纵坐标即可。

代入x = 0到函数方程中，可以求得焦点的纵坐标为：y = -3 * (0^(1/2)) + 4y = 4综上所述，该抛物线的焦点坐标为(0, 4)。

通过以上两道综合算式专项练习题的实例分析，我们可以看出参数方程在解决数学问题中的灵活应用。

在学习初一数学上册综合算式时，我们要注意理解参数方程的定义和特点，并且在实际问题中善于运用参数方程的知识，灵活解决各类数学计算题。