《电工学》上册课后答案解析

电工学秦曾煌第七版上册课后答案【篇一：电工学第七版课后答案_秦曾煌第二章习题解答_2】2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中i3。

【篇二：电工学(电子技术)课后答案秦曾煌】大作用的外部条件，发射结必须正向偏置，集电结反向偏置。

晶体管放大作用的实质是利用晶体管工作在放大区的电流分配关系实现能量转换。

2．晶体管的电流分配关系晶体管工作在放大区时，其各极电流关系如下：ic??ibie?ib?ic?(1??)ibicibicib3．晶体管的特性曲线和三个工作区域（1）晶体管的输入特性曲线：晶体管的输入特性曲线反映了当uce等于某个电压时，ib和ube之间的关系。

晶体管的输入特性也存在一个死区电压。

当发射结处于的正向偏压大于死区电压时，晶体管才会出现ib，且ib随ube线性变化。

（2）晶体管的输出特性曲线：ic随uce变化的关系曲线。

晶体管的输出特性曲线反映当ib为某个值时，在不同的ib下，输出特性曲线是一组曲线。

ib=0以下区域为截止区，当uce比较小的区域为饱和区。

输出特性曲线近于水平部分为放大区。

（3）晶体管的三个区域：晶体管的发射结正偏，集电结反偏，晶体管工作在放大区。

此时，ic=?ib，ic与ib成线性正比关系，对应于曲线簇平行等距的部分。

晶体管处于截止工作状态，对应输出特性曲线的截止区。

此时，ib=0，ic=iceo。

晶体管发射结和集电结都处于正向偏置，即uce很小时，晶体管工作在饱和区。

此时，ic虽然很大，但ic??ib。

即晶体管处于失控状态，集电极电流ic不受输入基极电流ib的控制。

14．3 典型例题例14．1 二极管电路如例14．1图所示，试判断二极管是导通还是截止，并确定各电路的输出电压值。

设二极管导通电压ud=0.7v。

25610v(a)(b)d1(c)(d)例14.1图1图（a）电路中的二极管所加正偏压为2v，大于u=0.7v，二极管处于导通状态，解：○d则输出电压u0=ua—ud=2v—0.7v=1.3v。

图1: 习题1.5.1图I1 = −4A U1 = 140V U4 = −80V I2 = 6AU2 = −90V U5 =30VI3 = 10AU3 = 60V1 电路的基本概念与定律1.5 电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。

电流和电压的参考方向如图中所示。

今通过实验测量得知1 试标出各电流的实际方向和各电压的实际极性。

2 判断哪些元件是电源？哪些是负载？3 计算各元件的功率，电源发出的功率和负载取用的功率是否平衡？[解]:2 元件1，2为电源；3，4，5为负载。

3 P1 = U1I1 = 140 ×(−4)W = −560W P2 = U2I2 = (−90) ×6W =−540W P3= U3I3 = 60 ×10W =600WP4 = U4I1 = (−80) ×(−4)W =320W P5 = U5I2 = 30 ×6W = 180WP1 + P2 =1100W负载取用功率P = P3 + P4 + P5 =1100W两者平衡电源发出功率P E = 1.5.2专业知识分享在图2中，已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3，并说明它是电源还是负载。

校验整个电路的功率是否平衡。

专业知识分享专业 知识分享[解] 首先根据基尔霍夫电流定律列出图 2: 习题1.5.2图−I 1 + I 2 − I 3 = 0−3 + 1 − I 3 =可求得I 3 = −2mA, I 3的实际方向与图中的参考方向相反。

根据基尔霍夫电流定律可得U 3 = (30 + 10 × 103 × 3 × 10−3 )V =60V其次确定电源还是负载： 1 从电压和电流的实际方向判定：电路元件3 80V 元件 30V 元件电流I 3 从“+”端流出,故为电源; 电流I 2 从“+”端流出，故为电源； 电流I 1 从“+”端流出，故为负载。

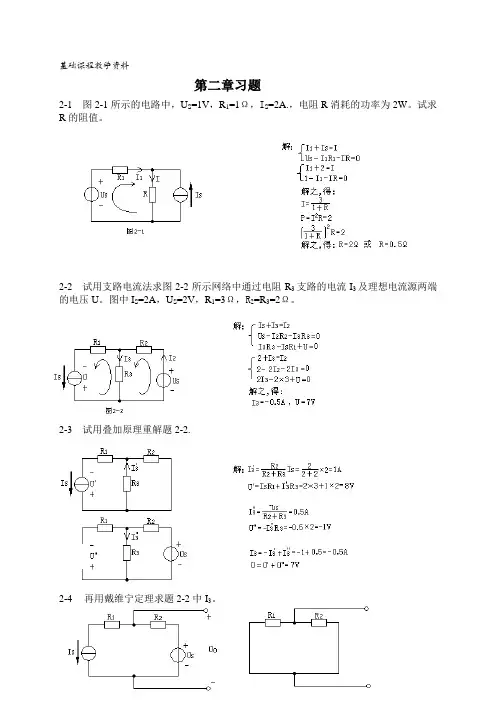
基础课程教学资料第二章习题2-1 图2-1所示的电路中，U S=1V，R1=1Ω，I S=2A.，电阻R消耗的功率为2W。

试求R的阻值。

2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。

图中I S=2A，U S=2V，R1=3Ω，R2=R3=2Ω。

2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。

2-5 图2-3所示电路中,已知U S1=6V，R1=2Ω，I S=5A，U S2=5V，R2=1Ω，求电流I。

2-6 图2-4所示电路中，U S1=30V，U S2=10V，U S3=20V，R1=5kΩ，R2=2kΩ，R3=10kΩ，I S=5mA。

求开关S在位置1和位置2两种情况下，电流I分别为多少？2-7 图2-5所示电路中，已知U AB=0，试用叠加原理求U S的值。

2-8 电路如图2-6所示，试用叠加原理求电流I。

2-9 电路如图2-7所示，试用叠加原理求电阻R4上电压U的表达式。

2-10电路如图2-8所示,已知R1=Ω，R2=R3=2Ω，U S=1V，欲使I=0，试用叠加原理确定电流源I S的值。

2-11 画出图2-9所示电路的戴维宁等效电路。

2-12 图2-10所示的电路接线性负载时，U 的最大值和I的最大值分别是多少？2-13 电路如图2-11所示，假定电压表的内阻无穷大，电流表的内阻为零。

当开关S处于位置1时，电压表的读数为10V，当S处于位置2时，电流表的读数为5mA。

试问当S处于位置3SHI 4，电压表和电流表的读数各为多少？2-14 图2-12所示电路中，各电源的大小和方向均未知，只知每个电阻均为6Ω，又知当R=6Ω时，电流I=5A。

今欲使R支路电流I=3A，则R应该多大？2-15 图2-13所示电路中，N为线性有源二端网络，测得AB之间电压为9V，见图（a）；若连接如图（b）所示，可测得电流I=1A。

现连接如图（c）所示形式，问电流I为多少？2-16 电路如图2-14所示，已知R1=5Ω时获得的功率最大，试问电阻R是多大？本章小结1、支路电流法是分析和计算电路的基本方法，适用于任何电路。

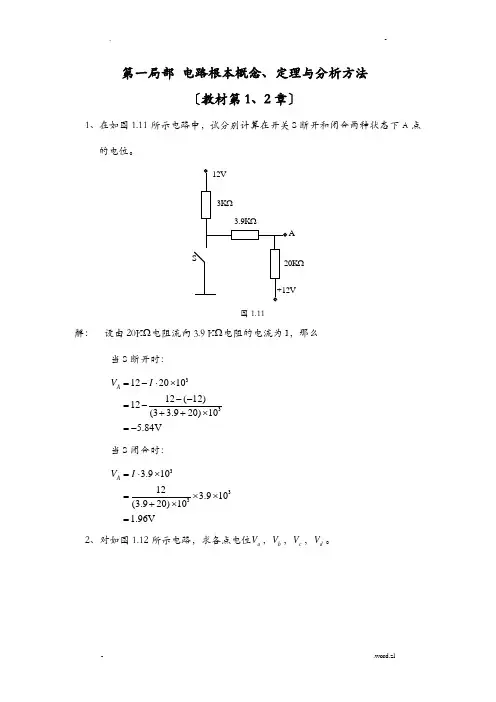
第一局部 电路根本概念、定理与分析方法〔教材第1、2章〕1、在如图1.11所示电路中，试分别计算在开关S 断开和闭合两种状态下A 点的电位。

AΩ图1.11解： 设由20K Ω电阻流向3.9 K Ω电阻的电流为I ，那么当S 断开时：3312201012(12)12(3 3.920)105.84V =-⋅⨯--=-++⨯=-A V I 当S 闭合时：3333.91012 3.910(3.920)101.96V =⋅⨯=⨯⨯+⨯=A V I 2、对如图1.12所示电路，求各点电位a V ，b V ，c V ，d V 。

E 290VE 1图1.12解： 设b 为参考点，那么0V =b V10660V ==⨯=a ab V U 1140V ===c cb V U E 290V ===d db V U E ab bU3、在如图1.13所示电路中，求电压ab U 。

+__U图1.13解： 设通过10Ω电阻由上向下的电流为1I ，通过5Ω电阻由上向下的电流为2I ，那么由KCL 知1123A =--=-I ，214341A =+=-+=I I ，25514A =-=-=I I所以1231053310(3)513440V=-++-=-+⨯-+⨯-⨯=-ab U I I I4、在如图1.14所示电路中，10.01μA I =，20.3μA I =，59.61μA I =。

求其余电流3I ，4I 和6I 。

图1.14解： 由KCL 可得3120.010.30.31μA =+=+=I I I 4539.610.319.3μA =-=-=I I I 6240.39.39.6μA =+=+=I I I5、在图1.15所示电路中，假设欲使指示灯上的电压3U 和电流3I 分别为12V 和0.3A ，试求电源电压U 。

图1.15解： 综合运用KVL 与KCL ，可得334412200.6V 2020=⇒===U U I I 2340.30.60.9A =+=+=I I I2424551020100.9200.6102015 1.4A 1515+⨯+⨯+=⇒===I I I I I I1250.9 1.4 2.3A =+=+=I I I123101010 2.3100.91244V =++=⨯+⨯+=U I I U6、如图1.16所示电路中，110V U =，2A S I =，11R =Ω，22R =Ω，35R =Ω，1R =Ω。

1 电路的基本概念与定律电源有载工作、开路与短路电源发出功率P E =在图2中，已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3，并说明它是电源还是负载。

校验整个电路的功率是否平衡。

[解] 首先根据基尔霍夫电流定律列出图 2: 习题图−I1 + I2 −I3=−3 + 1 −I3=可求得I3= −2mA, I3的实际方向与图中的参考方向相反。

根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10−3 )V= 60V其次确定电源还是负载：1 从电压和电流的实际方向判定：电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出，故为电源；电流I1从“+”端流出，故为负载。

2 从电压和电流的参考方向判别：电路元件3 U3和I3的参考方向相同P= U3I3 = 60 ×(−2) ×10−3W =−120 ×10−3W （负值），故为电源；80V元件U2和I2的参考方向相反P = U2I2 = 80 ×1 ×10−3W =80 ×10−3W （正值），故为电源；30V元件U1和I1参考方向相同P= U1I1 = 30 ×3 ×10−3 W =90 ×10−3W （正值），故为负载。

两者结果一致。

最后校验功率平衡：电阻消耗功率:2 2P R= R1I= 10 ×3 mW = 90mW12 2P R= R2I= 20 ×1 mW = 20mW2电源发出功率:P E = U2I2 + U3I3 = (80 + 120)mW =200mW负载取用和电阻损耗功率:P = U1I1 + R1 I2 + R2I2 = (90 + 90 + 20)mW =200mW1 2两者平衡基尔霍夫定律试求图6所示部分电路中电流I、I1和电阻R，设U ab = 0。

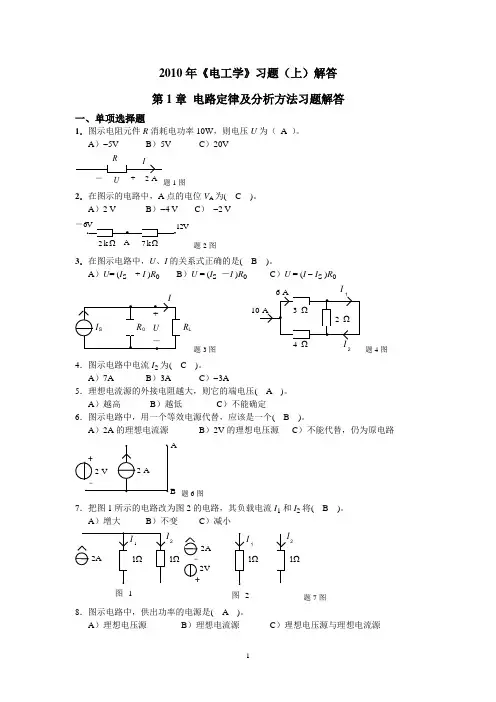
2010年《电工学》习题（上）解答 第1章 电路定律及分析方法习题解答一、单项选择题1．图示电阻元件R 消耗电功率10W ，则电压U 为（ A ）。

A ）-5V B ）5V C ）20VUR 题1图2．在图示的电路中，A 点的电位V A 为( C )。

A ）2 V B ）-4 V C ） -2 V－ 2 k 7 k ΩΩ题2图3．在图示电路中，U 、I 的关系式正确的是( B )。

A ）U = (I S + I )R 0 B ）U = (I S －I )R 0 C ）U = (I - I S )R 0R L题3图I 2题4图4．图示电路中电流I 2为( C )。

A ）7AB ）3AC ）-3A5．理想电流源的外接电阻越大，则它的端电压( A )。

A ）越高 B ）越低 C ）不能确定6．图示电路中，用一个等效电源代替，应该是一个( B )。

A ）2A 的理想电流源 B ）2V 的理想电压源 C ）不能代替，仍为原电路2 V题6图7．把图1所示的电路改为图2的电路，其负载电流I 1和I 2将( B )。

A ）增大B ）不变C ）减小221Ω2V 2A图 1图 2+题7图8．图示电路中，供出功率的电源是( A )。

A ）理想电压源 B ）理想电流源C ）理想电压源与理想电流源U4VS题8图S题9图9．在图示电路中，各电阻值和U S 值均已知。

欲用支路电流法求解流过电阻R G 的电流I G ，需列出独立的电流方程数和电压方程数分别为( B )。

A ）4和3 B ）3和3 C ）3和410．在计算线性电阻电路的电压和电流时，用叠加原理。

在计算线性电阻电路的功率时，加原理( B )。

A ）可以用 B ）不可以用 C ）有条件地使用11．在图示电路中，已知U S =12V ，I S =2A 。

A 、B 两点间的电压U AB 为( A )。

A ）-18VB ）18VC ）-6VU I SS+题11图SA题12图12．在图示电路中，当开关S 闭合时A 点的电位V A ( C )。

晶体管起放大作用的外部条件，发射结必须正向偏置，集电结反向偏置。

晶体管放大作用的实质是利用晶体管工作在放大区的电流分配关系实现能量转换。

2．晶体管的电流分配关系晶体管工作在放大区时，其各极电流关系如下：C B I I β≈(1)E B C B I I I I β=+=+C C BB I I I I ββ∆==∆3．晶体管的特性曲线和三个工作区域 （1）晶体管的输入特性曲线：晶体管的输入特性曲线反映了当UCE 等于某个电压时，B I 和BE U 之间的关系。

晶体管的输入特性也存在一个死区电压。

当发射结处于的正向偏压大于死区电压时，晶体管才会出现B I ，且B I 随BE U 线性变化。

（2）晶体管的输出特性曲线：晶体管的输出特性曲线反映当B I 为某个值时，C I 随CE U 变化的关系曲线。

在不同的B I 下，输出特性曲线是一组曲线。

B I =0以下区域为截止区，当CE U 比较小的区域为饱和区。

输出特性曲线近于水平部分为放大区。

（3）晶体管的三个区域：晶体管的发射结正偏，集电结反偏，晶体管工作在放大区。

此时，C I =b I β，C I 与b I 成线性正比关系，对应于曲线簇平行等距的部分。

晶体管发射结正偏压小于开启电压，或者反偏压，集电结反偏压，晶体管处于截止工作状态，对应输出特性曲线的截止区。

此时，B I =0，C I =CEO I 。

晶体管发射结和集电结都处于正向偏置，即CE U 很小时，晶体管工作在饱和区。

此时，C I 虽然很大，但C I ≠b I β。

即晶体管处于失控状态，集电极电流C I 不受输入基极电流B I 的控制。

14．3 典型例题例14．1 二极管电路如例14．1图所示，试判断二极管是导通还是截止，并确定各电路的输出电压值。

设二极管导通电压D U =。

25610VD1(a)(b)(c)(d)例图解：○1图（a ）电路中的二极管所加正偏压为2V ，大于DU =，二极管处于导通状态，则输出电压0U =A U —D U =2V —=。

第1章 习题解答(部分)1.5.3 有一直流电源，其额定功率P N =200 W ，额定电压U N ＝50 V ，内阻只ＲN ＝0.5Ω，负载电阻Ｒ0可以调节，其电路如图所示。

试求： (1)额定工作状态下的电流及负载电阻， (2)开路状态下的电源端电压，分析 电源的额定值有额定功率P N 。

额定电压U N 和额定电流I N 。

三者间的关系为 P N =U N I N 。

额定电压U N 是指输出额定电流I N 时的端电压，所以额定功率P N 也就是电源额定工作状态下负载所吸收的功率。

解 （1）额定电流 A U P I N N N 450200===负载电阻 5.12450===N N I U R Ω （2）开路状态下端电压U 0 等于 电源电动势E 。

U 0＝E ＝U N ＋I N Ｒ0＝50＋4×0.5＝52 V1.5.6 一只100V ，8W 的指示灯，现在要接在380V 的电源上，问要串多大阻值的电阻?该电阻应选用多大瓦数的?分析 此题是灯泡和电阻器额定值的应用。

白炽灯电阻值随工作时电压和电流大小而变，但可计算出额定电压下的电阻值。

电阻器的额定值包括电阻值和允许消耗功率。

解 据题给的指示灯额定值可求得额定状态下指示灯电流I N 及电阻只R NΩ≈==≈==1510073.0110A 073.01108N N N N N N U U R U P I串入电阻R 降低指示灯电压，使其在380V 电源上仍保持额定电压U N ＝110V 工作，故有Ω≈-=-=3710073.01103800N N I U U R 该电阻工作电流为I N =0.073 A,故额定功率为W R I P N R 6.193710073.022≈⨯=⋅=可选额定值为3.7k Ω,20 W 的电阻。

1.5.7在图1.03的两个电路中，要在12V 的直流电源上使6V ，50 mA 的电珠正常发光，应该采用哪 一个联接电路？ 解 要使电珠正常发光，必须保证电珠 获得6V ，50mA 电压与电流。

图1: 习题1.5.1图I1 = −4A U1 = 140V U4 = −80V I2 = 6AU2 = −90V U5 =30VI3 = 10AU3 = 60V1 电路的基本概念与定律1.5 电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。

电流和电压的参考方向如图中所示。

今通过实验测量得知1 试标出各电流的实际方向和各电压的实际极性。

2 判断哪些元件是电源？哪些是负载？3 计算各元件的功率，电源发出的功率和负载取用的功率是否平衡？[解]:2 元件1，2为电源；3，4，5为负载。

3 P1 = U1I1 = 140 ×(−4)W = −560W P2 = U2I2 = (−90) ×6W =−540W P3 = U3I3 = 60 ×10W =600WP4 = U4I1 = (−80) ×(−4)W =320W P5 = U5I2 = 30 ×6W =180WP1 + P2 =1100W负载取用功率P = P3 + P4 + P5 =1100W两者平衡电源发出功率P E =1.5.2在图2中，已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3，并说明它是电源还是负载。

校验整个电路的功率是否平衡。

[解] 首先根据基尔霍夫电流定律列出图 2: 习题1.5.2图−I 1 + I 2 − I 3 = 0−3 + 1 − I 3 =可求得I 3 = −2mA, I 3的实际方向与图中的参考方向相反。

根据基尔霍夫电流定律可得U 3 = (30 + 10 × 103 × 3 × 10−3 )V= 60V其次确定电源还是负载： 1 从电压和电流的实际方向判定：电路元件3 80V 元件 30V 元件电流I 3 从“+”端流出,故为电源; 电流I 2 从“+”端流出，故为电源； 电流I 1 从“+”端流出，故为负载。

图 1: 习题1.5.1图I1 = 4A U1 = 140V U4 = 80V I2 = 6AU2 = 90VU5 = 30VI3 = 10AU3 = 60V1 电路的基本概念与定律电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。

电流和电压的参考方向如图中所示。

今通过实验测量得知1 试标出各电流的实际方向和各电压的实际极性。

2 判断哪些元件是电源哪些是负载3 计算各元件的功率，电源发出的功率和负载取用的功率是否平衡[解]:2 元件1，2为电源；3，4，5为负载。

3 P1 = U1I1 = 140 ×(4)W = 560W P2 =U2I2 = (90) ×6W = 540W P3 = U3I3 =60 ×10W = 600WP4 = U4I1 = (80) ×(4)W = 320W P5 =U5I2 = 30 ×6W = 180WP1 + P2 = 1100W负载取用功率P = P3 + P4 + P5 = 1100W两者平衡电源发出功率P E =1.5.2在图2中，已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3，并说明它是电源还是负载。

校验整个电路的功率是否平衡。

[解] 首先根据基尔霍夫电流定律列出图 2: 习题1.5.2图I1 + I2 I3= 03 + 1 I3= 0可求得I3= 2mA, I3的实际方向与图中的参考方向相反。

根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×103 )V = 60V 其次确定电源还是负载：1 从电压和电流的实际方向判定：电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出，故为电源；电流I1从“+”端流出，故为负载。

2 从电压和电流的参考方向判别：电路元件3 U3和I3的参考方向相同P= U3I3 = 60 ×(2) ×103W = 120 ×103W （负值），故为电源；80V元件U2和I2的参考方向相反P = U2I2 = 80 ×1 ×103W =80 ×103W （正值），故为电源；30V元件U1和I1参考方向相同P= U1I1 = 30 ×3 ×103 W = 90 ×103W （正值），故为负载。

基础课程教学资料第二章习题2-1 图2-1所示的电路中，U S=1V，R1=1Ω，I S=2A.，电阻R消耗的功率为2W。

试求R的阻值。

2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。

图中I S=2A，U S=2V，R1=3Ω，R2=R3=2Ω。

2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。

2-5 图2-3所示电路中,已知U S1=6V，R1=2Ω，I S=5A，U S2=5V，R2=1Ω，求电流I。

2-6 图2-4所示电路中，U S1=30V，U S2=10V，U S3=20V，R1=5kΩ，R2=2kΩ，R3=10kΩ，I S=5mA。

求开关S在位置1和位置2两种情况下，电流I分别为多少？2-7 图2-5所示电路中，已知U AB=0，试用叠加原理求U S的值。

2-8 电路如图2-6所示，试用叠加原理求电流I。

2-9 电路如图2-7所示，试用叠加原理求电阻R4上电压U的表达式。

2-10电路如图2-8所示,已知R1=Ω，R2=R3=2Ω，U S=1V，欲使I=0，试用叠加原理确定电流源I S的值。

2-11 画出图2-9所示电路的戴维宁等效电路。

2-12 图2-10所示的电路接线性负载时，U 的最大值和I的最大值分别是多少？2-13 电路如图2-11所示，假定电压表的内阻无穷大，电流表的内阻为零。

当开关S处于位置1时，电压表的读数为10V，当S处于位置2时，电流表的读数为5mA。

试问当S处于位置3SHI 4，电压表和电流表的读数各为多少？2-14 图2-12所示电路中，各电源的大小和方向均未知，只知每个电阻均为6Ω，又知当R=6Ω时，电流I=5A。

今欲使R支路电流I=3A，则R应该多大？2-15 图2-13所示电路中，N为线性有源二端网络，测得AB之间电压为9V，见图（a）；若连接如图（b）所示，可测得电流I=1A。

现连接如图（c）所示形式，问电流I为多少？2-16 电路如图2-14所示，已知R1=5Ω时获得的功率最大，试问电阻R是多大？本章小结1、支路电流法是分析和计算电路的基本方法，适用于任何电路。

图 1: 习题1.5.1图I1 = ?4A U1 = 140V U4 = ?80V I2 = 6AU2 = ?90VU5 = 30VI3 =10A U3 =60V1 电路的基本概念与定律电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。

电流和电压的参考方向如图中所示。

今通过实验测量得知1 试标出各电流的实际方向和各电压的实际极性。

2 判断哪些元件是电源？哪些是负载？3 计算各元件的功率，电源发出的功率和负载取用的功率是否平衡？[解]:2 元件1，2为电源；3，4，5为负载。

3 P1 = U1I1 = 140 ×(?4)W= ?560W P2 = U2I2 = (?90) ×6W= ?540W P3 = U3I3 = 60 ×10W= 600WP4 = U4I1 = (?80) ×(?4)W =320W P5 = U5I2 = 30 ×6W =180WP1 + P2 =1100W负载取用功率P = P3 + P4 + P5 =1100W两者平衡电源发出功率P E =1.5.2在图2中，已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3，并说明它是电源还是负载。

校验整个电路的功率是否平衡。

[解] 首先根据基尔霍夫电流定律列出图 2: 习题1.5.2图?I1 + I2 ? I3=?3 + 1 ? I3=可求得I3= ?2mA, I3的实际方向与图中的参考方向相反。

根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10?3 )V= 60V其次确定电源还是负载：1 从电压和电流的实际方向判定：电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出，故为电源；电流I1从“+”端流出，故为负载。

2 从电压和电流的参考方向判别：电路元件3 U3和I3的参考方向相同P= U3I3 = 60 ×(?2) ×10?3W =?120 ×10?3W （负值），故为电源；80V元件U2和I2的参考方向相反P = U2I2 = 80 ×1 ×10?3W =80 ×10?3W （正值），故为电源；30V元件U1和I1参考方向相同P= U1I1 = 30 ×3 ×10?3 W =90 ×10?3W （正值），故为负载。

课后A选择题部分参考解答（第七版教材）第1章电路的基本概念与基本定律1.5.1 负载也指输出功率，此题答案不清1.5.2 ( 3 ) 开路电压等于电源电动势，可先比上短路电流求内阻1.5.3 ( 3 ) 1.5.4 ( 3 ) 1.5.5 ( 1 )1.5.6 ( 2 ) 1.5.7 ( 2 ) 1.6.1 ( 2 )1.6.2 ( 3 ) 1.7.1 ( 2 ) 1.7.2 ( 3 )第2章电路的分析方法2.1.1 ( 1 ) 2.1.2 ( 1 ) 2.1.3 ( 3 ) 2.1.4 ( 2 ) 2.1.5 ( 2 ) 2.1.6 ( 3 ) 2.1.7 ( 2 ) 2.3.1 ( 2 ) 2.3.2 ( 2 ) 2.3.3 ( 1 ) 2.3.4 ( 3 ) 2.5.1 ( 2 ) 2.6.1 ( 3 ) 2.6.2 ( 2 ) 2.7.1 ( 3 ) 2.7.2 ( 1 )第3章电路的暂态分析3.1.1 ( 2 ) 3.1.2 ( 2 ) 3.2.1 ( 2 )3.2.2 ( 2 ) 3.2.3 ( 3 ) 3.2.4 ( 2 )3.3.1 ( 2 ) 3.3.2 ( 2 ) 3.6.1 ( 2 )3.6.2 ( 2 )第4章正弦交流电路4.1.1 ( 2 ) 4.1.2 ( 2 ) 电压的瞬时值前负号去掉后，其初相角为负90度4.2.1 ( 2 ) 4.2.2 ( 3 ) 4.2.3 ( 2 )4.3.1 ( 1 ) 4.3.2 ( 3 ) 4.3.3 ( 3 )4.4.1 ( 2 ) 4.4.2 ( 3 ) 4.4.3 ( 2 )4.4.4 ( 1 ) 4.4.5 ( 3 ) 4.5.1 ( 4 )4.5.2 ( 1 ) 4.5.3 ( 2 ) 4.7.1 ( 3 )4.7.2 ( 3 )第5章三相电路5.2.1 ( 3 ) 5.2.2 ( 3 )5.2.3 ( 3 ) 此三电灯为星形接法，其上三电流相位互差120度可用平行四边形法则画相量图求解5.2.4 ( 3 ) L1相断路，只剩其它两相电流，同上5.3.1 ( 3 ) 5.4.1 ( 2 ) 第6章磁路与铁心线圈电路6.1.1 ( 2 ) 6.1.2 ( 1 ) 6.2.1 ( 3 )6.2.2 ( 2 ) 6.2.3 ( 2 ) 6.2.4 ( 3 )第7章交流电动机7.2.1 ( 3 ) 7.2.2 ( 1 ) 7.2.3 ( 1 )7.2.4 ( 2 ) 7.3.1 ( 3 ) 7.3.2 ( 2 ) ( 1 ) 7.4.1 ( 2 ) ( 1 ) 7.4.2 ( 2 ) ( 1 ) 7.4.3 ( 1 ) ( 1 ) 7.4.4 ( 2 ) ( 2 ) 7.4.5 ( 1 ) ( 1 ) 7.4.6 ( 3 ) 7.4.7 ( 2 ) 7.5.1 ( 3 ) 7.5.2 ( 3 ) 7.5.3 ( 1 ) 7.8.1 ( 3 ) 7.8.2 ( 2 ) 7.8.3 ( 2 )第10章继电接触器控制系统10.1.1（3）10.1.2 （3）10.2.1 （c）10.2.2 （2）10.3.1（2）不要求的内容可不看。

第1章 习题解答(部分)1.5.3 有一直流电源，其额定功率P N =200 W ，额定电压U N ＝50 V ，内阻只ＲN ＝0.5Ω，负载电阻Ｒ0可以调节，其电路如图所示。

试求： (1)额定工作状态下的电流及负载电阻， (2)开路状态下的电源端电压，分析 电源的额定值有额定功率P N 。

额定电压U N 和额定电流I N 。

三者间的关系为 P N =U N I N 。

额定电压U N 是指输出额定电流I N 时的端电压，所以额定功率P N 也就是电源额定工作状态下负载所吸收的功率。

解 （1）额定电流 负载电阻 5.12450===N N I U R Ω（2）开路状态下端电压U 0 等于 电源电动势E 。

U 0＝E ＝U N ＋I N Ｒ0＝50＋4×0.5＝52 V1.5.6 一只100V ，8W 的指示灯，现在要接在380V 的电源上，问要串多大阻值的电阻?该电阻应选用多大瓦数的?分析 此题是灯泡和电阻器额定值的应用。

白炽灯电阻值随工作时电压和电流大小而变，但可计算出额定电压下的电阻值。

电阻器的额定值包括电阻值和允许消耗功率。

解 据题给的指示灯额定值可求得额定状态下指示灯电流I N 及电阻只R N串入电阻R 降低指示灯电压，使其在380V 电源上仍保持额定电压U N ＝110V 工作，故有该电阻工作电流为I N =0.073 A,故额定功率为 可选额定值为3.7k Ω,20 W 的电阻。

，要在12V 的直流电源上使6V ，50 mA 的电珠正常发光，应该采用哪 一个联接电路？ 解 要使电珠正常发光，必须保证电珠 获得6V ，50mA 电压与电流。

此时电珠 的电阻值为120506==R Ω。

在图1.03(a)中，电珠和120Ω电阻将12V 电源电压平分，电珠能获得所需的6V 电压和50mA 电流，发光正常。

在图1.03(b)中，电珠与120Ω电阻并联后再串联120Ω电阻。

并联的120Ω电阻产生分流作用，使总电流大于50mA ，串联的120Ω电阻压降大于6V ，电珠电压将低于6V ，电流将小于50mA ，不能正常发光。

电工学课后习题答案电工学是一门研究电能的产生、传输、分配和使用的学科，它在现代工业和日常生活中扮演着极其重要的角色。

学习电工学，不仅要理解理论知识，还要通过课后习题来巩固和应用所学。

以下是一些电工学课后习题的参考答案，供同学们参考。

习题1：直流电路分析问题：计算电路中R1和R2的等效电阻。

答案：如果R1和R2是串联的，那么等效电阻R_eq = R1 + R2。

如果它们是并联的，那么1/R_eq = 1/R1 + 1/R2。

习题2：交流电路功率计算问题：已知一个交流电路中的电压有效值为220V，电流有效值为10A，求功率。

答案：功率P = V * I，其中V是电压有效值，I是电流有效值。

所以P = 220V * 10A = 2200W。

习题3：三相电路问题：一个三相电路的线电压是380V，相电压是多少？答案：在星形连接的三相电路中，相电压等于线电压的√3/2倍。

所以相电压V_phase = 380V * √3/2 ≈ 220V。

习题4：电磁感应问题：一个线圈在磁场中旋转，产生感应电动势。

如果线圈的电阻为10Ω，磁通量变化率为10 Wb/s，求感应电流。

答案：感应电动势E = -dΦ/dt，感应电流I = E/R。

所以I = -10 Wb/s / 10Ω = -1 A。

习题5：变压器原理问题：一个理想变压器的原边匝数为1000，副边匝数为500，输入电压为220V，求输出电压。

答案：理想变压器的电压比等于匝数比，即V2/V1 = N2/N1。

所以V2 = (500/1000) * 220V = 110V。

习题6：电动机的工作原理问题：一个三相异步电动机的转子转速为1500转/分钟，同步转速为1800转/分钟，求滑差。

答案：滑差s = (Ns - Nr) / Ns，其中Ns是同步转速，Nr是转子转速。

所以s = (1800 - 1500) / 1800 ≈ 0.167。

习题7：电路的谐振问题：一个RLC串联谐振电路，已知电阻R=100Ω，电容C=10μF，电感L=0.1H，求谐振频率。

第一章 电路的基本概念和基本定律习题解答1-1 在图1-39所示的电路中，若I 1=4A ，I 2=5A ，请计算I 3、U 2的值；若I 1=4A ，I 2=3A ，请计算I 3、U 2、U 1的值，判断哪些元件是电源？哪些是负载？并验证功率是否平衡。

解：对节点a 应用KCL 得 I 1+ I 3= I 2 即4+ I 3=5, 所以 I 3=1A 在右边的回路中，应用KVL 得6⨯I 2+20⨯I 3= U 2，所以U 2=50V 同理，若I 1=4A ，I 2=3A ，利用KCL 和KVL 得I 3= -1A ，U 2= -2V 在左边的回路中，应用KVL 得20⨯I 1+6⨯I 2= U 1，所以U 1=98V 。

U 1，U 2都是电源。

电源发出的功率：P 发= U 1 I 1+ U 2 I 3=98⨯4+2=394W 负载吸收的功率：P 吸=2021I +622I +2023I =394W 二者相等，整个电路功率平衡。

1-2 有一直流电压源，其额定功率P N =200W ，额定电压U N =50V ，内阻R o =0.5Ω，负载电阻R L 可以调节，其电路如图1-40所示。

试求：⑴额定工作状态下的电流及负载电阻R L 的大小；⑵开路状态下的电源端电压；⑶电源短路状态下的电流。

解：⑴A U P I N N N 450200===Ω===5.12450NN L I U R ⑵ =⨯+==0R I U U U N N S OC 50+4⨯0.5 = 52V ⑶ A R U I S SC 1045.0520===图1-39 习题1-1图 图1-40 习题1-2图1-3 一只110V 、8W 的指示灯，现在要接在220V 的电源上，问要串多大阻值的电阻？该电阻的瓦数为多大？解：若串联一个电阻R 后，指示灯仍工作在额定状态，电阻R 应分去110V 的电压，所以阻值Ω==5.151281102R 该电阻的瓦数W RP R 81102== 1-4 图1-41所示的电路是用变阻器R P 调节直流电机励磁电流I f 的电路。