2016-2017年安徽省淮北市濉溪县八年级(下)期中数学试卷(解析版)

淮北市八年级下学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共7题；共14分)1. （2分）下列各式是二次根式的是（）A .B .C .D .2. （2分） (2017八下·泰兴期末) 下列运算正确的是（）A . － =B . ÷ =4C . =－2D . (－ )2=23. （2分） (2019八下·师宗月考) 张大爷离家出门散步，他先向正东走了30 m，接着又向正南走了40 m，此时他离家的距离为（）A . 30 mB . 40 mC . 50 mD . 70 m4. （2分） (2016八下·和平期中) 下列命题中，是真命题的是（）A . 两条对角线互相平分的四边形是平行四边形B . 两条对角线相等的四边形是矩形C . 两条对角线互相垂直的四边形是菱形D . 两条对角线互相垂直且相等的四边形是正方形5. （2分）△ABC的三边分别是a、b、c，由以下条件不能得出△ABC是直角三角形的是（）A . a=1，b= ，c=B . ∠A+∠B=∠CC . a2﹣b2=c2D . ∠A：∠B：∠C=3：4：56. （2分）已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选一个作为补充条件后，使得四边形ABCD是菱形，现在下列四种选法，其中都正确的是（）A . ①或②B . ②或③C . ③或④D . ①或④7. （2分）(2016·河南) 如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（）A . （1，﹣1）B . （﹣1，﹣1）C . （，0）D . （0，﹣）二、填空题 (共7题；共7分)8. （1分） (2017七下·柳州期末) 计算： =________．9. （1分）如图，四边形ABCD中，已知AB=10，CD=12，对角线BD平分∠ABC，∠ADB=45°，∠BCD=90°，则边BC的长度为________ ．10. （1分） (2019九上·凤翔期中) 如图，如图，在正方形ABCD中，点P在AB边上，于E点，于F点，若，，则 ________.11. （1分）使式子有意义的最小整数m是________12. （1分） (2018九上·长宁期末) 如图，在Rt ABC中，∠BAC=90°，点G是重心，联结AG，过点G作DG//BC，DG交AB于点D，若AB=6，BC=9，则 ADG的周长等于________．13. （1分） (2016八下·龙湖期中) 如图，在矩形ABCD中，O是对角线的交点，AE⊥BD于E，若OE：OD=1：2，AC=18cm，则AB=________cm．14. （1分） (2019八上·榆树期末) 如图，矩形ABCD边AD沿折痕AE折叠，使点D落在BC上的点F处，已知AD＝10，AB＝6，则FC的长是________．三、解答题 (共10题；共95分)15. （15分） (2016八下·大石桥期中) 计算（1）（﹣2 ）× ﹣6（2）（ + ）÷（3）（﹣2）2015（ +2）2016．16. （5分）(2016九下·重庆期中) 已知：x，y为实数，且，化简：．17. （5分） (2016八下·安庆期中) 勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2证明：连结DB，过点D作BC边上的高DF，则DF=EC=b﹣a∵S四边形ADCB=S△ACD+S△ABC= b2+ ab．又∵S四边形ADCB=S△ADB+S△DCB= c2+ a（b﹣a）∴ b2+ ab= c2+ a（b﹣a）∴a2+b2=c2请参照上述证法，利用图2完成下面的证明．将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．求证：a2+b2=c2 ．18. （15分）(2018·舟山) 已知，△ABC中，∠B=∠C，P是BC边上一点，作∠CPE=∠BPF，分别交边AC，AB于点E，F。

安徽省淮北市八年级下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分）(2020·湛江模拟) 下列图形中，既是轴对称图形，又是中心对称图形的是（）A .B .C .D .2. （2分） (2019八上·武汉月考) 如图，画∠AOB 的角平分线的方法步骤是：①以 O 为圆心，适当长度为半径作弧，交 OA 于 M 点，交 OB 于 N 点.②分别以 M，N 为圆心，以大于 MN 的长为半径作弧，两弧在∠AOB 的内部交于C.③过点 C 作射线 OC，射线 OC 就是∠AOB 的角平分线，这样作角平分线的依据是（）A . SSSB . SASC . ASAD . AAS3. （2分） (2020八上·丹江口期末) 在直角坐标系中，点与点关于轴对称，则点的坐标为（）A .B .C .D .4. （2分） (2020八上·五常期末) 如图所示，在△ABC中，∠C=90°，AD平分∠BAC ，DE⊥AB于E ， DE=4，BC=9，则BD的长为（）A . 6B . 5C . 4D . 35. （2分） (2020七下·江苏月考) 若一个多边形的外角和与它的内角和相等，则这个多边形是（）A . 三角形B . 四边形C . 五边形D . 六边形6. （2分） (2017八上·衡阳期末) 下列命题是真命题的是（）A . 如果 =1，那么a=1；B . 三个内角分别对应相等的两个三角形全等；C . 如果a是有理数，那么a是实数；D . 两边一角对应相等的两个三角形全等。

7. （2分）(2017·嘉兴) 长度分别为，，的三条线段能组成一个三角形，的值可以是（）A .B .C .D .8. （2分） (2020七下·金昌期末) 如图，已知AE =AF，那么添加下列一个条件后，仍无法判定AED≌AFD的是（）A . ED =FDB . ∠EAD=∠FADC . ∠AED=∠AFD= 90°D . ∠EDA =∠FDA9. （2分）如图，在△ABC中，∠BAD=∠DAE=∠EAF=∠FAC，则（）是△ABC的角平分线．A . ADB . AEC . AFD . AC10. （2分）下列图形中具有稳定性的有（）A . 2个B . 3个C . 4个D . 5个二、填空题 (共10题；共10分)11. （1分） (2020九上·余姚月考) 有一个二次函数的图象，三位同学分别说出了它的一些特点:甲:对称轴为直线x=2;乙:与x轴两个交点的横坐标都是整数;丙:与y轴交点的纵坐标也是整数，且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式________12. （1分） (2020九上·台州月考) 已知抛物线y＝ x2+bx经过点A（4，0）.设点C（1，-3），请在抛物线的对称轴上确定一点D，使得|AD-CD|的值最大，则D点的坐标为________13. （1分） (2020八下·中卫月考) 如图，△ABC中，∠C=90°，∠A＝30° ，BD平分∠ABC交AC于D，若CD＝2cm，则AC=________.14. （1分） (2020八上·当涂期末) 如图，≌ ，其中，，则________．15. （1分） (2020八上·合肥月考) 一个锐角三角形，所有内角的度数均为正整数，且最小角是最大角的，则这个锐角三角形三个内角的度数为________．16. （1分） (2019七下·城固期末) 如图,在△ABC中,AE是∠BAC的角平分线,AD是BC边上的高,且∠B=40°,∠C=60°，则∠EAD度数是________.17. （1分） (2016八上·萧山期中) 已知等腰三角形的一边等于3cm，别一边等于6cm，则周长为________cm。

2016－2017学年度第二学期期中检测八年级数学试题（全卷共120分，考试时间90分钟）一．选择题（本大题有8个小题，每小题3分，共24分，将正确选项填写在表格中相应位置）1．下列图形中，是中心对称图形的是（▲）A B C D2．下列调查中，适宜采用普查方式的是（▲）A．调查市场上某品牌老酸奶的质量情况B．调查某品牌圆珠笔芯的使用寿命C．调查乘坐飞机的旅客是否携带了危禁物品D．调查我市市民对《徐州夜新闻》的认可情况3．下列调查的样本选取方式，最具有代表性的是（▲）A．在青少年中调查年度最受欢迎的男歌手B．了解班上学生的睡眠时间．调查班上学号为双号的学生的睡眠时间C．为了了解你所在学校的学生每天的上网时间，向八年级的同学进行调查D．对某市的出租司机进行体检，以此反映该市市民的健康状况4．下列事件中，属于确定事件的是（▲）A．掷一枚硬币，着地时反面向上B．买一张福利彩票中奖了C．投掷3枚骰子，面朝上的三个数字之和为18D．五边形的内角和为540度5．如图，E、F、G、H分别是□ABCD各边的中点，按不同方式连接分别得到图○1、○2中两个不同的阴影部分甲、乙，关于甲、乙两个阴影部分，下列叙述正确的是（ ▲ ）A ．甲和乙都是平行四边形B ．甲和乙都不是平行四边形C ．甲是平行四边形，乙不是平行四边形D ．甲不是平行四边形，乙是平 行四边形6． 如图，在菱形ABCD 中，AC ＝6，BD ＝8，则菱形的周长是（ ▲ ）A ．24B ．48C ．40D ．207． 若依次连接四边形ABCD 各边的中点所得四边形是矩形，则四边形ABCD 一定是（ ▲ ）A ．矩形B ．菱形C ．对角线互相垂直的四边形D ．对角线相等的四边形 8． 如图，在□ABCD 中，AD =2AB ，F 是AD 的中点，作CE ⊥AB 于E ，在线段AB 上，连接EF 、CF ．则下列结论：○1∠BCD =2∠DCF ；○2∠ECF =∠CEF ；○3S △BEC =2S △CEF ；○4∠DFE =3∠AEF ，其中一定正确的是（ ▲ ）A ．○1○2○4B ．○1○2○4C ．○1○2○3○4D ．○2○3○4图（1）图（2）GF E HCDGF E HCDABBA 第5题图CDAB第6题图EFCDBA 第8题图二． 填空题（本大题有8个小题，每小题3分，共24分）9． 如图是某校参加各兴趣小组的学生人数分布扇形统计图，其中“演艺”兴趣小组一项所对应的角度是 ▲ °．10． 一只不透明的袋子里装有1个白球，3个黄球，6个红球，这些球除了颜色外都相同，将球搅匀，从中任意摸出1个球，有下列事件：○1该球是红球，○2该球是黄球，○3该球是白球．它们发生的概率分别记为P 1，P 2，P 3．则P 1，P 2，P 3的大小关系 ▲ ．11． 在一个不透明的袋子里，装有若干个小球．这些小球只有颜色上的区别．已知其中只有两个红球．每次摸球前都将袋子里的球搅匀．随机摸出一个小球，记下颜色并将球放回袋子里．通过大量重复试验后，发现摸出红球的频率稳定在0.2，那么据此估计，袋子里的球的总数大约是 ▲ 个． 12． 在□ABCD 的周长是32cm ，AB =5cm ，那么AD = ▲ cm ．13． 如图，在□ABCD 中，∠ABC 的平分线交AD 于点E ，AB =4，BC =6，则DE = ▲ ． 14． 如图，在□ABCD 中，AD =6，点E 、F 分别是BD 、CD 的中点，则EF = ▲ ． 15． 如图，G 为正方形ABCD 的边AD 上的一个动点，AE ⊥BG ，CF ⊥BG ，垂足分别为点E ，F ，已知AD =4，则AE 2+CF 2= ▲ ．第9题图第13题图EABCD第14题图EF DABC第15题图FE CDABG16． 如图，在Rt △ABC 中，∠ACB =90，AC =3，BC =4，分别以AB 、AC 、BC 为边在AB 同侧作正方形ABEF ，ACPQ ，BDMC ，记四块阴影部分的面积分别为S 1、S 2、S 3、S 4，则1234S S S S +++= ▲ ．三． 解答题（本大题共8小题，共72分）17． （本题8分）某自行车公司调查阳光中学学生对其产品的了解情况，随机抽取部分学生进行问卷，结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型，分别记为A 、B 、C 、D ．根据调查结果绘制了如下尚不完整的统计图．根据所给数据，解答下列问题： （1）本次问卷共随机调查了名学生，扇形统计图中m = ． （2）请根据数据信息补全条形统计图．（3）若该校有1000名学生，估计选择“非常了解”、“比较了解”共约有多少人？18． （本题8分）为了了解某中学初三年级650名学生升学考试的数学成绩，从中随机抽取了50名学生的数学成绩进行分析，并求得样本的平均成绩是93.5分．下面是根据抽取的学生数学成绩制作的统计表：分组频数累计频数 频率问卷情况条形统计图6168类型人数DCBA2468101214161820第16题图4321S S S S LMDMPQE F CAB60.5～70.5 正3 a70.5～80.5 正正6 0.1280.5～90.5 正正9 0.1890.5～100.5 正正正正17 0.34100.5～110.5 正正b 0.2110.5～120.5正5 0.1 合计501根据题中给出的条件回答下列问题： （1）表中的数据a = ，b = ；（2）在这次抽样调查中，样本是 ；（3）在这次升学考试中，该校初三年级数学成绩在90.5～100.5范围内的人数约为 人．19． （本题8分）在如图所示的网格纸中，建立了平面直角坐标系xOy ，点P （1，2），点A （2，5），B （-2，5），C （-2，3）．（1） 以点P 为对称中心，画出△A ′B ′C ′，使△A ′B ′C ′与△ABC 关于点P对称，并写出下列点的坐标：B ′ ，C ′ ； yB A（2） 多边形ABCA ′B ′C ′的面积是 ．20． （本题8分）如图，在□ABCD 中， AE ⊥BD ，CF ⊥BD ，垂足分别为E 、F ．求证：（1）AE =CF ；（2）四边形AECF 是平行四边形． 证明：21． （本题8分）如图，已知矩形ABCD 中，E 是AD 上的一点，F 是AB 上的一点，EF ⊥EC ，且EF =EC ，DE =4cm ，矩形ABCD 的周长为32cm ，求AE 的长．解：22． （本题10分）如图，在平面直角坐标系xOy 中，点A (3，4)，B (5，0)，C (0，第20题图FEDABCBCA EDF 第22题图-2)．在第一象限找一点D ，使四边形AOBD 成为平行四边形， （1） 点D 的坐标是 ；（2） 连接OD ，线段OD 、AB 的关系是 ；（3） 若点P 在线段OD 上，且使PC +PB 最小，求点P 的坐标． 解：23． （本题10分）将两张完全相同的矩形纸片ABCD 、FBED 按如图方式放置，BD 为重合的对角线．重叠部分为四边形DHBG ，（1） 试判断四边形DHBG 为何种特殊的四边形，并说明理由； （2） 若AB =8，AD =4，求四边形DHBG 的面积． 解：（1） （2）xyO AB CEGHFCDAB第23题图24． （本题12分）如图，正方形ABCO 的边OA 、OC 分别在x 、y 轴上，点B 坐标为（6，6），将正方形ABCO 绕点C 逆时针旋转角度a （0°＜a ＜90°），得到正方形CDEF ，ED 交线段AB 于点G ，ED 的延长线交线段OA 于点H ，连CH 、CG ． （1）求证：△CBG ≌△CDG ；（2）求∠HCG 的度数；并判断线段HG 、OH 、BG 之间的数量关系，说明理由；（3）连结BD 、DA 、AE 、EB 得到四边形AEBD ，在旋转过程中，四边形AEBD 能否为矩形？如果能，请求出点H 的坐标；如果不能，请说明理由． （1） 证明：（2）解：（3）解：x yOGHFEDACB第24题图2016－2017学年度第二学期第一次质量抽测八年级数学试题答案四．选择题（本大题有8个小题，每小题3分，共24分）题号 1 2 3 4 5 6 7 8答案 A C B D A D C B五．填空题（本大题有8个小题，每小题3分，共24分）9．108．10．P1>P2>P3．11．10．12．11．13．2．14．3．15．16．16．18．六．解答题（本大题共10小题，共72分）17．答案：（1）50，m=32；……4分（2）图略；……6分（3）1000(16%40%)100056%560⨯+=⨯=．答约有560人．……8分18．答案：（1）a=0.06，b=10；……4分（2）50名学生的数学成绩；……6分（3）221．……8分19．解：（1）B′（4，-1），C′（4，1），图， (4)分（其中图2分）（2）28．……8分xyB'C'CA'OB AP20． （本题8分）证明：（1）因为四边形ABCD 是平行四边形，所以AD =BC ，…1分因为AD ∥BC ，所以∠ADE =∠CBF ，……2分 因为AE ⊥BD ，CF ⊥BD ，所以∠AED =∠CFB =90°，…3分所以△ADE ≌△CBF ，……4分 所以AE =CF ．……5分（2）因为AE ⊥BD ，CF ⊥BD ，所以∠AEF =∠CFE =90°，…6分 所以AE ∥CF ，……7分由（1）得AE =CF ，所以四边形AECF 是平行四边形．……8分 21． 解：因为EF ⊥EC ，所以∠CEF =90°，………………1分 所以∠AEF +∠DEC =90°，………………2分因为四边形ABCD 是矩形，所以∠A =∠D =90°，………………3分 所以∠AFE +∠AEF =90°，所以∠AFE =∠DEC ，………………4分又EF =EC ，所以△AEF ≌△DCE ，………………5分 所以AE =DC ，………………6分因为2(AD +DC )=32，所以2(AE +DE +AE )=32，………………7分 因为DE =4cm ，所以AE =6cm ．………………8分第20题图FEDABC22． 解答：（1）（8，4），图．…………2分 （2）OD 与AB 互相垂直平分．图…………4分（3）连接AC 交OD 于点P ，点P 即是所求点．…………5分（有图也可以）设经过点O 、D 的函数表达式为1y k x =，则有方程148k =，所以112k =，所以直线OD 的函数表达式为12y x =．………………6分设过点C 、A 的一次函数表达式为2y k x b =+，则有方程组22,3 4.b k b =-⎧⎨+=⎩解得22,2.b k =-⎧⎨=⎩所以过点C 、A 的一次函数表达式为22y x =-，………………8分解方程组1,22 2.y y x ⎧=⎪⎨⎪=-⎩得4,32.3x y ⎧=⎪⎪⎨⎪=⎪⎩，所以点P （43，23）．………………10分xyEPO ADBCEGCD23． （本题10分）解：（1）四边形DHBG 是菱形．………………1分 理由如下：因为四边形ABCD 、FBED 是完全相同的矩形， 所以∠A =∠E =90°，AD =ED ， …………2分 所以DA ⊥AB ，DE ⊥BE ，所以∠ABD =∠EBD ，………………3分 因为AB ∥CD ，DF ∥BE ，所以四边形DHBG 是平行四边形，∠HDB =∠EBD ，………………5分 所以∠HDB =∠ABD ， 所以DH =BH ， 所以□DHBG 是菱形．………………6分 （2）由（1），设DH =BH =x ，则AH =8-x ，在Rt △ADH 中，222AD AH DH +=，即得2224(8)x x +-=， 解得5x =，即BH =5，………………9分所以菱形DHBG 的面积为5420HB AD ??． (10)分24． （本题12分） 解：（1）证明：∵正方形ABCO 绕点C 旋转得到正方形yGFECBCDEF ，∴CD =CB ，∠CDG =∠CBG =90°．………2分在Rt △CDG 和Rt △CBG 中，CD =CB ，CG =CG ，∴△CDG ≌△CBG （HL ）．………………3分（2）解：∵△CDG ≌△CBG ，∴∠DCG =∠BCG 12DCB =∠，DG =BG ．……………4分在Rt △CHO 和Rt △CHD 中，CH =CH ，CO =CD ，∴△CHO ≌△CHD （HL ）．……………5分∴∠OCH =∠DCH 12OCD =∠，OH =DH ，…6分∴∠HCG =∠HCD +∠GCD 11145222OCD DCB OCB =∠+∠=∠=︒，…7分HG =HD +DG =HO +BG ．………………8分（3）解：四边形AEBD 可为矩形． 如图，连接BD 、DA 、AE 、EB ，因为四边形AEBD 若为矩形，则四边形AEBD 为平行四边形，且AB =ED ，则有AB 、ED 互相平分，即G 为AB 中点的时候．因为DG =BG ，所以此时同时满足DG =AG =EG =BG ，即平行四边形AEBD 对角线相等，则其为矩形．所以当G 点为AB 中点时，四边形AEBD 为矩形．………………10分 ∵四边形DAEB 为矩形，∴AG =EG =BG =DG ． ∵AB =6，∴AG =BG =3．………………11分 设H 点的坐标为（x ，0），则HO =x ， ∵OH =DH ，BG =DG ，∴HD =x ，DG =3．在Rt △HGA 中，∵HG =x +3，GA =3，HA =6-x ，∴(x +3)2=32+(6-x )2，∴x =2． ∴H 点的坐标为（2，0）．………………12分。

淮北市八年级下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分）若使分式的值为0，则x的取值为（）A . 1或-1B . -3或１C . -3D . -3或-12. （2分）﹣4.5×10﹣5表示（）A . ﹣0.00045B . ﹣0.000045C . ﹣450000D . ﹣450003. （2分）下列分式变形中，正确的是（）A . =a+bB . =﹣1C . =n﹣mD . =4. （2分） (2017八下·民勤期末) 若无解，则m的值是（）A . 3B . ﹣3C . ﹣2D . 25. （2分） (2019七下·荔湾期末) 已知点在第二象限且到轴的距离为3，到轴的距离为2，则点坐标为（）A .B .C .D .6. （2分）函数y=和y=在第一象限内的图象如图，点P是y=的图象上一动点，PC⊥x轴于点C，交y=的图象于点B．给出如下结论：①△ODB与△OCA的面积相等；②PA与PB始终相等；③四边形PAOB的面积大小不会发生变化；④CA=AP．其中所有正确结论的序号是（）A . ①②③B . ②③④C . ①③④D . ①②④7. （2分）函数y= 的图象可能是（）A .B .C .D .8. （2分）如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（）A . AB=BEB . DE⊥DCC . ∠ADB=90°D . CE⊥DE9. （2分） (2018八上·重庆期末) 如图，在平面直角坐标系中，函数和的图象分别为直线，，过点作x轴的垂线交于点，过点作y轴的垂线交于点，过点作x轴的垂线交于点，过点作y轴的垂线交于点，依次进行下去，则点的坐标是（）A .B .C .D .10. （2分） (2016九上·苏州期末) 下列四个函数图象中，当时，随的增大而增大的是（）A .B .C .D .二、填空题 (共5题；共5分)11. （1分）化简：÷=________ ．12. （1分）如图，一次函数y=kx+b（k＞0）的图象与x轴的交点坐标为（﹣2，0），则关于x的不等式kx+b ＜0的解集是________13. （1分）(2017·枣庄) 如图，在▱ABCD中，AB为⊙O的直径，⊙O与DC相切于点E，与AD相交于点F，已知AB=12，∠C=60°，则的长为________．14. （1分）已知一次函数y=kx+b的图象如图，则关于x的不等式kx+b＞0的解集是________15. （1分） (2017八下·大冶期末) 如图，在▱ABCD中，∠ABC的平分线交AD于点E，且AE=3.5，ED=2，则▱ABCD的周长是________．三、解答题 (共8题；共95分)16. （10分）(2017·青岛模拟) 计算题（1）解不等式组：．（2）化简：（x﹣）÷ ．17. （5分）先化简，再求值：．其中x为不等式组的整数解．18. （15分） (2019八下·泗洪开学考) 已知点在直线上，（1）直线解析式为________；（2）画出该一次函数的图象；（3）将直线向上平移个单位长度得到直线，与轴的交点的坐标为________；（4）直线与直线相交于点，点坐标为________；（5）三角形ABC的面积为________；（6）由图象可知不等式的解集为________.19. （10分）(2019·中山模拟)图①图②图③（1）【问题提出】如图①，在△ABC中，∠A＝120°，AB＝AC＝5，则△ABC的外接圆半径R的值为________.（2）【问题探究】如图②，⊙O的半径为13，弦AB＝24，M是AB的中点，P是⊙O上一动点，求PM的最大值.（3）【问题解决】如图③所示，AB、AC、BC是某新区的三条规划路其中，AB＝6km，AC＝3km，∠BAC＝60°，BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P，在AB、AC路边分别建物资分站点E、F.也就是，分别在、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短，试求PE＋EF＋FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).20. （15分）(2019·南京模拟) 小明和小亮分别从甲地和乙地同时出发，沿同一条路相向而行，小明开始跑步，中途改为步行，到达乙地恰好用40min.小亮骑自行车以300m/min的速度直接到甲地，两人离甲地的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示，（1）甲、乙两地之间的路程为________m，小明步行的速度为________m/min；（2）求小亮离甲地的路程y关于x的函数表达式，并写出自变量x的取值范围；（3）求两人相遇的时间.21. （15分） (2017八下·邵阳期末) 随着地球上的水资源日益枯竭，各级政府越来越重视倡导节约用水，某市的生活用水按“阶梯水价”方式进行收费，人均月生活用水收费标准如图所示，图中x表示人均月生活用水的吨数，y 表示收取的人均月生活用水费（元）。

安徽省淮北市八年级下学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）(2017·长春模拟) 使二次根式有意义的x的取值范围是（）A . x＞2B . x≥2C . x＜2D . x＞﹣22. （2分） (2018八上·张家港期中) 下列各组数中，不能构成直角三角形的一组是（）A . 1，2，B . 1，2，C . 3，4，5D . 6，8，123. （2分） (2015八下·福清期中) 下列各式属于最简二次根式是（）A .B .C .D .4. （2分）如图,以等边三角形ABC的BC边为直径画半圆,分别交AB,AC于点E,D,DF是半圆O的切线,过点F 作BC的垂线交BC于点G.若AF的长为2,则FG的长为（）A . 4B . 3C . 6D . 25. （2分） (2016八下·凉州期中) 等腰梯形的两底之差等于腰长，则腰与下底的夹角为（）A . 120°B . 60°C . 45°D . 135°6. （2分）如图，在Rt△ABC中，∠ACB=90°，D，E，F分别是AB，BC，CA的中点，若CD=5cm，则EF为（）A . 5B . 10C . 15D . 207. （2分） (2019八下·北京期末) 函数中，自变量的取值范围是（）A .B .C .D .8. （2分）过平面上A,B,C三点中的任意两点作直线，可作（）A . 1条B . 3条C . 1条或3条D . 无数条9. （2分） (2019八下·绍兴期中) 如图，DE，EF是△ABC的中位线，AB＋BC＝10，则四边形BFED的周长是（）A . 5B . 10C . 15D . 2010. （2分）(2017·洛阳模拟) 如图，在平面直角坐标系xOy中，点A（1，0），B（2，0），正六边形ABCDEF沿x轴正方向无滑动滚动，每旋转60°为滚动1次，那么当正六边形ABCDEF滚动2017次时，点F的坐标是（）A . （2017，0）B . （2017 ，）C . （2018，）D . （2018，0）11. （2分）如图，已知正六边形ABCDEF的边长为2，G，H分别是AF和CD的中点，P是GH上的动点，连接AP，BP，则AP+BP的最小值为（）A . 4B . +2C . +1D . 212. （2分） (2017八下·磴口期中) 如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为（）A . 4B . 6C . 16D . 55二、填空题 (共8题；共8分)13. （1分）在实数范围内分解因式：x3－3x＝________．14. （1分）(2017·孝感模拟) 如图，矩形OABC的边OA，OC分别在坐标轴上，OA=4，OC=8，把△ABC沿着AC折叠．点B落在点B′处，AB′交y轴于点D，则点D的坐标是________．15. （1分）如图，在△ABC中，已知E、F、D分别是AB、AC、BC上的点，且DE∥AC，DF∥AB，要使四边形AEDF是菱形，在不改变图形的前提下，你需添加的一个条件是________就可以证明这个多边形是菱形．16. （1分） (2020八上·张店期末) 如图，一根橡皮筋放置在x轴上，固定两端A和B，其中A点坐标（0,0）,B 点坐标（8,0），然后把中点C向上拉升3cm到D，则橡皮筋被拉长了________cm.17. （1分） (2019九上·南开月考) ）如图，Rt△ABC中，C= 90o ，以斜边AB为边向外作正方形 ABDE，且正方形对角线交于点D，连接OC，已知AC=5，OC=6 ，则另一直角边BC的长为________．18. （1分）等边三角形的一边上的高线长为，那么这个等边三角形的中位线长为________．19. （1分）如图所示，一个圆柱体高20cm，底面半径为5cm，在圆柱体下底面的A点处有一只蚂蚁，想吃到与A点相对的上底面B处的一只已被粘住的苍蝇，这只蚂蚁从A点出发沿着圆柱形的侧面爬到B点，则最短路程是________．（结果用根号表示）20. （1分）观察下列运算过程：……请运用上面的运算方法计算：＝________.三、解答题 (共6题；共56分)21. （10分） (2018八上·茂名期中) 计算（1）；（2） .22. （5分） (2017八下·文安期中) 如图，铁路上A、B两点相距25km，C、D为两村庄，DA⊥AB于A，CB⊥AB 于B，已知DA=15km，CB=10km，现在要在铁路AB上建一个土特产品收购站E，使得C、D两村到E站的距离相等，则E站应建在距A站多少千米处？23. （5分）如图，矩形的长与宽分别为a和b，在矩形中截取两个大小相同的圆作为圆柱的上下底面，剩余的矩形作为圆柱的侧面，刚好能组合成一个没有空隙的圆柱，则a和b要满足什么数量关系？24. （10分） (2019八上·萧山期末) 已知是等边三角形，点D是BC边上一动点，连结AD（1）如图1，若，，求AD的长；（2）如图2，以AD为边作，分别交AB，AC于点E，F．小明通过观察、实验，提出猜想：在点D运动的过程中，始终有，小明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的两种想法想法1：利用AD是的角平分线，构造角平分线的性质定理的基本图形，然后通过全等三角形的相关知识获证．想法2：利用AD是的角平分线，构造的全等三角形，然后通过等腰三角形的相关知识获证．请你参考上面的想法，帮助小明证明一种方法即可小聪在小明的基础上继续进行思考，发现：四边形AEDF的面积与AD长存在很好的关系若用S表示四边形AEDF的面积，x表示AD的长，请你直接写出S与x之间的关系式．25. （15分）(2020·长宁模拟) 如图，在平面直角坐标系中，已知抛物线经过点，对称轴是直线，顶点为点，抛物线与轴交于点．（1）求抛物线的表达式和点的坐标；（2）将上述抛物线向下平移个单位，平移后的抛物线与轴正半轴交于点，求的面积；（3）如果点在原抛物线上，且在对称轴的右侧，联结交线段于点，，求点的坐标．26. （11分） (2018九上·宁都期中) 如图 1，在Rt△ABC 中，∠A=90°，AB=AC，点 D、E 分别在边 AB、AC 上，AD=AE，连接DC，点 M、P、N 分别为 DE、DC、BC 的中点,（1）观察猜想：如图 1 中，△PMN 是________三角形；（2）探究证明：把△ADE 绕点 A 逆时针方向旋转到图 2 的位置，连接 MN，BD， CE．判断△PMN 的形状，并说明理由；（3）拓展延伸：将△ADE 绕点 A 在平面内自由旋转，若 AD=4，AB=10，请求△PMN 面积的取值范围．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共8题；共8分)13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、三、解答题 (共6题；共56分)21-1、21-2、22-1、23-1、24-1、25-1、25-2、25-3、26-1、26-2、26-3、。

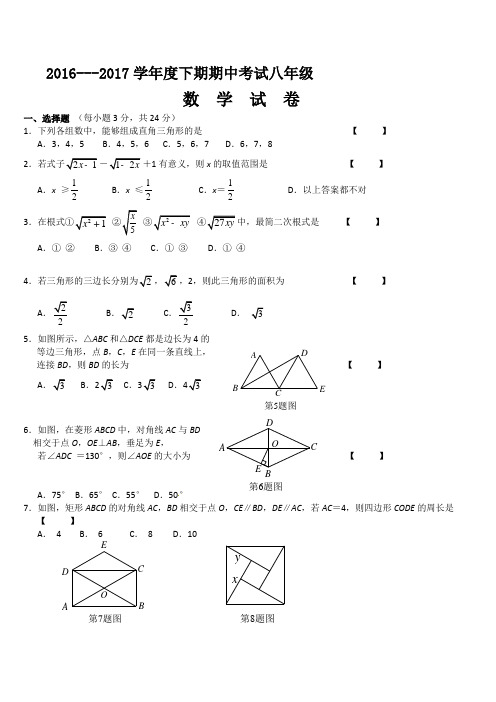
2016---2017学年度下期期中考试八年级数 学 试 卷一、选择题 （每小题3分，共24分）1．下列各组数中，能够组成直角三角形的是 【 】 A ．3，4，5 B ．4，5，6 C ．5，6，7 D ．6，7，8 2－1有意义，则x 的取值范围是 【 】 A ．x ≥12 B ．x ≤12 C ．x ＝12D ．以上答案都不对3【 】 A ．① ② B ．③ ④ C ．① ③ D ．① ④42，则此三角形的面积为 【 】 A．2BC．2 D ．5．如图所示，△ABC 和△DCE 都是边长为4的等边三角形，点B ，C ，E 在同一条直线上， 连接BD ，则BD 的长为【 】 A B ． C ． D ．6．如图，在菱形ABCD 中，对角线AC 与BD 相交于点O ，OE ⊥AB ，垂足为E ， 若∠ADC ＝130°，则∠AOE 的大小为 【 】A ．75°B ．65°C ．55°D ．50°7．如图，矩形ABCD 的对角线AC ，BD 相交于点O ，CE ∥BD ，DE ∥AC ，若AC ＝4，则四边形CODE 的周长是 【 】A ． 4B ． 6C ． 8D ．10第5题图ABD E第6题图O E AB C D第7题图ABC OE D y x第8题图8．如图，是4个全等的直角三角形镶嵌而成的正方形图案，已知大正方形的面积为49，小正方形的面积为4，若用x ，y 表示直角三角形的两条直角边（x ＞ y ），请观察图案，指出下列关系式不正确．．．的是 【 】A ．2249x y +=B ．2x y -=C ．2449xy +=D ．13x y +=二、填空题（ 每小题3分，共21分） 9．若x ，y 为实数，且∣x ＋2∣＋3y -＝0，则（x ＋y ）2017的值为．10 ．11. 实数a ，b 在数轴上的对应点如图所示，则∣a －b = ．12．若x ＝27＋x 2＋（2x ＝ ．13．如图，在平面直角坐标系中，若菱形ABCD 的顶点A ，B 的坐标分别为（－3，0）， （2，0），点D 在y 轴上，则点C 的坐标是 ．14．如图所示，直线a 经过正方形ABCD 的顶点A ，分别过顶点D ，B 作DE ⊥a 于点E ，BF ⊥a 于点F ，若DE ＝4，BF ＝3，则EF ＝ ．15．如图，R t △ABC 中，∠B ＝90°，AB ＝3，BC ＝4，将△ABC 折叠，使点B 恰好落在斜边AC 上，与点B ＇重合，AE 为折痕，则E B ＇＝ ．三、解答题：（本大题共8个小题，满分75分） 16．（每小题4分 共8分）计算：（101)2++； （2）a 532．第11题图0baB 'A BC E aA B C D E F第13题图第14题图第15题图17．(8分)x 的取值范围是什么？18．（9分）如图，每个小正方形的边长都是1， （1）求四边形ABCD 的周长和面积（2）∠BCD 是直角吗？19．(9分)如图所示，在□ABCD 中，点E ，F 分别在边BC 和AD 上，且CE ＝AF ，（1）求证：△ABE ≌ △CDF ；（2）求证：四边形AECF 是平行四边形．第18题图AB第19题图ABCDE F20．(10分) 如图所示，在菱形ABCD 中，点E ，F 分别是边BC ，AD 的中点，（1）求证：△ABE ≌ △CDF ；（2）若∠B ＝60°，AB ＝4，求线段AE 的长．21．（10分）如图所示，在矩形ABCD 中，对角线AC ，BD 相交于点O ，E 是CD 的中点，连接OE ，过点C 作CF∥BD 交线段OE 的延长线于点F ，连接DF ．求证： （1）OD ＝CF ； （2）四边形ODFC 是菱形．22．（10分）如图所示，矩形ABCD 的对角线相交于点O ，OF ⊥AD 于点F ，OF ＝2cm ，AE ⊥BD 于点E ，且BE ﹕BD ＝1﹕4，求AC 的长．第20题图AB C DFE第21题图A B C D F E OA B OED F C 第22题图23．（11分）在平面内，正方形ABCD 与正方形CEFH 如图放置，连接DE ，BH ，两线交于M ，求证：（1）BH ＝DE ；（2）BH ⊥DE ．HM A BF EC D 第23题图2016-2017学年度八年级（下）期中数学参考答案16．（1）1（4分） （2）7a 4分） 17．a ＝5； ……………………3分 5≤x ≤10 ……………………8分18．（1……………………3分面积14.5 ……………………6分（2）是……………………7分，证明：略．……………………9分 19．（1）略 5分 （2）略 9分20．（1）略 5分 （2）证出AE 是高 8分，AE ＝ 10分 21．证明：（1）∵CF ∥BD ∴∠DOE ＝∠CFE ，∵E 是CD 的中点，∴CE ＝DE在△ODE 和△FCE 中，DOE CFE CE DE DEO CEFì??ïïï=íïï??ïïî，∴△ODE ≌△FCE （ASA ）∴OD ＝CF ．……………………6分（2）由（1）知OD ＝CF ，∵CF ∥BD ，∴四边形ODFC 是平行四边形在矩形ABCD 中，OC ＝OD ，∴四边形ODFC 是菱形．……………………10分22．解法一：∵四边形ABCD 为矩形，∴∠BAD ＝90°，OB ＝OD ，AC ＝BD ，又∵OF ⊥AD ，∴OF ∥AB ，又∵OB ＝OD ，∴ AB ＝2OF ＝4cm ，∵BE ︰BD ＝1︰4，∴BE ︰ED ＝1︰3 ……………………3分 设BE ＝x ，ED ＝3 x ，则BD ＝4 x ，∵AE ⊥BD 于点E∴22222AE AB BE AD ED =-=-，∴16－x 2＝AD 2－9x 2………………6分 又∵AD 2＝BD 2－AB 2＝16 x 2－16 ，∴16－x 2＝16 x 2－16－9x 2，8 x 2＝32∴x 2＝4，∴x ＝2 ……………………9分 ∴BD ＝2×4 ＝8（cm ），∴AC ＝8 cm ． ……………………10分解法二：在矩形ABCD 中，BO ＝OD ＝12BD ，∵BE ︰BD ＝1︰4，∴BE ︰BO ＝1︰2， 即E 是BO 的中点 ……………………3分 又AE ⊥BO ，∴AB ＝A O ，由矩形的对角线互相平分且相等，∴AO ＝BO ……………………5分 ∴△ABO 是正三角形，∴∠BAO＝60°，∴∠OAD＝90°－60°＝30°……………………8分在Rt△AOF中，AO＝2OF＝4，∴AC＝2AO＝8 ……………………10分23．（1）提示：证明：△BCH≌△DCE（SAS）……………………6分（2）由（1）知△BCH≌△DCE∴∠CBH＝∠EDC设BH，CD交于点N，则∠BNC＝∠DNH∴∠CBH＋∠BNC＝∠EDC＋∠DNH＝90°∴∠DMN=180°-90°＝90°∴BH⊥DE．……………………11分。

安徽省淮北市八年级下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分） (2018八上·大田期中) 下列各组数据中，不是勾股数的是A . 3，4，5B . 7，24，25C . 8，15，17D . 5，7，92. （2分） (2018八上·大田期中) 如图，射线l是下列哪个函数的图象A .B .C .D .3. （2分） (2019九上·玉田期中) 如图，在平面直角坐标系中，点的坐标为，那么的值是（）A .B .C .D .4. （2分）正方形具有而矩形不一定具有的性质是（）A . 对角线相等B . 对角线互相平分C . 对边平行且相等D . 对角线互相垂直平分5. （2分）下面所给点的坐标满足y=﹣2x的是（）A . （2，﹣1）B . （﹣1，2）C . （1，2）D . （2，1）6. （2分）(2020·嘉兴模拟) 如图，在矩形纸片ABCD中，已知AD＝8，折叠纸片，使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF＝3，则AB的长为（）A . 3B . 4C . 5D . 67. （2分）(2019·行唐模拟) 如图矩形ABCD中，AB＝3，BC＝3 ，点P是BC边上的动点，现将△PCD 沿直线PD折叠，使点C落在点C1处，则点B到点C1的最短距离为（）A . 5B . 4C . 3D . 28. （2分） (2019八下·泉港期末) 如图，在▱ABCD中，若∠A+∠C＝130°，则∠D的大小为（）A . 100°B . 105°C . 110°D . 115°9. （2分） (2019八上·织金期中) 菱形具有而平行四边形不一定具有的性质是（）A . 对角线平分一组对角B . 对角线互相平分C . 对边相等D . 对角相等10. （2分）如图，在某中学生耐力测试比赛中，甲、乙两学生测试的路程s（米）与时间t（秒）之间的函数关系的图象分别为折线OABC和线段OD，下列说法正确的是（）A . 乙比甲先到终点；B . 乙测试的速度随时间增加而增大；C . 比赛进行到29.4秒时，两人出发后第一次相遇；D . 比赛全程甲的测试速度始终比乙的测试速度快。

2016~2017 学年度第二学期期中质量检测八年级数学试卷满分120 分，考试时间100 分钟命题人：朱春荣审核人：周华军一．选择题（共8 小题，每小题 2 分，满分16 分）1．下列图形中既是轴对称图形又是中心对称图形的是（）A． B．C． D．A，B，C，点A 的对应点A，落在AB 边上，则∠BCA'的度数为（）A．20°B．25°C．30°D．35°8.定义：[a，b]为反比例函数（ab≠0，a，b 为实数）的“关联数”．反比例函数的“关联数”为[m，m+2]，反比例函数的“关联数”为[m+1，m+3]，若m＞0，则（）A．k1=k2B．k1＞k2C．k1＜k2D．无法比较二．填空题（共 10 小题，每小题 3 分，满分 30 分）12.若代数式在x 3实数范围内有意义，则实数x 的取值范围是（）A．x＜3 B．x＞3 C．x≠3 D．x＝33.下列事件中，是不可能事件的是（）A．买一张电影票，座位号是奇数B．射击运动员射击一次，命中9 环C．明天会下雨D．度量三角形的内角和，结果是3604.若分式的值为0，则（）A．x=﹣2 B．x=0 C．x=1 D．x=1 或﹣2 5．能判定四边形ABCD 为平行四边形的题设是（）A．AB∥CD，AD=BC B．∠A=∠B，∠C=∠DC．AB=CD，AD=BC D．AB=AD，CB=CD6.如图，四边形ABCD 中，AC=BD，E，F，G，H 分别为AB，BC，CD，DA 的中点，则四边形EFGH 是（）A．平行四边形B．菱形C．矩形D．正方形（第6 题图）（第7 题图）（第12 题图）7.如图，△ABC 中，∠A=75°，∠B=50°，将△ABC 绕点C 按逆时针方向旋转，得到△9．约分：=．10.化简的结果是11.若分式方程有增根，则m=．12.如图，菱形ABCD 的对角线AC、BD 相交于点O，E 为AD 的中点，若OE=3，则菱形ABCD 的周长为．13.若反比例函数的图象过点（﹣1，2），则这个函数图象位于第象限．14.袋子里有5 只红球，3 只白球，每只球除颜色以外都相同，从中任意摸出1 只球，是红球的可能性（选填“大于”“小于”或“等于”）是白球的可能性．15.如图，A、B 两地间有一池塘阻隔，为测量A、B 两地的距离，在地面上选一点C，连接CA、CB 的中点D、E．若DE 的长度为30m，则A、B 两地的距离为m．16.如图，点A 在函数y=（x＞0）的图象上，且OA=4，过点A 作AB⊥x 轴于点B，则△ABO 的周长为．17.点（a﹣1，y1）、（a+1，y2）在反比例函数y=（k＞0）的图象上，若y1＜y2，则a 的范围是．18.如图，矩形ABCD 中，AB=8，BC=6，P 为AD 上一点，将△ABP 沿BP 翻折至△EBP，PE 与CD 相交于点O，且OE=OD，则AP 的长为．三．解答题（共 10 小题，每小题 3 分，满分 74 分）19计算（每小题5 分，满分10 分）：（1）（a+1﹣）÷（）（2）解方程：=+2；20．（满分6 分）化简：，然后在不等式x≤2 的非负整数解中选择一个适当的数代入求值．21．（满分6 分）若关于x 的方程﹣2=的解为正数，求m 的取值范围．22．（满分12 分）某区对即将参加中考的 5000 名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和频数分布直方图的一部分．请根据图表信息回答下列问题：视力频数（人）频率4.0≤x＜4.3 20 0.14.3≤x＜4.6 40 0.24.6≤x＜4.9 70 0.354.9≤x＜5.2 a 0.35.2≤x＜5.5 10 b（1）本次调查的样本为，样本容量为；（2）在频数分布表中，a=，b=，并将频数分布直方图补充完整；（3）若视力在 4.6 以上（含4.6）均属正常，根据上述信息估计全区初中毕业生中视力正常的学生有多少人？23．（满分8 分）如图，AC 为矩形ABCD 的对角线，将边AB 沿AE 折叠，使点B 落在AC 上的点M 处，将边CD 沿CF 折叠，使点D 落在AC 上的点N 处．（1）求证：四边形AECF 是平行四边形；（2）若AB=6，AC=10，求四边形AECF 的面积．24．（满分10 分）已知：如图，在矩形 ABCD 中，M，N 分别是边 AD，BC 的中点，E，F 分别是线段BM，CM 的中点．（1）求证：△ABM≌△DCM；（2）判断四边形 MENF 是什么特殊四边形，并证明你的结论；（3）当AD：AB= 时，四边形MENF 是正方形（只写结论，不需证明）．25．（满分10 分）如图，BD 是△ABC 的角平分线，它的垂直平分线分别交AB，BD，BC 于点E，F，G，连接ED，DG．（1）请判断四边形EBGD 的形状，并说明理由；（2）若∠ABC=30°，∠C=45°，ED=2 ，点H 是BD 上的一个动点，求HG+HC 的最小值．26．（满分12 分）顺风车行经营的A 型车去年6 月份销售总额为3.2 万元，今年经过改造升级后A 型车每辆销售价比去年增加400 元，若今年6 月份与去年6 月份卖出的A 型车数量相同，则今年6 月份A 型车销售总额将比去年6 月份销售总额增加25%．（1）求今年6 月份A 型车每辆销售价多少元（用列方程的方法解答）；（2）该车行计划7 月份新进一批A 型车和B 型车共50 辆，且B 型车的进货数量不超过A 型车数量的两倍，应如何进货才能使这批车获利最多？最大利润是多少？A、B 两种型号车的进货和销售价格如表：A 型车B 型车进货价格（元/辆）1100 1400销售价格（元/辆）今年的销售价格2400故答案是：m＞﹣6 且m≠﹣3．22 解：（1）20÷0.1=200（人），参考答案1 2 3 4 5 6 7 8A C D C CB B C9 --10 x 11 2 12 24 13 二四14 大于15 60 16 2+4 17 ﹣1＜a＜1 18 4.819 (1) a（a﹣2）（2） 3 是增根，方程无解20解：原式====∵不等式x≤2 的非负整数解是0，1，2∵（x+1）（x﹣1）≠0，x+2≠0，∴x≠±1，x≠﹣2，∴把x=0 代入．21 解：去分母，得x﹣2（x﹣3）=﹣m，解得：x=m+6，根据题意得：m+6﹣3≠0 且m+6＞0，解得：m＞﹣6 且m≠﹣3．所以本次调查的样本为 200 名初中毕业生的视力情况，样本容量为 200；（2）a=200×0.3=60，b=10÷200=0.05；故答案为 200 名初中毕业生的视力情况，200；60，0.05；（2）5000×（0.35+0.3+0.05）=3500（人），估计全区初中毕业生中视力正常的学生有 3500 人．23 （1）证明：由折叠可知，∴AM=AB，CN=CD，∠FNC=∠D=90°，∠AME=∠B=90°，∴∠ANF=90°，∠CME=90°，∵四边形ABCD 为矩形，∴AB=CD，AD∥BC，∴AM=CN，∴AM﹣MN=CN﹣MN，即AN=CM，在△ANF 和△CME 中，，∴△ANF≌△CME（ASA），∴AF=CE，又∵AF∥CE，∴四边形AECF 是平行四边形；（2）解：∵AB=6，AC=10，∴BC=8，设CE=x，则EM=8﹣x，CM=10﹣6=4，在R t△C EM 中，（8﹣x）2+42=x2，解得：x=5，∴四边形AECF 的面积的面积为：EC•AB=5×6=30．24（1）证明：∵四边形 ABCD 是矩形，∴AB=CD，∠A=∠D=90°，又∵M 是 AD 的中点，∴AM=DM．在△ABM 和△DCM 中，，∴△ABM≌△DCM（SAS）．（2）解：四边形 MENF 是菱形．证明如下：∵E，F，N 分别是 BM，CM，CB 的中点，∴NE∥MF，NE=MF．∴四边形 MENF 是平行四边形．由（1），得 BM=CM，∴ME=MF．∴四边形 MENF 是菱形．（3）解：当AD：AB=2：1 时，四边形 MENF 是正方形．理由：∵M 为 AD 中点，∴AD=2AM．∵AD：AB=2：1，∴AM=AB．∵∠A=90，∴∠ABM=∠AMB=45°．同理∠DMC=45°，∴∠EMF=180°﹣45°﹣45°=90°．∵四边形 MENF 是菱形，∴菱形 MENF 是正方形．故答案为：2：1．25解：（1）四边形 EBGD 是菱形．理由：∵EG 垂直平分 BD，∴EB=ED，GB=GD，∴∠EBD=∠EDB，∵∠EBD=∠DBC，∴∠EDF=∠GBF，在△EFD 和△GFB 中，，∴△EFD≌△GFB，∴ED=BG，∴BE=ED=DG=GB，∴四边形 EBGD 是菱形．（2）作EM⊥BC于M，DN⊥BC于N，连接 EC 交BD 于点H，此时 HG+HC 最小，在RT△EBM中，∵∠EMB=90°，∠EBM=30°，EB=ED=2，∴EM=BE= ，∵DE∥BC，EM⊥BC，DN⊥BC，∴EM∥DN，EM=DN=，MN=DE=2，在RT△DNC 中，∵∠DNC=90°，∠DCN=45°，∴∠NDC=∠NCD=45°，∴DN=NC=，∴MC=3，在RT△EMC中，∵∠EMC=90°，EM=．MC=3，∴EC===10．∵HG+HC=EH+HC=EC，∴HG+HC 的最小值为 10．26(1) 今年6 月份A 型车每辆销售价2000 元(2) A 型车17 辆，B 型车33 辆时获利最多。

安徽省淮北市八年级下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分） (2019八下·嘉兴期中) 二次根式中，字母的取值范围是（）A .B .C .D .2. （2分） (2016九上·市中区期末) 如图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于（）A . 0.75B .C . 0.6D . 0.83. （2分） (2019七上·苍南期中) 下列选项中的计算，不正确的是（）A .B .C .D .4. （2分） (2018九上·浙江月考) 下列命题是真命题的是（）A . 平分弦的直径垂直于弦；B . 弧相等，所对的圆周角相等；C . 弦相等，所对的圆心角相等；D . 圆心角相等，所对的弦相等5. （2分） (2018九上·温州开学考) 菱形的两条对角线长分别为3和4，那么这个菱形的面积为（）A . 12B . 6C . 5D . 76. （2分）以下列各组线段为边长，能构成直角三角形的是（）A . 1，1，B . 3，4，5C . 5，10，13D . 2，3，47. （2分）下列说法中，正确的个数有（）①已知直角三角形的面积为2，两直角边的比为1：2，则斜边长为；②直角三角形的最大边长为，最短边长为1，则另一边长为；③在△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC为直角三角形；④等腰三角形面积为12，底边上的高为4，则腰长为5．A . 1个B . 2个C . 3个D . 4个8. （2分） (2020八下·江岸期中) 如图，有一个水池，水面是一边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺.如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，这根芦苇的长度为（）尺A . 10B . 12C . 13D . 149. （2分） (2018八上·栾城期末) 如图，三个正方形围成如图所示的图形，已知两个正方形的面积分别是25和169，则字母B所代表的正方形的面积是（）A . 125B . 135C . 144D . 16010. （2分）(2013·桂林) 下列运算正确的是（）A . 52•53=56B . （52）3=55C . 52÷53=5D . （）2=5二、填空题 (共6题；共7分)11. （1分）(2018·建湖模拟) 已知实数a在数轴上的位置如图所示，化简的结果是 ________．12. （1分）(2018·扬州) 如图，已知的半径为2，内接于，，则________．13. （1分）(2019·德惠模拟) 如图，在菱形ABCD中，若AC=6，BD=8，则菱形ABCD的面积是________.14. （2分）(2020·盐城模拟) 如图，在四边形ABCG中，AG∥BC，BC>AG，∠B=90°，AB=BC=12，E是AB上一点，且∠GCE=45°，BE=4，则GE=________.15. （1分） (2020九上·沈阳月考) 等边三角形的两条中线所夹的锐角的度数为________16. （1分） (2019八下·钦州期末) 正方形，，，…按如图所示的方式放置.点，，，…和点，，，…分别在直线和轴上，则点的坐标是________.三、解答题 (共9题；共54分)17. （10分） (2017七下·马龙期末) 计算18. （5分）(2017·许昌模拟) 先化简，再求值：（﹣）÷ ，其中实数a，b满足（a ﹣2）2+|b﹣2a|=0．19. （5分）如图，直径是50cm圆柱形油槽装入油后，油深CD为15cm，求油面宽度AB。