广东省实验中学2013-2014学年高一数学上学期期末模块考试卷新人教A版

广东省汕头市澄海实验高级中学2013-2014学年高一数学上学期期末考试试题新人教A 版参考公式：球的表面积、体积公式 24πS R =，34π3V R =第Ⅰ卷 （选择题 共50分）一.选择题：(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的，将答案代号填入答案卷表格中)1.在y 轴上的截距是2，且与x 轴平行的直线方程为（ ）A ． 2y =B ． 2y =-C ． 2x =D ．22y y ==-或 2.已知集合{}{2,A y y x B x y ==+==,则=⋂B A （ ）A. (1,)+∞B. (2,)+∞C. [1,)+∞D. φ3. 已知M （2,2）和N （5，-2），点P 在x 轴上，90MPN ∠=，则点P 的坐标为（ ） A. （1,6） B. （1,0） C. （6,0） D. （1,0）或（6,0） 4．若直线0ax by c ++=在第一、二、三象限，则（ ）A ．0,0ab bc >>B ． 0,0ab bc <<C ．0,0ab bc <>D ．0,0ab bc >< 5．已知,αβ是两个不同的平面，,,l m n 是不同的直线，下列命题不正确．．．的是 ( ) A ．若,,,,l m l n m n αα⊥⊥⊂⊂则l α⊥； B ．若//,,,l m l m αα⊂⊂/则//l α； C ．若,,,,l m m l αβαβα⊥=⊂⊥则m β⊥；D ．若,,,m n αβαβ⊥⊥⊥，则m n ⊥6. 入射光线 从P （2，1）出发，经x 轴反射后，通过点Q （4，3）,则入射光线 所在直线的方程为（ ） A ． 0y = B ． 250x y -+= C ． 250x y +-= D ．250x y -+=7.. 一个几何体的三视图如右图所示，则该几何体的体积等于（ ）主视图 左视图俯视图A ． 483π+B ． 443π+ C ．84π+ D ． 103π8．已知PD ⊥矩形ABCD 所在的平面（图2），图中相互垂直的平面有( ) A ．1对 B ．2对 C ．3对 D ．5对 9．设函数22(0)()(0)x f x x bx c x - >⎧=⎨++ ≤⎩，若(4)(0),(2)0,f f f -=-=则关于x 的不等式()f x ≤1的解集为（ ）A ．(][),31,-∞--+∞） B ．[]()3,10,--+∞ C ．[]3,1-- D ．[)3,-+∞ 10.下列函数图象中，正确的是（ ）．第II 卷 （非选择题 共100分）二．填空题：(本大题共4小题，每小题５分，共20分)11．计算：()1325354log ⎡⎤-+=⎣⎦12．如图所示，水平放置的直三棱柱的侧棱长和底面边长均为2，正视图是边长为2的正方形，该三棱柱的侧视图面积为＿＿＿＿＿．PABCD图213．若两条直线260ax y ++=与2(1)(1)0x a y a +-+-=平行，则a 的取值集合是____； 14．已知圆锥的表面积为23m π，且它的侧面展开图是一个半圆，求这个圆锥的底面直径 。

宁波效实中学二○一三学年度第一学期高一期中数学试卷说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共100分． 第Ⅰ卷（选择题 共30分）一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中只有一项是符合题目要求的． 1.已知函数()f x =A ．(,1)-∞B ．(,1]-∞C ．(1,)+∞D ．[1,)+∞2．已知集合{|2}S x x =<，2{|340}T x x x =--≤，则()R S T =ðA ．(2,4)B ．[2,4]C ．(,4)-∞D ． (,4]-∞3．在区间(,0)-∞上为增函数的是A ．1=yB ．21x y +=C ．122---=x x yD ． 21xy x-=- 4．设函数221,1()2,1,x x f x x x x ⎧-≤⎪=⎨+->⎪⎩则1(2)f f ⎛⎫⎪⎝⎭的值为A ．18B ．89C ．1516D ．2716-5．若函数()f x = 3442++-mx mx x 的定义域为R ,则实数m 的取值范围是 A ．(,)-∞+∞ B ．3[0,)4 C ．3(,)4+∞ D ．3(0,)46．设,a b 是非零实数，若a b <，则下列不等式一定成立的是k*s@5%uA ．22a b <B ．22ab a b <C ．2211ab a b<D ．b aa b< 7．已知函数25,1,()11, 1.x ax x f x x x ⎧-+<⎪=⎨+≥⎪⎩在定义域R 上单调，则实数a 的取值范围为 A ．(,2]-∞B ．[2,)+∞C ．[4,)+∞D ． [2,4]8．已知集合23{|0,(1,1)}2A x x x k x =--=∈-，若集合A 有且仅有一个元素，则实数k 的取值范围是A ．159[,){}2216--B ．15(,)22C ．95[,)162-D ．9[,)16-+∞ 9．已知{},,,,,a ab Max a b b a b ≥⎧=⎨<⎩若函数{}2()|4|,f x Max x x x =-则函数()f x k*s@5%uA ．有最小值为0，有最大值为4B ．无最小值，有最大值为4C ．有最小值为0，无最大值D ．无最值10．若0,0,22a b a b >>+=，则下列不等式：○11ab ≤；22≤；○3222a b +≥； ○43383a b +≥；○5112a b+≥．对一切满足条件的,a b 成立的是 A ．○1○2○4B ．○1○2○5C ．○1○4○5D ．○2○3○4第Ⅱ卷（非选择题 共70分）二、填空题：本大题共7小题，每小题3分，共21分．11．已知函数()f x =()2f a =，则实数a = ▲ ．12．已知集合2{|230}M x x x =--=，{|20}N x ax =-=．若N M ⊆，则实数a 取值构成的集合为 ▲ ．13．关于x 的不等式2440x mx -+≥对任意[1,)x ∈+∞恒成立，则实数m 的取值范围为 ▲ ．14．已知条件：{}1⇐{}||23|1M x Z x x ⊆∈-<+，则满足条件的集合M 有 ▲ 个．15．函数222331x x y x x -+=-+的值域为 ▲ ．16．若关于x 的不等式|23||21|x x a ++-≤有解，则实数a 的取值范围为 ▲ ．17． 已知22()53196|53196|f x x x x x =-++-+，则(1)(2)(50f f f +++=▲ ．三、解答题：本大题共6小题，共49分． 解答应写出文字说明，证明过程或演算步骤． 18．已知定义在R 上的偶函数()f x ．当0x ≥时，2()1x f x x -+=-且(1)0f =． （Ⅰ）求函数()f x 的解析式并画出函数的图象； （Ⅱ）写出函数()f x 的值域．19．已知集合2{|230}A x x x =-->，集合4{|2}2B x x x =≤--． （Ⅰ）求A ，B ； （Ⅱ）求A B 及()R C A B ．20．已知定义域为(1,1)-的函数2()1xf x x =+．（Ⅰ）判断函数()f x 奇偶性并加以证明； （Ⅱ）判断函数()f x 的单调性并用定义加以证明； （Ⅲ）解关于x 的不等式(1)()0f x f x -+<．xyO21．已知集合{}22|280A x x ax a =--<，{}22|5(1)4,B x x x m x m R =-=--∈．（Ⅰ）若12(,)A x x =且2115x x -=，求实数a 的值； （Ⅱ）若存在实数m 使得B A ⊆，求实数a 范围．22．已知定义在R 上的奇函数()f x ．当0x <时，2()2f x x x =+． （Ⅰ）求函数()f x 的解析式；（Ⅱ）问：是否存在实数,()a b a b ≠，使()f x 在[,]x a b ∈时，函数值的集合为11[,]b a？若存在，求出,a b ；若不存在，请说明理由．附加题：已知*,,N a b c ∈，方程2=0ax bx c ++在区间(1,0)-上有两个不同的实根，求a b c ++的最小值．宁波效实中学二○一三学年度第一学期高一期中数学参考答案11、7 12、{0,2,}3- 13、 (,1]-∞ 14、 3 15、5[,3]316、 [4,)+∞ 17、66018、(I)2,[0,1)(1,)1()0,{1,1}2,(,1)(1,0)1x x x f x x x x x -+⎧∈+∞⎪-⎪=∈-⎨⎪+⎪-∈-∞--+⎩;图象如图： (II)值域为(,2](1,)-∞--+∞u19、（I ）(,1)(3,)A =-∞-+∞，[0,2)[4,)B =+∞；（II ）[4,)AB =+∞， ()[1,3][4,)RC AB =-+∞。

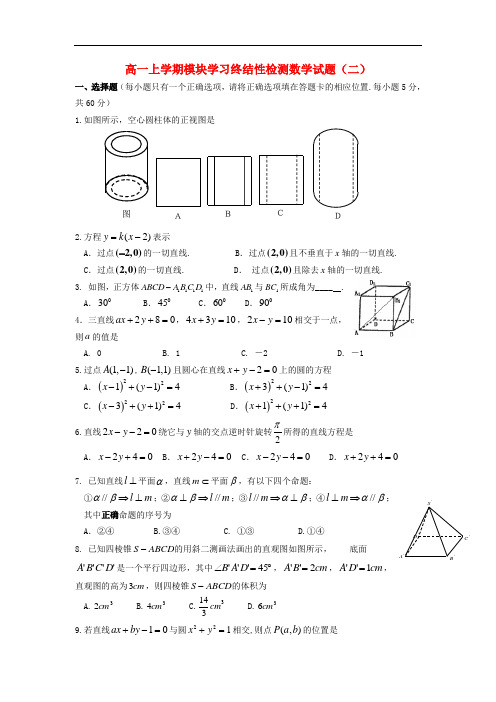
高一上学期模块学习终结性检测数学试题（二）一、选择题（每小题只有一个正确选项，请将正确选项填在答题卡的相应位置.每小题5分，共60分）1.如图所示，空心圆柱体的正视图是2.方程)2(-=x k y 表示A ．过点(2,0)-的一切直线.B ．过点(2,0)且不垂直于x 轴的一切直线.C ．过点(2,0)的一切直线.D ． 过点(2,0)且除去x 轴的一切直线. 3. 如图，正方体1111ABCD A B C D -中，直线1AB 与1BC 所成角为____ . A ．030 B ．045 C ．060 D ．0904．三直线280ax y ++=，4310x y +=，210x y -=相交于一点，则a 的值是A. 0B. 1C. －2D. －1 5.过点(1,1)A -,(1,1)B -且圆心在直线20x y +-=上的圆的方程 A ．()221(1)4x y -+-=B ．()223(1)4x y ++-=C ．()223(1)4x y -++= D ．()221(1)4x y +++=6.直线220x y --=绕它与y 轴的交点逆时针旋转2π所得的直线方程是A ．240x y -+=B ．240x y +-=C ．240x y --=D ．240x y ++= 7.已知直线l ⊥平面α，直线m ⊂平面β，有以下四个命题：①//l m αβ⇒⊥；②//l m αβ⊥⇒；③//l m αβ⇒⊥；④//l m αβ⊥⇒； 其中正确命题的序号为A ．②④ B.③④ C. ①③ D.①④8. 已知四棱锥ABCD S -的用斜二测画法画出的直观图如图所示， 底面''''D C B A 是一个平行四边形，其中︒=∠45'''D A B ，cm B A 2''=，cm D A 1''=，直观图的高为cm 3，则四棱锥ABCD S -的体积为 A.32cm B.34cm C.3314cmD.36cm 9.若直线10ax by +-=与圆221x y +=相交,则点(,)P a b 的位置是A ''A ．在圆上B ．在圆外C ．在圆内D ．以上皆有可能10.P 是ABC ∆所在平面α外一点，且P 到ABC ∆三边的距离相等，PO α⊥于O ，O 在ABC ∆内，则点O 是ABC ∆的A ．外心B ．内心C ．重心D ．垂心11. 已知点(2,3),(3,2)A B --，若直线l 过点(1,1)P 与线段AB 始终没有交点，则直线l 的斜率k 的取值范围是A ．324k ＜＜B ．324k k ＞或＜ C ． 34k ＞D ．2k ＜ 12．如果直线l 将圆22240x y x y +--=平分，且不通过第四象限，那么l 的斜率的取值范围是A ．[0]，1B ．[0]，2C ．1[0]2，D ．1[0]3， 二、填空题（每小题5分，共20分.请将正确答案填写在答题卡上）13．圆22250x y x +--=和圆222440x y x y ++--=的位置关系是 . 14．已知直线062:1=++y ax l 与01)1(:22=-+-+a y a x l 平行，则a 的取值是 . 15.一条线段，其长度为10cm ，两端点到平面的距离分别是2cm ，3cm ，这条线段与平面α所成的角的正弦值是16．若点P 在直线1l ：03=++y x 上，过点P 的直线2l 与曲线C ：()16522=+-y x 相切于点M ，则PM 的最小值是________．武威六中2013～2014学年度第一学期高一数学《必修2》模块学习终结性检测试卷答题卡二、填空题13． . 14． . 15. . 16．________． 三、解答题（17小题10分，其余各题12分，共70分）17.如图所示，已知ABC ∆中，点D 是边AB 的中点，边BC 与x 轴交于点E ，︒=∠45BEA .求（1）直线AB的方程；（2）直线BC 的方程；（3）直线CD的方程.18.已知圆222:(0)O x y r r +=>与直线0x y -+=相切． （1）求圆O 的方程； （2）过点的直线l 截圆所得弦长为l 的方程；19．如图所示，已知PA 垂直于⊙O 所在的平面，AB 是⊙O 的直径，C 是⊙O 上任意一点，过点A 作AE PC ⊥于点E .求证：AE ⊥平面PBC .20．已知圆经过点(2,1)A -，圆心在直线20x y +=上且与直线10x y --=相切，求圆的方程．21．如图，四棱锥P ABCD -中，底面ABCD 是矩形，PA ⊥底面ABCD ，1PA AB ==，AD F 是PB 的中点，点E 在边BC上移动．(1)求三棱锥E PAD -的体积；(2)点E 为BC 的中点时，试判断EF 与平面PAC 的位置关系，并说明理由；(3)求证：无论点E 在BC 边的何处，都有PE AF ⊥.22．已知三条直线1l ：20x y a -+=（a ＞0），直线2l ：4210x y --=和直线3l ：10x y +-=且，1l 与2l 的距离是5107. ⑴求a 的值；⑵能否找到一点P ，使得P 同时满足下列3个条件：①P 是第一象限的点；②P 点到1l 的距离是P 点到2l 的距离的21；③P 点到1l 的距离与P 点到3l 的距离之比是2∶5；若能，求P 点的坐标；若不能，说明理由.高一数学试卷答案三、解答题17.解：（1）依题意，可知)2,0(),0,1(B A -，代入截距式得直线AB 的方程为121=+-y x，化为一般式得022=+-y x ..................................................3分 （2）因为︒=∠45BEA ，所以直线BC 的倾斜角为︒=︒-︒13545180，所以1135tan -=︒=BC k ，又)2,0(B ，由斜截式得直线BC 的方程为2+-=x y ，化为一般式得02=-+y x ....................................................6分 （3）把3=x 代入02=-+y x ，得1-=y ，即)1,3(-C ，又由中点坐标公式得)1,21(-D ，代入两点式得直线CD 的方程为)21(3)21(111----=---x y ，化为一般式得0574=-+y x ....10分⑵若直线l 的斜率不存在，直线l 为1x =，此时直线l截圆所得弦长为意. ……………………………………………… … ……7分若直线l的斜率存在，设直线为(1)3y k x -=-，即3330kx y k -=，由题意知，圆心到直线的距离为1d ==，所以k =， 则直线l为20x -=．… ……11分 因此，所求的直线为1x =或20x -=．… ……12分 19．解析：略20．解析：设圆的方程为(x －a )2＋(y －b )2＝r 2(r >0)．∵圆心在直线2x ＋y ＝0上，∴b ＝－2a ，即圆心为C (a ，－2a )．又∵圆与直线x －y －1＝0相切，且过点(2，－1)， ∴|a ＋2a －1|2＝r ，(2－a )2＋(－1＋2a )2＝r 2， 即(3a －1)2＝2[(2－a )2＋(－1＋2a )2]，解得a ＝1或a ＝9，∴a ＝1，b ＝－2，r ＝2或a ＝9，b ＝－18，r ＝13 2.故所求圆的方程为(x －1) 2＋(y ＋2)2＝2或(x －9)2＋(y ＋18)2＝338.22.解析：⑴2l 即为2x -y -21= 0，∴1l 与2l 的距离d =1057)1(2|)21(|22=-+--a ， ∴|a +21|=27，∵a ＞0，∴a =3.................... .........5分 ⑵设点P （0x ，0y ），若P 点满足条件②，则P 点在与1l 、2l 平行的直线/l ：2x -y +c =0上，且5|21|215|3|+⨯=-c c ， 即c =213或c =611.∴20x -0y +213= 0或20x -0y +611 = 0. 若P 点满足条件③，由点到直线的距离公式2|1|·525|32|0000-+=+-y x y x ， ∴0x -20y +4 = 0或30x +2 = 0.由Ｐ在第一象限，∴30x +2 = 0（舍去）.联立方程20x -0y +213=0和0x -20y +4 = 0，解得0x = -3，0y =21应舍去. 由20x -0y +611 = 0和0x -20y +4 = 0联立，解得0x =91，0y =1837，∴P （91，1837）即为同时满足3个条件的点. ............... .........12分21.解析：(1)∵PA ⊥底面ABCD ，∴PA ⊥AD ，∴V E －PAD ＝13S △PAD ·AB ＝13×12×1×3×1＝36. ............ .........3分(2)当点E 为BC 的中点时，EF 与平面PAC 平行． 证明如下：∵在△PBC 中，E 、F 分别为BC 、PB 的中点， ∴EF ∥PC ，又EF ⊄平面PAC ， 而PC ⊂平面PAC ，∴EF∥平面PAC. ................................ ..........7分(3)证明：∵PA⊥平面ABCD，BE⊂平面ABCD，∴BE⊥PA.又BE⊥AB，AB∩PA＝A，∴BE⊥平面PAB，。

2013-2014学年广东省实验中学高一（上）期末数学试卷一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）直线（a为实常数）的倾斜角的大小是（）A．30°B．60°C．120°D．150°2．（5分）如图是水平放置的三角形的直观图，A′B′∥y′轴，则△ABC是（）A．等边三角形B．等腰三角形C．直角三角形D．等腰直角三角形3．（5分）给出下列命题：（1）垂直于同一直线的两直线平行．（2）同平行于一平面的两直线平行．（3）同平行于一直线的两直线平行．（4）平面内不相交的两直线平行．其中正确的命题个数是（）A．1 B．2 C．3 D．44．（5分）三棱锥的高为3，侧棱长均相等且为2，底面是等边三角形，则这个三棱锥的体积为（）A．B．C．D．5．（5分）给岀四个命题：（1）若一个角的两边分别平行于另一个角的两边，则这两个角相等；（2）α，β为两个不同平面，直线a⊂α，直线b⊂α，且a∥β，b∥β，则α∥β；（3）α，β为两个不同平面，直线m⊥α，m⊥β则α∥β；（4）α，β为两个不同平面，直线m∥α，m∥β，则α∥β．其中正确的是（）A．（1） B．（2） C．（3） D．（4）6．（5分）在正方体ABCD﹣A1B1C1D1中，异面直线B1C与A1C1所成角为（）A．30°B．45°C．60°D．90°7．（5分）直线2x+y+m=0和x+2y+n=0的位置关系是（）A．平行 B．垂直 C．相交但不垂直 D．不能确定8．（5分）将正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C，有如下四个结论：①AC⊥BD；②△ACD是等边三角形；③AB与平面BCD所成的角为60°；④AB与CD所成的角为60°．其中错误的结论是（）A．①B．②C．③D．④二、填空题：本大题共4小题，每小题6分，共24分．9．（6分）过点（1，2）且与直线x+2y﹣1=0平行的直线方程是．10．（6分）已知直线a，b和平面α，且a⊥b，a⊥α，则b与α的位置关系是．11．（6分）已知点A（﹣3，﹣2），B（6，1），点P在y轴上，且∠BAP=90°，则点P的坐标是．12．（6分）如图，一个底面半径为R的圆柱形量杯中装有适量的水．若放入一个半径为r 的实心铁球，水面高度恰好升高r，则=．三、解答题：本大题共3小题，每小题12分，共36分．解答应写出文字说明、证明过程或演算步骤．13．（12分）如图，在空间四边形ABCD中，E，F分别是AB和CB上的点，G，F分别是CD和AD上的点，且==1，==2，求证：EH，BD，FG三条直线相交于同一点．14．（12分）求经过点A（﹣2，2）并且和x轴的正半轴、y轴的正半轴所围成的三角形的面积是1的直线方程．15．（12分）如图，已知点M、N是正方体ABCD﹣A1B1C1D1的两棱A1A与A1B1的中点，P是正方形ABCD的中心，（1）求证：MN∥平面PB1C．（2）求证：D1B⊥平面PB1C．四、选择题：本大题共2小题，每小题5分，共10分．16．（5分）若直线a不平行于平面α，则下列结论成立的是（）A．平面α内所有的直线都与a异面B．平面α内不存在与a平行的直线C．平面a内所有的直线都与α相交D．直线α与平面α有公共点17．（5分）如图，正四面体ABCD的顶点A，B，C分别在两两垂直的三条射线Ox，Oy，Oz上，则在下列命题中，错误的为（）A．O﹣ABC是正三棱锥B．直线OB∥平面ACDC．直线AD与OB所成的角是45°D．二面角D﹣OB﹣A为45°五、解答题：本大题共3小题，共40分．解答应写出文字说明、证明过程或演算步骤．18．（13分）已知四棱锥P﹣ABCD的正视图是一个底边长为4、腰长为3的等腰三角形，图1、图2分别是四棱锥P﹣ABCD的侧视图和俯视图．求四棱锥P﹣ABCD的侧面PAB和PBC的面积．19．（13分）如图，在长方体ABCD﹣A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动．（1）证明：D1E⊥A1D；（2）当E为AB的中点时，求点E到面ACD1的距离；（3）AE等于何值时，二面角D1﹣EC﹣D的大小为．20．（14分）如图，棱柱ABC﹣A1B1C1中，四边形AA1B1B是菱形，四边形BCC1B1是矩形，AB⊥BC，CB=1，AB=2，∠A1AB=60°．（1）求证：平面CA1B⊥平面A1ABB1；（2）求B1C1到平面A1CB的距离；（3）求直线A1C与平面BCC1B1所成角的正切值．2013-2014学年广东省实验中学高一（上）期末数学试卷参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）（2013秋•忻州期末）直线（a为实常数）的倾斜角的大小是（）A．30°B．60°C．120°D．150°【解答】解：∵直线（a为实常数）的斜率为﹣令直线（a为实常数）的倾斜角为θ则tanθ=﹣解得θ=150°故选D2．（5分）（2013秋•越秀区校级期末）如图是水平放置的三角形的直观图，A′B′∥y′轴，则△ABC是（）A．等边三角形B．等腰三角形C．直角三角形D．等腰直角三角形【解答】解：由题意，直观图中A′B′∥y′轴，由斜二测画法得：原图△ABC中：AB∥y轴，AC在x轴上，如图．则△ABC是直角三角形，故选C．3．（5分）（2014•埇桥区校级学业考试）给出下列命题：（1）垂直于同一直线的两直线平行．（2）同平行于一平面的两直线平行．（3）同平行于一直线的两直线平行．（4）平面内不相交的两直线平行．其中正确的命题个数是（）A．1 B．2 C．3 D．4【解答】解：（1）如图，在正方体中，AB⊥BC，BB1⊥BC，但AB与BB1不平行，故（1）错误（2）如图，AB∥平面A1B1C1D1，BC∥平面A1B1C1D1，但AB与BC不平行，故（2）错误（3）由平行公理知（3）正确（4）同一平面内的两条直线若没有公共点，则一定平行，故（4）正确故正确的命题个数是2，故选B4．（5分）（2013秋•越秀区校级期末）三棱锥的高为3，侧棱长均相等且为2，底面是等边三角形，则这个三棱锥的体积为（）A．B．C．D．【解答】解：由题意，在正三棱锥S﹣ABC中，设H为ABC的中心，连接SH，则SH为该正三棱锥的高．连接AH，延长后交BC于E，∵三棱锥的高为3，侧棱长均相等且为2，∴AH=，∴AE=，∴AB=3，∴三棱锥的体积为=．故选：D．5．（5分）（2013秋•越秀区校级期末）给岀四个命题：（1）若一个角的两边分别平行于另一个角的两边，则这两个角相等；（2）α，β为两个不同平面，直线a⊂α，直线b⊂α，且a∥β，b∥β，则α∥β；（3）α，β为两个不同平面，直线m⊥α，m⊥β则α∥β；（4）α，β为两个不同平面，直线m∥α，m∥β，则α∥β．其中正确的是（）A．（1） B．（2） C．（3） D．（4）【解答】解：（1）如图，∠1，∠2，∠3的两边互相平行，∴∠3=∠4，∠4=∠1，∠4+∠2=180°；∴∠3=∠1，∠3+∠2=180°，∴这两个角相等或互补，故（1）不正确．（2）α，β为两个不同平面，直线a⊂α，直线b⊂α，且a∥β，b∥β，a，b相交时，α∥β，故（2）不正确；（3）由线面垂直的性质可知，两个不同平面分别垂直于同一条直线，则这两个平面相互平行，即α∥β，正确；（4）α，β为两个不同平面，直线m∥α，m∥β，则α∥β，也有可能α∩β=m，故不正确．故选：C．6．（5分）（2014秋•咸阳期末）在正方体ABCD﹣A1B1C1D1中，异面直线B1C与A1C1所成角为（）A．30°B．45°C．60°D．90°【解答】解：正方体ABCD﹣A1B1C1D1中，连接B1C、A1C1、AC、AB1，∵AC∥A1C1，∴∠ACB1就是异面直线B1C与A1C1所成角或所成角的补角，∵AC=B1C=AB1，∴∠ACB1=60°．故选C．7．（5分）（2015•广西校级学业考试）直线2x+y+m=0和x+2y+n=0的位置关系是（）A．平行 B．垂直 C．相交但不垂直 D．不能确定【解答】解：由方程组可得3x+4m﹣n=0，由于3x+4m﹣n=0有唯一解，故方程组有唯一解，故两直线相交．再由两直线的斜率分别为﹣2和﹣，斜率之积不等于﹣1，故两直线不垂直．故选C．8．（5分）（2013秋•越秀区校级期末）将正方形ABCD沿对角线BD折成直二面角A﹣BD ﹣C，有如下四个结论：①AC⊥BD；②△ACD是等边三角形；③AB与平面BCD所成的角为60°；④AB与CD所成的角为60°．其中错误的结论是（）A．①B．②C．③D．④【解答】解：取BD的中点E，则AE⊥BD，CE⊥BD．∴BD⊥面AEC．∴BD⊥AC，故①正确．设正方形边长为a，则AD=DC=a，AE=a=EC．∴AC=a．∴△ACD为等边三角形，故②正确．∠ABD为AB与面BCD所成的角为45°，故③不正确．以E为坐标原点，EC、ED、EA分别为x，y，z轴建立直角坐标系，则A（0，0，a），B（0，﹣a，0），D（0，a，0），C（a，0，0）．=（0，﹣a，﹣a），=（a，﹣a，0）．cos＜，＞==∴＜，＞=60°，故④正确．故选C二、填空题：本大题共4小题，每小题6分，共24分．9．（6分）（2010春•宣武区期末）过点（1，2）且与直线x+2y﹣1=0平行的直线方程是x+2y ﹣5=0．【解答】解：设过点（1，2）且与直线x+2y=0平行的直线方程为x+2y+m=0，把点（1，2）代入直线方程得，1+4+m=0，m=﹣5，故所求的直线方程为x+2y﹣5=0，故答案为：x+2y﹣5=0．10．（6分）（2015春•海南校级期末）已知直线a，b和平面α，且a⊥b，a⊥α，则b与α的位置关系是b⊂α或b∥α．【解答】解：当b⊂α时，a⊥α，则a⊥b当b∥α时，a⊥α，则a⊥b故当a⊥b，a⊥α⇒b⊂α或b∥α故答案为：b⊂α或b∥α11．（6分）（2013秋•越秀区校级期末）已知点A（﹣3，﹣2），B（6，1），点P在y轴上，且∠BAP=90°，则点P的坐标是（0，﹣11）．【解答】解：设点P（0，y），∵，=，∠BAP=90°．∴k AP•k AB=﹣1，∴，解得y=﹣11．∴P（0，﹣11）．故答案为：（0，﹣11）．12．（6分）（2003•北京）如图，一个底面半径为R的圆柱形量杯中装有适量的水．若放入一个半径为r的实心铁球，水面高度恰好升高r，则=．【解答】解：半径为r的实心铁球的体积是：升高的水的体积是：πR2r所以：∴故答案为：．三、解答题：本大题共3小题，每小题12分，共36分．解答应写出文字说明、证明过程或演算步骤．13．（12分）（2013秋•越秀区校级期末）如图，在空间四边形ABCD中，E，F分别是AB 和CB上的点，G，F分别是CD和AD上的点，且==1，==2，求证：EH，BD，FG三条直线相交于同一点．【解答】解：连接EF，GH，因为==1，==2，所以EF∥AC，HG∥AC且EF≠AC …（2分）所以EH，FG共面，且EH与FG不平行，…（3分）不妨设EH∩FG=P …（4分）则P∈EH，EH⊂面ABD，所以P∈面ABD；…（6分）同理P∈面BCD…（8分）又因为平面ABD∩平面BCD=BD，所以P∈BD，…（10分）所以EH，BD，FG三条直线相交于同一点P．…（12分）14．（12分）（2013秋•越秀区校级期末）求经过点A（﹣2，2）并且和x轴的正半轴、y轴的正半轴所围成的三角形的面积是1的直线方程．【解答】解：∵直线的斜率存在，∴可设直线l的方程为：y﹣2=k（x+2）．即y=kx+2k+2．令x=0，得y=2k+2；令y=0，解得x=﹣．由，解得﹣1＜k＜0．∵S△=1，∴，解得：k=﹣2或﹣．∵﹣1＜k＜0，∴．∴直线l的方程为：x+2y﹣2=0．15．（12分）（2013秋•越秀区校级期末）如图，已知点M、N是正方体ABCD﹣A1B1C1D1的两棱A1A与A1B1的中点，P是正方形ABCD的中心，（1）求证：MN∥平面PB1C．（2）求证：D1B⊥平面PB1C．【解答】证明：（1）连接AC，则AC一定过点P，连接AB1．∵A1M=MA，A1N=NB1，∴MN∥AB1．又MN⊄平面AB1C，AB1⊂平面AB1C，∴MN∥平面AB1C，即MN∥平面PB1C．（2）连D1B1，PB，∵=，∠D1DB=∠PBB1=90°，∴△D1DB∽△PBB1，∴∠D1DB=∠BB1P，∵∠PBB1=90°，∴∠B1PB+∠D1BD=90°，∴PB1⊥D1B①∴B1B⊥平面ABCD，∵AC⊂平面ABCD，∴B1B⊥AC，∵AC⊥BD，BD∩B1B=B，∴AC⊥平面B1D∵BD1⊂平面B1D，∴AC⊥D1B②∵PB1∩AC=P以及①②得：D1B⊥平面PB1C．四、选择题：本大题共2小题，每小题5分，共10分．16．（5分）（2013秋•越秀区校级期末）若直线a不平行于平面α，则下列结论成立的是（）A．平面α内所有的直线都与a异面B．平面α内不存在与a平行的直线C．平面a内所有的直线都与α相交D．直线α与平面α有公共点【解答】解：∵直线a不平行于平面α，∴直线a与平面α相交，或直线a⊂平面α．∴直线α与平面α有公共点．故选D．17．（5分）（2009•江西）如图，正四面体ABCD的顶点A，B，C分别在两两垂直的三条射线Ox，Oy，Oz上，则在下列命题中，错误的为（）A．O﹣ABC是正三棱锥B．直线OB∥平面ACDC．直线AD与OB所成的角是45°D．二面角D﹣OB﹣A为45°【解答】解：对于A，如图ABCD为正四面体，∴△ABC为等边三角形，又∵OA、OB、OC两两垂直，∴OA⊥面OBC，∴OA⊥BC．过O作底面ABC的垂线，垂足为N，连接AN交BC于M，由三垂线定理可知BC⊥AM，∴M为BC中点，同理可证，连接CN交AB于P，则P为AB中点，∴N为底面△ABC中心，∴O﹣ABC是正三棱锥，故A正确．对于B，将正四面体ABCD放入正方体中，如图所示，显然OB与平面ACD不平行．则答案B不正确．对于C，AD和OB成的角，即为AD和AE成的角，即∠DAE=45°，故C正确．对于D，二面角D﹣OB﹣A即平面FDBO与下底面AEBO成的角，故∠FOA为二面角D﹣OB﹣A的平面角，显然∠FOA=45°，故D正确．综上，故选：B．五、解答题：本大题共3小题，共40分．解答应写出文字说明、证明过程或演算步骤．18．（13分）（2013秋•越秀区校级期末）已知四棱锥P﹣ABCD的正视图是一个底边长为4、腰长为3的等腰三角形，图1、图2分别是四棱锥P﹣ABCD的侧视图和俯视图．求四棱锥P﹣ABCD的侧面PAB和PBC的面积．【解答】解：依题意，可知点P在平面ABCD上的正射影是线段CD的中点E，连接PE，则PE⊥平面ABCD．…（2分）在等腰三角形PCD中，PC=PD=3，DE=EC=2，在Rt△PED中，PE=，…（4分）过E作E⊥AB，垂足为F，则F为AB中点，连接PF，…（5分）在Rt△PEF中，PF=，…（6分）∵Rt△ADE≌Rt△BEC，∴AE=BE∴Rt△PAE≌Rt△PBE，∴PA=PB，∵F为中点∴AB⊥PF．…（8分）∴△PAB的面积为S=．…（9分）∵PE⊥平面ABCD，BC⊂平面ABCD，∴BC⊥PE．∵BC⊥CD，CD∩PE=C，∴BC⊥平面PCD．…（11分）∵PC⊂平面PCD，∴BC⊥PC依题意得PC=3，BC=2．∴△PBC的面积为S=．…（13分）19．（13分）（2005•江西）如图，在长方体ABCD﹣A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动．（1）证明：D1E⊥A1D；（2）当E为AB的中点时，求点E到面ACD1的距离；（3）AE等于何值时，二面角D1﹣EC﹣D的大小为．【解答】解法（一）：（1）证明：∵AE⊥平面AA1DD1，A1D⊥AD1，∴A1D⊥D1E（2）设点E到面ACD1的距离为h，在△ACD1中，AC=CD1=，AD1=，故，而．∴，∴，∴．（3）过D作DH⊥CE于H，连D1H、DE，则D1H⊥CE，∴∠DHD1为二面角D1﹣EC﹣D 的平面角．设AE=x，则BE=2﹣x在Rt△D1DH中，∵，∴DH=1．∵在Rt△ADE中，DE=，∴在Rt△DHE中，EH=x，在Rt△DHC中CH=，在Rt△CBE中CE=．∴．∴时，二面角D1﹣EC﹣D的大小为．解法（二）：以D为坐标原点，直线DA，DC，DD1分别为x，y，z轴，建立空间直角坐标系，设AE=x，则A1（1，0，1），D1（0，0，1），E（1，x，0），A（1，0，0）C（0，2，0）（1）因为=（1，0，1）•（1，x，﹣1）=0，所以．（2）因为E为AB的中点，则E（1，1，0），从而，，设平面ACD1的法向量为，则也即，得，从而，所以点E到平面AD1C 的距离为．（3）设平面D1EC的法向量，∴，由令b=1，∴c=2，a=2﹣x，∴．依题意．∴（不合，舍去），．∴AE=时，二面角D1﹣EC﹣D的大小为．20．（14分）（2013秋•越秀区校级期末）如图，棱柱ABC﹣A1B1C1中，四边形AA1B1B是菱形，四边形BCC1B1是矩形，AB⊥BC，CB=1，AB=2，∠A1AB=60°．（1）求证：平面CA1B⊥平面A1ABB1；（2）求B1C1到平面A1CB的距离；（3）求直线A1C与平面BCC1B1所成角的正切值．【解答】解：（1）证明：∵四边形BCC1B1是矩形，AB⊥BC∴AB⊥BC，BC⊥BB1，AB∩BB1=B∴CB⊥平面A1ABB1∵CB∈平面CA1B∴平面CA1B⊥平面A1ABB1（2）依题意的：A1B=2，AB1=2，B1C=，A1C=∵B1C1∥BC，B1C1⊄平面A1CB，BC⊂平面A1CB∴B1C1∥平面A1CB则B1C1到平面A1CB的距离等于点C1到平面A1CB的距离为H′∵△A1CB的面积S1=1∵AB1⊥A1B，CB⊥AB1∴AB1⊥平面A1CB∴三棱锥C1﹣A1CB的体积等于三棱锥B1﹣A1CB的体积∴H′=AB1=即B1C1到平面A1CB的距离等于（3）设A1到平面BCC1B1的距离为H∴平行四边形BCC1B1的面积S=2，则△A1B1C1的面积为1，BB1=2．由棱锥A1﹣B1BC1的体积等于棱锥B﹣A1B1C1的体积，得：H=∴sinθ=∴直线A1C与平面BCC1B1所成角的正切值tanθ=参与本试卷答题和审题的老师有：豫汝王世崇；minqi5；xize；刘长柏；zlzhan；caoqz；lily2011；沂蒙松；qiss（排名不分先后）菁优网2016年12月21日。

2013～2014学年第一学期期末考试试卷高一数学注意事项：1.请在答题纸上作答，在试卷上作答无效.2.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟.第Ⅰ卷 选择题 （共60分）一．选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合={1,2}A ,={2,3}B ,则=B A （ ）A.{2}B.{1,2,3}C.{1,3}D.{2,3}2．一个几何体的三视图如图1所示,则该几何体可以是 （ ）A.棱柱B.棱台C.圆柱D.圆台3.若直线210ax y a ++-=与直线2340x y +-=垂直，则a 的值为 （ ） A.3 B.-3 C.43 D.43- 4．圆柱底面圆的半径和圆柱的高都为2，则圆柱侧面展开图的面积为 （ ）A.4πB. C.8πD.5.过点(1,3)-且与直线230x y -+=平行的直线方程为 （ ）A.270x y -+=B.210x y +-=C.250x y --=D.250x y +-=6．用斜二测画法画出长为6，宽为4的矩形水平放置的直观图，则该直观图面积为（ ）A.12B.24C.7．圆1O ：2220x y x +-=和圆2O ：2260x y y +-=的位置关系 （ ）A.相交B.相切C.外离D.内含8．已知函数()f x 为奇函数，且当0x <时，21()f x x x =-，则(1)f = （ ） A.2 B.1 C.0D.-2图19．函数()3x f x x =+的零点所在的区间为 （ ）A.()2,1--B.()1,0-C.()0,1D.()1,210.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是 （ ）A.若//l α,//l β,则//αβB.若l α⊥,l β⊥,则//αβC.若//αβ,//l α,则//l βD.若αβ⊥,//l α,则l β⊥11.若正方体1111ABCD A BC D -的外接球O的体积为，则球心O 到正方体的一个面ABCD 的距离为 （ ）A.1B.2C.3D.412．已知,x y 满足22(1)16x y -+=，则22x y +的最小值为 （ ）A.3B.5C.9D.25第Ⅱ卷 非选择题（共90分）二．填空题（本大题共4小题,每小题5分,共20分,把答案填在答卷卡的相应位置上）13.直线20x y +-=与两条坐标轴围成的三角形面积为____________.14.已知一个正棱锥的侧棱长是3cm ，用平行于正棱锥底面的平面截该棱锥，若截面面积是底面面积的19，则截去小棱锥的侧棱长是 cm.15.如图2所示，三棱柱111ABC A B C -，则11111B A BC ABC A B C V V --= .16.已知某棱锥的俯视图如图3所示，主视图与左视图都是边长为2的等边三角形，则该棱锥的全面积是________.图2三．解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)已知平面内两点A （-1,1），B （1,3）.(Ⅰ)求过,A B 两点的直线方程；(Ⅱ)求过,A B 两点且圆心在y 轴上的圆的方程.18.(本小题满分12分) 设函数1221(0)()log (0)x x f x x x ⎧-≤⎪=⎨>⎪⎩,如果0()1f x <，求0x 的取值范围.19.(本小题满分12分)如图4，已知AB 是圆的直径，PA 垂直圆所在的平面，C 是圆上任一点,D 是线段PA 的中点，E 是线段AC 上的一点.求证： (Ⅰ)若E 为线段AC 中点，则DE ∥平面PBC ；(Ⅱ)无论E 在AC 何处，都有BC DE ⊥.20.(本小题满分12分)已知关于,x y 的方程C :04222=+--+m y x y x ，m ∈R.(Ⅰ)若方程C 表示圆，求m 的取值范围；(Ⅱ)若圆C 与直线l ：4370x y -+=相交于,M N 两点，且MN=求m 的值.21.（本小题满分12分） 如图5，长方体1111ABCD A BC D -中，E 为线段BC 的中点,11,2,AB AD AA ===. 图3图4(Ⅰ)证明：DE ⊥平面1A AE； (Ⅱ)求点A 到平面ED A 1的距离.22.（本小题满分12分）已知点(1,2),(0,1),A B -动点P满足PA PB =.(Ⅰ)若点P 的轨迹为曲线C ,求此曲线的方程；(Ⅱ)若点Q 在直线1l ：34120x y -+=上，直线2l 经过点Q 且与曲线C 有且只有一个公共点M ，求QM 的最小值．2013～2014学年第一学期期末考试参考答案与评分标准高一数学说明：一、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二、对解答题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．四、只给整数分数，选择题和填空题不给中间分．一．选择题（1）B ； （2）D ； （3）B ； （4）C ； （5）A ； （6）C ；（7）A ； （8）D ； （9）B ； （10）B ； （11）A ； (12) C ．二．填空题（13）2； （14）1； （15）13； （16）12．三.解答题(17) 解：(Ⅰ)31=11(1)AB k -=--， ·················· 2分 图5AB ∴⋅直线的方程为：y-3=1(x-1)，20x y -+=即. ························· 4分 (Ⅱ)0,2AB 的中点坐标为（），C ∴由已知满足条件的圆的圆心即为（0,2）, ·············· 6分|BC |r ===半径············· 8分∴圆的方程为22(y 2)2x +-= . ·················· 10分（18）解：当0x ≤o 时，211,x -<······························ 2分 122,22,x x <<1x ∴<, 0x ∴≤. ······························ 5分 当0x >时12log 1,x <····························· 7分 11221log log ,2x < 12x ∴>， ····························· 10分 综上0x ≤或12x >. ························· 12分 （19）解：（I ）,D E 分别为,PA AC 的中点,DE ∴∥PC . ··························· 4分 又,,DE PBC PC PBC ⊄⊂Q 平面平面DE ∴∥.PBC 平面 ·························· 6分 （II ）AB Q 为圆的直径,∴⊥AC BC .,PA ABC BC ABC BC PA ⊥⊂∴⊥又平面平面Q ．····································· 8分 PA AC =A ,BC PAC ∴⊥平面. ···························· 10分 无论D 在AC 何处,DE PAC ⊂平面,BC DE ∴⊥. ···························· 12分（20）解：（1）方程C 可化为 m y x -=-+-5)2()1(22, ·········· 2分 显然 5,05<>-m m 即时时方程C 表示圆． ············ 4分（2）圆的方程化为m y x -=-+-5)2()1(22,圆心C （1，2），半径 m r -=5, ··············· 6分则圆心C （1，2）到直线l: 4370x y -+=的距离为1d ==． ························· 8分1||||2MN MN ==则 2221(||)2r d MN =+,2251,m ∴-=+ ··························· 10分 得 1m =． ······························· 12分(21) (Ⅰ)1AA ABCD ⊥平面,DE ABCD ⊂平面1AA DE ∴⊥， ······ 2分E 为BC 中点，1BE EC AB CD ====,AE DE ∴==2AD =又222AE DE AD ∴+=,AE DE ∴⊥. ···················· 4分 又1111,,,AE A AE A A A AE AEA A A ⊂⊂=面面且 ∴ DE ⊥平面1A AE ···························· 6分(Ⅱ)设点A 到1A ED 平面的距离为d ,1A -AED 11V =323⨯ ····················· 8分1111==2AA ABCD AA AE AA AE AE ⊥∴⊥∴平面，，又由(Ⅰ)知DE ⊥平面1A AE ，1DE A E ∴⊥1122A ED S ∆∴=⨯=························ 10分1133A A ED V d -==1d ∴= ···················· 12分(22)解：（Ⅰ）设(,)P x y ，由|PA |PB |得=··············· 2分 两边平方得222221442(21)x x y y x y y +++-+=+-+ ··········· 3分 整理得22230x y x +--= ························· 5分 即22(1)4x y -+= ···························· 6分 （Ⅱ）当1|QC|QC l 与垂直时，最小.min |QC|3d ===,····················· 8分又||QM ==················· 10分min ||QM ∴==························ 12分。

太和二中2013-2014年度上学期高一数学期末考试题考试时间：90分钟 满分150分2014年1月18日一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知全集U=Z ，集合A={-2，-l ，1，2}，B={1，2}，则()U A B ð=（ ）A 、{-2，1}B ．{1，2} C{-1，-2} D ．{-1，2} 2.函数22)(3-+=x x f x 在区间(0,1)内的零点个数是 （ ）A. 0B. 1C. 2D. 33.已知过点P(-2，m)，Q(m ，4)的直线的倾斜角为45o，则m 的值为（ ） A 、l B 、2 C 、3 D 、4 4. 已知22log 3a =，22()3b =，121log 3c =，则,,a b c 的大小关系是（ ）。

A 、a b c >> B 、b c a >> C 、c a b >> D 、c b a >>5. 圆(x －3)2＋(y ＋4)2＝1关于直线y ＝—x+6对称的圆的方程是 ( )A ．(x ＋10)2＋(y ＋3)2＝1 B ．(x －10)2＋(y －3)2＝1 C ．(x －3)2＋(y ＋10)2＝1 D ．(x －3)2＋(y －10)2＝1 6．函数)13lg(13)(2++-=x xx x f 的定义域是（ ）A ．),31(+∞- B ． )1,31(-C ． )31,31(-D ．)31,(--∞ 7. 函数9f (x )lg x x=-的零点所在的大致区间是（ ） A 、(6，7) B 、(7，8) C 、(8，9) D 、(9，10) 8.设函数21(),()(,,0)f x g x ax bx a b R a x==+∈≠，若()y f x =的图像与()y g x =图像有且仅有两个不同的公共点1122(,),(,)A x y B x y ,则下列判断正确的是( ) A. 当0a >时，12120,0x x y y +<+< B. 当0a >时，12120,0x x y y +>+> C. 当0a <时，12120,0x x y y +<+> D. 当0a <时，12120,0x x y y +>+<二．填空题（每小题5分，共30分）9. 若函数22f (x )x x m =-+在区间[2，+∞)上的最小值为 -3，则实数m 的值为 ．10.如图所示,空间四边形ABCD 中,AB ＝CD,AB⊥CD,E、F 分别为BC 、AD 的中点，则EF 和AB 所成的角为11.已知直线l 经过点(7,1)且在两坐标轴上的截距互为相反数，则直线l 的方程 12．如图，正方体1111ABCD A B C D -的棱长为1，,E F 分别为线段11,AA B C 上的点，则三棱锥1D EDF -的体积为 ____________.13．三棱锥P-ABC 的两侧面PAB ，PBC 都是边长为2的正三角形，则二面角A —PB —C 的大小为 ．14. 定义在R 上的偶函数f (x )满足2f (x )f (x )+=，且当[10)x ,∈-时12x f (x )()=，则28f (log ) 等于 ．三、解答题(共6题,共80分，解答写出必要的证明过程、文字说明) 15. （本题满分12分）平行四边形的两邻边所在直线的方程为x ＋y ＋1＝0及3x －4＝0，其对角线的交点是D (3,3)，求另两边所在的直线的方程．16.（本题满分12分）如图，在四棱锥ABCD P -中，平面PAD⊥平面ABCD ，AB=AD ，∠BAD=60°，E 、F 分别是AP 、AD 的中点.求证：（1）直线EF∥平面PCD ； （2）平面BEF⊥平面PAD17. （本题满分14分）已知定义在R 上的函数221xx a f (x )-=+是奇函数．(I)求实数a 的值；(Ⅱ)判断f (x )的单调性，并用单调性定义证明；(III)若对任意的t R ∈，不等式22220f (t t )f (t k )-+-<恒成立，求实数k 的取值范围．18、（本题满分14分）如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，AB AD AC CD ⊥⊥，， 60ABC ∠=°，PA AB BC ==，E 是PC 的中点． （Ⅰ）求PB 和平面PAD 所成的角的大小； （Ⅱ）证明⊥AE 平面PCD ；（Ⅲ）求二面角A PD C --的正弦值．19．（本题满分14分）已知坐标平面上点(,)M x y 与两个定点12(26,1),(2,1)M M 的距离之比等于5. (1)求点M 的轨迹方程，并说明轨迹是什么图形；(2)记(1)中的轨迹为C ，过点(2,3)A -的直线l 被C 所截得的线段的长为8，求直线l 的方程．20. （本题满分14分）已知()f x 是定义在R 上的奇函数，当0x ≥时，()1(01)xf x a a a =->≠且. (1)求(2)(2)f f +-的值； (2)求()f x 的解析式；(3)解关于x 的不等式1(1)4f x -<-<，结果用集合或区间表示．太和二中2013-2014年度上学期高一数学期末考试题答案''二、填空题（）9、3-； 10、45； 11、x －7y ＝0或x －y －6＝0． 12、61； 13、060； 14、2 部分解析2.【解析】函数22)(3-+=x x f x 单调递增，又0121)0(<-=-=f ，01212)1(>=-+=f ，所以根据根的存在定理可知在区间)1,0(内函数的零点个数为1个，选B.4.【解析】由32<+x ，得323<+<-x ，即15<<-x ，所以集合}15{<<-=x x A ，因为)1(n B A ，-= ，所以1-是方程0)2)((=--x m x 的根，所以代入得0)1(3=+m ，所以1-=m ，此时不等式0)2)(1(<-+x x 的解为21<<-x ，所以)11(，-=B A ，即1=n 。

2013~2014学年度第一学期期末试卷高一数学第Ⅰ卷客观卷（共36分）一、选择题（每小题3分，共36分）1. 设集合A＝{1,2}，则满足A∪B＝{1,2,3}的集合B的个数是( )A．1 B．3 C．4 D．8 2. 若f(x)＝2x＋3，g(x＋2)＝f(x)，则g (x)的表达式为( )A．g(x)＝2x＋1 B．g(x)＝2x－1C．g(x)＝2x－3 D．g(x)＝2x＋73．函数f(x)＝11＋|x|的图象是( )4. 已知f(x)为定义在(－∞，＋∞)上的偶函数，且f(x)在[0，＋∞)上为增函数，则f(－2)，f(－π)，f(3)的大小顺序是( )A．f(－π)<f(3)<f(－2)B．f(－π)<f(－2)<f(3)C．f(－2)<f(3)<f(－π)D．f(3)<f(－2)<f(－π)5. 程序框图如图所示：如果输入x＝5，则输出结果为( )A.109 B．325C．973 D．2956．右下面为一个求20个数的平均数的程序，则在横线上应填的语句为( )．A．i ＞20 B．i ＜20C．i ＞＝20 D．i ＜＝207. 用秦九韶算法计算多项式f(x)＝34x ＋33x ＋22x ＋6x ＋1，当x ＝0.5时的值，需要做乘法的次数是( )A ．9B ．14C ．4D ．58. 某学校有体育特长生25人，美术特长生35人，音乐特长生40人．用分层抽样的方法从中抽取40人，则抽取的体育特长生、美术特长生、音乐特长生的人数分别为（ ）A ．8，14，18B ．9，13，18C ．10，14，16D ．9，14，179．某市要对两千多名出租车司机的年龄进行调查，现从中随机抽出100名司机，已知抽到的司机年龄都在[20,45)岁之间，根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示，利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )A ．31.6岁B ．32.6岁C ．33.6岁D ．36.6岁10．给出以下三个命题：(1) 将一枚硬币抛掷两次，记事件A ：“两次都出现正面”，事件B ：“两次都出现反面”，则事件A 与事件B 是对立事件；(2) 在命题(1)中，事件A 与事件B 是互斥事件；(3) 在10件产品中有3件是次品，从中任取3件，记事件A ：“所取3件中最多有2件是次品”，事件B ：“所取3件中至少有2件是次品”，则事件A 与事件B 是互斥事件．其中真命题的个数是( )．A ．0B ．1C ． 2D ．311．一个样本的频率分布直方图共有4个小长方形，它们的高的比从左到右依次为2：4：3：1，若第4组的频数为3，则第2组的频率和频数分别为A ．0.4，12B ．0.6，16C ．0.4，16D ．0.6，1212．设关于x 的一元二次方程2220x ax b ++=。

广东实验中学2012—2013学年（上）高一级期末考试数 学本试卷共23小题，满分150分，考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的班级、姓名、考号填写在答题卷上。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其它答案；不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡的整洁，考试结束后，将答题卷收回。

第一部分（基础检测100分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．67sinπ的值为（ *** ） A ．21B ．23C ． 21-D ．23-2．已知,2,21tan παπα<<-=则αsin 等于 （ *** ） 55.552.55.552.D C B A --3．函数y ＝cos x ·|tan x | ⎝⎛⎭⎫－π2<x <π2 的大致图象是( *** )4．在锐角ABC ∆中，若31tan ,55sin ==B A ，则=+B A （ *** ） 434.ππ或A 4.πB 43.πC 22.D5．下列不等式中，正确的是（ *** ）A ．tan513tan413ππ< B ．sin )7cos(5ππ-> C ．tan ⎝⎛⎭⎫－13π7<tan ⎝⎛⎭⎫－15π8 D ．cos )52cos(57ππ-<6．函数]0,[),3sin(2)(ππ-∈-=x x x f 的单调递增区间是（ *** ）A ．]65,[ππ-- B ．]6,65[ππ-- C ．]0,3[π- D ．]0,6[π- 7．已知函数sin cos 1212y x x ππ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭，则下列判断正确的是（ ***） A ．此函数的最小周期为2π，其图像的一个对称中心是,012π⎛⎫⎪⎝⎭B ．此函数的最小周期为π，其图像的一个对称中心是,012π⎛⎫⎪⎝⎭ C ．此函数的最小周期为2π，其图像的一个对称中心是,06π⎛⎫⎪⎝⎭D ．此函数的最小周期为π，其图像的一个对称中心是,06π⎛⎫⎪⎝⎭8．已知2tan α·sin α＝3，－π2<α<0，则cos ⎝⎛⎭⎫α－π6的值是(*** ) A ．0 B.32 C ．1 D.129．若10sin 3cos =-αα，则=αtan （*** ） A ．3； B ．53-; C ．3-; D ．8310．定义在R 上的函数满足，当时，，则（*** ）A ．B ．C ．)45(tan)6(tanππf f < D ．NMDCBA二、填空题： (每题5分,共20分)11. 已知扇形的弧长和面积的数值都是2，则其圆心角的正的弧度数为____***____.12．若集合M ＝⎩⎨⎧⎭⎬⎫θ⎪⎪ sin θ≥12，0≤θ≤π，N ＝⎩⎨⎧⎭⎬⎫θ⎪⎪cos θ≤12，0≤θ≤π，则M ∩N =___***___.13．如图,在正方形ABCD 中,M 是边BC 的中点,N 是边CD 的中点,设α=∠MAN ,那么αsin 的值等于_______***_____. 14．给出下列四个结论：①若角的集合{|,},{|,}244k A k B k k πππααββπ==+∈==±∈Z Z ， 则A B =；②函数|tan |x y =的周期和对称轴方程分别为)(2,Z k k x ∈=ππ ③ 已知sin ⎝⎛⎭⎫π6－α＝14，则sin ⎝⎛⎭⎫π6＋2α＝78 ④要得到函数cos()24x y π=-的图象，只需将sin 2x y =的图象向右平移2π个单位； 其中正确结论的序号是 *** ．（请写出所有正确结论的序号）。

广东实验中学2013—2014学年（上）高二级模块考试数 学 （文科）本试卷分模块测试和能力测试两部分，共4页，满分150分，考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的校名、姓名、考号填写在答题卷的密封线内。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其它答案；不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在另发的答题卷各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卷的整洁，考试结束后，将答题卷一并收回。

参考公式：1．母线底面底面侧面底面圆锥表面积l r r S S S ππ+=+=22．h S V 底面锥31=3．设具有线性相关关系的两个变量x,y 的一组观察值为),,2,1)(,(n i y x j i =，则回归直线x b a y ˆˆˆˆ+=的系数为：⎪⎪⎪⎩⎪⎪⎪⎨⎧-=---=-⋅-=∑∑∑∑===x b y ax xy y x xx n x y x n y x b ni ini i ii ni i i ˆˆ)())((ˆ121221第一部分 模块测试题（共100分） 一. 选择题 （每题5分 共50分） 1．下列说法中正确的是 （ ）A ．棱柱中两个互相平行的面一定是棱柱的底面B ．以直角三角形的一条边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体叫做圆锥C ．一个棱锥至少有四个面D ．用一平面去截圆锥，底面与截面之间的部分叫做圆台 2．若直线上有两个点在平面外．．．，则 （ ） A ．直线上至少有一个点在平面内 B ．直线上有无穷多个点在平面内 C ．直线上所有点都在平面外 D ．直线上至多有一个点在平面内3．一个几何体的三视图如图所示，则该几何体可以是（ ）1 32 7 01 8 12 3 2 69A BCEDA ．棱柱B ．棱台C ．圆柱D ．圆台4．某社区有500个家庭，其中高收入家庭160户，中等收入家庭280户，低收入家庭60户，为了调查社会购买力的某项指标，要从中抽取一个容量为100户的样本，记作①；我校高二级有12名女游泳运动员，为了调查学习负担情况，要从中选出3人的样本，记作②.那么完成上述两项调查应采用的最合适的抽样方法是 ( )A ．①用随机抽样，②用系统抽样B ．①用分层抽样，②用随机抽样C ．①用系统抽样，②用分层抽样D ．①用随机抽样，②用分层抽样 5．下列说法正确的是 ( )A ．对立事件也是互斥事件B ．某事件发生的概率为1.1C ．不能同时发生的的两个事件是两个对立事件D ．某事件发生的概率是随着实验次数的变化而变化的 6．下列判断正确的是 ( )A ．若βαβα//,//b ,//a ,则a//bB ．β⊥αβ⊥α⊥,b ,a ,则a⊥bC ．若b //a ,b ,a β⊂α⊂，则βα//D ．若n m ,m ⊥α⊥，则α//n7．已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积是 ( ) A ．1cm3B ．2cm 3C ．3cm 3D ．6cm 38．若将一颗质地均匀的骰子（一种各面上分别标有1，2，3，4，5，6个点的正方体玩具），先后抛掷两次，则出现向上的点数之和为4的概率是 ( ) A ．121 B ．212 C ．181 D ．719．下图是某公司10个销售店某月销售某产品数量（单位：台）的茎叶图，则数据落在区间[20,30）内的概率为 ( ) A ．0.2 B ．0.4 C ．0.5 D ．0.610．如图，矩形ABCD 中，点E 为边CD 的中点，若在矩形ABCD 内部随机取一个点Q ，则点Q 取自△ABE 内部的概率等于 ( ) A ．14 B ．13 C ．12 D ．23二、填空题 （每题5分 共20分）11．已知一组数据为-2，0，4，x ，y ，6,15，且这组数据的众数为6，平均数为5，则这组ACBDA 1B 1C 1D 1/秒0.040.20 0.320.38 0.06数的中位数为_____________.12．某设备的使用年限x （年）和所支出的维修费用y （万元），有如下表所示的统计资料：由资料知y 对x 呈线性相关关系，则其回归直线方程y=bx+a 为________________ (其中3.1120.765.655.548.332.22=⨯+⨯+⨯+⨯+⨯）13．给出下列四个命题：①设α是平面，m 、n 是两条直线，如果α⊄α⊂n ,m ，m 、n 两直线无公共点，那么α//n . ②设α是一个平面，m 、n 是两条直线，如果αα//,//n m ，则m//n.. ③若两条直线都与第三条直线平行，则这两条直线平行.④三条直线交于一点，则它们最多可以确定3个平面.其中正确的命题是________14．如图，在棱长为1的正方体ABCD-1111D C B A 中， C B 1与BD 所成角为 _________.三、解答题 （每题10分 共30分）15．(10分) 如图，三棱锥A-BCD 中，E 、F 分别是棱AB 、BC 的中点，H 、G 分别是棱AD 、CD 上的点，且K FG EH = . 求证：（1）EH ，BD ，FG 三条直线相交于同一点K; （2）EF//HG.16．（10分）某班50名学生在一次百米测试中，成绩（单位：秒）全部介于13与18秒之间，将测试结果按如下方式分成五组：第一组[13,14)，第二组[14,15)，…，第五组[17,18]，如图是按上述分组方法得到的频率分布直方图.若从第一、第五组中随机取出两个成绩，求这两个成绩一个在第一组，一个在第五组的概率. 17．(10分) 如图，母线长为2的圆锥PO 中，已知AB 是半径为1的⊙O 的直径，点C 在AB 弧上， DAEBF CG D HKAA 1EBFCMND B 1D 1 C 1为AC 的中点． （1）求圆锥PO 的表面积； （2）证明：平面ACP⊥平面POD.第二部分 能力测试（共50分） 18．“21m =”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0互相垂直”的_____________条件（填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”）19．如图，已知E ，F ，M ，N 分别是棱长为2的正方体ABCD-A 1B 1C 1D 1的棱AB 、BC 、CC 1、A 1B 1的中点，则三棱锥N-EFM 的体积为_____________ 20．(13分) 数列{n a } 中1a ＝13，前n 项和n S 满足1n S +-n S ＝113n +⎛⎫ ⎪⎝⎭（n ∈*N ）．（1）求数列{n a }的通项公式n a 以及前n 项和n S ；（2）若S 1, t ( S 1+S 2 ), 3( S 2+S 3 ) 成等差数列，求实数t 的值。