华师大版八年级数学下册《16.4 零指数幂与负整指数幂(一)》教案
- 格式:doc
- 大小:115.50 KB
- 文档页数:2

华师大版数学八年级下册《零指数幂与负整数指数幂》教学设计一. 教材分析《零指数幂与负整数指数幂》是华师大版数学八年级下册的一章内容。
这一章主要介绍了零指数幂和负整数指数幂的概念及其运算性质。
教材通过具体的例子引导学生理解并掌握零指数幂和负整数指数幂的定义,再通过大量的练习让学生熟练运用其运算性质进行计算。
二. 学情分析学生在学习这一章内容之前,已经学习了有理数、实数等基础知识,对幂的概念和运算已经有了一定的了解。
但学生对负数和零的指数幂的理解可能会存在一定的困难,因此需要通过具体的例子和练习让学生加深对这两个概念的理解。
三. 教学目标1.了解零指数幂和负整数指数幂的概念。
2.掌握零指数幂和负整数指数幂的运算性质。
3.能够运用零指数幂和负整数指数幂的概念和运算性质解决实际问题。
四. 教学重难点1.零指数幂和负整数指数幂的概念。
2.零指数幂和负整数指数幂的运算性质。
五. 教学方法1.采用问题驱动的教学方法,通过引导学生思考和解决问题,让学生理解零指数幂和负整数指数幂的概念及其运算性质。
2.运用多媒体教学,通过动画和图片等形式展示零指数幂和负整数指数幂的运算过程,帮助学生形象地理解概念和运算性质。
3.提供大量的练习,让学生在实践中掌握零指数幂和负整数指数幂的运算。
六. 教学准备1.PPT课件七. 教学过程1.导入(5分钟)通过复习实数和幂的知识,引导学生思考零和负数的指数幂是什么。
2.呈现(15分钟)通过具体的例子,呈现零指数幂和负整数指数幂的定义和运算性质。
3.操练(15分钟)让学生进行一些零指数幂和负整数指数幂的计算练习,帮助学生理解和掌握其运算性质。
4.巩固(10分钟)通过一些应用题,让学生运用零指数幂和负整数指数幂的概念和运算性质解决实际问题。
5.拓展(5分钟)引导学生思考零指数幂和负整数指数幂在其他领域的应用,如科学研究、工程技术等。
6.小结(5分钟)对本节课的内容进行小结,强调零指数幂和负整数指数幂的概念及其运算性质。
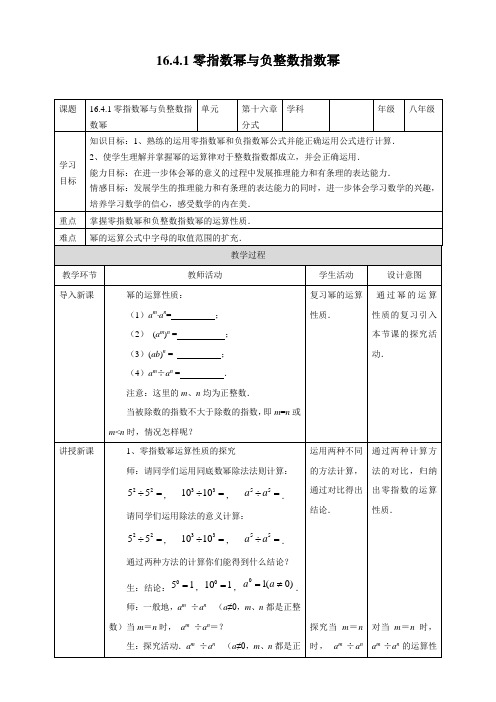

16.4零指数幂与负整数指数幂16.4.1零指数幂与负整数指数幂【教学目标】知识与技能1.了解零指数幂与负整数指数幂意义,理解零指数幂与负整数指数幂的概念;2.会进行相关计算;过程与方法1.学生经历探索零指数幂与负整数指数幂的过程,提升学生发现、观察、理解、归纳的能力;【教学重、难点】重点:①理解零指数幂与负整数指数幂的概念,并会进行相关计算;难点:①了解零指数幂与负整数指数幂意义,理解零指数幂与负整数指数幂的概念;【教学过程】一、旧知回顾同底数幂的运算回顾:(1) 同底数幂的除法运算法则① 32a a ÷② 43x x x ÷• ③ ()432xy xy x ÷• (引导学生:复习同底数幂的运算) (2)出题2:47a a ÷ 44x x ÷观察新题,提出问题:①在前面,我们学习过同底数幂的除法公式a m ÷a n =a m-n (m >n ), 即被除数的指数大于除数的指数.当被除数的指数不大于除数的指数, ②m=n 或m <n 时,情况怎样呢?二、抛出问题,活动探究探究1:零指数幂(1)出题① 3333÷ ② 4444÷ ③ 551010÷ ④ 33a a ÷⑤ 4400÷ (2)观察新题:①仿照同底数幂的除法公式计算;()3333044440555505555033334444101010100a a a a a ----÷==÷==÷==÷==≠②根据除法的意义:被除式等于除式(除式不为零)所得的商等于1;()3333444455555555333134441410101011010a a a a a ÷==÷==÷==÷==≠ 【归纳+板书】我们规定:()010a a =≠任何不等于零的数的零次幂都等于1;探究2:负整数指数幂(1)出题① 3533÷ ② 4844÷ ③ 581010÷ ④ 37a a ÷⑤ 4600÷ (2)观察新题:①仿照同底数幂的除法公式计算;()35352484845858337374463333444410101010000(0)a a a a a --------÷==÷==÷==÷==≠÷无意义不能做除式②利用约分的性质:直接算出这两个分式的结果;()335524488455883337743133334144441011010101010a a a a a a ÷==÷==÷==÷==≠ 【归纳+板书】我们规定:()10,n n a a n a -=≠是正整数任何不等于零的数的-n 次幂(n 为正整数),等于这个数的n 次幂的倒数。


华师大版八下数学16.4.1零指数幂与负整指数幂教学设计一. 教材分析《华师大版八下数学》16.4.1节主要介绍零指数幂与负整指数幂的概念及其运算性质。
这部分内容是指数幂的基础,对于学生理解指数幂的概念和运算规则具有重要意义。
教材通过具体的例子引导学生探究零指数幂和负整指数幂的定义和性质,并通过练习题帮助学生巩固所学知识。
二. 学情分析学生在学习本节内容前,已经掌握了有理数的乘方和指数幂的基本概念。
但零指数幂和负整指数幂的概念较为抽象,学生可能难以理解。
因此,在教学过程中,需要帮助学生建立直观的认识,并通过大量的例题和练习题让学生熟悉和掌握相关概念和运算性质。
三. 教学目标1.理解零指数幂和负整指数幂的概念。
2.掌握零指数幂和负整指数幂的运算性质。
3.能够运用零指数幂和负整指数幂解决实际问题。
四. 教学重难点1.零指数幂和负整指数幂的概念。
2.零指数幂和负整指数幂的运算性质。
五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。
通过设置问题引导学生思考,利用具体案例让学生感受零指数幂和负整指数幂的应用,小组讨论,促进学生之间的交流和学习。
六. 教学准备1.准备相关教案和教学课件。
2.准备典型例题和练习题。
3.准备教学道具和实物模型。
七. 教学过程1.导入(5分钟)通过复习有理数的乘方和指数幂的基本概念,引导学生进入本节内容的学习。
2.呈现(15分钟)利用课件展示零指数幂和负整指数幂的定义和运算性质,让学生直观地感受这两个概念。
3.操练(20分钟)让学生分组讨论,分析并解决典型例题。
教师巡回指导,解答学生疑问。
4.巩固(10分钟)布置练习题,让学生独立完成。
教师选取部分题目进行讲解,巩固所学知识。
5.拓展(10分钟)利用实际问题,让学生运用零指数幂和负整指数幂解决实际问题。
引导学生思考这两个概念在实际生活中的应用。
6.小结(5分钟)教师总结本节课的主要内容和知识点,强调零指数幂和负整指数幂的运算性质。

华师大版八下数学16.4零整数幂与负整数指数幂,科学记数法教学设计一. 教材分析华师大版八下数学第16.4节主要介绍了零整数幂与负整数指数幂,以及科学记数法。
这一节的内容是学生学习指数幂的基础,对于学生理解指数幂的概念和应用具有重要意义。
教材通过例题和练习,帮助学生掌握零整数幂和负整数指数幂的运算规则,以及科学记数法的表示方法和转换方法。
二. 学情分析学生在学习这一节内容时,已经掌握了有理数、整数幂的基本概念和运算规则,具备一定的逻辑思维能力和运算能力。
但学生对于负整数指数幂和科学记数法的理解可能存在一定的困难,因此需要通过实例和练习,帮助学生深入理解这两个概念。
三. 教学目标1.理解零整数幂和负整数指数幂的概念,掌握其运算规则。
2.掌握科学记数法的表示方法和转换方法。
3.能够运用零整数幂、负整数指数幂和科学记数法解决实际问题。
四. 教学重难点1.零整数幂和负整数指数幂的运算规则。
2.科学记数法的表示方法和转换方法。
五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。
通过设置问题,引导学生思考和探索,通过案例分析和练习,帮助学生理解和掌握知识,通过小组合作学习,培养学生的团队协作能力和解决问题的能力。
六. 教学准备1.PPT课件2.小组合作学习指南七. 教学过程1.导入(5分钟)通过一个实际问题,引入零整数幂和负整数指数幂的概念,激发学生的兴趣。
2.呈现(15分钟)讲解零整数幂和负整数指数幂的运算规则,通过PPT课件和例题,帮助学生理解和掌握。
3.操练(15分钟)学生独立完成练习题,教师巡回指导,及时纠正错误,巩固所学知识。
4.巩固(10分钟)通过小组合作学习,让学生互相讨论和解答疑问,进一步巩固知识。
5.拓展(10分钟)讲解科学记数法的表示方法和转换方法,通过案例和练习,帮助学生理解和掌握。
6.小结(5分钟)教师总结本节课的主要内容和知识点,提醒学生注意零整数幂、负整数指数幂和科学记数法的运用。
华师大版八下数学16.4零指数幂与负整指数幂16.4.1零指数幕与负整数指数幕教学设计一. 教材分析华东师范大学版八年级下册数学第16章是关于指数幂的学习,而16.4节是零指数幂与负整数指数幂的内容。
这部分教材主要让学生理解并掌握零指数幂和负整数指数幂的概念,并能运用它们进行简单的运算和解决问题。
在编写教学设计时,需要充分理解教材的编写意图,深入研究教材内容,把握教学内容的逻辑结构和知识体系。
二. 学情分析在八年级下册的学生已经学习了有理数、代数、方程等数学知识,对数的概念和运算有一定的掌握。
但是,对于零指数幂和负整数指数幂的理解可能存在一定的困难,需要通过实例和实际操作来帮助学生理解和掌握。
三. 教学目标通过本节课的学习,学生需要达到以下目标:1.理解零指数幂和负整数指数幂的概念。
2.掌握零指数幂和负整数指数幂的运算方法。
3.能够运用零指数幂和负整数指数幂解决实际问题。
四. 教学重难点1.零指数幂的概念和运算。
2.负整数指数幂的概念和运算。
3.运用零指数幂和负整数指数幂解决实际问题。
五. 教学方法采用问题驱动的教学方法,通过实例和实际操作,引导学生探究零指数幂和负整数指数幂的概念和运算方法。
同时,运用分组讨论和互助合作的学习方式,提高学生的参与度和合作能力。
六. 教学准备1.PPT课件:制作相关的PPT课件,内容包括零指数幂和负整数指数幂的概念、运算方法和实际应用等。
2.实例和练习题:准备一些相关的实例和练习题,用于引导学生探究和巩固所学知识。
3.教学工具:准备黑板、粉笔等教学工具,用于板书和讲解。
七. 教学过程1.导入(5分钟)通过一个实际问题引出零指数幂和负整数指数幂的概念,激发学生的学习兴趣。
2.呈现(15分钟)讲解零指数幂和负整数指数幂的概念和运算方法,引导学生理解和掌握。
3.操练(15分钟)让学生分组讨论,互相交流,通过实例和练习题来巩固所学知识。
4.巩固(10分钟)对学生的学习情况进行检查,对存在的问题进行讲解和解答,帮助学生巩固知识。
华师大版八下数学16.4零整数幂与负整数指数幂,科学记数法说课稿一. 教材分析华师大版八下数学第16.4节讲述了零整数幂与负整数指数幂,以及科学记数法。
这一节内容是初中学段数学的重要内容,也是学生进一步学习高中数学的基础。
通过本节内容的学习,学生能够理解并掌握零整数幂与负整数指数幂的定义和性质,以及科学记数法的表示方法,提高学生的数学素养和解决问题的能力。
二. 学情分析学生在学习本节内容前,已经学习了有理数的乘方,对幂的概念有一定的了解。
但是,对于零整数幂与负整数指数幂的定义和性质,以及科学记数法的表示方法,学生可能还存在一定的困惑。
因此,在教学过程中,需要针对学生的实际情况进行引导和讲解,帮助学生理解和掌握。
三. 说教学目标1.知识与技能:学生能够理解并掌握零整数幂与负整数指数幂的定义和性质,以及科学记数法的表示方法。
2.过程与方法:通过探究零整数幂与负整数指数幂的定义和性质,培养学生的逻辑思维能力和归纳总结能力。
3.情感态度价值观:激发学生对数学的兴趣,培养学生的团队合作意识和自主学习能力。
四. 说教学重难点1.零整数幂与负整数指数幂的定义和性质。
2.科学记数法的表示方法。
五. 说教学方法与手段本节课采用问题驱动法、案例教学法和小组合作学习法。
通过设置问题,引导学生思考和探究,从而理解和掌握零整数幂与负整数指数幂的定义和性质。
同时,通过案例分析和小组合作学习,培养学生的实践能力和团队合作意识。
六. 说教学过程1.导入:通过复习有理数的乘方,引导学生回顾幂的概念,为新课的学习做好铺垫。
2.探究零整数幂与负整数指数幂的定义和性质:通过设置问题,引导学生进行自主探究,总结零整数幂与负整数指数幂的定义和性质。
3.科学记数法的表示方法:通过案例分析,引导学生理解和掌握科学记数法的表示方法。
4.巩固练习:布置一些相关的练习题,让学生巩固所学知识,提高解决问题的能力。
5.总结与反思:引导学生总结本节课所学内容,反思自己的学习过程,提高自主学习能力。
16.4.1零整数幂与负整数指数幂一、教学目标:1.知道任何不等于零的零指数幂等于1.1(a≠0,n是正整数).2.知道负整数指数幂na =na2.掌握整数指数幂的运算性质.二、重点、难点重点:掌握零整数幂与负整数指数幂的运算性质.难点:会进行整数指数幂的运算.三、教学过程:(一)知识回顾,导入新课1.口算:56÷54= (-3)5÷(-3)3=a4÷a3= a m÷a n= (a≠0,m>n)2.回顾同底数幂的除法法则,a m÷a n=a m-n (a≠0,m>n的正整数)思考:当被除数的指数大于除数的指数,又如何计算呢?分m=n,m ﹤n两种情况探究。
(二)自主探究,获得新知1.用同底数幂的除法运算方法及除法的意义两种方法计算下面各题:52÷52= 103÷103= a5÷a5= (a≠0)学生通过计算便可从中得出;任何不等于零的零次幂都等于1.用数学符号表示为:a0=1 (a ≠0)2.同样用以上两种方法计算:52÷55= 103÷107= a m÷a n= (m﹤n) 学生通过计算可以发现:任何不等于零的数的负整数指数幂等于正整数指数幂的倒数。
1(a≠0,n是正整数)用数学符号表示为:a-n=na3.例1.计算:(1)3-2 (2)(31)0×10-2 4.例2.用小数表示下列各数:(1)10-4 (2)2.1×10-55. 知识延伸:正整数指数幂的相关运算性质:(1)同底数幂的乘法:n m n m a a a +=⋅(m,n 是整数);(2)幂的乘方:mn n m a a =)((m,n 是整数);(3)积的乘方:n n n b a ab =)((n 是整数);(4)同底数的幂的除法:n m n m a a a -=÷( a ≠0,m,n 是整数); 综合上面的学习,可以得出:a m ÷a n =a m-n 这条性质适用于m,n 是任意整数的结论,说明正整数指数幂的运算性质具有延续性.其它的正整数指数幂的运算性质,在整数范围里也都适用.四、随堂练习1.用小数或分数表示下列各数;(1)10-3=(2)70×8-2= (3)1.6×10-4= 2.计算(1) (x 3y -2)2 (2)x 2y -2 ·(x -2y)3(3)(3x 2y -2) 2 ÷(x -2y)33.若x 3x-1=1,则x=4.若a 0=1,则a= 若(x-1)0=1,则x= 若(1-x x )0=1,则x= 5.若10a =20,10b =5-1,求3a ÷3b 的值。
华师大版数学八年级下册16.4《零指数幂与负整数指数幂》(第1课时)说课稿一. 教材分析《零指数幂与负整数指数幂》是华师大版数学八年级下册第16.4节的内容。
本节内容是在学生已经掌握了有理数的乘方、正整数指数幂的基础上进行学习的。
本节课的主要内容是让学生理解并掌握零指数幂和负整数指数幂的定义及其性质,能够运用它们进行有关的运算和解决问题。
二. 学情分析学生在学习本节内容之前,已经掌握了有理数的乘方和正整数指数幂的知识,具备了一定的逻辑思维和运算能力。
但是,对于零指数幂和负整数指数幂的理解可能会存在一定的困难,因此,在教学过程中,需要引导学生通过观察、思考、讨论等方式,逐步理解和掌握相关概念和性质。
三. 说教学目标1.知识与技能目标:让学生理解并掌握零指数幂和负整数指数幂的定义及其性质,能够运用它们进行有关的运算和解决问题。
2.过程与方法目标:通过观察、思考、讨论等方式,培养学生的逻辑思维和运算能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的团队合作意识和自主学习能力。
四. 说教学重难点1.教学重点:零指数幂和负整数指数幂的定义及其性质。
2.教学难点:零指数幂和负整数指数幂在实际问题中的应用。
五.说教学方法与手段1.教学方法:采用问题驱动法、案例教学法和小组合作学习法。
2.教学手段:利用多媒体课件、实物模型和数学软件进行辅助教学。
六.说教学过程1.导入新课:通过复习正整数指数幂的知识,引导学生思考零指数幂和负整数指数幂的概念。
2.探究新知:引导学生观察、分析、讨论零指数幂和负整数指数幂的定义及其性质,总结出相关的运算规律。
3.巩固新知:通过例题和练习题,让学生运用零指数幂和负整数指数幂的知识解决问题,加深对知识点的理解和掌握。
4.拓展应用:引导学生思考零指数幂和负整数指数幂在实际问题中的应用,提高学生的解决问题的能力。
5.小结总结:对本节课的内容进行总结,强调零指数幂和负整数指数幂的定义及其性质,提醒学生注意相关运算规律的应用。