高等几何课件上课版PPT课件
- 格式：ppt
- 大小：11.71 MB
- 文档页数：10
下载文档原格式
合集下载
高等几何课件上课版PPT课件
的仿x 射y变换0,。x y 0, x 2y 1 0
• 2、已知仿射变换
x/ 2x y 1
• 求点 P1(1, 0), P2 (1, 0)
y/
x
y
3
• 的像点，及直线 x y 2 0的像直线。
29
4、特殊的仿射变换
正交变换
x'
y'
a11x a21x
a12 y a13 a22 y a23
称为透视仿射对应。 注：透视仿射对应与L的方向无关。若a与b相交，交 点称为自对应点。
14
两条直线间的透视仿射对应
a
C B A
o L
A/ B/ C/
b
特征：对应点的连线互相平行
15
两个平面间的透视仿射对应
A1 B1
C1
1
M对应点的连线互相平行
16
第一章、仿射坐标与仿射变换
2、单比
31
例1 证明：两平行直线经过仿射变换后仍变为平行直线
• 证明：设变换为：T:
x' y'
A
x y
a b
,
直线l1
:u
u1
u2
,l2
:
v
v1
v2
l1
//
l2
u
v即
u1 u2
v1 v2
u1' u2'
A
u1 u2
A
v1 v2
A
v1 v2
•且
o', e1' , e2' 在{o;e1, e2}下的坐标分别为： （a13, a23), (a11, a21), (a12, a22 )
26
平比行不四变边，形 故POP' 在x P坐Py变标为系平{O行';四e1' ,边e2' }形中O的'P坐x'P标P，y为' 且(保x,y)持单
• 2、已知仿射变换
x/ 2x y 1
• 求点 P1(1, 0), P2 (1, 0)
y/
x
y
3
• 的像点，及直线 x y 2 0的像直线。
29
4、特殊的仿射变换
正交变换
x'
y'
a11x a21x
a12 y a13 a22 y a23
称为透视仿射对应。 注：透视仿射对应与L的方向无关。若a与b相交，交 点称为自对应点。
14
两条直线间的透视仿射对应
a
C B A
o L
A/ B/ C/
b
特征：对应点的连线互相平行
15
两个平面间的透视仿射对应
A1 B1
C1
1
M对应点的连线互相平行
16
第一章、仿射坐标与仿射变换
2、单比
31
例1 证明：两平行直线经过仿射变换后仍变为平行直线
• 证明：设变换为：T:
x' y'
A
x y
a b
,
直线l1
:u
u1
u2
,l2
:
v
v1
v2
l1
//
l2
u
v即
u1 u2
v1 v2
u1' u2'
A
u1 u2
A
v1 v2
A
v1 v2
•且
o', e1' , e2' 在{o;e1, e2}下的坐标分别为： （a13, a23), (a11, a21), (a12, a22 )
26
平比行不四变边，形 故POP' 在x P坐Py变标为系平{O行';四e1' ,边e2' }形中O的'P坐x'P标P，y为' 且(保x,y)持单
大学高等几何课件
空间几何体的分类
多面体、旋转体、组合体等。
空间几何体的性质
体积、表面积、重心等。
平面几何与立体几何的关系
平面几何是立体几何的基础
01
立体几何中的许多概念和性质都可以从平面几何中推广而来。
空间几何体的投影
02
通过投影将三维空间中的几何体投影到二维平面上，从而将三
维问题转化为平面问题。
空间几何体的展开
数形结合的思想方法
数形结合
在高等几何中，数和形是密不可分的，通过数形结合可以将几何问 题转化为代数问题，或者将代数问题转化为几何问题。
代数方法
利用代数方法研究几何问题，如线性代数中的矩阵和向量等，可以 更深入地研究几何图形的性质和关系。
几何直观
通过几何直观来理解代数概念和性质，使得代数问题更加直观易懂。
05
CATALOGUE
高等几何中的数学思想与方法
抽象思维与具体表达的结合
1 2
抽象思维
高等几何中，点、线、面等基本元素不再是具体 的实物，而是通过抽象思维来定义和理解。
具体表达
高等几何中，通过几何图形、图像等方式将抽象 的数学概念具体化，便于理解和应用。
3
结合应用
抽象思维与具体表达的结合，使得高等几何能够 更深入地探索和研究几何学中的本质和规律。
差异性
然而，射影几何和仿射几何也存在差异性。例如，在射影空 间中，无穷远点是重要的元素，而在仿射空间中则不重要。 此外，射影变换通常会改变图形的形状和大小，而仿射变换 则不会。
04
CATALOGUE
欧式几何与非欧式几何
欧式几何的基本概念
欧式几何
基于平面的二维空间，研究点 、线、面及其性质和关系。
不同空间结构
多面体、旋转体、组合体等。
空间几何体的性质
体积、表面积、重心等。
平面几何与立体几何的关系
平面几何是立体几何的基础
01
立体几何中的许多概念和性质都可以从平面几何中推广而来。
空间几何体的投影
02
通过投影将三维空间中的几何体投影到二维平面上，从而将三
维问题转化为平面问题。
空间几何体的展开
数形结合的思想方法
数形结合
在高等几何中，数和形是密不可分的，通过数形结合可以将几何问 题转化为代数问题，或者将代数问题转化为几何问题。
代数方法
利用代数方法研究几何问题，如线性代数中的矩阵和向量等，可以 更深入地研究几何图形的性质和关系。
几何直观
通过几何直观来理解代数概念和性质，使得代数问题更加直观易懂。
05
CATALOGUE
高等几何中的数学思想与方法
抽象思维与具体表达的结合
1 2
抽象思维
高等几何中，点、线、面等基本元素不再是具体 的实物，而是通过抽象思维来定义和理解。
具体表达
高等几何中，通过几何图形、图像等方式将抽象 的数学概念具体化，便于理解和应用。
3
结合应用
抽象思维与具体表达的结合，使得高等几何能够 更深入地探索和研究几何学中的本质和规律。
差异性
然而，射影几何和仿射几何也存在差异性。例如，在射影空 间中，无穷远点是重要的元素，而在仿射空间中则不重要。 此外，射影变换通常会改变图形的形状和大小，而仿射变换 则不会。
04
CATALOGUE
欧式几何与非欧式几何
欧式几何的基本概念
欧式几何
基于平面的二维空间，研究点 、线、面及其性质和关系。
不同空间结构
大学高等几何课件第一讲
1.3 仿射不变性与不变量 定理1 间的平行性是 仿射不变 . 性 定理1.1 两条直线 射不变 形；梯 图 形是 仿射不变 形 图 . 推论 平行四边形是仿 述 定义1 , ( 定义1.1 设A,B,C为共线三点 这三点的简比 ABC)定义为下 有向线段 的比 ： AC . BC C在 线段AB上 ,简 ( ABC) < 0, C在 的延长线上 , ( ABC) > 0. 时 比 AB 时 ( ABC) = 在 解析 几何中讲过 线段 定比 的 分割 若点 分割线段 的分割比 , C AB 记 λ,则 为 AC AC λ= =− = −( ABC). CB BC 所 以简 ( ABC)等于点 分割线段 的 比 C AB 分割 比的相反数 .
例如 ，人眼 O处 在 观察水 平面 上的矩 ABCD时 形 ， 从O到矩 形的各 点连线 形成一个 投影棱 。若在 眼 锥 人 和矩 形之间 插入一 个平面 ，该平 面截棱 锥所得四边 形 A′B′C′D′即为 矩形ABCD的截 影。 但直观 上看 截影 ， 和 原矩 形既不 全等 ，又不相似， 那么 截影与 原形究竟 有 何关 系呢？ 这正 是阿尔贝 蒂苦 苦思索 而未 找到答案 的 问题 。 阿 尔贝 蒂还思 考了 以下问题 ：同一 原形的 不同截 影之 间究竟 有何关 ？ 系 这 些问 题成为 研究 射影几何 的出发 。 点
2. 平 π 到平 π ′的 行 影 透 仿 T 面 面 平 பைடு நூலகம் 或 视 射 平行 射影 的方 l要 既 与π 平 又 与 向 求 不 行 不 注： π′ 平行射影方向改变了 就得出另外的从π到π′ . , 的透 视仿 . 射
⇒(i)透 视仿射 保留同 素性(即几 何元素 点与线 保持原 先的种 ). 类 即: 两平面 间的 平行射 影将一 平面上 的点映 射为第 二平面 上的 , 点 将一平 面上的 直线映 第 为 二平面 上的直 . 线 ⇒(ii)透 . 视仿射 保留结 合性 ( 果这两 直线与 直线间 的透视 射有 仿 一个自 对应点 如 条直线 相 , 两平面 , 交线g 交).同 , 在平面 样 到平面 的透视 射下 若 仿 相交 则 为 自对应 点的轨 , 称为 迹 对应轴 对 , 应直线 与 ′或相 a a 交于轴 , 上 或都 与轴平 . 行 平面的 仿射是 有限 由 回的平 行射影 组成的 即仿 , 射是 ⇒平面到 透视仿 射链 .
2017年《高等几何》教学课件
影消线的存在，导致两平面间的中心射影不是一个双射!
§1.1 拓广平面
一、中心射影
1、平面上两直线间的中心射影 定义1.1
: l l'
2、平面到平面的中心射影
定义1.2
: '
}
均不是双射
中心射影不是双射的原因：存在影消点、影消线
存在影消点、影消线的原因：平行的直线没有交点
如何使得中心射影成为一个双射？
课 程 概 论
一、高等几何的内容 二、高等几何的方法 综合法
给定公理系统(一套相互独立、 无矛盾、完备的命题系统)，演 绎出全部内容 形、数结合，利用代数、分析 的方法研究问题 以解析法为主，兼用综合法
解析法 本课程
课 程 概 论
一、高等几何的内容 二、高等几何的与方法 三、开课目的
• 学习射影几何，拓展几何空间概念，引入几何变换 知识，接受变换群思想 • 训练理性思维、抽象思维、逻辑推理能力，增强数 学审美意识，提高数学修养 • 新颖性，趣味性，技巧性，反馈于初等几何和其他 学科，提高观点，加深理解，举一反三
区别起见，称平面上原有的点为有穷远点(通常点)，记作P
约定1.1 (3) 按约定(1), (2)添加无穷远点之后，平面上全体 无穷远点构成一条直线，称为无穷远直线(理想直线)，记作l∞ 区别起见，称平面上原有的直线为有穷远直线(通常直线)，l 总结：在平面上添加无穷远元素之后，没有破坏点与直线 的关联关系，同时使得中心射影成为双射.
1、平面上两直线间的中心射影 定义1.1
: l l'
O投射中心(O l l ') OP 投射线 P' l 上的点P在l'上的像 P l' 上的点P'在l上的像 因此 ，φ–1: l' → l是 l' 到 l 的中心射影 三个特殊的点： X=l×l' 自对应点(不变点) OU//l', 与l'不相交， U为l上的影消点 OV'//l, 与l不相交， V'为l'上的影消点 影消点的存在，导致两直线间的中心射影不是一个双射!
§1.1 拓广平面
一、中心射影
1、平面上两直线间的中心射影 定义1.1
: l l'
2、平面到平面的中心射影
定义1.2
: '
}
均不是双射
中心射影不是双射的原因：存在影消点、影消线
存在影消点、影消线的原因：平行的直线没有交点
如何使得中心射影成为一个双射？
课 程 概 论
一、高等几何的内容 二、高等几何的方法 综合法
给定公理系统(一套相互独立、 无矛盾、完备的命题系统)，演 绎出全部内容 形、数结合，利用代数、分析 的方法研究问题 以解析法为主，兼用综合法
解析法 本课程
课 程 概 论
一、高等几何的内容 二、高等几何的与方法 三、开课目的
• 学习射影几何，拓展几何空间概念，引入几何变换 知识，接受变换群思想 • 训练理性思维、抽象思维、逻辑推理能力，增强数 学审美意识，提高数学修养 • 新颖性，趣味性，技巧性，反馈于初等几何和其他 学科，提高观点，加深理解，举一反三
区别起见，称平面上原有的点为有穷远点(通常点)，记作P
约定1.1 (3) 按约定(1), (2)添加无穷远点之后，平面上全体 无穷远点构成一条直线，称为无穷远直线(理想直线)，记作l∞ 区别起见，称平面上原有的直线为有穷远直线(通常直线)，l 总结：在平面上添加无穷远元素之后，没有破坏点与直线 的关联关系，同时使得中心射影成为双射.
1、平面上两直线间的中心射影 定义1.1
: l l'
O投射中心(O l l ') OP 投射线 P' l 上的点P在l'上的像 P l' 上的点P'在l上的像 因此 ，φ–1: l' → l是 l' 到 l 的中心射影 三个特殊的点： X=l×l' 自对应点(不变点) OU//l', 与l'不相交， U为l上的影消点 OV'//l, 与l不相交， V'为l'上的影消点 影消点的存在，导致两直线间的中心射影不是一个双射!
最新人教版高中数学必修三几何概型课件(公开课)(28张PPT)幻灯片
（2）x的取值是区间[1,4]中的实数，任取一 个x的值，求 “取得值大于2”的概率。
1
2
34
几何概型 P = 2/3
总长度3
• 问题3：有根绳子长为3米，拉直后 任意剪成两段，每段不小于1米的 概率是多少？
P（A)=1/3
思考：怎么把随机事件转化为线段？
四、例题讲解
例1.某人午觉醒来，发现表停了，他打开 收音机想听电台整点报时，求他等待
解: 设A= 等待的时间不多于10分钟
则事件A发生恰好是打开收音机的 时刻位于[50，60]时间段内，因此 由几何概型的求概率公式得
P（A）= 60-50 60
1 =
6
即“等待报时的时间不多于10分钟”的概率为
1 6
.
点评:
0
10
20
30 40
50
60
打开收音机的时刻X是随机的，可以是0~60 之间的任何时刻，且是等可能的．我们称X服从[0， 60]上的均匀分布，X称为[0，60]上的均匀随机数.
每箭都能中靶,且射中靶面内任一点都是等可能的, 请问射中黄心的概率是多少?
不是为古典概 型？
设“射中黄心”为事件A
P(A)试验A全 对部 应结 区果 域构 的 的成 面 面区 积 积 1域 100
几何概型定义 如果每个事件发生的概率只与构成该事
件区域的长度（面积和体积）成比例，则称 这样的概率模型为几何概率模型，简称几何 概型。
几何概型的特点:
(1)基本事件有无限多个; (2)基本事件发生是等可能的.
在几何概型中,事件A的概率的计算公式如下
P (A ) 全 部 构 结 成 果 事 所 件 构 A 的 成 区 的 域 区 长 域 度 长 （ 度 面 （ 积 面 或 积 体 或 积 体 ） 积 ）
1
2
34
几何概型 P = 2/3
总长度3
• 问题3：有根绳子长为3米，拉直后 任意剪成两段，每段不小于1米的 概率是多少？
P（A)=1/3
思考：怎么把随机事件转化为线段？
四、例题讲解
例1.某人午觉醒来，发现表停了，他打开 收音机想听电台整点报时，求他等待
解: 设A= 等待的时间不多于10分钟
则事件A发生恰好是打开收音机的 时刻位于[50，60]时间段内，因此 由几何概型的求概率公式得
P（A）= 60-50 60
1 =
6
即“等待报时的时间不多于10分钟”的概率为
1 6
.
点评:
0
10
20
30 40
50
60
打开收音机的时刻X是随机的，可以是0~60 之间的任何时刻，且是等可能的．我们称X服从[0， 60]上的均匀分布，X称为[0，60]上的均匀随机数.
每箭都能中靶,且射中靶面内任一点都是等可能的, 请问射中黄心的概率是多少?
不是为古典概 型？
设“射中黄心”为事件A
P(A)试验A全 对部 应结 区果 域构 的 的成 面 面区 积 积 1域 100
几何概型定义 如果每个事件发生的概率只与构成该事
件区域的长度（面积和体积）成比例，则称 这样的概率模型为几何概率模型，简称几何 概型。
几何概型的特点:
(1)基本事件有无限多个; (2)基本事件发生是等可能的.
在几何概型中,事件A的概率的计算公式如下
P (A ) 全 部 构 结 成 果 事 所 件 构 A 的 成 区 的 域 区 长 域 度 长 （ 度 面 （ 积 面 或 积 体 或 积 体 ） 积 ）
大学高等几何课件第二讲
x2 y2 例 . 求 圆 2 + 2 =1的 积 题 椭 面 。 a b
′ b x = x 2 2 ： 取 射 换 椭 变 圆 2 解 选 仿 变 a 将 圆 成 x′ + y′ = b . y′ = y S椭圆 S∆OAB 因 面 之 是 射 变 ， 为 积 比 仿 不 量 故 = , S圆 S∆OA′B ab 所 S椭圆 = 2 ⋅πb2 = π ab. 以 b
推论1 仿 变 下 何 对 应 边 面 之 等 推论1 在 射 换 , 任 一 对 多 形 积 比 于 数换 话 , 任 两 多 形 积 比 仿 不 常 . 句 说 意 个 边 面 之 是 射 变 量 . 推论2 仿 变 下 意 条 闭 曲 所 成 面 推论2 在 射 换 , 任 两 封 凸 线 围 的 积 比 仿 不 量 之 是 射 变 .
α1 β1
α2 a1 − a0 = b − b0 β2 1
a2 − a0 b2 − b0
≠ 0.
最 一 等 不 于 是 为 共 的 点 后 个 式 等 零 因 不 线 三 ′ 不 线 O, E , E2的 O′, E′, E2也 共 。 像 1 1
射 换 特 仿 变 的 例 x′ = ax, 1. 位 变 (a ≠ 0) 似 换 y′ = ay x′ = x, 2. x轴 的 匀 缩 换 (a > 0). 上 均 伸 变 y′ = ay 当 =1 为 等 换 a 时 恒 变 . x′ = x, 过 缩 换 例 ， x2 + y2 = a2经 伸 变 如 圆 b (a > 0, b > 0)后 y′ = a y, x′2 y′2 变 椭 为 圆 2 + 2 =1. a b 3. 运 变 （ 移 旋 或 移 旋 的 统 为 动 动 换 平 ， 转 平 与 转 积 称 运 ） x′ = x cosθ − y sinθ +α0 y′ = x sinθ + y cosθ + β0 x′ = x 4. 关 x轴 反 于 的 射 y′ = −y
《高数空间解析几何》PPT课件
类似地， 方程 f( y , z)= 0在空间表示以 yoz 坐标面上的 曲线为准线，平行于 x 轴的直线为母线的柱面. 方程 f( x , z)= 0在空间表示以 xoz 坐标面上的曲线为准线， 平行于 y 轴的直线为母线的柱面.
8
椭圆柱面：
z
x2 a2
y2 b2
1
xoy 坐标面上的椭圆为准线、
3
P26例 5
xoz 坐标面上的双曲线
x2 a2
z2 c2
1分别绕 x、z 轴旋
转一周，求所得旋转曲面方程
x2 y2y2 z2
绕 x 轴转所得曲面称为旋转双叶双曲面,
z
曲面方程为
x2 y2 z2 a2 c2 c2 1
o
x
绕 z 轴转所得曲面称为旋转单叶双曲面,
z
曲面方程为
x2 y2 z2 a2 a2 c2 1
曲面讨论的两个基本问题： （1）已知曲面的形状，建立这曲面的方程； （2）已知方程 F(x, y, z) =0，研究这方程的图形；
二、旋转曲面 一条平面曲线 C 绕其平面上 一条直线 L 旋转所形成的曲面，称为旋转曲面 . 定直线 L 称为旋转轴.
1
建立 y oz 面上曲线 C : f ( y , z ) = 0绕 z 轴旋转所成
例
求曲线
:
x2
x
2
y2 y2
z2 8y
64
,
在 xoy, y0z 坐标面上的投影曲线的方程.
解 关于xo y 坐标面的投影
柱面方程 x 2 y 2 8 y
因而曲线 在 xo y 坐标
面上的投影曲线是圆.
1
y 0
y2 z2
b2
c2
8
椭圆柱面：
z
x2 a2
y2 b2
1
xoy 坐标面上的椭圆为准线、
3
P26例 5
xoz 坐标面上的双曲线
x2 a2
z2 c2
1分别绕 x、z 轴旋
转一周，求所得旋转曲面方程
x2 y2y2 z2
绕 x 轴转所得曲面称为旋转双叶双曲面,
z
曲面方程为
x2 y2 z2 a2 c2 c2 1
o
x
绕 z 轴转所得曲面称为旋转单叶双曲面,
z
曲面方程为
x2 y2 z2 a2 a2 c2 1
曲面讨论的两个基本问题： （1）已知曲面的形状，建立这曲面的方程； （2）已知方程 F(x, y, z) =0，研究这方程的图形；
二、旋转曲面 一条平面曲线 C 绕其平面上 一条直线 L 旋转所形成的曲面，称为旋转曲面 . 定直线 L 称为旋转轴.
1
建立 y oz 面上曲线 C : f ( y , z ) = 0绕 z 轴旋转所成
例
求曲线
:
x2
x
2
y2 y2
z2 8y
64
,
在 xoy, y0z 坐标面上的投影曲线的方程.
解 关于xo y 坐标面的投影
柱面方程 x 2 y 2 8 y
因而曲线 在 xo y 坐标
面上的投影曲线是圆.
1
y 0
y2 z2
b2
c2
大学高等几何课件第七讲
例如: 例如: 最 单 最 价 的 全 面 图 由 个 共 的 和 简 且 有 值 完 平 构 是 三 不 线 点 它 们 连 所 成 完 三 形 及 三 不 点 直 和 们 的 线 构 的 全 点 以 由 条 共 的 线 它 的 交 所 成 完 三 形 在 一 这 图 中 有 11 = 3个 和 点 构 的 全 线 . 每 个 种 形 都 a 点 a22 = 3条 线 及 每 点 有 12 = 2条 线 在 一 直 上 直 以 在 一 上 a 直 , 每 条 线 有 3 a21 = 2个 , 其 示 阵 点 表 矩 为 2 2 . 3
两 三 形 三 对 的 点 线 三 对 点 对偶定理: 设 个 角 中 双 边 交 共 ,则 对 顶 的 线 点 联 共 . 德 格 理 其 偶 理 射 几 中 有 其 要 地 .它 萨 定 及 对 定 在 影 何 占 极 重 的 位 表 述 两 三 (线 形 于 视 态 的 何 征 利 射 的 点 把 了 个 点 ) 处 透 状 下 几 特 ; 用 影 观 可 德 格 理 其 偶 理 造 各 不 形 的 等 何 理 萨 定 及 对 定 改 成 种 同 式 初 几 定 .
比 这 式得 较 三 , R = αA− βB = −(α′A′ − β′B′), P = βB −γC = −(β′B′ −γ ′ ′), C Q = γC −αA = −(γ ′ ′ −α′A′). C
从 1)式 A− βB = −(α′A′ − β′B′)左 观 , 它 表 点 和 联 上 一 ; ( α 端 之 代 两 A B 线 的 点 从 端 之 它 表 点 ′和 ′联 上 一 , 所 它 表 和 ′B′的 点 右 观 , 代 两 A B 线 的 点 以 代 AB A 交 R. 其 类 . 余 推 由 三 P, Q, R的 标 量 有 显 线 相 式: 于 点 坐 矢 间 明 的 性 关 P + Q + R = 0, 故 , Q, R三 共 . P 点 线 证 既 用 两 三 形 面 场 , 适 于 们 共 的 注: 此 法 适 于 个 角 共 的 合 也 用 它 不 面 场 . 合
高中数学立体几何知识点PPT课件
创设情境 兴趣导入
观察平静的湖面、窗户的玻璃面、黑板面、课桌面、
9.
墙面等，发现它们都有一个共同的特征：平坦、光滑，
1
给我们以平面的形象，但是它们都是有限的．
平
面
的
基
本
性
质
第1页/共144页
动脑思考 探索新知
平面的概念就是从这些场景中抽象出来的．数学中的平面是指光滑
并且可以无限延展的图形．
9. 平静的湖面、窗户的玻璃面、黑板面、课桌面、墙面等，都是平面
面
有其他公共. 点，并且所有公共点的集合是过这个点的 一条直线．
的
性质3：不在同一条直线上的三个点，可以确定一 个平面．
基
本
性
质
第17页/共144页
自我反思 目标检测
学习方法
学习行为
学习效果
9.
1
平 面 的 基 本 性 质
第18页/共144页
第九章 立体几何
9．2 直线与直线、直线与平面、平面与平面平行的判定与性质
内且m ∥ 则 m ∥ l ．
9.2 直线与直线、直线与平面、平面与平面平行的判定与性质
第36页/共144页
巩固知识 典型例题
例3 在如图所示的一块木料中，已知 BC∥平面 A1C1，BC∥ B1C1 ， 要经过平面 A1C1内的一点P与棱BC将木料锯开，应当怎样画线？ 解 画线的方法是： 在平面A1B1C1D1内， 过点P作直线B1C1的平行线EF， 分别交直线A1B1及直线D1C1与点E、F， 连接EB和FC．
面
公共点的集合就是这两个墙面的交线．
的
基
本
性
质
第8页/共144页
动脑思考 探索新知
观察平静的湖面、窗户的玻璃面、黑板面、课桌面、
9.
墙面等，发现它们都有一个共同的特征：平坦、光滑，
1
给我们以平面的形象，但是它们都是有限的．
平
面
的
基
本
性
质
第1页/共144页
动脑思考 探索新知
平面的概念就是从这些场景中抽象出来的．数学中的平面是指光滑
并且可以无限延展的图形．
9. 平静的湖面、窗户的玻璃面、黑板面、课桌面、墙面等，都是平面
面
有其他公共. 点，并且所有公共点的集合是过这个点的 一条直线．
的
性质3：不在同一条直线上的三个点，可以确定一 个平面．
基
本
性
质
第17页/共144页
自我反思 目标检测
学习方法
学习行为
学习效果
9.
1
平 面 的 基 本 性 质
第18页/共144页
第九章 立体几何
9．2 直线与直线、直线与平面、平面与平面平行的判定与性质
内且m ∥ 则 m ∥ l ．
9.2 直线与直线、直线与平面、平面与平面平行的判定与性质
第36页/共144页
巩固知识 典型例题
例3 在如图所示的一块木料中，已知 BC∥平面 A1C1，BC∥ B1C1 ， 要经过平面 A1C1内的一点P与棱BC将木料锯开，应当怎样画线？ 解 画线的方法是： 在平面A1B1C1D1内， 过点P作直线B1C1的平行线EF， 分别交直线A1B1及直线D1C1与点E、F， 连接EB和FC．
面
公共点的集合就是这两个墙面的交线．
的
基
本
性
质
第8页/共144页
动脑思考 探索新知
高中数学立体几何PPT课件
目录
旋转 体
(1)圆柱可以由____矩__形____绕其任一边所在直线旋 转得到． (2)圆锥可以由直角三角形绕其____直__角__边____所在 直线旋转得到． (3)圆台可以由直角梯形绕___直__角__腰___所在直线或 等腰梯形绕_上__、__下__底__中__点__连__线___旋转得到，也可 由___平__行__于__底__面____的平面截圆锥得到． (4)球可以由半圆或圆绕__地，它的水平放置的平面图形的斜二测直 观图是直角梯形(如图)，∠ABC＝45°，AB＝AD＝1，DC⊥ BC，则这块菜地的面积为________．
答案：2＋
2 2
目录
5．(2011·高考北京卷改编)某四面体的三视图如图所示，该四 面体四个面的面积中最大的是________．
目录
3．(教材习题改编)有下列四个命题：
①底面是矩形的平行六面体是长方体；
②棱长相等的直四棱柱是正方体；
③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体；
④对角线相等的平行六面体是直平行六面体．
其中真命题的个数是( )
A．1
B．2
C．3
D．4
目录
解析：选A.命题①不是真命题，因为底面是矩形，但侧棱不 垂直于底面的平行六面体不是长方体； 命题②不是真命题， 因为底面是菱形(非正方形)，底面边长与侧棱长相等的直四棱 柱不是正方体；命题③也不是真命题，因为有两条侧棱都垂 直于底面一边不能推出侧棱与底面垂直；命题④是真命题， 由对角线相等，可知平行六面体的对角面是矩形，从而推得 侧棱与底面垂直，故平行六面体是直平行六面体．
目录
解析：
将三视图还原成几何体的直观图如图所示． 它的四个面的面积分别为 8,6,10,6 2，故面积最大的应为 10.
旋转 体
(1)圆柱可以由____矩__形____绕其任一边所在直线旋 转得到． (2)圆锥可以由直角三角形绕其____直__角__边____所在 直线旋转得到． (3)圆台可以由直角梯形绕___直__角__腰___所在直线或 等腰梯形绕_上__、__下__底__中__点__连__线___旋转得到，也可 由___平__行__于__底__面____的平面截圆锥得到． (4)球可以由半圆或圆绕__地，它的水平放置的平面图形的斜二测直 观图是直角梯形(如图)，∠ABC＝45°，AB＝AD＝1，DC⊥ BC，则这块菜地的面积为________．
答案：2＋
2 2
目录
5．(2011·高考北京卷改编)某四面体的三视图如图所示，该四 面体四个面的面积中最大的是________．
目录
3．(教材习题改编)有下列四个命题：
①底面是矩形的平行六面体是长方体；
②棱长相等的直四棱柱是正方体；
③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体；
④对角线相等的平行六面体是直平行六面体．
其中真命题的个数是( )
A．1
B．2
C．3
D．4
目录
解析：选A.命题①不是真命题，因为底面是矩形，但侧棱不 垂直于底面的平行六面体不是长方体； 命题②不是真命题， 因为底面是菱形(非正方形)，底面边长与侧棱长相等的直四棱 柱不是正方体；命题③也不是真命题，因为有两条侧棱都垂 直于底面一边不能推出侧棱与底面垂直；命题④是真命题， 由对角线相等，可知平行六面体的对角面是矩形，从而推得 侧棱与底面垂直，故平行六面体是直平行六面体．
目录
解析：
将三视图还原成几何体的直观图如图所示． 它的四个面的面积分别为 8,6,10,6 2，故面积最大的应为 10.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
点集拓扑 代数拓扑 解析拓扑
分形几何
微分拓扑 微分流形 纤维丛
11
五、课程简介
• 周学时2，一个学期，学习第一章～第五章
• 主要参考书：
•梅向明、门淑惠等编《高等几何》,高等教育出版社出版， 2008年; • 朱德祥、朱维宗等编《高等几何》（第二版）,高等教育出 版社出版，2010年; •罗崇善编《高等几何》,高等教育出版社出版,1999年6月； •朱德祥、李忠映、徐学钰等编《高等几何习题解答》。 •周兴和编《高等几何》，科学出版社，2010年
• 学习射影几何，拓展几何空间概念，引入几何变换 知识，接受变换群思想
• 训练理性思维、抽象思维、逻辑推理能力，增强数 学审美意识，提高数学修养
• 新颖性，趣味性，技巧性，反馈于初等几何和其他 学科，提高观点，加深理解，举一反三
8
四、几何的发展历史线索
射影几何学是一切的几何学 ──[英] Cayley
教师授课助手 学生自修向导——
高等几何多媒体课件
1
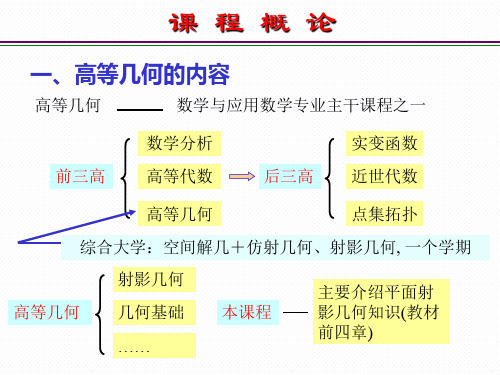
课程概论
一、高等几何的内容
高等几何
数学与应用数学专业主干课程之一
前三高
数学分析 高等代数
后三高
实变函数 近世代数
高等几何
点集拓扑
综合大学：空间解几＋仿射几何、射影几何, 一个学期
高等几何
射影几何 几何基础 ……
本课程
主要介绍平面射 影几何知识(教材 前五章)
这个对应称为 a1到an 的仿射对应。
记作： nn1 L 21
19
直线间的仿射对应
如图所示：
20
平面间的仿射对应
21
二、性质
（1）保持同素性和结合性； （2）保持共线三点的单比不变； （3）保持直线的平行性不变。 注：仿射对应下，对应点的连线不一定平行。
为什么？
22
定义2.2 若两个平面间的一个点对应（变换）保持同素 性、结合性和共线三点的单比不变，则这个点对应（变 换）称为仿射对应（变换）
代数法 代数几何 代数曲面 代数族 域上多胞形
微分几何
(19世纪)
（分析方法）
张量分析 微分流形、黎曼流形、复流形 大范围微分几何
射影几何
(19世纪)
（综合法、爱尔 兰根纲领代数法）
仿射几何 画法几何
10
四、几何的发展历史线索
罗氏几何 非欧几何 （19世纪） 黎曼几何
拓扑学
（几何与代数、 分析相结合， 多样化发展）
1)设 P1, P2 , P 为共线三点
P1
P2
P
称
( P1P2 P)
P1P P2 P
为共线三点 P1, P2 , P
的单比，P1, P2 叫基点
P 叫分点。
uuur uuur P1P, P2P 是有向线段 P1P, P2P 的数量
2). 符号
17
§ 1 透视仿射对应
3）单比与定比的区别
(P1P2P)表示一个数, 是有向线段P1P与P2P的比值, 与解几中的定比
称为透视仿射对应。 注：透视仿射对应与L的方向无关。若a与b相交，交 点称为自对应点。
14
两条直线间的透视仿射对应
a
C B A
o L
A/ B/ C/
b
特征：对应点的连线互相平行
15
两个平面间的透视仿射对应
A1 B1
C1
1
M
A
BC
L
特征：对应点的连线互相平行
16
第一章、仿射坐标与仿射变换
2、单比
2
课程概论
一、高等几何的内容 什么是射影几何？
直观描述
鸟瞰下射影几何
十九世纪名言
一切几何学都是射影几何
3
欧氏几何(初等几何)
研究图形在“搬动”之下保持不变的性质和数 量(统称不变性，如距离、角度、面积、体积等)
搬动
正交变换
对图形作有限次的平移、 旋转、轴反射的结果
欧氏几何
例１、平行四边形经仿射（对应）变换仍变为平行 四边形 例２、两平行线段之比经仿射对应不变 例３、仿射对应保持平形性不变
23
1.3 仿射坐标系
１、定义 笛卡尔坐标系在仿射对应下的像叫做
仿射坐标系， (x', y') 叫点 P' 的仿射坐标
记为 P' (x', y' )
２、设共线三点 P1, P2, P3 的仿射坐标为
分点反号. 二、性质
1、保同素性和结合性 2、保单比不变
3、保平行性
18
•1.2 仿射对应与仿射变换
一、概念
设同一平面内有n条直线，a1, a2 ,L , an 如下图 1,2 ,L ,n 是 a1到a2, a2到a3,L , an1到an 的透视仿射对应
经过这一串对应，得到 a1到an 的透视仿射对应，
非欧几何
经验几何
演绎化
论证几何 （欧氏几何）
（远古─元前600年）
（元前600年─ 400年）
积累了丰富的 经验，但未上 升成系统理论
埃及几何跟希腊逻辑 方法相结合，以抽象 化、逻辑化为特点
几何基础 （公理几何）
解析几何
微分几何
射影几何
拓扑学
9
四、几何的发展历史线索
代数曲线
解析几何
(17世纪)
（坐标法）
(x1, y1), (x2 , y2 ), (x3, y3)
则单比为
( p1, p2 , p3 )
x3 x1 x3 x2
y3 y1 y3 y2
24
25
3、仿射变换的坐标表示
• 已知仿射坐标：{o, e1, e2} 仿射变换为:T
• 变换将 ： {o, e1, e2} {o', e1' , e2' }
12
第一章 仿射坐标与仿射变换
本章地位 本章内容
学习射影几何的基础
阐明仿射变换的概念，研 究仿射变换的不变量与不 变性质。
学习注意
仿射变换在初等几何中的 应用
13
第一章、仿射坐标与仿射变换
1.1 透视仿射对应
一、概念 1、同一平面内两直线a到b间的透视对应，
设L为平面上另外一直线,a与 b不平行。过a上的点A, B,CL 作与L平行的直线与b交于 A', B', C ',L即得a到b的一个一一映射，
射影变换将彻底改变我们原有的几何
空间观念！
6
课程概论
一、高等几何的内容
二、高等几何的方法
综合法
给定公理系统(一套相互独立、 无矛盾、完备的命题系统)，演 绎出全部内容
解析法
形、数结合，利用代数、分析 的方法研究问题
本课程
以解析法为主，兼用综合法
7
课程概论
一、高等几何的内容 二、高等几何的方法 三、开课目的
研究图形的 正交变换不变性的科学
4
仿射几何
平行射影
透视仿射变换
有限次平行射影的结果
仿射变换
仿射几何 仿射不变性
研究图形的
仿射变换不变性的科学
比如——平行性、两平行 线段的比等等
5
射影几何
中心射影
透视变换
有限次中心射影的结果
射影变换
射影几何
研究图形的 射影变换不变性的科学
射影不变性
比如——几条直线共点、 几个点共线等等