直角三角形存在性问题专项训练(一)

直角三角形的性质练习题一、选择题1. 在直角三角形ABC中，角A为90°，且满足AB = 3，AC = 4，BC = 5，那么∠B的度数是：A) 30°B) 45°C) 60°D) 90°2. 直角三角形PQR中，∠P = 90°，PR = 5，RQ = 12，那么∠Q的度数是：A) 30°B) 45°C) 60°D) 90°3. 若一个直角三角形的一个锐角的度数是30°，那么另一个锐角的度数是：A) 30°B) 45°C) 60°D) 90°4. 若三角形ABC是直角三角形，其中∠A = 90°，AB = 8，AC = 15，则BC的长度为：A) 7B) 9C) 17D) 245. 直角三角形XYZ中，∠X = 90°，XY = 5，YZ = 12，则∠Y的正弦值是：A) 5/12B) 12/13C) 5/13D) 12/5二、填空题1. 直角三角形ABC中，∠C = 90°，AC = 7，BC = 24，则AB的长度为 ________。

2. 设直角三角形XYZ中，∠Y = 90°，XY = 6，则YZ的长度为________。

3. 直角三角形PQR中，PR = 5，RQ = 12，则∠P的度数为________。

4. 若直角三角形ABC中，∠B = 90°，AB = 14，则AC的长度为________。

5. 若直角三角形XYZ中，∠Y = 90°，XY = 9，则∠Z的度数为________。

三、解答题1. 已知直角三角形ABC，其中∠A = 90°，AB = 5，AC = 12，求BC的长度。

解析：根据直角三角形的性质，可使用勾股定理求解。

根据勾股定理，若AC、BC、AB分别表示直角三角形ABC的三条边的长度，则有AC² = AB² + BC²。

直角三角形存在性问题1．如图1，在平面直角坐标系中，直线y＝﹣x+m与y轴交于点B，与x轴交于点C，OC＝8，直线y＝kx+n经过点B与x轴负半轴交于点A，13 AOBO，（1）求直线AB的解析式；（2）如图2，以线段AB为斜边作等腰直角三角形ABD（点D在y轴右侧），直线OD 与BC交于E，求点E的坐标；2．如图，一次函数y1＝x+n与x轴交于点B，一次函数y2＝﹣x+m与y轴交于点C，且它们的图象都经过点D（1，﹣）．（1）则点B的坐标为，点C的坐标为；（2）在x轴上有一点P（t，0），且t＞，如果△BDP和△CDP的面积相等，求t的值；（3）在（2）的条件下，在y轴的右侧，以CP为腰作等腰直角△CPM，直接写出满足条件的点M的坐标．3．[模型建立]（一线三等角）（1）如图1，等腰Rt△ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过点A 作AD⊥ED于点D，过点B作BE⊥ED于点E，求证：△BEC≌△CDA；[模型应用]（2）如图2，直线l1：y＝x+4与坐标轴交于点A、B，直线l2经过点A与直线l1垂直，求直线l2的函数表达式．（3）如图3，平面直角坐标系内有一点B（6，﹣8），过点B作BA⊥x轴于点A、BC⊥y轴于点C，点P是线段AB上的动点，点D是直线y＝﹣2x+2上的动点且在第四象限内．若△CPD成为等腰直角三角形，请直接写出点D的坐标．4．如图，直线l1：y＝x和直线l2：y＝kx+3交于点A（2，2），P（t，0）是x轴上一动点，过点P作平行于y轴的直线，使其与直线l1和直线l2分别交于点D，E．（1）求k的值．（2）用t表示线段DE的长．（3）点M是y轴上一动点，当△MDE是等腰直角三角形时，求出t的值及点M的坐标．。

中考数学复习---二次函数中三角形存在性问题压轴题练习（含答案解析）一．相似三角形的存在性1．（2022•陕西）已知抛物线y＝ax2+bx﹣4经过点A（﹣2，0），B（4，0），与y 轴的交点为C．（1）求该抛物线的函数表达式；（2）若点P是该抛物线上一点，且位于其对称轴l的右侧，过点P分别作l，x 轴的垂线，垂足分别为M，N，连接MN．若△PMN和△OBC相似，求点P的坐标．【解答】解：（1）把A（﹣2，0），B（4，0）代入y＝ax2+bx﹣4得：，解得，∴抛物线的函数表达式为y＝x2﹣x﹣4；（2）如图：∵y＝x2﹣x﹣4＝（x﹣1）2﹣，∴抛物线y＝x2﹣x﹣4的对称轴是直线x＝1，在y＝x2﹣x﹣4中，令x＝0得y＝﹣4，∴C（0，﹣4），∴OB＝OC＝4，∴△BOC是等腰直角三角形，∵△PMN和△OBC相似，∴△PMN是等腰直角三角形，∵PM⊥直线x＝1，PN⊥x轴，∴∠MPN＝90°，PM＝PN，设P（m，m2﹣m﹣4），∴|m﹣1|＝|m2﹣m﹣4|，∴m﹣1＝m2﹣m﹣4或m﹣1＝﹣m2+m+4，解得m＝+2或m＝﹣+2或m＝或m＝﹣，∵点P是该抛物线上一点，且位于其对称轴直线x＝1的右侧，∴P的坐标为（+2，+1）或（，1﹣）．2．（2022•绵阳）如图，抛物线y＝ax2+bx+c交x轴于A（﹣1，0），B两点，交y轴于点C（0，3），顶点D的横坐标为1．（1）求抛物线的解析式；（2）在y轴的负半轴上是否存在点P使∠APB+∠ACB＝180°，若存在，求出点P的坐标，若不存在，请说明理由；（3）过点C作直线l与y轴垂直，与抛物线的另一个交点为E，连接AD，AE，DE，在直线l下方的抛物线上是否存在一点M，过点M作MF⊥l，垂足为F，使以M，F，E三点为顶点的三角形与△ADE相似？若存在，请求出M点的坐标，若不存在，请说明理由．【解答】解：（1）∵顶点D的横坐标为1，∴抛物线的对称轴为直线x＝1，∵A（﹣1，0），∴B（3，0），∴设抛物线的解析式为：y＝a（x+1）（x﹣3），将C（0，3）代入抛物线的解析式，则﹣3a＝3，解得a＝﹣1，∴抛物线的解析式为：y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3．（2）存在，P（0，﹣1），理由如下：∵∠APB+∠ACB＝180°，∴∠CAP+∠CBP＝180°，∴点A，C，B，P四点共圆，如图所示，由（1）知，OB＝OC＝3，∴∠OCB＝∠OBC＝45°，∴∠APC＝∠ABC＝45°，∴△AOP是等腰直角三角形，∴OP＝OA＝1，∴P（0，﹣1）．（3）存在，理由如下：由（1）知抛物线的解析式为：y＝﹣x2+2x+3，∴D（1，4），由抛物线的对称性可知，E（2，3），∵A（﹣1，0），∴AD＝2，DE＝，AE＝3．∴AD2＝DE2+AE2，∴△ADE是直角三角形，且∠AED＝90°，DE：AE＝1：3．∵点M在直线l下方的抛物线上，∴设M（t，﹣t2+2t+3），则t＞2或t＜0．∴EF＝|t﹣2|，MF＝3﹣（﹣t2+2t+3）＝t2﹣2t，若△MEF与△ADE相似，则EF：MF＝1：3或MF：EF＝1：3，∴|t﹣2|：（t2﹣2t）＝1：3或（t2﹣2t）：|t﹣2|＝1：3，解得t＝2（舍）或t＝3或﹣3或（舍）或﹣，∴M的坐标为（3，0）或（﹣3，﹣12）或（﹣，）．综上，存在点M，使以M，F，E三点为顶点的三角形与△ADE相似，此时点M的坐标为（3，0）或（﹣3，﹣12）或（﹣，）．3．（2022•恩施州）在平面直角坐标系中，O为坐标原点，抛物线y＝﹣x2+c与y 轴交于点P（0，4）．（1）直接写出抛物线的解析式．（2）如图，将抛物线y＝﹣x2+c向左平移1个单位长度，记平移后的抛物线顶点为Q，平移后的抛物线与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C．判断以B、C、Q三点为顶点的三角形是否为直角三角形，并说明理由．（3）直线BC与抛物线y＝﹣x2+c交于M、N两点（点N在点M的右侧），请探究在x轴上是否存在点T，使得以B、N、T三点为顶点的三角形与△ABC相似，若存在，请求出点T的坐标；若不存在，请说明理由．（4）若将抛物线y＝﹣x2+c进行适当的平移，当平移后的抛物线与直线BC最多只有一个公共点时，请直接写出抛物线y＝﹣x2+c平移的最短距离并求出此时抛物线的顶点坐标．【解答】解：（1）∵抛物线y＝﹣x2+c与y轴交于点P（0，4），∴c＝4，∴抛物线的解析式为y＝﹣x2+4；（2）△BCQ是直角三角形．理由如下：将抛物线y＝﹣x2+4向左平移1个单位长度，得新抛物线y＝﹣（x+1）2+4，∴平移后的抛物线顶点为Q（﹣1，4），令x＝0，得y＝﹣1+4＝3，∴C（0，3），令y＝0，得﹣（x+1）2+4＝0，解得：x1＝1，x2＝﹣3，∴B（﹣3，0），A（1，0），如图1，连接BQ，CQ，PQ，∵P（0，4），Q（﹣1，4），∴PQ⊥y轴，PQ＝1，∵CP＝4﹣3＝1，∴PQ＝CP，∠CPQ＝90°，∴△CPQ是等腰直角三角形，∴∠PCQ＝45°，∵OB＝OC＝3，∠BOC＝90°，∴△BOC是等腰直角三角形，∴∠BCO＝45°，∴∠BCQ＝180°﹣45°﹣45°＝90°，∴△BCQ是直角三角形．（3）在x轴上存在点T，使得以B、N、T三点为顶点的三角形与△ABC相似．∵△ABC是锐角三角形，∠ABC＝45°，∴以B、N、T三点为顶点的三角形与△ABC相似，必须∠NBT＝∠ABC＝45°，即点T在y轴的右侧，设T（x，0），且x＞0，则BT＝x+3，∵B（﹣3，0），A（1，0），C（0，3），∴∠ABC＝45°，AB＝4，BC＝3，设直线BC的解析式为y＝kx+b，则，解得：，∴直线BC的解析式为y＝x+3，由，解得：，，∴M（﹣，），N（，），∴BN＝×＝，①当△NBT∽△CBA时，则＝，∴＝，解得：x＝，∴T（，0）；②当△NBT∽△ABC时，则＝，∴＝，解得：x＝，∴T（，0）；综上所述，点T的坐标T（，0）或（，0）．（4）抛物线y＝﹣x2+4的顶点为P（0，4），∵直线BC的解析式为y＝x+3，∴直线BC与y轴的夹角为45°，当抛物线沿着垂直直线BC的方向平移到只有1个公共点时，平移距离最小，此时向右和向下平移距离相等，设平移后的抛物线的顶点为P′（t，4﹣t），则平移后的抛物线为y＝﹣（x﹣t）2+4﹣t，由﹣（x﹣t）2+4﹣t＝x+3，整理得：x2+（1﹣2t）x+t2+t﹣1＝0，∵平移后的抛物线与直线BC最多只有一个公共点，∴Δ＝（1﹣2t）2﹣4（t2+t﹣1）＝0，解得：t＝，∴平移后的抛物线的顶点为P′（，），平移的最短距离为．二．直角三角形的存在性4．（2022•广安）如图，在平面直角坐标系中，抛物线y＝ax2+x+m（a≠0）的图象与x轴交于A、C两点，与y轴交于点B，其中点B坐标为（0，﹣4），点C 坐标为（2，0）．（1）求此抛物线的函数解析式．（2）点D是直线AB下方抛物线上一个动点，连接AD、BD，探究是否存在点D，使得△ABD的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由．（3）点P为该抛物线对称轴上的动点，使得△P AB为直角三角形，请求出点P 的坐标．【解答】解：（1）∵抛物线y＝ax2+x+m（a≠0）的图象经过点B（0，﹣4），点C（2，0），∴，解得，∴抛物线的解析式为y＝x2+x﹣4；（2）存在．理由：如图1中，设D （t ，t 2+t ﹣4），连接OD ．令y ＝0，则x 2+x ﹣4＝0，解得x ＝﹣4或2，∴A （﹣4，0），C （2，0），∵B （0，﹣4），∴OA ＝OB ＝4，∵S △ABD ＝S △AOD +S △OBD ﹣S △AOB ＝×4×（﹣﹣t +4）+×4×（﹣t ）﹣×4×4＝﹣t 2﹣4t ＝﹣（t +2）2+4，∵﹣1＜0，∴t ＝﹣2时，△ABD 的面积最大，最大值为4，此时D （﹣2，﹣4）； （3）如图2中，设抛物线的对称轴交x 轴于点N ，过点B 作BM ⊥抛物线的对称轴于点M ．则N （﹣1.0）．M （﹣1，﹣4）；∵OA＝OB＝4，∠AOB＝90°，∴∠OAB＝∠OBA＝45°，当∠P1AB＝90°时，△ANP1是等腰直角三角形，∴AN＝NP1＝3，∴P1（﹣1，3），当∠ABP2＝90°时，△BMP2是等腰直角三角形，可得P2（﹣1，﹣5），当∠APB＝90°时，设P（﹣1，n），设AB的中点为J，连接PJ，则J（﹣2，﹣2），∴PJ＝AB＝2，∴12+（n+2）2＝（2）2，解得n＝﹣2或﹣﹣2，∴P3（﹣1，﹣2），P4（﹣1，﹣﹣2），综上所述，满足条件的点P的坐标为（﹣1，3）或（﹣1，﹣5）或（﹣1，﹣2）或（﹣1，﹣﹣2）．5．（2022•辽宁）如图，抛物线y＝ax2﹣3x+c与x轴交于A（﹣4，0），B两点，与y轴交于点C（0，4），点D为x轴上方抛物线上的动点，射线OD交直线AC 于点E，将射线OD绕点O逆时针旋转45°得到射线OP，OP交直线AC于点F，连接DF．（1）求抛物线的解析式；（2）当点D在第二象限且＝时，求点D的坐标；（3）当△ODF为直角三角形时，请直接写出点D的坐标．【解答】解：（1）将点A（﹣4，0），C（0，4）代入y＝ax2﹣3x+c，∴，解得，∴y＝﹣x2﹣3x+4；（2）过点D作DG⊥AB交于G，交AC于点H，设直线AC的解析式为y＝kx+b，∴，解得，∴y＝x+4，设D（n，﹣n2﹣3n+4），H（n，n+4），∴DH＝﹣n2﹣4n，∵DH∥OC，∴＝＝，∵OC＝4，∴DH＝3，∴﹣n2﹣4n＝3，解得n＝﹣1或n＝﹣3，∴D（﹣1，6）或（﹣3，4）；（3）设F（t，t+4），当∠FDO＝90°时，过点D作MN⊥y轴交于点N，过点F作FM⊥MN交于点M，∵∠DOF＝45°，∴DF＝DO，∵∠MDF+∠NDO＝90°，∠MDF+∠MFD＝90°，∴∠NDO＝∠MFD，∴△MDF≌△NOD（AAS），∴DM＝ON，MF＝DN，∴DN+ON＝﹣t，DN＝ON+（﹣t﹣4），∴DN＝﹣t﹣2，ON＝2，∴D点纵坐标为2，∴﹣x2﹣3x+4＝2，解得x＝或x＝，∴D点坐标为（，2）或（，2）；当∠DFO＝90°时，过点F作KL⊥x轴交于L点，过点D作DK⊥KL交于点K，∵∠KFD+∠LFO＝90°，∠KFD+∠KDF＝90°，∴∠LFO＝∠KDF，∵DF＝FO，∴△KDF≌△LFO（AAS），∴KD＝FL，KF＝LO，∴KL＝t+4﹣t＝4，∴D点纵坐标为4，∴﹣x2﹣3x+4＝4，解得x＝0或x＝﹣3，∴D（0，4）或（﹣3，4）；综上所述：D点坐标为（，2）或（，2）或（0，4）或（﹣3，4）．三．等腰三角形的存在性6．（2022•百色）已知抛物线经过A（﹣1，0）、B（0，3）、C（3，0）三点，O 为坐标原点，抛物线交正方形OBDC的边BD于点E，点M为射线BD上一动点，连接OM，交BC于点F．（1）求抛物线的表达式；（2）求证：∠BOF＝∠BDF；（3）是否存在点M，使△MDF为等腰三角形？若不存在，请说明理由；若存在，求ME的长．【解答】（1）解：设抛物线的表达式为y＝ax2+bx+c，把A（﹣1，0）、B（0，3）、C（3，0）代入得：，解得，∴抛物线的表达式为：y＝﹣x2+2x+3；（2）证明：∵正方形OBDC，∴∠OBC＝∠DBC，BD＝OB，∵BF＝BF，∴△BOF≌△BDF，∴∠BOF＝∠BDF；（3）解：∵抛物线交正方形OBDC的边BD于点E，∴令y＝3，则3＝﹣x2+2x+3，解得：x1＝0，x2＝2，∴E（2，3），①如图，当M在线段BD的延长线上时，∠BDF为锐角，∴∠FDM为钝角，∵△MDF为等腰三角形，∴DF＝DM，∴∠M＝∠DFM，∴∠BDF＝∠M+∠DFM＝2∠M，∵BM∥OC，∴∠M＝∠MOC，由（2）得∠BOF＝∠BDF，∴∠BDF+∠MOC＝3∠M＝90°，∴∠M＝30°，在Rt△BOM中，BM＝，∴ME＝BM﹣BE＝3﹣2；②如图，当M在线段BD上时，∠DMF为钝角，∵△MDF为等腰三角形，∴MF＝DM，∴∠BDF＝∠MFD，∴∠BMO＝∠BDF+∠MFD＝2∠BDF，由（2）得∠BOF＝∠BDF，∴∠BMO＝2∠BOM，∴∠BOM+∠BMO＝3∠BOM＝90°，∴∠BOM＝30°，在Rt△BOM中，BM＝，∴ME＝BE﹣BM＝2﹣，综上所述，ME的值为：3﹣2或2﹣．7．（2022•山西）综合与探究如图，二次函数y＝﹣x2+x+4的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．点P是第一象限内二次函数图象上的一个动点，设点P的横坐标为m．过点P作直线PD⊥x轴于点D，作直线BC交PD于点E．（1）求A，B，C三点的坐标，并直接写出直线BC的函数表达式；（2）当△CEP是以PE为底边的等腰三角形时，求点P的坐标；（3）连接AC，过点P作直线l∥AC，交y轴于点F，连接DF．试探究：在点P 运动的过程中，是否存在点P，使得CE＝FD，若存在，请直接写出m的值；若不存在，请说明理由．【解答】解：（1）在y＝﹣x2+x+4中，令x＝0得y＝4，令y＝0得x＝8或x＝﹣2，∴A（﹣2，0），B（8，0），C（0，4），设直线BC解析式为y＝kx+4，将B（8，0）代入得：8k+4＝0，解得k＝﹣，∴直线BC解析式为y＝﹣x+4；（2）过C作CG⊥PD于G，如图：设P（m，﹣m2+m+4），∴PD＝﹣m2+m+4，∵∠COD＝∠PDO＝∠CGD＝90°，∴四边形CODG是矩形，∴DG＝OC＝4，CG＝OD＝m，∴PG＝PD﹣DG＝﹣m2+m+4﹣4＝﹣m2+m，∵CP＝CE，CG⊥PD，∴GE＝PG＝﹣m2+m，∵∠GCE＝∠OBC，∠CGE＝90°＝∠BOC，∴△CGE∽△BOC，∴＝，即＝，解得m＝0（舍去）或m＝4，∴P（4，6）；（3）存在点P，使得CE＝FD，理由如下：过C作CH⊥PD于H，如图：设P（m，﹣m2+m+4），由A（﹣2，0），C（0，4）可得直线AC解析式为y＝2x+4，根据PF∥AC，设直线PF解析式为y＝2x+b，将P（m，﹣m2+m+4）代入得：﹣m2+m+4＝2m+b，∴b＝﹣m2﹣m+4，∴直线PF解析式为y＝2x﹣m2﹣m+4，令x＝0得y＝﹣m2﹣m+4，∴F（0，﹣m2﹣m+4），∴OF＝|﹣m2﹣m+4|，同（2）可得四边形CODH是矩形，∴CH＝OD，∵CE＝FD，∴Rt△CHE≌Rt△DOF（HL），∴∠HCE＝∠FDO，∵∠HCE＝∠CBO，∴∠FDO＝∠CBO，∴tan∠FDO＝tan∠CBO，∴＝，即＝，∴﹣m2﹣m+4＝m或﹣m2﹣m+4＝﹣m，解得m＝2﹣2或m＝﹣2﹣2或m＝4或m＝﹣4，∵P在第一象限，∴m＝2﹣2或m＝4．8．（2022•东营）如图，抛物线y＝ax2+bx﹣3（a≠0）与x轴交于点A（﹣1，0），点B（3，0），与y轴交于点C．（1）求抛物线的表达式；（2）在对称轴上找一点Q，使△ACQ的周长最小，求点Q的坐标；（3）点P是抛物线对称轴上的一点，点M是对称轴左侧抛物线上的一点，当△PMB是以PB为腰的等腰直角三角形时，请直接写出所有点M的坐标．【解答】解：（1）将点A（﹣1，0），点B（3，0）代入y＝ax2+bx﹣3，∴，解得，∴y＝x2﹣2x﹣3；（2）连接CB交对称轴于点Q，∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴抛物线的对称轴为直线x＝1，∵A、B关于对称轴x＝1对称，∴AQ＝BQ，∴AC+AQ+CQ＝AC+CQ+BQ≥AC+BC，当C、B、Q三点共线时，△ACQ的周长最小，∵C（0，﹣3），B（3，0），设直线BC的解析式为y＝kx+b，∴，解得，∴y＝x﹣3，∴Q（1，﹣2）；（3）当∠BPM＝90°时，PM＝PB，∴M点与A点重合，∴M（﹣1，0）；当∠PBM＝90°时，PB＝BM，如图1，当P点在M点上方时，过点B作x轴的垂线GH，过点P作PH⊥GH 交于H，过点M作MG⊥HG交于G，∵∠PBM＝90°，∴∠PBH+∠MBG＝90°，∵∠PBH+∠BPH＝90°，∴∠MBG＝∠BPH，∵BP＝BM，∴△BPH≌△MBG（AAS），∴BH＝MG，PH＝BG＝2，设P（1，t），则M（3﹣t，﹣2），∴﹣2＝（3﹣t）2﹣2（3﹣t）﹣3，解得t＝2+或t＝2﹣，∴M（1﹣，﹣2）或（1+，﹣2），∵M点在对称轴的左侧，∴M点坐标为（1﹣，﹣2）；如图2，当P点在M点下方时，同理可得M（3+t，2），∴2＝（3+t）2﹣2（3+t）﹣3，解得t＝﹣2+（舍）或t＝﹣2﹣，∴M（1﹣，2）；综上所述：M点的坐标为（1﹣，﹣2）或（1﹣，2）或（﹣1，0）．9．（2022•枣庄）如图①，已知抛物线L：y＝x2+bx+c经过点A（0，3），B（1，0），过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E，点P是抛物线上的一个动点．（1）求抛物线的关系式；（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当△OPE面积最大时，求出P点坐标；（3）将抛物线L向上平移h个单位长度，使平移后所得抛物线的顶点落在△OAE 内（包括△OAE的边界），求h的取值范围；（4）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线L：y＝x2+bx+c经过点A（0，3），B（1，0），∴，解得，∴抛物线的解析式为：y＝x2﹣4x+3；（2）如图，过P作PG∥y轴，交OE于点G，设P（m，m2﹣4m+3），∵OE平分∠AOB，∠AOB＝90°，∴∠AOE＝45°，∴△AOE是等腰直角三角形，∴AE＝OA＝3，∴E（3，3），∴直线OE的解析式为：y＝x，∴G（m，m），∴PG＝m﹣（m2﹣4m+3）＝﹣m2+5m﹣3，∴S△OPE ＝S△OPG+S△EPG＝PG•AE＝×3×（﹣m2+5m﹣3）＝﹣（m2﹣5m+3）＝﹣（m﹣）2+，∵﹣＜0，∴当m＝时，△OPE面积最大，此时，P点坐标为（，﹣）；（3）由y＝x2﹣4x+3＝（x﹣2）2﹣1，得抛物线l的对称轴为直线x＝2，顶点为（2，﹣1），抛物线L向上平移h个单位长度后顶点为F（2，﹣1+h）．设直线x＝2交OE于点M，交AE于点N，则E（3，3），∵直线OE的解析式为：y＝x，∴M（2，2），∵点F在△OAE内（包括△OAE的边界），∴2≤﹣1+h≤3，解得3≤h≤4；（4）设P（m，m2﹣4m+3），分四种情况：①当P在对称轴的左边，且在x轴下方时，如图，过P作MN⊥y轴，交y轴于M，交l于N，∴∠OMP＝∠PNF＝90°，∵△OPF是等腰直角三角形，∴OP＝PF，∠OPF＝90°，∴∠OPM+∠NPF＝∠PFN+∠NPF＝90°，∴∠OPM＝∠PFN，∴△OMP≌△PNF（AAS），∴OM＝PN，∵P（m，m2﹣4m+3），则﹣m2+4m﹣3＝2﹣m，解得：m＝（舍）或，∴P的坐标为（，）；②当P在对称轴的左边，且在x轴上方时，同理得：2﹣m＝m2﹣4m+3，解得：m1＝（舍）或m2＝，∴P的坐标为（，）；③当P在对称轴的右边，且在x轴下方时，如图，过P作MN⊥x轴于N，过F作FM⊥MN于M，同理得△ONP≌△PMF，∴PN＝FM，则﹣m2+4m﹣3＝m﹣2，解得：m1＝或m2＝（舍）；P的坐标为（，）；④当P在对称轴的右边，且在x轴上方时，如图，同理得m2﹣4m+3＝m﹣2，解得：m＝或（舍），P的坐标为：（，）；综上所述，点P的坐标是：（，）或（，）或（，）或（，）．方法二：作直线DE：y＝x﹣2，E（1，﹣1）是D点（2，0）绕O点顺时针旋转45°并且OD缩小倍得到，易知直线DE即为对称轴上的点绕O点顺时针旋转45°，且到O点距离缩小倍的轨迹，联立直线DE和抛物线解析式得x2﹣4x+3＝x﹣2，解得x1＝，x2＝，同理可得x3＝或x4＝；综上所述，点P的坐标是：（，）或（，）或（，）或（，）．10．（2023•澄城县一模）如图，抛物线y＝﹣x2+bx+c与x轴交于点A（﹣1，0）、B，与y轴交于点C（0，3），直线l是抛物线的对称轴．（1）求抛物线的函数解析式；（2）在对称轴l上是否存在点M，使△MAC为等腰三角形，若存在，求出所有符合条件的点M的坐标；若不存在，请说明理由．【解答】解：（1）把点A（﹣1，0）、点C（0，3）分别代入y＝﹣x2+bx+c，得．解得．故该抛物线解析式为：y＝﹣x2+2x+3；（2）由（1）知，该抛物线解析式为：y＝﹣x2+2x+3．则该抛物线的对称轴为直线x＝﹣＝1．故设M（1，m）．∵A（﹣1，0）、点C（0，3），∴AC2＝10，AM2＝4+m2，CM2＝1+（m﹣3）2．①若AC＝AM时，10＝4+m2，解得m＝±．∴点M的坐标为（1，）或（1，﹣）；②若AC＝CM时，10＝1+（m﹣3）2，解得m＝0或m＝6，∴点M的坐标为（1，0）或（1，6）．当点M的坐标为（1，6）时，点A、C、M共线，∴点M的坐标为（1，0）；③当AM＝CM时，4+m2＝1+（m﹣3）2，解得m＝1，∴点M的坐标为（1，1）．综上所述，符合条件的点M的坐标为（1，）或（1，﹣）或（1，0）或（1，1）．11．（2023•碑林区校级一模）二次函数y＝ax2+bx+2的图象交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接AC，设运动的时间为t秒．（1）求二次函数y＝ax2+bx+2的表达式；（2）在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标．【解答】解：（1）将点（﹣1，0），B（4，0）代入y＝ax2+bx+2，∴a＝﹣，b＝，∴y＝﹣x2+x+2；（2）∵BM＝5﹣2t，∴M（2t﹣1，0），设P（2t﹣1，m），∵PC2＝（2t﹣1）2+（m﹣2）2，PB2＝（2t﹣5）2+m2，∵PB＝PC，∴（2t﹣1）2+（m﹣2）2＝（2t﹣5）2+m2，∴m＝4t﹣5，∴P（2t﹣1，4t﹣5），∵PC⊥PB，∴×＝﹣1，∴t＝1或t＝2，∴M（1，0）或M（3，0），∴D（1，3）或D（3，2）．12．（2023•东洲区模拟）抛物线y＝ax2+bx+3经过A（﹣1，0），B（3，0）两点，与y轴正半轴交于点C．（1）求此抛物线解析式；（2）如图①，连接BC，点P为抛物线第一象限上一点，设点P的横坐标为m，△PBC的面积为S，求S与m的函数关系式，并求S最大时P点坐标；（3）如图②，连接AC，在抛物线的对称轴上是否存在点M，使△MAC为等腰三角形？若存在，请直接写出符合条件的点M的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+bx+3经过A（﹣1，0），B（3，0）两点，∴，解得：，∴抛物线解析式为y＝﹣x2+2x+3；（2）点P作PF⊥x轴于点F，交BC于点E，设BC直线解析式为：y＝kx+b，∵B（3，0），C（0，3），∴，解得，∴y＝﹣x+3，由题意可知P（m，﹣m2+2m+3），E（m，﹣m+3），S＝S△PBE+S△PCE，S＝PE•OB＝（﹣m2+2m+3+m﹣3）×3，，∵，∴当时，S有最大值，此时P点坐标为；（3）存在，M1（1，0），，，M4（1，1），①当AC＝AM时，如图，设对称轴l与AB交于点E，则，∵AM2＝AE2+EM2，∴，解得：，∴M点的坐标为或，②当AC＝MC时，则OC为AM的垂直平分线．因此M与E重合，因此，M点的坐标为（1，0），③当AM＝CM时，如图，设M点的坐标为（1，n），则AM2＝22+n2＝4+n2，CM2＝12+（3﹣n）2，∴4+n2＝12+（3﹣n）2，解得：n＝1，∴M点的坐标为（1，1），综上可知，潢足条件的M点共四个，其坐标为M1（1，0），，，M4（1，1）．13．（2023•三亚一模）如图，抛物线y＝ax2+3x+c（a≠0）与x轴交于点A（﹣2，0）和点B，与y轴交于点C（0，8），顶点为D，连接AC，CD，DB，直线BC 与抛物线的对称轴l交于点E．（1）求抛物线的解析式和直线BC的解析式；（2）求四边形ABDC的面积；（3）P是第一象限内抛物线上的动点，连接PB，PC，当S△PBC ＝S△ABC时，求点P的坐标；（4）在抛物线的对称轴l上是否存在点M，使得△BEM为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+3x+c（a≠0）过点A（﹣2，0）和C（0，8），∴，解得，∴抛物线的解析式为y＝﹣x2+3x+8．令y＝0，得．解得x1＝﹣2，x2＝8．∴点B的坐标为（8，0）．设直线BC的解析式为y＝kx+b．把点B（8，0），C（0，8）分别代入y＝kx+b，得，解得，∴直线BC的解析式为y＝﹣x+8．（2）如图1，设抛物线的对称轴l与x轴交于点H．∵抛物线的解析式为，∴顶点D的坐标为．∴S四边形ABDC ＝S△AOC+S梯形OCDH+S△BDH＝＝＝70．（3）∵．∴．如图2，过点P作PG⊥x轴，交x轴于点G，交BC于点F．设点．∵点F在直线BC上，∴F（t，﹣t+8）．∴．∴．∴．解得t1＝2，t2＝6．∴点P的坐标为（2，12）或P（6，8）．（4）存在．∵△BEM为等腰三角形，∴BM＝EM或BE＝BM或BE＝EM，设M（3，m），∵B（8，0），E（3，5），∴BE＝＝5，EM＝|m﹣5|，BM＝＝，当BM＝EM时，＝|m﹣5|，∴m2+25＝（m﹣5）2，解得：m＝0，∴M（3，0）；当BE＝BM时，5＝，∴m2+25＝50，解得：m＝﹣5或m＝5（舍去），∴M（3，﹣5）；当BE＝EM时，5＝|m﹣5|，解得：m＝5+5或m＝5﹣5，∴M（3，5+5）或（3，5﹣5），综上所述，点M的坐标为（3，0）或（3，﹣5）或（3，5+5）或（3，5﹣5）．14．（2023•南海区一模）如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣3（a ＞0）与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）点P为直线BC下方抛物线上的一动点，PM⊥BC于点M，PN∥y轴交BC 于点N．求线段PM的最大值和此时点P的坐标；（3）点E为x轴上一动点，点Q为抛物线上一动点，是否存在以CQ为斜边的等腰直角三角形CEQ？若存在，请直接写出点E的坐标；若不存在，请说明理由．【解答】解：（1）将A（﹣1，0），B（3，0）代入函数y＝ax2+bx﹣3（a＞0）中，得，解得，∴解析式为y＝x2﹣2x﹣3，故抛物线解析式为y＝x2﹣2x﹣3；（2）当x＝0时，y＝3，∴C（0，﹣3），∵B（3，0），∴∠OCB＝∠OBC＝45°，∵PN∥y轴，∴∠MNP＝45°，∵PM⊥BC，∴PM＝PN，则当PN最大时，PM也最大，设BC的解析式为y＝mx+n，∴，解得，∴BC解析式为y＝x﹣3，设P（x，x2﹣2x﹣3），N（x，x﹣3），∴PN＝x﹣3﹣（x2﹣2x﹣3）＝﹣（x﹣）2+，当x＝时，PN最大，则PM＝PN＝×＝，∴P（，），故PM最大值为，P点坐标为（，﹣）；（3）存在，点E的坐标为（﹣5，0），（，0），（0，0），（，0）．∵CEQ是以CQ为斜边的等腰直角三角形，∴设Q（x，x2﹣2x﹣3），①如图，过点E作x轴的垂线l，再分别过点C和点Q作垂线l的垂线，分别交于点M和点N，∵∠CEQ＝90°，∴∠QEM+∠CEN＝90°，∵∠QEM+∠MQE＝90°，∴∠EQM＝∠CEN，∵∠CNE＝∠QME＝90°，EC＝EQ，∴△EMQ≌△CNE（AAS），∴CN＝EM＝x2﹣2x﹣3，MQ＝EN＝3，∴|x Q|+MQ＝CN，﹣x+3＝x2﹣2x﹣3，解得x＝﹣2，x＝3（舍去），∴OE＝CM＝2+3＝5，E（﹣5，0），②如图，过点E作x轴的垂线l，再分别过点C和点Q作垂线l的垂线，分别交于点M和点N，同理：△EMC≌△QNE（AAS），CM＝EN＝x2﹣2x﹣3，NQ＝EM＝3，∴﹣x+x2﹣2x﹣3＝3，解得x＝，x＝（舍去），∴OE＝CM＝，E（，0），③如图，点E和点O重合，点Q和点B重合，此时E（0，0），④如图，过点E作x轴的垂线l，再分别过点C和点Q作垂线l的垂线，分别交于点M和点N，同理：△EMC≌△QNE（AAS），CM＝EN＝x2﹣2x﹣3，NQ＝EM＝3，∴x+3＝x2﹣2x﹣3，解得x＝，x＝（舍去），∴OE＝CM＝，E（，0），综上所述，点E的坐标为（﹣5，0），（，0），（0，0），（，0）41。

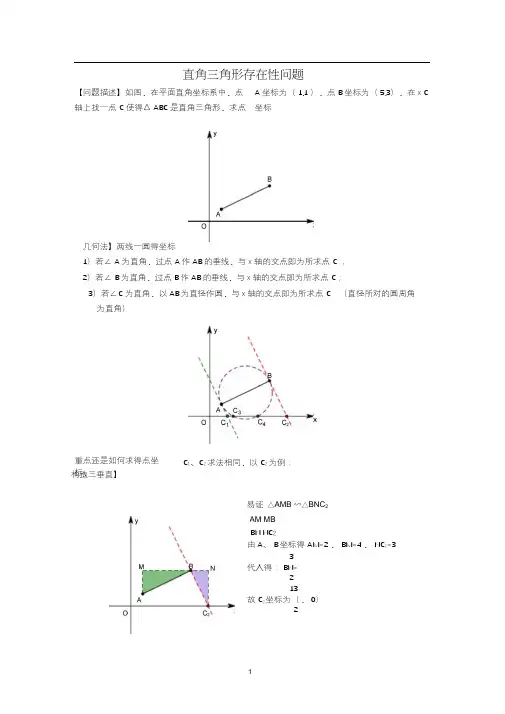
直角三角形存在性问题【问题描述】如图，在平面直角坐标系中，点轴上找一点C 使得△ ABC 是直角三角形，求点A 坐标为（1,1 ），点B 坐标为（5,3），在x C坐标．几何法】两线一圆得坐标1）若∠ A 为直角，过点A 作AB 的垂线，与x 轴的交点即为所求点C ；2）若∠ B 为直角，过点B 作AB 的垂线，与x 轴的交点即为所求点C；3）若∠C 为直角，以AB为直径作圆，与x轴的交点即为所求点C．（直径所对的圆周角为直角）构造三垂直】BN NC2由A、B坐标得AM=2 ，BM=4 ，NC2=33代入得：BN=213故C2坐标为（，0）2重点还是如何求得点坐标，C1、C2 求法相同，以C2为例：易证△AMB ∽△BNC 2AM MBAM MC3易证△AMC3∽△C3NB，C3N= NB由A、B坐标得AM=1，BN=3，设MC3=a，C3N=b1a代入得：= ，即ab=3 ，又a+b=4，故a=1 或3 b3故C3坐标为（2,0），C4坐标为（4,0）构造三垂直步骤：第一步：过直角顶点作一条水平或竖直的直线；第二步：过另外两端点向该直线作垂线，即可得三垂直相似．【代数法】表示线段构勾股还剩下C1待求，不妨来求下C1 ：1）表示点：设C1坐标为（2）表示线段：AB 2 5，AC13）分类讨论：当BAC1 为直角时，24）代入得方程：20 m 1 122222m11，BC1m 532AB2AC12BC12；m5222 32，解得： 3 m．2C3、C4 求法相同，以C3为例：m，0），又A（1，1）、B（5，3）；还有个需要用到一个教材上并没有出现但是大家都知道的算法：互相垂直的两直线斜率之积为-1．考虑到直线AC1与AB 互相垂直，k AC1 k AB 1，可得：k AC1 2，又直线AC1过点A（1,1），可得解析式为：y=-2x+3，33所以与x 轴交点坐标为3,0 ，即C1坐标为3,0 ．22 确实很简便，但问题是这个公式出现在高中的教材上~【小结】几何法：（1）“两线一圆”作出点；（2）构造三垂直相似，利用对应边成比例求线段，必要时可设未知数．代数法：（1）表示点A、B、C 坐标；（2）表示线段AB、AC、BC；（3）分类讨论① AB2+AC2=BC2、② AB2+BC2=AC2、③ AC2+BC2=AB2；（4）代入列方程，求解．如果问题变为等腰直角三角形存在性， 则同样可采取上述方法， 只不过三垂直得到的不是相 似，而是全等．三垂直构造等腰直角三角形】 中考真题（删减）】通过对下面数学模型的研究学习，解决问题． 模型呈现】如图，在 Rt △ABC ，∠ACB=90°，将斜边 AB 绕点 A 顺时针旋转 90 得到 AD ，过点 D 作DE ⊥AC 于点 E ，可以推理得到△ ABC ≌△ DAE ，进而得到 AC=DE ，BC=AE ． 我们把这个数学模型成为 “K 型 ”． 推理过程如下：【模型迁移】二次函数 y ax 2 bx 2的图像交 x 轴于点 A （ -1,0）， B （ 4,0）两点，交 y 轴于点 C ．动点 M 从点 A 出发，以每秒 2 个单位长度的速度沿 AB 方向运动，过点 M 作MN x 轴交直线 BC 于点 N ，交抛物线于点 D ，连接 AC ，设运动的时间为 t 秒． （1）求二次函数 y ax 2 bx 2 的表达式；（2）在直线 MN 上存在一点 P ，当 PBC 是以 BPC 为直角的等腰直角三角形时，求此时 点 D 的坐标．E A C分析】1 2 3 1）yx x 2 ； 222）本题直角顶点 P 并不确定，以 BC 为斜边作等腰直角三角形，直角顶点即为 P 点，再 过点P 作水平线，得三垂直全等．设 HP=a ，PQ=b ，则 BQ=a ， CH=b ，故 D 点坐标为（ 1,3 ）思路 2：等腰直角的一半还是等腰直角．如图，取BC 中点 M 点，以BM 为一直角边作等腰直角三角形， 则第三个顶点即为 P 点．根 据 B 点和 M 点坐标，此处全等的两三角形两直角边分别为 1 和 2 ，故 P 点坐标易求．由图可知：b aa b 42 ，解得：a1 b3同理可求此时解得： m 1 12 ， m 2 1 2 ， m3 1 6 ， m4 1 6 （舍）如下图，对应 P 点坐标分别为 1 2, 11 2, 1 、 1 6,1中考真题】12如图，在平面直角坐标系中，抛物线 y x 2bx c 与 x 轴交于 A 、B 两点，点 B （3,0），25经过点 A 的直线 AC 与抛物线的另一交点为 C （4, ），与 y 轴交点为 D ，点 P 是直线 AC 下2 方的抛物线上的一个动点（不与点A 、C 重合）．（1）求该抛物线的解析式．（2）点Q 在抛物线的对称轴上运动， 当 OPQ 是以OP 为直角边的等腰直角三角形时， 请直接写出符合条件的点 P 的坐标．分析】2）①当∠ POQ 为直角时，考虑 Q 点在对称轴上，故过点 Q 向 y 轴作垂线，垂线段长为 垂线，长度必为 1，故 P 的纵坐标为 ±1．如下图，不难求出 P 点坐标．13设 P 点坐标为 m,1 m 2 m 3 ，22可得： 1 m 2 m 3 1．2212 3； xx2 21) y1，可知过点 P 向 x 轴作②当∠ OPQ 为直角时，如图构造△ OMP ≌△ PNQ ，可得： PM=QN ． 设 P 点坐标为 m,21m 2 m 32 ，1，若 1m 2 m 3 m 1 ，解得： m 1 5 ， m 25 （舍）．22若 1m 2 m 3 m 1，解得： m 1 2 5， m 2 2 5（舍） 22对于构造三垂直来说，直角顶点已知的和直角顶点的未知的完全就是两个题目！也许能画出大概位置，但如何能画出所有情况，才是问题的关键．其实只要再明确一点， 构造出三垂直后， 表示出一组对应边， 根据相等关系列方程求解即可．则PM 01 2 3 mm2212 m 23， QN= m 21， 如下图，对应 P 点坐标分别为 5,1 5中考真题】如图，抛物线y ax2 bx 2交x轴于点A( 3,0)和点B(1,0)，交 y轴于点C． (1)求这个抛物线的函数表达式．(2)点 D的坐标为( 1,0) ，点 P为第二象限内抛物线上的一个动点，求四边形ADCP 面积的最大值．( 3)点 M 为抛物线对称轴上的点，问：在抛物线上是否存在点N ，使MNO 为等腰直角三角形，且MNO 为直角？若存在，请直接写出点N 的坐标；若不存在，请说明理由．x备用图分析】2 2 41) y x x 2 ；332) 连接AC，将四边形面积拆为△ APC 和△ADC 面积，考虑△ ADC 面积为定值，故只需△APC 面积最大即可，铅垂法可解；过点N 作NE⊥x 轴交x 轴于E 点，如图1，过点M 向NE 作垂线交EN 延长线于易证△OEN≌△ NFM ，可得：NE=FM．22 m3当直角顶点不确定时，问题的一大难点是找出所有情况，而事实上，所有的情况都可以归结为同一个方程：NE=FM ．故只需在用点坐标表示线段时加上绝对值，便可计算出可能存在的其他情况．3)F 点，设N 点坐标为m, 24 m3，则NE22m3 ，FM m 1 ，22m34m 2=m31，解得：m17 731) m27 737 73（图4）4对应N 点坐标分别为3 734734m 2=31，解得：m373(图2)、m41 73（图3）4 对应N 点坐标分别为7343 7343 734一般直角三角形存在性，同样构造三垂直，区别于等腰直角构造的三垂直全等，没了等腰的条件只能得到三垂直相似．而题型的变化在于动点或许在某条直线上，也可能在抛物线上等．对称轴上寻找点】（中考真题）如图，已知抛物线y ax2 bx c（a 0）的对称轴为直线x 1 ，且抛物线与x 轴交于 A、B两点，与 y轴交于C点，其中A（1,0），C （0,3）．（1）若直线y mx n 经过 B 、C 两点，求直线BC 和抛物线的解析式；（2）在抛物线的对称轴x 1上找一点 M ，使点 M 到点 A的距离与到点C 的距离之和最小，求出点 M 的坐标；（3）设点 P为抛物线的对称轴x 1上的一个动点，求使BPC 为直角三角形的点 P坐标．分析】1）直线BC：y x3抛物线：y x2 2x3；2）将军饮马问题，考虑到M 点在对称轴上，且点 A 关于对称轴的对称点为点B ，故MA+MC=MB+MC，∴当B、M、C 三点共线时，M到A和C的距离之后最小，此时M 点坐标为（-1，2）；3）两圆一线作点P：yx以 P 1 为例，构造△ PNB ∽△ BMC ，考虑到 BM =MC =3，易求 P 2 坐标为（ 1,4）．P 3、 P 4求法类似，下求 P 3：已知 PN=1， PM=2，设 CN=a ，BM=b ， 1a，即 ab=2，由图可知： b-a=3， b2∴BN=PN=2，故 P 1 点坐标为（ -1， -2）． xx舍），对应 x故可解： 类似可求P 3坐标为1,3217．2由相似得：2 抛物线 y ax 2 2x c 与 x 轴交于 A( 1,0) ，B (3,0)两点，与 y 轴交于点 C ，点 D 是该抛物线的顶点．1）求抛物线的解析式和直线 AC 的解析式；2）请在 y 轴上找一点 M ，使 BDM 的周长最小，求出点 M 的坐标；3）试探究：在拋物线上是否存在点 P ，使以点 A ， P ， C 为顶点， AC 为直角边的三角形是直角三角形？若存在，请求出符合条件的点 P 的坐标；若不存在，请说明理由．抛物线上寻找点】中考真题） 如图，在平面直角坐标系中，分析】1）抛物线：y x2 2x 3 ，直线AC：y=3x+3；2）看图，M 点坐标为（0,3）与C 点重合了．3）考虑到AC 为直角边，有如下两种情况，故分别过A、C 作AC 的垂线，与抛物线交点即为所求P 点，xP：x先求过A 点所作垂线得到的点设P 点坐标为 m, m22m3，则PM=m+1，AM= 0 m22m2m3，易证△ PMA∽△ ANC，且AN =3，m 1 m2 2m 3 ∴ ，解得：31CN=1，m110，3m21（舍），故第1个P点坐标为130, 193再求过点C 所作垂线得到的点PM 3m2m 2m故第2 个P 点坐标为综上所述，P 点坐标为3 2 m2m，CN=m，m17，m2（舍）37,203,910137, 20或3939P：3，解得：1m22m动点还可能在⋯⋯】中考真题)如图，抛物线y ax2 bx 2(a 0)与x轴交于A( 3,0) ，B(1,0)两点，与 y轴交于点C ，直线 y x 与该抛物线交于 E ， F 两点．1)求抛物线的解析式．2) P 是直线 EF 下方抛物线上的一个动点，作 PH EF 于点 H ，求 PH 的最大值．3) 以点C 为圆心，1 为半径作圆，e C 上是否存在点 M ，使得BCM 是以CM 为直角边的直角三角形？若存在，直接写出 M 点坐标；若不存在，说明理由．分析】CM 为直角边，故点C 可能为直角顶点，点M 也可能为直角顶点．①当 BCM 为直角时，如图：1)22x32；2) 过点P 作x 轴的垂线交EF 于点Q，所谓PH 最大，即PQ 最大，易解．3)M 1 ：不难求得 CF=1，BF=2，故 M 1 坐标为同理可求 M 2 坐标为【总结】 对于大部分直角三角形存在性问题， 构造三垂直全等或相似基本上可解决问题， 牢 记构造步骤：（ 1）过直角顶点作水平或竖直线；（ 2）过另外两端点向其作垂线．∴ EM 1 : EC 1: 2，又 CM 1 1， 可得： EM 155，EC525 5BOCM 44M 3 ：不难发现 CM=1，BC= 5 ，∴ BM 2，即△ MEC ∽△ BFM ，且相似比为 1：2， 设 EC=a ， EM=b ，则 FM=2a ， BF=2b ， 2a 由图可知： 2a2b22，解得：13 54 5故点M 3 的坐标为至于 M 4坐标，显然 1, 2．综上所述， M 点坐标为或 255, 2或 1, 2 ．如图： yBO放大C②当∠ BMC 为直角时，y。

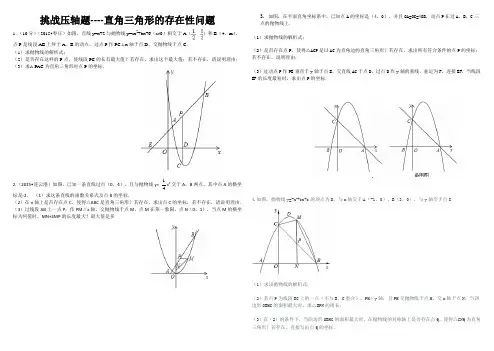
挑战压轴题----直角三角形的存在性问题1．（10分）（2015•枣庄）如图，直线y=x+2与抛物线y=ax 2+bx+6（a ≠0）相交于A （，）和B （4，m ），点P 是线段AB 上异于A 、B 的动点，过点P 作PC ⊥x 轴于点D ，交抛物线于点C ． （1）求抛物线的解析式；（2）是否存在这样的P 点，使线段PC 的长有最大值？若存在，求出这个最大值；若不存在，请说明理由； （3）求△PAC 为直角三角形时点P 的坐标．2.（2015•连云港）如图，已知一条直线过点（0，4），且与抛物线y=41x 2交于A ，B 两点，其中点A 的横坐标是-2． （1）求这条直线的函数关系式及点B 的坐标．（2）在x 轴上是否存在点C ，使得△ABC 是直角三角形？若存在，求出点C 的坐标，若不存在，请说明理由． （3）过线段AB 上一点P ，作PM ∥x 轴，交抛物线于点M ，点M 在第一象限，点N （0，1），当点M 的横坐标为何值时，MN+3MP 的长度最大？最大值是多3. 如图，在平面直角坐标系中，已知点A 的坐标是（4，0），并且OA=OC=4OB ，动点P 在过A ，B ，C 三点的抛物线上． （1）求抛物线的解析式；（2）是否存在点P ，使得△ACP 是以AC 为直角边的直角三角形？若存在，求出所有符合条件的点P 的坐标；若不存在，说明理由；（3）过动点P 作PE 垂直于y 轴于点E ，交直线AC 于点D ，过点D 作y 轴的垂线．垂足为F ，连接EF ，当线段EF 的长度最短时，求出点P 的坐标．4.如图，抛物线y=-x 2+bx+c的顶点为D ，与x 轴交于A （-1，0）、B （3，0），与y 轴交于点C ．（1）求该抛物线的解析式；（2）若点P 为线段BC 上的一点（不与B 、C 重合），PM ∥y 轴，且PM 交抛物线于点M ，交x 轴于点N ，当四边形OBMC 的面积最大时，求△BPN 的周长；（3）在（2）的条件下，当四边形OBMC 的面积最大时，在抛物线的对称轴上是否存在点Q ，使得△CNQ 为直角三角形？若存在，直接写出点Q 的坐标．5.（2015宜宾）如图，抛物线y=- 1/2x2+bx+c与x轴分别相交于点A（-2，0），B（4，0），与y轴交于点C，顶点为点P．（1）求抛物线的解析式；（2）动点M、N从点O同时出发，都以每秒1个单位长度的速度分别在线段OB、OC上向点B、C方向运动，过点M作x轴的垂线交BC于点F，交抛物线于点H．①当四边形OMHN为矩形时，求点H的坐标；②是否存在这样的点F，使△PFB为直角三角形？若存在，求出点F的坐标；若不存在，请说明理由．6.如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2．点P 从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒．将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA．（1）请用含t的代数式表示出点D的坐标；（2）求t为何值时,△DPA的面积最大,最大为多少？（3）在点P从O向A运动的过程中,△DPA能否成为直角三角形？若能,求t的值．若不能,请说明理由；（4）请直接写出随着点P的运动,点D运动路线的长．2.如图，在平面直角坐标系xoy中，已知抛物线经过点A（0，4），B（1，0），C（5，0），抛物线对称轴l与x轴相交于点M。

中考数学翻折专题训练直角三角形存在性问题1.（2017•河南）如图，在Rt△ABC中，∠A＝90°，AB＝AC，BC＝+1，点M，N分别是边BC，AB上的动点，沿MN所在的直线折叠∠B，使点B的对应点B′始终落在边AC上，若△MB′C为直角三角形，则BM 的长为．2.（2020•郑州二模）如图，矩形ABCD中，AB＝3，BC＝4，对角线AC，BD相交于点O，点E是AD边上一动点，将△AEO沿直线EO折叠，点A落在点F处，线段EF，OD相交于点G．若△DEG是直角三角形，则线段DE的长为．3.（2020•恩施市校级模拟）如图，在矩形ABCD中，AB＝4，BC＝6，E是BC的中点，连接AE，P是边AD 上一动点，沿过点P的直线将矩形折叠，使点D落在AE上的点D′处，当△APD′是直角三角形时，PD＝．4.（2020•洛阳一模）如图，在Rt△ABC中，∠C＝90°，∠A＝30°，AB＝2，BD平分∠ABC，点E是边AB上一动点（不与A、B重合），沿DE所在的直线折叠∠A，点A的对应点为F，当△BFC是直角三角形且BC为直角边时，则AE的长为．5.（2020春•二七区校级月考）如图，在矩形ABCD中，AB：BC＝3：4，点E是对角线BD上一动点（不与点B，D重合），将矩形沿过点E的直线MN折叠，使得点A，B的对应点G，F分别在直线AD与BC上，当△DEF为直角三角形时，CN：BN的值为．6.（2019•临颍县一模）如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点E、F分别在边AC、BC上，连接EF，沿EF折叠该三角形，使点C的对应点D落在边AB上．若△BDF是直角三角形，则CF的长为．7.（2019•包河区一模）如图，在矩形ABCD中，AD＝4，AC＝8，点E是AB的中点，点F是对角线AC上一点，△GEF与△AEF关于直线EF对称，EG交AC于点H，当△CGH中有一个内角为90°时，则CG的长为．8.（2018秋•蜀山区校级期中）如图，矩形ABCD中，AB＝3，AD＝9，将△ABE沿BE翻折得到△A′BE，点A落在矩形ABCD的内部，且∠AA′G＝90°，若以点A′、G、C为顶点的三角形是直角三角形，则AE＝．9.（2019秋•川汇区期末）如图，在矩形ABCD中，已知AB＝2，点E是BC边的中点，连接AE，△AB′E和△ABE关于AE所在直线对称，若△B′CD是直角三角形，则BC边的长为．10.（2019秋•建湖县期中）如图，长方形ABCD中，∠A＝∠ABC＝∠BCD＝∠D＝90°，AB＝CD＝5，AD＝BC ＝13，点E为射线AD上的一个动点，若△ABE与△A'BE关于直线BE对称，当△A'BC为直角三角形时，AE 的长为．11.（2020•梁园区校级二模）如图所示，在矩形ABCD中，AB＝2，AD＝2，对角线AC与BD交于点O，E 是AD边动点，作直线OE交BC于点G，将四边形DEGC沿直线EG折叠，点D落在点D′处，点C落在点C′处，ED′交AC于F，若△AEF是直角三角形，则AE＝．12.（2020•望城区模拟）如图，在矩形ABCD中，AB＝3，BC＝4，点E为射线CB上一动点（不与点C重合），将△CDE沿DE所在直线折叠，点C落在点C′处，连接AC′，当△AC′D为直角三角形时，CE的长为．13.（2020•宜城市模拟）如图，矩形ABCD 中，AB ＝8，AD ＝6，E 为AB 边上一点，将△BEC 沿着CE 翻折，使点B 落在点F 处，连接AF ，当△AEF 为直角三角形时，BE ＝ ．14.（2020•沈阳）如图，在矩形ABCD 中，AB ＝6，BC ＝8，对角线AC ，BD 相交于点O ，点P 为边AD 上一动点，连接OP ，以OP 为折痕，将△AOP 折叠，点A 的对应点为点E ，线段PE 与OD 相交于点F ．若△PDF 为直角三角形，则DP 的长为 ．15.如图，在三角形ABC 中，∠C=90°，AC=3，BC=4，D,E 分别是AB ，BC 上的动点，将BDE Δ沿着直线DE 翻折得到FDE Δ，使点F 落在射线AC 上，当BE 的长为 时，ADF Δ是直角三角形。

一次函数之存在性（直角三角形）（人教版）一、单选题(共3道，每道33分)1.如图，直线y=2x+4与坐标轴交于A，B两点，P为直线x=1上一动点，连接AP，BP．当△ABP是以点A，B为直角顶点的直角三角形时，点P的坐标为( )A. B.C. D.答案：D解题思路：1．解题要点①首先研究基本图形，对信息进行标注；②研究目标△ABP，A，B为定点，P为动点，若△ABP是直角三角形，需要根据直角顶点进行分类，根据题目信息，分别以B，A作为直角顶点；③对于直角，需要结合题目背景灵活处理，如以点B，点A为直角顶点时，可以借助坐标系背景用函数解析式来求点坐标．2．解题过程由题意得，A（-2，0），B（0，4）．①当时，如图所示，．∵点的横坐标为1，∴．②当时，如图所示，，∴．综上得，点P的坐标为．试题难度：三颗星知识点：直角三角形的存在性2.如图，直线交y轴于点A，且经过点B（4,1）．若P是y轴上的一动点，当△ABP是以点A，B为直角顶点的直角三角形时，点P的坐标为( )A. B.C. D.答案：A解题思路：1．解题要点①首先研究基本图形，对信息进行标注；②研究目标△ABP，A，B为定点，P为动点，若△ABP是直角三角形，需要根据直角顶点进行分类，根据题意信息，点A，B轮流作为直角顶点；③对于直角，需要结合题目背景灵活处理，如以点B为直角顶点时，可以借助坐标系背景用函数解析式来求点坐标；④审题需要注意，点P是y轴上的一动点，需要弄清目标．2．解题过程①若点Ａ充当直角顶点，即时，显然不成立；②若点Ｂ充当直角顶点，即时，过点B作⊥AB，交y轴于点，如图所示，则，∴．综上所述，符合题意的点P的坐标为．试题难度：三颗星知识点：直角三角形的存在性3.如图，将△ABC放在平面直角坐标系中，三个顶点的坐标分别为A（-1，0），B（3，0），C （0，2），P是线段AC上的一个动点（不与点A，C重合），过点P作平行于x轴的直线，交BC于点Q，若在x轴上存在点R，使得△PQR是等腰直角三角形，则点R的坐标为( )A. B.C. D.答案：C解题思路：1．解题要点①观察题目特征，确定为等腰直角三角形存在性问题．②分析定点、动点、不变特征．从直角入手，分类讨论．③画图，表达线段长，借助等腰直角三角形性质建等式．2．解题过程由题意，得A（-1，0），B（3，0），C（0，2），则，．设，则，PQ=-2m+4．①如图，当点Q为直角顶点时，PQ=RQ．，，由-2m+4=m，得，∴．②如图，当点P为直角顶点时，PQ=PR．，，由-2m+4=m，得，∴．③如图，当点R为直角顶点时，RP=RQ．过点R作RD⊥于点D，则，由，得m=1，∴．综上得，点R的坐标为．试题难度：三颗星知识点：等腰直角三角形存在性。

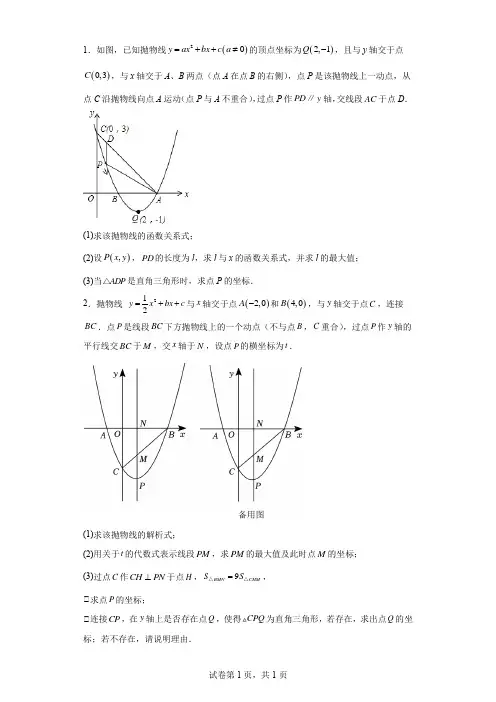
1．如图，已知抛物线()20y ax bx c a =++≠的顶点坐标为()2,1Q -，且与y 轴交于点()0,3C ，与x 轴交于A 、B 两点（点A 在点B 的右侧），点P 是该抛物线上一动点，从点C 沿抛物线向点A 运动（点P 与A 不重合），过点P 作PD y ∥轴，交线段AC 于点D ．(1)求该抛物线的函数关系式；(2)设(),P x y ，PD 的长度为l ，求l 与x 的函数关系式，并求l 的最大值；(3)当ADP △是直角三角形时，求点P 的坐标．2．抛物线 212y x bx c =++与x 轴交于点()2,0A -和()4,0B ，与y 轴交于点C ，连接BC ．点P 是线段BC 下方抛物线上的一个动点（不与点B ，C 重合），过点P 作y 轴的平行线交BC 于M ，交x 轴于N ，设点P 的横坐标为t ．(1)求该抛物线的解析式；(2)用关于t 的代数式表示线段PM ，求PM 的最大值及此时点M 的坐标；(3)过点C 作CH PN ⊥于点H ，9BMN CHM S S =△△，①求点P 的坐标；①连接CP ，在y 轴上是否存在点Q ，使得CPQ 为直角三角形，若存在，求出点Q 的坐标；若不存在，请说明理由．3．如图，抛物线22y x x k =-+与x 轴交于A 、B 两点，与y 轴交于点()0,3C -．(1)求抛物线的解析式和点A 和点B 的坐标；(2)在x 轴下方的抛物线上是否存在一点D ，使四边形ABDC 的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由；(3)在抛物线22y x x k =-+上求点Q ，使BCQ △是以BC 为直角边的直角三角形． 4．如图，抛物线22y x x k =-+与x 轴交于A 、B 两点，与y 轴交于点()0,3C -．(1)求抛物线的解析式和点A 和点B 的坐标；(2)在x 轴下方的抛物线上是否存在一点D ，使四边形ABDC 的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由；(3)在抛物线22y x x k =-+上求点Q ，使BCQ △是以BC 为直角边的直角三角形． 5．已知抛物线y ＝﹣x 2+bx +c 与x 轴交于A （﹣1，0），B （m ，0）两点，与y 轴交于点C （0，5）．(1)求b ，c ，m 的值；(2)如图1，点D 是抛物线上位于对称轴右侧的一个动点，且点D 在第一象限内，过点D 作x 轴的平行线交抛物线于点E ，作y 轴的平行线交x 轴于点G ，过点E 作EF ①x 轴，垂足为点F ，当四边形DEFG 的周长最大时，求点D 的坐标；(3)如图2，点M 是抛物线的顶点，将△MBC 沿BC 翻折得到△NBC ，NB 与y 轴交于点Q ，在对称轴上找一点P ，使得△PQB 是以QB 为直角边的直角三角形，求出所有符合条件的点P 的坐标．6．如图，抛物线()224y x m x =-++的顶点C 在x 轴的正半轴上，直线2y x =+与抛物线交于A ，B 两点，且点A 在点B 的左侧．(1)求m 的值；(2)点P 是抛物线()224y x m x =-++上一点，当PAB 的面积是ABC 面积的2倍时，求点P的坐标；(3)将直线AB 向下平移(0)k k >个单位长度，平移后的直线与抛物线交于D ，E 两点(点D 在点E的左侧)，当DEC为直角三角形时，求k的值．。

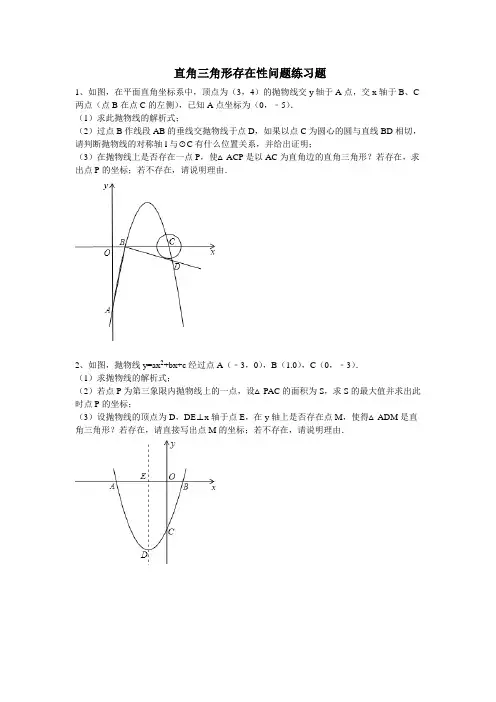
直角三角形存在性问题练习题
1、如图，在平面直角坐标系中，顶点为（3，4）的抛物线交y轴于A点，交x轴于B、C 两点（点B在点C的左侧），已知A点坐标为（0，﹣5）．
（1）求此抛物线的解析式；
（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l与⊙C有什么位置关系，并给出证明；
（3）在抛物线上是否存在一点P，使△ACP是以AC为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．
2、如图，抛物线y=ax2+bx+c经过点A（﹣3，0），B（1.0），C（0，﹣3）．
（1）求抛物线的解析式；
（2）若点P为第三象限内抛物线上的一点，设△PAC的面积为S，求S的最大值并求出此时点P的坐标；
（3）设抛物线的顶点为D，DE⊥x轴于点E，在y轴上是否存在点M，使得△ADM是直角三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
3、如图14，已知抛物线与x轴的一个交点A的坐标为（-1,0），对称轴为直线x = 2.
（1）求抛物线与x轴的另一个交点B的坐标；
（2）点D是抛物线与y轴的交点，点C是抛物线上的另一点。

已知以AB为一底边的梯形ABCD的面积为9.求此抛物线的解析式，并指出顶点E的坐标；
（3）点P是（2）中抛物线对称轴上一动点，且以1个单位/秒的速度从此抛物线的顶点E向上运动。

设点P运动的时间为t秒。

①当t为秒是，△PAD的周长最小？当t为秒时，△PAD是以AD为腰
的等腰三角形？（结果保留根号）
②点P在运动过程中，是否存在一点P，使△PAD是以AD为斜边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由。

直角三角形的存在性问题（因动点产生的直角三角形的存在性问题）课前预热1、两点式2、两直线互相垂直，两直线的解析式为11b x k y +=与22b x k y += → 121-=⋅k k3、三角形相似：射影定理在直角三角形中，斜边上的高线是两直角边在斜边上的摄影的比例中项，每条直角边是它们在斜边上的摄影和斜边的比例中项∠ACB=90° BD AD CD •=2⇒ AB AD AC •=2CD ⊥AB AB BD BC •=24、三角函数求解新课认知问题提出：已知直角三角形的一边（即直角三角形的两个点确定），求 解第三点解决方法：1、找点方法：双线一圆（两垂线一圆）一圆指以已知边为直径作圆，双线指过线段（边）端点（顶点）做垂线. 2、分析题目中的定长、定角3、确定点的坐标情况分类：（1）当动点在直线上运动时常用方法:①121-=⋅k k ；②三角形相似；③勾股定理；（2）当动点在曲线上运动是时情况分类：①已知点处做直角方法：①121-=⋅k k ；②三角形相似；③勾股定理.②动点处做直角方法：寻找特殊角.动点在直线上运动时例1如图，已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为（-1，0），对称轴为直线x=-2．（1）求抛物线与x轴的另一个交点B的坐标；（2）点D是抛物线与y轴的交点，点C是抛物线上的另一点．已知以AB为一底边的梯形ABCD的面积为9．求此抛物线的解析式，并指出顶点E的坐标；（3）点P是（2）中抛物线对称轴上一动点，且以1个单位/秒的速度从此抛物线的顶点E向上运动．设点P运动的时间为t秒．①当t为秒时，△PAD的周长最小？当t为秒时，△PAD是以AD为腰的等腰三角形？（结果保留根号）②点P在运动过程中，是否存在一点P，使△PAD是以AD为斜边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由当动点在曲线上运动时 (1)求解过程中只有已知点处做直角例2 如图，抛物线213442y x x =--与x 轴交于A 、B 两点（点B 在点A 的右侧），与y 轴交于点C ，连结BC ，以BC 为一边，点O 为对称中心作菱形BDEC ，点P 是x 轴上的一个动点，设点P 的坐标为(m , 0)，过点P 作x 轴的垂线l 交抛物线于点Q ．（1）求点A 、B 、C 的坐标；（2）当点P 在线段OB 上运动时，直线l 分别交BD 、BC 于点M 、N ．试探究m 为何值时，四边形CQMD 是平行四边形，此时，请判断四边形CQBM 的形状，并说明理由；（3）当点P 在线段EB 上运动时，是否存在点Q ，使△BDQ 为直角三角形，若存在，请直接写出点Q 的坐标；若不存在，请说明理由．（2）求解过程中动点处做直角例3 如图，已知抛物线y=x 2+bx+c 与x 轴交于A 、B 两点（A 点在B 点左侧），与y 轴交于点C （0，-3），对称轴是直线x=1，直线BC 与抛物线的对称轴交于点D ．（1）求抛物线的函数表达式；（2）求直线BC 的函数表达式；（3）点E 为y 轴上一动点，CE 的垂直平分线交CE 于点F ，交抛物线于P 、Q 两点，且点P 在第三象限．①当线段PQ=43AB,求tan ∠CED 的值②当以点C 、D 、E 为顶点的三角形是直角三角形时，请直接写出点P 的坐标． 温馨提示：考生可以根据第（3）问的题意，在图中补出图形，以便作答．1、（2012山东枣庄10分）在平面直角坐标系中，现将一块等腰直角三角板ABC 放在第二象限，斜靠在两坐标轴上，点C为 (－1，0) ．如图所示，B 点在抛物线y ＝12x 2＋12x －2图象上，过点B 作BD ⊥x 轴，垂足为D ，且B 点横坐标为－3．（1）求证：△BDC ≌△COA ； （2）求BC 所在直线的函数关系式；（3）抛物线的对称轴上是否存在点P ，使△ACP 是以AC为直角边的直角三角形？若存在，求出所有点P 的坐标；若不存在，请说明理由．2.已知抛物线y=ax 2+bx+3（a ≠0）经过A （3，0），B （4，1）两点，且与y 轴交于点C ．（1）求抛物线y=ax 2+bx+3（a ≠0）的函数关系式及点C 的坐标；（2）如图（1），连接AB ，在题（1）中的抛物线上是否存在点P ，使△PAB 是以AB 为直角边的直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由；（3）如图（2），连接AC ，E 为线段AC 上任意一点（不与A 、C 重合）经过A 、E 、O 三点的圆交直线AB 于点F ，当△OEF 的面积取得最小值时，求点E 的坐标．3、（2012内蒙古）如图，抛物线2y x bx 5=--与x 轴交于A ．B 两点（点A 在点B 的左侧），与y 轴交于点C ，点C 与点F 关于抛物线的对称轴对称，直线AF 交y 轴于点E ，|OC|：|OA|=5：1．（1）求抛物线的解析式；（2）求直线AF 的解析式；（3）在直线AF 上是否存在点P ，使△CFP 是直角三角形？若存在，求出P 点坐标；若不存在，说明理由．例1（1）由抛物线的轴对称性及A（﹣1，0），可得B（﹣3，0）．（2）设抛物线的对称轴交CD于点M，交AB于点N，由题意可知AB∥CD，由抛物线的轴对称性可得CD=2DM．∵MN∥y轴，AB∥CD，∴四边形ODMN是矩形．∴DM=ON=2，∴CD=2×2=4．∵A（﹣1，0），B（﹣3，0），∴AB=2，∵梯形ABCD的面积=（AB+CD）•OD=9，∴OD=3，即c=3．∴把A（﹣1，0），B（﹣3，0）代入y=ax2+bx+3得，解得．∴y=x2+4x+3．将y=x2+4x+3化为顶点式为y=（x+2）2﹣1，得E（﹣2，﹣1）．（3）①当t为2秒时，△PAD的周长最小；当t为4或4﹣或4+秒时，△PAD是以AD为腰的等腰三角形．②存在．∵∠APD=90°，∠PMD=∠PNA=90°，∴∠PDM+∠APN=90°，∠DPM+∠PDM=90°，∴∠PDM=∠APN，∵∠PMD=∠ANP，∴△APN∽△PDM，∴=，∴=，∴PN2﹣3PN+2=0，∴PN=1或PN=2．∴P（﹣2，1）或（﹣2，2）．故答案为：2；4或4﹣或4+例2（1）当y=0时，x2﹣x﹣4=0，解得x1=﹣2，x2=8，∵点B在点A的右侧，∴点A的坐标为（﹣2，0），点B的坐标为（8，0）．当x=0时，y=﹣4，∴点C的坐标为（0，﹣4）．（2）由菱形的对称性可知，点D的坐标为（0，4）．设直线BD的解析式为y=kx+b，则，解得k=﹣，b=4．∴直线BD的解析式为y=﹣x+4．∵l⊥x轴，∴点M的坐标为（m，﹣m+4），点Q的坐标为（m，m2﹣m﹣4）．如图，当MQ=DC时，四边形CQMD是平行四边形，∴（﹣m+4）﹣（m2﹣m﹣4）=4﹣（﹣4）．化简得：m2﹣4m=0，解得m1=0（不合题意舍去），m2=4．∴当m=4时，四边形CQMD是平行四边形．此时，四边形CQBM是平行四边形．解法一：∵m=4，∴点P是OB的中点．∵l⊥x轴，∴l∥y轴，∴△BPM∽△BOD，∴==，∴BM=DM，∵四边形CQMD是平行四边形，∴DM CQ，∴BM CQ，∴四边形CQBM是平行四边形．解法二：设直线BC的解析式为y=k1x+b1，则，解得k1=，b1=﹣4．故直线BC的解析式为y=x﹣4．又∵l⊥x轴交BC于点N，∴x=4时，y=﹣2，∴点N的坐标为（4，﹣2），由上面可知，点M的坐标为（4，2），点Q的坐标为（4，﹣6）．∴MN=2﹣（﹣2）=4，NQ=﹣2﹣（﹣6）=4，∴MN=QN，又∵四边形CQMD是平行四边形，∴DB∥CQ，∴∠3=∠4，∵在△BMN与△CQN中，，∴△BMN≌△CQN（ASA）∴BN=CN，∴四边形CQBM是平行四边形．（3）抛物线上存在两个这样的点Q，分别是Q1（﹣2，0），Q2（6，﹣4）．若△BDQ为直角三角形，可能有三种情形，如答图2所示：①以点Q为直角顶点．此时以BD为直径作圆，圆与抛物线的交点，即为所求之Q点．∵P在线段EB上运动，∴﹣8≤x Q≤8，而由图形可见，在此范围内，圆与抛物线并无交点，故此种情形不存在．②以点D 为直角顶点．连接AD ，∵OA=2，OD=4，OB=8，AB=10，由勾股定理得：AD=，BD=，∵AB 2+BD 2=AB 2，∴△ABD 为直角三角形，即点A 为所求的点Q ． ∴Q 1（﹣2，0）；③以点B 为直角顶点．如图，设Q 2点坐标为（x ，y ），过点Q 2作Q 2K ⊥x 轴于点K ，则Q 2K=﹣y ，OK=x ，BK=8﹣x ． 易证△QKB ∽△BOD ， ∴，即，整理得：y=2x ﹣16．∵点Q 在抛物线上，∴y=x 2﹣x ﹣4． ∴x 2﹣x ﹣4=2x ﹣16，解得x=6或x=8，当x=8时，点Q 2与点B 重合，故舍去；当x=6时，y=﹣4，∴Q 2（6，﹣4）．例3 ⑴∵抛物线的对称轴为直线x=1， ∴1221b b a -=-=⨯ ∴b =－2．∵抛物线与y 轴交于点C （0，－3），∴c =－3，∴抛物线的函数表达式为y =x 2－2x －3．⑵∵抛物线与x 轴交于A 、B 两点，当y =0时，x 2－2x －3=0．∴x 1=－1,x 2=3.∵A 点在B 点左侧，∴A （－1，0），B （3，0）设过点B （3，0）、C （0，－3）的直线的函数表达式为y =kx ＋m ， 则033k m m =+⎧⎨-=⎩，∴13k m =⎧⎨=-⎩∴直线BC 的函数表达式为y =x －3． ⑶①∵AB =4，PO =34AB ， ∴PO =3∵PO ⊥y 轴∴PO ∥x 轴，则由抛物线的对称性可得点P 的横坐标为12-， ∴P （12-，74-）∴F（0，74 -），∴FC=3－OF=3－74=54．∵PO垂直平分CE于点F，∴CE=2FC=5 2∵点D在直线BC上，∴当x=1时，y=－2，则D（1，－2）．过点D作DG⊥CE于点G，∴DG=1，CG=1，∴GE=CE－CG=52－1=32．在Rt△EGD中，tan∠CED=23 GDEG=．②P1（12），P2（1－252）．练习1、【答案】解：（1）证明：∵∠BCD ＋∠ACO ＝90°，∠ACO ＋∠OAC ＝90°，∴∠BCD ＝∠OAC 。