数学理卷·2014届广东省中山市华侨中学高三上学期第三次模拟考试试卷(2013.12)

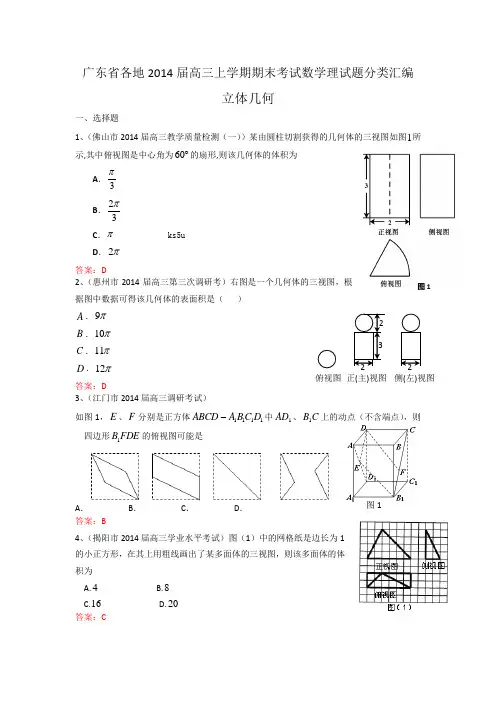
图1图1广东省各地2014届高三上学期期末考试数学理试题分类汇编立体几何一、选择题1、（佛山市2014届高三教学质量检测（一））某由圆柱切割获得的几何体的三视图如图1所示,其中俯视图是中心角为60︒的扇形,则该几何体的体积为A ．3πB ．23πC ．π ks5uD ．2π答案：D 2、（惠州市2014届高三第三次调研考）右图是一个几何体的三视图，根据图中数据可得该几何体的表面积是（ ）A ．9πB ．10πC ．11πD ．12π答案：D 3、（江门市2014届高三调研考试）如图1，E 、F 分别是正方体1111D C B A ABCD -中1AD 、C B 1上的动点（不含端点），则四边形FDE B 1的俯视图可能是A ．B ．C ．D ． 答案：B4、（揭阳市2014届高三学业水平考试）图（1）中的网格纸是边长为1的小正方形，在其上用粗线画出了某多面体的三视图，则该多面体的体积为A.4B.8C.16D.20 答案：C俯视图正(主)视图 侧(左)视图5、（汕头市2014届高三上学期期末教学质量监测）三棱柱的侧棱与底面垂直，且底面是边长为2的等边三角形，其正视 图(如图所示)的面积为8，则侧视图的面积为( )A. 8B. 4C.答案：C 6、（肇庆市2014届高三上学期期末质量评估）某几何体的三视图如图2所示(单位：cm), 则其体积和表面积分别是（ ）A. 6π3cm 和12(1)π+2cmB. 6π3cm 和12π2cm C. 12π3cm 和12(1)π+2cm D. 12π3cm 和12π2cm答案：A 7、（中山市2014届高三上学期期末考试）把边长为1的正方形ABCD 沿对角线BD 折起，使得平面⊥ABD 平面CBD ，形成三棱锥ABD C -的正视图与俯视图如下图所示，则侧视图的面积为 （ ）A BC D ． 答案：B8、（珠海市2014届高三上学期期末）一个四棱锥的三视图如图所示，其中主视图是腰长为1的等腰直角三角形，则这个几何体的体积是（ ） A 、12 B 、1 C 、23D 、2 答案：A 9、（珠海一中等六校2014届高三第三次联考）已知正方形ABCD 的对角线AC 与BD 相交于E 点，将ACD ∆沿对角线AC 折起，使得平面ABC ⊥平面ADC （如图），则下列命题中正确的为( C )A. 直线AB ⊥直线CD, 且直线AC ⊥直线BDB. 直线AB ⊥平面BCD ，且直线AC ⊥平面BDEC. 平面ABC ⊥平面BDE ，且平面ACD ⊥平面BDED. 平面ABD ⊥平面BCD ，且平面ACD ⊥平面BDE 答案：C10、（东莞市2014届高三上学期期末调研测试）一个空间几何体的正视图与侧视图都是边长为2的正三角形，俯视图是半径为1的圆，则该几何体的体积是答案：A 二、填空题1、（省华附、省实、广雅、深中四校2014届高三上学期期末）某几何体的三视图如图所示,其中正（主）视图与侧（左）视图的边界均为直角三角形，俯视图的边界为直角梯形，则该几何体的体积为 .答案：8 2、（江门市2014届高三调研考试）若α、β是不重合的平面，a 、b 、c 是互不相同的空间直线，则下列命题中为真命题的是 ．（写出所有真命题的序号） ① 若α//a ，α//b ，则b a // ② 若α//c ，α⊥b ，则b c ⊥解法二图ABCD PEFH. .ACDB EF图5 图6ABCD PEF③ 若α⊥c ，β//c ，则βα⊥④ 若α⊂b ，α⊂c 且b a ⊥，c a ⊥，则α⊥a答案：②③（对1个3分，错1个2-分）三、解答题 1、（佛山市2014届高三教学质量检测（一））如图5,矩形ABCD 中,12AB =,6AD =,E 、F 分别为CD 、AB 边上的点,且3DE =,4BF =,将BCE ∆沿BE 折起至PBE ∆位置(如图6所示),连结AP 、EF 、PF ,其中PF =(Ⅰ)求证:PF ⊥平面ABED ； (Ⅱ)求直线AP 与平面PEF 所成角的正弦值.【解析】(Ⅰ)由翻折不变性可知,6PB BC ==,9PE CE ==,在PBF ∆中,222201636PF BF PB +=+==,所以PF BF⊥ ……………2分 在图1中,易得EF ==………3分在PEF ∆中,222612081EF PF PE +=+==,所以PF EF ⊥ …………………4分 又BF EF F = ,BF ⊂平面ABED ,EF ⊂平面ABED ,所以PF ⊥平面ABED . ………………6分（注：学生不写BF EF F = 扣1分）(Ⅱ)方法一:以D 为原点,建立空间直角坐标系D xyz -如图所示,则()6,0,0A ,(6,8,P , ()0,3,0E ,()6,8,0F ,所以(0,,25AP = ,(0,0,FP =,()6,5,0EF = , …………8分设平面PEF 的法向量为(),,x y z =n ,则0FP EF ⎧⋅=⎪⎨⋅=⎪⎩n n ,即0650z x y ⎧=⎪⎨+=⎪⎩,解得560x y z ⎧=-⎪⎨⎪=⎩ 令6y =-,得()5,6,0=-n ,……………………………………………12分设直线AP 与平面PEF 所成角为θ,则sin AP AP θ⋅===nn. 所以直线AP 与平面PEF. ……………………14分 方法二:过点A 作AH EF ⊥于H ,由(Ⅰ)知PF ⊥平面ABED ,而AH ⊂平面ABED所以PF AH ⊥,又EF PF F = ,EF ⊂平面PEF ,PF ⊂平面PEF , 所以AH ⊥平面PEF ,所以APH ∠为直线AP 与平面PEF 所成的角. ………………………9分 在Rt APF ∆中,AP ===…………………………11分在AEF ∆中,由等面积公式得AF ADAH EF ⋅==………………………………13分 在Rt APH ∆中,sin AH APH AP ∠===所以直线AP 与平面PEF. ………………………14分 2、（广州市2014届高三1月调研测试）在如图6的几何体中，平面CDEF 为正方形，平面ABCD 为等腰梯形，AB ∥CD ，BC AB 2=，60ABC ︒∠=，AC FB ⊥．（1）求证：⊥AC 平面FBC ；（2）求直线BF 与平面ADE 所成角的正弦值．（1）证明1：因为BC AB 2=，60ABC ︒∠=，在△ABC 中，由余弦定理可得BC AC 3=．……………………………2分 所以222AC BC AB +=．所以BC AC ⊥．………………………………………………………………3分 因为AC FB ⊥，BF BC B = ，BF 、BC ⊂平面FBC ，所以⊥AC 平面FBC ．……………………………………………………………4分证明2：因为60ABC ︒∠=，设BAC α∠=()0120α<<，则120ACB α∠=-．在△ABC 中，由正弦定理，得()sin sin 120BC ABαα=- ．……………………1分 因为BC AB 2=，所以()sin 1202sin αα-=．整理得tan 3α=，所以30α=．……………………………………………2分 所以BC AC ⊥．………………………………………………………………3分 因为AC FB ⊥，BF BC B = ，BF 、BC ⊂平面FBC ，所以⊥AC 平面FBC ．…………………………………………………4分（2）解法1：由（1）知，⊥AC 平面FBC ，FC ⊂平面FBC ，所以FC AC ⊥．因为平面CDEF 为正方形，所以FC CD ⊥．因为AC CD C = ，所以⊥FC 平面ABCD ．……………………………6分取AB 的中点M ，连结MD ，ME ，因为ABCD 是等腰梯形，且BC AB 2=，60DAM ∠=，所以MD MA AD ==．所以△MAD 是等边三角形，且ME BF ．………………7分取AD 的中点N ，连结MN ，NE ，则MN AD ⊥．………8分 因为MN ⊂平面ABCD ，ED FC ，所以ED MN ⊥． 因为AD ED D = ，所以MN ⊥平面ADE ． ……………9分 所以MEN ∠为直线BF 与平面ADE 所成角． ……………10分 因为NE ⊂平面ADE ，所以MN ⊥NE ．…………………11分因为2MN AD =，ME ==，……………………………12分 在Rt △MNE中，sin MN MEN ME ∠==．………………………………13分 所以直线BF 与平面ADE14分 解法2：由（1）知，⊥AC 平面FBC ，FC ⊂平面FBC ，所以FC AC ⊥．因为平面CDEF 为正方形，所以FC CD ⊥．因为AC CD C = ，所以⊥FC 平面ABCD ．……………………………………6分所以CA ，CB ，CF 两两互相垂直，建立如图的空间直角坐标系xyz C -．………………………7分 因为ABCD 是等腰梯形，且BC AB 2=，60ABC ︒∠= 所以CB CD CF ==．不妨设1BC =，则()0,1,0B ，()0,0,1F，)A，1,02D ⎫-⎪⎪⎝⎭，1,12E ⎫-⎪⎪⎝⎭， 所以()0,1,1BF =-，1,022DA ⎛⎫= ⎪ ⎪⎝⎭，()0,0,1DE = ．………………………9分设平面ADE 的法向量为=()x,y,z n ，则有0,0.DA DE ⎧⋅=⎪⎨⋅=⎪⎩ n n即0,20.y x z +=⎪=⎩ 取1x =，得=n ()1,是平面ADE 的一个法向量．…………………………11分 设直线BF 与平面ADE 所成的角为θ，则sin cos ,4BF BF BF ⋅θ=〈〉===n n n．………………13分 所以直线BF 与平面ADE 所成角的正弦值为4．………………………………14分 3、（增城市2014届高三上学期调研）如图3，边长为2的正方形ABCD ，E,F 分别是AB,BC 的中点，将△AED ， △DCF 分别沿DE,DF 折起，使A,C 两点重合于A '。

中山市高三级2013—2014学年度第一学期期末统一考试数学试卷（理科）本试卷共4页，20小题，满分150分．考试用时120分钟．注意事项：1、答卷前，考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上。

2、每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题上。

3、不可以使用计算器。

4、考试结束，将答题卡交回，试卷不用上交。

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设复数113i z =-，21i z =-，则12z z +在复平面内对应的点在( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．设全集U 是实数集,R {}22,M x x x =><-或{}2430N x x x =-+> 则图中阴影部分所表示的集合是 （ ） A ．{|21}x x -≤< B ．{|22}x x -≤≤ C ．{|12}x x <≤D ．{|2}x x <3．已知平面向量()21=，a ，()2x =-，b ，若a ∥b ， 则a +b 等于( ) A ．()2,1--B ．()2,1C ．()3,1-D ．()3,1-4．定义某种运算a S b =⊗，运算原理如上图所示，则式子131100lg ln )45tan 2(-⎪⎭⎫⎝⎛⊗+⊗e π的值为（ ）A ．4B ．8C ．11D ．135．把边长为1的正方形ABCD 沿对角线BD 折起，使得平面⊥ABD平面CBD ，形成三棱锥ABD C -的正视图与俯视图如下图所示，则侧视图的面积为 （ ）（第2题图）（第4题图）A B C D ． 6．下列四个命题中，正确的有①两个变量间的相关系数r 越小，说明两变量间的线性相关程度越低；②命题p ：“R ∈∃0x ，01020>--x x ”的否定p ⌝：“R ∈∀x ，012<--x x ”；③用相关指数2R 来刻画回归效果，若2R 越大，则说明模型的拟合效果越好； ④若23.0=a ，3.02=b ，2log 3.0=c ，则b a c <<． A ．①③④B ．①④C ．③④D ．②③7．对a ∀、b R ∈，运算“⊕”、“⊗”定义为：a b ⊕=,().()a a b b a b <⎧⎨≥⎩，a b ⊗=,().()a ab b a b ≥⎧⎨<⎩，则下列各式其中不恒成立的是（ ） ⑴a b a b a b =+⊗+⊕ ⑵a b a b a b =-⊗-⊕ ⑶[][]a b a b a b =⋅⊗⋅⊕ ⑷[][]a b a b a b =÷⊗÷⊕ A ．⑴、⑶B ． ⑵、⑷C ．⑴、⑵、⑶D ．⑴、⑵、⑶、⑷8. 已知函数)(x f y =)(R x ∈满足(2)2()f x f x +=，且[1,1]x ∈-时，()1f x x =-+，则当[10,10]x ∈-时，)(x f y =与4()log g x x =的图象的交点个数为( ) A ．13B ．12二、填空题：本大题共6小题，每小题5分，满分9．已知函数3log ,0()2,0x x x f x x >⎧=⎨≤⎩，则1(())9f f 10．如图，一不规则区域内，有一边长为1区域内随机地撒1000（含边界）的黄豆数为 375 平方米.（用分数作答）11．在二项式521x x ⎛⎫- ⎪⎝⎭的展开式中，含4x 的项的系数是 ．12．已知20πα<<,=+)6cos(πα53,则=αcos . 13．已知数列{}n a 为等差数列，若23a =，1612a a +=，则789a a a ++= .14．如图, //AB MN ，且2OA OM =，若OP xOA yOB =+，（其中,x y R ∈），则终点P 落在阴影部分（含边界） 时，21y x x +++的取值范围是 .三、解答题： 本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤． 15．（本题满分12分）设平面向量)sin ,(cos x x a =，31(,)2b =，函数()1f x a b =⋅+. （Ⅰ）求函数)(x f 的值域和函数的单调递增区间; （Ⅱ）当9()5f α=,且263ππα<<时,求2sin(2)3πα+的值. 16．（本题满分12分）某校从参加高三年级期末统考测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．（Ⅰ）估计这次测试数学成绩的平均分和众数； （Ⅱ）假设在[90，100]段的学生的数学成绩都不相同，且都超过94分．若将频率视为概率，现用简单随机抽样的方法，从95，96，97，98，99，100这6个数中任意抽取2个数，有放回地抽取了3次，记这3次抽取中，恰好是两个学生的数学成绩的次数为ξ，求ξ的分布列及数学期望E ξ．17．（本小题满分14分）如图，在底面是矩形的四棱锥ABCD P -中，PA ⊥平面ABCD ， 2==AB PA ，4=BC . E 是PD 的中点，（Ⅰ）求证：平面PDC ⊥平面PAD ；（Ⅱ）求二面角D AC E --的余弦值； （Ⅲ）求直线CD 与平面AEC 所成角的正弦值 18．（本小题满分14分）数列{n a }的前n 项和为n S ，2131(*)22n n S a n n n N +=--+∈． （Ⅰ）设n n b a n =+，证明：数列{}n b 是等比数列； （Ⅱ）求数列{}n nb 的前n 项和n T ；PBEDCA（Ⅲ）若1n n n b c b =-，数列{}n c 的前n 项和n T ，证明：n T <53． 19．（本小题满分14分）已知函数()x f x e kx =-，.（Ⅰ）若0k >，且对于任意0)(,>∈x f R x 恒成立，试确定实数k 的取值范围； （Ⅱ）设函数)()()(x f x f x F -+=，求证：1ln (1)ln (2)ln ()ln(2)()2n nF F F n e n N +*+++>+∈20．（本题满分14分）已知函数2()()f x x x a =-，2()(1)g x x a x a =-+-+（其中a 为常数）； （Ⅰ）如果函数()y f x =和()y g x =有相同的极值点，求a 的值；（Ⅱ）设0a >，问是否存在0(1,)3ax ∈-，使得00()()f x g x >，若存在，请求出实数a 的取值范围；若不存在，请说明理由．（Ⅲ）记函数()[()1][()1]H x f x g x =-⋅-，若函数()y H x =有5个不同的零点，求实数a 的取值范围．中山市高三级2013—2014学年度第一学期期末统一考试理科数学参考答案一、选择题：本大题共8小题，每小题5分，共40分．DAAD BCBC二、填空题：本大题共6小题，每小题5分，满分30分． 9.14 ; 10. 8311. 10;12.； 13. 45； 14. 4[,4]3三、解答题： 本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．15．（本题满分12分）设平面向量)sin ,(cos x x a =，)21,23(=b ，函数1)(+⋅=b a x f 。

12014年中山一中理科数学调研联考试卷本试题卷分第I 卷（选择题）和第II 卷（非选择题）.满分150分. 考试时间120分钟. 注意事项：1．答卷前，考生务必用2B 铅笔在“考生号”处填涂考生号。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；不按以上要求作答的答案无效。

参考公式：①锥体的体积公式Sh V 31=，其中S 是锥体的底面积，h 是锥体的高． ②22()()()()()n ad bc K a b c d a c b d -=++++，其中.n a b c d =+++③()22333311234n n n +++++=第I 卷（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分.只有一个是符合题目要求的.1.设集合2{|60}M x x x =+-<，{|13}N x x =≤≤，则M N ⋂= （ ） A ．[1,2) B ．[1,2] C ．(2,3] D ．[2,3]2.复数2(1)z i =+的实部是 ( )A.1B.0C.1-D. 23. 已知)(x f 是定义在R 上的函数， 命题:p )(x f 满足R x ∈∀，)()(x f x f -=-， 命题q ：0)0(=f ，则命题p 是命题q 的 ( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D.既不充分又不必要条件4、已知(3,2)a =-，(1,0)b =-， 向量a b λ+与向量2a b -垂直， 实数λ值为( )A ．17-B. 17C. 16-D. 165. 已知点F 是抛物线24y x =焦点， ,M N 是该抛物线上两点， ||||6MF NF +=则MN 中点到准线距离为 （ ）A ．32B ．2C ．3D ．46、已知l 是直线，α、β是两个不同的平面，下列命题中的真命题是 （ ）A. 若//l α，//l β，则//αβB. 若βα⊥，//l α，则β⊥l . C ．若//l α，βα//，则//l β D. 若α⊥l ，//l β，则 βα⊥7.设0ω>，函数sin()3y x πω=+的图象向右平移43π个单位长度后与原图象重合，则ω的最小值为 （ ）A ．23B ．43C ．32 D ．3 8. 非空集合G 关于运算⊕满足：（1）对任意的,,a b G ∈都有,a b G ⊕∈(2)存在,e G ∈都有,a e e a a ⊕=⊕= (3) 对任意的,,,a b c G ∈ 都有()()a b c a b c ⊕⊕=⊕⊕，则称G 关于运算⊕为“融洽集”。

90t ≤？开始1k = 1t =是t t t k =+⋅1k k =+否 输出t 结束第6题图中山市2014届高三数学综合试题（三）理科一、选择题：本大题共8小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）复数3212i Z i-=-，则复数Z 对应的点在 （ ）A ．第一象限或第三象限B ．第二象限或第四象限C ．x 轴正半轴上D ．y 轴负半轴上 （2）已知椭圆的一个焦点为F(1,0),离心率21=e ，则椭圆的标准方程为（ ） A.122=+y x 2 B.1222=+y x C.14=+3y x 22 D.13=+4y x 22(3) ,a b 为非零向量，“函数2()()f x ax b =+ 为偶函数”是“a b ⊥”的（ ） （A ） 充分但不必要条件 （B ） 必要但不充分条件 （C ） 充要条件 （D ） 既不充分也不必要条件（4）如图所示，茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为（ ）（A ）52 （B ）107 （C ）54 （D ）109 （5）已知实数x 、y 满足⎪⎩⎪⎨⎧≤≤--≥-+301,094y y x y x ，则x －3y 的最大值是（ ）A ．－1B ．0C ．1D ．2 （6）如果执行右面的程序框图，那么输出的t =（ ） A ．96 B ．120C ．144D ．300(7)已知二项式21()2n x x+（n N +∈）展开式中，前三项的二项式系数和是56，则展开式中的常数项为 （ ）A ．45256B ．47256C ．49256D ．51256(8)函数的定义域为D ，若满足：①()x f 在D 内是单调函数；②存在],[b a 使得()x f 在],[b a 上的值域为甲 8 99 8 0 1 2 3 3 79 乙∙OAB CDP图4]2,2[ba ，那么就称函数()x f y =为“成功函数”,若函数()()()1,0l o g ≠>+=c c t c x f x c 是“成功函数”，则t 的取值范围为（ ）A.()∞+，0B.⎪⎭⎫ ⎝⎛∞-41, C.⎪⎭⎫⎝⎛+∞,41 D.⎪⎭⎫ ⎝⎛41,0第Ⅱ卷本卷包括必考题和选考题两部分。

幂函数与函数的零点一、选择题（9*5=45分）1. 【广东省中山市华侨中学2014届高三第一次模拟考试】下列命题中正确的是( )①幂函数的图象都经过点()1,1和点()0,0； ②幂函数的图象不可能在第四象限；③当0=n 时，函数=n y x 的图象是一条直线； ④幂函数=n y x 当0>n 时是增函数；⑤幂函数=n y x 当0<n 时在第一象限内函数值随x 值的增大而减小．A. ①和④B.④和⑤C.②和③D.②和⑤2. 【山西省太原市2014届高三第二次学段评】若()f x 是幂函数，且满足()()422f f =，则()2f =（ ）A.4B.1C.3D.23. 【陕西省澄城县寺前中学2014届高三第二次月考】）设1310.4y =，1320.5y =，1430.5y =，则（ ）A.321y y y <<B.123y y y <<C.231y y y <<D.132y y y <<4. 【2011·石家庄月考】如图中曲线是幂函数α=y x 在第一象限的图象．已知α取122，±±四个值，则相应于曲线1234 ， ， ，C C C C 的α值依次为( )A.11222-2 ，- ， ，B.112222 ， ， - ， - C.112222- ，-， ， D.112222 ， ， -， -5. 【山东省德州市2014届高三上学期期末考试】函数()2xf x e x =+-的零点所在的区间为（ ）A.()2,1--B.()1,0-C.()0,1D.()1,26. 【广东省中山市华侨中学2014届高三第二次模拟考试】已知函数()()()4040x x x f x x x x +<⎧⎪=⎨-≥⎪⎩，，，则函数()f x 的零点个数为（ ） A.1 B.2 C.3 D.47.【2011·烟台模拟】若定义在R 上的偶函数()f x 满足()()2+=f x f x ，且当(]0,1∈x 时，()=f x x ，则函数()3log =-y f x x 的零点个数是( )A.多于4个B.4个C.3个D.2个8. 【天津市和平区2014届高三上学期期末考试】函数()22,01ln ,0x x x f x x x ⎧+≤=⎨-+>⎩的零点个数为（ ）A.4B.3C.2D.1 9. 【2011年高考陕西卷文】方程cos x x =在(),-∞+∞内（ ） A.没有根 B.有且仅有一个根 C.有且仅有两个根 D.有无穷多个根二、填空题（5*5=25分）1. 【2010年高考安徽卷文】设2535a ⎛⎫= ⎪⎝⎭，3525b ⎛⎫=⎪⎝⎭，2525c ⎛⎫= ⎪⎝⎭，则a 、b 、c 的大小关系是2. 【四川省自贡市普高2014届高三第二次诊断性考试】已知幂函数()y f x =的图象过点12,22⎛⎫ ⎪ ⎪⎝⎭，则()4f 的值为 3. 【广东省中山市华侨中学2014届高三第三次模拟考试】函数()1212xf x x ⎛⎫=- ⎪⎝⎭的零点个数为4. 【2011·深圳模拟】已知函数()2=+xf x x ，()ln =+g x x x ，()1=--h x x x 的零点分别为123,,x x x ，则123,,x x x 的大小关系是______________．5. 【2011·葫芦岛模拟】已知函数()()223--*=∈mm f x xm N 的图象关于y 轴对称，且在()0,+∞上是减函数，则满足33(1)(32)--+<-m m a a 的a 的取值范围 ．。

广东省各地2014届高三上学期期末考试数学理试题分类汇编圆锥曲线一、选择题1、（广州市2014届高三1月调研测试）若点(1,0)A 和点(4,0)B 到直线l 的距离依次为1和2，则这样的直线有A ．1条B ．2条C ．3条D ．4条 答案：C2、（惠州市2014届高三第三次调研考）设椭圆22221(0,0)x y m n m n+=>>的右焦点与抛物线28y x =的焦点相同，离心率为12，则此椭圆的方程为（ ）A ．2211612x y +=B ．2211216x y +=C ．2214864x y +=D ．2216448x y += 答案：A3、（揭阳市2014届高三学业水平考试）若双曲线22221x y a b-=的离心率为3，则其渐近线的斜率为-A.2±B.2±C.12±D. 22± 答案：B4、（增城市2014届高三上学期调研）与圆221x y +=及圆228120x y x +-+=都相外切的圆的圆心在(A)一个椭圆上 (B) 一支双曲线上 (C) 一条抛物线上 (D) 一个圆上 答案：B5、（江门市2014届高三调研考试）已知点)2 , 1(A ，)1 , 2(B ，则线段AB 的垂直平分线的方程是 A ．03=-+y x B ．01=+-y x C ．0=-y x D ．0=+y x 答案：C6、（江门市2014届高三调研考试）平面直角坐标系中，抛物线x y 212=与函数x y ln =图象的交点个数为A ．0B ．1C ．2D ．3 答案：D 二、填空题1、（佛山市2014届高三教学质量检测（一））设12,F F 是双曲线22124y x -=的两个焦点，P 是双曲线与椭圆2214924x y +=的一个公共点，则12PF F ∆的面积等于_________答案：242、（省华附、省实、广雅、深中四校2014届高三上学期期末）已知直线:l x p =过抛物线2:4C y x =的焦点，直线l 与抛物线C 围成的平面区域的面积为,S 则p =______ ，S = .答案：81,.3三、解答题1、（佛山市2014届高三教学质量检测（一）） 如图7所示,已知椭圆C 的两个焦点分别为()11,0F -、()21,0F ,且2F 到直线390x y --=的距离等于椭圆的短轴长. (Ⅰ) 求椭圆C 的方程；(Ⅱ) 若圆P 的圆心为()0,P t (0t >),且经过1F 、2F ,Q 是椭圆C 上的动点且在圆P 外,过Q 作圆P 的切线,切点为M ,当QM 的最大值为322时,求t 的值.【解析】(Ⅰ)设椭圆的方程为22221x y a b+=(0a b >>),依题意,19242b -==, …………………………………………1分所以2b = ……………………………………2分 又1c =, ……………………………………3分所以2225a b c =+=, ………………………………………4分所以椭圆C 的方程为22154x y +=. ……………………………………………………5分 (Ⅱ) 设(),Q x y (其中22154x y +=), ……………………………………………6分 圆P 的方程为()2221x y t t +-=+,………………………………………7分因为PM QM ⊥, 所以221QM PQ t =--()2221x y t t =+---…………………………………8分()2214444y t t =-+++ ……………………………9分 当42t -≤-即12t ≥时,当2y =-时,QM 取得最大值, ……………………10分且max 32432QM t =+=,解得3182t =<(舍去). ……………………11分. . xyF1F 2O 图7当42t ->-即102t <<时,当4y t =-时,QM 取最大值, ……………………12分 且2max 32442QM t =+=,解得218t =,又102t <<,所以24t =.………13分综上,当24t =时,QM 的最大值为322. ……………………………………14分2、（广州市2014届高三1月调研测试）如图7，已知椭圆C 的方程为()222210x y a b a b +=>>，双曲线12222=-by a x 的两条渐近线为21,l l ．过椭圆C 的右焦点F 作直线l ，使1l l ⊥，又l 与2l 交于点P ，设l 与椭圆C 的两个交点由上至下依次为A ，B ．（1）若1l 与2l 的夹角为60°，且双曲线的焦距为4，求椭圆C 的方程；（2）求||||AP FA 的最大值． 解：（1）因为双曲线方程为12222=-by a x ，所以双曲线的渐近线方程为x aby ±=．………………………………………………1分 因为两渐近线的夹角为60且1<ab，所以30POF ∠= ． 所以a b 3tan 303==．…………………………………………………………2分 所以b a 3=．因为2c =，所以2222=+b a ， 所以3a =，1b =．所以椭圆C 的方程为2213x y +=．…………………………………………4分 （2）因为1l l ⊥，所以直线l 与的方程为()ay x c b=-，其中22c a b =-．………………5分 因为直线2l 的方程为by x a=， 联立直线l 与2l 的方程解得点2,a ab P c c ⎛⎫⎪⎝⎭．……………………………………6分Ox yBAF P l 1l l 2O x yBA F P l 1l l 2图7设||||FA AP λ=，则FA AP λ= ．……………………………………………………7分 因为点(),0F c ，设点()00,A x y ，则有()20000,,a abx c y x y c c λ⎛⎫-=-- ⎪⎝⎭．解得()2201c a x c λλ+=+，()01ab y c λλ=+．………………………………………………8分因为点()00,A x y 在椭圆22221x y a b+=上，所以()()()()2222222222111c a ab a c b c λλλλ++=++．即()()222224221c aa a c λλλ++=+．等式两边同除以4a 得22222()(1),(0,1).e e e λλλ++=+∈……………………10分所以24222222322e e e e e λ-⎛⎫==--++ ⎪--⎝⎭………………………………………11分 ()()2222223322212e e ≤--⋅+=-=--．………………………12分所以当22222e e -=-，即22e =-时，λ取得最大值21-．………………13分故||||AP FA 的最大值为21-．………………………………………14分 3、（增城市2014届高三上学期调研）已知点()()1,0,1,0,A B -直线AM,BM 相交于点M ，且2MA MB k k ⨯=-.（1）求点M 的轨迹C 的方程；（2）过定点（0,1）作直线PQ 与曲线C 交于P,Q 两点，且322PQ =，求直线PQ 的方程.（1）解：设M(x,y), 1分 则(),,111MA Mb y y k k x x x ==≠±+- 3分 ∴211y y x x ⨯=-+- 4分∴2212y x +=()1x ≠± 6分（条件1分） （2）当直线PQ 的斜率不存在时，即PQ 是椭圆的长轴，其长为22，显然不合，即直线PQ 的斜率存在， 7分设直线PQ 的方程是y=kx+1,()()1122,,,,P x y Q x y则1212()y y k x x -=-， 8分联立22121y x y kx ⎧+=⎪⎨⎪=+⎩，消去y 得()222210k x kx ++-= 9分 ∵()()()222442810k k k ∆=++=+>，∴k R ∈, 10分12122221,22k x x x x k k +=-=-++ 11分 ∴()()()()22221212121214PQ x x y y k x x x x ⎡⎤=-+-=++-⎣⎦221222k k +=+， 12分∴322PQ =221222k k +=+，22,2k k ==±， 13分所以直线PQ 的方程是y=2±x+1。

中山市华侨中学2014届高考模拟（三）数 学 试 卷（文）考试范围：集合、逻辑用语、函数导数、三角函数、解三角、向量、复数、立体几何 本试卷共4页，20小题，满分150分．考试用时120分钟． 2013-11-01 15：00-17：00 参考公式：柱体体积公式 锥体体积公式 球体积公式 球的表面积， （其中S 为底面面积，h 为高）V Sh = =13V sh334R V π= 24R S π= （其中R 为球的半径） 一、选择题：(本大题共 10 小题；每小题 5 分，满分 50 分) 1．已知{}{}|10,2,1,0,1A x x B =+>=--，则()R C A B⋂=------（ ）A ．{}2,1--B ．{}2-C ．{}1,0,1-D ．{}0,12．复数()1()z a a ia R =++∈是纯虚数，则2z 的值为------（ ）A ．0B ．1-C ．iD ． i -3．命题“042,2≤+-∈∀x x R x ”的否定为------------------ --（ ） A ． 042,2≥+-∈∀x x R x B. 042,2≤+-∉∀x x R x C ．042,2>+-∉∃x x R x D ．042,2>+-∈∃x x R x [ 4. 下列函数中,既是偶函数又在区间(0,+ ∞)上单调递减的是-----（ ）A ．1y x =B ．lg ||y x =C ．21y x =-+D ．xy e -= 5．函数f （x ）＝x121x 2⎛⎫- ⎪⎝⎭的零点个数为-----（ ）A .0 B.1 C.2 D.36.如右上图，在ABC ∆中，点D 是BC 边上靠近B 的三等分点，则=AD ---（ ）A ． AC AB 3132- B ． 3231+C ． 3132+ D ． 3231-7．已知函数3()sin 2()2f x x x π⎛⎫=+∈ ⎪⎝⎭R ，下面结论错误．．的是---（ ）（第9题）A ．函数)(x f 的最小正周期为πB ．函数)(x f 是偶函数C ．函数)(x f 的图象关于直线4x π=对称 D ．函数)(x f 在区间0,2π⎡⎤⎢⎥⎣⎦上是增函数 8.设α、β是两个不重合的平面，m 、n 是两条不重合的直线，则以下结论错误．．的是--（ ） A.若α//β，m ⊂α，则 m//β B. 若m//α，m//β，n αβ=I ，则 m//n C. 若m ⊂α，n ⊂α，m//β，n//β，则 α//β D.若m//α， m ⊥β，则 α⊥β 9、（2013深圳二模）某几何体的三视图如图所示,其俯视图是由一个半圆与其直径组成的图形,则此几何体的体积是 -------（ ）A ．20π3B ．6πC ．10π3D ．16π310．已知定义在R 上的函数)(x f 满足1)2()4(=-=f f ， )(x f '为)(x f 的导函数，且导函数)(x f y '=的图象如右图所示． 则不等式1)(<x f 的解集是-----（ ）A ．)0,2(-B ．)4,2(-C ．)4,0(D ．),4()2,(+∞--∞Y二．填空题(共4小题，每小题5分，共20分，将正确答案填在题中横线上)11.已知向量=1），)1,0(b -=，=（k。

中山市华侨中学2014届高三第三次模拟考试理科综合科试题本试卷分第Ⅰ卷（选择题)和第Ⅱ卷（非选择题)两部分.满分300分，考试时间:150分钟第Ⅰ卷(选择题，共118分）相对原子质量:H─1C─l2、N─14、O─16、Na─23、Si─24、S─32、Mg─24、Na─23、Al─27、Cl─35。

5一、单选题（每小题只有一个选项是符合题意，每小题4分，共64分)1．下列对有关实验的叙述，正确的是( )A．在叶绿体色素提取实验中,研磨绿叶时应加有机溶剂，如无水乙醇B．做植物细胞质壁分离和复原实验时,可用30%的KNO3溶液代替30％的蔗糖溶液C．观察洋葱根尖细胞有丝分裂实验中，用卡诺氏液对根尖进行解离D．检测试管中的梨汁是否有葡萄糖，可加入适量斐林试剂后，摇匀并观察颜色变化2．生物膜将真核细胞分隔成不同的区室，使得细胞内能够同时进行多种化学反应，而不会相互干扰.下列叙述正确的是( ）A．细胞核是mRNA合成的主要场所B．高尔基体是肽链合成和加工的场所C．线粒体将葡萄糖氧化分解成CO2和H2O D．溶酶体合成和分泌多种酸性水解酶3．如图所示细胞膜的亚显微结构，其中a和b为物质的两种运输方式，下列对细胞膜结构和功能的叙述错误的是（）A．若图示为肝细胞膜，则b可代表CO2进出细胞的方向B．细胞间的识别、细胞的癌变与①有密切的关系C．适当提高温度将加快②和③的流动速度D．不同物种的细胞中①②③的种类均不相同4．下列关于细胞生命历程的叙述,正确的是( ）A．人体细胞的衰老就是人体的衰老B．细胞分化导致遗传物质发生改变C．脑细胞因缺氧而死亡的现象属于细胞坏死D．癌变细胞的呼吸速率降低、核体积增大5．图甲所示为基因表达过程,图乙为中心法则，①~⑤表示生理过程。

下列叙述正确的是（）A．图甲所示为染色体DNA上的基因表达过程B．红霉素影响核糖体在mRNA上的移动，从而影响转录过程C．图甲所示过程为图乙中的①②③过程D．图乙中涉及碱基互补配对的过程为①②③④⑤6．大豆植株的体细胞含40条染色体。

中山市华侨中学2014届高三第三次模拟考试理科综合科试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

满分100分，考试时间：50分钟第Ⅰ卷(选择题，共36分)相对原子质量：H─1C─l2、N─14、O─16、Na─23、Si─24、S─32、Mg─24、Na─23、Al─27、Cl─35.5一、单选题（每小题只有一个选项是符合题意，每小题4分，共24分）7．化学与生产、生活密切相关。

下列叙述正确的是（）A．合金材料中不可能含有非金属元素B．信息产业中的光缆的主要成分是单质硅C．采用催化措施，将汽车尾气中的CO和NO转化为无害气体D．14C可用于文物年代的鉴定，14C与12C互为同素异形体8．能在水溶液中大量共存的一组离子是（）A．H+、Fe3+、I－、SO42－B．Al3+、Mg2+、HCO3－、Cl－C．K+、Ag+、Ca2+、NO3－D．H+、Na+、AlO2－、Cl－9．设N A为阿伏加德罗常数的数值，下列叙述正确的是（）A．60g SiO2中含有N A个SiO2分子B．标况下，22.4L SO3的分子数为N AC．1L 0.5 mol·L－1 CuCl2溶液中含有0.5N A个Cu2＋D．15.6 g Na2O2与过量CO2反应时，转移的电子数为0.4N A1011．下列有关反应的化学方程式或离子方程式正确的是（）A．硫酸铝与过量的氨水反应：Al3+ + 4OH—== AlO2—+ 2H2OB．除去铁粉中的铝：2Al + 2NaOH == 2NaAlO2 + H2↑C．实验室制取Cl 2的离子方程式：MnO2 + 4HCl(浓) Mn2+ + 2Cl—+ Cl2↑+ 2H2OD．浓硫酸与铜的反应：Cu + 2H2SO4 (浓) CuSO4 + SO2↑+ 2H2O12．从石英砂制取并获得高纯硅的主要化学反应如下（）①SiO2+ 2C Si（粗）+2CO↑SiCl4②Si(粗) +2Cl③SiCl 4 + 2H2 Si（纯）+ 4HCl 关于上述反应的分析不正确的是A．①、③是置换反应，②是化合反应B．高温下，焦炭与氢气的还原性均强于硅C．粗硅中可能含有SiO2、C等杂质D．高温下将石英砂、焦炭、氯气、氢气按一定比例混合可得高纯硅二、双项选择题（每小题中只有两个答案是正确的，全部选对得6分，只选对一个答案的得3分，有错选或不选得零分，每题6分，共12分）22．有关下列物质说法正确的是（）A．Na、Mg、Fe等金属在一定条件下与水反应都生成H2和对应的碱B．相同温度下，等物质的量浓度的Na2CO3和NaHCO3溶液pH：Na2CO3 > NaHCO3C．将两支蘸有浓盐酸和浓氨水的玻璃棒相互靠近有大量白烟产生D．HCl、NH3、CO2都极易溶于水，都可用水作吸收剂做喷泉实验23．下列实验装置设计正确、且能达到目的的是（）A．实验Ⅰ：制取纯净氢氧化亚铁B．实验Ⅱ：证明非金属性强弱：S＞C＞SiC．实验Ⅲ：除去CO2中的HClD．实验Ⅳ：继续煮沸溶液至红褐色，停止加热，当光束通过体系时可产生丁达尔效应第Ⅱ卷（共64分）三、非选择题30.（16分）Na2SO3是抗氧剂。

一、选择题：本大题共8小题，每小题5分，满分40分.1.已知集合2{0,1,2,3,4},{|20}U A x x x ==-=，则U A ð=（ ） A ．{1,2,3} B ．{0,1,3,4} C ．{1,3,4} D ．{0,3,4}2. 复数32i1i+等于（ ） A.1i - B. 1i -+ C. 1i + D.1i -- 3.已知1sin cos 3αα+=，则22cos ()14πα--=（ ）A.89 B. 1718 C. -89 D. 23- 4．已知数列{n a ｝是各项均为正数的等比数列，若2342,216a a a =+=，则5a =（ ）A.4B.8C.16D.325. 关于函数3()31f x x x =-+，下列说法正确的是（ ） A ．()f x 是奇函数且x=-1处取得极小值 B ．()f x 是奇函数且x=1处取得极小值 C ．()f x 是非奇非偶函数且x=-1处取得极小值 D ．()f x 是非奇非偶函数且x=1处取得极小值6.一简单组合体的三视图及尺寸如下图所示，则该组合体的体积是（ ）A. 76B. 80C. 96D. 1127.已知不共线的平面向量a ，b ，c ，两两所成的角相等，且｜a ｜＝1，｜b ｜＝1，｜c ｜＝3，则｜a ＋b ＋c ｜等于（ ）A ．2 B.5 C.2或5 8.各大学在高考录取时采取专业志愿优先的录取原则．一考生从某大学所给的7个专业中，选择3个作为自己的第一、二、三专业志愿，其中甲、乙两个专业不能同时兼报，则该考生不同OCBAD的填报专业志愿的方法有（ ）A.210种B. 180种C.120种D.95种二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分。

(一）必做题（9-13题）9.在△ABC 中，角A B C ，，的对边分别为a b c ，，，且a b c <<2sin b A =． 则角B 的大小为 ；10．由曲线1,1,===y x e y x 所围成的图形面积是 .11. 在平面直角坐标系xOy 中，抛物线22(0)x py p =>上纵坐标为1的点到焦点的距离为3，则焦点到准线的距离为 .12. 下图是某算法的程序框图，当输出的结果100>T 时，整数s 的最小值是 .13. 已知O 是坐标原点，点()1,0A -，若()y x M ,为平面区域⎪⎩⎪⎨⎧≤≤≥+212y x y x上的一个动点，则 OA OM +的最小值是 . （二）选做题（14 - 15题，考生只能从中选做一题）14．(几何证明选做题)如下图，AB 是圆O 的直径，延长AB 至C ， 使2AB BC =，且2BC =，CD 是圆O 的切线，切点为D ，连接AD ， 则CD =________，DAB ∠=________．15.（极坐标与参数方程选讲选做题）极坐标系中，曲线4sin ρθ=-和cos 1ρθ=相交于点,A B ，则AB ＝ .三、解答题：本大题共6小题，满分80分。