中心对称(一)

《中心对称》作业设计方案（第一课时）一、作业目标本作业设计旨在通过《中心对称》的学习，使学生能够理解并掌握中心对称的基本概念、性质和判断方法，能够运用所学知识解决简单的几何问题，并培养学生的空间想象能力和逻辑思维能力。

二、作业内容（一）知识回顾1. 复习已学过的轴对称、平移等基本图形变换。

2. 回顾对称图形的特点，引出中心对称的概念。

（二）新课内容1. 中心对称定义：一个图形关于某一点做180度旋转后与原图重合，则称该图形为中心对称图形。

2. 中心对称的性质：中心对称的两个对应点与对称中心的连线互相垂直且平分对方线段。

3. 判断方法：通过观察图形的性质或作图法判断是否为中心对称图形。

（三）应用练习1. 基础练习：选择简单的图形判断其是否为中心对称，并说明理由。

2. 进阶练习：利用中心对称的性质，在给定的图形中找出所有中心对称的子图形。

3. 综合练习：结合其他几何知识，解决一些实际问题，如利用中心对称设计图案等。

三、作业要求1. 学生需认真完成每一道题目，理解并掌握中心对称的基本概念和性质。

2. 在完成进阶练习时，学生应注重运用所学知识分析问题、解决问题，提高自己的空间想象能力和逻辑思维能力。

3. 综合练习部分，学生可以尝试自己设计一些简单的图案，并判断其是否为中心对称图形，以增强学习的趣味性和实践性。

4. 作业完成后，学生需自行检查答案，确保准确无误。

如有疑问，可向老师或同学请教。

四、作业评价1. 教师将根据学生的作业完成情况，对学生的学习情况进行评估和反馈。

2. 评价标准包括学生对中心对称概念的理解程度、对性质的掌握情况以及解题的准确性和条理性等。

3. 对于优秀作业，教师将给予表扬和鼓励，以激发学生的学习积极性和自信心。

五、作业反馈1. 教师将针对学生在作业中出现的错误和不足进行讲解和指导，帮助学生查漏补缺。

2. 学生应根据教师的反馈，及时改正错误，巩固所学知识，提高学习效果。

3. 教师和学生应保持良好的沟通，共同探讨学习中遇到的问题，促进教学相长。

10.4.中心对称图形（1）
1.了解什么是中心对称图形，能判断一个图形是否是中心对称图形；
2.掌握中心对称的慨念，能找出图形对应的点和线段；
3.理解轴对称、中心对称、旋转对称这三种变换的区别和联系。

教材第127-129页，完成填空。

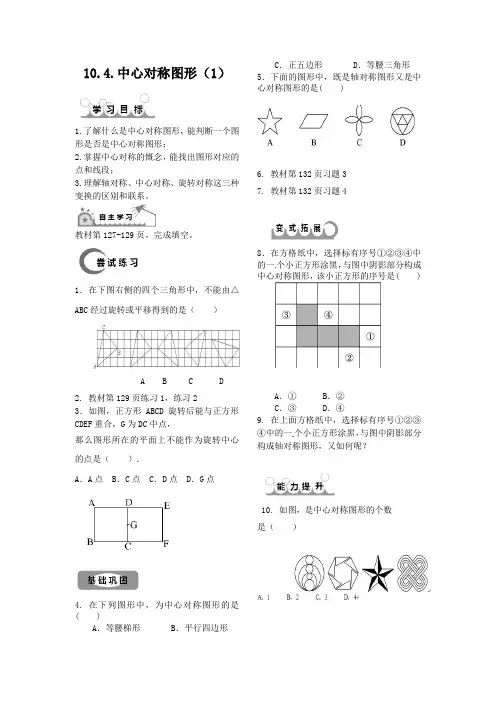
1．在下图右侧的四个三角形中，不能由△
ABC经过旋转或平移得到的是（）
A B C D
2. 教材第129页练习1，练习2
3．如图，正方形ABCD旋转后能与正方形CDEF重合，G为DC中点，
那么图形所在的平面上不能作为旋转中心
的点是（）．
A．A点B．C点C．D点D．G点
4. 在下列图形中，为中心对称图形的是( )
A．等腰梯形 B．平行四边形
C．正五边形 D．等腰三角形5．下面的图形中，既是轴对称图形又是中心对称图形的是( )
6. 教材第132页习题3
7. 教材第132页习题4
8．在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形，该小正方形的序号是(
)
A．① B．②
C．③ D．④
9. 在上面方格纸中，选择标有序号①②③
④中的一个小正方形涂黑，与图中阴影部分构成轴对称图形，又如何呢？
10. 如图，是中心对称图形的个数
是（）
11.下列图案中，既是轴对称图形又是中心对称图形的是（）
A．B．
C．D．
12.下列图形中，是中心对称图形但不是轴对称图形的是
答案：
1.B;3.A;4.B.5.C;8.B;9.有两种情
况：②左边第二格或②上边第二格；
10.B;11.B;12.A.。

图形的平移轴对称（图形）中心对称（图形）对称轴——直线对称中心——点图形沿某方向平移一定距离图形沿对称轴对折（翻折180°）后重合图形绕对称中心旋转180°后重合对应点的连线平行或在同一直线上，对称点的连线被对称轴垂直平分对应点的连线段相等。

对称点连线经过对称中心，且被对称中心平分中心对称图形（一）知识点一．图形旋转1．图形旋转的有关概念：图形的旋转、旋转中心、旋转角；在平面内,将一个图形一个定点转动一定的角度,这样的图形运动称为图形的旋转。

这个定点称为旋转中心，旋转的角度称为旋转角。

注意点：旋转角通常与旋转方向有关，因此在写旋转角时通常要说明旋转方向。

2．旋转图形的性质：（1）旋转前、后的图形全等。

（2）对应点到旋转中心的距离相等。

（3）每一对对应点与旋转中心的边线所成的角彼此相等。

二．中心对称 1．中心对称的有关概念：中心对称、对称中心、对称点把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么称这两个图形关于这点对称，也称这两个图形成中心对称，这个点叫做对称中心，两个图形中的对应点叫做对称点。

2．中心对称的基本性质：（1）成中心对称的两个图形具有图形旋转的一切性质。

（2）成中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。

三．中心对称图形1.中心对称图形的有关概念：中心对称图形、对称中心把一个平面图形绕某一点旋转180 °，如果旋转后的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形。

这个点就是它的对称中心。

2.中心对称与中心对称图形的区别与联系如果将成中心对称的两个图形看成一个图形，那么这个整体就是中心对称图形；反过来，如果把一个中心对称图形沿着过对称中心的任一条直线分成两个图形，那么这两个图形成中心对称。

3.图形的平移、轴对称（折叠）、中心对称（旋转）的对比四．平行四边形1.定义：两组对边分别平行的四边形叫做平行四边形。

点对称图形（中心对称图形）教学目的:1、了解中心对称图形的概念、知道与轴对称图形之间的区别与联系；能找出线段、平行四边形的对称中心；会画矩形、菱形、正方形的对称轴。

2、培养学生的观察能力、动手能力、自学能力、计算能力、逻辑思维能力；3、在教学中渗透事物总是相互联系又相互区别的辨证唯物主义观点。

教学重点：定理1、定理2及逆定理。

教学难点：理解中心对称的概念。

教学程序一、复习创情导入什么叫做轴对称图形？轴对称图形有什么性质？如何判定两个图形关于对称中心对称？二、授新1、提出问题（1）什么叫做点对称（中心对称）图形？对称中心？中心对称图形与中心对称有何联系和区别？（2）点对称与轴对称有什么区别和联系？（3）用硬纸做一个中心对称图形。

（4）线段、平行四边形、矩形、菱形、正方形是否都是中心对称图形？是否都是轴对称图形？（5）举例说明中心对称图形的应用。

2、自学质疑：自学课本P106--108页，完成预习题，并提出疑难问题。

3、分组讨论；讨论自学中不能解决的问题及学生提出问题。

4、反馈归纳（1）什么叫做点对称（中心对称）图形？对称中心？中心对称图形与中心对称有何联系和区别？把一个图形绕它的某一点旋转1800，如果旋转后的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形。

完成预习思考题（1）；（2）用硬纸做一个中心对称图形。

观察说明自制中心对称图形，说明它是中心对称图形；（3）线段、平行四边形、矩形、菱形、正方形是否都是中心对称图形？是否都是轴对称图形？（4）举例说明中心对称图形的应用。

中心对称图形形状匀称美观：建筑、工艺做装饰图案；能够在所在平面内绕对称中心平稳旋转：旋转的零部件，如叶轮等。

5、尝试练习（1）完成跟踪练习（1）---（3）题，并总结，为什么三叶轮、五角星不是中心对称图形，有什么规律？中心对称图形中的对比数为偶数，才有对应点。

（2）完成达标练习和综合练习；（3）其它；6、深化创新（1）什么是中心对称？（两个图形）（2）中心对称的性质定理1：关于中心对称的两个图形是全等的中心对称的性质定理2：关于中心对称的两个图形，对称点连线都经过对称中心，并被对称中心平分。

中心对称例子
以下是 9 条关于中心对称例子：
1. 嘿，你看蝴蝶的翅膀，那两边是不是完美的中心对称呀！就像是我们照镜子，左边和右边简直一模一样，这多神奇啊！
2. 哇塞，扑克牌里的桃心不也是中心对称的嘛！那桃心的左右两边，可不就像是双胞胎一样嘛！
3. 哎呀呀，剪纸中的一些图案也是中心对称的呀！比如那些漂亮的花朵剪纸，把它对折起来两边完全重合，这难道不令人惊叹吗？
4. 想想看，圆形的盘子也是中心对称的哦！不管你怎么旋转它，看起来都是一样的，这多有趣呀！
5. 嘿，你知道吗，雪花的形状好多都是中心对称的呢！那精致的模样，就如同大自然精心雕琢的艺术品一样，难道你不觉得很奇妙吗？
6. 哇哦，古代建筑中的一些图案装饰也是中心对称的呢！那工整对仗的样子，真的是太美啦！
7. 咦，太极图呀，多么典型的中心对称例子！那黑白两半，和谐又平衡，不正像生活中的阴阳两面吗？
8. 哈哈，我们每天都能看到的时钟盘面其实也是中心对称的呀！时针和分针走过的轨迹，左右两边不也是对称的嘛，多有意思！
9. 啧啧，天安门城楼左右两边也是中心对称的呢！那宏伟的气势，真的是让人肃然起敬啊！
我觉得中心对称真的是无处不在，给我们的生活带来了很多奇妙和美好的感受呢！。

中心对称（优秀5篇）篇一：知识归纳篇一1．中心对称把一个图形绕着某一点旋转，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称，这个点叫做对称中心，两个图形关于点对称也称中心对称，这两个图形中的对应点，叫做关于中心的对称点．中心对称的两个图形具有如下性质：（1）关于中心对称的两个图形全等；（2）关于中心对称的两个图形，对称点的连线都过对称中心，并且被对称中心平分．判断两个图形成中心对称的方法是：如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称．2．中心对称图形把一个图形绕某一点旋转，如果旋转后的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．矩形、菱形、正方形、平行四边形都是中心对称图形，对角钱的交点就是它们的对称中心；圆是中心对称图形，圆心是对称中心；线段也是中心对称图形，线段中点就是它的对称中心．知识结构重点、难点分析：本节课的重点是中心对称的概念、性质和作已知点关于某点的对称点。

因为概念是推导三个性质的主要依据、性质是今后解决有关问题的理论依据；而作已知点关于某个点的对称点又是作中心对称图形的关键。

本节课的难点是中心对称与中心对称图形之间的联系和区别。

从概念角度来说，中心对称图形和中心对称是两个不同而又紧密相联的概念。

从学生角度来讲，在学习轴对称时，有相当一部分学生对轴对称和轴对称图形的概念理解上出现误点。

因此本节课的难点是中心对称与中心对称图形之间的联系和区别。

教法建议本节内容和生活结合较多，新课导入可考虑以下方法：（1）从相似概念引入：中心对称概念与轴对称概念比较相似，中心对称图形与轴对称图形比较相似，可从轴对称类比引入，（2）从汉字引入：有许多汉字都是中心对称图形，如“田”、“日”、“曰”、“中”、“申”、“王”，等等，可从汉字引入，（3）从生活实例引入：生活中有许多中心对称实例和中心对称图形，如飞机的螺旋桨，风车的风轮，纽结，雪花，等等，可从生活实例引入，（4）从商标引入：各公司、企业的商标中有许多中心对称实例和中心对称图形，如联想，联合证券，湘财证券，中国工商银行，中国银行，等等，可从这些商标引入，（5）从车标引入：各品牌汽车的车标中有许多都是中心对称图形，如奥迪，韩国现代，本田，富康，欧宝，宝马，等等，可从车标引入，（6）从几何图形引入：学习过的许多图形都是中心对称图形，如圆，平行四边形，矩形，菱形，正方形，等等，可从几何图形引入，（7）从艺术品引入：艺术品中有许多都是呈中心对称或是中心对称图形，如下图，可从艺术品引入。

《中心对称》教学设计方案（第一课时）一、教学目标1. 理解中心对称的概念，掌握其定义和性质。

2. 能够识别中心对称图形，并确定其对称中心。

3. 通过观察、分析和讨论，培养学生的观察能力和抽象思维能力。

二、教学重难点1. 教学重点：理解中心对称的概念，掌握其定义和性质。

2. 教学难点：能够识别中心对称图形，并确定其对称中心。

三、教学准备1. 准备教学PPT，包含图片、动画和相关概念的解释。

2. 准备中心对称的实例，如钟表、风扇、旋转门等。

3. 准备小组讨论的材料，以便学生交流和讨论。

4. 准备练习题，用于学生巩固所学知识。

四、教学过程：（一）课前准备1. 学生复习相关知识，为新课学习做好准备。

2. 教师准备教学用具，如黑板、白板、中心对称图形等。

（二）导入新课1. 提问学生：大家还记得我们之前学过的图形对称吗？你能举出一些例子吗？2. 引导学生回顾轴对称图形，并让学生讨论和总结轴对称和中心对称的区别。

3. 教师解释中心对称的概念，并引导学生了解中心对称在实际生活中的应用。

（三）探究学习1. 教师出示一些中心对称图形，如正方形、矩形、平行四边形等，让学生观察它们的特征，并讨论它们如何通过旋转和反射实现中心对称。

2. 教师引导学生探究中心对称图形的性质，如对应点连线交于对称中心，图形沿对称中心翻折180度后能够完全重合等。

3. 学生分组讨论和总结中心对称的性质，教师给予指导和帮助。

（四）课堂活动1. 完成课后习题和相关练习题，巩固学生对中心对称知识的掌握。

2. 进行小组讨论和展示，让学生分享自己的学习成果和经验，教师给予评价和反馈。

3. 引导学生运用中心对称知识解决实际问题，如设计图案、测量实物等。

（五）小结作业1. 教师总结本节课的重点和难点，强调中心对称的性质和应用。

2. 布置与中心对称相关的作业，让学生回家后继续思考和实践。

希望中心对称的性质：1. 中心对称的两个图形，交换对称点，可以重合。

2. 中心对称不改变图形的形状和大小。

第三章 中心对称图形（一）一、选择题：1．下列图形中，是中心对称图形而不是轴对称图形的是 （ ） A ．平行四边形 B ．矩形 C ．菱形 D ．正方形 2．正方形具有而菱形不一定具有的性质是 （ ） A ．对角线互相垂直 B ．对角线互相平分 C ．对角线相等 D ．对角线平分一组对角3．平行四边形的对角线长为x 、y ，一边长为12，则x 、y 的值可能是 （ ） A ．8和14 B ．10和14 C ．18和20 D ．10和34 4．下面说法正确的是 （ ）A ．一个三角形中，至多只能有一个锐角B ．一个四边形中，至少有一个锐角C ．一个四边形中，四个内角可能全是锐角D ．一个四边形中，不能全是钝角 5．一个凸n 边形的边数与对角线条数的和小于20，且能被5整除，则n 为 （ ） A ．4 B ．5 C ．6 D ．5或6 6．如图：在□ABCD 中，AE ⊥BC 于E ，AF ⊥CD 于F 。

若AE=4，AF=6，且□ABCD 的周长为40，则ABCD 的面积为 （ ） A ．24 B ．36C ．40D ．487．顺次连接四边形四边中点所组成的四边形是菱形， 则原四边形为 （ ） A ．平行四边形 B ．菱形 C ．对角线相等的四边形 D ．直角梯形8．平行四边形ABCD 的周长为2a ，两条对角线相交于O ，△AOB 的周长比△BOC 的周长大b ，则AB 的长为 （ ） A ．2ba - B ．2ba + C ．22ba + D ．22ba + 9．菱形的周长为20cm ，两邻角的比为1：2，则较长的对角线长为 （ ）A ．4.5 cmB ．4 cmC ．53 cmD ．43 cm10．在四边形ABCD 中，从①AB ∥CD ；②AB=CD ；③BC ∥AD ；④BC=AD 中任选两个使四边形ABCD 为平行四边形的选法有 （ ） A ．3 B ．4 C ．5 D ．6 二、填空题：11．一个正方形要绕它的中心至少旋转_______度，才能与原来的图形重合．A B C D EF12．从数学对称的角度看：下面的几组大写英文字母：①ANEG；②KBXM；③XIHO；④HWDZ不同于另外三组的一组是__________，这一组的特点是_______________．13．若一个正方形的周长为x cm，面积为x cm2,则它的对角线长为_________．14．一个菱形的两条对角线长分别为6cm、8cm，则这个菱形的面积S为___________．15．若矩形的一个角的平分线分一边为4cm和3cm的两部分，则矩形的周长为__________．16．把边长为3、5、7的两个全等三角形拼成四边形，一共能拼成____________种不同的四边形，其中有____________个平行四边形．17．如图：点E、F分别是菱形ABCD的边BC、CD上的点且∠EAF=∠D=60°，∠FAD=45°，则∠CFE=___________．18．矩形的两条对角线的夹角为60°，一条对角线与短边的和为15，则长边的长为___________．三、解答题：19．作一直线，将下图分成面积相等的两部分（保留作图痕迹）．20．如图：□ABCD中，MN∥AC，试说明MQ=NP．D C21．矩形ABCD中，AC、BD相交于O，AE平分∠BAD交BC于E．若∠CAE=15°，求∠BOE的度数．Array 22．如图：菱形ABCD中，E是AB的中点，且DE⊥AB，AB=a．求：①∠ABC的度数；②对角线AC的长；③菱形ABCD的面积．23．矩形ABCD中AB=6cm,BC=8cm,AE平分∠BAC交BC于E，CF平分∠ACD交AD于F．①说明四边形AECF为平行四边形；②求四边形AECF的面积．24．点D是等腰Rt△ABC的直角边BC上一点，AD的中垂线EF分别交AC、AD、AB 于E、O、F，且BC=2．①当CD=2时，求AE；②当CD=2（2-1）时，试证明四边形AEDF是菱形．B D参考答案1．A 2．C 3．C 4．D 5．D 6．D 7．C 8．B 9．C 10．B11．0°；12．③，各个字母成中心对称；13．14．24cm2；15．22㎝或20cm16．6、3；17．45°18．.19．提示：将此图形分成两个矩形，找出两矩形的对称中心，连结两中心的直线即是所作线；20．提示：先证AMQC为平行四边形，得AC＝MQ，再证APNC为平行四边形，得AC＝NP；21．∠BOE＝75°；22．①∠ABC＝120°②BD2223．①（略）②平行四边形AECF的面积等于30；24．①AE＝32②提示：过D作DG⊥AB于G，通过计算得DG＝CD，则AD平分∠CAB，从而得证.。