九年级数学下册知识点----- 确定圆的条件

九年级下圆知识点总结九年级下学期的数学课程中，圆是一个非常重要的知识点。

圆的性质和相关的定理是我们在高中阶段学习几何的基础，因此在这个学期中我们要掌握圆的相关概念、性质以及与圆相关的定理。

本文将对九年级下学期涉及的圆相关的知识点进行总结。

1. 圆的定义与性质圆是平面上所有离一个固定点的距离都相等的点的集合。

圆的性质主要包括：任意两点之间都存在唯一的弧长、半径与切线的垂直关系、半径相等的圆的圆心距相等等。

2. 圆的周长与面积圆的周长是圆周上任意两点间的弧长之和，用C表示。

圆的面积是圆内部所有点到圆心的距离之和，用S表示。

圆的周长公式为C=2πr，圆的面积公式为S=πr²。

3. 圆心角与弧度制圆心角是由圆心和圆上两点所围的角。

圆心角的度数叫做角的度数，用°表示。

弧度制是另一种角度单位制，用角所对弧长与半径相等的角的度数来表示。

圆心角的度数和所对弧的弧度数之间的关系为：1°=π/180 rad。

4. 弧长与扇形面积弧长是弧所对的圆心角度数的一部分。

弧长的计算公式为：L= (θ/360) × 2πr。

扇形面积是由圆心角所对的弧与与其相交的两条半径围成的区域的面积。

扇形面积的计算公式为：S = (θ/360)×πr²。

5. 切线与切线定理切线是与圆只有一个交点的直线。

圆上任意一点到切线的距离等于半径的长度，在该点处切线垂直于半径。

切线定理指出，从圆外一点引出的切线与此点到圆心的半径所夹的角等于圆上此切点所对的弧所对的圆心角的一半。

6. 弦与弦长弦是圆上任意两点之间的线段。

弦与圆的周长和半径有一定的关系：相等的两弦所对的圆心角相等，且圆内弦所对的圆心角大于相同弧所对的圆心角。

7. 弧扫定理弧扫定理是一个基本的几何定理，它表明，由圆心角所对的圆弧等于该圆弧所扫过的圆心角。

8. 正多边形的内角和与外角和正多边形是指所有边长相等、所有内角相等的多边形。

正n边形的每个内角的度数为A = (n-2)×180° ÷ n，每个外角的度数为B = 360° ÷ n。

九年级数学下册圆的知识点整理圆的应用在数学领域中非常的广泛且常见，下面是小编给大家带来的九年级数学下册《圆》知识点整理，希望能够帮助到大家!九年级数学下册《圆》知识点整理第十章圆★重点★①圆的重要性质;②直线与圆、圆与圆的位置关系;③与圆有关的角的定理;④与圆有关的比例线段定理。

☆内容提要☆一、圆的基本性质1.圆的定义(两种)2.有关概念：弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆。

3.三点定圆定理4.垂径定理及其推论5.等对等定理及其推论5. 与圆有关的角：⑴圆心角定义(等对等定理)⑵圆周角定义(圆周角定理，与圆心角的关系)⑶弦切角定义(弦切角定理)二、直线和圆的位置关系1.三种位置及判定与性质：初中数学复习提纲2.切线的性质(重点)3.切线的判定定理(重点)。

圆的切线的判定有⑴⑵4.切线长定理三、圆换圆的位置关系初中数学复习提纲1.五种位置关系及判定与性质：(重点：相切)2.相切(交)两圆连心线的性质定理3.两圆的公切线：⑴定义⑵性质四、与圆有关的比例线段初中数学复习提纲1.相交弦定理2.切割线定理五、与和正多边形1.圆的内接、外切多边形(三角形、四边形)2.三角形的外接圆、内切圆及性质3.圆的外切四边形、内接四边形的性质4.正多边形及计算中心角：初中数学复习提纲内角的一半：初中数学复习提纲(右图)(解Rt△OAM可求出相关元素, 初中数学复习提纲、初中数学复习提纲等)六、一组计算公式1.圆周长公式2.圆面积公式3.扇形面积公式初中数学复习提纲4.弧长公式5.弓形面积的计算方法6.圆柱、圆锥的侧面展开图及相关计算七、点的轨迹六条基本轨迹八、有关作图1.作三角形的外接圆、内切圆2.平分已知弧3.作已知两线段的比例中项4.等分圆周：4、8;6、3等分九、基本图形十、重要辅助线1.作半径2.见弦往往作弦心距3.见直径往往作直径上的圆周角4.切点圆心莫忘连5.两圆相切公切线(连心线)6.两圆相交公共弦。

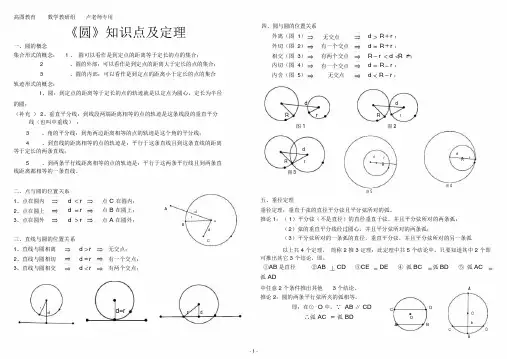
高图教育数学教研组卢老师专用《圆》知识点及定理一、圆的概念集合形式的概念： 1 、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充） 2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；四、圆与圆的位置关系外离（图 1）无交点d R r ；外切（图 2）有一个交点d R r ；相交（图 3）有两个交点R r d R r ；内切（图 4）有一个交点d R r ；内含（图 5）无交点d R r ；d dR r R r图 1图 23、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

dR r图3d rRdR图4r二、点与圆的位置关系1、点在圆内d r点 C 在圆内；2、点在圆上d r点 B 在圆上；A d3、点在圆外d r点 A 在圆外；r OBd三、直线与圆的位置关系C1、直线与圆相离d r无交点；2、直线与圆相切d r有一个交点；3、直线与圆相交d r有两个交点；rd d=r r d图 5五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论 1：（ 1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共 4 个定理，简称 2 推 3 定理：此定理中共 5 个结论中，只要知道其中 2 个即可推出其它 3 个结论，即：①AB是直径②AB CD③CE DE④ 弧BC弧BD⑤ 弧AC弧 AD中任意 2 个条件推出其他 3 个结论。

初中九年级圆的知识点详解在初中九年级数学课程中，圆是一个重要的几何概念。

我们将在本文中详细解释圆的知识点，包括定义、性质和常见的相关公式。

一、圆的定义圆是一个平面上所有到圆心距离都相等的点的集合。

这个距离被称为半径，用字母r表示。

圆的圆心和半径是确定一个圆的基本要素。

二、圆的性质1. 圆的直径和半径关系：圆的直径是通过圆心，并且两个端点在圆上的线段，它的长度是半径的两倍，即直径d=2r。

2. 圆的周长和面积：圆的周长是指圆上一周的长度，用字母C表示，它可以通过公式C=2πr来计算，其中π≈3.14是一个无理数，代表圆周率。

圆的面积是指圆内部的区域，用字母A表示，它可以通过公式A=πr²来计算。

3. 圆的切线和法线：圆上的切线是与圆切于一点的直线，切线与半径的夹角为90度。

圆上的法线是与圆相交于一点，并且与切线垂直的直线。

4. 圆的弧度制和度制：在解决一些圆相关问题时，我们通常使用弧度制来度量角度。

弧度制的角度是通过圆的弧长和半径之间的比值来定义的。

一个完整的圆的弧长等于2πr，所以一个完整圆的角度为360°。

三、常见的圆相关公式1. 圆的周长公式：C = 2πr2. 圆的面积公式：A = πr²3. 圆的弧长公式：L = 2πr(θ/360°)，其中θ是所对应的圆心角的角度。

4. 扇形面积公式：S = 0.5r²(θ/360°)，其中θ是所对应的圆心角的角度。

五、相关解题方法1. 已知圆的半径求周长和面积：根据上述公式直接计算即可。

2. 已知圆的周长求半径和面积：由C=2πr可得r=C/(2π)，再带入A=πr²即可计算面积。

3. 已知圆的面积求半径和周长：由A=πr²可得r=√(A/π)，再带入C=2πr即可计算周长。

4. 已知圆心角和半径求弧长和扇形面积：根据相应的公式计算即可。

六、例题解析1. 已知一个圆的半径为5cm，求其周长和面积。

九年级圆知识点归纳总结圆是数学中的一个基本几何概念，在九年级的几何学学习中占据重要的地位。

了解和掌握圆的相关知识点对于解决与圆相关的问题至关重要。

本文将对九年级圆的知识点进行归纳总结，帮助学生们更好地理解和应用这些知识。

一、圆的定义与性质1. 圆的定义：圆是一个平面上所有到圆心的距离都相等的点的轨迹。

2. 圆的要素：圆心、半径。

3. 圆的性质：- 圆上的任意一点到圆心的距离都相等。

- 圆的直径是通过圆心的一条线段，它的长度等于圆的半径的两倍。

- 圆的周长是圆周上的任意一点至邻近点的距离之和，也可以通过公式C=2πr计算（其中C表示圆的周长，r表示半径）。

- 圆的面积是圆内所有点构成的区域，可以通过公式A=πr²计算（其中A表示圆的面积）。

二、圆与直线的关系1. 切线：切线是与圆相切于一点的直线，且与半径垂直。

2. 弦：弦是圆上任意两点所确定的线段。

3. 弧：弧是圆周上两点之间的一段弧线。

4. 弧度与弧长的关系：弧度是角度的一种衡量单位，可以用弧长与半径之比来表示。

弧度制中一周对应的弧长等于圆的周长，即2πr。

三、圆的角关系1. 圆心角：由半径的两条边所夹的角称为圆心角。

2. 圆周角：由两条弧线所夹的角称为圆周角。

3. 圆心角与弧度的关系：圆心角的度数等于它所对应的弧度的长度。

四、圆的相交关系1. 相离：两个圆没有任何交点。

2. 外切：两个圆相切于一点，且其中一个圆位于另一个圆的外部。

3. 内切：两个圆相切于一点，且其中一个圆位于另一个圆的内部。

4. 相交：两个圆有两个交点。

五、圆的应用1. 利用圆求解问题：通过已知条件和圆的性质，可以解决与圆相关的实际问题，如求解圆的面积、周长等。

2. 圆的建模：在数学建模中，圆的概念具有广泛应用，可用于描述自然界中的许多现象和实际问题，如行星运动、电子轨道等。

六、圆的常见误区与解决方法1. 误区一：将弦与半径混淆。

解决方法：理解弦是由圆上的两点所确定的线段，半径是由圆心到圆上一点的线段。

九年级下册圆的知识点汇总圆是数学中的一个重要概念，也是几何学的基础之一。

在九年级下册学习中，涉及了很多关于圆的知识点。

下面将对这些知识点进行汇总和概述。

一、圆的定义与基本属性圆是平面上的一个几何图形，由到一个固定点的距离始终相等的所有点组成。

这个固定点称为圆心，距离称为半径（r）。

圆的完整曲线称为圆周，圆周上的任意两点与圆心之间的距离都相等，这个距离等于半径。

二、圆与直径圆的直径是连接圆周上两个点并经过圆心的线段。

直径的长度等于半径的两倍，即直径d = 2r。

三、圆与弦圆的弦是连接圆周上的两点的线段。

四、圆与弧圆的弧是圆周的一部分。

弧可以用中心角的度数来表示。

圆周的度数是360度，所以圆周被分为四个相等的弧，每个弧都是90度。

五、弦割定理在一个圆上，若两弦交于一点，那么两条弦分别乘以自己的弦长和求得的割线长度相等。

六、切线与切点切线是与圆只有一个交点的直线。

与切线相交的点称为切点。

切线与半径在切点处相互垂直。

七、弦切角定理当一个角的顶点在圆上，而角的两边分别交于圆上的两点，那么角对应的弦的弦长等于角两边相交的弧的弧长。

八、相交圆的位置关系当两个圆相交时，可能出现以下几种情况：1. 外切：两个圆相切于一个点，并且其中一个圆完全包含在另一个圆的外部。

2. 内切：两个圆相切于一个点，并且一个圆完全包含在另一个圆的内部。

3. 互相交错：两个圆没有相交，但是它们的内部存在交点。

4. 互相外离：两个圆没有相交，它们的外部也没有交点。

5. 互相内离：两个圆没有相交，但是它们的内部存在交点。

九、圆内接四边形圆内接四边形是指一个四边形的四个顶点都位于同一个圆上的情况。

圆内接四边形的对角线互相垂直并且相互平分。

十、角度的测量与圆周角圆周角是以圆心为顶点的角。

圆周角的度数等于所对应的弧的弧度数。

一个圆的角度总和是360度。

以上就是九年级下册关于圆的知识点的汇总。

通过学习这些知识，可以帮助我们更好地理解和应用圆的概念，在解决几何问题时能够得到更准确和全面的答案。

九年级下圆章节知识点圆是我们初中数学中最重要的几何图形之一，它的相关知识点在九年级下册中被广泛讲解和应用。

本篇文章将对圆的知识点进行深入分析和讨论，从基本概念到圆的性质和应用，帮助学生更好地理解和掌握这一内容。

一、基本概念圆是一个闭合的曲线，由与位于同一平面的一点到另一固定点的距离相等的所有点组成。

圆由圆心和半径组成。

圆心是圆的中心点，通常用字母O来表示；半径是圆心到圆上任意一点的距离。

根据圆的直径的不同，可以分为大圆和小圆，直径是圆的两个任意点之间的最长线段。

二、圆的性质1. 弧度与圆周角圆的周长被称为圆周长，用字母C表示。

对于同一个圆，它的圆周长与直径之间有一个特殊的关系：C = πd，其中π是一个数学常数，约等于3.14159，d是圆的直径。

与圆有密切关系的一个概念是圆心角。

圆心角是以圆心为顶点的角，其两条边分别由圆上的两个点确定。

圆心角所对的弧被称为圆心角所对弧。

圆心角的度数等于其所对弧的弧度数。

2. 弧长与扇形面积弧长是圆的一部分的长度，它是圆周长的一部分。

弧长与圆心角有一个简单的关系：弧长 = 弧度 ×半径。

当弧度为1时，弧长等于半径，也就是弧长等于圆的半径时，所对圆心角的度数为180度。

扇形是由一条弧和与圆心连线所围成的部分，扇形面积可以通过扇形的弧长和半径计算得出：扇形面积 = 弧长 ×半径 / 2。

三、圆的应用圆的应用非常广泛，涉及到物理、建筑、机械以及日常生活中的各个方面。

1. 物理学中的圆在物理学中，圆被广泛应用于描述天体运动的轨道，如行星绕太阳的运动轨道。

行星绕太阳移动总是在几乎完全圆形的椭圆轨道上。

2. 圆在建筑中的运用圆形的建筑物在建筑设计中经常用来表达某种意境或象征含义。

例如，圆形的穹顶被广泛运用于教堂和礼堂，它代表着一种庄严和安定的感觉，同时也能够提供优秀的声学效果。

3. 机械领域中的圆机械领域中，轮胎被设计成圆形，这是因为圆形的轮胎可以更好地承受来自各个方向的压力。

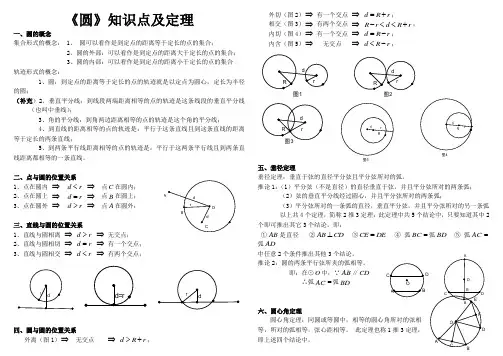
《圆》知识点及定理一、圆的概念集合形式的概念： 1、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

二、点与圆的位置关系1、点在圆内⇒d r<⇒点C在圆内；2、点在圆上⇒d r=⇒点B在圆上；3、点在圆外⇒d r>⇒点A在圆外；三、直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一个交点；3、直线与圆相交⇒d r<⇒有两个交点；四、圆与圆的位置关系外离（图1）⇒无交点⇒d R r>+；外切（图2）⇒有一个交点⇒d R r=+；相交（图3）⇒有两个交点⇒R r d R r-<<+；内切（图4）⇒有一个交点⇒d R r=-；内含（图5）⇒无交点⇒d R r<-；图1五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB是直径②AB CD⊥③CE DE=④弧BC=弧BD⑤弧AC=弧AD中任意2个条件推出其他3个结论。

专题30 圆的基本性质【知识要点】知识点一圆的基础概念圆的概念：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫圆．这个固定的端点O叫做圆心，线段OA叫做半径．以O点为圆心的圆记作⊙O，读作圆O．特点：圆是在一个平面内，所有到一个定点的距离等于定长的点组成的图形．确定圆的条件：⑴圆心；⑵半径，⑶其中圆心确定圆的位置，半径长确定圆的大小．补充知识：1）圆心相同且半径相等的圆叫做同圆；2）圆心相同，半径不相等的两个圆叫做同心圆；3）半径相等的圆叫做等圆．弦的概念：连结圆上任意两点的线段叫做弦。

经过圆心的弦叫做直径，并且直径是同一圆中最长的弦．⏜，读作弧AB．在同圆或弧的概念：圆上任意两点间的部分叫做圆弧，简称弧．以A、B为端点的弧记作AB等圆中，能够重合的弧叫做等弧．圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．在一个圆中大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧．弦心距概念：从圆心到弦的距离叫做弦心距．弦心距、半径、弦长的关系：（考点）知识点二垂径定理垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；常见辅助线做法（考点）：1）过圆心，作垂线，连半径，造RT△，用勾股，求长度；2）有弧中点，连中点和圆心，得垂直平分．知识点一圆的基础概念圆的概念：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫圆．这个固定的端点O叫做圆心，线段OA叫做半径．以O点为圆心的圆记作⊙O，读作圆O．特点：圆是在一个平面内，所有到一个定点的距离等于定长的点组成的图形．确定圆的条件：⑷圆心；⑸半径，⑹其中圆心确定圆的位置，半径长确定圆的大小．补充知识：1）圆心相同且半径相等的圆叫做同圆；2）圆心相同，半径不相等的两个圆叫做同心圆；3）半径相等的圆叫做等圆．弦的概念：连结圆上任意两点的线段叫做弦。

九年级圆的所有知识点圆是几何学中的重要概念，它在我们的日常生活中无处不在。

在九年级的数学学习中，我们将学习关于圆的各种知识点。

本文将全面介绍九年级圆的所有知识点，包括圆的定义、性质、常见公式以及应用等内容。

一、圆的定义及性质圆是由平面上所有到定点的距离都相等的点构成的集合。

圆由圆心和半径来确定，圆心是圆上任何一点到定点的距离都相等，半径则是圆心到圆上任何一点的距离。

圆的性质包括：1. 圆上任意两点之间的线段都是弦，而直径是一条通过圆心且两端点在圆上的弦，它将圆分为两个相等的半圆。

2. 圆上任意一条弦都可作为直径，且直径的长度是半圆周长的两倍。

3. 圆上每个点到圆心的距离都相等，这个距离就是半径，圆周上所有点到圆心的距离都等于半径的长度。

4. 圆周上的一个角，其对应的弧所对应的圆心角相等，即圆心角的度数等于弧度数。

5. 切线与半径的垂直性质：一条切线与通过切点的半径垂直相交。

二、圆的周长和面积公式1. 周长公式：圆的周长等于直径的长度乘以π（圆周率）。

周长 = 直径× π 或者周长 = 2 ×半径× π。

2. 面积公式：圆的面积等于半径的平方乘以π。

面积 = 半径² × π 或者面积 = （直径/2）² × π。

三、圆的应用圆不仅仅在数学中有着重要的地位，它也广泛应用于生活和其他学科中。

以下是圆的一些常见应用：1. 几何设计：圆形是设计中最基本的形状之一，它常常被用来表达和传达各种美学和构图原则。

2. 圆形建筑：许多建筑物采用圆形设计，如剧院、圆形体育场等，这样可以使观众坐在任何位置上都能获得更好的视觉体验。

3. 圆形运动：许多体育运动中都有圆形运动的要素，例如足球、篮球等球类运动，球场也常常是圆形或半圆形的。

4. 圆的应用于物理学中的轨迹：圆形轨迹出现在一些著名的物理学定律中，如牛顿的万有引力定律中行星的椭圆轨道。

综上所述，九年级圆的知识点包括了圆的定义、性质、周长和面积公式以及常见应用等方面。

初三下册数学圆知识点定理总结研究必备精品知识点——初三圆的定理总结1.垂径定理及推论：在圆中，如果一条直径垂直于一条弦，那么这条直径将这条弦平分，并且这条直径还垂直于弦的两个端点所在的直线。

还有其他三个定理：中径定理、弧径定理和中垂定理。

2.平行线夹弧定理：圆的两条平行弦所夹的弧相等。

3.“角、弦、弧、距”定理：在同一个圆或等圆中，如果两个角相等，那么它们所对的弦也相等；如果两个弦相等，那么它们所对的角也相等；如果两个角所对的弧相等，那么这两个角也相等；如果两个弧所对的角相等，那么这两个弧也相等；如果两个弧所对的弦相等，那么这两个弧也相等；如果两个弦所对的弦心距相等，那么这两个弦也相等；如果两个弦所对的弦心距相等，那么这两个弦也相等。

4.圆周角定理及推论：圆周角的度数等于它所对的弧的度数的一半。

如果一个直径平分一个圆，那么它所对的两个弧是等弧，它所对的两个角是等角，它所对的两个弦是等弦，它所对的两个弦心距是相等的。

如果一条弦所对的圆心角是直角，那么这条弦是直径。

5.圆内接四边形性质定理：圆内接四边形的对角互补，并且任何一个外角都等于它的内对角。

6.切线的判定与性质定理：如果一条直线通过圆上的一个点，并且垂直于这个点到圆心的半径，那么这条直线是圆的切线。

圆的切线垂直于经过切点的半径。

如果一条直线经过圆心并且垂直于切线，那么它必须经过切点。

如果一条直线经过切点并且垂直于切线，那么它必须经过圆心。

7.切线长定理：从圆外一点引圆的两条切线，它们的切线长相等；圆心和这一点的连线平分两条切线的夹角。

2.因为OC是半径，AB是切线，所以OC⊥AB。

3.弦切角定理及其推论：1) 弦切角等于它所夹的弧对的圆周角；2) 如果两个弦切角所夹的弧相等，那么这两个弦切角也相等；3) 弦切角的度数等于它所夹的弧的度数的一半。

举例：1) 因为BD是切线，BC是弦，所以∠CBD =∠CAB。

2) 因为ED，BC是切线，所以∠CBA =∠DEF。

圆1．圆的认识（1）以点O 为圆心的圆叫作“圆O ”，记为“⊙O ”。

（2）线段OA 、OB 、OC 都是圆的半径，线段AC 为直径。

（3）连结圆上任意两点之间的线段叫做弦。

直径是圆中最长的弦。

（4）圆上任意两点间的部分叫做弧。

小于半圆周的圆叫做劣弧。

大于半圆周的圆弧叫做优弧。

（5）圆心角：顶点在圆心，两边与圆相交的角叫做圆心角。

如∠AOB 、∠AOC 、∠BOC 就是圆心角。

2．圆的对称性（1）圆是轴对称图形，任意一条直径所在的直线都是它的对称轴。

圆是中心对称图形，圆心是它的对称中心。

（2）垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

推论：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧； （2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。

推论2：圆的两条平行弦所夹的弧相等。

即：在⊙O 中，∵AB ∥CD ∴弧AC =弧BD 3.圆心角定理：同圆或等圆中，相等的圆心角所对的弦相等，所对的弧相等，弦心距相等。

即：①AOB DOE ∠=∠；②AB DE =；③OC OF =；④ 弧BA =弧BD上述四个结论中，只要知道其中的1个相等，则可以推出其它的3个结论， 4．圆周角（1）圆周角：顶点在圆上，两边与圆相交的角叫做圆周角。

（2）半圆或直径所对的圆周角都相等，都等于90°（直角）。

90°的圆周角所对的弦是圆的直径。

（3）同圆或等圆中，一条弧所对的圆周角等于该弧所对的圆心角的一半。

（4）同弧（或等弧）所对的圆周角相等；相等的圆周角所对的弧相等。

人教版初三数学下册-圆-知识点归纳-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN圆的知识点归纳圆的半径相等，所以两条半径与圆心构成的三角形是等腰三角形直径d与半径r的关系：d=2r直径所对圆周角等于90°；90°的圆周角所对的弦是直径圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等、所对的弦相等、所对的弦心距相等圆周角定理：1、在同圆或等圆中，相等的圆周角所对的弧相等、所对的弦相等、所对的弦心距相等 2、同弧所对圆周角是圆心角的一半垂径定理：一条直线，只要具备下列5条中的2条作为条件，就可以推出其他三条结论。

称为：知二推三1、平分弦所对的优弧2、平分弦所对的劣弧3、平分弦（这条弦不是直径）4、垂直于弦5、过圆心圆内接四边形对角互补切线的判定：①作半径，证垂直；②作垂直，证半径切线定理：圆的切线垂直于过其切点的半径切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角三角形的内接圆圆心，是这个三角形三条角平分线的交点三角形的外接圆圆心，是这个三角形三条垂直平分线的交点圆的周长：C圆=2πr 圆的面积：S圆=πr2弧长公式：l=nπr180扇形面积：S扇=nπr2360圆柱侧面积：S圆柱侧面=πdh圆锥侧面积：S圆锥侧面=πrl（其中l是母线）圆柱体积：V圆柱=S底h圆锥体积：V圆锥=13S底h圆的常见辅助线：1、作垂线2、连半径3、构造直径三角形点与圆的位置关系（以下d代表点到圆心距离，r代表圆的半径）：1、点在圆外 d>r2、点在圆上 d=r3、点在圆内 d<r直线与圆的位置关系（以下d代表直线到圆心距离，r代表圆的半径）：1、相离 d>r2、相切 d=r3、相交 d<r圆与圆的位置关系（以下d代表两圆的圆心距离，R、r分别代表两圆的半径）：1、外离d>R+r2、外切d=R+r3、相交R-r<d<R+r4、内切d=R-r5、内含d<R-r。

课题：3.5确定圆的条件一：备课标（一）内容标准：：知道三角形的外心，在尺规作图方面，过不在同一直线上的三点做圆，做三角形的外接圆。

（二）数学思想、方法（十大核心概念）：本节课的教学内容是确定圆的条件，即探索经过一个点、两个点、三个点分别能否作出圆、能作出几个圆的问题，归纳总结出不在同一条直线上的三点作圆的问题，得出重要结论“不在同一条直线上的三个点确定一个圆”．从而培养学生的探索精神，同时可以使学生体会在这一过程中所体现的归纳思想．十大核心概念：几何直观、空间观念。

二、备重点、难点（一）教材分析：本节课是九年级下册第三章《圆》的第五节“确定圆的条件”，属于“图形与几何”领域图形性质部分。

通过本章前面几节课的学习，学生知道经过一点可以画无数条直线，经过两点有且只有一条直线等知识。

同时具备了用尺规作“线段垂直平分线”等操作技能，掌握了“线段垂直平分线的性质”。

（二）重点、难点分析：重点：经历不在同一条直线上的三个点确定一个圆的探索过程，并能掌握这个结论．掌握过不在同一条直线上的三个点作圆的方法．了解三角形的外接圆、三角形的外心等概念．难点：经历不在同一条直线上的三个点确定一个圆的探索过程，并能过不在同一条直线上的三个点作圆．三、备学情（一）学习条件和起点能力分析：1.学习条件分析：（1）必要条件：学生已学习了线段垂直平分线的做法和性质。

圆的两要素：圆心，半径（2）支持性条件：在经过点画直线等知识的学习过程中，学生具备了一定的合作精神和探究能力，具有一定的分类讨论的数学思想方法和类比方法。

2.起点能力分析：学生在小组活动中所表现出来的合作交流意识，鼓励学生动手、动口、动脑，尽可能设计具有挑战性的情境，激发学生的求知、借助实际问题情景，激发学生解决问题的兴趣，为解决本节课的目标“确定圆的条件”和下环节的探究活动注入动力。

（二）学生可能达到的程度和存在的普遍性问题：本节课主要经历不在同一条直线上的三个点确定一个圆的探索过程，并能过不在同一条直线上的三个点作圆．学生理解操作难度较大。