四年级数学上册运算律知识点

北师大版四年级数学上册第四单元《运算律》知识点总结一、买文具1、只有加减或只有乘除运算时，从左到右依次计算。

既有加减又有乘除运算时，先算乘除后算加减。

如果有括号，要先算（）里的，再算[ ]里的，最后算括号外面的。

2、用“小括号”“中括号”改变原式的运算顺序，二、加法交换律和乘法交换律1、加法交换律：两个数相加，交换加数的位置，和不变。

用字母表示为：a+b=b+a 。

2、乘法交换律：两个数相乘，交换乘数的位置，积不变。

用字母表示为：a×b=b×a三、加法结合律1、加法结合律：三个数相加，先把前两个数相加，再和第三个数相加，或者先把后两个数相加，再和第一个数相加，和不变。

用字母表示为：(a+b)+c=a+(b+c) 。

2、应用加法运算律进行简便计算在连加计算中，当某些加数相加可以凑成整十、整百、整千的数时，运用加法运算律可使计算简便。

3、口诀：连加计算仔细看，考虑加数是关键。

整十、整百与整千，结合起来更简单。

运算定律记心间，交换位置和不变。

结合定律应用广，加数凑整更简便。

4、减法的运算性质：（1）一个数连续减去两个数等于这个数减去这两个减数的和。

用字母表示：a-b-c=a-(b+c)（2）一个数减去两个数的和等于这个数连续减去和里每个加数。

乘四、乘法结合律1、乘法结合律：三个数相乘，先把前两个数相乘，再和第三个数相乘；或者先把后两个数相乘，再和第一个数相乘，积不变。

用字母表示为：(a×b)×c=a×(b×c)2、应用乘法运算律进行简便计算在连乘计算中，当某两个乘数的积正好是整十、整百、整千的数时，运用乘法运算律可使计算简便。

3、运用分解的方法，将某个乘数拆分成几个数相乘的形式，使其中的乘数与其他乘数的乘积“凑整”。

如;25X32=25X(8X4)=25X4X8 =100X8=8004、除法的运算性质：（1）一个数连续除以两个数（每次都能除尽）等于这个数除以这两个除数的积。

2020-2021学年北师大版四年级上册数学第四单元《运算律》知识点运算律知识点：运算顺序：先算中括号，再算小括号，先乘除再加减练习：简便算法知识点1：加法交换律：交换两个加数的位置，结果不变字母表示：a + b = b + a乘法交换律：交换两个因数的位置，结果不变字母表示：a × b = b × a练习：23+87=（）+23 78+65=（）+（）65× 98=（）+（） 678+987=（）+（）看清符号哦~25+89+75+11= 342+79+58=54+67+46+33= 123+43+77+57=拓展：减法和除法也满足交换律吗？举例试一试。

知识点2：加法结合律：三个数相加，先把前两个数相加，再和第三个数相加，或者先把后两个数相加，再和第一个数相加，它们的和不变。

字母表示：（a+b）+c=a+（b+c）注意：连加！！！乘法结合律：三个数相乘，先把前两个数相乘，再和第三个数相乘，或者先把后两个数相乘，再和第一个数相乘，它们的积不变。

字母表示：（a×b）×c=a×(b×c)注意：连乘！！！使用时机：当几个数相乘时，如果其中两个数相乘得整十、整百、整千的数就可以应用乘法交换律和乘法结合律。

乘法结合律可以改变乘法运算中的顺序。

数字如;25和4、50和2、125和8、50和4、500和2等。

练习：73×25×4 125×63×8 4×（25×93）50+7+40+9 78+98+22+12拓展提高：上述规律可推广到更多个数相乘。

如：125×4×8×25=（125×8）×（25×4）=1000×100=100000练习：25×50×4×2×8×12525×25×4×8125×50×8×2根据上述推广可以拆分组合：25×32×125=25×4×8×125=（25×4）×（8×125）=100×1000=100000练习：125×64×25×516×125×525×16×550×25×16知识点3：乘法分配律：两个数的和（或差）与一个数相乘，可以把两个加数（或被减数、减数）分别与这个数相乘，在把两个积相加（或相减），结果不变。

四年级上册数学思维导图第五单元运算律
1.10个一万是十万，10个十万是一百万，10个一百万是一千万，10个一千万是一亿。

相邻两个计数单位之间的进率是“十”，这种计数方法叫做十进制计数法。

特别注意：计数单位与数位的区别。

2、在用数字表示数的时候，这些计数单位要按照一定的顺序排列起来，它们所占的位置叫做数位。

3、位数：一个数含有几个数位，就是几位数，如652100是个六位数。

4、按照我国的计数习惯，从右边起，每四个数位是一级。

6、亿以上数的读法：
①先分级，从高位开始读起。

先读亿级，再读万级，最后读个级。

②亿级的数要按照个级的数的读法来读，再在后面加上一个“亿”字。

万级的数要按照个级的数的读法来读，再在后面加上一个“万”字。

③每级末尾不管有几个0，都不读。

其他数位有一个“0”或连续几个“0”，都只读一个“0”。

7、亿以上数的写法：
①从最高位写起，先写亿级，再写万级，最后写个级。

②哪个数位上一个单位也没有，就在那个数位上写0。

8、比较数的大小：
①位数不同的两个数，位数多的数比较大。

②位数相同的两个数，从最高位开始比较。

9、求近似数：
省略万位后面的尾数，要看千位上的数;省略亿位后面的尾数，要看千万位上的数。

这种求近似数的方法叫“四舍五入法”，是“舍”还是“入”，要看省略的尾数最高位上的数是小于5还是等于或大于5。

小于5就舍去尾数，等于或大于5就向前一位进1，再舍去尾数。

第四单元《运算律》知识点归纳及练习乘法结合律1、乘法结合律：三个数相乘，先把前两个数相乘，再和第三个数相乘，或者先把后两个数相乘，再和第一个数相乘，它们的积不变。

用字母表示是：（a×b）×c=a×(b×c).使用时机：当几个数相乘时，如果其中两个数相乘得整十、整百、整千的数就可以应用乘法交换律和乘法结合律。

乘法结合律可以改变乘法运算中的顺序。

数字如;25和4、50和2、125和8、50和4、500和2等。

加法运算时也有结合律。

如果用a/b/c表示三个数，那么加法结合律表示为：（a+b）+c=a+（b+c）2、认识乘法交换律a、b表示两个数，那么乘法交换律用字母表示为：a×b=b×a。

1）上述规律可推广到更多个数相乘。

如：125×4×8×25=（125×8）×（25×4）=1000×100=1000002）加法运算时也有交换律，如用字母a、b表示两个数，那么加法交换律用字母表示为：a+b=b+a。

3）运用加法交换律和结合律可以使得一些运算简便。

50+7+40+9=（50+40）+（7+9）=90+16=106练习题：73×25×4 125×63×8 4×（25×93）12×125×5×8 32×125×25 48×125×5乘法分配律1、乘法分配律：两个数的和（或差）与一个数相乘，可以把两个加数（或被减数、减数）分别与这个数相乘，在把两个积相加（或相减），结果不变。

用字母表示数：（a+b）×c=a×c+b×c或（a-b）×c=a×c－b×c1、式子的特点：式子的原算符号一般是×、+(-)、×的形式；在两个乘法式子中，有一个相同的因数；另为两个不同的因数之和(或之差)是能凑成整十、整百、整千的数。

运算律和运算性质
四则混合运算
1．加法和减法称为第一级运算。

乘法和除法称为第二级运算。

2．没有括号的混合运算：同级运算从左往右依次运算；两级运算先算乘、除法，后算加减法；有括号的混合运算：先算小括号里面的，再算中括号里面的，最后算括号外面的。

加法交换律：a+b=b+a、a+b+c=a+c+b
加法结合律：（a+b）+c=a+（b+c）
乘法交换律：a×b = b×a、a×b×c = a×c×b
乘法结合律：（a×b）×c = a×（b×c）
乘法分配律：
（a＋b）×c = a×c＋b×c a×c＋b×c =（a＋b）×c （a－b）×c = a×c－b×c a×c－b×c =（a－b）×c
注：乘法分配律：两个数的和（或差）与一个数相乘，可以把两个加数（或被减数、减数）分别与这个数相乘，再把两个积相加（或相减），结果不变。

运算性质
1．减法的性质：一个数连续减去几个数，相当于减去这几个数的和。

a－b－c = a－（b＋c）
2．除法的性质：a÷b÷c=a÷（b×c）
（a＋b）÷c = a÷c＋b÷c。

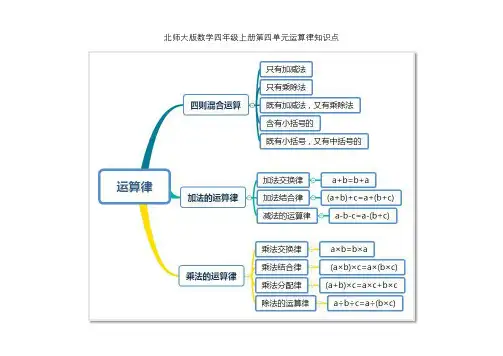
第1节买文具知识点1：四则混合运算的运算顺序。

如果只有加减法或者只有乘除法，从左往右进行计算；如果既有加减法，又有乘除法时，先算乘除法，后算加减法；如果有小括号的，应该先算小括号里面的；如果有小括号，还有中括号的，先算小括号里面的，后算中括号里面的，最后算括号外面的。

知识点2：用四则混合运算，解决实际问题。

在解决实际问题时，可以根据数量关系列出分步算式，然后再根据四则混合运算的规则写成综合算式。

知识点3：把分步算式写成综合算式。

列综合算式时，书写顺序与分步算式的计算顺序相同；列综合算式时，只使用分布算式的已知数量，不使用分布算式中任何计算出来的数量；列综合算式时，要学会使用算式来表示算式的得数；列综合算式时，要注意书写的算式，在下一步中做的是算式中的什么数，应该处于什么位置。

第2节加法交换律和乘法交换律知识点1：加法交换律和乘法交换律的含义。

两个数相加，交换加数的位置，和不变，这就是加法交换律；两个数相乘，交换乘数的位置，积不变，这就是乘法交换律。

知识点2：加法交换律和乘法交换律的字母表达式。

加法交换律：a+b = b+a乘法交换律：a×b = b×a知识点3：加法交换律和乘法交换律的应用。

在两个数的加法中，使用加法交换律可以对加法进行验算。

在两个数的乘法中，使用乘法交换律可以对乘法进行验算。

在三个数的加法中，使用加法交换律，有时可以使计算简便；在三个数的乘法中，使用乘法交换律可以使计算简便。

第3节加法结合律知识点1：加法结合律的含义。

三个数相加，先把前两个数相加，再和第三个数相加；也可以先把后两个数相加，再和第一个数相加，和不变，这就是加法结合律。

知识点2：加法结合律的字母表达。

（a+b）+c = a+（b+c）知识点3：使用加法结合律进行简便计算。

在连加的算式中，加法交换律可以改变加速出现的位置，加法结合律用来改变运算顺序，把能凑成整十、整百或整千的数先相加，在使用加法结合律改变应运算顺序时，应注意给先计算的那一步算式添上括号，这样既符合四则混合运算的顺序，又能够起到凑成整十、整百、整千的数，使计算简便。

四 运 算 律一、买文具1. 不含括号的混合运算的运算顺序:在没有括号的算式里,有乘除法和加减法,要先算乘除法,再算加减法;如果加法或减法两边同时有乘除法,那么乘除法可同时计算。

2. 含有括号的四则混合运算的运算顺序:在有括号的算式里,如果有小括号,要先算小括号里面的,再算小括号外面的;如果有中括号,先算中括号里面的,再算中括号外面的。

有中括号时,一定要把中括号里面的算式全部算完才能去掉中括号。

3. 混合运算图示如下:二、加法交换律和乘法交换律1. 加法交换律:两个数相加,交换加数的位置,和不变。

用字母表示为a +b =b +a 。

2. 乘法交换律:两个数相乘,交换乘数的位置,积不变。

用字母表示为a ×b =b ×a 。

3. 加法交换律和乘法交换律的应用:运用加法交换律和乘法交换律可以验算加法和乘法的计算是否准确。

三、加法结合律1. 加法结合律:三个数相加,先把前两个数相加,再加第三个数,或者先把后两个数相加,再与第一个数相加,和不变。

用字母表示为(a +b )+c =a +(b +c )。

2. 加法运算律的应用:在连加算式中,当某些加数可以凑成几百几十数或整百数时,可以运用加法交换律、加法结合律改变加数的位置或改变运算顺序,使计算简便。

易错提示:计算时,没有参加运算的数要连同前面的运算符号抄写下来。

知识巧记: 混合运算并不难,明确顺序是关键。

同级运算最好办,从左到右依次算。

两级运算都出现,先算乘除后加减。

遇到括号更简单,先算里面后外面。

要点提示:用字母表示运算律,更为直观方便。

易错提示:减法和除法中不存在交。

北师大四年级数学上册第四单元《运算律》知识点2第四单元《运算律》加法交换律和结合律1．加法交换律：两个数相加，交换加数的位置，和不变。

用字母表示为：a+b=b+a2．加法结合律：三个数相加，先把前两个数相加，再和第三个数相加，或者先把后两个数相加，再和第一个数相加，和不变。

用字母表示为：(a+b)+c=a+(b+c)3.在连加计算中，当某些加数相加可以凑成整十、整百、整千的数时，运用加法运算律可使计算简便。

口诀：连加计算仔细看，考虑加数是关键。

整十、整百与整千，结合起来更简单。

交换定律记心间，交换位置和不变。

结合定律应用广，加数凑整更简便。

4.减法的运算性质一个数连续减去两个数等于这个数减去这两个减数的和。

用字母表示：a-b-c=a-(b+c)减法的运算性质一个数减去两个数的和等于这个数连续减去和里每个加数。

5.乘法的交换律和结合律（1）．乘法交换律：两个数相乘，交换乘数的位置，积不变。

用字母表示为：a×b=b×a（2）．乘法结合律：三个数相乘，先把前两个数相乘，再和第三个数相乘；或者先把后两个数相乘，再和第一个数相乘，积不变。

用字母表示为：(a×b)×c=a×(b×c)6.应用乘法运算律进行简便计算在连乘计算中，当某两个乘数的积正好是整十、整百、整千的数时，运用乘法运算律可使计算简便。

运用分解的方法，将某个乘数拆分成几个数相乘的形式，使其中的乘数与其他乘数的乘积“凑整”。

乘除的规律：先乘后除等于先除后乘。

除法的运算性质：（1）一个数连续除以两个数（每次都能除尽）等于这个数除以这两个除数的积。

除法的运算性质：（2）一个数除以两个数的积等于这个数连续除以积里每个乘数。

7.乘法分配律乘法分配律特别要注意“两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加”中的分别两个字。

注意：（1）一定要括号外的数分别乘括号里的两个数，再把积相加。

四年级上册数学•运算律知识★加法交换律和乘法交换律1.加法交换律：任意两个数相加，交换加数的位置，和不变。

用字母表示： a+b=b+a2.乘法交换律：任意两个数相乘，交换乘数的位置，积不变。

用字母表示：a×b=b×a★加法结合律1.加法结合律：三个数相加，先把前两个数相加，再加第三个数，或者先把后两个数相加，再与第一个数相加，它们的和不变。

用字母表示：(a+b)+c=a+(b+c)目的：为了运算更简便，用小括号把两个能够凑成整十、整百、整千的数括起来先相加，再加其他数。

例：57+288+43 =(57+43)+288 =100+288=388 (51+29)+71=51+(29+71)=51+100=15115+34+85+66=(15+85)+(34+66)=100+100=2002.减法性质：一个数连续减去两个数，等于这个数减去这两个数的和。

用字母表示： a-b-c=a-(b+c)目的：为了运算更简便，把减数先加起来（凑整十、整百、整千数）再一次性减掉。

例：238-44-56=238-（44+56）=238-100★乘法结合律黄金搭档：2×5=10 4×25=100 8×125=10001.乘法结合律：三个数相乘，先乘前两个数或者先乘后两个数，积不变。

用字母表示： (a×b)×c= a×(b×c)目的：为了运算更简便，用小括号把两个能够凑成整十、整百、整千的数括起来先相乘，再乘其他数。

拆分例： 125×9×8 =(125×8)×9 =1000×9=9000 (25×60)×4=（25×4）×60 =100×60=6000125×25×32←拆分=（125×8）×（4×25）=1000×100=100000 125×64←拆分=（125×8）×8 =1000×8=8000★乘法分配律1.乘法分配律：两个数的和与一个数相乘，可以把这两个数分别与这个数相乘，再相加，结果不变。

北师大版小学数学四年级上册第4单元(运算律)知识点整理加法乘法名称加法交换律加法结合律乘法交换律乘法结合律乘法分配律两个数相加，交换加数的位置，和不变。

三个数相加，先算前两个数相加或先算后两个数相加，和不变。

两个数相乘，交换乘数的位置，积不变。

三个数相乘，先算前两个数相乘或先算后两个数相乘，积不变。

两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再相加。

字母表示a+b=b+a(a+b)+c=a+(b+c)a某b=b某a(a某b)某c=a某(b某c)(a+b)某c=a某c+b某c实例4+6=6+462+53=53+62385+276=276+385(4+8)+6=4+(8+6)(19+62)+38=19+(62+38)(51+29)+91=51+(29+91)3某5=5某345某102=102某45296某200=200某296(2某4)某3=2某(4某3)(7某4)某25=7某(4某25)(40某3)某6=40某(3某6)（3+5）某10=3某10+5某10（4+6）某8=4某8+6某8（46+54）某28=46某28+54某28应用加法的交换律和加法的结合律在简便计算的过程中往往是一起使用的。

157+78+322=157+（78+322）=157+400=557554+249+146=249+（554+146）=249+700=949在简便计算题目中，乘法的交换律与结合律往往是一起使用的；乘法分配律的应用可以正向用、反向用；还可以想办法凑出所需要的形式，再计算。

125某9某8=9某（125某8）=9某1000=9000125某9某8=（125某8）某9=9000（25某125）某（8某4）=25某125某8某4=（25某4）某（125某8）=100某1000=10000044某25=11某4某25=11某（4某25）=11某100=1100（80+4）某25=80某25+4某25=2000+100=210034某72+34某28=34某（72+28）=34某100=3400=（100+4）某25=100某25+4某25=2500+100=260035某99+35=35某99+35某1=35某（99+1）=35某100=3500。

第四单元运算律知识点一：买文具-四则混合运算顺序（1）四则混合运算顺序在没有括号的算式里，当只有加、减运算或乘、除运算时，按从左到右的顺序进行计算，既有加、减运算，又有乘、除运算时，要先算，再算。

（2）含有中括号的四则混合运算在一个算式里，如果既有小括号又有中括号，要先算的，再算面的，最后算。

知识点二：运算律及其应用加法交换律用字母表示为 a＋b＝加法结合律用字母表示为（a+b）+c=乘法交换律用字母表示为 a×b＝乘法结合律用字母表示为 (a×b) ×c=乘法分配律用字母表示为 (a+b) ×c=1.在连加计算中，运用可以让一些加法计算简便。

2.乘法结合律只适用于运算，不可以在乘加或乘减运算中运用。

3.乘法分配律可以正用，也可以逆用。

如果a×c和b×c计算简便时，可以先算a×c和b×c，再把两个积相加；如果a＋b的和正好是整十、整百、整千数时，可以用来计算。

4.运用乘法分配律进行计算时，两个加数要，然后再把。

【易错典例1】（2019秋•嘉陵区期末）实践探究．【思路引导】根据整数乘法的竖式计算法则解答即可．【完整解答】解：乘数14个位上的4与326相乘，表示4×326的积是1304，十位上的1与326相乘，表示10×326的积是3260；【易错注意点】此题考查了整数乘法的竖式计算方法．【易错典例2】（2019秋•洛川县期末）如图算式中的汉字各代表什么数字？我＝3；是＝9；中＝7；国＝1；人＝0．【思路引导】根据整数乘法的运算法则，第一个因数与第二个因数的个位相乘得：3438，所以第二个因数的个位为9，第一个因数的百位为3．原式为：382×29＝11078，完成竖式，并找到各汉字代表的数字．【完整解答】解：原式为：所以：我＝3；是＝9；中＝7；国＝1；人＝0．故答案为：3；9；7；1；0．【易错注意点】本题主要考查凑数谜，关键根据整数乘法及加法的运算法则，找到合适的数，完成计算．【易错典例3】点A表示的数可能是算式（）的积．A．201×51B．199×45C．199×51【思路引导】根据题意，点A介于1与10000之间，且更接近10000；根据估算的计算方法，分别求出各个算式的结果，再进一步解答．【完整解答】解：201×51≈200×50＝10000，等于10000，不符合题意；199×45≈200×45＝9000，接近10000，符合题意；199×51≈200×50＝10000，等于10000，不符合题意；故选：B．【易错注意点】考查了三位数乘两位数的估算，把两位数看作与它接近的整十整百数，然后再进一步解答．【易错典例4】（2018秋•单县期末）学校准备发练习本，发给15个班，每班144本，还要留40本作为备用．学校应买多少练习本？【思路引导】首先用发给每个班的练习本的数量乘班级的数量，求出发给15个班多少本练习本；然后用它加上备用的练习本的数量，求出学校应买多少练习本即可．【完整解答】解：144×15+40＝2160+40＝2200（本）答：学校应买2200本练习本．【易错注意点】此题主要考查了整数乘法的意义和应用，要熟练掌握，解答此题的关键是求出发给15个班多少本练习本．:考点1：带括号的混合运算（含较大数的除法）1．（2020春•江北区期末）把方框中的三个分步算式合并成综合算式是（）12+6＝1836÷18＝220+2＝22A．36÷（12+6）+20B．20+36÷（12+6）C．36÷12+6+20D．36÷（12+6）+22．（270+770÷55）﹣190÷10正确的运算顺序是（）A．②除法→①加法→③减法→④除法B．②除法→①加法→③减法→②除法C．②除法→①加法→④除法→③减法3．（2021春•浑源县期中）用计算器计算（801﹣576）÷15时，当按到“÷”的时候，显示屏上显示接着按“15”，再按“＝”，显示屏上显示的是。