当前位置：文档之家 › 第7章--非线性系统分析--练习与解答

第7章--非线性系统分析--练习与解答

  • 格式：doc
  • 大小：4.17 MB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

非线性系统分析(精)

非线性系统分析(精)


7.3 非线性特性的描述函数法
(3)相平面法的特点

① 适用于一、二阶非线性系统的分析 ② 方法：首先将二阶非线性微分方程变写为以 输出量及输出量导数为变量的两个一阶微分方程；然 后依据这一对方程，设法求出其在上述两变量构成的 相平面中的轨线，并由此对系统的时间响应进行判别。 ③ 该方法所得结果比较精确和全面。 ④ 对于高于二阶的系统，需要讨论变量空间中 的曲面结构，从而大大增加了工程使用的困难。
7.3 非线性特性的描述函数法
1. 2. 3. 4.

基本概念 谐波线性化 非线性特性的描述函数 典型非线性特性的描述函数
7.3 非线性特性的描述函数法
1. 基本概念
(1) 分析非线性系统的两种工程方法
相平面法 描述函数法
(2) 描述函数法（谐波平衡法）的特点

描述函数法是一种近似方法，相当于线性理论中频率法 的推广。方法不受阶次的限制，且所得结果也比较符合实际，故 得到了广泛应用。


7.2 非线性环节及其对系统结构的影响
3.回环（间隙）特性
x1表示输入 x2表示输出
b表示间隙。
7.2 非线性环节及其对系统结构的影响
回环（间隙）特性的影响

(1) 降低了定位精度，增大了系统的静差。 (2) 使系统动态响应的振荡加剧，稳定性变坏。
7.2 非线性环节及其对系统结构的影响
7.1 非线性系统动态过程的特点
4. 非线性系统的运动形式
（1）非线性系统在小偏离时单调变化，大 偏离时很可能就出现振荡。 （2）非线性系统的动态响应不服从叠加原 理。
7.1 非线性系统动态过程的特点
5. 非线性系统的自振
非线性系统的自振却在一定范围内能够长期 存在，不会由于参数的一些变化而消失。
第7章非线性系统

第7章非线性系统

2．饱和特性 饱和特性的输入输出关系 如图7－2，有时为简化，可把它近似为理想 饱和特性，即由两条直线来表示。也就是说， 当输入低于某值时，输出与输入成正比，而
当输入超过此值后，输出就保持定值而不再变化。例如电机的 磁化特性曲线，线性放大器设置限幅时都具有这种饱和特性。 饱和特性使系统在大信号时增益降低，稳态误差增大，还可能 影响系统的稳定性。但饱和特性也可以起保护等有利的作用。 3 ．间隙( 回环 ) 特性 间隙特性的输入输 出关系如图 7-3 所示。输出在输入增加、减 少时与输入成不同的直线关系，当输入 x 在 不断增大时，输出 y 与输入 x 的关系由图 7-3 中箭头向右的线段确定，当输入 x 在不断减 小时，输出y与输入x的关系由图7-3中箭头 向左的线段确定。即输出不仅与输入量的大小有关，而且还与 输入量的变化状态有关。例如齿轮传动中的间隙，这是由于制 造精度所限和为保证转动灵活而不卡死所必需的，它使齿轮传 动时在由正向变反向时，必须经转动了间隙间距后，才会有力 矩传递的作用，在铁心中，由于磁滞的存在，磁化曲线也具有 这种特性。
于是有
1 x2 x 2 f (x 1) x 2 x
dx f (x )x 2 2 1 dx x 1 2
0 ,x 3 , x 0 10 20 初始状态确定后，例如 r ，将状态变量值代入上式就可开始绘图 了，由于非线性特性f(e)有三种可能的值， 因此在计算斜率时，要根据χ1 的大小正 确选用f(e)三种取值中的一个。绘出的相 轨迹如图7-8 例7-1的相轨迹所示。
x f ( x , x ) 2 dx 2 12 x x 1 dx 1 2 式可知，相轨迹的斜 率完全取决于它的微分方程，因此不同的系统有不同的相轨 迹，与线性系统的根轨迹、频率特性一样，相轨迹完全反映 系统的特性。 根据式（7-2）可以得到绘制相轨迹的方法。若要绘制从初 始状态开始的相轨迹，只要把状态变量值代入式（7-2）算出 该点相轨迹的斜率，由于在小范围内，曲线的切线与曲线是 重合的，因此沿着该点的切线画一小段，这段也近似为相轨 迹上的一小段，得到新的状态变量值后，重复以上步骤就可 绘出系统的相轨迹了。 xoBox分析软件包含了用上述方法编制的绘制相轨迹子程序 ，下面举一个例子来说明相轨迹的绘制方法及xoBox软件绘制 相轨迹子程序的使用方法。
(第七章 非线性系统分析)

(第七章 非线性系统分析)

或
2 & & 2ζω n x + ω n x dx =− & dt x
（7-14）
31
（1）无阻尼运动
由方程（7-14），相轨迹方程为：
(ζ = 0)
=A
ω
& x
2 0 2 n
x (t ) +
2
& (t ) x
2
2
ω
2 0
2 n
（7-16）
其中
A =
x +
相轨迹如图7－24所示，在相平面上是为一族同心 的椭圆。 每个椭圆相当于一个简谐振动。
8
二.非线性系统和线性系统有不同的 运动规律
① 在线性系统中，系统的稳定性只取决于系统的 结构和参数，对常参量线性系统，只取决于系统 特征方程根的分布，而和初始条件、外加作用没 有关系。 对于非线性系统，不存在系统是否稳定的笼统概 念。必须具体讨论某一运动的稳定性问题。 非线性系统运动的稳定性，除了和系统的结构形式及 参数大小有关以外，还和初始条件有密切的关系。
返回子目录
3
⑤
对分段线性的非线性系统，能决定开关线,写出分 区域相轨迹的方程式。
⑥ 对具有外作用和或具有速度反馈的情况能合适地选 取相坐标作出相轨迹图。 ⑦ 正确理解谐波线性化的条件及描述函数的概念。 ⑧ 了解描述函数建立的一般方法，明确几种典型非线 性特性负倒描述函数曲线的特点。 ⑨ 熟练掌握运用描述函数法分析系统中是否有周期运 动, 判断周期运动的稳定性。
式中
⎧+ 1 x1 > 0 signx1 = ⎨ ⎩− 1 x1 < 0
15
图7-8 斜坡输入时 的系统输出量
图7-7 包含死区的非线性系统
非线性系统分析方法

非线性系统分析方法


解：1. 死去继电特性的描述函数
4M N(X)
1 ( )2
X
X
2. 绘制描述函数的负倒数特性
1
X
N(X ) 4M 1 ( )2
X
3. 绘制线性部分的极坐标图
4. 判断稳定性，分析两曲线相交点的性质
1 N(X)
X
-1.56 300 400 B -1 -0.5
X 130 A 140
120 G(j)
趋于奇点 远离奇点 包围奇点
例：二阶线性定常系统
••
•
x 2n x n2 x 0
试分析其奇点运动性质。
dx/dt x
稳定节点
••
•
x 2n x n2 x 0
dx/dt x
1
稳定节点
相轨迹趋于原点，该奇点称为 稳定节点
••
•
x 2n xn2 x 0
dx/dt x
1
不稳定节点
相轨迹远离原点，该奇点为 不稳定节点
者是自持振荡的
自持振荡点 a 振荡幅值=Xa
振荡频率=a
Im Re
X a
0
1 G(j) N ( X )
例：已知死区继电非线性系统如图
R(s)
+M
460
C(s)
+-
- -M
( j)(0.01 j 1)(0.005 j 1)
继电参数： M 1.7 死区参数：Δ 0.7 应用描述函数法作系统分析。
•
x
-1 -5/4
-3/2
-5/3
=
-2
-3/7
-3
-5 - x
3
1 1/3
0 -3/4 -1/2 -1/3
第7章非线性系统分析

第7章非线性系统分析


描述函数的定义是：输入为正弦函数时，输 出的基波分量与输入正弦量的复数比。
其数学表达式为
N
X
R
X
Y1
sin(t X sint
1)
Y1 X
1
A12 B12 arctan A1
A1
1
2
y(t) costdt
0
X
B1
1
B1
2
y(t ) sin tdt
0
7.3 非线性特性的描述函数法
（2）举例说明描述函数
(1) 降低了定位精度，增大了系统的静差。 (2) 使系统动态响应的振荡加剧，稳定性变坏。
7.2 非线性环节及其对系统结构的影响
4.摩擦特性
Mf
M1 •
M2
•
M f 摩擦力矩
转速
M1 静摩擦力矩
M 2 动摩擦力矩
7.2 非线性环节及其对系统结构的影响
摩擦特性的影响
(1)对随动系统而言，摩擦会增加静差，降低精 度。
7.2 非线性环节及其对系统结构的影响
2.饱和特性
x1 a ，等效增益 为常值，即线性段 斜率；
而 x1 a ，输出饱
和，等效增益随输 入信号的加大逐渐 减小。
7.2 非线性环节及其对系统结构的影响
饱和特性的影响
(1) 饱和特性使系统开环增益下降， 对动态响应的 平稳性有利。
(2) 如果饱和点过低，则在提高系统平稳性的同时， 将使系统的快速性和稳态跟踪精度有所下降。
7.3 非线性特性的描述函数法
KX sint
y(t) Ka
0 t 1 1 t / 2
∵ y(t) 单值奇对称， A0 0 A1 0
B1
4
第7章 非线性系统的分析

第7章 非线性系统的分析


某一初始条件出发在相平面上按照式(7-13)或式(7-14)绘出的
曲线称为相平面轨迹,简称相轨迹。不同初始条件下构成的
相轨迹,称为相轨迹簇。由相轨迹簇构成的图称为相平面图。
利用相平面图分析系统性能的方法,称为相平面分析法。
图7-6为某个非线性系统的相平面图。图中,相轨迹上的
箭头表示相变量随着时间的增加沿相轨迹运动的方向。
第7章 非线性系统的分析 7.2 相平面分析法
7.2.1 相平面的基本概念 设二阶非线性系统的微分方程为
第7章 非线性系统的分析
第7章 非线性系统的分析
1.相平面和相轨迹
前面已经设定
我们称以x1(或x)为横坐
标、以x2(或 )为纵坐标构成的平面为相平面(注意,纵坐标x2
是横坐标x1的一阶导数),如图7-6所示。x1、x2为相变量。由
7.2.2 线性系统的相轨迹 在学习非线性系统的相平面分析法之前,我们先对非常
熟悉的线性系统做相平面分析。设二阶线性系统的微分方程 为
第7章 非线性系统的分析
也就是说,无论系统特征参数ωn和ξ是何值,系统的奇点是 不变的。此外,式(7-21)的特征方程为
系统的特征根为
对于不同的阻尼比ξ,二阶系统特征根的形式是不同的,而 线性系统的时域响应是由特征根决定的。下面介绍系统特征 根与系统的奇点(0,0)以及相轨迹的关系。
行线性化。我们只研究系统平衡点附近的特性时,就可以采 用平衡点附近的线性化方法,将非线性系统在平衡点附近小 范围线性化。当然,也可以将非线性系统分为几个区域,对每 个区域进行分段线性化。
第7章 非线性系统的分析
2.相平面分析法 相平面分析法简称相平面法,是非线性系统的图解分析 法。其基本思路是:建立一个相平面,在相平面上根据非线性 系统的结构和特性,绘制非线性系统的相轨迹。相轨迹就是 非线性系统中的变量在不同初始条件下的运动轨迹,根据相 轨迹就可以对非线性系统进行分析。该方法只适用于一阶和 二阶非线性微分方程。
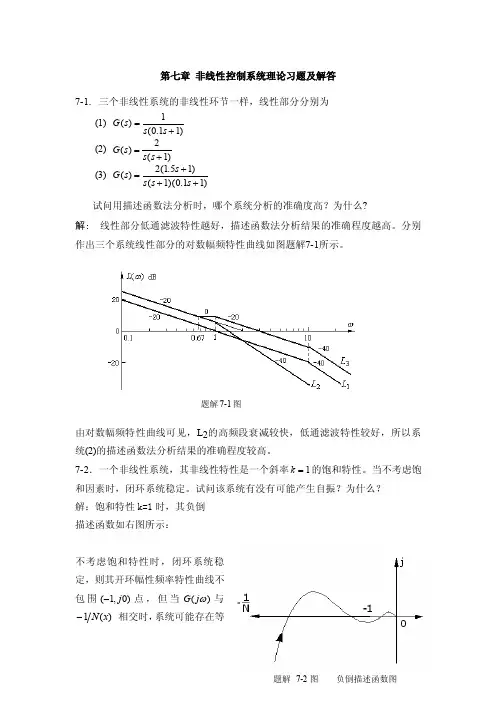
非线性控制系统理论习题及解答

非线性控制系统理论习题及解答

题解 7-2图 负倒描述函数图第七章 非线性控制系统理论习题及解答7-1. 三个非线性系统的非线性环节一样，线性部分分别为(1) G s s s ()(.)=+1011(2) G s s s ()()=+21(3) G s s s s s ()(.)()(.)=+++21511011试问用描述函数法分析时，哪个系统分析的准确度高？为什么?解: 线性部分低通滤波特性越好，描述函数法分析结果的准确程度越高。

分别作出三个系统线性部分的对数幅频特性曲线如图题解7-1所示。

由对数幅频特性曲线可见，L 2的高频段衰减较快，低通滤波特性较好，所以系统(2)的描述函数法分析结果的准确程度较高。

7-2．一个非线性系统，其非线性特性是一个斜率1=k 的饱和特性。

当不考虑饱和因素时，闭环系统稳定。

试问该系统有没有可能产生自振？为什么？ 解：饱和特性k=1时，其负倒 描述函数如右图所示：不考虑饱和特性时，闭环系统稳定，则其开环幅性频率特性曲线不包围(1,0)j -点，但当)(ωj G 与)(1x N - 相交时，系统可能存在等题解7-1图幅振荡，如图所示,因此，该系统有可能产生自振。

7-3．将下列图7-50 所示非线性系统简化成非线性部分)(X N 和等效的线性部分)(s G 相串联的单位反馈系统，并写出线性部分的传递函数)(s G 。

解：(1)系统结构图可等效变换为题解7-3(1)的形式:其中)()(1)()(211s G s G s G s G +=(2)将系统结构图等效变换为题解7-2(2)的形式:G s G s H s ()()[()]=+111(3)将系统结构图等效变换为题解7-3(3)的形式:G s H s G s G s ()()()()=+1111题解7-3(1)图题解 7-3(2)图 题解 7-3(3)图7-4．判别图7-51所示各系统是否存在自振点。

解: （a）不是（b）是（c）是（d）ca、点是，b点不是（e）是（f）a点不是，b点是（g）a点不是，b点是（h）系统不稳定（i）系统不稳定（j）系统稳定（k）7-5．非线性系统如图7-52所示。

第七章非线性控制系统分析习题答案.

第七章非线性控制系统分析习题答案.

解： y(t) = A3 sin3 ωt
∫ ∫ 1
B=
2π
A3 sin 4 ωt
4 A3
dωt =
π
2
1
(1
− cos
2ωt) 2
dωt
1
π0
π 04
∫ [ ] A3
=
π
2 (1 − 2 c os 2ω t + c os 2 2ω t )
A3
dωt =
π
A3
π
− sin 2ωt 2
π0
π2 π
0
A 3 π c o s 4ω t + 1
G1 ( s) +G1 ( s)
4 、 判 断 题 7 -2 图 中 各 系 统 是 否 稳 定 ； −1 N( A) 与 G ( j ω ) 两 曲 线 交 点 是 否 为 自 振 点 。
2
解 ：（ a ） 不 是 ； （ b） 是 ； （c）是；
（ d） a、c 点 是， b 点 不 是；
（ e） 是 ；
（ 2 ） 由 图 解 7 -5 可 见 ， 当 −1 N( A) 和 G ( j ω ) 相 交 时 ， 系 统 一 定 会 自 振 。 由 自 振 条 件
A + 6 −K −( A + 6) K
N ( A)G( jω ) =
=
= −1
ω =1 A + 2 2
2( A+2)
( A +6) K = 2 A +4
10
−1 0
10
G( jω ) =
=
−j
j ω( j ω + 1) ω2 + 1
ω( ω2 + 1)
非线性系统的分析

非线性系统的分析

可利用继电控制实现快速跟踪。
带死区的继电特性，将会增加系统的定 位误差，对其他动态性能的影响，类似 于死区、饱和非线性特性的综合效果。
式中
a — —继电器吸合电压； ma — —继电器释放电压； M — —常值输出。
当a=0时，继电器的吸合及释放电压为零，此种情况亦 称零值切换，又称理想继电器特性，如 图7-1-5a所示。
增长，时间响应都逐渐衰减为零，非线性系统也 是稳定系统 。
当x0 1时， 线性系统的响应仍与 x0 1时一样。
但非线性系统的响应则不然，它随时间增长而发散
到。系统呈不稳定状态。
2、系统的自持振荡
在非线性系统中，在无外部激励时，发生某一固定 振幅和频率的振荡，称为自持振荡（或自激振荡）。
例 7-1-2 范德波尔方程是
如图7-1-4c所示，其数学描述是
kxt a
yt kxt a
c sgn xt
•
y(t) 0
•
y(t) 0
(7-1-5)
•
y(t) 0
式中 a — —间隙宽度；
k — —线性输出特性的斜率，k tan
间隙（回环）特性的影响
降低了定位精度，增大了系统的静差。
使系统动态响应的振荡加剧，稳定性 变坏。
图 7-1-1 b) 弹簧力的非线性特性
考虑到作用于质量m上的全部力，其运动 可用下面的非线性微分方程描述：
m
d2y dt 2
fv
dy dt
kyy
F
(7-1-1)
描述大多数非线性物理系统的数学模型是n阶非线性 微分方程，其形式为
m
dn dt
y
n
h t, yt, dyt
dt, d 2 yt
第七章 非线性系统的分析讲解

第七章 非线性系统的分析讲解


分析方法：频域上有描述函数法和波波夫法；时域 上有相平面法和李亚普诺夫第二法。计算机仿真的 方法也可以分析复杂的非线性系统。
§7.2
x(t)
非线性系统的描述函数分析法
n(t)
e
一、描述函数法的基本概念
非线性环节N
＋ －
N
非线性部分
x
G(s) 线性部分
c
假设非线性系统的输入函数为
x(t ) A sin(t )
(t ) 0 y (t ) 0 y (t ) 0 y
间隙输出相位滞后，减小稳定性裕量，动特性变坏自 持振荡。同时使稳态误差增大。
5. 继电器特性
y M -a -ma ma a －M
y y M -a x －M a －M x -a a －M x M y
x
0 m a x(t ) a, 0 a x(t ) m a, y (t ) M sgn x(t ) M x(t ) m a, x(t ) m a, M
输出n(t)将是非正弦的周期信号。可以展成傅利叶级数， y(t)是由恒定分量、基波分量、和高次谐波组成。 பைடு நூலகம்设1：如果非线性部分的特性曲线具有中心对称性质，那以 输出信号y(t)的波形具有奇次对称性（波形的后半个周期重复 前半个周期的变化，但符号相反）输出不含直流分量，输出响 应的平均值为零。
假设2：线性部分具有良好的低通滤波性，那么高次谐波的幅值 远小于基波。闭环通道内近似地只有一次谐波信号流通。对于 一般的非线性系统而言这个条件是满足的，线性部分的低通滤 波性越好，用描述函数法分析的精度越高。 上述两个假设满足时，非线性环节的输入是一个正弦信号，系 统的输出是相同频率的正弦信号，对于非线性环节的输出只研 究其基波成分就足够了。 假设系统中非线性环节的输入函数为
第7章 非线性系统分析

第7章 非线性系统分析

1 2 1 2 1 2 2
x 0

1
x 0

4. 间隙特性
齿轮传动中的齿隙
a
输出
b
液压传动中的油隙
b
a
输入
元件开始运动 输入信号<2 a 时，输出信号不变； 当输入信号>2 a 以后，输出随输入线性变化。 元件反向运动 保持在运动方向发生变化瞬间的输出值； 输入反向变化>2 a ，输出随输入线性变化。
理想饱和特性的数学描述为：
ka y kx ka
x a | x | a xa
饱和特性的存在，将使系统的开环增益有所 降低，对系统的稳定性有利。 出于对系统安全性的考虑，常常加入各种限 幅装置，其特性也属饱和特性。
3．继电特性
继电特性顾名思义就是继电器所具有的特性 , 继
一种近似分析法。也可采用基于
Simulink的非线性系统分析方法。
§7-2
常见非线性特性
一个单输入单输出静态非线性特性的数 学描述为：
y f ( x)
静态非线性特性中，死区特性、饱和特性、继
电特性、间隙特性是最常见的，也是最简单。
1. 死区特性
输出
（不灵敏区特性）
各类液压阀的正重叠量； 系统的库伦摩擦； 测量变送装置的不灵敏区； 调节器和执行机构的死区； 弹簧预紧力；等等。
2.稳定性
线性系统的稳定性仅和系统的结构和参数有关，
而和系统的输入信号大小，初始状态无关。
而非线性系统的稳定性，除了和系统的结构，
参数有关外，还与系统的初始状态及输入信号大
小有密切关系，这一点非常重要。即可能在某个
初始条件下稳定，而在另一个初始条件下系统可
能不稳定。

7第七章非线性系统的分析


第七章 非线性系统的分析
5、 ( 1)
jω
××
λ1 λ2
x
x
系统的运动是非周期发散运动。相轨迹是由原点出发的发散 型抛物线。原点处的奇点称为不稳定节点。
第七章 非线性系统的分析
6、
, 为一正一负两实根
12
jω
×
λ1
0
×
λ2

x
x
系统的自由运动是发散运动，原点处的奇点称为鞍点。 以上6种奇点，类似的奇点在非线性系统中也常见到。
复平面中，根据二者的相对位置可分析非线性系统的稳定
性。
一、非线性系统稳定
Im
1 不被G(j)包围
N(X)
x a
1 N(X)
0
Re

G( j)
第七章 非线性系统的分析
二、非线性系统不稳定 1 被G( j)包围
N(X)
三、非线性系统产生自持振荡
1 与G(j)相交
N(X)
图示系统在a点产生稳定的自 持振荡。由交点可确定自持 振荡的频率和幅值。
Im
0
Re
x a
G( j) 1
N(X)
Im
1 N(X)
a0
Re
x b a

G( j)
非线性系统即使无外界作用，也可能会发生某一 固定振幅和频率的振荡，称为自持振荡。
３、频率响应畸变 非线性系统在输入为正弦函数时，输出为包含一定数
量的高次谐波的非正弦周期函数。
第七章 非线性系统的分析
线性系统分析可用叠加原理，在典型输入信号下系 统分析的结果也适用于其它情况。
非线性系统不能应用叠加原理，没有一种通用的方 法来处理各种非线性问题。

自动控制原理-第七章 非线性系统分析


p p p ( x1 , x 2 ) ( x1 x 10 ) ( x 2 x 20 ) x1 x 2 Q ( x , x ) Q ( x x ) Q ( x x ) 1 2 1 10 2 20 x1 x 2
p ( x1 , x 2 ) a ( x1 x10 ) b( x 2 x 20 ) Q( x1 , x 2 ) c( x1 x10 ) d ( x 2 x 20 )

c 区域： a Tc c k m
c k m c 1 （k m c) T T ct 0 由奇点定义： k m c 0 c 常数 c k m 1 k m c dc T dc c 区域： c 常数 奇线： c k m
§7-4
奇点及极限环
dx 0 奇点概念：相轨迹上满足 dx 0 不定式的特殊点，称为奇点。
在奇点处有多条相轨迹穿过或趋于该奇点，相当于系统处于 平衡状态 一 奇点分类：(线性系统)
2 2 n x n x 0 x 2 2 n x n x x dx 2 x dx 2 n x n x dt (*) 相轨迹方程 dx x dx x dt
介绍：典型非线性特性、相平面法、描述 函数法
§7-1引言
稳定性 1．线性系统与非线性系统区别： 输出曲线 等幅振荡 稳态输出
2．非线性特性（典型） 1）死区
0 x a y k ( x a ) x a k ( x a ) x a
0 = k ( x aSignx)
x1 a ( x1 x 10 ) b( x 2 x 20 ) x 2 c( x1 x10 ) d ( x 2 x 20 )

非线性系统的分析

非线性系统理论1.1.非线性系统特点非线性系统与线性控制系统相比，具有一系列新的特点］，线性系统满足叠加原理，而非线性控制系统不满足叠加原理。

图8-1带滤波器的非线性系统2•非线性系统的稳定性不仅取决于控制系统的固有结构和参数， 而且与系统的初始条件以及外加输入有关系。

例：对于一由非线性微分方程 X=-x(1 ―) 描述的非线性系统，显然有两个平衡点，即x 1=0和x 2=1。

将上式改写为=—dt x(l - x)设20吋，系统的初态为咛积分上式可得dx3•非线性系统可能存在自激振荡现象 的情况： (1) 如图跳跃谐振和多值响应8 — 3 所砂)其输出存在极其复杂图8—3跳跃谐振与多值响应(2)分频振荡和倍频振荡非线性系统在正弦信号作用下， 其稳态分量除产生同频率振荡外,和分频振荡。

如图 8—4所示波形。

还可能产生倍频振荡4•非线性系统在正弦信号作用下, 的输入信号倍频信号分频信图8—4倍频撮荡与分频振荡8.1.2 研究非线性系统的意义与方法1•研究非线性系统的意义1）实际的控制系统，存在着大量的非线性因素。

这些非线性因素的存在，使得我们用线性系统理论进行分析时所得出的结论，与实际系统的控制效果不一致。

线性系统理论无法解释非线性因素所产生的影响。

2）非线性特性的存在，并不总是对系统产生不良影响。

2•研究非线性系统的方法1）相平面法是用图解的方法分析一阶，二阶非线性系统的方法。

通过绘制控制系统相轨迹,达到分析非线性系统特性的方法。

2）描述函数法是受线性系统频率法启发，而发展出的一种分析非线性系统的方法。

它是一种谐波线性化的分析方法，是频率法在非线性系统分析中的推广。

3）计算机求解法是利用计算机运算能力和高速度对非线性微分方程的一种数值解法。

8.2典型非线性特性的数学描述及其对系统性能的影响8.2.1饱和特性在电子放大器中常见的一种非线性，如图8-5所示，饱和装置的输入特性的数学描述如下：［辰。

sig 滋(f)8.2.2死区特性死区特性也称为不灵敏区，如图8-6所示。

《非线性系统分析》PPT课件


0
M
x h2 h2 x h1
x h1
(7 4a)
.
当x 0:
M
y
0
M
x h1 h1 x h2
x h2
(7 4b)
19
图（b）所示继电特性的数学描述由 读者自行导出。
20
4、间隙特性
传动机构的间隙也是控制系统中常见的非线性 特性，齿轮传动是典型的间隙特性，图7-4（a） 表示齿轮传动原理，图7-4（b）表示主动轮位移 与从动轮位移的关系。设主动轮与从动轮间的最 大间隙为2b，那么当主动轮改变方向时，主动轮 最大要运动2b从动轮才能跟随运动。间隙特性类 似于线性系统的滞后环节，但不完全等价，它对 控制系统的动态、稳态特性都不利。设齿轮传动 速比为，则图7-4间隙特性的数学描述为：
22相平面法是庞加莱poincare1885年首先提出的本来它是一种求解二元一阶非线性微分方程组的图解法两个变量构成的直角坐标系称为相平面方程组的解在相平面上的图象称为相轨这里是将相平面法用于分析一阶尤其是二阶非线性控制系统并形成了一种特定的相平面法它对弄清非线性系统的稳定性稳定域等基本属性解释极限环等特殊现象起到了直观形象的作23因为绘制两维以上的相轨迹是十分困难的所以相平面法对于二阶以上的系统几乎无能为力
一点在 x x平面上绘出的曲线，表征了系统的
运动过程，这个曲线就是相轨迹。我们用一个二 阶线性时不变系统来体验一下相平面和相轨迹。
26
例7-1 考虑二阶系统：
..
x ax 0 , a 0, x(t0 ) x0 ,
将它写成微分方程组：
dx
.
x
dt.
d x ax
dt
两式相除得到：
.
dx dx

第七章非线性系统的分析


2、死区非线性
x1 ≤ ∆ 0, x2 = k ( x1 − ∆signx1 ), x1 > ∆
1 signx1 = −1
x1 > 0 x1 < 0
在实际系统中死区可由众多原因引起，它对系统可产生不同的 影响：一方面它使系统不稳定或者产生自振荡；另一方面有时 人们又人为的引入死区特性，使系统具有抗干扰能力。
第七章 非线性控制系统
7-2
1、饱和非线性
kx1 = x2 = ka x2 m −ka = − x 2m
典型非线性环节
x1 < a x1 ≥ a x1 ≤ −a
x2m
x2
−a
0
k
a
x1
此处：输入 x1 − − − − x2 − − − −输出 k − − − −比例系数
− x2m
第七章 非线性控制系统
第七章 非线性控制系统
4）混沌(Chaos)
蝴蝶效应（ The Butterfly Effect） 是指在一个动力系统中，初始条 件下微小的变化能带动整个系统 的长期的巨大的连锁反应。这是 一种混沌现象。 核心理念：看似微不足道的细小 变化，却能以某种方式对社会产 生微妙的影响，甚至影响整个社 会系统的正常运行。
第七章 非线性控制系统
r(t)
e(t)
N(A,ω) NLS
x(t)
G(s)
c(t)
非线性系统的闭环“传递函数”：
G ( jω ) N ( A, ω ) Φ ( jω ) = 1 + G ( jω ) N ( A, ω )
0 闭环“特征方程”： 1 + G ( jω ) N ( A, ω ) =
即
1 G ( jω ) = − N ( A, ω )

非线性系统的一般分析方法试题

非线性系统的一般分析方法【课后自测】7-1 判断题7-31图中各系统是否稳定，)(1A N -与)(ωj G 两曲线交点是否为自振点。

图7-1 题7-1图解：（a ）系统不稳定 曲线G(jw)与曲线()1N A -有交点a 、b 。

对于a 点，当A 增大时，()1N A -由G(jw)左侧稳定区进入右侧不稳定区，所以交点a 不是自振点。

对于b 点，当A 点增大时时，由G(jw)右侧不稳定区进入左侧稳定区，所以交点b 是稳定工作点，是自振点。

(b)系统不稳定 G(jw)曲线与()1N A -曲线有交点a 、b ，对于a 点，当A 增大时，()1N A -由G(jw)左侧稳定区进入右侧不稳定区，所以交点a 不是自振点。

对于b 点，当A 点增大时时，()1N A -由G(jw) 右侧不稳定区进入左侧稳定区，所以交点b 是自振点。

（c ）()1N A -曲线被G(jw)曲线所包围，系统不稳定。

（d ）系统不稳定 曲线G(jw)与曲线()1N A -曲线有一个交点，在交点处，当A 增大时，()1N A -由G(jw)右侧不稳定区进入左侧稳定区，所以交点是自振点。

（e ）系统稳定（f ）系统不稳定 G(jw)曲线与()-1N A 曲线有交点a 、b ，对于a 点，当A 增大时，()1N A -由G(jw)右不侧稳定区进入左侧稳定区，所以交点a 是自振点。

对于b 点，当A 点增大时时，()1N A -由G(jw) 右侧稳定区进入左侧不稳定区，所以交点b 不是自振点。

7-2 试求图7-32所示非线性特性的描述函数，画出-1/N 曲线，并指出X=0，X=1和X=∞时的-1/N 值。

图7-2 题7-2图解：由图可得非线性元件特性为1221()k xx a y k x k k ax a⎧≤⎪=⎨-->⎪⎩令sin x X t ω=,当x a ≥时，arcsin aa t Xω==1221sin 0()sin ()k X t t ay t k X t k k at aωωωω<<⎧=⎨-->⎩因()y t 是t 的奇函数，故10A =1212214()sin ()sin 2002()(arcsin )B y t td t y t td ta k X k k Xππωωωωπππ===+-⎰⎰ 所以11212()(arctan )2(arcsin )()AN X B ak k k XX a π==+-≥当X a <时，1sin y k X t ω=,02t πω<≤此时10A = 210221021011()sin 1sin 11cos 22B y t td t k X td t tk Xd t k xπππωωπωωπωωπ==-==⎰⎰⎰则1()N X k = ()X a <7-3 某单位反馈系统，其前向通道有一描述函数A eA N j/)(4π-=的非线性元件，线性部分的传递函数为)15.0(/15)(+=s s s G ，试用描述函数法确定系统是否存在自振？若有，参数是多少？解：非线性部分负倒数描述函数为：π-=-41()j Ae N A作()-1N A 和()G j ω曲线如图1所示。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第七章 非线性控制系统分析习题与解答7-1 设一阶非线性系统的微分方程为3x x x+-= 试确定系统有几个平衡状态，分析平衡状态的稳定性，并画出系统的相轨迹。

解 令 x=0 得 -+=-=-+=x x x x x x x 321110()()()系统平衡状态x e =-+011,,其中：0=e x ：稳定的平衡状态；1,1+-=e x ：不稳定平衡状态。

计算列表，画出相轨迹如图解7-1所示。

可见：当x ()01<时，系统最终收敛到稳定的平衡状态；当x ()01>时，系统发散；1)0(-<x 时，x t ()→-∞; 1)0(>x 时，x t ()→∞。

注：系统为一阶，故其相轨迹只有一条，不可能在整个 ~xx 平面上任意分布。

7-2 试确定下列方程的奇点及其类型，并用等倾斜线法绘制相平面图。

(1) x xx ++=0 (2) ⎩⎨⎧+=+=2122112x x xx x x解 （1） 系统方程为x -2 -1 -13 0 131 2x-6 0 0.385 0 -0.385 0 6 x 11 2 01 0211图解7-1 系统相轨迹⎩⎨⎧<=-+I I >=++I )0(0:)0(0:x x x x x x x x令0x x ==，得平衡点：0e x =。

系统特征方程及特征根：21,221,21:10,()2:10, 1.618,0.618()s s s s s s I II ⎧++==-±⎪⎨⎪+-==-+⎩稳定的焦点鞍点(, ) , , x f x x x x dxdxxx x dx dx x x x x x==--=--==--=-+=ααβ111⎪⎪⎩⎪⎪⎨⎧<-=>--=)0(11:II )0(11:I x x βαβα计算列表用等倾斜线法绘制系统相平面图如图解7-2（a ）所示。

图解7-2（a ）系统相平面图（2） xx x 112=+ ① 2122x x x+= ② 由式①： x xx 211=- ③ 式③代入②： ( )( )x xx x x 111112-=+- 即 x x x 11120--= ④ 令 x x110== 得平衡点： x e =0 由式④得特征方程及特征根为 ⎩⎨⎧-==--414.0414.20122,12λs s （鞍点） 画相轨迹，由④式x xdxdx x x x 1111112===+α xx 112=-α 计算列表用等倾斜线法绘制系统相平面图如图解7-2（b ）所示。

7-3 已知系统运动方程为sin x x +=0，试确定奇点及其类型，并用等倾斜线法绘制相平面图。

解 求平衡点，令 x x==0 得 sin x =0平衡点 x k k e ==±±π(,,,012 )。

将原方程在平衡点附近展开为台劳级数，取线性项。

设 F x x x () sin =+=0∂∂∂∂F x x Fx x xx ee∆∆+=0∆∆ cos x x x e +⋅=0⎩⎨⎧±±±===∆-∆±±===∆+∆),5,3,1(0),4,2,0(0k k x x x k k x x x e e ππ特征方程及特征根： k 为偶数时 s j 21210+==±λ, （中心点） k 为奇数时 s 212101-==±λ, （鞍点）用等倾斜线法作相平面sin sin sin xdxdx x xx xx +=⋅+==α01作出系统相平面图如图解7-3所示。

7-4 若非线性系统的微分方程为(1) ( .) x x x x x +-++=30502 (2) x xxx ++=0 试求系统的奇点，并概略绘制奇点附近的相轨迹图。

解（1） 由原方程得(, )( .) . x f x xx x x x x x x x ==----=-+--305305222 令 x x110== 得 x x x x +=+=210() 解出奇点 x e =-01,在奇点处线性化处理。

在x e =0处：(, )(, ) ()( .) . x f x x xx f x xxxx x xx x x x xx xx x x x =⋅+⋅=--⋅+-+⋅=-+========∂∂∂∂0000001260505即. x x x -+=050 特征方程及特征根s j 1220505420250984,....=±-=± （不稳定的焦点） 在x e =-1处x x xxx x xxx xx 5.0)5.06()21(0101+=⋅+-+⋅--==-==-= 即. x x x --=050 特征根 ⎩⎨⎧-=+±=718.0218.1245.05.022,1s （鞍点） 概略画出奇点附近的相轨迹如图解7-4（1）所示：（2） 由原方程(, ) x f x xxx x ==-- 令x x ==0 得奇点 x e =0,在奇点处线性化( ) xfxx fxxx x x x x xx xx x x x =⋅+⋅=--⋅-⋅========∂∂∂∂00001得 x x =- 即x x +=0 特征根 s j 12,=±。

奇点x e =0（中心点）处的相轨迹如图解7-4(2)所示。

7-5 非线性系统的结构图如图7-36所示。

系统开始是静止的，输入信号)(14)(t t r ⨯=，试写出开关线方程，确定奇点的位置和类型，画出该系统的相平面图，并分析系统的运动特点。

解 由结构图，线性部分传递函数为C s M s s()()=12 得 ()()c t m t = ①由非线性环节有⎪⎩⎪⎨⎧III -<+II>-I ≤=22)(22)(20)(e t e e t e e t m ②由综合点得c t r t e t e t ()()()()=-=-4 ③ 将③、②代入①得⎪⎩⎪⎨⎧-<-->-≤=III2)(2II 2)(2I 20)(e t e e t e e t e开关线方程为 e t ()=±202:)(0)(:=-+I I ==I e ec e t e常数令 e e ==0 得奇点 e 02II =特征方程及特征根 s s j 21210+==±,, （中心点）III ：e e ++=20 令 e e ==0 得奇点 e 02III=-特征方程及特征根 s s j 21210+==±,, （中心点）绘出系统相轨迹如图解7-5所示，可看出系统运动呈现周期振荡状态。

7-6 图7-37所示为一带有库仑摩擦的二阶系统，试用相平面法讨论库仑摩擦对系统单位阶跃响应的影响。

解 由系统结构图有⎩⎨⎧<->+±+⋅=0:0:215.015)()(ccs s s E s C s s C s E s (.)()()05125+±=⎩⎨⎧<=->=+II055.0I 0535.0ce c cc e c c ①因为 c r e e =-=-1 ②②代入①式有 ⎩⎨⎧>=+-<=++II00102I 00106ee e eee e e特征方程与特征根⎪⎩⎪⎨⎧±==+-±-==++)(310102:II )(30106:I 2,122,12不稳定的焦点稳定的焦点j s s s j s s s依题意 0)0(,0)0(==c c 可得0)0()0(1)0(1)0(===-=c ec e以)0,1(为起点概略作出系统相轨迹。

可见系统阶跃响应过程是振荡收敛的。

7-7 已知具有理想继电器的非线性系统如图7-38所示。

图7-38 具有理想继电器的非线性系统试用相平面法分析：（1）T d =0时系统的运动；（2）T d =05.时系统的运动，并说明比例微分控制对改善系统性能的作用； （3）T d =2时系统的运动特点。

解 依结构图，线性部分微分方程为c u = ① 非线性部分方程为 ⎩⎨⎧II <+-I >+=0101eT e eT e u d d ②开关线方程： eT e d=-1 由综合口： c r e e =-=-1 ③ ③、②代入①并整理得⎩⎨⎧II<++I>+-=0101d d eT e eT e e在 I 区： e edede ==-1 解出： ()e e e 220=-> （抛物线） 同理在 II 区可得：()ee e 220=< （抛物线）开关线方程分别为T d =0时， e =0;T d =05.时， ee =-2; T d =2 时， .ee =-05. 概略作出相平面图如图解7-7所示。

图习题集P178 T8-10由相平面图可见：加入比例微分控制可以改善系统的稳定性；当微分作用增强时，系统振荡性减小，响应加快。

7-8 具有饱和非线性特性的控制系统如图7-39所示，试用相平面法分析系统的阶跃响应。

解 非线性特性的数学表达式为III-<II >I <⎪⎩⎪⎨⎧-=ae a e a e M Me y || 线性部分的微分方程式为Ky c cT =+ 考虑到e c r =-，上式又可以写成rr T Ky e e T +=++ 输入信号为阶跃函数，在0>t 时有，0==rr ，因此有 0=++Ky e eT 根据已知的非线性特性，系统可分为三个线性区域。

Ⅰ区：系统的微分方程为)(0a e Ke e e T <=++按前面确定奇点的方法，可知系统在该区有一个奇点（0，0），奇点的类型为稳定焦点。

图解7-8（a ）为Ⅰ区的相轨迹，它们是一簇趋向于原点的螺旋线。

Ⅱ区：系统的微分方程为)(0a e KM e eT >=++设一般情况下，初始条件为00)0(,)0(e ee e ==。

则上式的解为 KMt Te KM e T KM ee t e T t -+-++=-)()()(000 对上式求一次导数，得KM e KM e t eT t -+=-)()(0 故当初始条件KM e -=0'时，相轨迹方程为KM e -='。

当KM e -≠0'时，相轨迹方程为KM eKM eKMT T e ee e +++-+=000ln )(图7-39 非线性系统结构图由此可作出该区的相轨迹，如图解7-8(b )所示，相轨迹渐进于直线KM e-= 。

Ⅲ区：此时系统的微分方程为)(0a e KM e eT -<=-+将Ⅱ区相轨迹方程中的KM 改变符号，即得Ⅲ区的相轨迹方程⎪⎩⎪⎨⎧≠++--+===)(ln )()(00000KM eKM e KM e KMT T e e e e KM e KM e该区的相轨迹如图解7-8（b ）所示。