一元二次方程应用题微课
- 格式:doc
- 大小:18.00 KB
- 文档页数:2

第9课时一元二次方程及其应用知识梳理素养形成,定义:只含有一个未知数并且未知数的最高次数是2的整式方程,叫做一元二次方程Mw A tM A W一般形式:aj∙2+〃/+c=0(αz ≠0,α•〃,c 为常数)【易错提醒】对于二次项系数含有字母的方程,根据根的情况求字母取值范围时,一定要先确定该方程是一元二次方程还是一元一次方程,然后进行判断.根与系数的关系(*选学):若一元二次方程α/+^■+c=0(α≠0)有两个实数根中,/2,则b c +J*2=-------------- »Xj *Xi —-a a设α为原来一•变化后的♦为H1地H 点(下窿蓟"川味,当连续两次增长,平均每次增K 率为1时,有"U+])?=优I∙H 、率下降率题当连续两次下降.平均每次下降率为工时,有一上仁 k 温•提示】增长率问题所列方程在求解时一般使用直接开平方法.际2.利涧等量关系:利润率=艘XK)0%应] ((D 如图①,设空白部分的宽为工,则Sm^=(α-2x)(6-2x)芳I 考法聚焦素养提升旺・浙江中考命题点元 次方程及其应用元次方程的解法解法适用情况注意事项直接开平方法 (1)当方程续少一次项时•即a√+c=(Xα≠0皿V0); (2)形如α(ι+")2=M!>o)的方程开方后取值符号一般是“土”公式法 适用于所有一元二次方程,求根公式为/=土约蚂"4Qn 1a(1)使用求根公式时要先把一元二次方程化为一般形式,方程的右边一定要化为0? (2)将α,仇C 代入公式时应注意其符号; (3)若加-4αcV0,则原方程无实数解因式分解法 (D 方程缺少常数项.即α/+6a∙=0(α≠0); (2)将方程右边化为0后.方程的左边可以提出含有∙τ的公因式,形如x(αj∙÷Λ)=0或(αz÷6)(cx+J)=0 方程两边含有I 的相同的因式时•不能约去.以免丢根•如对于一元二次方程(工一2)(∙r+2)=∙r—2,不能两边同时约去1—2,否则会造成漏解 配方法 将二次项系数化为1后,一次项系数为绝对值较小的偶数时•考虑使用配方法:方程两边同时加上一次项系数一半的平方(1)在配方过程中,一定要在等号两边同时加上一个相同的数;(2)将方程的二次项系数化为1后•一次项的正负决定配方后括号里面是加还是减根的判别式 (I)A 2-4αc>(×n 一元二次方程行两个不相等的实数根 (2)为一we=。








一元二次方程的实际应用1、阅读下面解题过程,解方程x²-1x1-2=0 解分以下两种情况:(1)当x≥0时,原方程可化为x阅读下面解题过程,解方程x²-1x1-2=0解分以下两种情况:(1)当x≥0时,原方程可化为x²-x=0,解得x1=2 x2=-1(不和题意,舍去)(2)当x<0时,原方程可化为x²+x-2=0,解得x1=-2 x2=1 (不合题意,舍去)∴原方程的根是x1=2 x2=-2请照此方法解方程x²-| x-1 |-1=02、已知关于x的方程x2-(k+2)x+2k=0.(1)求证:无论k取任意实数值,方程总有实数根.(2)若等腰三角形ABC的一边a=1,另两边长b、c恰是这个方程的两个根,求△ABC的周长.3、已知函数y=2/x和y=kx+1(k不等于0).(1)若这两个函数的图像都经过(1,a),求a和k的值(2)(2)当K取何值时,这两个函数的图像总有公共点4、已知,在矩形ABCD中,AB=a,BC=b,动点M从点A出发沿边AD向点D运动.(1)如图1,当b=2a,点M运动到边AD的中点时,请证明∠BMC=90°;(2)如图2,当b>2a时,点M在运动的过程中,是否存在∠BMC=90°,若存在,请给与证明;若不存在,请说明理由;(3)如图3,当b<2a时,(2)中的结论是否仍然成立?请说明理由.5、已知关于x的方程x²-(m+2)x+(2m-1)=0(1)求证:方程有两个不相等的实数根(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角三角形的周长.如图,要设计一幅宽20cm、长30cm的图案,其中有两横两竖的彩条,横、竖彩条的宽度比为3:2,如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度(结果保留小数点后一位)?7、已知:如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E分别是AC、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(s)(0<t<4).解答下列问题:(1)当t为何值时,PQ⊥AB?(2)当点Q在BE之间运动时,设五边形PQBCD的面积为y(cm2),求y与t之间的函数关系式;(3)在(2)的情况下,是否存在某一时刻t,使PQ分四边形BCDE两部分的面积之比为S△PQE:S四边形P=1:29?若存在,求出此时t的值以及点E到PQ的距离h;若不存在,请说明理由.QBCD8、某商场销售一批服装,平均每天可售出20件,每件盈利40元,经市场调查发现,每件服装每降价1元,商场平均每天就可以多售出2件,在国庆期间,商场决定采取降价促销的措施,以达到减少库存、扩大销售量的目的。

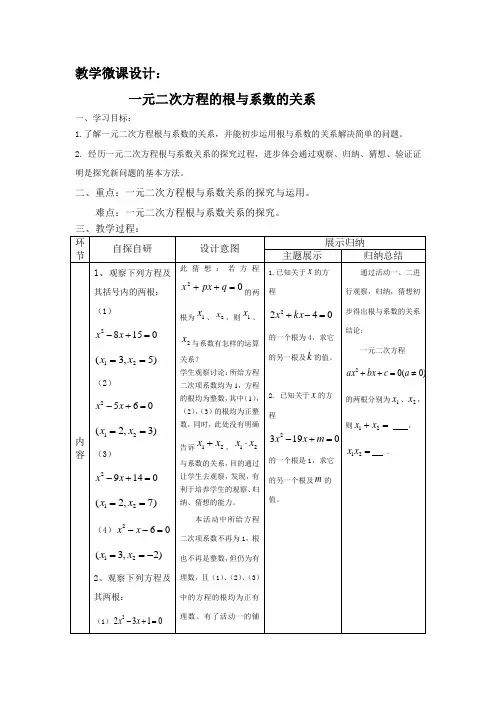
《一元二次方程根与系数的关系》“微课”教学设计
工具和方法:PPT多媒体
教学过程设计
教学目的:
1. 掌握一元二次方程根与系数的关系及其运用。
2.经历探索一元二次方程根与系数的关系的过程,体验观察→发现→猜想→验证的思维转化过程,培养学生分析问题和解
决问题的能力.
3.通过观察、归纳获得数学猜想,体验数学活动充满着探索性和创造性,掌握由“特殊——一般——特殊”的数学思想
方法:
培养学生勇于探索的精神.
教学重点难点
一元二次方程根与系数的关系及其应用.
教学过程
一、探索新知
下列一元二次方程有两个实数根分别是x1,x2,求出方程的两个根并观察方程的两根之和与系数的关系,两根之积与系数的关系,你有什么发现?
(1)x2-3x+2=0 (x1 =1 , x2=2) (2)x2+3x-10=0(x1= -5,x2=2)
二、根与系数的关系(韦达定理):
若一元二次方程ax2+bx+c=0(a≠0)有两实数根x1,x2,则
x1+x2=-ba ,x1·x2=ca
这表明两根之和为一次项系数与二次项系数的比的相反数,两根之积等于常数项与二次项系数的比。
三、典型例题
例 1.不解方程,求下列方程的两根之和与两根之积:x2 – 3x -1 =0 (2)3x2 – x + 2=0
教学设计说明:引导学生正确认识根与系数的关系例2. 已知方程x2-2x+c=0的一根为3,求方程的另一根及c的值.。
一元二次方程的应用
商品利润问题
【要点整理】
基本量:(1)进价(2)售价(3) 利润
基本关系式:(1)每件利润=售价-进价
(2)总利润=每件利润×销售件数
【经典范例】
1.合肥百货大搂服装柜在销售中发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元.为了迎接“十·一”国庆节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:如果每件童装降价4元,那么平均每天就可多售出8件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少?
2.西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价O.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元.该经营户要想每天盈利2O0元,应将每千克小型西瓜的售价降低多少元?
3.工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少元?
(2)若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元?
4.大宇商场在一种待处理的衣服共20件,每件原价为50元,因季节关系的影响,决定进行降价销售。
卖出10件后,商场为了让资金尽快回收,决定以同样的幅度再次下调价格,结
果很快全部售完了所有这种衣服,并共回收资金855元。
(1).求这两次降价的百分率是多少?(2).求后10件这种衣服每件的售价。