北师大版八年级上数学动点问题

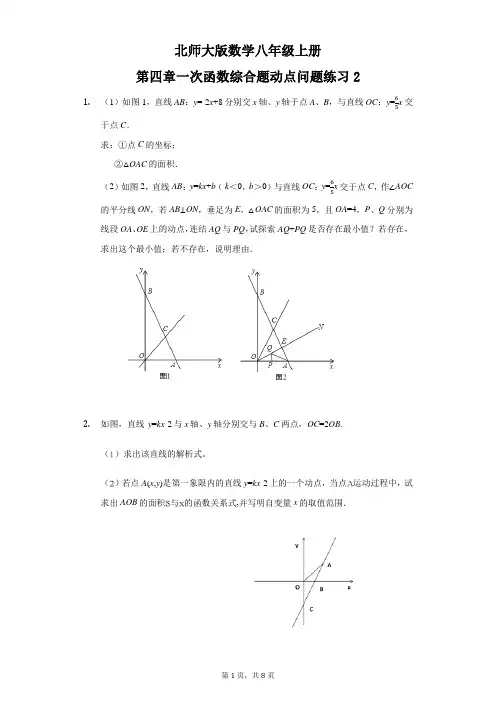
北师大版数学八年级上册第四章一次函数综合题动点问题练习21.（1）如图1，直线AB：y=-2x+8分别交x轴、y轴于点A、B，与直线OC：y=6x交5于点C．求：①点C的坐标；②△OAC的面积．x交于点C，作∠AOC （2）如图2，直线AB：y=kx+b（k＜0，b＞0）与直线OC：y=65的平分线ON，若AB⊥ON，垂足为E，△OAC的面积为5，且OA=4，P、Q分别为线段OA、OE上的动点，连结AQ与PQ，试探索AQ+PQ是否存在最小值？若存在，求出这个最小值；若不存在，说明理由．2.如图，直线y=kx-2与x轴、y轴分别交与B、C两点，OC=2OB.（）求出该直线的解析式。

（）若点A(x,y)是第一象限内的直线y=kx-2上的一个动点，当点运动过程中，试求出AOB的面积与的函数关系式,并写明自变量x的取值范围．3.如图，一次函数y=kx+b的图象分别与x轴、y轴相交于点E和点F，点E的坐标为（-8，0），点F的坐标为（0，6），点A的坐标为（0，4），点P为直线EF上的一个动点．（1）求直线EF的解析式；（2）若点P在点E、F之间运动（不包含E、F点），求△OPA的面积S与x的函数关系式；并写出自变量x的取值范围；（3）探充：若点P在直线EF上运动，当点P运动到什么位置时，△OPA的面积为12？4.如图，在平面直角坐标系xOy中，一次函数y=k1x+b的图象与x轴交于点A（-3，0），与y轴交于点B，且与正比例函数y=kx的图象交点为C（3，4）．（1）求k值与一次函数y=k1x+b的解析式；（2）在x轴上有一动点P，求当PB+PC最小时P点坐标．（3）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，请求出点D 的坐标．5.如图在平面直角坐标系中，直线l1：y=-x+4与y轴交于点A，与直线l2：y=kx+b交于点C（6，n），直线l2：与y轴交于点B（0，-4）．（1）求直线l2的函数表达式；（2）点D（m，0）是x轴上的一个动点，过点D作x轴的垂线，交l1于点M，交l2于点N，当S△AMB=2S△CMB时，请直接写出线段MN的长．x+2与x轴、y轴分别交于A、B两点，在y轴上有一点C 6.如图，直线l：y=−12（0，4）,动点M从A点以每秒1个单位的速度沿x轴向左移动，移动时间为t秒.（1）求A、B两点的坐标；（2）当t何值时△COM≌△AOB，并求此时M点的坐标.7.如图所示，直线y=kx-1与x轴、y轴分别交于B、C两点，OB=1OC.2（1）求B点的坐标和k的值；（2）若点A（x，y）是第一象限内的直线y=kx-1上的一个动点，在点A运动过程中，试写出△AOB的面积S与x的函数表达式；并在当A运动到什么位置时，△AOB .的面积是148.如图，直线y=-x+4与x轴交于点A，与y轴交于点B，点C的坐标是（1，0），P为直线AB上的动点，连接PO，PC．（1）求A，B两点的坐标；（2）当△PBO与△PAC面积相等时，求点P的坐标；（3）直接写出△PCO周长的最小值．9.如图，在平面直角坐标系中，过点A（0，6）的直线AB与直线OC相交于点C（2，4）动点P沿路线O→C→B运动．（1）求直线AB的解析式；（2）当△OPB的面积是△OBC的面积的1时，求出这时点P的坐标.310.如图，已知直线l1：y=1x+1和直线l2：y=3x+1，过点B（3，0）作AB⊥x轴，交直2线l1于点A，若点P是x轴上的一个动点，过点P作平行于y轴的直线，分别与l1、l2交于点C、D，连接AD、BC．（1）求线段AB的长；（2）当P的坐标是（2，0）时，求直线BC的解析式；（3）若△ABC的面积与△ACD的面积相等，求点P的坐标．11.如图，在平面直角坐标系中，过点C（0，6）的直线AC与直线OA相交于点A（4，2），动点M在线段OA和射线AC上运动，试解决下列问题：(1)求直线AC的表达式；(2)求△OAC的面积；(3)是否存在点M，使△OMC的面积是△OAC的面积的1？若存在，求出此时点M的2坐标；若不存在，请说明理由．12.已知，如图，在平面直角坐标系xOy中，直线l1：y=x+3分别交x轴、y轴于点A、B两点，直线l2：y=-3x过原点且与直线l1相交于C，点P为y轴上一动点．（1）求点C的坐标；（2）求出△BCO的面积；（3）当PA+PC的值最小时，求此时点P的坐标．13.如图，直线l1：y1=-x+2与x轴，y轴分别交于A，B两点，点P（m，3）为直线l1x+b过点P．上一点，另一直线l2：y2=12（1）求点P坐标和b的值；（2）若点C是直线l2与x轴的交点，动点Q从点C开始以每秒1个单位的速度向x轴正方向移动．设点Q的运动时间为t秒；①请写出当点Q在运动过程中，△APQ的面积S与t的函数关系式；②直接写出当t为何值时△APQ的面积等于4.5，并写出此时点Q的坐标．14.如图，直线l与x轴交于点A，与y轴交于点B（0，2）．已知点C（﹣1，3）在直线l上，连接OC．（1）求直线l的解析式；（2）P为x轴上一动点，若△ACP的面积是△BOC的面积的2倍，求点P的坐标．15.如图，在平面直角坐标系xOy中，已知直线l1：y=mx（m≠0）与直线l2：y=ax+b（a≠0）相交于点A（1，2），直线l2与x轴交于点B（3，0）．（1）求直线l2的表达式；（2）点Q在直线l2，△OBQ的面积为6，则点Q的坐标为多少？（3）过动点P（0，n）且平行于x轴的直线与l1，l2的交点分别为C，D，当点C 位于点D左方时，写出n的取值范围．16.如图，在平面直角坐标系中，直线l1：y=kx+b（k≠0）与直线l2：y=x交于点A（2，a），与y轴交于点B（0，6），与x轴交于点C．（1）求直线l1的函数表达式；（2）求△AOC的面积；（3）在平面直角坐标系中有一点P（5，m），使得S△AOP=S△AOC，请求出点P的坐标；（4）点M为直线l1上的动点，过点M作y轴的平行线，交l2于点N，点Q为y轴上一动点，且△MNQ为等腰直角三角形，请直接写出满足条件的点M的坐标．第9页，共1页。

初中数学动点问题(北师大版)1. 引言初中数学动点问题是数学中经常出现的一个考点，它涉及到点在平面内移动的问题。

通过解决这类问题，可以帮助学生理解和掌握坐标系、图形变换等数学概念。

本文将重点介绍北师大版初中数学教材中关于动点问题的内容。

2. 动点问题的基本概念动点问题是指一个点在平面内以一定的规律进行移动的情况。

这个点可以在平面内的不同位置上，可以沿直线、曲线等路径运动。

学生需要根据提供的条件，确定点的运动轨迹、速度、方向等。

解决动点问题需要运用坐标系、直线方程、参数方程等知识。

3. 动点问题的解决方法解决动点问题的方法有多种，下面介绍几种常见的方法：- 使用坐标系：通过建立合适的坐标系，将点的位置用坐标表示，便于进行计算和分析。

- 利用直线方程：当点在直线上运动时，可以通过直线方程来确定点的位置，进而求解相关问题。

- 应用参数方程：对于复杂的轨迹，可以使用参数方程来描述点的位置，通过确定参数值来求解问题。

- 运用速度概念：当点的位置随时间变化时，可以利用速度概念来描述点的运动，并解决相关问题。

4. 例题分析下面通过例题来具体说明解决动点问题的步骤和方法。

例题：一条船以每小时12公里的速度顺水航行，沿江下游行驶，下游距离为96公里。

一条狗站在江边，见船过去需0.5小时，它就跳入江中追船，每小时游5公里。

试问，狗游完全程需要多少时间？一条船以每小时12公里的速度顺水航行，沿江下游行驶，下游距离为96公里。

一条狗站在江边，见船过去需0.5小时，它就跳入江中追船，每小时游5公里。

试问，狗游完全程需要多少时间？解答：首先，设狗追船的时间为$t$小时，则船运动的时间为$t+0.5$小时。

根据题意可得：船的位移 = 船的速度 ×船的时间狗的位移 = 狗的速度 ×狗的时间根据题目中给出的数据，可列出方程组：$$12 \times (t+0.5) = 96$$$$5 \times t = 96$$解方程可得：$t=\frac{192}{17}$因此，狗游完全程需要$\frac{192}{17}$小时。

平行四边形之动点问题（北师版）（专题）一、单选题(共6道，每道15分)1.如图，在平行四边形ABCD中，AB=1，BC=3．动点P从点A出发，沿AD方向以每秒3个单位的速度向点D匀速运动；同时动点Q从点C出发，沿CD方向以每秒1个单位的速度向点D匀速运动．连接QP并延长，交BA的延长线于点M，设运动的时间为t秒，则当t=( )时，四边形AQDM是平行四边形．A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：略2.如图，平行四边形ABCD的对角线AC，BD相交于点O，BD=12cm，AC=6cm，点E在线段BO上从点B以1cm/s的速度运动，点F在线段OD上从点O以2cm/s的速度运动．若点E，F同时运动，设运动时间为t秒，当t=( )时，四边形AECF是平行四边形．A.2B.3C.6D.12答案：A解题思路：运动路线分析图：依题意，设BE=t，则OE=6-t，OF=2t．若四边形AECF为平行四边形，则OE=OF，即6-t=2t，解得t=2，故选A．试题难度：三颗星知识点：略3.如图，在四边形ABCD中，AD∥BC，且，BC=6cm，P，Q分别从A，C同时出发，P以1cm/s的速度由A向D运动，Q以2cm/s的速度由C出发向B运动．设运动时间为x秒，则当x=( )时，四边形ABQP是平行四边形．A.1B.2C.3D.4答案：B解题思路：运动路线分析图：依题意，AP=x，CQ=2x，∵BC=6，∴QB=6-2x，若四边形ABQP是平行四边形，则AP=BQ，∴x=6-2x，解得x=2．故选B．试题难度：三颗星知识点：略4.如图，在四边形ABCD中，AD∥BC，且BC=6cm，AD=9cm，P，Q分别从A，C同时出发，P以1cm/s的速度由A向D运动，Q以2cm/s的速度由C向B运动，( )秒时直线PQ将四边形截出一个平行四边形．A.3或B.或C.2或3D.2或答案：C解题思路：运动路线分析图：设运动时间为t，结合题意可得：CQ=2t，AP=t，共分两种情况：①当四边形APQB是平行四边形时，AP=BQ，即：t=6-2t，解得t=2；②当四边形CDPQ是平行四边形时，PD=CQ，即：9-t=2t，解得t=3．综上，故选C．试题难度：三颗星知识点：略5.如图，在平行四边形ABCD中，AB=5，AD=15，∠ABC=60°．点P从点B出发沿B→A→D以每秒2个单位长度的速度向点D匀速运动；同时点Q从点C出发沿C→B以每秒3个单位长度的速度向点B匀速运动，当点Q到达点B时，P，Q同时停止运动．设P，Q的运动时间为t秒．（1）点P在AD上运动过程中，当t=( )秒时，PQ∥AB．A.3B.4C.2D.2.5答案：B解题思路：试题难度：三颗星知识点：略6.（上接第5题）（2）如图，过点Q作QE⊥BC交线段DA或AB于点E，设△BQE的面积为S，则S与t的函数关系式为( )A.B.C.D.答案：D解题思路：试题难度：三颗星知识点：略。

学生做题前请先回答以下问题问题1：动点问题的处理框架是什么？问题2：在分析运动过程时常借助运动状态分析图，需要关注哪几个要素？四边形之动点问题（建等式一）（北师版）一、单选题(共5道，每道20分)1.如图，直线与x轴、y轴分别交于A，B两点，直线BC与x轴交于点C，∠ABC=60°．动点P从点A出发以每秒1个单位的速度沿AC向点C运动（不与点A，C重合），同时动点Q从点C出发以每秒2个单位的速度沿折线CB-BA向点A运动（不与点C，A重合）．设点P的运动时间为t秒，△APQ的面积为S，则S与t之间的函数关系式为( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：动点问题2.如图，在梯形ABCD中，AD∥BC，AD=6，BC=16，E是BC的中点．点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒2个单位长度的速度从点C出发，沿CB向点B运动．点P停止运动时，点Q也随之停止运动．当运动时间为( )秒时，以点P，Q，E，D为顶点的四边形是平行四边形．A. B.C.或D.或答案：D解题思路：试题难度：三颗星知识点：动点问题3.如图，在平行四边形OABC中，点A在x轴上，∠AOC=60°，OC=4cm，OA=8cm．动点P 从点O出发，以1cm/s的速度沿折线OA-AB运动；动点Q同时从点O出发，以相同的速度沿折线OC-CB运动．当其中一点到达终点B时，另一点也随之停止运动，设运动时间为t 秒．（1）设△OPQ的面积为S，要求S与t之间的函数关系式，根据表达的不同，t的分段应为( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：动点问题4.（上接第3题）（2）S与t之间的函数关系式为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：动点问题5.（上接第4题）（3）当点P在OA上运动，且△OPQ的面积为平行四边形OABC的面积的一半时，t的值为( )A.，8B.4C. D.8答案：D解题思路：试题难度：三颗星知识点：动点问题学生做题后建议通过以下问题总结反思问题1：动点问题的处理框架中的第三步：分析几何特征、表达、设计方案求解，具体的操作动作有哪些？问题2：表达线段长时有哪些手段？。

最新北师大版八年级数学上册动点问题专练1、已知，如图，点D是△ABC的边AB的中点，四边形BCED是平行四边形，（1）求证：四边形ADCE是平行四边形；（2）当△ABC满足什么条件时，平行四边形ADCE是矩形？2、如图，已知E是平行四边形ABCD的边AB上的点，连接DE．（1）在∠ABC的内部，作射线BM交线段CD于点F，使∠CBF=∠ADE；（要求：用尺规作图，保留作图痕迹，不写作法和证明）（2）在（1）的条件下，求证：△ADE≌△CBF．3、如图，已知E是▱ABCD中BC边的中点，连接AE并延长AE交DC的延长线于点F．（1）求证：△ABE≌△FCE．（2）连接AC、BF，若∠AEC=2∠ABC，求证：四边形ABFC为矩形．4、如图①所示，已知A、B为直线l上两点，点C为直线l上方一动点，连接AC、BC，分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作DD1⊥l于点D1，过点E作EE1⊥l于点E1．（1）如图②，当点E恰好在直线l上时（此时E1与E重合），试说明DD1=AB；（2）在图①中，当D、E两点都在直线l的上方时，试探求三条线段DD1、EE1、AB之间的数量关系，并说明理由；（3）如图③，当点E在直线l的下方时，请直接写出三条线段DD1、EE1、AB之间的数量关系．（不需要证明）5、如图1，矩形MNPQ中，点E，F，G，H分别在NP，PQ，QM，MN上，若∠1=∠2=∠3=∠4，则称四边形EFGH为矩形MNPQ的反射四边形．图2，图3，图4中，四边形ABCD为矩形，且AB=4，BC=8．理解与作图：（1）在图2，图3中，点E，F分别在BC，CD边上，试利用正方形网格在图上作出矩形ABCD 的反射四边形EFGH．计算与猜想：（2）求图2，图3中反射四边形EFGH的周长，并猜想矩形ABCD的反射四边形的周长是否为定值？启发与证明：（3）如图4，为了证明上述猜想，小华同学尝试延长GF 交BC 的延长线于M ，试利用小华同学给我们的启发证明（2）中的猜想．6、如图，矩形ABCD 中，AB ＝4cm ，BC ＝8cm ，动点M 从点D 出发，按折线DCBAD 方向以2cm/s 的速度运动，动点N 从点D 出发，按折线DABCD 方向以1cm/s 的速度运动．（1）若动点M 、N 同时出发，经过几秒钟两点相遇？（2）若点E 在线段BC 上，且BE ＝3cm ，若动点M 、N 同时出发，相遇时停止运动，经过几秒钟，点A 、E 、M 、N 组成平行四边形？7、已知：如图，在梯形ABCD 中，AB ∥DC ，∠B=90°，BC=8cm ，CD=24cm ，AB=26Cm ，点P 从C 出发，以1cm/s 的速度向D 运动，点Q 从A 出发，以3cm/s 的速度向B 运 动，其中一动点达到端点时，另一动点随之停止运动．从运动开始．（1）经过多少时间，四边形AQPD 是平行四边形？（2）经过多少时间，四边形AQPD 成为等腰梯形？（3）在运动过程中，P 、Q 、B 、C 四点有可能构成正方形吗？为什么？8、如图，已知平行四边形ABCD 的对角线AC 、BD 相交于点O ，AC=20cm 、BD=12cm ，两动点E 、F 同时分别以2cm/s 的速度从点A 、C 出发在线段AC 相对上运动．（1）求证：当E 、F 运动过程中不与点O 重合时，四边形BEDF 一定为平行四边形；（2）当E 、F 运动时间t 为何值时，四边形BEDF 为矩形？N M D C BA9、如图所示，在梯形ABCD中，AD∥BC，∠B=90°，AD=24 cm，BC=26 cm，动点P从点A 出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿着CB方向向点B以3cm/s 的速度运动．点P、Q分别从点A和点C同时出发，当其中一点到达端点时，另一点随之停止运动．（1）经过多长时间，四边形PQCD是平行四边形？（2）经过多长时间，四边形PQBA是矩形？（3）经过多长时间，四边形PQCD是等腰梯形？10、如图，平行四边形ABCD的对角线AC、BD相交于点O，BD=12cm，AC=6cm，点E在线段BO上从点B以1cm/s的速度运动，点F在线段OD上从点O以2cm/s的速度运动．（1）若点E、F同时运动，设运动时间为t秒，当t为何值时，四边形AECF是平行四边形．（2）在（1）的条件下，①当AB为何值时，四边形AECF是菱形；②四边形AECF可以是矩形吗？为什么？11、如图，在梯形ABCD中，AD∥BC，AD=4，DC=5，BC=11，梯形的高为4，动点M从B点出发沿线段BC以每秒1个单位长度的速度向终点C运动；动点N同时从C点出发沿CDA以每秒2单位长度的速度向终点A运动．若M，N两点同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动的时间为t秒．（1）t为何值时，四边形ABMN为平行四边形；（2）t为何值时，四边形CDNM为等腰梯形．12、如图，等腰梯形ABCD中，AD∥BC，AB=CD，AD=10cm，BC=30cm，动点P从点A开始沿AD 边向点以每秒1cm的速度运动，同时动点Q从点C开始沿CB边向点B以每秒3cm的速度运动，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒．（1）t为何值时，四边形ABQP是平行四边形？（2）四边形ABQP能成为等腰梯形吗？如果能，求出t的值；如果不能，请说明理由．13、如图，已知在四边形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P 从A开始沿AD边向点D以1cm/s的速度运动，动点Q从点C开始沿CB边向点B以3cm/s的速度运动，P、Q别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动的时间为t秒．（1）当t为何值时，四边形ABQP为矩形？（2）当t为何值时，四边形PQCD为平行四边形？（3）当t为何值时，四边形PQCD为等腰梯形？14、如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P 从点A开始沿AD边向点D以1cm/秒的速度运动；动点Q从点C开始沿CB边向点B以3cm/秒的速度运动，若P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t．（1）当t为何值时，线段AB与线段PQ相等；（2）当t为何值时，四边形PQCD为等腰梯形；（3）是否存在t值，使PQ把直角梯形分成周长相等的两部分？若存在，求出t的值；若不存在，请你说明理由．15、P、Q二人沿直角梯形ABCD道路晨练，如图，AD∥BC，∠B=90°，AD=240m，BC=270m，P 从点A开始沿AD边向点D以1m/s的速度行走，Q从点C开始沿CB边向点B以3m/s的速度跑步．（1）P、Q二人分别从A、C两点同时出发多少时间时，四边形PQCD（P、Q二人所在的位置为P、Q点）是平行四边形？（2）添加一个什么条件时，P、Q二人分别从A、C两点同时出发，在某时刻四边形PQCD是菱形？说明理由．（3）P、Q二人分别从A、C两点同时出发多少时间时，四边形PQCD是等腰梯形？16、如图，O为△ABC的边AC上一动点，过点O的直线MN∥BC，设MN分别交∠ACB的内、外角平分线于点E、F.（1）求证：OE=OF（2）当点O在何处时，四边形AECF是矩形？（3）请在ABC中添加条件，使四边形AECF变为正方形，并说明你的理由.。

八年级上册综合复习（十一）动点问题（北师版）一、单选题(共7道，每道14分)1.如图，直线：与x，y轴分别交于A，B两点，直线：与x轴交于点C，与直线交于点P．动点M从点A出发，以每秒1个单位的速度沿折线AP—PC 向点C匀速运动（点M不与点A，C重合），设△OMC的面积为S，运动时间为t秒，则S 与t之间的函数关系式为( )A.B.C.D.答案：B解题思路：试题难度：三颗星知识点：一次函数动点问题2.如图，在△AOB中，以点O为原点建立平面直角坐标系，A(16，0)，B(8，6).动点P从点A出发以每秒3个单位的速度沿AO向终点O运动，同时点Q从点O出发以每秒2个单位的速度沿OB—BA向终点A运动，当其中一点到达终点时，另一点也随之停止运动.设运动时间为t秒，则△OPQ的面积S与t之间的函数关系式为( )A.B.C.D.答案：B解题思路：试题难度：三颗星知识点：一次函数之动点问题3.如图，过A(8，0)，B两点的直线与直线交于点C，平行于y轴的直线从原点O出发，以每秒1个单位长度的速度沿x轴向右平移，到C点时停止；分别交线段BC，OC于点D，E，以DE为边向左侧作等边△DEF，设△DEF与△BCO重叠部分的面积为S （平方单位），直线的运动时间为t（秒）．（1）C点坐标是( )，根据S表达的不同，t的分段是( )A.B.C.D.答案：C解题思路：试题难度：三颗星知识点：一次函数动点问题4.（上接第3题）（2）S与t的函数关系式是( )A.B.C.D.答案：C解题思路：试题难度：三颗星知识点：一次函数动点问题5.如图，直线y=-x+18分别与x轴、y轴交于A，B两点；直线y=2x分别与AB交于点C，与过点A且平行于y轴的直线交于点D．点E从点A出发，以每秒1个单位长度的速度沿x 轴向左运动，过点E作x轴的垂线，分别交直线AB，OD于点P，Q，以PQ为边向右作正方形PQMN，设正方形PQMN与△ACD重叠部分的面积为S（平方单位），点E的运动时间为t （秒）．当0<t<12时，则S与t之间的函数关系式为（）<12时，则s与t之间的函数关系式为( )A.B.C.D.答案：B解题思路：试题难度：三颗星知识点：一次函数动点问题6.如图，已知一次函数y=-x+7与正比例函数的图象交于点A，且与x轴交于点B．过点A作AC⊥y轴于点C．动点P从点O出发，以每秒1个单位长度的速度，沿OC-CA的路线向点A运动；同时动点R从点B出发，以相同速度向左平移．当点P到达点A时，点P 和点R都停止运动．在运动过程中，设动点P运动的时间为t秒，△APR的面积为S，则S 关于t的函数关系式为( )A.B.C.D.答案：B解题思路：试题难度：三颗星知识点：一次函数动点问题7.如图，在平面直角坐标系中，四边形ABCD是梯形，AB∥CD，点B（10，0），C（7，4），∠DAB=45°．动点P从点A出发以每秒2个单位的速度向终点B运动，同时动点Q从点B出发以每秒5个单位的速度沿折线BC-CD的方向向点D运动，过点P作PM垂直于x轴，与折线AD-DC相交于点M，当P，Q两点中有一点到达终点时，另一点也随之停止运动．设点P，Q运动的时间为t秒（t＞0），△MPQ的面积为S．则点Q与点M相遇前S与t之间的函数关系式为( )A.B.C.D.答案：D解题思路：试题难度：三颗星知识点：一次函数动点问题。

北师大版八年级上数学动点问题初二动点问题1.如图，等腰梯形ABCD 中，AD ∥BC ，AB=CD ，AD=10cm ，BC=30cm ，动点P 从点A 开始沿AD 边向点D 以每秒1cm 的速度运动，同时动点Q 从C 开始沿CB 边向点B 以每秒3cm 的速度运动，当其中一点到达端点时，另一点也随之停止运动。

设运动时间为t 秒。

（1）t 为何值时，四边形ABQP 是平行四边形？（2）四边形ABQP 能成为等腰梯形吗？如果能，求出t 的值；如果不能，请说明理由。

2.如图，已知直线1l :2+-=x y 与直线2l ：82+=x y 相交于点F ，1l 、2l 分别交x 轴于点E 、G ，矩形ABCD 顶点C 、D 分别在直线1l 、2l ，顶点A 、B 都在x 轴上，且点B 与点G 重合。

（1）、求点F 的坐标和∠GEF 的度数；（2）、求矩形ABCD 的边DC 与BC 的长；（3）、若矩形ABCD 从原地出发，沿x 轴正方向以每秒1个单位长度的速度平移，设移动时间为t ()60≤≤t 秒，矩形ABCD 与△GEF 重叠部分的面积为s ，求s 关于t 的函数关系式，并写出相应的txy O x =4 A B C PH M 3.四边形OABC 是等腰梯形，OA ∥BC ，在建立如图的平面直角坐标系中，A （10，0），B （8，6），直线x =4与直线AC 交于P 点，与x 轴交于H 点；（1）直接写出C 点的坐标，并求出直线AC 的解析式；（2）求出线段PH 的长度，并在直线AC 上找到Q 点，使得△PHQ 的面积为△AOC 面积的51，求出Q 点坐标；（3）M 点是直线AC 上除P 点以外的一个动点，问：在x 轴上是否存在N 点，使得△MHN 为等腰直角三角形？若有，请求出M 点及对应的N 点的坐标，若没有，请说明理由．4．如图，正方形CGEF 的对角线CE 在正方形ABCD 的边BC 的延长线上（CG ＞BC ），M 是线段AE 的中点，DM 的延长线交CE 于N ．（1）线段AD 与NE 相等吗？请说明理由；（2）探究：线段MD 、MF 的关系，并加以证明．。

专题1.7动点问题1．在ABC 中，90ACB ，5AB cm ，3AC cm ，动点P 从点B 出发，沿射线BC 以1/cm s 的速度移动，设运动的时间为t 秒，当ABP 为直角三角形时，求t 的值．【解答】解：在Rt ABC 中，由勾股定理得：222225316BC AB AC ，4BC cm ．根据题意得：BP tcm ．①如图①，当BAP 为直角时，BP tcm ．(4)CP t cm ，3AC cm ，在Rt ACP 中，222223(4)AP AC CP t ，在Rt BAP 中，222AB AP BP ，222253(4)t t ，解得254t ．②如图②，当APB 为直角时，此时点P 与点C 重合，4BP BC cm ，4t ．当ABP 为直角三角形时，4t 或254．2．如图，ABC 中，20AB AC BC 厘米，如果点M 从点C 出发，点N 从点B 出发，沿着三角形三边以4厘米/秒的速度运动，当点N 第一次到达C 点时，M ，N 两点同时停止运动．运动时间为t （秒)．（1）当05t 且BMN 为直角三角形时，求t 的值；（2）当t 为何值，BMN 为等边三角形．【解答】解：（1）当05t 时，点M 在BC 上，点N 在AB 上，4BN t ，204MB t ，BMN 为直角三角形，则90BNM 或90NMB ，①当90BNM 时，60B ∵，90906030BMN B ，2BM BN ，20424t t ，解得：53t ；②当90NMB 时，60B ∵，90906030BNM B ，2BN BM ，42(204)t t ，解得：103t ．③点M 在AC 上，点N 在AB 上，404AN CM t ，(808)(404)20t t ，253t （不合题意舍去），综上，当53t 或103时，BMN 为直角三角形；（2）点N 第一次到达C 点时，M ，N 两点同时停止运动，则010t ，①当05t 时，当MB BN 时，BMN 为等边三角形，此时，4204t t ，解得：52t ；②当510t 时，BMN 为等边三角形，只能点M 与点A 重合，点N 与点C 重合，此时，10t ，综上，52t 或10t 时，BMN 为等边三角形．3．如图，已知ABC 中，90B ，16AB cm ，12BC cm ，P 、Q 是ABC 边上的两个动点，其中点P 从点A 开始沿A B 方向运动，且速度为每秒1cm ，点Q 从点B 开始沿B C A 方向运动，且速度为每秒2cm ，它们同时出发，同时停止．（1）P 、Q 出发4秒后，求PQ 的长；（2）当点Q 在边CA 上运动时，出发几秒钟后，CQB 能形成直角三角形？【解答】解：（1）由题意可得，248()BQ cm ，161412()BP AB AP cm ，90B ∵，)PQ cm ，即PQ 的长为；（2）当BQ AC 时，90BQC ，90B ∵，16AB cm ，12BC cm ，20()AC cm，∵22AB BC AC BQ ， 16122022BQ ，解得485BQ cm ，36()5CQ cm ， 当CQB 是直角三角形时，经过的时间为：36(1229.65（秒)；当90CBQ 时，点Q 运动到点A ，此时运动的时间为：(1220)216 （秒)；由上可得，当点Q 在边CA 上运动时，出发9.6秒或16秒后，CQB 能形成直角三角形．4．如图，在Rt ABC 中，90C ，10AB cm ，6AC cm ，动点P 从点B 出发，以2/cm 秒的速度沿BC 移动至点C ，设运动时间为t 秒．（1）求BC 的长；（2）在点P 的运动过程中，是否存在某个时刻t ，使得点P 到边AB 的距离与点P 到点C 的距离相等？若存在，求出t 的值；若不存在，请说明理由．【解答】解：（1）在Rt ABC 中，由勾股定理得：8()BC cm ；（2）存在，理由如下：如图，当点P 恰好运动到BAC 平分线上时，点P 到直线AB 的距离与点P 到点C 的距离相等，由已知可得：2BP t cm ，(82)PC BC BP t cm ，连接AP ，过点P 作PE AB 于E ，如图所示：则(82)PE PC t cm ，在AEP 与ACP 中，90PAE PAC AEP C AP AP，()AEP ACP AAS ，6AE AC cm ，1064()BE AB AE cm ，在Rt BEP 中，由勾股定理得：222BP BE PE ，即222(2)4(82)t t ，解得：52t ，即当t 的值为52时，点P 到边AB 的距离与点P 到点C的距离相等．5．如图，在Rt ABC 中，90B ，7AB cm ，25AC cm ．点P 从点A 出发沿AB 方向以1/cm s 的速度向终点B 运动，点Q 从点B 出发沿BC 方向以6/cm s 的速度向终点C 运动，P ，Q 两点同时出发，设点P 的运动时间为t 秒．（1）求BC 的长；（2）当2t 时，求P ，Q 两点之间的距离；（3）当AP CQ 时，求t 的值？【解答】解：（1）在Rt ABC 中，90B ，7AB cm ，25AC cm ，24BC cm ．（2）如图，连接PQ ，725BP ，6212BQ ，在直角BPQ 中，由勾股定理得到：13()PQ cm ；（3）设t 秒后，AP CQ ．则246t t ，解得247t ．答：P 、Q 两点运动247秒，AP CQ ．6．如图，在Rt ABC 中，90ACB ，10AB cm ，6AC cm ，动点P 从点B 出发沿射线BC 以1/cm s 的速度运动，设运动时间为()t s ．（1）当ABP 为直角三角时，求t 的值；（2）当ABP 为等腰三角形时，求t 的值．【解答】解：（1）当ABC 为直角三角时，8()BC cm ，①当90APB 时，点P 与点C 重合，8BP BC ，8t ，②当90BAP ，BP t ，8CP t ，6AC ，在Rt ACP 中，2226(8)AP t ，在Rt BAP 中，222AB AP BP ，222210[6(8)]t t ，解得：252t ，综上所述，8t 或252；（2）在ABC 中，90ACB ，由勾股定理得：8()BC cm ，ABP ∵为等腰三角形，当AB AP 时，则216BP BC cm ，即16t ；当10BA BP cm 时，则10t ；当PA PB 时，如图：设BP PA x ，则8PC x ，在Rt ACP 中，由勾股定理得：222PC AC AP ，222(8)6x x ，解得254x ，254t ．综上所述：t 的值为16或10或254．7．如图，在ABC 中，60A ，4AB cm ，12AC cm ．动点P 从点A 开始沿AB 边以1/cm s 的速度运动，动点Q 从点C 开始沿CA 边以3/cm s 的速度运动．点P 和点Q 同时出发，当点P 到达点B 时，点Q 也随之停止运动．设动点的运动时间为t (04)s t ，解答下列问题：（1）当t 为何值时，点A 在PQ 的垂直平分线上？（2）在运动过程中，是否存在某一时刻t ，使APQ 是直角三角形？若存在，求出t 的值；若不存在，请说明理由．【解答】解：（1）若点A 在线段PQ 的垂直平分线上，则AP AQ ，AP t ∵，123AQ t ，123t t ，解得：3t ，答：当3t 时，点A 在线段PQ 的垂直平分线上；（2）①若90APQ ，则APQ 是直角三角形，60A ∵，30AQP ，2AQ AP ，1232t t ，125t ，②若90AQP ，则APQ 是直角三角形，60A ∵，30APQ ，2AP AQ ，2(123)t t ，247t ． 当125t 或247时，APQ 是直角三角形．8．如图，在Rt ABC 中，3AB ，4BC ，动点P 从点A 出发沿AC 向终点C 运动，同时动点Q 从点B 出发沿BA 向点A 运动，到达A 点后立刻以原来的速度沿AB 返回．点P ，Q 的运动速度均为每秒1个单位长度，当点P 到达点C 时停止运动，点Q 也同时停止运动，连接PQ ，设它们的运动时间为(0)t t 秒．（1）设CBQ 的面积为S ，请用含有t 的代数式来表示S ；（2）线段PQ 的垂直平分线记为直线l ，当直线l 经过点C 时，求AQ 的长．【解答】解：（1）如图1，当03t 时，BQ t ，4BC ，1422S t t ；如图2，当35t 时，，3AQ t ，则3(3)6BQ t t ，14(6)1222S t t ；（2）连接CQ ，如图3，QP ∵的垂直平分线过点C ，CP CQ ，3AB ∵，4BC ，5AC ，2224(5)t t ，解得910t ；或2224(6)(5)t t ，显然不成立；92131010AQ ．9．如图，在Rt ABC 中，90ABC ，20AB ，15BC ，AD 为AC 边上的动点，点D 从点C 出发，沿边CA 往A 运动，当运动到点A 时停止，设点D 运动的时间为t 秒，速度为每秒2个单位长度．（1）当t 为何值时，CBD 是直角三角形；（2）若CBD 是等腰三角形，求t 的值．【解答】解：（1）2CD t ，90ABC ∵，20AB ，15BC ，25AC ，252AD AC CD t ；①90CDB 时，1122ABC S AC BD AB BC，即1125201522BD ，解得12BD ，9CD ，92 4.5t ；②90CBD 时，点D 和点A 重合，25212.5t ．综上所述， 4.5t 或12.5秒时，CBD 是直角三角形（2）①CD BC 时，15CD ，1527.5t ；②CD BD 时，C DBC ，90C A DBC DBA ∵，A DBA ，BD AD ，112.52CD AD AC ，12.52 6.25t ；③BD BC 时，如图，过点B 作BF AC 于F ，根据等腰三角形三线合一的性质可得2CD CF ；则CF DF ，12BF ∵，9CF ，29218CD CF ，1829t ．综上所述， 6.25t 或7.5或9秒时，CBD 是等腰三角形．10．已知ABC 中，90B ，8AB cm ，6BC cm ，P 、Q 是ABC 边上的两个动点，其中点P 从点A 开始沿A B 方向运动且速度为每秒1cm ，点Q 从点B 开始沿B C A 方向运动，在BC 边上的运动速度是每秒2cm ，在AC 边上的运动速度是每秒1.5cm ，它们同时出发，当其中一个点到达终点时，另一个点也随之停止，设运动时间为t 秒．（1）出发2秒后，求PQ 的长；（2）当点Q 在边BC 上运动时，t 为何值时，ACQ 的面积是ABC 面积的13；（3）当点Q 在边CA 上运动时，t 为何值时，PQ 将ABC 周长分为23:25两部分．【解答】解：（1）当2t s 时，点Q 在边BC 上运动，则2AP cm ，24()BQ t cm ，8AB cm ∵，826()BP AB AP cm ，在Rt BPQ 中，由勾股定理可得)PQ cm ，PQ 的长为；（2）12ACQ S CQ AB ∵，12ABC S BC AB ，点Q 在边BC 上运动时，ACQ 的面积是ABC 面积的13，1162()33CQ BC cm ，624()BQ BC CQ cm ，422t ，当点Q 在边BC 上运动时，t 为2时，ACQ 的面积是ABC 面积的13；（3）在Rt ABC 中，由勾股定理得：10()AC cm ，当点P 达到点B 时，881t ，当点Q 达到点A 时，610292 1.53t ，∵当其中一个点到达终点时，另一个点也随之停止，08t ，AP t ∵cm ，(8)BP t cm ，点Q 在CA 上运动时，61.5()(1.5 4.5)()2CQ t t cm ，10(1.5 4.5)(1.514.5)()AQ t t cm ，86 1.5 4.5(0.59.5)()BP BC CQ t t t cm ，(1.514.5)(0.514.5)()AP AQ t t t cm ，分两种情况：①2325BP BC CQ AP AQ ，即0.59.5230.514.525t t ，解得：4t ，经检验，4t 是原方程的解，4t ；②2523BP BC CQ AP AQ ，即0.59.5250.514.523t t ，解得：6t ，经检验，6t 是原方程的解，6t ；综上所述，当点Q 在边CA 上运动时，t 为4或6时，PQ 将ABC 周长分为23:25两部分．11．如图，在ABC 中，90C ，12AC ，5BC ，BD 平分ABC ．动点P 从点B 出发，沿折线BA AC 以每秒1个单位长度的速度向点C 运动，当点P 不与点D 重合时，连结P 、B 、D 三点．设点P 的运动时间为t 秒．（1）线段AB 的长为13；（2）当DP AB 时，t；（3）求线段BD 的长；（4）当DBP 与DPB 相等时，直接写出t 的值．【解答】解：（1）90C ∵，12AC ，5BC ，13AB ．故答案为：13．（2）BD ∵平分ABC ，DP AB ，DC CB ，DC DP ．在Rt DCB 和Rt DPB 中，BD BD DC DP，Rt DCB Rt DPB(HL) ．5BC BP ．15t BP．故答案为：5．（3）BD∵平分ABC，AD AB CD BC．12135CDCD．解得：103 CD ．在Rt CDB中，3BD ．（4）①当点P在AB上时，DBP DPB∵，DB DP．过点D作DE AB于点E，如图，由（2）知：Rt DCB Rt DEB，5BE BC．DB DP∵，DE AB，5PE BE．210PB BE．110t BP；②当点P在AC上时，DBP DPB∵，DB DP．由（3）知：3BD ，103CD ，PD ．PA AC CD PD ．点P 运动的距离为：653AB PA ．6565()133t ．综上，t 的值为：10或653 ．12．如图，在ABC 中，3AB ，4AC ，5BC ，P 为边BC 上一动点，PE AB 于E ，PF AC 于F ，M 为EF 中点，求AM 的最小值．【解答】解：∵在ABC 中，3AB ，4AC ，5BC ，222AB AC BC ，即90BAC ．又PE AB ∵于E ，PF AC 于F ，四边形AEPF 是矩形，EF AP ．M ∵是EF 的中点，1122AM EF AP ．当AP BC 时，AP 的最小值即为直角三角形ABC 斜边上的高125，AM 的最小值是65．13．如图，已知四边形ABCD 中，//AB CD ，4BC AD ，10AB CD ，90DCB ，E 为CD 边上的一点，7DE ，动点P 从点A 出发，以每秒1个单位的速度沿着边AB 向终点B 运动，连接PE ，设点P 运动的时间为t 秒．（1）求BE 的长；（2）若BPE 为直角三角形，求t 的值．【解答】解：（1）10CD ∵，7DE ，1073CE ，在Rt CBE 中，5BE ；（2）当90BPE 时，1037AP ，则717t （秒)，当90BEP 时，222BE PE BP ，即222254(7)(10)t t ，解得，53t ， 当7t 或53时，BPE 为直角三角形．14．如图，在Rt ABC 中，90ABC ，20AB ，15BC ，点D 为AC 边上的动点，点D 从点C 出发，沿边CA 往A 运动，当运动到点A 时停止，设点D 运动的时间为t 秒，速度为每秒2个单位长度．（1）填空：当t 4.5或12.5秒时，CBD 是直角三角形；（2）若CBD 是等腰三角形，求t 的值．【解答】解：（1）2CD t ，90ABC ∵，20AB ，15BC ，25AC ，252AD AC CD t ；①90CDB 时，1122ABC S AC BD AB BC，即1125201522BD ，解得12BD ，9CD ，92 4.5t ；②90CBD 时，点D 和点A 重合，25212.5t ．综上所述， 4.5t 或12.5秒时，CBD 是直角三角形（2）①CD BC 时，15CD ，1527.5t ；②CD BD 时，C DBC ，90C A DBC DBA ∵，A DBA ，BD AD ，112.52CD AD AC ，12.52 6.25t ；③BD BC 时，如图，过点B 作BF AC 于F ，根据等腰三角形三线合一的性质可得2CD CF ；则CF DF ，12BF ∵，9CF ，29218CD CF ，1829t ．综上所述， 6.25t 或7.5或9秒时，CBD 是等腰三角形．故答案为：4.5或12.5秒．15．如图，已知在Rt ABC 中，90ACB ，8AC ，16BC ，D 是AC 上的一点，3CD ，点P 从B 点出发沿射线BC 方向以每秒2个单位的速度向右运动．设点P 的运动时间为t ．连接AP ．（1）当3t 秒时，求AP 的长度（结果保留根号）；（2）当ABP 为等腰三角形时，求t 的值；（3）过点D 作DE AP 于点E ．在点P 的运动过程中，当t 为何值时，能使DE CD ？【解答】解：（1）根据题意，得2BP t ，162162310PC t ，8AC ，在Rt APC 中，根据勾股定理，得AP ．答：AP 的长为．（2）在Rt ABC 中，8AC ，16BC ，根据勾股定理，得AB若BA BP ，则2t ，解得t ；若AB AP ，则32BP ，232t ，解得16t ；若PA PB ，则222(2)(162)8t t ，解得5t ．答：当ABP 为等腰三角形时，t 的值为、16、5．（3）①点P 在线段BC 上时，过点D 作DE AP 于E ，如图1所示：则90AED PED ，90PED ACB ，PD 平分APC ，EPD CPD ，又PD PD ∵，()PDE PDC AAS ，3ED CD ，162PE PC t ，835AD AC CD ，4AE ，4162202AP AE PE t t ，在Rt APC 中，由勾股定理得：2228(162)(202)t t ，解得：5t ；②点P 在线段BC 的延长线上时，过点D 作DE AP 于E ，如图2所示：同①得：()PDE PDC AAS ，3ED CD ，216PE PC t ，835AD AC CD ，4AE ，4216212AP AE PE t t ，在Rt APC 中，由勾股定理得：2228(216)(212)t t ，解得：11t ；综上所述，在点P 的运动过程中，当t 的值为5或11时，能使DE CD ．16．如图，在ABC 中，5AC ，E 为BC 边上一点，且1CE ，AE ，4BE ，点F为AB 边上的动点，连接EF ．（1）求AB 的长；（2）当BEF 为等腰三角形时，求AF 的长．【解答】解：（1）5AC ∵，1CE ，AE 2226AC CE ，226AE ，222AC CE AE ，90ACE ，5BC CE BE ∵，5AC ，AB ；（2）①当4BF BE 时，4AF AB BF ；②如图，当BF EF 时，有45FEB B ，90BFE ，BF EF ，设BF EF x ，222BF EF BE ∵，2224x x ，x （负值舍去），AF AB BF ③如图，当BE EF 时，有45EFB B ，90BEF ，4EF BE ，BF，AF AB BF综上所述，AF 的长为4或．。