第六章 关系系统及其优化
- 格式:ppt
- 大小:317.50 KB
- 文档页数:51
第4章关系系统及其优化1.试述查询优化在关系数据库系统中的重要性和可能性。
答:查询优化在关系数据库系统中有着非常重要的地位。
关系数据库系统和非过程化的SQL语言能够取得巨大的成功,关键是得益于查询优化技术的发展。
关系查询优化是影响RDBMS性能的关键因素。
优化对关系系统来说既是挑战又是机遇。
所谓挑战是指关系系统为了达到用户可接受的性能必须进行查询优化。
由于关系表达式的语义级别很高,使关系系统可以从关系表达式中分析查询语义,提供了执行查询优化的可能性。
这就为关系系统在性能上接近甚至超过非关系系统提供了机遇。
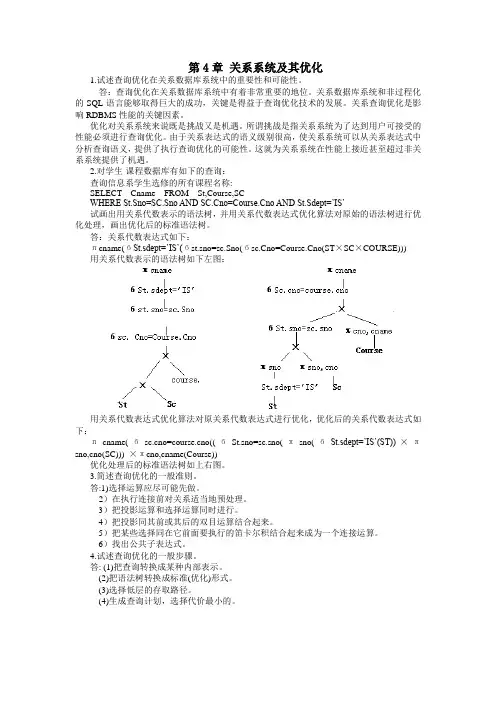
2.对学生-课程数据库有如下的查询:查询信息系学生选修的所有课程名称:SELECT Cname FROM St,Course,SCWHERE St.Sno=SC.Sno AND o=o AND St.Sdept=’IS’试画出用关系代数表示的语法树,并用关系代数表达式优化算法对原始的语法树进行优化处理,画出优化后的标准语法树。
答:关系代数表达式如下:πcname(бSt.sdept=’IS’(бst.sno=sc.Sno(бo=o(ST×SC×COURSE))) 用关系代数表示的语法树如下左图:用关系代数表达式优化算法对原关系代数表达式进行优化,优化后的关系代数表达式如下:πcname(бo=o((бSt.sno=sc.sno(πsno(бSt.sdept=’IS’(ST))×πsno,cno(SC))) ×πcno,cname(Course))优化处理后的标准语法树如上右图。
3.简述查询优化的一般准则。
答:1)选择运算应尽可能先做。
2)在执行连接前对关系适当地预处理。
3)把投影运算和选择运算同时进行。
4)把投影同其前或其后的双目运算结合起来。
5)把某些选择同在它前面要执行的笛卡尔积结合起来成为一个连接运算。
6)找出公共子表达式。
4.试述查询优化的一般步骤。

制造业智能化生产管理系统设计方案第一章绪论 (3)1.1 研究背景与意义 (3)1.2 系统设计目标 (3)第二章制造业智能化生产管理概述 (4)2.1 智能化生产管理的概念 (4)2.2 智能化生产管理的关键技术 (4)2.3 智能化生产管理的优势 (4)第三章系统需求分析 (5)3.1 功能需求 (5)3.1.1 基本功能需求 (5)3.1.2 扩展功能需求 (6)3.2 功能需求 (6)3.2.1 响应时间 (6)3.2.2 数据处理能力 (6)3.2.3 系统稳定性 (6)3.2.4 系统兼容性 (6)3.3 可靠性需求 (6)3.3.1 数据安全性 (6)3.3.2 系统恢复能力 (6)3.3.3 系统抗干扰能力 (6)3.3.4 系统可维护性 (7)第四章系统设计总体方案 (7)4.1 系统架构设计 (7)4.2 系统模块划分 (7)4.3 系统集成与交互 (8)第五章数据采集与处理 (8)5.1 数据采集方式 (8)5.2 数据处理方法 (8)5.3 数据存储与管理 (9)第六章生产调度与优化 (9)6.1 生产计划制定 (9)6.2 生产调度策略 (10)6.3 生产过程优化 (10)第七章质量管理与追溯 (11)7.1 质量检测方法 (11)7.1.1 概述 (11)7.1.2 常用质量检测方法 (11)7.1.3 智能化生产管理系统中的质量检测 (11)7.2 质量追溯系统 (11)7.2.1 概述 (12)7.2.2 质量追溯系统的组成 (12)7.2.3 智能化生产管理系统中的质量追溯 (12)7.3 质量改进与优化 (12)7.3.1 概述 (12)7.3.2 质量改进方法 (12)7.3.3 智能化生产管理系统中的质量改进与优化 (13)第八章设备维护与管理 (13)8.1 设备运行监控 (13)8.1.1 数据采集 (13)8.1.2 状态监测 (13)8.1.3 故障诊断 (13)8.2 设备维护策略 (13)8.2.1 预防性维护 (13)8.2.2 反应性维护 (14)8.2.3 预测性维护 (14)8.3 设备功能优化 (14)8.3.1 设备选型 (14)8.3.2 参数调整 (14)8.3.3 智能控制 (14)8.3.4 节能减排 (14)第九章仓储物流管理 (14)9.1 仓库管理策略 (14)9.1.1 仓库布局优化 (14)9.1.2 仓库物料管理 (14)9.1.3 仓库安全管理 (15)9.2 物流配送优化 (15)9.2.1 物流配送路线优化 (15)9.2.2 配送车辆管理 (15)9.2.3 配送人员管理 (15)9.3 仓储物流信息化 (16)9.3.1 信息管理系统构建 (16)9.3.2 信息安全与数据保护 (16)9.3.3 信息共享与协同办公 (16)第十章系统实施与评估 (16)10.1 系统开发与实施 (16)10.1.1 确定开发团队与分工 (16)10.1.2 系统需求分析与设计 (16)10.1.3 系统开发与集成 (16)10.1.4 系统部署与培训 (17)10.2 系统测试与验收 (17)10.2.1 单元测试 (17)10.2.2 集成测试 (17)10.2.3 系统测试 (17)10.2.4 验收测试 (17)10.3 系统运行与维护评估 (17)10.3.1 系统运行监控 (17)10.3.2 系统维护与升级 (17)10.3.3 用户满意度调查 (18)10.3.4 成效评估 (18)第一章绪论1.1 研究背景与意义科技的快速发展,我国制造业正面临着转型升级的压力。





第六章课程结构第六章课程结构与课程类型课程从理论上可以被分析为课程⽬标、课程内容和学习活动⽅式等诸种课程成分,但在现实中,学校课程总是作为⼀个整体⽽存在的。
课程设计⾸先要考虑的问题不是具体课程内容的选样与组织,或某种学习活动⽅式的设计,⽽是各类课程以及课程内部各成分的结合⽅式问题,即课程结构问题。
只有树⽴科学的课程结构观,才能从整体上把握课程的内部构成,为优化课程设计,增强课程的整体功能提供理论保证。
第⼀节课程结构的概念和属性⼀、课程结构及其相关概念探讨在课程论中,课程结构本⾝还不是像课程⽬标、课程评价等等名词那样有着相对确切含义,能够⽐较⼴泛和规范运⽤的概念。
在《简明国际教育百科全书·课程》中,与课程结构关系较为密切的词条有两个,具体的内容就反映这样的特点。
⼀条的英⽂是“Curriculum Organization”,中⽂译⽂为课程组织,“课程组织是指将构成教育系统或学校课程的要素,加以安排、联系和排列的⽅式。
这些要素包括这样⼀些⼀般因素:教学计划与⽅案,学习材料,学校器材与学校设备,教学⼒量的职业知识以及评价与检查体系的要求等。
学校或学院的⽓氛,社会、社区、家庭对学校的⽀持,学⽣的能⼒和兴趣以及教师的风格于策略,这些因素虽不很明显,但也是同样重要的。
准备加以组织的课程⽐各学科或领域的⼤纲内容要丰富得多:它是学习的环境,教师的⽬标与价值观,和学⽣的学习经验。
组织课程是⼀项关键⽽⼜复杂的任务,教育系统的全部⼯作都建⽴在它的上⾯。
”西⽅教育家⼀般都⽐较重视课程组织。
⼤多数国家的课程组织呈现三种⽔平:学校⽔平、地⽅⽔平、国家⽔平。
在课程研制过程中,课程组织的作⽤有两个层⾯,⼀是处理内容或学习经验的选择问题,建构⽆限的⽂化与有限的课程之间的关系;⼆是处理内容或学习经验的结构问题,建构课程内在的各种要素和各个部分之间的关系。
所以课程组织的实质是,⼈们在课程研制实践中针对课程结构,探讨解决课程的外部和内部平衡问题、探讨解决不同类型的课程之间的关系问题。

第六章 线性规划及其解的实现线性规划是目前应用最广泛的一种系统优化方法,它的理论和方法已十分成熟,可以应用于生产计划、物质调运、资源优化配置、地区经济规划等许多实际问题.线性规划最早由前苏联学者L V Kantorovich 于1939年提出,但他的工作当时并未为人所熟知.直到1947年,美国学者G B Danzing 提出求解线性规划最有效的算法-----单纯性算法后,才引起数学家、经济学家和计算机工作者的重视,并迅速发展成为一门完整的学科而得到广泛的应用.利用线性规划建立数学模型也是中国大学生数学建模竞赛中最常用的方法之一.优化模型的一般形式为T n Xx x x X X f z ),,,(),(min 21 == (1)m i X g t s i ,,2,1,0)(.. =≤ (2)其中)(x f 称为目标函数,)(X g i 称为约束条件.只满足式(2)的X 称为可行解;同时满足式(1)、式(2)两式的解*X X =称为最优解.由式(1)、式(2)组成的模型属于约束优化,若只有式(1)就是无约束优化.一般情况下,优化问题都是有约束的,但是如果最优解不是在可行域的边界上,而是在可行域的内部,那么就可以用无约束优化作比较简单的处理.若f ,i g 均为线性函数,优化模型式(1)、式(2)称为线性规划,否则称为非线性规划. 本章主要对线性规划问题及其解的实现作简要介绍.§6.1 线性规划模型形式及其性质线性规划是运筹学的一个重要分支,应用很广.线性规划问题可以描述为求一组非负变量,这些非负变量在一定线性约束的条件下,使一个线性目标函数取得极小(或极大)值的问题.1、线性规划的标准形式目标函数 n n x c x c x c z +++= 2211m in约束条件 ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥=+++=+++=+++0,,,2122112222212111212111n mn mn m m n n n n x x x bx a x a x a b x a x a x a b x a x a x a这里n x x x ,,,21 是变量,i ij i b a c ,,都是已知常数,且0≥i b ,约束条件常用..t s 表示.线性规划用矩阵表示就是T n x x x X cX z ),,,(,min 21 ==T n n m ij b b b b n m a A x b AX t s ),,,(),()(,0,..21 =≤=≥=⨯.2、线性规划的一般形式 目标函数 n n x c x c x c z +++= 2211m in约束条件 ⎪⎪⎩⎪⎪⎨⎧+++++++++mn mn m m n n n n b x a x a x a b x a x a x a b x a x a x a )()()(22112222212*********式中的( )可以是关系符号:≤≥=<>,,,,中的任意一个.3、线性规划化为标准形的方法 把线性规划化为标准形:(1)目标函数一律化为求极小(如果是求极大,则利用)m in(m ax z z -⇔化为求极小).(2)对约束条件中b Ax ≤的不等式,利用加入松弛变量的方法化为等式.如果原约束条件中有""b ≥形式的约束,可以在不等式两边同时加负号化为""b -≤的形式.(3)标准形中一般要求0≥i x .如果某个i x 无此约束,可以引入两个新变量''',i i x x ,令'''i i i x x x -=,0,'''≥i i x x ;如果原来的约束为i i l x ≥,可以令i i i l x x -=',0'≥i x .4、线性规划的基本性质 线性规划有以下基本性质:1)若存在可行域,可行域必为凸集; 2)基可行解对应于可行域的顶点;3)若有最优解,必在可行域的顶点取得.§6.2 线性规划问题的数学模型及其解的基本概念1、线性规划问题的数学模型例1 (生产计划问题)某工厂生产甲、乙两种产品,甲产品每生产一件需耗黄铜2kg 、3个工作日、两个外协件,每件可获利润60元;乙产品每生产一件需耗黄铜4kg 、1个工作日、不需外协件,每件可获利润30元,该厂每月可供生产用的黄铜320kg ,总工作日180个,外协件100个.问应怎样安排生产才能使工厂的利润最高?分析问题,建立数学模型.问题:怎样安排生产,即甲、乙两种产品各生产多少才能使工厂的利润最高?用1x ,2x 分别表示甲、乙两种产品生产的件数,该厂追求的目标是获取最高利润,用数学表达式表示为:213060m axx x f +=.由于生产甲、乙产品的件数要受到生产能力的约束,即 黄铜约束:3204221≤+x x ,工作日约束:180321≤+x x , 外协件约束:10021≤x , 非负约束:0,21≥x x .这样,该厂生产计划问题就归结为如下数学模型:⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤++=.0,,1002,1803,32042..,3060max 211212121x x x x x x x t s x x f例2 (运输问题)计划由三个粮站1A ,2A ,3A 运输某种粮食至三个加工厂1B ,2B ,3B ,三个粮站的供应量和三个加工厂的需求量以及各供应地至需求地的单位运输价(元/t)如表1所示,试作出运费最省的调运计划方案.表 1问题:如何调运,才能使运费最省?设ij x 表示第i 个粮站到第j 个加工厂的粮食数量(单位:3,2,1,,=j i t ),则总运费3332312322211312112050603040709080120x x x x x x x x x f ++++++++=.从各粮站运出的粮食数量不能超过供应量,20131211=++x x x ,30232221=++x x x ,50333231=++x x x ,同时还要保证各加工厂的需要,25312111=++x x x ,50322212=++x x x ,25332313=++x x x ,而运输量应满足0≥ij x .则上述运输问题的数学模型为⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥=++=++=++=++=++=++++++++++=.0255025503020..2050603040709080120min 332313322212312111333231232221131211333231232221131211ij x x x x x x x x x x x x x x x x x x x t s x x x x x x x x x f从上述两个例子可以看出,虽然两个问题的具体内容和性质不同,但它们都属于优化问题,它们的数学模型都有相同的数学形式,即在一定的线性等式或不等式的条件下,使某一线性函数达到最大(或最小).所谓线性规划问题的数学模型是将实际问题转化为一组线性不等式获等式约束下求线性目标函数的最小(大)值问题.2、解的基本概念对于线性规划问题的标准形式..min ≥==x b Ax t s cx z 其中系数矩阵A 是行满秩的,即)()(n m m A R ≤=,并引入列向量),,2,1(n j P j =表示系数矩阵的列向量.满秩约束条件的解称为线性规划问题的可行解,可行解的全体}0,|{≥==x b Ax x D 称为线性规划问题的可行域.满足目标函数的可行解称为线性规划问题的最优解.系数矩阵A 的任意一个m 阶的可逆方阵B 称为线性规划问题的一个基.显然,A 最多有mn C 个基.基B 中的任意一列向量j P 称为基向量.系数矩阵A 中除基B 外的其余m n -个列向量称为非基向量.显然,选择的基不同,与基对应的非基向量也不尽相同.与基向量j P 对应的变量j x 称为基变量.与非基向量j P 对应的变量j x 称为非基变量.为叙述方便,不妨假设基B 是阵A 的前m 列构成的,即),,,(21m P P P B =,如若不然,则可通过调整变量顺序达到此目的.按上述定义,),,2,1(m j x j =为基变量,),,2,1(n m m j x j ++=为非基变量,记T m B x x x X ),,,(21 =,T n m m N x x x X ),,,(21 ++=,),,,(21n m m P P P N ++=那么约束条件可用分块矩阵表示为b X X N B N B =⎪⎪⎭⎫ ⎝⎛),(令0=N X ,由b BX B =得b B X B 1-= (3) 称⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=-01b B X X X N B为对应于基B 的基解.很显然,由于m B R =)(,即0||≠B ,所以式(3)的解是惟一的.即对应于某个基的基解是惟一的,从而一个线性规划问题最多有mn C 个基解.若基解满足0≥x ,则称基解为基可行解。



第六章领导关系与角色一、单项选择题1.领导关系的两重属性中,()占据主导地位。
A.自然属性B.管理属性C.权力属性D.社会属性2.()是领导关系存在的前提。
A.职位B.组织C.权力D.权利3.()是领导关系中的核心。
A.领导B.被领导C.群体D.人4.首先提出正式群体和非正式群体分类的是()。
A.梅奥B.马斯洛C.弗洛伊德D.赫茨伯格5.冲突属于()。
A.低对抗行为B.高对抗性行为C.无对抗性行为D.对抗性行为参考答案:1.D 2.C 3.D 4.A 5.B二、多项选择题1.群体的主要特征包括()。
A.有一定数量的人B.是一种社会组织C.有稳定持续的社会互动关系D.心理上有归属感E.具有独立的意义2.非正式群体形成的基础主要有()。
A.利益之间的矛盾B.价值观的一致C.个体互补D.个性差异大E.利益的一致3.与领导关系最为密切的非正式群体类型有()。
A.纵向寄生型B.纵向共栖型C.横向进取型D.横向防守型E.矛盾冲突型4.下列关于冲突哪些说法是正确的()。
A.冲突发生于个人与组织之间B.冲突是目标和利益不一致情况下发生的C.冲突是一种静态的相互作用D.单方面的态度和行为不构成冲突E.冲突是在目标和利益一致情况下发生的5.从冲突的表现形式来看,冲突的主要类型有()。
A.目标冲突B.认识冲突C.情感冲突D.行为冲突E.自我冲突6.角色冲突的表现形式有()。
A.角色外冲突B.角色内冲突C.角色间冲突D.个体之间的冲突E.目标冲突7.按照老子原则处理冲突的主要方法有()。
A.主动出击B.理顺法C.避开法D.不干涉法E.预防法8.沟通的主要功能包括()。
A.控制B.激励C.情绪表达D.信息E.引起冲突参考答案:1.ACD 2.BCE 3.ABCD 4.ABD 5.ABCD 6.ABC 7.CDE 8.ABCD三、问答题1.什么是领导关系?它具有哪些特点?领导关系是指领导者在进行领导活动的过程中,领导者和被领导者及领导者和领导者相互之间发生、发展和建立起来的一种工作和感情交往的关系,即领导主体在领导活动中与组织系统中的其他成员发生的工作关系和非工作关系的总和。