单元静定结构的内力分析
- 格式:ppt
- 大小:2.78 MB
- 文档页数:29

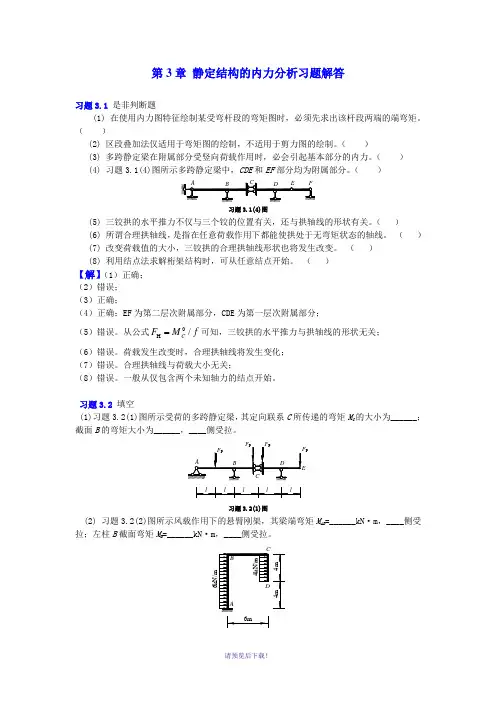
第3章 静定结构的内力分析习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
( )(2) 区段叠加法仅适用于弯矩图的绘制,不适用于剪力图的绘制。
( ) (3) 多跨静定梁在附属部分受竖向荷载作用时,必会引起基本部分的内力。
( ) (4) 习题3.1(4)图所示多跨静定梁中,CDE 和EF 部分均为附属部分。
( )习题3.1(4)图(5) 三铰拱的水平推力不仅与三个铰的位置有关,还与拱轴线的形状有关。
( ) (6) 所谓合理拱轴线,是指在任意荷载作用下都能使拱处于无弯矩状态的轴线。
( ) (7) 改变荷载值的大小,三铰拱的合理拱轴线形状也将发生改变。
( ) (8) 利用结点法求解桁架结构时,可从任意结点开始。
( )【解】(1)正确;(2)错误; (3)正确;(4)正确;EF 为第二层次附属部分,CDE 为第一层次附属部分;(5)错误。
从公式0H /C F M f 可知,三铰拱的水平推力与拱轴线的形状无关;(6)错误。
荷载发生改变时,合理拱轴线将发生变化; (7)错误。
合理拱轴线与荷载大小无关;(8)错误。
一般从仅包含两个未知轴力的结点开始。
习题3.2 填空(1)习题3.2(1)图所示受荷的多跨静定梁,其定向联系C 所传递的弯矩M C 的大小为______;截面B 的弯矩大小为______,____侧受拉。
P习题3.2(1)图(2) 习题3.2(2)图所示风载作用下的悬臂刚架,其梁端弯矩M AB =______kN ·m ,____侧受拉;左柱B 截面弯矩M B =______kN ·m ,____侧受拉。
习题3.2(2)图(3) 习题3.2(3)图所示三铰拱的水平推力F H 等于 。
习题3.2(3)图(4) 习题3.2(4)图所示桁架中有 根零杆。
习题3.2(4)图【解】(1)M C = 0;M C = F P l ,上侧受拉。
![静定结构内力计算全解[详细]](https://uimg.taocdn.com/290a22ba7cd184254b3535d4.webp)


力学与结构—静定结构内力计算静定结构是指在静态平衡的情况下,具有确定的结构稳定的结构体系。
在静定结构内力计算中,我们主要关注结构中的受力情况,以及内力的计算和分析。
本文将介绍静定结构内力计算的基本原理和方法。
一、静定结构的受力情况静定结构中,每一点的受力都可以通过平衡方程来计算。
平衡方程包括力的平衡方程和力矩的平衡方程。
力的平衡方程:在静态平衡状态下,结构的受力合力为零,即ΣF=0力矩的平衡方程:在静态平衡状态下,结构的受力合力矩为零,即ΣM=0根据这两个平衡方程,我们可以计算出结构中各个节点的受力情况。
二、内力的计算和分析在静定结构中,内力是指结构中材料的内部受力情况。
在计算内力时,我们主要关注结构中的悬臂梁、简支梁、悬链线等情况。
1.悬臂梁悬臂梁是一种固定在一端的梁。
在计算悬臂梁的内力时,我们需要知道梁的长度、材料的性质、外力的作用点和大小等信息。
对于悬臂梁,内力可以通过以下公式计算:弯矩M=Px(P为力的大小,x为力的作用点到悬臂梁左端的距离)剪力V=P2.简支梁简支梁是一种两端都可以自由转动的梁。
在计算简支梁的内力时,我们同样需要知道梁的长度、材料的性质、外力的作用点和大小等信息。
对于简支梁,内力可以通过以下公式计算:弯矩M=Px(P为力的大小,x为力的作用点到简支梁左端的距离)剪力V=03.悬链线悬链线是一种线性受力的结构,常见于吊桥和高空绳索走廊等场景。
在计算悬链线的内力时,我们需要知道悬链线的长度、绳子的重力、外力的作用点和大小等信息。
对于悬链线,内力可以通过以下公式计算:水平力H=水平方向的外力的合力垂直力V=绳子的重力+垂直方向的外力的合力张力T = sqrt(H^2 + V^2)通过以上的方法,我们可以计算得到静定结构中各个节点的受力情况和内力。
三、静定结构内力计算的应用静定结构内力计算在结构工程中具有重要的应用价值。
通过计算内力,我们可以了解结构的受力情况,选择合适的材料和结构参数,保证结构的安全性和稳定性。




