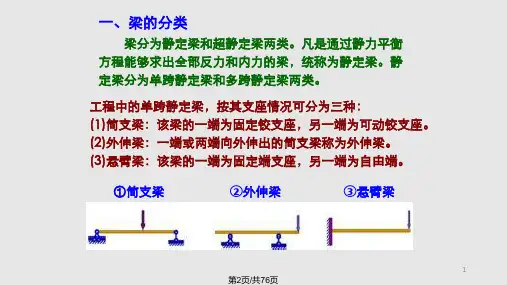
静定结构的内力计算..
- 格式:ppt
- 大小:1.34 MB
- 文档页数:35






![静定结构内力计算全解[详细]](https://uimg.taocdn.com/290a22ba7cd184254b3535d4.webp)


第三章静定结构的内力计算学习目的和要求不少静定结构直接用于工程实际,另外,它还是静定结构位移计算及超静定结构的计算基础。
所以静定结构的内力计算是十分重要的,是结构力学的重点内容之一。
通过本章学习要求达到:1、练掌握截面内力计算和内力图的形状特征。
2、练掌握截绘制弯矩图的叠加法。
3、熟练掌握截面法求解静定梁、刚架及其内力图的绘制和多跨静定梁及刚架的几何组成特点和受力特点。
4、了解桁架的受力特点及按几何组成分类。
熟练运用结点法和截面法及其联合应用,会计算简单桁架、联合桁架既复杂桁架。
5、掌握对称条件的利用;掌握组合结构的计算。
6、熟练掌握截三铰拱的反力和内力计算。
了解三铰拱的内力图绘制的步骤。
掌握三铰拱合理拱轴的形状及其特征学习内容梁的反力计算和截面内力计算的截面法和直接内力算式法;内力图的形状特征;叠加法绘制内力图;多跨静定梁的几何组成特点和受力特点。
静定梁的弯矩图和剪力图绘制。
桁架的特点及分类,结点法、截面法及其联合应用,对称性的利用,几种梁式桁架的受力特点,组合结构的计算。
三铰拱的组成特点及其优缺点;三铰拱的反力和内力计算及内力图的绘制;三铰拱的合理拱轴线。
§3.1梁的内力计算回顾一、截面法1、平面杆件的截面内力分量及正负规定:轴力N (normal force) 截面上应力沿轴线切向的合力以拉力为正。
剪力Q (shearing force)截面上应力沿轴线法向的合力以绕隔离体顺时针转为正。
弯矩M (bending moment) 截面上应力对截面中性轴的力矩。
不规定正负,但弯矩图画在拉侧。
2、截面内力计算的基本方法:截面法:截开、代替、平衡。
内力的直接算式:直接由截面一边的外力求出内力。
1、轴力=截面一边的所有外力沿轴切向投影代数和。
2、剪力=截面一边的所有外力沿轴法向投影代数和,如外力绕截面形心顺时针转动,投影取正否则取负。
3、弯矩=截面一边的所有外力对截面形心的外力矩之和。
弯矩及外力矩产生相同的受拉边。