初等数学研究答案1
- 格式:doc
- 大小:4.53 MB
- 文档页数:76

习题解答第一讲 自然数的基数理论与序数理论1、在自然数的基数理论中,证明自然数的乘法满足交换律证明:对于{(,)|,}A B a b a A b B ⨯=∈∈与{(,)|,}B B b a b B a A ⨯=∈∈,定义A B ⨯到B A ⨯的映射为:(,)(,),(,),(,)fa b b a a b A B b a B A −−→∈⨯∈⨯显然这个映射是A B ⨯到B A ⨯的一一映射,所以A B B A ⨯=⨯,于是按定义有:A B B A ⋅=⋅,即乘法满足交换律。
2、利用最小数原理证明定理14.定理14的内容是:设()p n 是一个与自然数有关的命题,如果:(1)命题()p n 对无穷多个自然数成立;(2)假如命题对0()n k k n =≥成立时,能够推出命题对1n k =-也成立,那么对一切自然数不小于n 0的自然数n ,命题()p n 必然成立。
证明:如果命题不真,设使命题不成立的自然数构成集合M ,那么M 非空,因此,M 中必有一个最小数000()r r n ≥。
此时,由于不大于0r 的自然数只有有限个,按照条件(1),至少有一个自然数0()r r r >,命题在r 处成立;于是由条件(2),命题对1r -也成立,连锁应用条件(2),那么命题在12,,,,, r r r r k ---处都成立,而这个序列是递减的,因此0r 必然出现在这个序列中,这与0r 的假定不符,这个矛盾说明定理14成立。
3、用序数理论证明3+4=7证明:313432313145,(),''''+==+=+=+==33323256(),'''+=+=+== 34333367()'''+=+=+==4、设平面内两两相交的n 个圆中,任何三个不共点,试问这n 个圆将所在的平面分割成多少个互不相通的区域?,证明你的结论。
解:设这n 个圆将所在平面分割成()f n 个部分,显然1224(),()f f ==; 如果满足条件的n 个圆把平面分割成()f n 个部分,那么对于满足条件的n+1个圆来说,其中的n 个圆一定已经把平面分割成()f n 个部分,而最后一个圆由于与前面的每个圆都相交,并且由于任何三个圆不共点,所以这最后的圆与前面的n 个圆必然产生2n 个交点,这2n 个交点必然把这最后一个圆分割成2n 段圆弧,这些圆弧每一段都把自己所在的一个区域一分为二,从而12()()f n f n n +-=, 于是得:212324121()(),()(),,()()() f f f f f n f n n -=-=--=- 将这n-1个等式相加得:124211()()()() f n f n n n -=+++-=- 即 2122()()f n n n n n =-+=-+ 5、设平面上的n 条直线最多可以把平面分割成 f (n )个互不相通的区域,证明:112()()n n f n +=+ 证明:显然1111212()()f +⨯==+成立; 假将设平面上的k 条直线最多可以把平面分割成 f (k )112()k k +=+个互不相通的区域,那么对于平面上的k+1条直线来说,其中的任意k 条直线最多把平面分割成112()k k +=+个互不相通的区域,对于最后的直线来说,它如果与前面的每条直线都相交,那么在这条直线上最多可以产生k 个交点,这k 个交点可以把最后的这条直线分割成k+1段,每一段都将自己所在的区域一分为二,从而11()()f k f k k +-=+所以:111112()()()k k f k f k k k ++=++=+++ 121121122()()()()k k k k k +++++=+=+所以公式112()()n n f n +=+在1n k =+时也成立, 于是公式对一切自然数n 都成立。

初等数学研究(程晓亮、刘影)版课后习题答案 第一章 数1添加元素法和构造法,自然数扩充到整数可以看成是在自然数的基础上添加0到扩大的自然数集,再添加负数到整数集;实数扩充到复数可以看成是在实数的基础上构造虚数单位i 满足12-=i ,和有序实数对),(b a 一起组成一个复数bi a +. 2(略)3从数的起源至今,总共经历了五次扩充:为了保证在自然数集中除法的封闭性,像b ax =的方程有解,这样,正分数就应运而生了,这是数的概念的第一次扩展,数就扩展为正有理数集.公元六世纪,印度数学家开始用符号“0”表示零.这是数的概念的第二次扩充,自然数、零和正分数合在一起组成算术数集.为了表示具有相反意义的量,引入了负数.并且直到17世纪才对负数有一个完整的认识,这是数的概念的第三次扩充,此时,数的概念就扩展为有理数集.直到19世纪下半叶,才由皮亚诺、戴德金、维尔斯特拉斯等数学家的努力下构建了严格的实数理论.这是数的概念的第四次扩充,形成了实数集.虚数作为一种合乎逻辑的假设得以引进,并在进一步的发展中加以运用.这是数学概念的第五次扩充,引进虚数,形成复数集.4证明:设集合D C B A ,,,两两没有公共元素d c b a ,,,分别是非空有限集D C B A ,,,的基数,根据定义,若b a >,则存在非空有限集'A ,使得B A A ~'⊃;若d c ≥从而必存在非空有限集'C ,使得D C C ~'⊃,所以)(C A ⋃)(D B ⋃⊃所以集合C A ⋃的基数c a +大于集合D B ⋃的基数d b +,所以d b c a +>+.5(1)解:按照自然数序数理论加法定义, 1555555155155)25(2535''=++=++⋅=+⋅=+⋅=⋅=⋅ (2)解:按照自然数序数理论乘法定义87)6(])15[()15()25(2535'''''''''===+=+=+=+=+ 6证明:︒1当2=n 时,命题成立.(反证法)()()()()()()()01121,1111111,111101111111,,2,1,0111,,2,1,0)2(212122121212121212122221212122111112111212222121≥++-+⇒≥++-++≥+-+-≥++++∴≥⎪⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛->-=-++-+-=+++++=>+=≥+++=+++=>≥=︒+++++++++++++++++k k k k k k k k k k k k k k k i k k k k k k i k k i a k a k k a k k a k k a ka a ka a a a a k a a a a a a a a a a a a a a a a a a k i a k n ka a a a a a k i a k k n ,即要证由归纳假设,得,且得,,且时,由当。
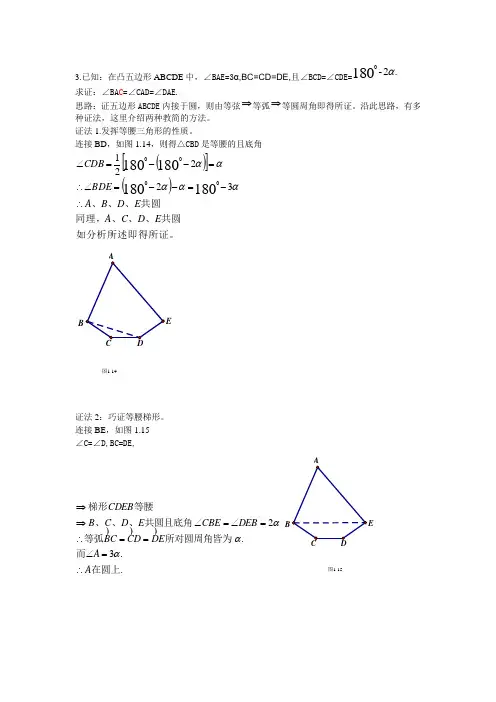
3.已知:在凸五边形ABCDE 中,∠BAE=3α,BC=CD=DE,且∠BCD=∠CDE=.2-1800α求证:∠BA C =∠CAD=∠DAE.思路:证五边形ABCDE 内接于圆,则由等弦⇒等弧⇒等圆周角即得所证。
沿此思路,有多种证法,这里介绍两种教简的方法。
证法1.发挥等腰三角形的性质。
连接BD ,如图1.14,则得△CBD 是等腰的且底角()[]()如分析所述即得所证。
共圆、、、同理,共圆、、、E D C A E D B A BDE CDB ∴-=--=∠∴=--=∠ααααα322211801801801800图1.14EDBCA证法2:巧证等腰梯形。
连接BE ,如图1.15 ∠C=∠D,BC=DE,..3.2在圆上而所对圆周角皆为等弧共圆且底角、、、等腰梯形A A E D D C C B DEB CBE E D C B CDEB ∴=∠==∴=∠=∠⇒⇒ααα图1.15EDACB4.设H 为锐角△ABC 之垂心,若AH 等于外接圆半径,求证:∠BAC=600分析:因条件中的等量关系含有外接圆半径,故宜画出外接圆,以便发现隐含的联系,现介绍三种较简的证法。
证法1:借助平行四边形。
连接CO 并延长交外接圆于D ,如图1.17,则有直径所对圆周角为直角易证BD//AH(同⊥BC), AD//BH(同⊥AC),⇒AHBD 是平行四边形;图1.17DOHCBA60600,21=∠∴=∠∴===A BDC CD R AH BD ,证法2.利用欧拉线的预备定理60600212121217.118.1,=∠=∠=∠∴=∠∴===⊥MOC BOC A MOC OC R AH OM M BC OM 知则由例如图于作图1.18KMDO ABC证法3.利用正弦定理60sin 2sin 2219.1,,=∠∴=∠=∠=⊥⊥A AB C R AHF AH AF AC BF BC AE ,则有如图设图1.19FEABC6.在△ABC 中,先作角A 、B 的平分线,再从点C 作上二角的平分线之平行线,并且连D 、E,若DE//BA ,求证:△ABC 等腰。

初等数学研究答案1习题一1答:原那么:〔1〕A ⊂B〔2〕A 的元素间所定义的一些运算或基本关系,在B 中被重新定义。
而且关于A 的元历来说,重新定义的运算和关系与A 中原来的意义完全分歧。
〔3〕在A 中不是总能实施的某种运算,在B 中总能实施。
(4) 在同构的意义下,B 应当是A 满足上述三原那么的最小扩展,而且由A 独一确定。
方式:〔1〕添加元素法;〔2〕结构法2证明:(1)设命题能成立的一切c 组成集合M 。
a=b ,M 11b 1a ∈∴⋅=⋅∴, 假定bc ac M c =∈,即,那么M c c b b bc a ac c a ∈'∴'=+=+=', 由归结公理知M=N ,所以命题对恣意自然数c 成立。
〔2〕假定a <b ,那么bc kc ac bc,k)c (a )1(b k a N k =+=+=+∈∃即,,由,使得 那么ac<bc 。
〔3〕假定a>b ,那么ac m c bc ac,m )c (b )1(a m b N m =+=+=+∈∃即,,由,使得那么ac>bc 。
3证明:(1)用反证法:假定b a b,a b a <>≠或者,则由三分性知。
当a >b 时,由乘法单调性知ac >bc. 当a <b 时,由乘法单调性知ac<bc.这与ac=bc 矛盾。
那么a=b 。
〔2〕用反证法:假定b a b,a b a =>或者,则由三分性知不小于。
当a >b 时,由乘法单调性知ac >bc. 当a=b 时,由乘法单调性知ac=bc.这与ac<bc 矛盾。
那么a <b 。
〔3〕用反证法:假定b a b,a b a =<或者,则由三分性知不大于。
当a<b 时,由乘法单调性知ac<bc. 当a=b 时,由乘法单调性知ac=bc.这与ac>bc 矛盾。
那么a>b 。

习题一5证明:当n=1时,的倍数。
是9181n 154n=-+ 假设当n=k 时的倍数。
是91k 154k-+则当n=k+1时的倍数。
是)()(918k 451k 154411k 154k 1k +--+=-+++则对∀N n ∈,1n 154n -+是9的倍数. 6证明:当1n =时,141-=3-,n21n21-+=3-;则当1n =时成立。
假设当k n =时成立,即(141-)(941-)(2541-)……… (21k 241)(--)=k 21k21-+ 当1k n +=时,(141-)(941-)(2541-)……… (21k 241)(--)(21k 241)(+-) =k 21k 21-+(21k 241)(+-)=)()(1k 211k 21k 21k 23+-++=++- 当1k n +=时成立。
7解:(1)01x 3x 132=---==+,则,αββα (2)3311=-=---ββαα,131313A n2n n 2n nn 2n 2n 2n ββααβαβα+--+-=-=∴+++++131311n 11n nn )()(-+-+---+-=βββαααβα133131n 1n nn ++-+-=βαβα;n 1n A A 3+=+(3)当n=1时,1013A 333=-=βα的倍数。
是10 假设当n=k 时13A 3k3k 3k βα-=的倍数。
是10则当n=k+1时131313A 33k 33k 3k 33k 33k 31k 31k 31k 3)()()()()(βαβαβαββααβα-+-=⋅-⋅=-=+++k 333k3k 1013βαβα+-=则对∀N n ∈,n 3A 是10的倍数. 21 解:Z=72i 31)(++=+=++1)6isin 6(cos 17ππ)67isin 67(cos ππ+=i 21231--则|Z|=22263241)23-(12-=-=+;则.23arctan 2)(+-=πθ 22 解: |z|=1,,则令ααisin cos z +=∴1z z 2+-=)i sin -sin (2cos cos cos 22ααααα+-则u=222)21(cos 41cos 4cos 4|1z z |-=+-=+-ααα当3u ,1cos max =-=时α;当.0u ,21cos min ==时α 25解:由图像知20)-(-10)-3(-|OD |22=+=;则.312||||||max =+=+=AD OD Z .112||||||min =-=-=BD OD Z,24060180)(arg .30,21sin max =+=∴=∴=Z αα.180)(arg min =Z 习题二1解:设这个多项式为)1()(10-+=x a a x f )4)(2)(1(2)(1(32---+--+x x x a x x a ).然后将已知点依次代入:;10,10)1(00-=∴=-=a a f ;9,1)2(110=∴+=-=a a a f ;14,63101)4(2210=∴++==a a a a f ;2,21812124218)5(33210=∴=+++==a a a a a f因此,)1(910)(-+-=x x f )4)(2)(1(22)(1(14---+--+x x x x x )7523--=x x 即.32)3(=f2解:d x c x b x a x x f +-+-+-+-=-)2()2()2()2()2(234令2=x 得165=d ;令0=x 得;8624,165248169=+-+-+-=c b a c b a 即 令1=x 得.119=+-c b a 令3=x 得.269=++c b a 则165,180,75,14====d c b a即165)2(180)2(75)2(14)2()2(234+-+-+-+-=-x x x x x f =.5432234+-+-x x x x7解:(1)法一:原式为对称式,但显然原式没有一个因式,又由于原式为四次式,则设有一个二次对称式的因式=+++444)(y x y x ])([22nxy y x m ++])([22lxy y x k ++则;1;2====l k n m 444)(y x y x +++=222)(2xy y x ++ 法二:22222222444]2)[(2)()(xy y x y x y x y x y x +++-+=+++ =2222222222)(22)(4)(2xy y x y x y x xy y x ++=++++ (2) 2222222)1(122)()1(++++=++++x x x x x x x x2222)1()1()1(21++=++++=x x x x x x(3) 原式为对称式,当)(z y x +-=时原式为零,故z y x ++为原式的一个因式,又由于原式为三次式,则还有另一个二次对称式的因式.设=++++xyz y x x z z y ))()(((z y x ++))()([222yz xz xy n z y x m +++++]令120,1,1=+===n m z y x 得,令;131,1,1-=-=-=-=n m z y x 得 则).)((),,(.1,0yz xz xy z y x z y x f n m ++++=∴==(4)原式为轮换式,当y x =时原式为零,故))()((x z z y y x ---为原式的一个因式,又由于原式为四次式,则还有另一个一次对称式的因式.设=++++xyz y x x z z y ))()((k ))()((x z z y y x ---(z y x ++)令.2,1260,2,1-=∴-====k k z y x 得则=++++xyz y x x z z y ))()((-2))()((x z z y y x ---(z y x ++) 8解:(1)))((15x x 6x x 22234l nx x k mx x ++++=+-+- =kl x nk ml x l mn k x n m x ++++++++)()()(234比较系数得:⎪⎪⎩⎪⎪⎨⎧=-=+=++-=+15161kl nk m l l m n k n m ;设;5,3==l k 则.2,1-==n m则).52)(3(15x x 6x x 22234+-++=+-+-x x x x(2)=++++21x 29x 20x 7x 234))((22l nx x k mx x ++++ =kl x nk ml x l mn k x n m x ++++++++)()()(234比较系数得:⎪⎪⎩⎪⎪⎨⎧==+=++=+2129207kl nk m l l m n k n m ;设;7,3==l k 则.5,2==n m则=++++21x 29x 20x 7x 234).75)(32(22++++x x x x9解:(1))5()3()152)(3(45x 21x x 2223+-=-+-=+--x x x x x (2))6792)(1(6x 13x 2x 72x 23234-++-=+--+x x x x=)2)(12)(3)(1(+-+-x x x x(3)原式为轮换式,当y x -=时原式为零,故))()((x z z y y x +++为原式的一个因式,.设=-+++++xyz 4y)z(x z)y(x z)x(y 222))()((x z z y y x k +++ 令.10,1,1====k z y x 得则=-+++++xyz 4y)z(x z)y(x z)x(y 222))()((x z z y y x +++ (4))2)(12]()6)(4[(4x -24)14x 24)(x 11x (x 222+++++=++++x x x x x=-24x 242)(12()2)(12)(6)(4(x x x x x x x x -+++++++)=)2410()2)(12)(6)(4(2+++++++x x x x x x x =)2415)(6)(4(2++++x x x x10解:(1)]6016)[(60164(x 3x -12)10)(x 6)(x 5)(x (x 4222x x x x +++++=++++)=-23x 222236016(4)60164(x x x x x x -+++++)=]6016(2][3)6016[2(x 22x x x x x -+++++) =)120312)(12035(2x 22++++x x x )426535(+-=x )8)(152)(426535(++--x x x (2)7x 44x 27x 2x 234+---))((22l nx x k mx x ++++= =kl x nk ml x l mn k x n m x ++++++++)()()(234比较系数得:⎪⎪⎩⎪⎪⎨⎧=-=+-=++-=+744272kl nk m l l m n k n m ;设;1,7==l k 则.7,5-==n m则7x 44x 27x 2x 234+---)17)(75(22+-++=x x x x)2537)2537)(75(2--+-++=x x x x ( 16解;(1)5432534)2()2()2()2(2-x A 2)-(x 6x 2x x 2-+-+-+-+=-+-x Ex D x C x B 设 通分并合并同类项后与原式比较系数,得:.22,54,42,15,2=====E D C B A则.)2(22)2(54)2(42)2(152-x 22)-(x 6x 2x x 25432534-+-+-+-+=-+-x x x x(2)2222221)x (13-x A 1)x -3)(x -(x 16x 4x 5+-+++-++=++-x EDx x x c Bx 通分并合并同类项后与原式比较系数,得:.3,2,2,1,1-=-=-=-==E D C B A则.1)x (32123-x 11)x -3)(x -(x 16x 4x 5222222+---++---+=++-x x x x x 22 解:;471,71,3xx 222121=+=+∴=+-xx x x 则.18)11(x x (21212323=+-+=+--x x xx 即.52347218x3x x 2x 2223-23=++=++++-28. (1) =72cos7cos0cos ππ++)73-cos(73cos πππ++)7-cos()72-cos(ππππ++=1 (2) =)( 1tg 1+)( 2tg 1+)( 3tg 1+)]145(tg 1[ -+ =)(1tg 1+)(2tg 1+)(3tg 1+)1tan 11tan 11(+-+ =2)( 2tg 1+)( 3tg 1+)43tan 1( +=222 (3) =++2)240cos 1(++2)280cos 1( ++2)2120cos 1( 2)2160cos 1( + =+++++++280cos 1)160cos 120cos 80cos 40(cos 24[412160cos 1 ++++2240cos 1 ]2320cos 1+=++++++280cos )160cos 120cos 80cos 40(cos 26[412160cos ++2240cos ]2320cos=]40cos 2120cos 80cos )20cos 2180cos 40(cos 412[81+--+--++=]25)20cos 80cos 40(cos 512[81--++=1619)20cos 20cos 2120cos 2(8516523=-+- 。

初等数学研究,李长明,周焕山版 高等教育出版社习题一1答:原则:(1)A ⊂B(2)A 的元素间所定义的一些运算或基本关系,在B 中被重新定义。
而且对于A 的元素来说,重新定义的运算和关系与A 中原来的意义完全一致。
(3)在A 中不是总能施行的某种运算,在B 中总能施行。
(4) 在同构的意义下,B 应当是A 满足上述三原则的最小扩展,而且由A 唯一确定。
方式:(1)添加元素法;(2)构造法2证明:(1)设命题能成立的所有c 组成集合M 。
a=b ,M 11b 1a ∈∴⋅=⋅∴, 假设bc ac M c =∈,即,则M c c b b bc a ac c a ∈'∴'=+=+=',由归纳公理知M=N ,所以命题对任意自然数c 成立。
(2)若a <b ,则bc kc ac bc,k)c (a )1(b k a N k =+=+=+∈∃即,,由,使得 则ac<bc 。
(3)若a>b ,则ac mc bc ac,m)c (b )1(a m b N m =+=+=+∈∃即,,由,使得 则ac>bc 。
3证明:(1)用反证法:若b a b,a b a <>≠或者,则由三分性知。
当a >b 时,由乘法单调性知ac >bc. 当a <b 时,由乘法单调性知ac<bc.这与ac=bc 矛盾。
则a=b 。
(2)用反证法:若b a b,a b a =>或者,则由三分性知不小于。
当a >b 时,由乘法单调性知ac >bc. 当a=b 时,由乘法单调性知ac=bc.这与ac<bc 矛盾。
则a <b 。
(3)用反证法:若b a b,a b a =<或者,则由三分性知不大于。
当a<b 时,由乘法单调性知ac<bc. 当a=b 时,由乘法单调性知ac=bc.这与ac>bc 矛盾。
则a>b 。

1、 已知21-=i z ,则150100++z z 的值等于( )A 、1B 、1-C 、iD 、i -2、 已知53sin =θ,02sin <θ,则2tan θ的值等于() A 、21B 、21-C 、31D 、3 3、 函数136-+-=x x y 的值域是()A 、⎥⎦⎤ ⎝⎛∞-317,B 、⎥⎦⎤ ⎝⎛∞-1277,C 、(]5,∞-D 、[)+∞,5 4、 若实数y x ,满足()()22214125=-++y x ,则22y x +的最小值为()A 、2B 、1C 、3D 、25、 曲线()x x x f -=4在点P 处的切线平行于直线03=-y x ,则P 点坐标为()A 、()3,1B 、()3,1-C 、()0,1D 、()0,1-6、 设集合{}1>=x x M ,{}12>=x x P ,则下列关系中正确的是() A 、P M =B 、P P M = C 、M P M = D 、P P M =7、 设α是锐角,2234tan +=⎪⎭⎫ ⎝⎛+πα,则αcos 的值等于() A 、22B 、23C 、33D 、36 8、 设()x f 是定义在R 上以2为周期的偶函数,已知()1,0∈x 时,()()x x f -=1log 21,则函数()x f 在()2,1上()A 、是增函数,且()0<x f ;B 、是增函数,且()0>x fC 、是减函数,且()0<x f ;D 、是减函数,且()0>x f9、 已知锐角βα,满足()21sin ,1tan =-=αβα,则βcos 等于() A 、426+B 、426-C 、462-D 、426-- 10、分解因式:y x y x 62922-+-(x-3y)(x+3y+2)分解因式:3542322+++++y x y xy x=(x+y)(x+2y)+3(x+y)+(x+2y)+3 =(x+y)(x+2y+3)+(x+2y+3) =(x+y+1)(x+2y+3) 已知200420052004112004--+-=x x y ,则()2004y x +的值是; x=1/2004,y= -2005/2004,代入得1 已知实数m 满足m m m =-+-20082007,则=-22007m 2008 计算⎥⎦⎤⎢⎣⎡--+÷⎥⎦⎤⎢⎣⎡-++x x x x x x xx 1111=1/2x-1 自然数集的两种主要理论是 基数理论 、 序数理论 。

《初等数学研究》习题解答第一章 数系1.1 集合论初步·自然数的基数理论习题1.11.证明集合0{|}x x >与实数集对等。
证明:取对应关系为ln y x =,这个函数构成0(,)+∞与(,)-∞+∞的一一对应,所以集合0{|}x x >与实数集对等。
2.证明()()()A B C A B A C = 证明:()x AB C x A ∀∈⇒∈或x B C ∈,x A ⇒∈或(x B ∈且x C ∈),那么有x A ∈或x B ∈同时还有x A ∈或x C ∈,即x A B ∈同时还有x A C ∈,所以()()()()()x A B A C A B C A B A C ∈⇒⊆反过来:()()x AB AC x A B ∀∈⇒∈且x A C ∈,对于前者有x A ∈或者x B ∈;对于后者有x A ∈或者x C ∈,综合起来考虑,x B ∈与x C ∈前后都有,所以应是“x B ∈且x C ∈”即“x B C ∈”,再结合x A ∈的地位“或者x A ∈”以及前后关系有“x A ∈或x BC ∈”即()x A B C ∈,所以()()()()x AB C A B C A B A C ∈⇒⊇所以()()()A B C A B A C =。
3.已知集合A 有10个元素,,B C 都是A 的子集,B 有5个元素,C 有4个元素,B C有2个元素,那么()BA C -有几个元素?解:集合()BA C -如图1所示:由于452(),(),()r C r B r B C ===,所以32(),()r B C r C B -=-=, 从而1028(())r B A C -=-=, 即()BA C -有8个元素4.写出集合{,,,}a b c d 的全部非空真子集。
图1CBA5.证明,按基数理论定义的乘法对加法的分配律成立。
证明:设,,A B C 是三个有限集合,并且B C φ=,记(),(),()a r A b r B c r C ===首先:由于BC φ=,所以A B A C φ⨯⨯=,所以其次:对于(,)(){(,)|,}a x A B C a x a A x B C ∀∈⨯=∈∈,由于x B C ∈,那么若x B ∈,于是(,)a x A B ∈⨯; 若x C ∈,于是(,)a x A C ∈⨯,所以总有(,){(,)|,}{(,)|,}a x a x a A x B a x a A x C A B A C ∀∈∈∈∈∈=⨯⨯即()(())()A BC A B A C r A B C r A BA C ⨯⊆⨯⨯⇒⨯≤⨯⨯反过来:(,)a x A B A C ∀∈⨯⨯,那么(,)a x A B ∈⨯或者(,)a x A C ∈⨯于是有,a A ∈x B ∈或者x C ∈,即,a A ∈x B C ∈,所以(,)()a x A B C ∈⨯即()(())()A BC A B A C r A B C r A BA C ⨯⊇⨯⨯⇒⨯≥⨯⨯所以()a b c ab ac +=+6.在基数理论定义的乘法下,证明1a a ⨯=。

习题二1.2.3.解:()()()则有设.2112444222234b ax x m x m p qx px x ++=+++-+-2223422342)4(44)1()1(2444b abx x a b ax x m x m p qx px x +++++=+++++- ⎪⎪⎩⎪⎪⎨⎧=+=++==∴222)1(2)1(24444-bm ab m p a b q a p ⎪⎩⎪⎨⎧--=+=-=∴1412n m b a q a p4.证明:(1)因个互异的根的是方程501,,,,15432=-x λλλλ 又()())()1(1112345x F x x x x x x x -=++++-=- 所以的根,依据因式定理,(是方程0)F ,,,432=x λλλλ()()())1.....(..........)()F(432λλλλ----=x x x x x(2)设)2.......().........()()(()()(G 5255x S x F x R x x xQ x F x =++=) ()()而)知,由(,0)()G (1432====λλλλG G G⎪⎪⎩⎪⎪⎨⎧=++=++=++=++0)1(R )1()1(0)1()1()1(0)1()1()1(0)1()1()1(342422λλλλλλλλQ p R Q p R Q p R Q p 因为由以上方程组易得:,01)(234=++++=λλλλλT0)1(R ,0)1(,0)1(P ===Q故由因式定理可知,x-1是P(x),Q(x)和R(x)的因式,又根据(2),x-1也是F(x),S(x)的因式,但x-1不是F(x)的因式,所以x-1是S(x)的因式 5.即(,推出由题设,3),2-0c b a 333222abc c b a ca bc ab c b a =++++=++=++)(21(-222c b a ca bc ab ++=++) )(31333c b a abc ++=))(222333c b a c b a ++++因此()c a c a c b c b b a b a c b a ++++++++=()()(222222555 )()()(222222555b c a a c b c b a c b a -+-+-+++= )(555ac bc ab abc c b a +++++=2.3222333555c b a c b a c b a +++++++=)).(65222333555c b a c b a c b a ++++=++∴(2.35222333555c b a c b a c b a ++++=++∴6.解:由试除法知,当k=2时,有一次因式,为了探求二次因式,可用待定系数法,求得当k=1时,)2)(1()(22-+-=x x x x f))(-22234q px x n mx x a akx kx x ++++=-+-(设nq x np mq x n mp q x m p x ++++++++=)()()(234⎪⎪⎩⎪⎪⎨⎧-==+-=++-=+)4.......(....................23.....................2)2.(....................)1...(..........1nq k np mq k n mp q m p )(则有: 由(4),有⎩⎨⎧=-=⎩⎨⎧-==⎩⎨⎧=-=⎩⎨⎧==1212,212-1q n q n q n q n ,)5.....(....................22-),321k p m q n =+⎩⎨⎧-==有代入(把 ⎪⎪⎩⎪⎪⎨⎧===-==⎪⎩⎪⎨⎧-=-+-=21011K )6(........................................)1(3232)1(151q n p m k p k m 故当)得:)(由( 不合)不满足,故代入(⎩⎨⎧-==212q n………………….7.解:(1)原式=2222444y x y x y x y x -++++)( =[][]222244)(.)(y x xy y x xy y x y x +++-+++ ()()[]()[]xy y x xy y x y x y x ++-++-+=222222.()[]()[]()[]()xy y x xy y x xy y x xy y x +++++-+++=2222222.()()[]xy y x xy y x xy y x +++-+++=22222()()xy y x y xy x ++⋅++=22222 ()2222y xy x ++=(2)原式=()[]()11212++++x x x x ()[]211++=x x=()221++x x(3)此多项式是对称多项式。

《初等数学研究》习题解答第一章 数系1.1 集合论初步·自然数的基数理论习题1.11.证明集合0{|}x x >与实数集对等。
证明:取对应关系为ln y x =,这个函数构成0(,)+∞与(,)-∞+∞的一一对应,所以集合0{|}x x >与实数集对等。
2.证明()()()A B C A B A C =证明:()x A B C x A ∀∈⇒∈或x B C ∈,x A ⇒∈或(x B ∈且x C ∈),那么有x A ∈或x B ∈同时还有x A ∈或x C ∈,即x A B ∈同时还有x A C ∈,所以()()()()()x A B A C A B C A B A C ∈⇒⊆反过来:()()x A B A C x A B ∀∈⇒∈且x A C ∈,对于前者有x A ∈或者x B ∈;对于后者有x A ∈或者x C ∈,综合起来考虑,x B ∈与x C ∈前后都有,所以应是“x B ∈且x C ∈”即“x B C ∈”,再结合x A ∈的地位“或者x A ∈”以与前后关系有“x A ∈或x B C ∈”即()x A B C ∈,所以()()()()x A B C A B C A B A C ∈⇒⊇ 所以()()()A B C A B A C =。
3.已知集合A 有10个元素,,B C 都是A 的子集,B 有5个元素,C 有4个元素,B C 有2个元素,那么()B A C -有几个元素?解:集合()B A C -如图1所示:由于452(),(),()r C r B r B C ===,所以32(),()r B C r C B -=-=,图1CBA从而1028(())r B A C -=-=, 即()B A C -有8个元素4.写出集合{,,,}a b c d 的全部非空真子集。
{,}{},{},{},{,},{,},{,},{,},{,},{,},{,,},{,,},{,,},{,,}a b c d a b a c a d b c b d c d a b c a b d a c d b c d5.证明,按基数理论定义的乘法对加法的分配律成立。

A 卷一1.在三线段a,b,c 中,欲证a=b+c ,可做线段p=b+c ,然后证 a=p2.反射轴相同的两个反射之积是 恒等变换3.轨迹的基本属性是指 纯粹性和完备性4.三大尺规作图的不可能问题是 化圆为方、倍立方、三等分角5.在ABC 与'''A B C 中,若'A A ∠=∠ ()'180A A ∠+∠=则'''''''ABC A B C S AB AC S A B A C = 二1. 三角形的三条中位线形成的三角形与原三角形关系是 相似2. 设E 、F 、G 、H 分别是ABCD 的AB 、BC 、CD 、AD 边上的中点,则四边形EFGH 是 平行四边形3. 下列变换中不是合同变换的是 位似比不等于±1的位似变换4.5三1. 设ABC 由一点M 与顶点A 、B 、C 的连线分别交BC 、CA 、AB 于点D 、E 、F ,求AM BM CM AD BE CF++2. 在ABC 的三边上分别取111,,222AE EC CD DB BF FA ===,求:DEF ABC S S1.在ABC中,M是BC的中点,求证:AB+AC>2AM2.证三角形三高线交于一点(西瓦准则)3.求作三角形,已知它的三条中线一1. 梅涅劳斯定理是证明 共线点 的有力工具2. 反射相同的两个反射的积是 恒等变换3. 在ABC 与'''A B C 中,若'A A ∠=∠ ()'180A A ∠+∠=则'''''''ABC A B C S AB AC S A B A C =4.轨迹的纯粹性是指 属于轨迹上的每一点都符合给定的条件 5.三大尺规作图的不可能问题是 化圆为方、倍立方、三等分角 二1.三角形的三条中位线形成的三角形与原三角形的面积之比是 1:4 2.在三角形的三高线、三中垂线和三中位线中,不共点的三线是 三中位线 3.正方形的一边与对角线之间 无公度 4.欧拉线上的三点是指 外心、垂心、重心 5.位似比为-1的位似变换是 中心对称 三1. 已知ABC 中,AB=8cm ,BC=6cm ,AC=10cm.求:(1)ABC S(2)AB 边上的高BD 的长2. 在ABC S 的三边上分别取111,,333AD AB BE BC CF CA ===,已知ABC S =3, 求:DEF S。
《初等数学研究》习题解答第一章 数系1.1 集合论初步·自然数的基数理论习题1.11.证明集合0{|}x x >与实数集对等。
证明:取对应关系为ln y x =,这个函数构成0(,)+∞与(,)-∞+∞的一一对应,所以集合0{|}x x >与实数集对等。
2.证明()()()A B C A B A C = 证明:()x AB C x A ∀∈⇒∈或x B C ∈,x A ⇒∈或(x B ∈且x C ∈),那么有x A ∈或x B ∈同时还有x A ∈或x C ∈,即x A B ∈同时还有x A C ∈,所以()()()()()x A B A C A B C A B A C ∈⇒⊆反过来:()()x AB AC x A B ∀∈⇒∈且x A C ∈,对于前者有x A ∈或者x B ∈;对于后者有x A ∈或者x C ∈,综合起来考虑,x B ∈与x C ∈前后都有,所以应是“x B ∈且x C ∈”即“x B C ∈”,再结合x A ∈的地位“或者x A ∈”以及前后关系有“x A ∈或x BC ∈”即()x A B C ∈,所以()()()()x AB C A B C A B A C ∈⇒⊇所以()()()A B C A B A C =。
3.已知集合A 有10个元素,,B C 都是A 的子集,B 有5个元素,C 有4个元素,B C有2个元素,那么()BA C -有几个元素?解:集合()BA C -如图1所示:由于452(),(),()r C r B r B C ===,所以32(),()r B C r C B -=-=, 从而1028(())r B A C -=-=, 即()BA C -有8个元素4.写出集合{,,,}a b c d 的全部非空真子集。
图1CBA{,}{},{},{},{,},{,},{,},{,},{,},{,},{,,},{,,},{,,},{,,}a b c d a b a c a d b c b d c d a b c a b d a c d b c d5.证明,按基数理论定义的乘法对加法的分配律成立。
初等代数研究第一章课后答案
1.对于阖其各自属于实数的解,其有限解总数是什么?
答:对于一个方程有n个未知数的情况,若其各自属于实数,其有限
解总数就是n个实数的组合数。
2.多项式的降幂性质是什么?
答:多项式的降幂性质是指把多项式的次方降低,可以说出此多项式
的系数与高次幂的多项式的系数之间存在特殊的关系。
3.方程的求根方法有哪些?
答:方程的求根方法有移项法、分式法、因式分解法、求根公式法、
四则运算法、代数位移法和零点求取法等。
4.展开某一代数式有什么用处?
答:展开某一代数式是用来求该多项式的某一特定幂次的系数,并可
以帮助我们在后续不同多项式的乘积和幂次的降低中得到精确的结果。
习题一1、数系扩展的原则是什么?有哪两种扩展方式?(P9——P10) 答:设数系A 扩展后得到新数系为B ,则数系扩展原则为:(1)B A ⊂(2)A 的元素间所定义的一些运算或几本性质,在B 中被重新定义。
而且对于A 的元素来说,重新定义的运算和关系与A 中原来的意义完全一致。
(3)在A 中不是总能实施的某种运算,在B 中总能施行。
(4)在同构的意义下,B 应当是A 的满足上述三原则的最小扩展,而且有A 唯一确定。
数系扩展的方式有两种:(1)添加元素法。
(2)构造法。
2、对自然数证明乘法单调性:设,,,a b c N ∈则(1),;a b ac bc ==若则(2),;a b ac bc <<若则(3),a b ac bc >>若则;证明:(1)设命题能成立的所有C 组成集合M 。
a b,a a 1,b b 1,P13(1),(1)a 111,a ac a c ac a bc b c bc b b Mc M c bc==⋅=⋅=+=+=+=+''∴⋅=⋅∴∈∈= (规定)假设即ac ,ac a c .bc a ba bcbc bc M ==∴+=+∴=''∴∈'又 由归纳公理知,,N M =所以命题对任意自然数成立。
(2),,.a b b a k k N <=+∈若则有 (P17定义9)由(1)有()bc a k c =+a c kc =+ac bc ∴< (P17.定义9)或:,,.a b b a k k N <=+∈若则有 bc ()a k c ac kc =+=+ ()ac ac kc a k c bc ∴<+=+=.ac bc ∴=(3),,.a b a b k k N >=+∈若则有a ().cb kc bc kc =+<+ac bc ∴>3、对自然数证明乘法消去律:,,,a b c N ∈设则(1),;ac bc a b ==若则(2)ac bc a b <<若,则;(3)ac bc a b >>若,则。
初等代数研究课后习题20071115033 数学院 07(1) 杨明1、证明自然数的顺序关系具有对逆性与全序性,即(1)对任何N b a ∈,,当且仅当b a <时,a b >.(2))对任何N b a ∈,,在b a <,b a =,b a >中有且只有一个成立.证明:对任何N b a ∈,,设a A ==,b B ==(1)“⇒” b a <,则B B ⊂∃,,使,~B A ,A B B ~,⊃∴,a b >∴“⇐” a b >,则B B ⊂∃,,使A B ~,,B B A ⊂∴,~,b a <∴综上 对任何N b a ∈,,b a <⇔a b >(2)由(1)b a <⇔a b > b a <∴与b a >不可能同时成立,假设b a <∴与b a =同时成立,则B B ⊂∃,,使,~B A 且B A ~, ,~B B ∴与B 为有限集矛盾,b a <∴与b a =不可能同时成立,综上,对任何N b a ∈,,在b a <,b a =,b a >中有且只有一个成立..2、证明自然数的加法满足交换律.证明:对任何N b a ∈,设M 为使等式a b b a +=+成立的所有b 组成的集合先证 a a +=+11,设满足此式的a 组成集合k ,显然有1+1=1+1成立φ≠∈∴k 1,设k a ∈,a a +=+11,则+++++++=+=+==+a a a a a 1)1()1()(1k a ∈∴+,N k =∴, 取定a ,则1M φ∈≠,设,b M a b b a ∈+=+,则 ()()a b a b b a b a +++++=+=+=+ ,b M M N +∴∈∴= ∴ 对任何N b a ∈,,a b b a +=+3、证明自然数的乘法是唯一存在的证明:唯一性:取定a ,反证:假设至少有两个对应关系,f g ,对b N ∀∈,有 (),()f b g b N ∈,设M 是由使()()f b g b =成立的所有的b 组成的集合,()()1f b g b a ==⋅ 1M φ∴∈≠ 设b N ∈则()()f b g b =()()f b a g b a ∴+=+ ()()f b g b ++∴=,b M +∴∈,M N ∴= 即b N ∀∈,()()f b g b =乘法是唯一的存在性:设乘法存在的所有a 组成集合K 当1a =时,b N ∀∈,111,1111b b b b ++⋅=⋅==+=⋅+ φ≠∈∴k 1,设a K ∈,b N ∀∈,有,a b 与它对应,且1a a ⋅=,ab ab a +=+,对b N ∀∈,令a b ab b +=+ 1111a a a a ++⋅=⋅+=+=1()(1)a b ab b ab a b ab b a a b a ++++++=+=+++=+++=+a K +∴∈ K N ∴= 即乘法存在p24—5、解:满足条件的A 有1{1,2}A =,2{1,2,3}A =,3{1,2,4}A =,4{1,2,5}A = 5{1,2,3,4}A =,6{1,2,3,5}A =,7{1,2,4,5}A =,8{1,2,3,4,5}A =123456782,3,4,5A A A A A A A A ========∴========基数和为23343528+⨯+⨯+= p24—6、证明:,A a B b ==,A 中的x 与B 中的y 对应 A B ab ∴⨯=,B A ba ab ∴⨯==A B ab ⨯= A B A B B A ∴⨯=⋅=⨯p24—8、证明:1)3+4=73134++== 3231(31)45++++=+=+== 3332(32)56++++=+=+==3433(33)67++++=+=+==2)3412⋅= 313⋅= 32313136+⋅=⋅=⋅+=33323239+⋅=⋅=⋅+=343333312+⋅=⋅=⋅+=p24—12、证明:1)()m n m n +++++=+()1(1)m n m n m n m n +++++++=++=++=+2)()mn nm m +++=+ ()1(1)mn mn mn m nm m ++++=+=++=+p26—36、已知(,)f m n 对任何,m n N ∈满足(1,)1(1,1)(,2)(1,1)(,(1,))f n n f m f m f m n f m f m n =+⎧⎪+=⎨⎪++=+⎩求证:1)(2,)2f n n =+2)(3,)22f n n =+3)1(4,)22n f n +=-证明:1)当1n =时,(2,1)(11,1)(1,2)2112f f f =+==+=+结论成立,假设n k =时,结论成立,即(2,)2f k k =+,当1n k =+时,(2,1)(11,1)(1,(2,))(1,2)(2)1(1)2f k f k f f k f k k k +=++==+=++=++ 所以对一切自然数结论都成立2)当1n =时,(3,)(21,)(2,2)22212f n f n f =+==+=⋅+结论成立假设n k =时,结论成立,即(3,)22f k k =+当1n k =+时,(3,1)(21,1)(2,(3,))(2,22)2222(1)2f k f k f f k f k k k +=++==+=++=++ 所以对一切自然数结论都成立3)当1n =时,11(4,1)(31,1)(3,2)22222f f f +=+==⨯-=-结论成立 假设n k =时,结论成立,即1(4,)22k f k +=- 当1n k =+时,112(4,1)(3,(4,))(3,22)2(22)222k k k f k f f k f ++++==-=-+=-所以对一切自然数结论都成立p62—1、证明定理2.1证明:[,],[,]a b c d Z ∀∈,[,][,][,]a b c d a c b d +=++因为自然数加法满足交换律[,][,]a c b d c a d b ∴++=++而[,][,][,]c d a b c a d b +=++[,][,][,][,]a b c d c d a b ∴+=+[,],[,],[,]a b c d e f Z ∀∈,[,][,][,][,][,][(),()]a b c d e f a c b d e f a c e b d f ++=+++=++++以为自然数满足加法结合律([,][,])[,][,]([,][,])a b c d e f a b c d e f ∴++=++ 即整数加法满足交换律和结合律p62—2、已知[,],[,]a b c d Z ∈,求证[,][,]a b c d =的充要条件是[,][,][1,1]a b c d -= 证明:“⇒” 已知[,][,]a b c d =则a d b c +=+[,][,][,][1,1]a b c d a d b c ∴-=++=“⇐” 已知[,][,][1,1]a b c d -=则[,][1,1]a d b c ++=,a d b c +=+[,][,]a b c d ∴=p62—4、已知N b a ∈,,求证([,])[,]a b a b --=证明:[,][,]a b b a -= ([,])[,][,]a b b a a b --=-=p62—5、已知[,],[,]a b c d Z ∈,求证([,][,])[,][,]a b c d a b c d --=-+证明:左边([,][,])[,][,]a b c d a d b c b c a d --=-++=++右边[,][,][,][,][,]a b c d b a c d b c a d -+=+=++所以左边等于右边([,][,])[,][,]a b c d a b c d ∴--=-+p62—7、已知,,a b c N ∈,求证当且仅当a d b c +<+时[,][,]a b c d <证明:“⇒” 已知a d b c +<+,[,][,][,]a b c d a d b c -=++因为 a d b c +<+ [,]a d b c ∴++是负数,[,][,]a b c d ∴<“⇐” 已知[,][,]a b c d <则[,][,][,]a b c d a d b c -=++因为[,]a d b c ++是负数,a d b c ∴+<+p62—9、已知,Z αβ∈,求证:1)αβαβ+≤+ ,2) αβαβ=证明:设[,],[,]a b c d αβ== 1)[,]a c b d αβ+=++ ()()a c b d αβ∴+=+-+而,a b c d αβ=-=-()()()()a c b d a b c d a b c d +-+=-+-≤-+-αβαβ∴+≤+2)[,]ac bd ad bc αβ=++ ()ac bd ad bc αβ∴=+-+而,a b c d αβ=-=-()()()()()ac bd ad bc a c d b d c a b c d a b c d +-+=-+-=--=-- αβαβ∴=p63—12、n 名棋手每两个比赛一次,没有平局,若第k 名胜负的次数各为,k k a b ,1,2,........,k n =,求证:2222221212......n n a a a b b b +++=+++ 证明:对于(1,2,...,)k a k n =,必存在一个(1,2,...,)j b j n =使得k j a b =⇒22(,1,2,...,)k j a b k j n == 2222221212......n n a a a b b b ∴+++=+++p63—16、已知10p a b -,10p c d -,求证p ad bc -证明:由已知:,s t Z ∃∈使10a b ps -=,10c d pt -=⇒ 10,10b a ps d c pt =-=-10(10)()ad bc ac apt ac cps p cs at ∴-=---=-p ad bc ∴-p63—17、设2不整除a ,求证281a +证明:因为2不整除a ,所以存在唯一一对,q r Z ∈,使2a q r =+,其中02r <<⇒1r =,22441a q q ∴=++⇒214(1)a q q -=+ 281a ∴-p63—20、设a Z ∈,求证(1)(2)(3)1a a a a ++++是奇数的平方证明:22222(1)(2)(3)1[(1)1](1)[(2)(2)1]1[(1)(1)][(2)(2)]1(1)(2)2(1)(2)1[(1)(2)1]a a a a a a a a a a a a a a a a a a ++++=+-+++++=+-+++++=++-+++=++- 1,2a a ++肯定一奇一偶(1)(2)a a ∴++肯定为偶数(1)(2)1a a ∴++-肯定为奇数p63—22、证明:前n 个自然数之和的个位数码不能是2、4、7、9证明:前n 个自然数的和为(1)2n n + 因为:n 个自然数的和仍为自然数∴ 1+n 与n 中必定一个为奇数一个为偶数若个位数码为2则1+n 与n 的个位数码只能是1,4或4,1而(1+n )- n=1 ∴个位数码不能为2若个位数码为4则1+n 与n 的个位数码只能是1,8或8,1也不可能成立若个位数码为7则1+n 与n 的个位数码有2种可能,则2,7或1,14也不可能成立,若个位数码为9则1+n 与n 的个位数码有2种可能,即2,9或1,18也不可能成立,综上,前n 个自然数和的个位数码不能是2,4,7,9p63—26、证明2.3定理1(12,,......,n a a a )=(12,,......n a a a )证明:因为:(12,,......,n a a a )是12,,......n a a a 的公因数中的最大数所以R 需考虑非负整数 ∴(12,,......,n a a a )=(12,,......n a a a ) p63—29、证明2.3定理4的推论(,)1a b =的充要条件是有,x y Z ∈使得1ax by += 证明:因为(,)1a b = ,a b ∴不全为0“⇒” 由定理4 ,x y Z ∃∈使(,)1ax by a b +==“⇐” 设(,)a b d =则,d a d b ,d ax by ∴+ 1d ∴ (,)1d a b ∴== p63—30、证明2.3定理6及其推论。
初等数学研究(程晓亮、刘影)版课后习题答案 第一章 数1添加元素法和构造法,自然数扩充到整数可以看成是在自然数的基础上添加0到扩大的自然数集,再添加负数到整数集;实数扩充到复数可以看成是在实数的基础上构造虚数单位i 满足12-=i ,和有序实数对),(b a 一起组成一个复数bi a +. 2(略)3从数的起源至今,总共经历了五次扩充:为了保证在自然数集中除法的封闭性,像b ax =的方程有解,这样,正分数就应运而生了,这是数的概念的第一次扩展,数就扩展为正有理数集.公元六世纪,印度数学家开始用符号“0”表示零.这是数的概念的第二次扩充,自然数、零和正分数合在一起组成算术数集.为了表示具有相反意义的量,引入了负数.并且直到17世纪才对负数有一个完整的认识,这是数的概念的第三次扩充,此时,数的概念就扩展为有理数集.直到19世纪下半叶,才由皮亚诺、戴德金、维尔斯特拉斯等数学家的努力下构建了严格的实数理论.这是数的概念的第四次扩充,形成了实数集.虚数作为一种合乎逻辑的假设得以引进,并在进一步的发展中加以运用.这是数学概念的第五次扩充,引进虚数,形成复数集.4证明:设集合D C B A ,,,两两没有公共元素d c b a ,,,分别是非空有限集D C B A ,,,的基数,根据定义,若b a >,则存在非空有限集'A ,使得B A A ~'⊃;若d c ≥从而必存在非空有限集'C ,使得D C C ~'⊃,所以)(C A ⋃)(D B ⋃⊃所以集合C A ⋃的基数c a +大于集合D B ⋃的基数d b +,所以d b c a +>+.5(1)解:按照自然数序数理论加法定义, 1555555155155)25(2535''=++=++⋅=+⋅=+⋅=⋅=⋅ (2)解:按照自然数序数理论乘法定义87)6(])15[()15()25(2535'''''''''===+=+=+=+=+ 6证明:︒1当2=n 时,命题成立.(反证法)()()()()()()()01121,1111111,111101111111,,2,1,0111,,2,1,0)2(212122121212121212122221212122111112111212222121≥++-+⇒≥++-++≥+-+-≥++++∴≥⎪⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛->-=-++-+-=+++++=>+=≥+++=+++=>≥=︒+++++++++++++++++k k k k k k k k k k k k k k k i k k k k k k i k k i a k a k k a k k a k k a ka a ka a a a a k a a a a a a a a a a a a a a a a a a k i a k n ka a a a a a k i a k k n ,即要证由归纳假设,得,且得,,且时,由当。
2.对自然数证明乘法单调性:设a,b,c∈N则(1)若a=b,则ac=bc(2)若a<b,则ac<bc(3)若a>b,则ac>bc证明:(1)设命题能成立的所有c组成的集合M.∵a·1=b·1∴1∈M假设c∈M即则(ac) ′= (bc) ′﹤=﹥ac + 1 = bc + 1 重复以上过程a次,可得到ac + a = bc + a = bc + b即a(c+1) = b(c+1)∴c∈M由归纳公理知M = N.所以命题对任意自然数c成立(2)若a < b,则有k∈N,使得a + k = b,由(1) (a + k)c = bcac + kc = bc﹤=﹥ac < bc(3)依据(2)由对逆性可得。
7.设α=(3+13) / 2 , β=( 3-13) / 2 , An= (αn-βn)/ 13(n=1,2,…..).(1) 以α,β为根作一元二次方程;(2) 证明A n+2=3A n+1+A n;(3) 用数学归纳法证明A3n 是10的倍数;解:(1) α+ β=3, α β=-1,∴由韦达定理得以α,β为根作一元二次方程为:X2-3X-1=0(2) 证:3A n+1+A n=3(αn+1-βn+1)/13+(αn-βn)/13=( α+ β) (αn+1-βn+1) /13+(αn-βn)/13= (αn+2 -βn+2 - α βn+1 + β αn+1 + αn- βn)/13= (αn+2 -βn+2)/13=A n+2(3) 证:①当n=1时,有A3 =10,则10| A3。
②假设当n=k时,有10| A3k则当n=k+1时,A3k+3 = 3A 3k+2+A3k+1=3(3A 3k+1+A3k) +A3k+1=10 A 3k+1 +3 A3k10|10 A 3k+1 , 10| 3A3。
∴ 10|10 A 3k+3由①②得,对∀n∈N*,有10| A3n。
初等数学研究答案1大学数学之初等数学研究,李长明,周焕山版,高等教育出版社 习题一1答:原则:(1)A ⊂B(2)A 的元素间所定义的一些运算或基本关系,在B 中被重新定义。
而且对于A 的元素来说,重新定义的运算和关系与A 中原来的意义完全一致。
(3)在A 中不是总能施行的某种运算,在B 中总能施行。
(4) 在同构的意义下,B 应当是A满足上述三原则的最小扩展,而且由A 唯一确定。
方式:(1)添加元素法;(2)构造法 2证明:(1)设命题能成立的所有c 组成集合M 。
a=b ,M 11b 1a ∈∴⋅=⋅∴,假设bcac M c =∈,即,则Mc c b b bc a ac c a ∈'∴'=+=+=',由归纳公理知M=N ,所以命题对任意自然数c 成立。
(2)若a <b ,则bc kc ac bc,k)c (a )1(b k a N k =+=+=+∈∃即,,由,使得则ac<bc 。
(3)若a>b,则acm c bc ac,m )c (b )1(a m b N m =+=+=+∈∃即,,由,使得 则ac>bc 。
3证明:(1)用反证法:若ba b,ab a <>≠或者,则由三分性知。
当a >b 时,由乘法单调性知ac >bc. 当a <b 时,由乘法单调性知ac<bc.这与ac=bc 矛盾。
则a=b 。
(2)用反证法:若ba b,ab a =>或者,则由三分性知不小于。
当a >b时,由乘法单调性知ac >bc. 当a=b 时,由乘法单调性知ac=bc.这与ac<bc 矛盾。
则a <b 。
(3)用反证法:若ba b,ab a =<或者,则由三分性知不大于。
当a<b时,由乘法单调性知ac<bc. 当a=b 时,由乘法单调性知ac=bc.这与ac>bc 矛盾。
则a>b 。
4. 解:(1)4313='=+ 541323='='+=+652333='='+=+ 763343='='+=+874353='='+=+(2)313=⋅631323=+⋅=⋅93232333=+⋅='⋅=⋅123333343=+⋅='⋅=⋅153434353=+⋅='⋅=⋅5证明:当n=1时,的倍数。
是9181n 154n=-+假设当n=k 时的倍数。
是91k 154k-+则当n=k+1时的倍数。
是)()(918k 451k 154411k 154k1k +--+=-+++则对∀N n ∈,1n 154n-+是9的倍数.6证明:当1n =时,141-=3-,n21n21-+=3-;则当1n =时成立。
假设当k n =时成立,即(141-)(941-)(2541-)……… (21k 241)(--)=k 21k21-+ 当1k n +=时,(141-)(941-)(2541-)……… (21k 241)(--)(21k 241)(+-) =k21k21-+(21k 241)(+-)=)()(1k 211k 21k 21k 23+-++=++- 当1k n +=时成立。
7解:(1)01x 3x 132=---==+,则,αββα(2)3311=-=---ββαα,131313An2n n 2n n n 2n 2n 2n ββααβαβα+--+-=-=∴+++++131311n 11n nn )()(-+-+---+-=βββαααβα133131n 1n nn ++-+-=βαβα;n 1n A A 3+=+(3)当n=1时,1013A 333=-=βα的倍数。
是10假设当n=k 时13A3k3k 3kβα-=的倍数。
是10则当n=k+1时131313A 33k33k 3k 33k 33k 31k 31k 31k 3)()()()()(βαβαβαββααβα-+-=⋅-⋅=-=+++k333k3k 1013βαβα+-=则对∀N n ∈,n3A 是10的倍数. 8证明:;,,则,,使得,;,lar lc kaq kb ar c aq b Z r q c |a b |a ====∈∃∴ 。
;)(lc kb |a a lr kq lc kb +∴+=+∴ 9证明:假设存在b ,使得,1a +<<a b 由得,b <a ,,使得k a b N k +=∈∃若,则1k =;1a b +=若,则1k >;即1a k a b +>+=;1a b +>因此.1a 是不可能的+<b 10证明:);,,,,,,(,,设*321321332211Z q q q Z p p p p q c p qb p q a ∈∈===则a(bc)===⋅321321332211p p p )q q q p q p q pq)(()()()(321321p p p q q q a(bc)p q p q p q 332211=⋅=)(11答:(1)加法,乘法,减法; 构成数环 (2)乘法,除法; (3)加法,乘法; (4)加法,乘法; (5)加法,乘法,除法; (6)乘法; (7)加法,乘法,减法;构成数环(8)加法,乘法,减法;构成数环 12 证明:方法一nn 332211b a b a b a b a <<<< 即n11n 2112b a b a ,b a b a >>=-++++++∴11n 21n 21b a b b b a a a 1n 21n 2111n 21b b b b b b b a b a a a )()()(++++++-+++b b b b b a b a b a -b a 1n 21n 11n 2112>+++-++=)()()(nn 332211b a b a b a b a <<<<即1-n n n 1-n 1n n 1b a b a ,b a b a <<,=-++++++∴n n n21n 21b a b b ba a an n 21n 21n n n 21b b b b b b b a b a a a )()()(++++++-+++b b b b b a b a b a -b a nn 211-n n n 1-n 1n n 1<+++-++=)()()(方法二:设p,b a 11=q,b a nn=则由p=nn 332211b a b a b a ba<<<<=q 得,p b a 11=, p b a 22>,p b a n n> ; qb a 11<,qb a 22<,qb an n= ;则n 21n 21b b b p b p b p b ++++++ n21n21b b b a a a ++++++<<n21n21bb b qb q b q b ++++++ 即q.b b b a a a p n21n21<++++++<则.b a b b b a a a b a n nn 21n 2111<++++++< \13.(1);109.16.5003105.1102.16.50031053.1102.143434⨯≈+⨯+⨯≈+⨯+⨯(2);88.4238.026.433824.026.43=-≈- (3);7.6872232.687138.6813.2264.32≈==⨯ (4)≈÷⨯43564.2)1063.2(3.1008.163875.1079436.2)1063.2(33⨯≈=÷⨯14 解:5.046308.0%02.04.2315|a |≈=⨯==∆δ 则它的有效数字的个数为4。
15 解:551.45511.47321.11416.3232≈=-⨯≈-π16 证明:方法一:⇒dcx bax S ++= 是有理数,则其不包含x ;dcx kdb x d cx kc a kd cx kd b x kc a d cx k d cx b ax S +-++-+=+-+-++=++=)()(又。
;即,bc ad kd b kc a ===∴,代入,,则;令其为b p c a p d p bc ad ===⇐ dcx bax S ++=得,为有理数。
p abap x b p b ax d cx b ax S =++=++=方法二:⇒dcx b ax S ++=是有理数,则dcx b ax S Z,n m,++=∈∃使得=.nm ;bn.-dm cm )x -(an d)m (cx b)n (ax =+=+,即则bc.ad ;bn dm mc an ,x Q d c b a *=⎩⎨⎧==∈即则是无理数,,,,又由于⇐ 又;d)d (cx b)d (ax d cx b ax S 2d cdx bdadx ++=++=++=bc.ad =则.)(d)b(cx d)d (cx b)d (ax d cx b ax S 2dbd cx d d cdx bd adx =++=++=++=++=dcx bax S ++=∴是有理数17 证明:cd c d c d b a +-=-=-∴+=+,d b c a则若。
时,c d b a ==若⎪⎩⎪⎨⎧=-=+≠b-a c d b-a c -d c d b a 时由得b -a b-a c-d d 2+=;即无理数等于有理数矛盾,则。
c d =18解:(1) ≥++≥≥≥≥≤+≤≤≤≤1n 2n 4534231n n 433221; 并且时并且当∞→>+=+-++n ;01n 21n n 1n 2n 01n 21n n 1n 2n →+=+-++∴此序列为退缩有理闭区间序列,且它所确定的实数为1.(2) ≥+≥≥≥≥≤≤≤≤≤1n 14131210000; 并且时并且当∞→>+=-+n ;01n 101n 101n 101n 1→+=-+∴此序列为退缩有理闭区间序列,且它所确定的实数为0.(3) ≥≥≥≥≥≤≤≤≤≤11112n1-2n 654321; 并且时并且当∞→>=-n ;02n 12n 1-2n 102n12n 1-2n 1→=- ∴此序列为退缩有理闭区间序列,且它所确定的实数为1.19.(1)(⨯)答:复数集与复平面内以0为起点的一切向量组成的集合一一对应;(2)(⨯) 答:两复数的和与积都是实数的充分条件是:这两个复数是共轭复数(3)(⨯)答:共轭虚数的正整数次幂仍是共轭复数;(4)(⨯) 答: 一个非零复数的模等于1的充分条件是它与它的倒数之和为实数.20 证明:当时k 3n =,++-3k2i31)(;)(22i 313k=--当时1k 3n +=,++-+13k 2i31)(;)(12i 3113k -=--+当时2k 3n +=,++-+23k 2i31)(;)(12i 3123k -=--+21解:Z=72i 31)(++=+=++1)6isin 6(cos 17ππ)67isin 67(cosππ+=i 21231--则|Z|=22263241)23-(12-=-=+;则.23arctan 2)(+-=πθ22 解: |z|=1,,则令ααisin cos z +=∴1z z 2+-=)i sin -sin (2cos cos cos 22ααααα+-则u=222)21(cos 41cos 4cos 4|1z z|-=+-=+-ααα当3u,1cos max=-=时α;当.0u,21cos min==时α23. 解方程N).n 1,n 1z 1z nn∈>-=+,()()( 即,则)()解:由于(,1)11(1z 1z nn =-+-=+nz z1)-n ,2,1,0(k ;nk 2isin n k 2cos 1-z 1z =+=+ππ; 则1)-n ,1,0(k 1nk 2isin n k 2cos n k 2isinn k 2cos 1z =-+++=;ππππ24解:(1);1)(,1)(1nn2n===nωωω ,次单位根);次方根(个不同的的是,,,n n n 1n2ωωω ∴(2))(1(1nωω-=-;0)11-n 2=++++ωωω而∴≠-,01ω;011-n 2=++++ωωω(3))(1(1n-=-z z)11-n 2z z z ++++=)1(-z );())()((1n 32-----ωωωωz z z z 当时,1≠z =++++1-n 21z zz )())()((132-----n z z z z ωωωω令时,1=z .)1()1(112n n =----ωωω )(25解:由图像知20)-(-10)-3(-|OD |22=+=;则.312||||||max=+=+=AD OD Z .112||||||min =-=-=BD OD Z,24060180)(arg .30,21sin max =+=∴=∴=Z αα.180)(arg min =Z26 解:设z=x+yi,则代入.4y 1)(x .3x 2y x 3z z z z 2222=++=++=++即,得27 证明:isinx ;cosx z isinx cosx z -=+=,则令isinx;cosx z isinx cosx z 22-=+=,;,isinnx cosnx z isinnx cosnx z n n -=+=而;,isinx 2z z cosx 2z z =-=+;,isinx 2z z cosx 2z z 2222=-=+;,isinx 2z z cosx 2z z nn n n =-=+则)z z z zz (z 2i 1sinnx sin2x sinx n n 22-++-+-=+++)z -z)(11(sin )1sin(sinx ]1)z 1(z 1)z -z(1[i 21n n -++-=----=nxx n z z )1)(z 1()2)2(cos 2(cos 2sin2z x n nx nx --+-=;)1)(z 1(2)1(sin 2sin 2sin 4z xn x nx --+=)z z z z (z 21cosnx cos2x cosx n n 22++++++=+++ z)z -z)(11(cos )1cos(1cosx ]1)z 1(z 1)z -z(1[21n n -++--=--+-=nx x n z z)1)(z 1()2)2(in 2sin (2sin 2z x n s nx nx --+-=;)1)(z 1(2)1(cos 2sin 2sin 4z x n x nx --+=x.21n tg cosnx cos2x cosx sinnx sin2x sinx +=++++++ 则28证明: 时,当0x ≠0p x p x p x p x n 1-n 2-n 21-n 1n=+++++ 方程 的两边同乘以得n x -0x p x p x p x p 1nn n -11-n -22-11=+++++-将x=代入上式得,ααisin cos ++++)]isin(-)[cos(-p 11αα0)]isin(-n )[cos(-n p n =++αα .按照复数相等的条件得++αcos p 110cosn p n=+α2sin p sin p 21++αα习题二1解:设这个多项式为)1()(10-+=x a a x f )4)(2)(1(2)(1(32---+--+x x x a x x a ).然后将已知点依次代入:;10,10)1(00-=∴=-=a a f ;9,1)2(110=∴+=-=a a a f;14,63101)4(2210=∴++==a a a a f ;2,21812124218)5(33210=∴=+++==a a a a a f因此,)1(910)(-+-=x x f )4)(2)(1(22)(1(14---+--+x x x x x )7523--=x x 即.32)3(=f2解:dx c x b x a x x f +-+-+-+-=-)2()2()2()2()2(234令2=x 得165=d ;令0=x 得;8624,165248169=+-+-+-=c b a c b a 即 令1=x 得.119=+-c b a 令3=x 得.269=++c b a 则165,180,75,14====d c b a 即165)2(180)2(75)2(14)2()2(234+-+-+-+-=-x x x x x f=.5432234+-+-x x x x 3解:由于22341)(m 1)x p(m 2qx 4px 4x4+++++-成为bax x22++的完全平方式,则 =++22b)ax x 2(22341)(m 1)x p(m 2qx 4px 4x 4+++++-得:;)1(2)1(24444222⎪⎪⎩⎪⎪⎨⎧=+=++==-b m ab m p ba q ap .)1(44;44)1(22p m q ba q mb p a =++⎪⎪⎩⎪⎪⎨⎧+=+-=-=∴即4证明: (1))1()1)((-=-x x x F )1x x x x(234++++=15-x=)1(-x );)()()((432λλλλ----x x x x即: );)()()(()(432λλλλ----=x x x x x F(2))()()R()Q()P(5255λλλλλλλS F ⋅=++,即.0)(0)1R()1Q()1P(2=⋅=++λλλS即: .0)1R()1Q()1P(===.0)1(,)1()1()1R()1Q()1P(=⋅=++S S F 得又由则1-x 是R(x)Q(x),P(x),和S(x)的一个公因式。