Z变换

信号与系统 z变换信号与系统是电子信息学科中的一门重要课程，其中的z变换是信号与系统分析的一种重要工具。

本文将介绍信号与系统中的z变换原理及应用。

一、z变换原理z变换是一种离散域的数学变换，它将离散时间序列转换为复平面上的函数。

在信号与系统中，我们常常需要对信号进行分析和处理，而z变换提供了一种方便且有效的方式。

它将离散时间序列变换为z域函数，从而可以对信号进行频域分析。

z变换的定义是：X(z) = ∑[x(n)·z^(-n)]，其中x(n)为离散时间序列，z为复变量。

通过z变换，我们可以将离散时间序列的差分方程转化为代数方程，从而简化信号与系统的分析和计算。

此外，z变换还具有线性性质和时移性质，使得我们可以方便地进行信号的加权叠加和时间偏移操作。

二、z变换的应用1. 系统的频域分析：z变换将离散时间序列转换为z域函数，可以方便地进行频域分析。

通过计算系统的传递函数在z域中的值，我们可以得到系统的频率响应，从而了解系统对不同频率信号的响应特性。

2. 系统的稳定性判断：通过z变换，可以将系统的差分方程转化为代数方程。

我们可以通过分析代数方程的根的位置，判断系统的稳定性。

如果差分方程的根都在单位圆内，说明系统是稳定的。

3. 离散时间系统的滤波设计：z变换为我们提供了一种方便的方法来设计离散时间系统的滤波器。

通过在z域中对滤波器的传递函数进行分析和调整，我们可以设计出满足特定需求的滤波器。

4. 信号的采样与重构：在数字信号处理中，我们常常需要对连续时间信号进行采样和重构。

通过z变换，我们可以将连续时间信号转换为离散时间信号，并在z域中进行处理。

然后再通过z逆变换将离散时间信号重构为连续时间信号。

5. 离散时间系统的时域分析：z变换不仅可以进行频域分析，还可以进行时域分析。

通过z变换，我们可以将离散时间系统的差分方程转换为代数方程，并通过对代数方程的分析，得到系统的时域特性。

z变换是信号与系统分析中非常重要的工具。

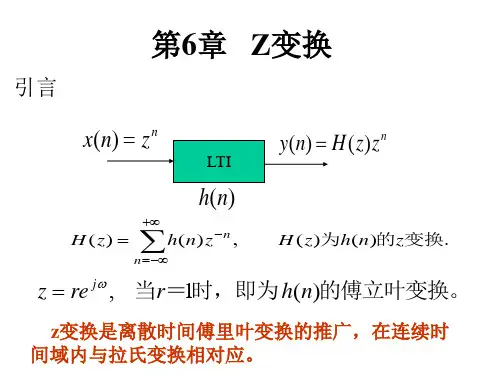
z变换公式在信号处理领域中，z变换是一种将离散时间序列转换为复频域的工具。

它在数字信号处理、控制系统分析和通信工程等领域中广泛应用。

本文将详细介绍z变换的概念、特性以及常见的z变换公式。

一、z变换的概念z变换是对离散时间信号进行频域分析的一种方法。

它类似于傅里叶变换，但傅里叶变换只适用于连续时间信号，而z变换适用于离散时间信号。

通过将离散时间序列表示为z的幂级数形式，可以将离散时间信号在复频域中进行表示和分析。

z变换的定义如下：X(z) = Z{x(n)} = ∑[ x(n) * z^(-n)] （1）其中，x(n)是离散时间序列，X(z)是x(n)的z变换。

二、z变换的特性与傅里叶变换类似，z变换也具有线性性、时移性、共轭性和卷积性质。

下面对每个特性进行详细讨论。

1. 线性性z变换具有线性性质，即对于任意常数a和b以及离散时间序列x1(n)和x2(n)，有以下公式成立：Z{a * x1(n) + b * x2(n)} = a * X1(z) + b * X2(z) （2）其中，X1(z)和X2(z)分别是x1(n)和x2(n)的z变换。

2. 时移性z变换具有时移性质，即对于离散时间序列x(n - k)，其z变换为Z{x(n - k)} = z^(-k) * X(z)。

3. 共轭性z变换具有共轭性质，即如果x(n)的z变换为X(z)，则x*(-n)的z 变换为X*(1/z*)，其中，*表示共轭。

4. 卷积性质z变换具有卷积性质，即对于离散时间序列x1(n)和x2(n)的卷积序列y(n) = x1(n) * x2(n)，其z变换为Y(z) = X1(z) * X2(z)，其中，*表示乘法运算。

三、常见的z变换公式根据z变换的定义和特性，可以得到一些常见的z变换公式，下面将逐个进行介绍。

1. 常数序列对于常数序列x(n) = C，其z变换为X(z) = C * (1 - z^(-1)) / (1 - z^(-1))。

第四章 Z 变换1 Z 变换的定义 (1) 序列)(n x 的ZT ：[]∑∞=-==0)()()(n nzn x n x Z z X(2) 复变函数)(z X 的IZT ：[])()(1z X Z n x -=，s e z =是复变量。

(3) 称)(n x 与)(z X 为一对Z 变换对。

简记为)()(z X n x ZT⇔或 )()(z X n x ⇔(4) 序列的ZT 是1-z 的幂级数。

n z -代表了时延，1-z 是单位时延。

(5) 单边ZT ：[]∑∞=-∆==0)()()(n nzn x z X n x Z(6) 双边ZT ：[]∑∞-∞=-∆==n nB B zn x z X n x Z )()()(2 ZT 收敛域ROC定义：使给定序列)(n x 的Z 变换)(z X 中的求和级数收敛的z 的集合。

∑∞-∞=-n nzn x )(收敛的充要条件是它∞<∑∞-∞=-n nzn x )((3) 有限长序列的ROC序列)(n x 在1n n <或2n n >(其中21n n <)时0)(=n x 。

收敛域至少是∞<<z 0。

序列的左右端点只会影响其在0和∞处的收敛情况： 当0,021><n n 时，收敛域为∞<<z 0(∞=,0z 除外)当0,021≤<n n 时，收敛域为∞<≤z 0(∞=z 除外) 当0,021>≥n n 时，收敛域为∞≤<z 0(=z 除外)右边序列的ROC序列)(n x 在1n n <时0)(=n x 。

如果01=n ，则序列为因果序列。

ROC 的情况：当01≥n 时，ROC 为∞≤<z R x 1； 当01<n 时，ROC 为∞<<z R x 1。

左边序列的ROC序列)(n x 在2n n >时0)(=n x 。

如果12-=n ，则序列为反因果序列。

常见序列的z变换什么是z变换？z变换是一种数学工具，用于分析和处理离散时间信号和系统。

它可以将离散时间信号从时域（时间）转换到z域（复平面），从而方便地进行频域分析和系统设计。

z变换在数字信号处理、控制系统和通信系统等领域中广泛应用。

z变换的定义对于一个离散时间序列x[n]，其z变换X(z)定义为：X(z)=∑x∞n=−∞[n]z−n其中，z是一个复数，x[n]是离散时间序列的值。

常见序列的z变换1. 单位序列单位序列u[n]是一个从n=0开始的离散时间序列，其值为1。

其z变换为：U(z)=∑u∞n=0[n]z−n=∑z−n∞n=0根据几何级数的公式，可以得到：U(z)=11−z−12. 单位阶跃序列单位阶跃序列u s[n]是一个从n=0开始的离散时间序列，其值在n≥0时为1，n< 0时为0。

其z变换为：U s(z)=∑u s∞n=0[n]z−n=∑z−n∞n=0根据几何级数的公式，可以得到：U s(z)=11−z−13. 指数序列指数序列x[n]=a n是一个常数a的离散时间序列。

其z变换为：X(z)=∑a n∞n=−∞z−n=∑(az−1)n∞n=−∞根据几何级数的公式，可以得到：X(z)=11−az−1,|az−1|<14. 正弦序列正弦序列x[n]=Asin(ωn+ϕ)是一个频率为ω、振幅为A、相位为ϕ的离散时间序列。

其z变换为：X(z)=∑A∞n=−∞sin(ωn+ϕ)z−n根据正弦函数的性质，可以将其拆分为实部和虚部的和：X(z)=∑A∞n=−∞sin(ωn+ϕ)z−n=∑A∞n=−∞sin(ωn)cos(ϕ)z−n+∑A∞n=−∞cos(ωn)sin(ϕ)z−n利用欧拉公式，可以将正弦函数转换为指数函数：X(z)=∑A∞n=−∞sin(ωn)cos(ϕ)z−n+∑A∞n=−∞cos(ωn)sin(ϕ)z−n=12j∑A∞n=−∞(e jωn−e−jωn)cos(ϕ)z−n+12j∑A∞n=−∞(e jωn+e−jωn)sin(ϕ)z−n=12j∑A∞n=−∞(e jωn cos(ϕ)−e−jωn cos(ϕ))z−n+12j∑A∞n=−∞(e jωn sin(ϕ)+e−jωn sin(ϕ))z−n根据欧拉公式的性质，可以得到：X(z)=12j∑A∞n=−∞(e jωn cos(ϕ)−e−jωn cos(ϕ))z−n+12j∑A∞n=−∞(e jωn sin(ϕ)+e−jωn sin(ϕ))z−n=12j∑A∞n=−∞(cos(ϕ)(z−1)n−cos(ϕ)(z−1)−n)+12j∑A∞n=−∞(sin(ϕ)(z−1)n+sin(ϕ)(z−1)−n)整理得到：X(z)=Acos(ϕ)2j∑((z−1)n−(z−1)−n)∞n=−∞+Asin(ϕ)2j∑((z−1)n+(z−1)−n)∞n=−∞利用几何级数的公式，可以得到：X(z)=Acos(ϕ)2j11−z−1+Asin(ϕ)2jz−11−z−15. 脉冲序列脉冲序列x[n]=δ[n]是一个在n=0时取值为1，其他时刻取值为0的离散时间序列。