分振幅法干涉原理及应用
- 格式:doc
- 大小:11.22 KB
- 文档页数:3

光的干涉分振幅干涉实验报告实验目的:观察光的干涉现象,学习分振幅干涉实验的基本原理和方法。
实验原理:1. 光的干涉现象:当两束光波相遇时,根据它们的相位差,可以出现相干加强或相干削弱的情况,这种现象就称为光的干涉。
2. 分振幅干涉:分振幅干涉是一种光的干涉形式,它是利用两个或多个来源的光波,通过干涉器件进行干涉实验。
光波在空间中叠加,产生干涉以形成明暗条纹。
实验仪器:1. He-Ne激光器:用于产生单色光。
2. 记录台:用于固定和调整干涉仪器件。
3. 分光镜:用于将激光分成两束。
4. 透镜:用于调整光束的直径和准直度。
5. 双缝:用于产生两束相干光。
6. 照相胶片或光敏纸:用于记录干涉条纹。
7. 干涉仪:用于观察干涉条纹,包括一块透明玻璃片和一块反射玻璃片。
实验步骤:1. 将激光器放置在记录台上,并调整光束直径和准直度。
2. 将分光镜放置在激光器前方,照射光通过分光镜后,分成两束光。
3. 将透镜放置在分光镜后方,调整光束的直径和准直度。
4. 将双缝放置在透镜后方,使两束光经过双缝。
5. 调整双缝宽度和距离,观察干涉条纹的形成和变化情况。
6. 将干涉仪放置在干涉条纹的位置,观察和记录干涉条纹。
7. 根据实验记录,分析干涉条纹的特点和规律。
实验结果与分析:通过实验观察和记录,我们可以得到明暗交替的干涉条纹。
根据条纹的间隔和明暗变化规律,我们可以得到光的干涉条件和干涉定律。
不同干涉条件下,干涉条纹的形态和间隔会有所不同。
结论:通过分振幅干涉实验,我们观察到了光的干涉现象,并得到了干涉条纹的特点和规律。
实验结果验证了光的干涉理论,并加深了我们对光的干涉现象的理解。

光的干涉分振幅干涉实验报告实验名称:光的干涉——分振幅干涉实验一、实验目的1.学习和掌握分振幅干涉的基本原理和方法。
2.通过实验观察和分析分振幅干涉现象,验证光的干涉现象。
3.运用波动理论解释实验现象,提高理论联系实际的能力。
二、实验原理分振幅干涉是指两列光波在空间某一点叠加,产生干涉现象。
干涉现象的产生需要满足相干条件,即两列光波的频率相同、相位差恒定、振动方向相同。
分振幅干涉实验是通过将一束光分成两束,使它们在空间某一点叠加,产生干涉现象。
本实验采用双缝干涉的方法,将一束光分成两束相干光,通过调节双缝之间的距离和角度,观察干涉条纹的变化。
三、实验步骤1.准备实验器材:激光器(或单色光源)、双缝装置、屏幕、尺子。
2.将激光器放置在双缝装置的一侧,屏幕放在双缝装置的另一侧。
3.打开激光器,调整激光器的位置,使光线正对双缝装置,并使光线恰好照射在双缝上。
4.观察屏幕上出现的干涉条纹,记录干涉条纹的位置和形状。
5.改变双缝之间的距离和角度,观察干涉条纹的变化,并记录实验数据。
6.根据干涉条纹的位置和形状,计算相干光的波长和波长差。
四、实验结果与分析1.实验结果:在实验中,我们观察到了明暗相间的干涉条纹。
随着双缝之间的距离和角度的变化,干涉条纹的位置和形状也会发生变化。
通过测量干涉条纹的位置和宽度,我们可以计算出相干光的波长和波长差。
2.结果分析:干涉条纹的位置取决于相干光的波长和双缝之间的距离。
当双缝之间的距离变化时,干涉条纹的位置会发生变化。
干涉条纹的宽度取决于相干光的波长和双缝之间的角度。
当双缝之间的角度变化时,干涉条纹的宽度会发生变化。
通过计算相干光的波长和波长差,我们可以进一步了解分振幅干涉现象的规律。
五、结论总结通过本次实验,我们验证了分振幅干涉现象的规律,深入了解了光的干涉原理和方法。
实验结果表明,当相干光的波长和双缝之间的距离、角度发生变化时,干涉条纹的位置和形状也会发生变化。
这一实验结果有助于我们更好地理解光的波动性质和光学现象。


分振幅干涉和分波面干涉
分振幅干涉和分波面干涉是光学干涉现象的两种主要类型,它们在光学实验和技术中有不同的应用。
以下是对这两种干涉的简要解释:
1.分振幅干涉(Amplitude Division Interference):
•原理:分振幅干涉是通过分割入射光波的振幅,使其沿不同光程传播,然后重新合成,产生干涉现象。
这通常涉
及将光波分成两个或多个振幅不同的部分。
•应用:分振幅干涉常用于Michelson干涉仪等设备中,用于测量光学元件的表面形状、厚度差异等。
2.分波面干涉(Wavefront Division Interference):
•原理:分波面干涉是通过分割入射光波的波面,使其沿不同光程传播,然后重新合成,产生干涉现象。
这涉及光
波的相位差异,而不是振幅。
•应用:分波面干涉广泛应用于干涉仪器,例如Twyman-Green干涉仪和Fizeau干涉仪。
它可用于测量光学表面
的平整度、透明膜的厚度、折射率差异等。
这两种干涉现象的共同点是都涉及将光波分成两个或多个部分,然后再合成,通过干涉条纹来测量光学性质。
区别在于分振幅干涉关注振幅差异,而分波面干涉关注波面差异。
在实际应用中,选择使用分振幅干涉还是分波面干涉取决于具体的实验需求和测量目标。
这两种方法都为光学领域提供了强大的工具,用于精密测量和实验研究。

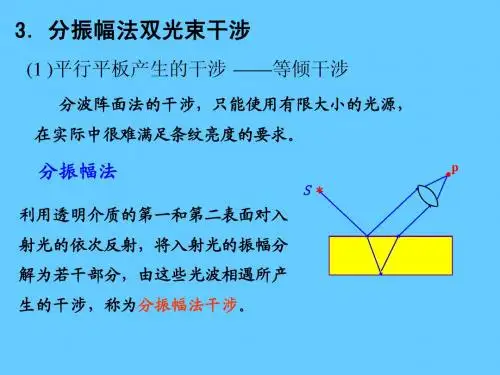
迈克尔逊干涉仪的调节和使用一.实验原理迈克尔逊干涉仪是一个分振幅法的双光束干涉仪,其光路如右图所示,它由反光镜M1,M2、分束镜P1和补偿板P2组成。
其中M1是一个固定反射镜,反射镜M2可以沿光轴前后移动,他们分别放置在两个相互垂直臂中,分束镜和补偿板与两个反射镜均成45°且相互平行,分束镜P1的一个面镀有半透半反膜,它能将入射光等强度的分为两束;补偿板是一个与分束镜厚度和折射率完全相同的玻璃板。
迈克尔逊干涉仪结构如下图所示,镜M1、M2的背面各有三个螺丝,调节M1、M2镜面的倾斜度,M1的下端还附有两个互相垂直的微动拉簧螺丝,用以精确的调整M1的倾斜度。
M2镜所在的导轨拖板由精密丝杠带动,可沿着导轨前后移动。
M2镜的位置由三个读数尺所读出的数值的和来确定,主尺、粗调手轮和微调手轮。
如图所示,躲光束激光器提供的每条光纤的输出端是一个短焦距凸透镜,经其汇聚后的激光束,可以认为是一个很好的点光源S发出的球面光波。
S1’为S经M1以及G1反射后所成的像,S2’为S经G1以及M2反射后所成的像。
S2’和S1’为两相干光源。
发出的球面波在其相遇的空间处处相干。
为非定域干涉,在相遇处都能产生干涉条纹。
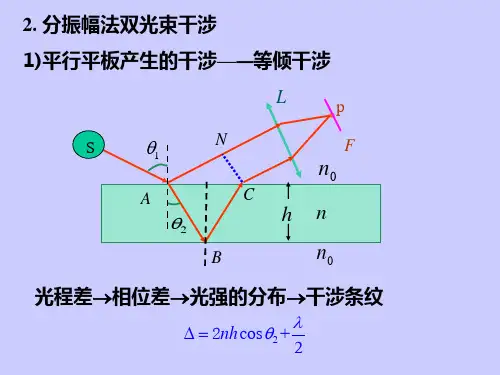
空间任一点P的干涉明暗由S2’和S1’到该点的光程差Δ=r2-r1决定,其中r2和r1分别为S2’和S1’到P点的光程。
P点的光强分布的极大和极小的条件是:Δ=kλ(k=0,1,2…)为亮条纹Δ=(2k+1)λ(k=0,1,2…)为暗条纹2.He-Ne激光波长的测定当M1’与M2平行时,将观察屏放在与S2’,S1’连线相垂直的位置上,可看到一组同心干涉圆条纹,如图所示。
设M1’与M2之间的距离为d,S2‘和S1‘之间的距离为2d,S2’和S1‘在屏上任一点P的光程差为Δ=2dcosφφ为S2’到P点的光线与M2法线的夹角。
当改变d,光程差也相应发生改变,这时在干涉条纹中心会出现“冒进”和“缩进”的现象,当d增加λ/2,相应的光程差增加λ,这样就会“冒出”一个条纹;当d减少λ/2,相应的光程差减少λ,这样就会“缩进”一个条纹;因此,根据“冒出”和“缩进”条纹的个数可以确定d的该变量,它可以用来进行长度测量,其精度是波长量级,当“冒出”或“缩进”了N个条纹,d的改变两δd为:Δd=Nλ/2二.实验内容1.调节干涉仪,观察非定域干涉(1)水平调节,调节干涉仪底角螺丝,使仪器导轨水平,然后用锁圈锁住。



1实验五迈克尔逊干涉仪的分振幅干涉研究光的干涉是重要的光学现象之一,是光的波动性的重要实验依据。
两列频率相同、振动方向相同和位相差恒定的相干光在空间相交区域将会发生相互加强或减弱现象,即光的干涉现象。
光的波长虽然很短(4×10-7~8×10-7m 之间),但干涉条纹的间距和条纹数却很容易用光学仪器测得。
根据干涉条纹数目和间距的变化与光程差、波长等的关系式,可以推出微小长度变化(光波波长数量级)和微小角度变化等,因此干涉现象在照相技术、测量技术等领域有着广泛地应用。
相干光源的获取除用激光外,在实验室中一般是将同一光源采用分波阵面或分振幅两种方法获得,并使其在空间经不同路径会合后产生干涉。
迈克尔逊干涉仪(如图5-1)是1883年美国物理学家迈克尔逊和莫雷合作,为研究“以太”漂移而设计制造出来的精密光学仪器。
它是利用分振幅法产生双光束以实现干涉。
在近代物理和近代计量技术中,如在光谱线精细结构的研究和用光波标定标准米尺等实验中都有着重要的应用。
利用该仪器的原理,研制出多种专用干涉仪。
[实验目的]1.了解迈克尔逊干涉仪的干涉原理和迈克尔逊干涉仪的结构,学习其调节方法。
2.调节观察干涉条纹,测量激光的波长。
3.测量钠双线的波长差。
4.练习用逐差法处理实验数据。
[实验仪器与器材]迈克尔逊干涉仪,钠灯,针孔屏,毛玻璃屏,多束光纤激光源(HNL 55700)。
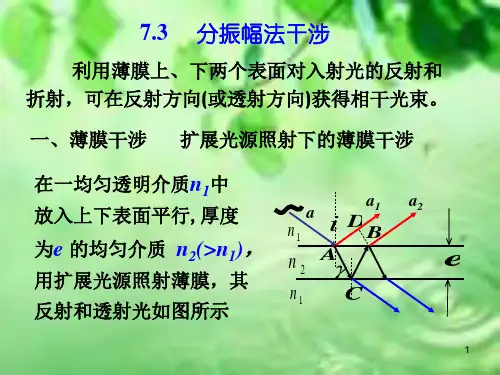
[实验原理]1.迈克尔逊干涉仪图5-1是迈克尔逊干涉仪实物图。
图5-2是迈克尔逊干涉仪的光路示意图,图中M 1和M 2是在相互垂直的两臂上放置的两个平面反射镜,其中M 1是固定的;M 2由精密丝杆控制,可沿臂轴前、后移动,移动的距离由刻度转盘(由粗读、细读刻度盘组合而成)读出。
在两臂轴线相交处,有一与两轴成45°角的平行平面玻璃板G 1,它的第二个平面上镀有半透(半反射)的银膜,以便将入射光分成振幅接近相等的反射光⑴和透射光⑵,故G 1又称为分光板。
分振幅法干涉原理及应用
分振幅法干涉是光学干涉现象中的一种干涉方式,它基于波的叠加原理,利用两个相干光源之间的干涉现象进行测量和分析。
该方法的原理和应用非常广泛,包括材料表面形貌测量、光栅测量、光学薄膜厚度测量等。
分振幅法干涉的基本原理是两个相干光源发出的光波在空间中叠加形成干涉图样,通过观察和记录干涉图样的变化来获得有关光学系统特
征的信息。
在分振幅法干涉中,两束光源的光波通过半透明镜或分束器分开,分别经过不同的路径到达接收器。
由于路径不同,光波的相位也会发生变化,当两束光波到达接收器时,它们会产生干涉现象。
干涉图样的变化可以用来分析光学系统的特点,比如材料表面的形貌、薄膜的厚度等。
分振幅法干涉的应用非常广泛。
其中一个重要的应用是材料表面形貌测量。
通过测量材料表面的形貌,可以了解材料的几何形状、表面粗糙度等信息,这对于材料加工、制造和表面质量控制等方面具有重要意义。
分振幅法干涉可以通过分析干涉图样的变化来测量物体表面的高度差
异,从而获得物体表面的形貌信息。
该方法具有高精度、非接触和无损测量等优点,广泛应用于航天、机械制造、电子器件等领域。
另一个重要的应用是光栅测量。
光栅是一种具有周期性结构的光学元件,对光的干涉具有很高的敏感性。
分振幅法干涉可以利用光栅的干涉现象来测量光栅的参数,比如周期、方位等。
这对于光栅的制造和使用具有重要意义。
光栅测量的结果可以用于光栅衍射效果的优化,提高光学系统的性能。
除了材料表面形貌测量和光栅测量,分振幅法干涉还广泛应用于光学薄膜厚度的测量。
光学薄膜是一种具有特殊光学性质的薄层材料,例如反射、透射等。
分振幅法干涉可以利用光的干涉现象来测量光学薄膜的厚度,这对于光学薄膜的研究和生产具有重要意义。
测量光学薄膜厚度的结果可以用于优化光学薄膜的制备过程,提高光学薄膜的性能。
总之,分振幅法干涉是一种基于波的叠加原理的具有高精度、非接触和无损测量的方法。
它在材料表面形貌测量、光栅测量、光学薄膜厚度
测量等方面具有重要的应用价值。
随着科技的不断发展,分振幅法干涉在光学测量领域的应用前景将会更加广阔。