下载文档原格式
For personal use only in study and research; not for commercial use第8章 稳恒磁场 习题及答案6. 如图所示，AB 、CD 为长直导线，C B为圆心在O 点的一段圆弧形导线，其半径为R 。
若通以电流I ，求O 点的磁感应强度。
解：O 点磁场由AB 、C B、CD 三部分电流产生，应用磁场叠加原理。
AB 在O 点产生的磁感应强度为01=BC B在O 点产生的磁感应强度大小为θπμR I B 402=RIR I 123400μππμ=⨯=，方向垂直纸面向里CD 在O 点产生的磁感应强度大小为)cos (cos 421003θθπμ-=r IB)180cos 150(cos 60cos 400︒︒-=R I πμ )231(20-=R I πμ，方向垂直纸面向里 故 )6231(203210ππμ+-=++=R I B B B B ，方向垂直纸面向里7. 如图所示，两根导线沿半径方向引向铁环上的A ，B 两点，并在很远处与电源相连。
已知圆环的粗细均匀，求环中心O 的磁感应强度。
解：圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生，但∞A 和∞B 在O 点产生的磁场为零。
且θπθ-==21221R R I I 电阻电阻 1I 产生的磁感应强度大小为）（θππμ-=24101RI B ，方向垂直纸面向外2I 产生的磁感应强度大小为θπμRIB 4202=，方向垂直纸面向里 所以， 1)2(2121=-=θθπI I B B环中心O 的磁感应强度为0210=+=B B B8. 如图所示，一无限长载流平板宽度为a ，沿长度方向通过均匀电流I ，求与平板共面且距平板一边为b 的任意点P 的磁感应强度。
解：将载流平板看成许多无限长的载流直导线，应用叠加原理求解。
以P 点为坐标原点，垂直载流平板向左为x 轴正方向建立坐标系。
稳恒磁场一、选择题1. 一圆电流在其环绕的平面内各点的磁感应强度B 【 】 (A) 方向相同， 大小相等； (B) 方向不同，大小不等； (C) 方向相同， 大小不等； (D) 方向不同，大小相等。
2. 电流由长直导线流入一电阻均匀分布的金属矩形框架，再从长直导线流出，设图中321O ,O ,O 处的磁感应强度为B B B 123,,,则 【 】(A)B B B 123==； (B) 0B 0B B 321≠== ；(C) 0B ,0B ,0B 321=≠= ； (D) 0B ,0B ,0B 321≠≠=3. 所讨论的空间处在稳恒磁场中，对于安培环路定律的理解，正确的是 【 】(A) 若⎰=⋅L0l d B ，则必定L 上B 处处为零(B) 若⎰=⋅L0l d B， 则必定L 不包围电流(C) 若⎰=⋅L0l d B， 则L 所包围电流的代数和为零(D) 回路L 上各点的B 仅与所包围的电流有关。
4. 在匀强磁场中，有两个平面线圈，其面积21A 2A =， 通有电流21I 2I =， 它们所受的最大磁力矩之比M M 12/等于 【 】 (A) 1 (B) 2(C) 4(D) 1/45. 由N 匝细导线绕成的平面正三角形线圈，边长为a ， 通有电流I ， 置于均匀外磁场B中，当线圈平面的法向与外磁场同向时，该线圈所受的磁力矩M m 值为： 【 】(2)选择题(A) 2/IB Na 32,(B)4/IB Na 32, (C) 60sin IB Na 32,(D) 06. 一带电粒子以速度v 垂直射入匀强磁场 B 中，它的运动轨迹是半径为R 的圆， 若要半径变为2R ，磁场B 应变为： 【 】 B 22)D (B 21)C (B 2)B (B 2)A ( 7. 图中所示是从云室中拍摄的正电子和负电子的轨迹照片，均匀磁场垂直纸面向里，由两条轨迹可以判断【 】(A) a 是正电子，动能大; (B) a 是正电子， 动能小; (C) a 是负电子，动能大; (D) a 是负电子，动能小。
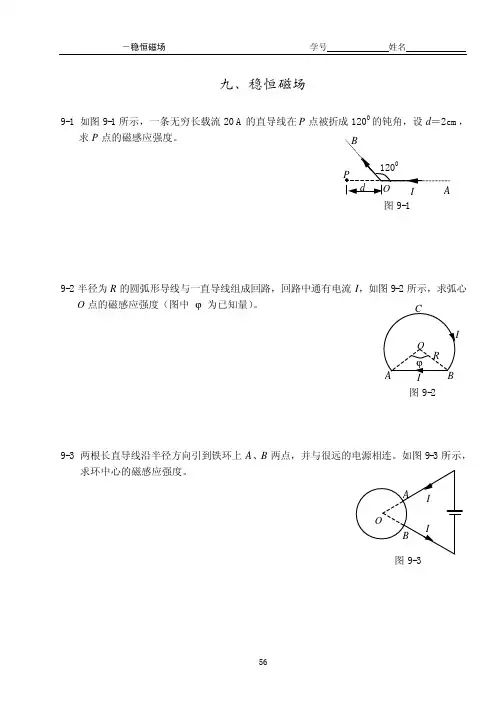
九、稳恒磁场磁感应强度9-1 如图9-1所示，一条无穷长载流20 A 的直导线在P 点被折成1200的钝角，设d ＝2cm ，求P 点的磁感应强度。
9-2半径为R 的圆弧形导线与一直导线组成回路，回路中通有电流I ，如图9-2所示，求弧心O 点的磁感应强度（图中 ϕ 为已知量）。
9-3 两根长直导线沿半径方向引到铁环上A 、B 两点，并与很远的电源相连。
如图9-3所示，求环中心的磁感应强度。
图9-1磁矩9-4一半径为R的薄圆盘，其中半径为r的阴影部分均匀带正电，面电荷密度为+s，其余部分均匀带负电，面电荷密度为-s（见图9-4）。
设此盘以角速度为ω绕其轴线匀速转动时，圆盘中心O处的磁感应强度为零，问R和r有什么关系？并求该系统的磁矩。
图9-49-5氢原子处在正常态（基态）时，它的电子可看作是在半径为a＝0.53×10－8cm的轨道（称为玻尔轨道）上作匀速圆周运动，若电子在轨道中心处产生的磁感应强度大小为12.5T，求（1）电子运动的速度大小？（2）该系统的磁矩。
（电子的电荷电量e＝1.6×10－19C）。
磁通量9-6已知一均匀磁场的磁感应强度B＝2T，方向沿x轴正方向，如图9-6所示，已知ab＝cd ＝40cm，bc＝ad＝ef＝30cm，be＝cf＝30cm。
求：（1）通过图中abcd面的磁通量；（2）通过图中befc面的磁通量；(3)通过图中aefd面的磁通量。
图9-69-7两平行长直导线相距d＝40cm，每根导线载有等量同向电流I，如图9-7所示。
求：（1）两导线所在平面内，与左导线相距x（x在两导线之间）的一点P处的磁感应强度。
(2)若I＝20A，通过图中斜线所示面积的磁通量（r1＝r3＝10cm，l＝25cm)。
图9-7安培环路定律9-8如图9-8所示的导体圆管，内、外半径分别为a和b，导体内载有电流I，设电流I均匀分布在导体圆管的横截面上，求：（1）磁感应强度的分布；（2）通过每米导体圆管S平面内（阴影部分）的磁感应通量。
第7章 稳恒磁场一、思考讨论题1、如图4.1所示的电流元Idl 是否在空间所有点的磁感应强度均不为零？请你指出Idl在a 、b 、c 、d 四点产生的磁感应强度的方向。
解：不是，电流元Idl在自身产生的磁感应强度为零。
a 、垂直纸面向外b 、垂直纸面向外c 、垂直纸面向内d 、垂直纸面向内2、分别求图4.2中的三种情况下，通有电流I 的直线电流在图中点产生磁感应强度B 的大小和方向。
解：a 图，()a I cos cos a I B πμπμ823145304--=-=方向垂直纸面向内 b 图，()aIcos cos a I B πμπμ82345604--=-= 方向垂直纸面向内 c 图() 30041cos cos a I B -=πμ () 1806030402cos cos tan c a I B -=πμ aIB B B πμ41312-=-= 方向垂直纸面向内3、电流分布如图4.3所示，分别求出各图中O 点的磁感应强度O B的大小和方向。
图4.1图4.2a图4.2ba图4.2c1 R 3解：a 图， 321B B B B ++=()30060431cos cos cos R IB B -==πμ23601202a I B μ=方向垂直纸面向内b 图， 01=B ，RIR I B 126122μμ==，()2322180150243-=-⋅=R I cos cos R I B πμπμ所以，⎪⎪⎭⎫⎝⎛-+=R R I B πμ432121 方向垂直纸面向内 c 图，RIR I B 834321μμ==，052==B B R I B B πμ16243==，所以，⎪⎪⎭⎫ ⎝⎛+=πμ238R I B 方向垂直纸面向外 4、若空间中存在两根无限长直载流导线，则磁场的分布就不存在简单的对称性，因此：（A ）安培环路定理已不成立，故不能直接用此定理计算磁场分布。
（B ）安培环路定理仍然成立，故仍可直接用此定理计算磁场分布。
第12单元 稳恒电流的磁场第七章 静电场和恒定磁场的性质(三)磁感应强度序号 学号 姓名 专业、班级一 选择题[ C ]1．一磁场的磁感应强度为B ai bj ck =++（T ），则通过一半径为R ，开口向z 正方向的半球壳表面的磁通量的大小是： (A) Wb 2a R π(B) Wb 2b R π (C) Wb 2c R π(D) Wb 2abc R π[ B ]2. 若要使半径为4×103-m 的裸铜线表面的磁感应强度为7.0×105- T ，则铜线中需要通过的电流为(μ0=4π×107-T ·m ·A1-)(A) 0.14A (B) 1.4A (C) 14A (D) 28A[ B ]3. 一载有电流I 的细导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管(R=2r)，两螺线管单位长度上的匝数相等，两螺线管中的磁感应强度大小R B 和r B 应满足： (A) R B =2r B(B) R B =rB (C) 2R B =r B (D) R B R=4r B[ D ]4．如图，两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上，稳恒电流I 从a 端流入而从d 端流出，则磁感应强度B沿图中闭合路径L 的积分l B d ⋅⎰等于(A)I 0μ(B)I 031μ (C) I 041μ(D)I 032μ[ D ]5. 有一由N 匝细导线绕成的平面正三角形线圈，边长为a ，通有电流I ，置于均匀外磁场 B 中，当线圈平面的法向与外磁场同向时，该线圈所受的磁力矩mM(A) 2/32IB Na (B) 4/32IB Na (C) 0260sin 3IB Na (D) 0二 填空题1.一无限长载流直导线，通有电流I ，弯成如图形状，设各线段皆在纸面内，则P 点磁感应强度 B 的大小为aIπμ830。
3.半径为0.5cm 的无限长直圆柱形导体上，沿轴线方向均匀地流着I=3A 的电流，作一个半径r=5cm 、长l=5cm 且与电流同轴的圆柱形闭合曲面S ，则该曲面上的磁感应强度 B 沿曲面的⎰=⋅Sd s B _______0_________________________。
第14章 稳恒电流的磁场 参考答案一、选择题1(B)，2(A)，3(D)，4(C)，5(B)，6(D)，7(B)，8(C)，9(D)，10(A) 二、填空题(1). 最大磁力矩，磁矩 ; (2). πR 2c ； (3). )4/(0a I μ； (4).RIπ40μ ；(5). μ0i ，沿轴线方向朝右. ； (6). )2/(210R rI πμ， 0 ; (7). 4 ; (8).B I R2，沿y 轴正向； (9). ωλB R 3π，在图面中向上； (10). 正，负.三 计算题1. 将通有电流I 的导线在同一平面内弯成如图所示的形状，求D 点的磁感强度B的大小．解：其中3/4圆环在D 处的场 )8/(301a I B μ=AB 段在D 处的磁感强度 )221()]4/([02⋅π=b I B μBC 段在D 处的磁感强度)221()]4/([03⋅π=b I B μ1B、2B 、3B 方向相同，可知D 处总的B 为)223(40baI B +ππ=μ2. 半径为R 的导体球壳表面流有沿同一绕向均匀分布的面电流，通过垂直于电流方向的每单位长度的电流为K ．求球心处的磁感强度大小．解：如图θd d d KR s K I ==2/32220])cos ()sin [(2)sin (d d θθθμR R R I B +=32302d sin R KR θθμ=θθμd sin 2120K =⎰π=020d sin 21θθμK B ⎰π-=00d )2cos 1(41θθμK π=K 041μ3. 如图两共轴线圈，半径分别为R 1、R 2，电流为I 1、I 2．电流的方向相反，求轴线上相距中点O 为x 处的P 点的磁感强度． 解：取x 轴向右，那么有2/322112101])([2x b R I R B ++=μ 沿x 轴正方向 2/322222202])([2x b R I R B -+=μ 沿x 轴负方向21B B B -=[2μ=2/32211210])([x b R I R ++μ]])([2/32222220x b R I R -+-μ若B > 0，则B方向为沿x 轴正方向．若B < 0，则B的方向为沿x 轴负方向．4．一无限长圆柱形铜导体(磁导率μ0)，半径为R ，通有均匀分布的电流I ．今取一矩形平面S (长为1 m ，宽为2 R )，位置如右图中画斜线部分所示，求通过该矩形平面的磁通量．解：在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小，由安培环路定 律可得： )(220R r rRIB ≤π=μ因而，穿过导体内画斜线部分平面的磁通Φ1为⎰⎰⋅==S B S B d d 1 Φr r RI Rd 2020⎰π=μπ=40Iμ在圆形导体外，与导体中心轴线相距r 处的磁感强度大小为)(20R r rIB >π=μ因而，穿过导体外画斜线部分平面的磁通Φ2为⎰⋅=S Bd 2Φr r I R Rd 220⎰π=μ2ln 20π=I μ穿过整个矩形平面的磁通量 21ΦΦΦ+=π=40I μ2ln 20π+I μ5. 一半径为 4.0 cm 的圆环放在磁场中，磁场的方向对环而言是对称发散的，如图所示．圆环所在处的磁感强度的大小为0.10 T ，磁场的方向与环面法向成60°角．求当圆环中通有电流I =15.8 A 时，圆环所受磁力的大小和方向．1 m解：将电流元I d l 处的B分解为平行线圈平面的B 1和垂直线圈平面的B 2两分量，则 ︒=60sin 1B B ； ︒=60cos 2B B分别讨论线圈在B 1磁场和B 2磁场中所受的合力F 1与F 2．电流元受B 1的作用力l IB lB I F d 60sin 90sin d d 11︒=︒=方向平行圆环轴线．因为线圈上每一电流元受力方向相同，所以合力⎰=11d F F ⎰π︒=Rl IB 20d 60sin R IB π⋅︒=260sin = 0.34 N ，方向垂直环面向上．电流元受B 2的作用力l IB lB I F d 60cos 90sin d d 22︒=︒= 方向指向线圈平面中心． 由于轴对称，d F 2对整个线圈的合力为零，即02=F ． 所以圆环所受合力 34.01==F FN ， 方向垂直环面向上．6. 如图所示线框，铜线横截面积S = 2.0 mm 2，其中OA 和DO ＇两段保持水平不动，ABCD 段是边长为a 的正方形的三边，它可绕OO ＇轴无摩擦转动．整个导线放在匀强磁场B中，B 的方向竖直向上．已知铜的密度ρ = 8.9×103 kg/m 3，当铜线中的电流I =10 A 时，导线处于平衡状态，AB段和CD 段与竖直方向的夹角α =15°．求磁感强度B的大小．解：在平衡的情况下，必须满足线框的重力矩与线框所受的磁力矩平衡(对OO ＇轴而言)． 重力矩 αραρs i n s i n 2121gSa a a gS a M +⋅=αρsin 22g Sa =B 2d l磁力矩ααcos )21sin(222B Ia BIa M =-π=平衡时 21M M = 所以 αρsin 22g Sa αcos 2B Ia = 31035.9/tg 2-⨯≈=I g S B αρT7. 半径为R 的半圆线圈ACD 通有电流I 2，置于电流为I 1的无限长直线电流的磁场中，直线电流I 1恰过半圆的直径，两导线相互绝缘．求半圆线圈受到长直线电流I 1的磁力．解：长直导线在周围空间产生的磁场分布为 )2/(10r I B π=μ取xOy 坐标系如图，则在半圆线圈所在处各点产生的磁感强度大小为：θμsin 210R I B π=， 方向垂直纸面向里，式中θ 为场点至圆心的联线与y 轴的夹角．半圆线圈上d l 段线电流所受的力为：l B I B l I F d d d 22=⨯= θθμd sin 2210R R I I π=θsin d d F F y =． 根据对称性知： F y =0d =⎰y F θcos d d F F x = ，⎰π=0x x dF F ππ=2210I I μ2210I I μ=∴半圆线圈受I 1的磁力的大小为： 2210I I F μ=，方向：垂直I 1向右．I 2I 1A DC8. 如图所示．一块半导体样品的体积为a ×b ×c ．沿c 方向有电流I ，沿厚度a 边方向加有均匀外磁场B (B的方向和样品中电流密度方向垂直)．实验得出的数据为 a ＝0.10 cm 、b ＝0.35 cm 、c ＝1.0 cm 、I ＝1.0 mA 、B ＝3.0×10-1 T ，沿b 边两侧的电势差U ＝6.65 mV ，上表面电势高．(1) 问这半导体是p 型(正电荷导电)还是n 型(负电荷导电)？(2) 求载流子浓度n 0 (即单位体积内参加导电的带电粒子数)．解：(1) 根椐洛伦兹力公式：若为正电荷导电，则正电荷堆积在上表面，霍耳电场的方向由上指向下，故上表面电势高，可知是p 型半导体。
第十章 稳恒电流的磁场1、四条相互平行的无限长直载流导线，电流强度均为I ，如图放置，若正方形每边长为2a ，求正方形中心O 点的磁感应强度的大小和方向。
解：43210B B B B B r r r r r +++=无限长载流直导线产生的磁感应强度 rI2B 0πμ=由图中的矢量分析可得a 2I a 2I22B B 0042πμ=πμ=+a I45cos a2I 2B 0000πμ=⋅πμ= 方向水平向左2、把一根无限长直导线弯成图 (a)、(b) 所示形状，通以电流I ，分别求出O 点的磁感应强度B 的大小和方向。
解：（a ）（b ）均可看成由两个半无限长载流直导线1、3和圆弧2组成，且磁感应强度在O 点的方向相同 （a ）方向垂直纸面向外。
)38(R16I43R 4I R 4I R 4I B 00000π+πμ=π⋅πμ+πμ+πμ=（b ）由于O 点在电流1、3的延长线上，所以0B B 31==r r方向垂直纸面向外。
R8I323R I 4B B 0020μ=π⋅πμ==14（a ） I（b ）3、真空中有一边长为l 的正三角形导体框架，另有互相平行并与三角形的bc 边平行的长直导线1和2分别在a 点和b 点与三角形导体框架相连 (如图) 。
已知直导线中的电流为I ，求正三角形中心点O 处的磁感应强度B 。
解：三角形高为 l l360sin h .0==4 它在 θθπμ=θ=d sin R 2Isin dB dB 20x θθπμ−=θ−=d cos R2I cos dB dB 20yRI d sin R2I dB B 20200x x πμ=∫θθπμ∫==π0d cos R2I dB B 020y y =∫∫θθπμ−==π)T (1037.6100.10.5104RI B B 522720x P −−−×=××π××π=πμ==∴轴正方向。
x2 27－3 图中三棱柱面高 h ＝1.0m ，底面各边长分别为 ab=0.6m ，bc=0.4m ，ac=0.3m ，沿 ad第七章 稳 恒 磁 场7－1 两根无限长直导线相互垂直地放置在两正交平面内， 分别通有电流 I 1=2A ，I 2=3A ， 如图所示。
求点 M 1和 M 2处的磁感应强度。
图中 AM 1＝AM 2=lcm ，AB=2cm. 。
解： 无限长电流的磁感应强度为 B 0I ，两无限长2d 电流在点 M 1 和 M 2 处的磁感应强度相互垂直，合磁感 应强度为I I 25T B M 1 2 0I 102 ( I 12 I 23 ) 2 33 10 54 1＝4.47 10 B M 20I ( I 12 I 22 ) 2 10 54 9＝7.21 10 5T 2 10 2习题 7－ 1 图7－ 2一无限长的载流导线中部被弯成圆弧形，圆弧半径 R=3cm ，导线中的电流 I=2A ， 如图所示，求圆弧中心 O 点的磁感应强度。
解：两半无限长电流在 O 点产生的磁感应强度 方向相同，叠加为 B O1 2 0方向 ? O14 R 3/4圆电流在 O 点产生的磁感应强度为 B O23 0I4 2R 方向 O 点的合磁感应强度为B OBO1BO2-74 10-722 3 10 20.43 1.8 10-5 T 方向x2 2习题 7－3 图边有直长导线，导线申通有电流 I=4A 。
求通过 cbef 面的磁通量。
解 ：通过 cbef 面的磁通量应与通过 gbje 面的磁通量相当ag=ac=0.3m ，有＝B SdS0.6 0I0.32xhdx 0Ih ln 0.60.34 10 1ln2 5.54 10-7 Wbd j e7－4 两根平行直长导线载有电流 I 1=I 2=20A 。
试求（ 1）两导线所在平面内与两导线等 A 处的磁感应强度； （ 2）通过图中矩形面积的磁通量。
图中 r 1=r 3=10cm ，r2=20cm ，1）两半无限长电流在中点 A 点产生的磁感应强度方向相同，叠加为B A 2 2)＝ BS 0Il22.2 20 1 0220 1dS 300I 102 1 1 (1 x40x 30410-740-x-610)ldx x 0I220 25 10 224 10 204 10-5T方向?2 ln37－ 5 两个半径为 R 示， o 点是两环心 o1、o 2 的中点，求在两环心 o 1、o 2连线上离 强度。
