ansys中的Beam188单元中文说明
- 格式:doc
- 大小:221.92 KB
- 文档页数:12

梁的概况梁单元用于生成三维结构的一维理想化数学模型。
与实体单元和壳单元相比,梁单元可以效率更高的求解。
两种新的有限元应变单元,BEAM188和BEAM189,提供了更强大的非线性分析能力,更出色的截面数据定义功能和可视化特性。
参阅ANSYS Elements Reference中关于BEAM188和BEAM189的描述。
何为横截面?横截面定义为垂直于梁的轴向的截面形状。
ANSYS提供了有11种常用截面形状的梁横截面库,并支持用户自定义截面形状。
当定义了一个横截面时,ANSYS 建立一个9结点的数值模型来确定梁的截面特性(lyy,lzz等),并求解泊松方程得到弯曲特征。
横截面和用户自定义截面网格划分将存储在横截面库文件中。
可以用LATT命令将梁横截面属性赋给线实体。
这样,横截面的特性将在用BEAM188或BEAM189对该线划分网格时包含进去。
如何生成横截面用下列步骤生成横截面:1.定义截面并与代表相应截面形状的截面号关联。
2.定义截面的几何特性数值。
ANSYS中提供了下表列出的命令完成生成、查看、列表横截面和操作横截面库的功能:参阅ANSYS Commands Reference可以得到横截面命令的完整集合。
定义截面并与截面号关联使用SECTYPE命令定义截面。
下面的命令将截面号2与定义号的横截面形状(圆柱体)关联:命令:SECTYPE,2,BEAM,CSOLIDSECDATA,5,8SECNUM,2GUI: Main Menu>Preprocessor>Settings>-Beam-Common SectsMain Menu>Preprocessor>-Attributes-Define>Default Attribs要定义自己的横截面,使用子形状(ANSYS提供的形状集合)MESH。
要定义带特殊特性如lyy和lzz的横截面,使用子形状ASEC。
定义横截面的几何特性数值使用SECDATA命令定义横截面的几何数值。

关于BEAM188单元输出结果的说民(有的别的梁单元也通
用)
1.梁单元可以输出轴力X,三个方向弯矩,以及两个方向的剪力Y,Z
2.梁单元在计算前,要搞清楚这个单元自身的坐
标系。
根据单元说明,我自己翻译了下。
BEAM188单元有IJ连个节点构成。
一般认为单元X方向,是在XY平面内的。
但是如果单元X轴垂直于XY平面,那么,就认为单元Y轴与整体坐标系Y轴平行。
根据右手定则来定义方向的正负。
对于弯矩,比如MX,右手握拳状,大拇指指向x方向,四指就是弯矩方向,当然要分清大拇指指向x正向还是负向。
这个坐标系依然是单元的坐标系。
不是整体坐标系。
一定要记住。
弯矩就是绕坐标轴转动的。
AFORCE。

ansys命令流中文说明KB、KE: 待划分线的定向关键点起始、终止号SECNUM: 截面类型号u SECPLOT,SECID,MESHKEY 画梁截面的几何形状及网格划分SECID:由SECTYPE命令分配的截面编号MESHKEY:0:不显示网格划分1:显示网格划分u /ESHAPE, SCALE 按看似固体化分的形式显示线、面单元SCALE: 0:简单显示线、面单元1:使用实常数显示单元形状u esurf, xnode, tlab, shape 在已存在的选中单元的自由表面覆盖产生单元xnode: 仅为产生surf151 或surf152单元时使用tlab: 仅用来生成接触元或目标元top 产生单元且法线方向与所覆盖的单元相同,仅对梁或壳有效,对实体单元无效Bottom产生单元且法线方向与所覆盖的单元相反,仅对梁或壳有效,对实体单元无效Reverse 将已产生单元反向Shape: 空与所覆盖单元形状相同Tri 产生三角形表面的目标元注意:选中的单元是由所选节点决定的,而不是选单元,如同将压力加在节点上而不是单元上u Nummrg,label,toler, Gtoler,action,switch 合并相同位置的itemlabel: 要合并的项目node: 节点, Elem,单元,kp: 关键点(也合并线,面及点)mat: 材料,type: 单元类型,Real: 实常数cp:耦合项,CE:约束项,CE: 约束方程,All:所有项toler: 公差Gtoler:实体公差Action: sele 仅选择不合并空合并switch: 较低号还是较高号被保留(low, high)注意:可以先选择一部分项目,再执行合并。
如果多次发生合并命令,一定要先合并节点,再合并关键点。
合并节点后,实体荷载不能转化到单元,此时可合并关键点解决问题。
u Lsel, type, item, comp, vmin, vmax, vinc, kswp 选择线type: s 从全部线中选一组线r 从当前选中线中选一组线a 再选一部线附加给当前选中组aunoneu(unselect)inve: 反向选择item: line 线号loc 坐标length 线长comp: x,y,zkswp: 0 只选线1 选择线及相关关键点、节点和单元u Nsel, type, item, comp, vmin, vmax, vinc, kabs 选择一组节点为下一步做准备Type: S: 选择一组新节点(缺省)R: 在当前组中再选择A: 再选一组附加于当前组U: 在当前组中不选一部分All: 恢复为选中所有None: 全不选Inve: 反向选择Stat: 显示当前选择状态Item: loc: 坐标node: 节点号Comp: 分量Vmin,vmax,vinc: ITEM范围Kabs: “0” 使用正负号“1”仅用绝对值u NSLL,type, nkey 选择与所选线相联系的节点u nsla, type, nkey: 选择与选中面相关的节点type:s 选一套新节点r 从已选节点中再选a 附加一部分节点到已选节点u 从已选节点中去除一部分nkey: 0 仅选面内的节点1 选所有和面相联系的节点(如面内线,关键点处的节点)u esel, type, item, comp, vmin, vmax, vinc, kabs 选择一组单元Type: S: 选择一组单元(缺省)R: 在当前组中再选一部分作为一组A: 为当前组附加单元U: 在当前组中不选一部分单元All: 选所有单元None: 全不选Inve: 反向选择当前组(?)Stat: 显示当前选择状态Item: Elem: 单元号Type: 单元类型号Mat: 材料号Real: 实常数号Esys: 单元坐标系号u ALLSEL, LABT, ENTITY 选中所有项目LABT: ALL: 选所有项目及其低级项目BELOW: 选指定项目的直接下属及更低级项目ENTITY: ALL: 所有项目(缺省)VOLU:体高级AREA:面LINE :线KP:关键点ELEM:单元NODE:节点低级u Tshap,shape 定义接触目标面为2D、3D的简单图形Shape: line:直线Arc:顺时针弧Tria:3点三角形Quad:4点四边形………….2.6 根据需要耦合某些节点自由度u cp, nset, lab,,node1,node2,……node17nset: 耦合组编号lab: ux,uy,uz,rotx,roty,rotznode1-node17: 待耦合的节点号。

Beam188/189单元基于Timoshenko梁理论(一阶剪切变形理论:横向剪切应变在横截面上是常数,也就是说,变形后的横截面保持平面不发生扭曲)而开发的,并考虑了剪切变形的影响,适合于分析从细长到中等粗细的梁结构。
该单元提供了无约束和有约束的横截面的翘曲选项。
Beam188是一种3D线性、二次或三次的2节点梁单元。
Beam189是一种3D二次3节点梁单元。
每个节点有六个或者七个自由度,包括x、y、z 方向的平动自由度和绕x、y、z 轴的转动自由度,还有一个可选择的翘曲自由度。
该单元非常适合线性、大角度转动或大应变非线性问题。
beam188的应力刚化选项在任何大挠度分析中都是缺省打开的,从而可以分析弯曲、横向及扭转稳定问题(进行特征值屈曲分析或(采用弧长法或非线性稳定法)破坏研究)。
Beam188/beam189单元支持弹性、塑性,蠕变及其他非线性材料模型。
这种单元还可以采用多种材料组成的截面。
该单元还支持横向剪力和横向剪应变的弹性关系,但不能使用高阶理论证明剪应力的分布变化。
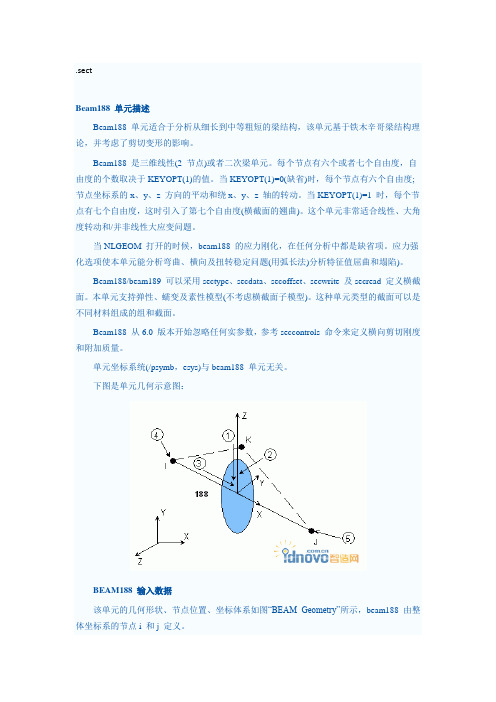
下图是单元几何示意图:该单元的几何形状、节点位置、坐标体系和压力方向如图所示,beam188 由整体坐标系的节点i 和j 定义。
对于Beam188梁单元,当采用默认的KEYOPT(3)=0,则采用线性的形函数,沿着长度用了一个积分点,因此,单元求解量沿长度保持不变;当KEYOPT(3)=2,该单元就生成一个内插节点,并采用二次形函数,沿长度用了两个积分点,单元求解量沿长度线性变化;当KEYOPT(3)=3,该单元就生成两个内节点,并采用三次形函数,沿长度用了三个积分点,单元求解量沿长度二次变化;当在下面情况下需要考虑高阶单元内插时,推荐二次和三次选项:1)变截面的单元;2)单元内存在非均布荷载(包含梯形荷载)时,三次形函数选项比二次选项提供更好的结果。
(对于局部的分布荷载和非节点集中荷载情况,只有三次选项有效);3)单元可能承受高度不均匀变形时。

Beam188/189单元基于Timoshenko梁理论(一阶剪切变形理论:横向剪切应变在横截面上是常数,也就是说,变形后的横截面保持平面不发生扭曲)而开发的,并考虑了剪切变形的影响,适合于分析从细长到中等粗细的梁结构。
该单元提供了无约束和有约束的横截面的翘曲选项。
Beam188是一种3D线性、二次或三次的2节点梁单元。
Beam189是一种3D二次3节点梁单元。
每个节点有六个或者七个自由度,包括x、y、z 方向的平动自由度和绕x、y、z 轴的转动自由度,还有一个可选择的翘曲自由度。
该单元非常适合线性、大角度转动或大应变非线性问题。
beam188的应力刚化选项在任何大挠度分析中都是缺省打开的,从而可以分析弯曲、横向及扭转稳定问题(进行特征值屈曲分析或(采用弧长法或非线性稳定法)破坏研究)。
Beam188/beam189单元支持弹性、塑性,蠕变及其他非线性材料模型。
这种单元还可以采用多种材料组成的截面。
该单元还支持横向剪力和横向剪应变的弹性关系,但不能使用高阶理论证明剪应力的分布变化。
下图是单元几何示意图:该单元的几何形状、节点位置、坐标体系和压力方向如图所示,beam188 由整体坐标系的节点i 和j 定义。
对于Beam188梁单元,当采用默认的KEYOPT(3)=0,则采用线性的形函数,沿着长度用了一个积分点,因此,单元求解量沿长度保持不变;当KEYOPT(3)=2,该单元就生成一个内插节点,并采用二次形函数,沿长度用了两个积分点,单元求解量沿长度线性变化;当KEYOPT(3)=3,该单元就生成两个内节点,并采用三次形函数,沿长度用了三个积分点,单元求解量沿长度二次变化;当在下面情况下需要考虑高阶单元内插时,推荐二次和三次选项:1)变截面的单元;2)单元内存在非均布荷载(包含梯形荷载)时,三次形函数选项比二次选项提供更好的结果。
(对于局部的分布荷载和非节点集中荷载情况,只有三次选项有效);3)单元可能承受高度不均匀变形时。

Release 10.0 Documentation for ANSYSBEAM1883—D Linear Finite Strain Beam三维线性有限应变梁单元BEAM188 Element DescriptionBEAM188单元描述BEAM188 is suitable for analyzing slender to moderately stubby/thick beam structures. This element is based on Timoshenko beam theory。
Shear deformation effects are included。
Beam188 单元适合于分析从细长到中等粗短的梁结构,该单元基于铁木辛哥梁结构理论,并考虑了剪切变形的影响。
BEAM188 is a linear (2—node) or a quadratic beam element in 3—D。
BEAM188 has sixor seven degrees of freedom at each node, with the number of degrees of freedom dependingon the value of KEYOPT(1). When KEYOPT(1) = 0 (the default), six degrees of freedomoccur at each node. These include translations in the x, y, and z directions and rotationsabout the x, y, and z directions。
When KEYOPT(1) = 1, a seventh degree of freedom(warping magnitude) is also considered。


ansys杆、梁和管单元讲解(1)杆单元,适用于弹簧、螺杆、预应力螺杆和薄膜桁架等,常用的杆单元有LINK8/LINK11/LINK180.LINK180:三维杆单元,根据各种情况可以看作桁架单元、索单元、链杆单元或弹簧单元等,本单元是一个轴向拉伸---压缩单元,每个节点有三个自由度:节点坐标系的X、Y、Z方向的平动。
本单元是一种顶端铰链结构,不考虑单元弯曲。
本单元具有塑性、蠕变、旋转、大变形和大应变功能。
当考虑大变形时(NLGEOM,ON)任何分析中LINK180单元都包括应力刚化选项。
本单元支持弹性、各向同性强化塑性、随动强化塑性、Hill各向异性强化、Chaboche 非线性强化塑性和蠕变。
LINK10与之类似仅压缩或仅拉伸。
输入参数:节点:I,J 自由度:UX、UY、UZ 实常数:AREA为面积,ADDMAS质量,TENSKEY 拉压选项,0为可以受拉压,1为只受拉,-1为只受压。
材料属性:EX,(PRXY或NUXY),ALPX(CTEX或THSX),DENS,GXY,ALPD,BETD 面载荷:无体载荷:温度T(I)、T(J)特殊属性:单元生死、初始状态、大挠度、大应变、线性扰动、非线性稳定、塑性、应力刚化、用户自定义材料、粘弹性、粘弹性/蠕变、(2)梁单元,用于螺栓(杆)、薄壁管件,C形截面构建,角钢或狭长薄膜构建(只有膜应力和弯应力)梁单元有弹性梁、塑性梁、渐变不对称梁、薄壁梁等,此处介绍BEAM188BEAM188:三维线性有限应变梁单元,适用于分析从细长到中等短粗的梁结构,基于铁木辛哥梁结构理论,考虑了剪切变形的影响。
BEAM188是三维线性(2节点)或者二次梁单元。
每个节点有6或者7个自由度,自由度的个数取决与KEYOPT(1)=0(默认),每个节点有6个自由度,即节点坐标系的X,Y,Z方向的平动和绕X,Y,Z轴的转动,当KEYOPT(1)=1时,7个自由度,引入横截面的翘曲。

BEAM188中文说明BEAM188 —3-D 线性有限应变梁(基于Ansys 5.61的help)MP ME ST PR PP ED元素描述BEAM188 适用于分析细长的梁。
元素是基于Timoshenko 梁理论的。
具有扭切变形效果。
BEAM188 是一个二节点的三维线性梁。
BEAM188 在每个节点上有6或7个自由度,(自由度)数目的变化是由KEYOPT(1)来控制的。
当 KEYOPT(1) = 0时 (默认), 每节点有6个自由度。
分别是沿x,y,z的位移及绕其的转动。
当 KEYOPT(1) = 1时,会添加第七个自由度 (翘曲量) 。
此元素能很好的应用于线性(分析),大偏转,大应力的非线性(分析)。
BEAM188包含应力刚度,在默认情况下,在某些分析中由NLGEOM来打开。
在进行弯曲( flexural),侧向弯曲( lateral), 和扭转稳定性( torsional stability)分析时,应力刚度应该是被打开的。
BEAM188 能够采用SECTYPE, SECDATA, SECOFFSET, SECWRITE,和SECREAD来定义任何截面(形状)。
. 弹性(elasticity),蠕变( creep),和塑性( plasticity)模型都是允许的 (不考虑次截面形状)。
图1. BEAM188 3-D 线性有限应变梁输入数据(元素的)几何形状,节点为止,即元素坐标系图示于BEAM188。
BEAM188在模型坐标系中是由节点 I 和节点 J 来定义的。
节点 K 是必需的元素方向点定义。
有关方向点的相关信息详见Generating a Beam Mesh With Orientation Nodes 在ANSYS Modeling and Meshing Guide中。
于LMESH和LATT命令说明中可见节点 K 的自动定义的详细说明。
在空间中这是一个没有量纲的元素。
截面形状是用SECTYPE和SECDATA命令(详见ANSYS Commands Reference )来独立定宓摹C恳桓鼋孛嫘巫淳囟ㄒ桓?ID 号(SECNUM)。
.sectBeam188 单元描述Beam188 单元适合于分析从细长到中等粗短的梁结构,该单元基于铁木辛哥梁结构理论,并考虑了剪切变形的影响。
Beam188 是三维线性(2 节点)或者二次梁单元。
每个节点有六个或者七个自由度,自由度的个数取决于KEYOPT(1)的值。
当KEYOPT(1)=0(缺省)时,每个节点有六个自由度;节点坐标系的x、y、z 方向的平动和绕x、y、z 轴的转动。
当KEYOPT(1)=1 时,每个节点有七个自由度,这时引入了第七个自由度(横截面的翘曲)。
这个单元非常适合线性、大角度转动和/并非线性大应变问题。
当NLGEOM 打开的时候,beam188 的应力刚化,在任何分析中都是缺省项。
应力强化选项使本单元能分析弯曲、横向及扭转稳定问题(用弧长法)分析特征值屈曲和塌陷)。
Beam188/beam189 可以采用sectype、secdata、secoffset、secwrite 及secread 定义横截面。
本单元支持弹性、蠕变及素性模型(不考虑横截面子模型)。
这种单元类型的截面可以是不同材料组成的组和截面。
Beam188 从6.0 版本开始忽略任何实参数,参考seccontrols 命令来定义横向剪切刚度和附加质量。
单元坐标系统(/psymb,esys)与beam188 单元无关。
下图是单元几何示意图:BEAM188 输入数据该单元的几何形状、节点位置、坐标体系如图“BEAM Geometry”所示,beam188 由整体坐标系的节点i 和j 定义。
节点K 是定义单元方向的所选方式,有关方向节点和梁的网格划分的信息可以参见A NSYS Modeling and Meshing Guide中的Generating a Beam Mesh With Orientation Node s。
参考lmesh 和latt 命令描述可以得到k 节点自动生成的详细资料。
Beam188 可以在没有方向节点的情况下被定义。


BEAM188中文说明BEAM188 — 3-D 线性有限应变梁(基于Ansys 5.61的help)MP ME ST PR PP ED元素描述BEAM188 适用于分析细长的梁。
元素是基于Timoshenko 梁理论的。
具有扭切变形效果。
BEAM188 是一个二节点的三维线性梁。
BEAM188 在每个节点上有6或7个自由度,(自由度)数目的变化是由KEYOPT(1)来控制的。
当KEYOPT(1) = 0时(默认), 每节点有6个自由度。
分别是沿x,y,z的位移及绕其的转动。
当KEYOPT(1) = 1时,会添加第七个自由度(翘曲量) 。
此元素能很好的应用于线性(分析),大偏转,大应力的非线性(分析)。
BEAM188包含应力刚度,在默认情况下,在某些分析中由NLGEOM来打开。
在进行弯曲(flexural),侧向弯曲(lateral), 和扭转稳定性(torsional stability)分析时,应力刚度应该是被打开的。
BEAM188 能够采用SECTYPE, SECDATA, SECOFFSET, SECWRITE,和SECREAD来定义任何截面(形状)。
. 弹性(elasticity),蠕变(creep),和塑性(plasticity)模型都是允许的(不考虑次截面形状)。
图1. BEAM188 3-D 线性有限应变梁输入数据(元素的)几何形状,节点为止,即元素坐标系图示于BEAM188。
BEAM188在模型坐标系中是由节点I 和节点J 来定义的。
节点K 是必需的元素方向点定义。
有关方向点的相关信息详见Generating a Beam Mesh With Orientation Nodes在ANSYS Modeling and Meshing Guide中。
于LMESH和LATT命令说明中可见节点K 的自动定义的详细说明。
在空间中这是一个没有量纲的元素。
截面形状是用SECTYPE和SECDATA命令(详见ANSYS Commands Reference )来独立定宓摹C恳桓鼋孛嫘巫淳囟ㄒ桓?ID 号(SECNUM)。

ANSYS使用心得BEAM188单元应力时程数据提取方法在ANSYS中,BEAM188单元是用来模拟横截面有限厚度的梁的单元类型。
在实际工程中,我们经常需要知道梁在不同时间点的应力情况,以了解其受力情况。
本文将介绍一种基于APDL命令的方法,用来提取BEAM188单元的应力时程数据。
首先,我们需要在ANSYS中建立梁的有限元模型,并设置好相应的边界条件和加载。
在这个过程中,我们需要注意梁的材料性质、几何尺寸以及加载方式等,这些都会影响到最终的应力分布。
在模型建立完成后,我们需要运行一个静态分析,以得到梁的静态应力。
在ANSYS中,我们可以使用“SOLU”命令来进行静态分析。
在静态分析完成后,我们可以使用以下命令来查看梁的应力分布:```*VWRITE, beam_stress, BEAM, 1, S, LOC, RANGE```其中,beam_stress是一个后处理变量名,用来存储梁的应力数据,BEAM表示只计算梁单元的应力,1表示第一组单元,S表示计算应力场,LOC表示输出位置信息,RANGE表示输出的范围。
通过运行上述命令,我们可以得到梁在不同位置的应力数据。
为了得到不同时间点的应力数据,我们需要使用ANSYS的时程分析功能。
假设我们需要在1秒、2秒和3秒时刻的应力数据,我们可以按照以下步骤进行操作:1.使用“TIME”命令来设置分析的总时间和时间步长。
在这个例子中,我们设置总时间为3秒,步长为1秒。
2.使用“NLSTEP”命令来指定非线性分析的步数。
由于我们只需要在1秒、2秒和3秒时刻的应力数据,所以我们设置步数为33.使用“SOLVE”命令来运行时程分析。
4.运行静态分析的命令来保存每个时间步的应力数据。
我们可以使用如下的APDL命令来保存每个时间步的应力数据:```*VWRITE, beam_stress_1s, BEAM, 1, S, LOC, AT, 1*VWRITE, beam_stress_2s, BEAM, 1, S, LOC, AT, 2*VWRITE, beam_stress_3s, BEAM, 1, S, LOC, AT, 3```以上命令中,beam_stress_1s、beam_stress_2s和beam_stress_3s是用来分别保存1秒、2秒和3秒时刻的应力数据的后处理变量名。

第七章练习3.钢架结构有限元分析。
单元类型:BEAM188。
1.定义文件名Utility Menu→File→Change Jobname…2.定义单元类型⑴设置分析类型:Main Menu→Preferences,→Structural。
⑵定义单元类型:Main Menu→Preprocessor→Element Type→Add/Edit/Delete,BEAM188。
3.定义材料力学参数Main Menu→Preprocessor→Material Props→Material Models,Structural→Linear→Elastic→Isotropic,弹性模量EX=2.1e5(N/mm2即MPa),泊松比PRXY=0.3。
4.定义BEAM188截面形状Main Menu:Preprocessor→Sections→Beam→Common Sectns,使ID=1,Name=S1,在Sub-Type中选择匚(槽形)截面形状。
按所给截面参数输入W1、W2、W3、t1、t2、t3。
截面单元网格精度:coarse即0。
5.创建几何模型⑴Main Menu:Preprocessor→Modeling→Create→Keypoints→In Actice CS,定义关键点1(0,0,0),2(0,1000,0),3(1200,1000,0),4(1200,0,0) 。
打开关键点号及线号:Utility Menu→PlotCtrls→Numbering,KP= On;LINK=On。
⑵Main Menu:Preprocessor→Modeling→Create→Lines→Straight Line,连接点1-2,2-3,3-4,生成三条线。
⑶Main Menu:Preprocessor→Modeling→Copy→Lines,沿Z正向拷贝上面三条线,ITIME=2,DZ=800。
⑷Main Menu:Preprocessor→Modeling→Create→Lines→Straight Line,连接点2—6,3—7,生成二条线。

ANSYS中BEAM188的使用方法1.创建几何模型:首先,在ANSYS中创建几何模型。
这可以通过使用ANSYS的几何设计工具或导入外部CAD文件来完成。
确保模型的尺寸和形状符合实际情况,并且需要考虑到适当的边界条件。
2.定义材料属性:在使用BEAM188元素之前,需要为梁材料定义适当的材料属性。
这些属性可以包括弹性模量、泊松比和密度等。
3.划分网格:应用BEAM188元素之前,需要对几何模型进行网格化。
使用ANSYS的网格划分工具,如Meshing,来划分合适的网格。
确保梁的划分足够细致以获得准确的结果。
4.定义截面属性:对于每个梁段,需要定义横截面的几何属性。
这包括梁截面的宽度、高度以及其他几何参数,如惯性矩等。
这些参数可以通过实验或计算获得。
5.定义边界条件:在模拟过程中,必须为梁结构定义适当的边界条件。
这包括约束和加载条件。
约束可以是固定端、铰接端或其他约束类型。
加载条件可以是点载荷、均布载荷或其他载荷。
6.定义材料非线性性质(如果适用):如果所模拟的材料具有非线性属性,如应力-应变曲线的非线性,在此步骤中需要定义这些属性以获得准确的结果。
7.定义分析类型:根据所需的分析类型,选择适当的分析类型,如静力分析、动力分析或稳态热传导分析等。
确保正确设置分析参数和求解选项。
8.指定BEAM188元素类型:在ANSYS中,BEAM188元素需要明确地指定为杆单元类型。
使用ANSYS的ELEMENTTYPE命令以及对应的单元类型编号来指定BEAM188元素。
9.定义杆单元属性:在ANSYS中,BEAM188元素具有多个属性,如截面属性、杆单元的长度、杆单元的方向等。
使用ANSYS的REALCONSTANT命令定义这些属性。
10.获取结果:设置求解选项后,使用ANSYS的求解器来解决模型。
求解过程可能需要一定的时间,具体取决于模型的复杂性和计算机性能。
完成求解后,可以使用ANSYS的后处理工具来查看和分析结果。

Beam1883 维线性有限应变梁单元Beam188 单元描述Beam188 单元适合于分析从细长到中等粗短的梁结构,该单元基于铁木辛哥梁结构理论,并考虑了剪切变形的影响。
Beam188 是三维线性(2 节点)或者二次梁单元。
每个节点有六个或者七个自由度,自由度的个数取决于KEYOPT(1)的值。
当KEYOPT(1)=0(缺省)时,每个节点有六个自由度;节点坐标系的x、y、z 方向的平动和绕x、y、z 轴的转动。
当KEYOPT(1)=1 时,每个节点有七个自由度,这时引入了第七个自由度(横截面的翘曲)。
这个单元非常适合线性、大角度转动和/并非线性大应变问题。
当NLGEOM 打开的时候,beam188 的应力刚化,在任何分析中都是缺省项。
应力强化选项使本单元能分析弯曲、横向及扭转稳定问题(用弧长法)分析特征值屈曲和塌陷)。
Beam188/beam189 可以采用sectype、secdata、secoffset、secwrite 及secread 定义横截面。
本单元支持弹性、蠕变及素性模型(不考虑横截面子模型)。
这种单元类型的截面可以是不同材料组成的组和截面。
Beam188 从6.0 版本开始忽略任何实参数,参考seccontrols 命令来定义横向剪切刚度和附加质量。
单元坐标系统(/psymb,esys)与beam188 单元无关。
下图是单元几何示意图:BEAM188 输入数据该单元的几何形状、节点位置、坐标体系如图“BEAM Geometry”所示,beam188 由整体坐标系的节点i 和j 定义。
节点K 是定义单元方向的所选方式,有关方向节点和梁的网格划分的信息可以参见ANSYS Modeling and Meshing Guide中的Generating a Beam Mesh With Orientation Nodes。
参考lmesh 和latt 命令描述可以得到k 节点自动生成的详细资料。

BEAM188中文说明BEAM188—3-D 线性有限应变梁(基于Ansys 的help)MP ME ST PR PP ED元素描述BEAM188 适用于分析细长的梁。
元素是基于Timoshenko 梁理论的。
具有扭切变形效果。
BEAM188 是一个二节点的三维线性梁。
BEAM188 在每个节点上有6或7个自由度,(自由度)数目的变化是由KEYOPT(1)来控制的。
当KEYOPT(1) = 0时(默认), 每节点有6个自由度。
分别是沿x,y,z的位移及绕其的转动。
当KEYOPT(1) = 1时,会添加第七个自由度(翘曲量) 。
此元素能很好的应用于线性(分析),大偏转,大应力的非线性(分析)。
BEAM188包含应力刚度,在默认情况下,在某些分析中由NLGEOM来打开。
在进行弯曲(flexural),侧向弯曲(lateral), 和扭转稳定性(torsional stability)分析时,应力刚度应该是被打开的。
BEAM188 能够采用SECTYPE, SECDATA, SECOFFSET, SECWRITE,和SECREAD来定义任何截面(形状)。
. 弹性(elasticity),蠕变(creep),和塑性(plasticity)模型都是允许的(不考虑次截面形状)。
图1. BEAM188 3-D 线性有限应变梁输入数据(元素的)几何形状,节点为止,即元素坐标系图示于BEAM188。
BEAM188在模型坐标系中是由节点I 和节点J 来定义的。
节点K 是必需的元素方向点定义。
有关方向点的相关信息详见Generating a Beam Mesh With Orientation Nodes在ANSYS Modeling and Meshing Guide中。
于LMESH和LATT命令说明中可见节点K 的自动定义的详细说明。
在空间中这是一个没有量纲的元素。
截面形状是用SECTYPE和SECDATA命令(详见ANSYS Commands Reference )来独立定宓摹C恳桓鼋孛嫘巫淳囟ㄒ桓ID 号(SECNUM)。

ANSYS杆单元,梁单元简介ANSYS中提供的杆单元简介LINK1二维杆单元,应用于平面桁架,杆件,弹簧等结构,承受轴向的拉力和压力,不考虑弯矩,每个节点具有X和Y位移方向的两个自由度,单元不能承受弯矩,只用于铰链结构应力沿单元均匀分布。
具体应用时存在如下假设和限制:1.杆件假设为均质直杆,在其端点受轴向载荷。
2.杆长应大于0,即节点i,j不能重合3.杆件必须位于x-y平面且横截面积要大于04.温度沿杆长方向线性变化5.位移函数的设置使得杆件内部的应力为均匀分布6.初始应变也参与应力刚度矩阵的计算LINK8三维杆单元,应用于空间桁架,是LINK2的三维情况,用来模拟桁架,缆索,连杆,弹簧等,这种三维杆单元是杆轴方向的拉压单元,每个节点有三个自由度,即沿节点坐标系x,y,z,方向的平动,就像在铰链结构中表现的一样,本单元不承受弯矩。
本单元具有塑性,蠕变,膨胀、应力刚化、大变形和大应变等功能。
具体应用时存在如下假设和限制:1.杆单元假定为直杆,轴向载荷作用在末端,自杆的一端至另一端均为统一属性2.杆长应大于0,即节点i,j不能重合3.横截面积要大于04.温度沿杆长方向线性变化5.位移函数暗含着在杆上有相同的应力6.即便是对于第一次累计迭代,初始应变也被用来计算应力刚度矩阵LINK10 三维仅受压或仅受拉杆单元,应用于悬索,它具有独一无二的双线性刚度矩阵特性,使用只受拉选项时,如果单元受压,刚度就消失,以此来模拟缆索的松弛或是链条的松弛,这一特性对于整个钢缆用一个单元来模拟的钢缆静力问题非常有用,当需要松弛单元的性能,而不关心松弛单元的运动时,他也可用于动力分析(带有惯性和阻尼效应)。
如果分析的目的是研究单元的运动(没有松弛单元),那那么应该使用类似于LINK10的不能松弛的单元,如LINK8或PIPE59。
对于最终收敛结果是紧绷状态的结构,如果迭代过程中可能出现松弛状态,那么这种静力收敛问题也不能使用LINK10单元。
BEAM188中文说明BEAM188 — 3-D 线性有限应变梁(基于Ansys 5.61的help)MP ME ST PR PP ED元素描述BEAM188 适用于分析细长的梁。
元素是基于Timoshenko 梁理论的。
具有扭切变形效果。
BEAM188 是一个二节点的三维线性梁。
BEAM188 在每个节点上有6或7个自由度,(自由度)数目的变化是由KEYOPT(1)来控制的。
当KEYOPT(1) = 0时(默认), 每节点有6个自由度。
分别是沿x,y,z的位移及绕其的转动。
当KEYOPT(1) = 1时,会添加第七个自由度(翘曲量) 。
此元素能很好的应用于线性(分析),大偏转,大应力的非线性(分析)。
BEAM188包含应力刚度,在默认情况下,在某些分析中由NLGEOM来打开。
在进行弯曲(flexural),侧向弯曲(lateral), 和扭转稳定性(torsional stability)分析时,应力刚度应该是被打开的。
BEAM188 能够采用SECTYPE, SECDATA, SECOFFSET, SECWRITE,和SECREAD来定义任何截面(形状)。
. 弹性(elasticity),蠕变(creep),和塑性(plasticity)模型都是允许的(不考虑次截面形状)。
图1. BEAM188 3-D 线性有限应变梁输入数据(元素的)几何形状,节点为止,即元素坐标系图示于BEAM188。
BEAM188在模型坐标系中是由节点I 和节点J 来定义的。
节点K 是必需的元素方向点定义。
有关方向点的相关信息详见Generating a Beam Mesh With Orientation Nodes在ANSYS Modeling and Meshing Guide中。
于LMESH和LATT命令说明中可见节点K 的自动定义的详细说明。
在空间中这是一个没有量纲的元素。
截面形状是用SECTYPE和SECDATA命令(详见ANSYS Commands Reference )来独立定宓摹C恳桓鼋孛嫘巫淳囟ㄒ桓?ID 号(SECNUM)。
截面号是特定的元素属性。
梁元素是基于Timoshenko 梁理论的,这是一个一阶切应变理论:横向切应变在截面中是常量;也就是说截面在变形后仍是平面。
BEAM188是一阶Timoshenko 梁元素,它用一个点在长度上来(代替截面)。
应此当在节点I 和J 上使用SMISC参数的话会显示每个端点节点的形心。
BEAM188 能被用于细长(slender)或粗壮(stout???)的梁。
因为一阶切应变理论的限制,自有适当厚度的梁能被分析。
梁结构上的细长比(GAL2/(EI)) 能够用来判断是否采用此元素:G切变模数A截面面积L构件长度EI弯曲刚度在整体(偏移)距离而不是单个元素的情况下记录这个比值是重要的。
悬臂梁受向下的负载提供了悬臂梁在受向下的负载的情况下横向切应变的一个估评。
虽然这个结果不能外推到所有的情况,但可以作为一个指导。
我们推荐细长比应大于30 。
图2. 悬臂梁受向下的负载细长比(GAL2/(EI)>30)Timoshenko/向剪切刚度。
扭转变形的St. Venant 翘曲决定了一个综合状态,它可以使(材料)在屈服后的切应力变得平均。
ANSYS 不提供对横截面或可能出现塑性屈服的横截面上的扭切分布情况的换算。
应此因扭转负载而引起的大的非弹性的变形应当进行讨论,(ansys)也会检查并给处警告。
在这种情况下推荐用实体或壳模型来代替。
在默认情况下BEAM188 元素假设横截面上的弯曲很小可以被忽略(KEYOPT(1) = 0)。
你可以使用KEYOPT(1) = 1来打开弯曲度的自由度。
如果此自由度被打开那每个节点会有7个自由度:UX, UY, UZ, ROTX, ROTY, ROTZ, 和WARP。
BEAM188 允许用一个轴向延伸率的函数来改变横截面的转动惯量。
默认情况下元素横截面的面积可以改变,但元素的体积在变形前后是相同的。
此默认同样适用于elasto-plastic 情况。
使用KEYOPT(2), 你能使横截面面积为一个常量或保持不变。
元素的输出在元素的积分位置和横截面的积分点上都是有效的。
梁在长度方向的积分点(高斯点)如(图)积分位置所示。
Figure 3. 3-D 线性有限应变梁元素的积分位置截面的应力与力(包含弯矩)都是在积分点上获得的。
元素基本点的输出会外推到元素的节点。
BEAM188 的一些剖面关联量(面积的积分,位置,泊松比函数,函数的导数等等) ,在使用SECTYPE和SECDATA命令定义截面时会自动分配到一个序列号。
每一个截面区域预定为由9个节点组成。
相交区域模型举例说明矩形块和槽形块的模型情况。
每个单元有4个积分点。
Figure 4. BEAM188 相交区域模型BEAM188 提供剖面积分点和节点的结果输出。
但你仅能查看边界上的输出。
(PRSSOL打印BEAM188 剖面节点和积分点的解。
应力和应变是在节点上的,塑性应力,塑性功,潜变应变则是在积分点上。
)当元素的材料具有非线性状态或有通过剖面的温度时,计算是在积分点上进行的。
在大量通用弹性应用中],元素采用剖面积分点的pre-calculated 特性。
应此,应力与应变的输出均是经过了积分点的计算的。
如果截面分配了次截面ASEC, 那么只有一般性的应力与应变(轴向力, 弯矩, 切向应变, (弯曲)曲率, 和切应力)能够输出。
3-D 的轮廓图和变形显示图是不可用的。
ASEC 次截面只能被作为一个薄矩形块来显示验证梁的方向。
质量矩阵与负载向量的相容性的评估,相对于使用的刚度矩阵来说是一个高阶积分。
元素提供包含相容性与集中的质量初矩阵。
使LUMPM,ON 可以让质量矩阵(质量)集中。
(系统)默认使用相容性矩阵。
单位长度的质量可以用ADDMAS 作为实常量来输入。
详见输入概述。
力是相加在节点上的(定义在元素主方向)。
如果形心轴不与元素主方向重合,那么附加的轴向力会引起弯曲。
(同样)如果形心和扭转中心不重合的话,扭转力也会引起扭转变形和扭矩。
应次节点的定位应当与力的中心向重合。
使用SECOFFSET命令可以适当的改变OFFSETY和OFFSETZ 的幅角。
默认情况下ANSYS 用形心来定义元素的主轴。
在节点和元素负载中有元素负载的描述。
压力是作为一种面负载来作用在元素表面上的,(元素的面可见)图BEAM188.中带圈文字的显示。
正向压力一压力(常规形式)输入。
侧向压力以单位长度上的力来输入。
尾端压力以力(的形式)输入。
BEAM188 与ansys中的其他基于埃尔米特多项式(Hermitian polynomial)的元素(f比如说BEAM4).不同,它是基于线性多项式(linear polynomials)的。
因此分布式(周延式)负载的偏移在说明中是不允许的。
此外不支持非节点上的集中力。
(必须加的话)推荐用加细元素的方法。
BEAM188 计算的准确性与收敛性与元素的细化程度相关。
温度作为一种体负载可以加在每个端点节点的三个方向上。
在端点上,加在元素主方向(x-axis)上的温度是(T(0,0)),y 方向上为(T(1,0)), z 方向上为(T(0,1)).。
第一个温度坐标T(0,0) 默认为TUNIF。
绻龆ㄒ辶说谝桓鑫露龋敲雌渌木衔谝桓觥?如果仅在节点I 上输入温度,那节点J 默认对应于节点I 。
其他的输入形式如果未定以均默认为TUNIF。
KEYOPT(10) = 1 用于从用户子程序中读入初始应力数据。
用户子程序的详细叙述请见ANSYS Guide to User Programmable Features 。
输入概述中给出了元素输入的一个概括说明。
BEAM188 输入概述ElementNameBEAM188Nodes I, J, KDegrees of Freedom UX, UY, UZ, ROTX, ROTY, ROTZ if KEYOPT(1) = 0UX, UY, UZ, ROTX, ROTY, ROTZ, WARP if KEYOPT(1) = 1RealConstants(Blank), TYZ1, TXZ1, ADDMASMaterial Properties EX, EY, EZ, (PRXY, PRYZ, PRXZ, or NUXY, NUYZ, NUXZ), ALPX, ALPY, ALPZ, DENS, GXY, GYZ, GXZ, DAMPSurface Loads Pressure - face 1 (I-J) (-z normal direction),face 2 (I-J) (-y normal direction),face 3 (I-J) (+x tangential direction),face 4 (I) (+x axial direction),face 5 (J) (-x direction).反方向请用负值。
Body Loads Temperatures-T(0,0), T(1,0), T(0,1) at each end nodeSpecial 塑性,潜变,应力强化,大变形,大应力,初始应力输入(Plasticity,Features Creep, Stress stiffening, Large deflection, Large strain,Initial stress import)。
提供如下的TB命令项:BISO, MISO,NLISO, BKIN, MKIN, KINH, CHABOCHE, and CREEP. 详见ANSYS Theory Reference 。
KEYOPT(1)0 - 默认; 六DOF, 无弯曲1 - 七DOF (包括弯曲)KEYOPT(2)0 - 默认; 截面随轴向变长的函数而变化,但须NLGEOM,ON 。
1 - 截面尺寸假定为常量(经典梁理论)KEYOPT(5)0 - 默认; 对称的压载荷刚度1 - 非对称的压载荷刚度2 - 忽略压载荷刚度Note - 只有在OUTPR,ESOL 激活时KEYOPT(6) 才能通过KEYOPT(9)激活。
当KEYOPTs 6, 7, 8, 和9 都被激活时,元素输出中的应力是一个总的应变。
"总" 意味着同时包含了热应变。
如果元素的材料定义是定义的塑性材料,那么可以包含塑性应变和塑性功。
可以在/POST1 中用PRSSOL显示。
KEYOPT(6)元素积分点输出控制0 - 默认; 输出截面力,截面应变,弯矩1 - 与KEYOPT(6) = 0 相同,增加截面面积2 - 与KEYOPT(6) = 1 相同,增加元素基本方向(x,y,z)3 - 输出截面向单元节点外推的力/力矩,应变/曲率KEYOPT(7)截面积分点输出控制(在截面压尺寸= ASEC时无效)0 - 默认;没有输出1 - (输出)最大最小应力/应变2 - 与KEYOPT(7) = 1 相同,增加每个截面节点的应力应变输出KEYOPT(8)截面节点输出控制(在截面压尺寸= ASEC时无效)0 - 默认;没有输出1 - (输出)最大最小应力/应变2 - 与KEYOPT(8) = 1 相同,增加沿截面外边界的应力应变输出3 - 与KEYOPT(8) = 1 相同,增加每个截面节点的应力应变KEYOPT(9)元素节点和截面节点的外推值的输出控制(在截面压尺寸= ASEC时无效)0 - 默认;没有输出1 - (输出)最大最小应力/应变2 - 与KEYOPT(9) = 1 相同,增加沿截面外边界的应力应变输出3 - 与KEYOPT(9) = 1 相同,增加每个截面节点的应力应变KEYOPT(10 )0 - 没有用户子程序来提供初始应力(默认)1 - 用USTRESS 从用户子程序中读取初始应力(详见ANSYSGuide to User Programmable Features关于用户子程序的章节).1.切向应变刚度输出数据单元解的输出有两种:•节点位移解包含于节点解中。