【精品】圆柱与圆锥易错题

小学数学圆柱圆锥易错题练习题问题一：已知一个圆柱的高度为10 cm，底面直径为6 cm。

求这个圆柱的体积和表面积。

解答：首先计算底面的半径，由于底面直径为6 cm，所以半径为3 cm。

接下来，我们可以使用下面的公式来计算圆柱的体积和表面积：体积公式：V = 底面积 ×高度表面积公式：A = 2πr² + 2πrh （其中π取3.14）将已知数据代入公式我们可以得到：底面积= πr² = 3.14 × 3² ≈ 28.26 cm²体积 = 底面积 ×高度 = 28.26 cm² × 10 cm = 282.6 cm³表面积= 2πr² + 2πrh = 2 × 3.14 × 3² + 2 × 3.14 × 3 × 10 ≈ 188.4 cm²因此，这个圆柱的体积约为282.6 cm³，表面积约为188.4 cm²。

问题二：已知一个圆锥的高度为8 cm，底面半径为4 cm。

求这个圆锥的体积和母线长度。

解答：首先我们可以使用下面的公式来计算圆锥的体积和母线长度：体积公式：V = 1/3 ×底面积 ×高度母线公式：l = √(高度² + 底面半径²) （其中√表示平方根）将已知数据代入公式我们可以得到：底面积= πr² = 3.14 × 4² = 50.24 cm²体积 = 1/3 ×底面积 ×高度= 1/3 × 50.24 cm² × 8 cm ≈ 133.18 cm³母线长度= √(高度² + 底面半径²) = √(8² + 4²) ≈ √80 ≈ 8.94 cm因此，这个圆锥的体积约为133.18 cm³，母线长度约为8.94 cm。

圆柱和圆锥易错题专项练习第四讲：圆柱和圆锥易错题专项练姓名：得分：一、认真审题，再填空（19×2=38分）1、等底等高的圆柱和圆锥，体积之比为（）：（）2、一个圆柱与一个圆锥等底等高，它们的体积之和是48dm²，圆柱的体积是（）dm³，圆锥的体积是（）dm³。

3、一个圆柱形与一个圆锥形的底面直径都是10cm，高都是12cm，先在圆锥形里注满水，再把圆锥形的水倒入圆柱形中，圆柱形里的水深（）厘米。

4、把一个棱长10dm的正方体切削成一个最大的圆柱，圆柱的体积是（）5、把一个高24cm的圆柱形铁块熔铸成一个和它等底的圆锥，圆锥高（）cm.6、一个圆锥，底面半径5cm，高3cm，这个圆锥的体积是（）cm³。

7、一个圆锥形沙堆，占地面积15㎡，高4m，这个沙堆的体积是（）m³。

8、把一个棱长6cm的正方体木块切削成一个最大的圆锥，得到的圆锥的体积是（）cm³。

9、在一个底面半径4dm，高6dm的圆柱形中装满水，再把一个与这个圆柱等底等高的圆锥放入圆柱形中，水会溢出（）立方分米。

10、把一个圆柱切削成一个最大的圆锥，削掉了60 cm³，原来这个圆柱的体积是（）。

11、一个圆锥的体积是12立方厘米，底面积是4平方厘米，高是（）。

12、一个圆锥形的，从内里量高9厘米，先装满水，然后把水所有倒入和它等底的圆柱描述器里，水面高（）厘米。

13、直角三角形ABC的AB边长为3厘米，BC边长为4厘米，AC边长为5厘米。

以AB边为轴旋转一周后，形成一个立体图形。

它的体积是（）。

14、一个圆柱与一个圆锥体积相等，高也相等。

圆柱的底面积是60平方厘米，圆锥的底面积是(。

)。

15、一个圆柱形水桶里装有一块与水桶（从里面量）等底等高的圆锥形铁锭，加入24升水，正好盛满一桶。

圆锥形铁锭的体积是（）立方分米，如果圆锥形铁锭的底面积是4平方分米，水桶的高是（）分米。

人教版六年级下册数学第三单元圆柱与圆锥测试卷一.选择题(共5题，共9分)1.做一根长2米，半径为10厘米的圆柱体水管需要多少铁皮，就是要计算这个圆柱体水管的（）。

A.侧面积B.表面积C.底面面积D.体积2.一个圆柱的底面半径是8厘米，高是7厘米，这个圆柱的体积是（）cm3。

3.下面说法正确的是（）。

A.一条直线长10m。

B.圆锥的体积比与它等底等高的圆柱的体积小。

C.一年中有6个大月、6个小月。

D.把一根木头锯成7段，若锯每一段所用的时间都相等，那么锯每一段的时间是锯完这根木头所用时间的。

4.小明做了一个圆柱形状的容器和三个圆锥形状的容器(如下图)，将圆柱形状容器中的水倒入第（）个圆锥形状的容器，正好可以倒满。

A. B. C.5.把圆柱的底面平均分成16份切开后，照图拼成近似的长方体，（）发生了变化。

A.底面积B.表面积C.体积二.判断题(共5题，共10分)1.等底等高的圆柱和长方体的体积相等。

（）2.如果一个圆锥的体积是一个圆柱体积的3倍，它们的底面积相等，那么圆锥的高一定是圆柱高的9倍。

（）3.圆柱的侧面展开是长方形，但不是正方形。

（）4.圆柱体的体积与圆锥体的体积比是3:1。

（）5.甲、乙两个圆柱的体积相等，如果甲圆柱的高是乙圆柱的，那么甲圆柱的半径则是乙圆柱的1.5倍。

（）三.填空题(共8题，共11分)1.一个圆柱的底面直径是15 cm，高是8 cm，这个圆柱的侧面积是（）cm2。

2.一个圆柱的侧面积是47.1cm2，高是5cm，它的表面积是（） cm2，体积是（）cm3。

3.一个圆锥的体积为81立方米，高为3米。

则底面积为（）平方米。

4.把一升水倒入容量为2升的圆柱形瓶中，水面约在瓶高的（）处；把2升水倒入容量为400毫升的杯中，可以倒满（）杯。

5.一个圆柱的体积是94.2立方分米，它的底面周长是12.56分米，这个圆柱的高是（）分米。

6.把一个圆锥沿底面直径纵切开，切面是一个（）形。

小升初必备：圆柱与圆锥典型及易错题型分析圆柱与圆锥典型及易错题型（一）关于圆锥与圆柱相互之间的关系：1.若圆锥与圆柱等底等高，则它们的体积不等（圆锥的体积是圆柱的三分之一）；2.若圆锥与圆柱等底等体积，则它们的高不等（圆锥的高是圆柱的3倍）；3.若圆锥与圆柱等高等体积，则它们的底不等（圆锥的底面积是圆柱的3倍）。

练：1、一个圆柱和一个圆锥等底等高，它们的体积和是24立方分米，那么圆柱的体积是_________立方分米．2、一个圆柱和一个圆锥的底面直径相等，圆锥的高是圆柱的3倍，圆锥的体积是12立方分米，圆柱的体积是（）立方分米。

A12B36C4D8（二）、关于圆柱、圆锥的典型实际问题：1.实质求圆柱的侧面积：通风管（如圆柱形烟囱）压路机1、做一根长1米，底面周长是2分米的圆柱形通风管，需要铁皮多少平方分米？（管壁厚度忽略不计）2.求的滚轮转动一周所压过的路面面积就是求圆柱（滚轮）的侧面积；（所压过的路面面积=圆柱（滚轮）的侧面积×转动速度×时间）1、压路机的滚筒是个圆柱，它的宽是3米，滚筒横截面半径是1米，那么滚筒转一周可压路面多少平方米？如果压路机的滚筒每分钟转10周，那么5分钟可以行驶多少米？3.求无盖的圆柱形表面积。

1、求圆柱形水桶能装水多少升，是求它的（）；做一节圆柱形通风管要多少铁皮，是求它的（）A．侧面积B．表面积C．体积D．容积2、一个圆柱形儿童游泳池底面半径是4米，深0.5米．在它的四周和池底抹上水泥，每平方米需要水泥10千克，一共用水泥多少千克？3、一个无盖的圆柱形铁皮水桶,高50厘米,底面直径30厘米,做这个水桶约莫需用几何铁皮? (得数保留整数)4、做一个无盖的圆柱形鱼缸，底面半径3dm，高5dm。

（1）做这个鱼缸至少要几何平方分米？（得数保留整十平方分米）（2）这个鱼缸能装几何千克水？（1升水重1千克）5、圆柱的体积求底面积或高时，要用体积除以底面积或高，圆锥的体积求底面积或高时，要先乘以3再除以底面积或高。

1500立方厘米=（1500 ）毫升=（ 1.5 ）升
圆锥的侧面展开图是一个（扇形），圆锥有（1）条高。

二、易错判断题
长方体中最多有4个面可能是正方形。

（×）
一个圆柱，如果底面直径和高相等，则圆柱的侧面展开是正方形。

（×）
如果一个物体上、下底面是面积相等的两个圆，那么这个物体一定是圆柱。

（×）
如果两个圆柱的侧面积相等，那么他们的底面周长也相等。

（×）
把一个圆柱的底面直径扩大2倍，高不变，那么它的侧面积也扩大2倍。

（√）
圆柱体的高越大，它的侧面积就越大。

( ×)
三、易错应用题
1.画出下面圆柱的展开图，并求出它的表面积。

(单位：厘米)。

第二单元《圆柱.圆锥》试卷错题【2 】（本质是几个公式的变形和对圆柱.圆锥的懂得）1.正方体内有一个最大的圆柱,圆柱的侧面积是75.36平方厘米,圆柱的直径=（）,圆柱的半径=（）的一半.圆柱的高=（）.这个正方体的表面积是（）.圆柱的底面积是正方体底面积的（）％,圆柱的4个侧面之和是正方体侧面积的（）％,圆柱的体积是正方体体积的（）％.2.正方体内有一个最大的圆锥,圆锥的直径=（）,圆锥的半径=（）的一半.圆锥的高=（）.圆锥的体积是正方体内挖出的最大的圆柱的体积的（）.3.有一个密封的容器,它是由一个圆柱和一个圆锥构成的.圆锥和圆柱等底等高,高都是6厘米,圆柱朝下,圆锥在上,容器内有一部分水,水的高度是4厘米,把容器倒过来圆锥朝下,圆柱在上,如今水面的高度是（）.4.把一个高100厘米的圆柱沿着直径切拼成一个近似的长方体,这时它的表面积增长200平方厘米,这个圆柱的体积是（）.5.一个圆柱高100厘米,假如把他它的高削减20厘米,表面积将削减251.2平方厘米,本来圆柱的体积是（）.6.一根2米长的圆柱形木柴,横截面的直径是20厘米,沿着横截面的直径锯开,分成相等的两部分,每一部分的体积和表面积各是（）（）.7.一根圆柱形木材长2米,把它截成相等的4段后,表面积增长18.84平方厘米,本来这根圆木的体积是（）.8.一个圆柱的体积是72立方厘米,与它等底等高的圆锥的体积是（）.假如圆锥的底面积是18平方厘米,那么圆锥的高是（）.假如圆锥的高是2厘米,圆锥的底面积是（）.9.一个圆锥和圆柱的底面积之比是3:1,假如高相等,则圆锥和圆柱的体积比是（）.假如高的比是2:1,则圆锥和圆柱的体积比是（）.10.一个圆锥和圆柱的高的比是3:1,假如底面积相等,则圆锥和圆柱的体积比是（）.圆锥的体积是12立方分米,则圆柱的体积是（）.假如底面积的比是2:1,则圆锥和圆柱的体积比是（）.圆锥的体积是12立方分米,则圆柱的体积是（）.11.一个圆锥和圆柱的体积比是3:1,假如底面积相等,则圆锥和圆柱的高的比是（）.假如底面积的比是2:1,则圆锥和圆柱的高比是（）.12.一个长方体.正方体.圆柱.圆锥等底等高,则体积比是（）.假如一个长方体.正方体.圆柱.圆锥体积和高都相等,则长方体的高是（）.圆锥的高是（）.13.圆柱的高不变,底面半径扩展2倍,直径扩展（）.底面积扩展（）,侧面积扩展（）,表面积扩展（）,体积扩展（）.14.圆锥的高不变,底面半径扩展2倍,直径扩展（）.底面积扩展（）,体积扩展（）.15.一个圆柱形汽油桶的容积是45立方分米,底面积是7.5平方分米,桶内装的汽油占油桶容积的十二分之七,桶内汽油高是（）.16.一个圆锥形沙堆的底面直径是4米,高4.2米,用这对沙在10米宽的公路上铺2厘米厚,能铺（）米长.17.将圆柱的底面平均分成若干份,拼成一个近似的长方体,表面积比本来增长400平方厘米,圆柱的高是20厘米,圆柱的体积是（）立方厘米.18.自来水水管的内直径是2厘米,水管内的水的流速是每秒8厘米,一位同窗去洗手,走时忘却关水龙头,5分钟糟蹋（）升水.19.将一个圆锥形的零件浸没在底面周长是12.56分米的圆柱形玻璃容器中,容器水面上升了0.4分米,这个零件的体积是（）.20.圆锥形沙岸的底面周长是12.56米,高1.2米,用这堆沙铺在一条长是20米.宽5米的长方形路上,能铺多厚？21.将一个长10分米.宽8分米.高6分米的长方体加工成一个最大的圆柱,所得圆柱的体积是（）.22.圆柱的侧面睁开是正方形,底面半径是10厘米,高是（）厘米.底面直径和高的比是（）.23.将棱长2分米的正方体木块,削成一个最大的圆锥,所得圆锥的体积是（）.削去部分的体积是（）.24.将体积为282.6立方厘米的长方体熔铸成一个底面半径是6厘米的圆锥形机械零件,圆锥形零件的高是（）.25.圆柱的高是8厘米,将它的高增长2厘米,表面积就增长25.12平方厘米,本来圆柱的体积是（）.26.圆柱的侧面积是50.24平方厘米,高和底面半径相等,它的表面积是（）.27.一个半径是10米地圆柱形水池,能蓄水1570立方米,假如再挖深2.5米,这个蓄水池能蓄水（）立方米.28.压路机滚筒的半径是0.8米,宽是1.5米,假如滚筒每分钟迁移转变5周,那么每分钟压路得面积是（）平方米.29.圆锥形容器（极点朝下）内装有0.2升水,水面高度正好是圆锥高度的一半,这个容器还能装水（）升.30.一个直角三角形三条边分离是4厘米.3厘米.5厘米,以斜边为轴扭转一周得到的立体图形的体积是（）.31.一个钝角三角形,最短边上的高是6厘米,以最短边（6厘米）为轴扭转一周,扭转后的大圆锥的高是10厘米,得到的立体图形的体积是（）.。

圆柱与圆锥易错题目(1)一、圆柱与圆锥1．看图计算．（1）求圆柱的表面积（单位：dm）（2）求零件的体积（单位：cm）【答案】（1）解：3.14×10×20+3.14×（10÷2）2×2＝628+3.14×25×2＝628+157＝785（平方分米）答：圆柱的表面积是785平方分米。

（2）解： ×3.14×（2÷2）2×3+3.14×（2÷2）2×4＝ ×3.14×1×3+3.14×1×4＝3.14+12.56＝15.7（立方厘米）答：零件的体积是15.7立方厘米。

【解析】【分析】（1）圆柱的表面积是两个底面积加上一个侧面积，根据圆面积公式计算出底面积，用底面周长乘高求出侧面积；（2）圆柱的体积=底面积×高，圆锥的体积=底面积×高×，根据公式计算，用圆柱的体积加上圆锥的体积就是总体积。

2．计算圆锥的体积。

【答案】解：3.14×2²×15×=3.14×4×5=62.8（dm³）【解析】【分析】圆锥的体积=底面积×高×，根据圆锥的体积公式计算体积即可。

3．一根圆柱形木材长20分米，把它截成3段，表面积增加了12.56平方分米。

这根木材体积是多少立方米?【答案】解：12.56÷4×20=62.8（立方分米）=0.0628（立方米）答：这根木材体积是0.0628立方米。

【解析】【分析】将圆柱形木材截成3段，增加了4个底面积，用增加的表面积除以4即可求出圆柱的底面积，然后用底面积乘高即可求出这根圆柱形木材的体积。

4．将一根底面直径是20厘米，长1米的圆木沿着直径劈成相等的两半。

每半块木头的表面积和体积是多少?【答案】解：1米=100厘米，表面积：3.14×（20÷2）2+[3.14×20×100]÷2+20×100=5454（平方厘米）体积：3.14×（20÷2）2×100÷2=15700（立方厘米）答：每半块木头的表面积是5454平方厘米，体积是15700立方厘米。

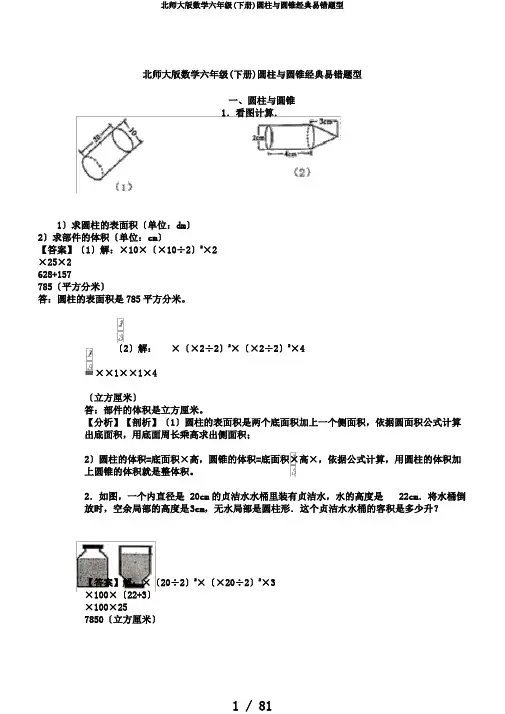
北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1．看图计算．1〕求圆柱的表面积〔单位：dm〕2〕求部件的体积〔单位：cm〕【答案】〔1〕解：×10×〔×10÷2〕2×2×25×2628+157785〔平方分米〕答：圆柱的表面积是785平方分米。

〔2〕解：×〔×2÷2〕2×〔×2÷2〕2×4＝××1××1×4〔立方厘米〕答：部件的体积是立方厘米。

【分析】【剖析】〔1〕圆柱的表面积是两个底面积加上一个侧面积，依据圆面积公式计算出底面积，用底面周长乘高求出侧面积；2〕圆柱的体积=底面积×高，圆锥的体积=底面积×高×，依据公式计算，用圆柱的体积加上圆锥的体积就是整体积。

2．如图，一个内直径是 20cm的贞洁水水桶里装有贞洁水，水的高度是22cm．将水桶倒放时，空余局部的高度是3cm，无水局部是圆柱形．这个贞洁水水桶的容积是多少升？【答案】解：×〔20÷2〕2×〔×20÷2〕2×3×100×〔22+3〕×100×257850〔立方厘米〕7850立方厘米＝升答：这个贞洁水水桶的容积是升。

【分析】【剖析】水桶的容积包含水的体积和空余局部的体积，依据圆柱的体积公式分别计算后再相加即可求出水桶的容积。

3．有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯，杯中水面距杯口厘9厘米的圆锥形铅锤完整浸入水中，水会溢出314立方厘米．求铅锤米．假定将一个半径为的高．【答案】解：×〔20÷2〕2×2.24+314×100×2.24+314703.36+314〔立方厘米〕，2〕÷〔×9×3÷÷12〔厘米〕，答：铅锤的高是12厘米。

《易错题》小学数学六年级下册第三单元圆柱与圆锥测试卷（包含答案解析）一、选择题1．一个底面积是20cm2的圆柱，斜着截去了一段后，剩下的图形如图．截后剩下的图形的体积是（）cm3．A. 140B. 180C. 220D. 3602．如图是一个直角三角形，两条直角边分别是6cm和2cm，以较长边为轴，旋转一周所形成的立体图形的体积是（）立方厘米．A. 25.12B. 12.56C. 75.363．把一个圆柱铸成一个圆锥体，它的（）不变。

A. 体积B. 表面积C. 侧面积4．两个圆柱的底面积相等，高之比是2：3 ，则体积之比是（）A. 2：3B. 4：9C. 8：27D. 4：6 5．把一个棱长是4分米的正方体木块削成一个最大的圆柱，体积是（）立方分米。

A. 50.24B. 100.48C. 646．正方体、圆柱和圆锥的底面积相等，高也相等，下面说法正确的是（）。

A. 圆柱的体积比正方体的体积小一些B. 圆锥的体积是正方体体积的C. 圆柱的体积与圆锥的体积相等D. 正方体的体积比圆柱的体积小一些7．有一个圆柱和一个圆锥的体积相等，圆柱的底面积是圆锥的2倍，圆锥的高是9cm，圆柱的高是（）。

A. 1.5cmB. 3cmC. 9cm8．圆柱的底面半径和高都乘3，它的体积应乘（）A. 3B. 6C. 279．如图所示，把一个底面积是24平方分米，高是8分米的圆柱木料，削成两个完全一样的圆锥体，并且每个圆锥的底面积与圆柱的底面积相等。

则削去部分的体积是（）A. 32立方分米B. 64立方分米C. 96立方分米D. 128立方分米10．一个圆锥的体积是12立方厘米，它的底面积是3平方厘米，高是（）。

A. 厘米B. 厘米C. 4厘米D. 12厘米11．两块同样的长方形纸板，卷成形状不同的圆柱（接头处不重叠），并装上两个底面，那么制成的两个圆柱体（）。

A. 底面积一定相等B. 侧面积一定相等C. 表面积一定相等D. 体积一定相等12．圆柱形通风管的底面周长是31.4厘米，高2分米，制作这样一节通风管需（）铁皮。

六年级圆柱与圆锥易错题
以下是一些六年级圆柱与圆锥的易错题：
1. 一个圆柱体和一个圆锥体的底面积相等、体积也相等，圆锥的高是27厘米，圆柱的高是多少厘米．
2. 一个圆柱体和一个圆锥体的底面积和体积都相等，圆锥的高是18厘米，圆柱的高是多少厘米．
3. 一个圆柱体和一个圆锥体的底面积相等、体积不相等，圆锥的体积是圆柱的(1/3)，圆锥的高是27厘米，圆柱的高是多少厘米．
4. 一个圆柱体和一个圆锥体的底面积相等、高相等，它们的体积之和是144立方厘米，圆锥的体积是多少立方厘米．
5. 圆锥体的底面积不变，高增加(1/5)，则体积增加多少
6. 圆柱体与一个圆锥体的底面积相等、高也相等，圆柱的体积是3立方分米，圆锥的体积是多少立方分米．
7. 圆柱体与一个圆锥体的底面积和体积都相等，圆锥的高是9分米，圆柱的高是多少分米．
8. 一个圆柱体和一个圆锥体的底面积和体积都相等，圆锥的高是24厘米，圆柱的高是多少厘米．
9. 一个圆柱体和一个圆锥体的底面积相等、高不相等，圆柱的体积是圆锥的(3/5)，圆锥的高是27厘米，圆柱的高是多少厘米．
10. 一个圆柱体和一个圆锥体的底面积和体积都相等，已知圆锥的高是18
厘米，则圆柱的高是多少厘米．
这些题目需要学生仔细理解并应用圆柱和圆锥的体积公式（V=πr^2h）以
及相关的数学知识。

如果他们在这方面有困难，可能需要更多的练习和解释。

六年级数学下册《第3单元圆柱与圆锥》易错题拔高训练人教版一．选择题1．如图形中，哪项是圆柱的展开图（）A．B．C．2．把一张直角三角形硬纸的一条直角边贴在木棒上快速旋转一周，形成的图形是（）A．三角形B．球体C．圆锥D．圆柱3．把一张长25.12cm、宽18.84cm的长方形纸卷成一个圆柱形纸筒（接头处刚好对接，没有重叠）。

这个纸筒的底面直径不可能是（）厘米。

A．8B．7C．64．一根圆柱形木料，如果沿着底面直径劈成两半，表面积增加120平方厘米。

如果拦腰平均截成两个小圆柱，表面积增加157平方厘米。

这根圆柱形木料原来的高是（）厘米。

A．2.4B．6C．12D．245．下面图形中，只有一条高的是（）A．三角形B．梯形C．圆柱D．圆锥6．将一个圆锥的底面直径扩大到原来的3倍，要使体积不变，高要缩小到原来的（）A．B．C．D．二．填空题7．一个圆柱的底面直径是2分米，高10分米，这个圆柱的侧面积是平方分米，表面积是平方分米，体积是立方分米。

8．把一个圆柱形木料削成一个最大的圆锥体，削去部分的体积是圆柱体的。

9．一个圆锥体的体积是4.5立方分米，高是4.5分米，底面积是平方分米．10．一个圆柱形茶叶筒的侧面正好包裹了一张长方形的商标纸。

圆柱底面半径是5cm，高是2dm。

这张商标纸的面积是cm2。

11．一个圆锥的底面直径是8厘米，高12厘米，沿底面直径将它切成两个完全相等的部分，表面积增加平方厘米．12．一个圆锥的底面半径是4厘米，高是6厘米，沿着顶点到圆心切开，表面积增加平方厘米．三．判断题13．把一个圆柱体拼成一个近似的长方体，体积不变，表面积变了．．14．一个圆柱形的玻璃杯可盛水1立方分米，我们就说玻璃杯容积是1升．．15．圆锥的高有无数条．．16．把一个圆柱体削成一个最大的圆锥体，削去的部分的体积与原来的体积之比是2：3．17．圆柱的侧面展开后是正方形，说明底面直径和高的比是1：1．．四．计算题18．计算下面立体图形的体积19．计算下面图形的表面积和体积．五．应用题20．把一个底面直径12厘米的圆锥形金属铸件浸没在棱长1.5分米的正方体容器中，水面比原来升高1.2厘米，求这个圆锥的体积．21．一个无盖的圆柱形铁桶，底面周长是6.28dm，桶深4dm．做这个铁桶至少需要多大面积的铁皮？这个铁桶最多能装多少升水（铁皮厚度忽略不计）？22．一张长方形的铁皮（如下图），剪下图中的阴影部分恰好可以做成一个油桶（接头处不计）。

六年级圆柱圆锥易错题精选圆柱圆锥易错题1.用一张长30厘米，宽18厘米的长方形纸，围成一个圆柱，这个圆柱体的侧面积是（）平方厘米。

解：首先，我们需要知道圆柱的侧面积公式为2πrh，其中r为底面半径，h为圆柱的高。

由于题目没有给出高，我们需要先求出底面半径。

根据长方形纸的长度和宽度，可以得到圆柱的底面周长为2(30+18)=96厘米，即2πr=96，解得r=48/π。

再根据圆柱的高为18厘米，代入公式2πrh，即可得到圆柱体的侧面积为2π×48/π×18=1728平方厘米。

2.一个圆柱的侧面展开是正方形，当圆柱的高是15分米时，圆柱的底面周长是（）分米。

解：根据题意，圆柱的侧面展开是正方形，说明圆柱的高等于底面周长。

因此，底面周长为15分米。

3.等底等高的圆柱和圆锥。

圆柱的体积是36立方厘米，圆锥的体积是（）立方厘米；圆锥的体积是36立方厘米圆柱体积比圆锥大（）立方厘米。

解：由于圆柱和圆锥等底等高，它们的底面积相等。

设它们的底面积为S，圆柱的高为h，圆锥的高为H，则圆柱的体积为V1=S×h=36，圆锥的体积为V2=1/3×S×H。

将V1代入可得S×h=36，带入V2可得V2=1/3×S×(3h)=1/3×36×3h=36h。

因此，圆锥的体积为36h立方厘米，圆柱的体积比圆锥大36-36h立方厘米。

如果圆锥的体积是36立方厘米，则圆柱的体积比圆锥大0立方厘米，圆锥的体积为1立方厘米。

4.把一个底面直径和高都是6分米的圆柱的，底面分成若干等份，再切开拼成一个长方体。

这个长方体的长是（）分米，宽是（）分米，高是（）分米，体积是（）立方分米。

解：首先，我们需要知道圆柱的底面积为πr²，其中r为底面半径。

由于底面直径为6分米，即r=3分米。

将底面分成n等份，则每份的弧长为2πr/n，每份的面积为πr²/n。

圆柱与圆锥典型及易错题型一、圆柱与圆锥1．一个圆锥体形的沙堆，底面周长是25.12米，高1.8米，用这堆沙在8米宽的公路上铺5厘米厚的路面，能铺多少米？【答案】解：5厘米= 0.05米沙堆的底面半径：25.12+ （2x3.14）=25.12+6.28=4 （米）1沙堆的体积：x3.14x42x1.8 = 3.14x16x0.6 = 3.14x9.6 = 30.144 （立方米）所铺沙子的长度：30.144+ （8x0.05）=30.144+0.4 = 75.36 （米）.答：能铺75.36米。

【解析】【分析】根据1米=100厘米，先将厘米化成米，除以进率100,然后求出沙堆的1底面半径，用公式：C+2n=r，要求沙堆的体积，用公式：V= nr2h，最后用沙堆的体积+ （公路的宽x铺沙的厚度）=铺沙的长度，据此列式解答.2．工地上有一个圆锥形的沙堆,高是1.5 米,底面半径是6 米,每立方米的沙约重1.7 吨。

这堆沙约重多少吨?（得数保留整吨数）【答案】解：3.14x62x1.5x x1.7=3.14x18x1.7=56.52x1.7，96 （吨）答：这堆沙约重96吨。

1【解析】【分析】圆锥的体积=底面积x高x ,先计算圆锥的体积，再乘每立方米沙的重量即可求出总重量。

3．如下图,爷爷的水杯中部有一圈装饰,是悦悦怕烫伤爷爷的手特意贴上的。

这条装饰圈宽5cm,装饰圈的面积是多少cm2?【答案】解：3.14x6x5 = 94.2 （cm2）答：装饰圈的面积是94.2cm2。

【解析】【分析】解：装饰圈的面积就是高5cm的圆柱的侧面积，用底面周长乘5即可求出装饰圈的面积。

4．一个圆柱体容器的底面直径是16 厘米，容器中盛有10 厘米深的水，现在把一个圆锥形铁块浸没到水中，水面上升了3厘米，圆锥形铁块的体积是多少立方厘米？【答案】解：3.14x （16“）2x3= 3.14x64x3= 200.96x3= 602.88 （立方厘米）答：圆锥形铁块体积是602.88立方厘米。

第3单元圆柱与圆锥-易错题-人教版易错点大集合易错点一：圆柱的表面积典例把一个圆柱体的侧面展开得到一个正方形，这个圆柱体的底面周长是10厘米，高是多少厘米，侧面积是多少平方厘米．跟踪训练1．将一个边长为5分米的正方形纸片卷成圆柱筒，这个圆柱的侧面积是多少平方分米．2．用铁皮制成一个高是5分米，底面周长是12.56分米的圆柱形水桶（没有盖），至少需要多少平方米铁皮？答：至少需要多0.7536平方米铁皮．3．一个圆柱底面半径是4分米，圆柱侧面积是62.8平方分米，这个圆柱的表面积是多少？4．一个圆柱体，底面半径是7厘米，表面积是1406.72平方厘米．这个圆柱的高是多少？5．圆柱侧面展开是一个正方形，已知圆柱的底面积是10平方厘米，则圆柱的侧面积是多少平方厘米？易错点二：圆柱的体积典例将一根长4米的圆柱形木料锯成3段，表面积增加了60平方分米。

这根木料的体积多少立方分米。

跟踪训练1．把一个棱长是6分米的正方体木块，削成一个最大的圆柱体，这个圆柱体的体积是多少立方分米。

2．把一个底面直径是20厘米的圆柱沿直径竖直切成两半，表面积比原来增加了400平方厘米，原来这个圆柱的底面积是多少，体积是多少。

3．一个长5cm、宽4cm的长方形纸，以这个长方形的长边为轴旋转一周，得到的立体图形是什么图形，它的体积是多少cm3。

4．一个圆柱底面半径是5cm，高是8cm，这个圆柱的侧面积是多少cm2，表面积是多少cm2，体积是多少cm3。

5．一个圆柱体油桶的体积是192dm3，底面积是16dm2，它的高是多少dm。

易错点三：圆锥的体积典例直角三角形的两条直角边分别是3厘米，4厘米。

若以其中一条直角边所在的直线为轴旋转一周，得到一个体积最大的圆锥，这个圆锥的体积是多少立方厘米。

跟踪训练1．一个圆锥形沙堆，高1.2m，底面直径是6m，这堆沙子的体积是多少m3。

2．一个圆锥的底面半径是3cm，高是4cm，它的体积是多少cm3。

圆柱与圆锥典型及易错题型一、圆柱与圆锥1．一个底面半径为12厘米的圆柱形杯中装有水，手里浸泡了一个底面直径是12厘米，高是18厘米的圆锥体铁块，当铁块从杯中取山来时，杯中的水面会下降多少厘米??【答案】解： ×3.14×（12÷2）2×18÷（3.14×122）= ×3.14×36×18÷（3.14×144）=1.5（厘米）答：桶内的水将下降1.5厘米。

【解析】【分析】水面下降部分水的体积就是圆锥的体积，根据圆锥的体积公式先计算出圆锥体铁块的体积，也就是水面下降部分水的体积。

用水面下降部分水的体积除以杯子的底面积即可求出水面下降的高度。

2．将一根底面直径是20厘米，长1米的圆木沿着直径劈成相等的两半。

每半块木头的表面积和体积是多少?【答案】解：1米=100厘米，表面积：3.14×（20÷2）2+[3.14×20×100]÷2+20×100=5454（平方厘米）体积：3.14×（20÷2）2×100÷2=15700（立方厘米）答：每半块木头的表面积是5454平方厘米，体积是15700立方厘米。

【解析】【分析】根据题意，劈开的每半块木头的表面积是原来木头的表面积的一半增加了一个切面的面积，据此代入公式解答即可；劈开的每半块木头的体积是原来木头的体积的一半，据此代入公式解答即可；圆柱表面积S=2×底面积+侧面积=2×3.14×r2+3.14×d×h；截面面积S=dh；体积V=3.14×r2×h。

3．计算下面圆柱的表面积。

（单位：厘米)【答案】解：3.14×（4÷2）²×2＋3.14×4×6＝100.48（平方厘米）【解析】【分析】圆柱体的表面积是两个底面积加上一个侧面积，底面积根据圆面积公式计算，用底面周长乘高求出侧面积。

六年级下学期圆柱与圆锥易错题专项训练50题1、圆柱的侧面展开是一个长方形，长方形的长等于圆柱的（底面周长），长方形的宽等于圆柱的（高）2、一个圆柱的底面半径扩大2倍，高不变，它的底面积扩大（4）倍，侧面积扩大（2）倍，体积扩大（4）倍；一个圆柱的底面半径扩大2倍，高也扩大2倍，它的底面积扩大（ 4 ）倍，侧面积扩大（4）倍，体积扩大（ 8）倍；一个圆柱的底面半径扩大2倍，高扩大3倍，它的底面积扩大（4）倍，侧面积扩大（ 6 ）倍，体积扩大（12 ）倍。

3、一个圆柱的底面半径为2厘米，侧面展开后正好是一个正方形，这个圆柱的体积是（157.7536立方厘米）4、等底等高的圆柱和圆锥的体积的和是96立方分米，这个圆柱的体积是（72 ）立方分米，这个圆锥的体积是（24）立方分米。

5、把一个圆锥体浸没在底面积是30平方厘米的圆柱形盛有水的容器里，水面升高4厘米，这个圆锥体的体积是（120 ）立方厘米。

6、用一个高36厘米的圆锥形容器盛满水，倒入和它等底等高的圆柱形容器中，水的高度是（ 12 ）厘米。

7、一个棱长是3分米的正方形容器装满水后，倒入一个底面积是3平方分米的圆锥形容器里正好装满，这个圆锥的高是（27）分米。

8、一个圆柱和一个圆锥的体积相等，底面积相等。

圆锥的高是6分米，圆柱的高是（ 2 ）分米。

9、一个圆锥的体积是126立方厘米，底面积是42平方厘米，高是（9）厘米。

10将一个边长为5分米的正方形纸片卷成圆柱筒，这个圆柱的侧面积是（25 ）平方分米。

11、一段圆钢长4米，底面半径是5厘米，把他平均分成3段后，表面积增加了（117.75）平方厘米。

12、一个圆柱的底面面积是25平方厘米，高是10分米，它的体积是（ 2500 ）立方厘米。

13、有一块正方体木料，棱长是6分米，把它削成为一个最大的圆柱体，这个圆柱体的体积是（169.56）立方分米。

14、一个圆柱体，把它削成一个与圆柱等底等高的圆锥体，圆锥体的体积是削去部分的（1/2）。

【精品】圆柱与圆锥易错题总结一、圆柱与圆锥1．将一根长16分米的圆柱形钢材截成三段较短的圆柱形，其表面积增加了24 平方分米，这根钢材原来的体积是多少？【答案】解：24÷4=6（平方分米）16×6=96（立方分米）答：这根钢材原来的体积是96立方分米。

【解析】【分析】将一根圆柱形钢材截成三段，增加了四个底面积，据此求出圆柱形钢材的底面积，再用底面积乘高即可求出这根钢材的体积。

2．一个圆锥形沙堆，底面周长是31.4米，高是1.2米．每立方米黄沙重2吨，这堆黄沙重多少吨？【答案】解：底面半径：31.4÷（2×3.14）＝31.4÷6.28＝5（米）这堆沙子的总重量： ×3.14×52×1.2×2＝3.14×25×0.4×2＝78.5×0.4×2＝31.4×2＝62.8（吨）答：这堆黄沙重62.8吨。

【解析】【分析】用底面周长除以圆周率的2倍即可求出底面半径。

根据圆锥的体积公式计算出沙子的体积，再乘每立方米沙子的重量即可求出总重量。

3．计算圆柱的表面积。

【答案】解：3.14×（6÷2）²×2+3.14×6×10=3.14×18+3.14×60=56.52+188.4=244.92（cm³）【解析】【分析】圆柱的表面积是两个底面积加上侧面积，根据圆面积公式计算底面积，用底面周长乘高求出侧面积。

4．一个圆锥体钢制零件，底面半径是3cm，高是2m，这个零件的体积是多少立方厘米？【答案】解： ×3.14×32×2＝3.14×6＝18.84（立方厘米）答：这个零件的体积是18.84立方厘米。

【解析】【分析】圆锥的体积=底面积×高×，根据公式计算体积即可。

圆柱圆锥12种易错题型
以下是一些与圆柱和圆锥相关的易错题型：
1. 计算圆柱或圆锥的体积时，忘记将高度和半径或直径的单位统一换算。

2. 混淆圆柱的体积公式和表面积公式，或者混淆圆锥的体积公式和表面积公式。

3. 在计算圆柱或圆锥的体积时，未正确平方或立方半径或直径的值。

4. 错误地将圆柱的底面面积与圆柱的侧面积相加来求圆柱的表面积。

5. 错误地将圆柱的表面积与圆柱的体积相加来求圆柱的总表面积。

6. 忽略圆锥的底面积，在计算圆锥的表面积时只考虑侧面积。

7. 错误地将圆锥的表面积与圆锥的体积相加来求圆锥的总表面积。

8. 混淆圆柱和圆锥的形状，例如将一个圆锥误认为是圆柱。

9. 在解决与圆锥相关的问题时，未将斜高或母线的长度考虑在内。

10. 未正确使用三角函数来计算圆锥的斜高或母线的长度。

11. 在计算圆锥的体积时，未正确将半径或直径的平方乘以高度再乘以π。

12. 忽略圆柱或圆锥的单位问题，在计算结果中缺少单位。

请注意，这只是一些常见的易错题型，根据具体的问题和知识点可能会有其他的易错点。

在解答题目时，请仔细阅读题目要求，理清思路，避免粗心导致的错误。

【精品】圆柱与圆锥易错题总结一、圆柱与圆锥1．如图，这是用塑料薄膜覆盖的蔬菜大棚，长15米，横截面是一个直径为2米的半圆。

大棚内的空间有多大?【答案】解：3.14×（2÷2）2×15÷2=23.55（立方米）答：大棚内的空间有23.55立方米。

【解析】【分析】观察图可知，大棚的形状是一个圆柱的一半，要求大棚内的空间大小，用圆柱的体积÷2=大棚内的空间大小，据此列式解答.2．一个圆柱形钢管，内直径是20cm，水在钢管内的流速是每秒40cm，每秒流过的水是多少cm3？【答案】解：3.14×（20÷2）2×40=314×40=12560（cm3）答：每秒流过的水是12560cm3。

【解析】【分析】钢管是圆柱形，流出的水也是圆柱形。

用钢管的横截面面积乘每秒流出水的长度即可求出流过水的体积。

3．计算下面圆柱的表面积。

（单位：厘米)【答案】解：3.14×（4÷2）²×2＋3.14×4×6＝100.48（平方厘米）【解析】【分析】圆柱体的表面积是两个底面积加上一个侧面积，底面积根据圆面积公式计算，用底面周长乘高求出侧面积。

4．一个圆锥形沙堆，底面积是45.9m2，高1.2m．用这堆沙在12m宽的路面上铺3cm厚的路基，能铺多少米？【答案】解：3厘米＝0.03米×45.9×1.2÷（12×0.03）＝18.36÷0.36＝51（米）答：能铺51米。

【解析】【分析】现根据圆锥的体积=×底面积×高求出圆锥形沙堆的体积，然后根据长方体的体积=长×宽×高，求出铺路的长度即可。

5．一个圆锥体钢制零件，底面半径是3cm，高是2m，这个零件的体积是多少立方厘米？【答案】解： ×3.14×32×2＝3.14×6＝18.84（立方厘米）答：这个零件的体积是18.84立方厘米。