六年级数学上圆知识结构图1

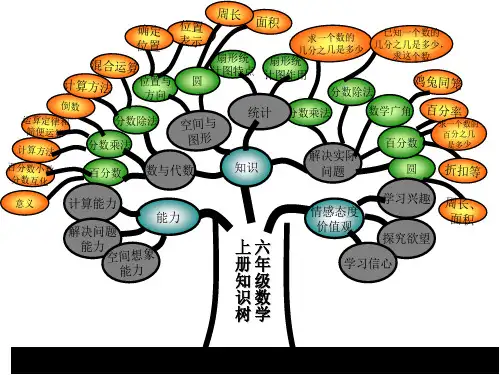
新人教版小学六年级数学上册圆的理解单元知识结构框架在各个学段中，《课程标准》安排了“数与代数”、“空间与图形”、“统计与概率”、“实践与综合应用”四个学习领域。

在空间与图形方面，本册教材安排了《位置》、《圆》两个单元。

在《圆》这个单元中，通过对曲线图形——圆的特征和相关知识的探索与学习，初步理解研究曲线图形的基本方法，促动学生空间观点的进一步发展。

下面，我将从以下几个方面来谈我对这个单元教材的理解和我的主要教学策略：（出示课件）一、课标要求：关于圆，在第一学段（1—3年级）的要求是：1．会辨认长方形、正方形、三角形、平行四边形、圆等简单图形。

2．能用简单的语言描述它的特征。

初步了解它是轴对称图形。

3．能对简单图形实行分类并会用各种平面图形拼图。

在本学段，即第二学段（4—6年级）的要求是：1．通过观察、操作，理解圆，掌握圆的特征，会用圆规画圆；2．知道圆是轴对称图形，进一步理解轴对称图形，能使用平移、轴对称和旋转设计简单的图案。

3．探索并掌握圆的周长和面积公式，能够准确计算圆的周长和面积。

4．经历从实际生活中发现问题、提出问题、解决问题的过程，体会圆的知识在生活中的广泛应用，初步形成综合使用数学知识解决问题的水平。

圆是一种曲线图形，它同直线图形有不同的特点。

在本册之前各册教材出现的平面图形都是直线图形。

所以“圆”的教学是学生系统理解曲线图形特征的开始。

在低年级的教学中虽然也出现过圆，但仅仅直观的理解，比如：人教版一年级上册第四、五单元《理解物体和图形》《分类》，初步理解圆并能够对基本图形实行分类。

一年级下册第三单元《图形的拼组》，尝试用不同的立体图形或平面图形实行设计和拼组。

二年级上册第五单元《观察物体》，初步了解圆是轴对称图形，并知道它有无数条对称轴。

本册的第四单元《圆》，要理解圆的基本特征，会画圆，会计算圆的周长和面积并会灵活应用这些知识解决实际问题。

从学习直线图形到学习曲线图形，不论是内容本身、还是研究问题的方法，都有所变化，教材通过对圆的研究，使学生初步理解研究曲线图形的基本方法，同时，也渗透了曲线图形与直线图形的内在联系。

圆规是数学几何中常见的工具之一，用于绘制和测量圆的各种属性。

下面是六年级圆规知识点的归纳：1.圆规的结构和使用方法：-圆规由固定的一只脚和可移动的一只脚组成，可移动脚上有一个锋利的笔尖或铅笔芯。

-圆规的固定脚上有一个可调节的刻度盘，用于测量圆的半径或直径。

-使用圆规时，应将固定脚放在画纸上，通过调节刻度盘使可移动脚与固定脚相切或相交，然后绘制所需要的线条。

2.圆的基本概念：-圆是由平面上任意一点到固定点的距离保持不变的点的集合。

-圆心是固定的点，圆心到圆上任意一点的距离称为半径，用字母r表示。

-直径是圆上任意两点之间通过圆心的线段，直径的长度为半径的两倍。

3.圆的相关性质：-圆的任意一条直径都将圆分为两个等分的半圆。

-圆的两条直径垂直相交。

-圆的半径相等。

-圆的半径垂直于其所在的切线。

4.利用圆规绘制圆的方法：-绘制半径：将圆规的可移动脚与固定脚相切于圆心，然后调整刻度盘的值，使可移动脚到达所需的半径长度，最后绘制半径线。

-绘制直径：将圆规的可移动脚与固定脚相交于圆心，然后调整刻度盘的值，使可移动脚到达所需的直径长度，最后绘制直径线。

-绘制切线：将圆规的可移动脚与固定脚相切于圆上一点，然后将可移动脚旋转一定角度，使可移动脚到达切线与圆的交点，最后绘制切线。

5.圆的计算：-计算圆的周长：圆的周长等于直径的长度乘以π（π≈3.14），即公式C=πd或C=2πr。

-计算圆的面积：圆的面积等于半径的平方乘以π，即公式A=πr²。

6.圆与其他几何图形的关系：-圆与正方形：正方形的对角线等于边长的√2倍，而圆的直径等于半径的2倍，因此正方形的对角线长度等于圆的直径的长度。

-圆与三角形：圆心到三角形的三个顶点的距离相等时，这个三角形是等边三角形，等边三角形的外接圆的圆心就是三角形的重心。

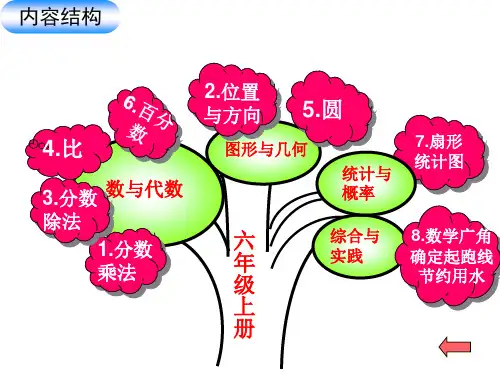
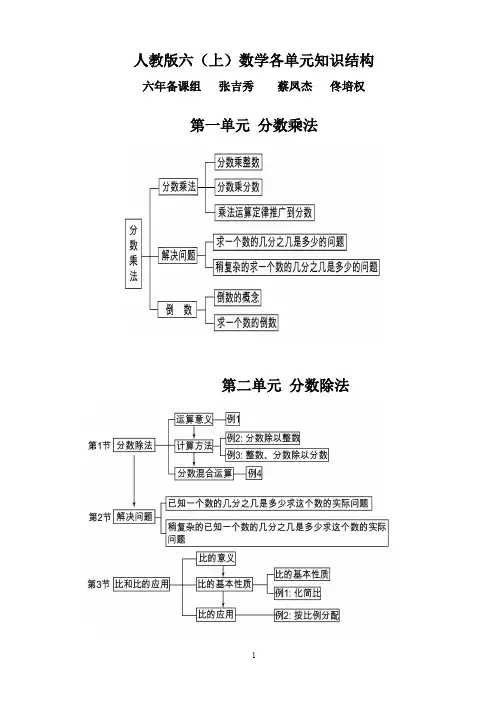
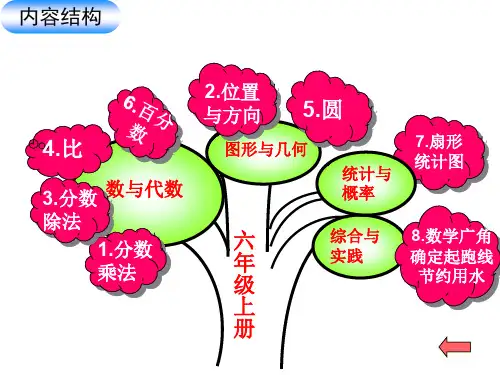
人教版六（上）数学各单元知识结构六年备课组张吉秀蔡凤杰佟培权第一单元分数乘法第二单元分数除法第三单元 圆第四单元 百分数圆的面积圆认识圆圆的周长第五单元 圆柱与圆锥第六单元 比例圆柱 圆柱的认识的表面积圆柱的体积圆锥圆锥的认识圆锥体积圆柱和圆锥 比例的意义比例的基本性质内项积=外项积判断改 写解比例（比例） 方程（乘法等式）变化的量没乘除关联变化有乘除关联变化正比例意义的量反比例意义的量正反比例意义的量对比比例尺数值比例尺线段比例尺图形的放大与缩小比例的应用比例六年级上册数学方法结构六年备课组 张吉秀 蔡凤杰 佟培权第一单元 分数乘法（一）分数乘法意义：1、分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

方法：“分数乘整数”指的是第二个因数必须是整数，不能是分数。

例如：53×7表示: 求7个53的和是多少？ 或表示：53的7倍是多少？ 2、一个数乘分数的意义就是求一个数的几分之几是多少。

方法：“一个数乘分数”指的是第二个因数必须是分数，不能是整数。

（第一个因数是什么都可以）例如：53×61表示: 求53的61是多少？9 ×61表示: 求9的61是多少？ A × 61表示: 求a 的61是多少？（二）分数乘法计算法则：1、分数乘整数的运算法则是：分子与整数相乘，分母不变。

方法：（1）为了计算简便能约分的可先约分再计算。

（整数和分母约分）（2）约分是用整数和下面的分母约掉最大公因数。

（整数千万不能与分母相乘，计算结果必须是最简分数）2、分数乘分数的运算法则是：用分子相乘的积做分子，分母相乘的积做分母。

（分子乘分子，分母乘分母）方法：（1）如果分数乘法算式中含有带分数，要先把带分数化成假分数再计算。

（2）分数化简的方法是：分子、分母同时除以它们的最大公因数。

（3）在乘的过程中约分，是把分子、分母中，两个可以约分的数先划去，再分别在它们的上、下方写出约分后的数。