多边形的面积知识结构图

多边形面积知识结构咱来唠唠多边形面积这事儿哈。

一、三角形面积。

1. 普通三角形。

- 最基本的求法就是底乘以高再除以2。

就好比你有个三角形的小旗，底就是旗底边的长度，高呢就是从底边相对的那个顶点垂直拉下来到底边的那条线的长度。

把底和高乘起来，再砍一半，就是这个三角形的面积啦。

- 为啥要除以2呢？你可以想象把两个一模一样的三角形拼起来，就变成一个平行四边形了，平行四边形面积是底乘高，那一个三角形不就是它的一半嘛。

2. 特殊三角形。

- 直角三角形。

- 它的面积求法也能用底乘高除以2。

不过它比较特殊，因为它的两条直角边就可以直接当底和高用。

比如说一个直角三角形，两条直角边分别是3厘米和4厘米，那它的面积就是3×4÷2 = 6平方厘米，简单得很。

- 等腰三角形。

- 它的面积还是底乘高除以2。

不过求高的时候可能要费点劲儿，得根据等腰三角形的一些特性来算高。

比如说等腰三角形的腰长是5厘米，底是6厘米，你得先算出高，再求面积。

二、平行四边形面积。

1. 平行四边形的面积就是底乘以高。

你可以把平行四边形想象成一个被推歪了的长方形。

底就是平行四边形的一条边，高就是这条底边对应的垂直高度。

比如说一个平行四边形底是5米，高是3米，那它的面积就是5×3 = 15平方米。

2. 这里要注意哦，可别把斜边当成高啦，高一定是垂直于底的那条线的长度。

三、梯形面积。

1. 梯形面积的公式是(上底 + 下底)×高÷2。

你可以把梯形想象成一个上窄下宽或者上宽下窄的四边形。

上底和下底就是梯形平行的那两条边，高就是这两条平行边之间的垂直距离。

2. 为啥是这个公式呢？你可以把两个一模一样的梯形拼起来，就变成一个平行四边形啦。

这个平行四边形的底就是梯形的上底加下底，高还是梯形的高，那一个梯形的面积不就是这个平行四边形面积的一半嘛，所以就有了这个公式。

四、多边形的分割与组合。

1. 有些复杂的多边形，咱们可以把它分割成几个咱们熟悉的三角形、平行四边形或者梯形来求面积。

四年级下册多边形的面积第二单元的思维导图
四下第二单元多边形的面积
1．通过整理与复习，进一步熟悉平行四边形、三角形、梯形面积的计算方法及公式的推导过程，加深对多边形面积计算公式间关系的理解。

2．利用平行四边形、三角形、梯形的面积公式解决与这些图形有关的实际问题,培养学生动手操作、观察、概括及解决问题的能力。

3．进一步体验图形与生活的联系，感受平面图形的学习价值，提高数学学习的兴趣和信心。

4．经历整理与复习的全过程，学习整理知识的方法，提高初步归纳，整理知识的能力，逐步养成梳理知识的习惯。

●平行四边形的面积
●面积公式：S=底a×高h
●h=S÷a
●a=S÷h
●面积计算的推导
●三角形的面积
●面积公式：S=底a×高h÷2
●h=2S÷a
●a=2S÷h
●怎么推导三角形面积公式
●梯形的面积
●面积公式：S=（上底a+下底b）×高h÷2
●h=2S÷（a+b）
●a+b=2S÷h
●怎么推导梯形的面积计算公式●组合图形的面积
●规则图形面积计算
●割补法
●拼接法
●和差法
●估计不规则图形的面积
●格点计算。

用思维导图的形式对多边形面积这一单元的知识进行回顾梳理步入小学我们了解到由三条或三条以上线段首尾依序连接组成的平面图形叫多边形。

三角形、平行四边形、梯形等都属于多边形，不少学生在学习时，对于多变的图形会混淆不清并难以计算相关内容。

为帮助学生灵活理解多边形图形，人教版五年级上册教材讲述了多边形的面积内容，助力学生理清多边形的面积知识。

学习知识时一般可以将其内容总结归纳至思维导图中，以便梳理，接下来就给大家分享关于多边形的面积思维导图及其相关内容。

一、多边形的面积梳理然而该如何将多边形的面积内容整理至思维导图呢？首先要做的势必是对多边形的面积知识内容进行梳理，而我们知道思维导图以层层递进的方式发散内容。

因此，梳理时也可以利用由浅入深的方式对知识内容进行汇总：例如，小学五年级多边形的面积一节主要内容有平行四边形的面积、三角形的面积、梯形的面积、组合图形的面积四部分。

在教材中展现了很多关于多边形面积的案例，但其主要目的则在于向学生梳理图形面积的推导过程以及公式计算。

因此在制作多边形的面积思维导图时可以将这些主要内容提取出来。

二、多边形的面积思维导图多边形的面积知识内容梳理完毕后，便可将其整理至思维导图。

当然了，梳理知识内容的同时将其同步至思维导图也是可以的。

对于多边形的面积思维导图的制作一般可以简单梳理为以下多个步骤：1、通过迅捷画图创建思维导图并进入编辑页面；2、将多边形的面积知识内容以层层递进、由浅入深的方式整理至节点；3、利用主题、样式、公式、备注等功能进一步完善思维导图；4、将制作好的多边形的面积思维导图存储为png、pdf、josn等格式。

注：绘制时注意节点层级的逻辑性；归纳小技巧：1、可利用“图标”的不同符号记录知识点的差异，如难易程度、重要程度、了解程度等；2、制作期间可通过“协作”功能邀请他人与自己一同编辑，集思广益梳理知识内容；3、对于知识中所包含的公式内容，可以使用“公式”功能快速编辑，使用方法可参考“思维导图怎么插入公式”了解；4、若梳理过程发现思路有误，或想要复现原有思路，可通过“历史版本”功能预览或恢复已记录版本。

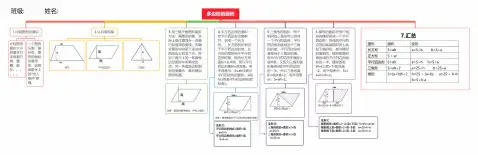
多边形的面积1.比较图形的面积①比较图形面积大小的基本方法有数方格、重叠、割补。

②一个图形分割、移补后，图形的面积没有改变，这就是数学上的“出入相补”原理。

2.认识底和高3.用三角尺画图形高的方法：画图形的高，实际上是过直线外一点画已知直线的垂线。

先确定图形中的某个顶点或图形边上的某个点，然后三角尺上的一条直角边过图形中所确定的点，另一条直角边和图形的底重合，最后画出图形的高。

注意：画高时要用虚线，并标上垂足。

4.平行四边形的面积：把平行四边形沿高剪开，拼成一个长方形，，长方形的长相当于平行四边形的底，长方形的宽相当于平行四边形的高，因为长方形面积=长X宽，所以平行四边形面积=底X高。

用字母表示：S=ah(S表示平行四边形的面积，a和h分别是平行四边形的底和高)。

注意：等底等高的平行四边形的面积相等变形式：平行四边形的底=面积÷高a=S÷h平行四边形的高=面积÷底h=S÷a5.三角形的面积：两个相同的三角形可以拼成一个平行四边形，平行四边形的底相当于三角形的底，平行四边形的高相当于三角形的高，因为平行四边形的面积=底X高，又因为三角形面积是拼成的平行四边形的一半，所以三角形面积=底X高÷2，用字母表示：S=ah÷2。

变形式：三角形的底=面积×2÷高a=2S÷h三角形的高=面积×2÷底h=2S÷a6.梯形的面积:把两个相同的梯形拼成一个平行四边形，拼成的平行四边形的底是梯形的上底和下底的和，高与梯形的高相同，梯形的面积是拼成的平行四边形面积的一半。

梯形的面积=(上底+下底)X高÷2，用字母表示：S=(a+b)×h÷2。

变形式梯形的高=面积×2÷(上底+下底) h=2S÷(a+b) 梯形的上底=面积×2÷高-下底 a=2S÷h-b 梯形的下底=面积×2÷高-上底 a=2S÷h-a7.汇总。