电路理论基础(陈希有)习题答案第十章

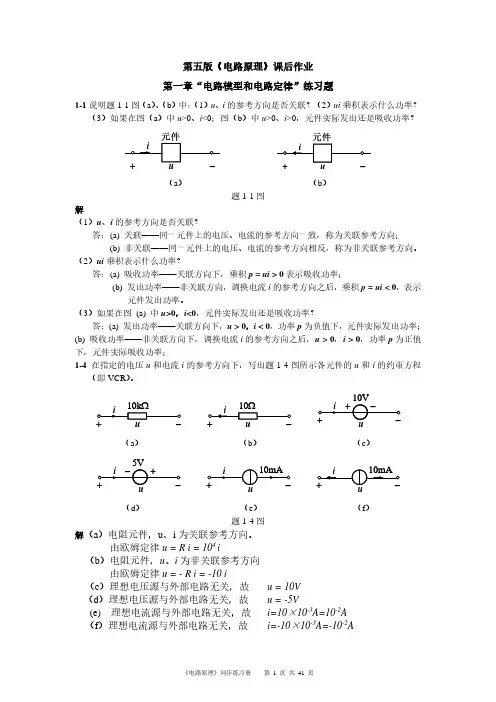
i答案10.1解：t ：：： 0时，电容处于开路，故u C (0 _) = 10mA 2k 「- 20V 由换路定律得：u C (0 .) +(0”20V换路后一瞬间，两电阻为串联，总电压为 u C (0 )。

所以再由节点①的KCL 方程得:i C (0 ) =10mA -i 1(0 .)二(10-5)mA =5mA答案10.2解：t ：：：0时电容处于开路，电感处于短路，3门电阻与61电阻相并联，所以45V6i(0J3A ，L(0Ji(0」= 2A(5+8 + 6 3)0 6+36+3u C (0J =8 i(0J = 24V 由换路定律得：U C (0 ) 7C (0J =24V ，匚(0.) “L (0_)=2A由KVL 得开关电压：u(0 ) --U c (0 ) 8 匚(0 .)=(-24 8 2)V 8V答案10.3解：t ：：： 0时电容处于开路，i =0 ,受控源源电压4i =0 ,所以U C (0 J =U C (0」=U 1(0」61.5V = 0.6V(9 6尸等效电阻i i (0 )=%(0 .) (2 2)k 」=5mA(b)所示。

R 段「4i (6 3)i容i时间常数二 R C 二 0 ・1st 0后电路为零输入响应，故电容电压为：u C (t)二 u C (0 ,)e~ =0.6e A0°V6“电阻电压为：“⑴工―6门 i 6门 ^C-dUc ^0.72e 10t V (t 0)dt答案10.43解：t ：：：0时电感处于短路，故L(0J= 39A=3A ，由换路定律得:6 + 3i L (0^i L (0J=3A求等效电阻的电路如图(b)所示。

等效电阻R 「6 •色卫=8」，时间常数.二L/R =0.5s6+3t 0后电路为零输入响应，故电感电流为i L (t) =i L (0 .)e^^ =3e 2t A (t _o ) 电感电压._2tu ,(t)二 L 匕二-24e V (t .0)dt31电阻电流为U 36C 汽L +U 1小2八i 3 2e A33「3「31电阻消耗的能量为：W3°= f 30i ；dt = f12/dt =12[-0.25ed=3W答案10.5解：由换路定律得i L (0.) “L (0」=0，达到稳态时电感处于短路，故LG) =20/4=5A求等效电阻的电路如图(b)所示。

《电路理论基础》(第三版--陈希有)习题答案第一章答案1.1解：图示电路电流的参考方向是从a 指向b 。

当时间t <2s 时电流从a 流向b,与参考方向相同，电流为正值；当t >2s 时电流从b 流向a ，与参考方向相反，电流为负值。

所以电流i 的数学表达式为2A 2s -3A 2s t i t <⎧=⎨>⎩答案1.2解：当0=t 时0(0)(59e )V 4V u =-=-<0其真实极性与参考方向相反，即b 为高电位端，a 为低电位端；当∞→t 时()(59e )V 5V u -∞∞=-=>0其真实极性与参考方向相同，即a 为高电位端，b 为低电位端。

答案1.3解：(a)元件A 电压和电流为关联参考方向。

元件A 消耗的功率为A A A p u i =则A A A 10W 5V 2Ap u i === 真实方向与参考方向相同。

(b) 元件B 电压和电流为关联参考方向。

元件B 消耗的功率为B B B p u i =则B B B 10W 1A 10Vp i u -===- 真实方向与参考方向相反。

(c) 元件C 电压和电流为非关联参考方向。

元件C 发出的功率为C C C p u i =则节点④：231A 0i i =--=若已知电流减少一个，不能求出全部未知电流。

(2)由KVL 方程得回路1l ：1412233419V u u u u =++=回路2l ：15144519V-7V=12V u u u =+=回路3l ：52511212V+5V=-7V u u u =+=-回路4l ：5354437V 8V 1V u u u =+=-=-若已知支路电压减少一个，不能求出全部未知电压。

答案1.6解：各元件电压电流的参考方向如图所示。

元件1消耗功率为:11110V 2A 20W p u i =-=-⨯=-对回路l 列KVL 方程得21410V-5V 5V u u u =+==元件2消耗功率为:2215V 2A 10W p u i ==⨯=元件3消耗功率为:333435V (3)A 15W p u i u i ===-⨯-=对节点①列KCL 方程4131A i i i =--=元件4消耗功率为:4445W p u i ==-答案1.7解：对节点列KCL 方程节点①:35A 7A 2A i =-+=节点③:47A 3A 10A i =+=节点②:5348A i i i =-+=对回路列KVL 方程得：回路1l ：13510844V u i i =-⨯Ω+⨯Ω=回路2l ：245158214V u i i =⨯Ω+⨯Ω=答案1.8解：由欧姆定律得130V 0.5A 60i ==Ω对节点①列KCL 方程10.3A 0.8A i i =+=对回路l 列KVL 方程1600.3A 5015V u i =-⨯Ω+⨯Ω=-因为电压源、电流源的电压、电流参考方向为非关联，所以电源发出的功率分别为S 30V 30V 0.8A 24W u P i =⨯=⨯=S 0.3A 15V 0.3A 4.5W i P u =⨯=-⨯=-即吸收4.5W 功率。

电路理论基础习题答案第一章1-1. (a)、(b)吸收10W ；(c)、(d)发出10W. 1-2. –1A; –10V; –1A; – 4mW.1-3. –0.5A; –6V; –15e –t V; 1.75cos2t A; 3Ω; 1.8cos 22t W.1-4. u =104 i ; u = -104 i ; u =2000i ; u = -104 i ;1-8. 2F; 4 C; 0; 4 J. 1-9. 9.6V,0.192W, 1.152mJ; 16V , 0, 3.2mJ.1-10. 1– e -106t A , t >0 取s .1-11. 3H, 6(1– t )2 J; 3mH, 6(1–1000 t ) 2 mJ;1-12. 0.4F, 0 .1-13. 供12W; 吸40W;吸2W; (2V)供26W, (5A)吸10W. 1-14. –40V , –1mA; –50V, –1mA; 50V , 1mA. 1-15. 0.5A,1W; 2A,4W; –1A, –2W; 1A,2W. 1-16. 10V ,50W;50V ,250W;–3V ,–15W;2V ,10W. 1-17. (a)2V;R 耗4/3W;U S : –2/3W, I S : 2W; (b) –3V; R 耗3W; U S : –2W, I S :5W; (c)2V ,–3V; R 耗4W;3W;U S :2W, I S :5W; 1-18. 24V , 发72W; 3A, 吸15W;24V 电压源; 3A ↓电流源或5/3Ω电阻. 1-19. 0,U S /R L ,U S ;U S /R 1 ,U S /R 1 , –U S R f /R 1 . 1-20. 6A, 4A, 2A, 1A, 4A; 8V, –10V , 18V . 1-21. K 打开：(a)0, 0, 0; (b)10V, 0, 10V; (c)10V,10V ,0; K 闭合: (a)10V ,4V ,6V; (b)4V ,4V ,0; (c)4V ,0,4V; 1-22. 2V; 7V; 3.25V; 2V. 1-23. 10Ω.1-24. 14V .1-25. –2.333V , 1.333A; 0.4V , 0.8A. 1-26. 80V . ※第二章2-1. 2.5Ω; 1.6R ; 8/3Ω; 0.5R ; 4Ω; 1.448Ω; . R /8; 1.5Ω; 1.269Ω; 40Ω; 14Ω.2-2. W P 484＝低,W P 4484⨯=高. 2-3. 1.618Ω.2-4. 400V;363.6V;I A =.5A, 电流表及滑线电阻损坏. 2-6. 5k Ω. 2-7. 0.75Ω.2-8.R 1=38K Ω,R 2=10/3K Ω 2-9. 10/3A,1.2Ω;–5V,3Ω; 8V ,4Ω; 0.5A,30/11Ω. 2-10. 1A,2Ω; 5V ,2Ω; 2A; 2A; 2A,6Ω. 2-11. –75mA; –0.5A. 2-12. 6Ω; 7.5Ω; 0; 2.1Ω. 2-13. 4Ω; 1.5Ω; 2k Ω. 2-14.1.6V ,-24V 2-15. (a) (b) –2 A ↓, 吸20W. 2-16. 2-17. 3A. 2-18. 7.33V . 2-19. 86.76W. 2-20. 1V, 4W. 2-21. 64W.2-22.电压源发50W ，电流源发1050W 2-232-24. 7V, 3A; 8V ,1A. 2-25. 4V, 2.5V, 2V. 2-26.2Ω 2-27. 60V . 2-28. 4.5V. 2-29. –18V .2-30. 原构成无解的矛盾方程组; (改后)4V,10V . 2-312-32.2.5A2-33. 3.33 k , 50 k .2-34 加法运算 )(3210i i i u u u u ++-= 2-35. R 3 (R 1 +R 2 ) i S /R 1 . 2-36. 可证明 I L =－ u S /R 3 . 2-37. –2 ; 4 . ※第三章3-1. 44V;–1+9=8V; 6+9=15V; sin t +0.2 e – t V.3-2. 155V.3-3. 190mA.3-4. 1.8倍.3-5. 左供52W, 右供78W.3-6. 1 ; 1A; 0.75A.3-7. 3A; 1.33mA; 1.5mA; 2/3A; 2A.3-8. 20V, –75.38V.3-9. –1A; 2A; 1A.3-10. 5V, 20 ; –2V, 4 .3-12. 4.6 .3-13. 2V; 0.5A.3-14. 10V, 5k .3-15.3-16.22.5V3-17. 4/3 , 75W; 4/3 , 4.69W.3-18. 3 , 529/12W.; 1 , 2.25W.3-193-20. 50 .3-21. 0.2A.3-22. 1A.3-23. 1.6V.3-24. 4A;3-25. 23.6V; 5A,10V.3-26.3-27 4V3-28. ※第四章4-1. 141.1V, 100V, 50Hz, 0.02s,0o, –120o; 120 o. 4-2. 7. o A, 1/–45 o A, 18.75/–40.9 o A.4-3. U, 7.75mA .4-4. 10/53.13A, 10/126.87o A, 10/–126.87o A, 10/–53.13o A；各瞬时表达式略。

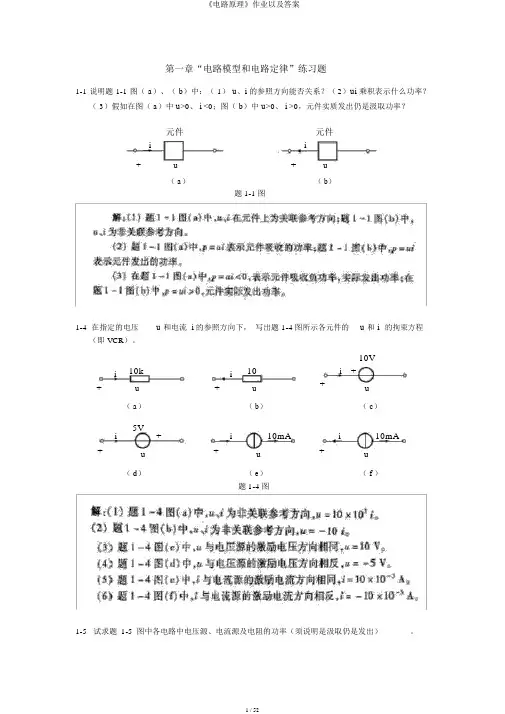
第一章“电路模型和电路定律”练习题1-1 说明题 1-1 图（ a）、（ b）中：（ 1）u、i的参照方向能否关系？（2）ui乘积表示什么功率？（ 3）假如在图（ a）中u>0、i <0；图（ b）中u>0、i >0，元件实质发出仍是汲取功率？元件元件i i+u+u（ a）（ b）题1-1图1-4 在指定的电压u 和电流 i 的参照方向下，写出题1-4图所示各元件的u 和 i的拘束方程（即 VCR）。

10k10i 10Vi i+++u+u u （ a）（ b）（ c）i 5V+i10mA i10mA+u+u+u（ d）（ e）（ f ）题1-4图1-5试求题1-5图中各电路中电压源、电流源及电阻的功率（须说明是汲取仍是发出）。

52A++15V515V 2A（ a）（b）题1-5图1-16电路如题1-16 图所示，试求每个元件发出或汲取的功率。

2I12+++U2U2V（a）题 1-16 图+515V2A（ c）A2I11I 2（b）1-20试求题1-20图所示电路中控制量u1及电压 u。

1k10k++++u1u10u12V题 1-20 图第二章“电阻电路的等效变换”练习题2-1电路如题2-1和电流 i 2、 i图所示，已知3：（1）R3=8ku S=100V，R1=2k，R2=8k。

试求以下 3 种状况下的电压；（ 2）R3=（R3处开路）；（3）R3=0（R3处短路）。

u2R1i2+i3+R2u2R3 u S题2-1 图2-5 用△— Y 等效变换法求题2-5 图中 a、b 端的等效电阻：（1）将结点①、②、③之间的三个 9 电阻组成的△形变换为 Y 形；（2）将结点①、③、④与作为内部公共结点的②之间的三个 9 电阻组成的 Y 形变换为△形。

①a999②③99b④题 2-52-11利用电源的等效变换，求题2-11 图所示电路的电流i 。

1A4424i+++1010 10V4V6V题 2-11 图2-13 题 2-13图所示电路中R1 R3 R4， R22R1，CCVS的电压u c4R1i1，利用电源的等效变换求电压u10。

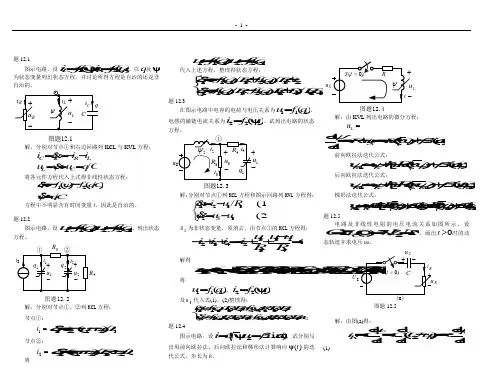
题12.1图示电路，设)(),(21R R L u f i f i ==ψ。

以q 及ψ为状态变量列出状态方程，并讨论所得方程是自治的还是非自治的。

图题12.1解：分别对节点①和右边回路列KCL 与KVL 方程：C q u u i i q i CL L R C C /===--==ψ将各元件方程代入上式得非线性状态方程：Cq C q f f q /)/()(21=--=ψψ方程中不明显含有时间变量t ，因此是自治的。

题12.2图示电路，设)(),(222111q f u q f u ==，列出状态方程。

4R R 图题12.2解：分别对节点①、②列KCL 方程： 节点①：=1i 321S 1/)(R u u i q --= 节点②：=2i 423212//)(R u R u u q --= 将)(),(222111q f u q f u == 代入上述方程，整理得状态方程：⎩⎨⎧+-=++-=)/())((/)(/)(/)(4343223112S3223111R R R R q f R q f q i R q f R q f q 题12.3在图示电路中电容的电荷与电压关系为)(111q f u =，电感的磁链电流关系为)(222ψf i =。

试列出电路的状态方程。

1u u 图题12.3解：分别对节点①列KCL 方程和图示回路列KVL 方程得：⎩⎨⎧-=-=(2) (1) /323321u u R u i q S ψ3u 为非状态变量，须消去。

由节点①的KCL 方程得：0413332432=-++-=++-R u u R u i i i i 解得()([)/()(224114332413f R q f R R R i R u u +=++=将)(111q f u =、)(222ψf i = 及3u 代入式(1)、(2)整理得：⎩⎨⎧++-+-=+++-=S u R R R R f R R R q f R R R f R R q f q )/()()/()()/()()/()(4343224331124332243111ψψψ 题12.4图示电路，设)sin(,S 3t u a i ωβ==ψ，试分别写出用前向欧拉法、后向欧拉法和梯形法计算响应)(t ψ的迭代公式，步长为h 。