材料力学第十一章习题选及其解答

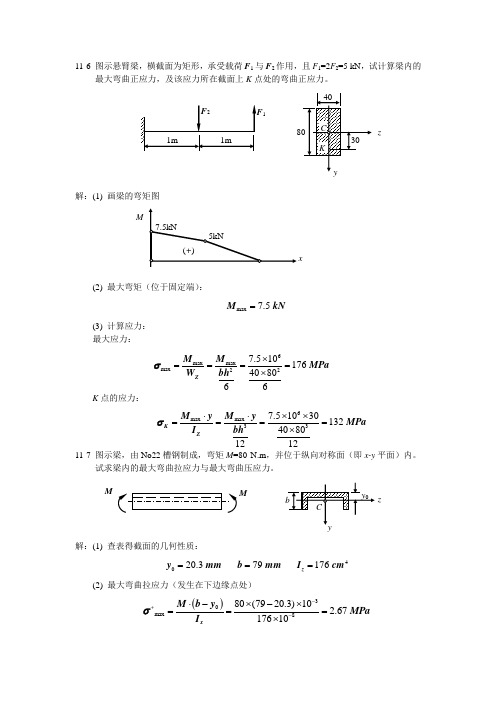
11-6 图示悬臂梁，横截面为矩形，承受载荷F 1与F 2作用，且F 1=2F 2=5 kN ，试计算梁内的最大弯曲正应力，及该应力所在截面上K 点处的弯曲正应力。

解：(1) 画梁的弯矩图(2) 最大弯矩（位于固定端）：max 7.5 M kN =(3) 计算应力： 最大应力：K 点的应力：11-7 图示梁，由No22槽钢制成，弯矩M =80 N.m ，并位于纵向对称面（即x-y 平面）内。

试求梁内的最大弯曲拉应力与最大弯曲压应力。

解：(1) 查表得截面的几何性质：4020.3 79 176 z y mm b mm I cm ===(2) 最大弯曲拉应力（发生在下边缘点处）()30max880(7920.3)10 2.67 17610x M b y MPa I σ-+-⋅-⨯-⨯===⨯6max max max227.510176 408066ZM M MPa bh W σ⨯====⨯6max max 337.51030132 ********K ZM y M y MPa bh I σ⋅⋅⨯⨯====⨯x M1zM M z(3) 最大弯曲压应力（发生在上边缘点处）30max88020.3100.92 17610x M y MPa I σ---⋅⨯⨯===⨯ 11-8 图示简支梁，由No28工字钢制成，在集度为q 的均布载荷作用下，测得横截面C 底边的纵向正应变ε=3.0×10-4，试计算梁内的最大弯曲正应力，已知钢的弹性模量E =200 Gpa ，a =1 m 。

解：(1) 求支反力31 44A B R qa R qa ==(2) 画内力图(3) 由胡克定律求得截面C 下边缘点的拉应力为：49max 3.010******* C E MPa σε+-=⋅=⨯⨯⨯=也可以表达为：2max4C C z zqa MW W σ+== (4) 梁内的最大弯曲正应力：2maxmax max 993267.5 8C zz qa M MPa W W σσ+====qxxF SM11-14 图示槽形截面悬臂梁，F =10 kN ，M e =70 kNm ，许用拉应力[σ+]=35 MPa ，许用压应力[σ-]=120 MPa ，试校核梁的强度。

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。

试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。

解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。

1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。

解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。

试问杆件横截面上存在何种内力分量，并确定其大小。

图中之C点为截面形心。

解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。

试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。

解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。

解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。

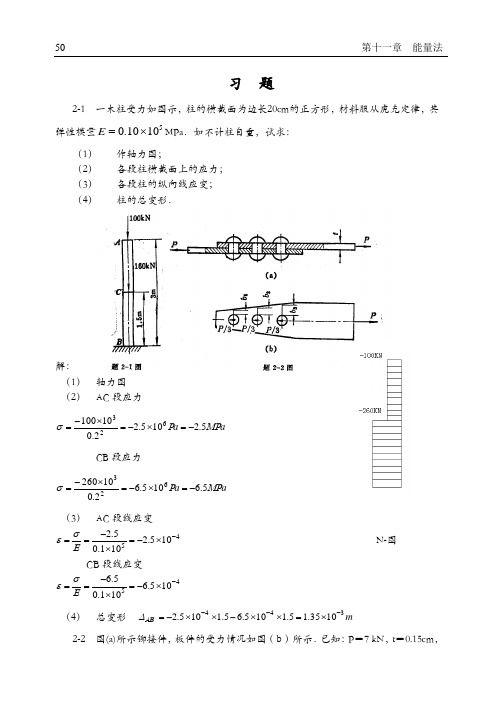
习 题2-1 一木柱受力如图示，柱的横截面为边长20cm 的正方形，材料服从虎克定律，其弹性模量51010.0⨯=E MPa ．如不计柱自重，试求：（1）作轴力图； （2）各段柱横截面上的应力； （3）各段柱的纵向线应变； （4） 柱的总变形．解：（1） 轴力图（2） AC 段应力a a MP P σ5.2105.22.010100623-=⨯-=⨯-=CB 段应力a a MP P σ5.6105.62.010260623-=⨯-=⨯-=（3） AC 段线应变45105.2101.05.2-⨯-=⨯-==E σε N-图 CB 段线应变45105.6101.05.6-⨯-=⨯-==E σε （4） 总变形 m 3441035.15.1105.65.1105.2---⨯=⨯⨯-⨯⨯-=AB ∆2-2 图(a)所示铆接件，板件的受力情况如图（ｂ）所示．已知：P ＝7 kN ，t ＝0.15cm ，b 1＝0.4cm ，b 2=0.5cm ，b 3=0.6cml 。

试绘板件的轴力图，并计算板内的最大拉应力。

解:（2）a MP σ4.194101024.015.0767311=⨯⨯⨯⨯⨯=- a MP σ1.311101025.015.0767322=⨯⨯⨯⨯⨯=-a MP σ9.388101026.015.07673=⨯⨯⨯⨯=- 最大拉应力a MP σσ9.3883max ==2-3 直径为１cm 的圆杆，在拉力P ＝10 kN 的作用下，试求杆内最大剪应力，以及与横截面夹角为α＝30o 的斜截面上的正应力与剪应力。

解:（1） 最大剪应力a d MP ππP στ66.6310101102212672241max =⨯⨯⨯⨯===- （2）︒=30α界面上的应力()a MP ασσα49.952366.632cos 12=⨯=+= a MP αστα13.5530sin 66.632sin 2=⨯=⨯=︒ 2-4 图示结构中ABC 与CD 均为刚性梁，C 与D 均为铰接，铅垂力P ＝20kN 作用在C 铰，若（1）杆的直径d 1=1cm ，（2）杆的直径d 2=2cm ，两杆的材料相同，E ＝200Gpa ，其他尺寸如图示，试求（1）两杆的应力；（2）C 点的位移。

如何处理合伙企业的协议纠纷1. 引言合伙企业是一种常见的商业组织形式，它由两个或更多个人或公司共同投资、经营和分享利润。

在合伙企业中，协议起着至关重要的作用，它规定了合伙人之间的权利和义务，为企业的稳定运行提供了法律保障。

然而，由于合伙人之间在商业活动中存在不可避免的分歧和冲突，协议纠纷也时有发生。

本文将详细介绍如何处理合伙企业的协议纠纷，帮助您在遇到类似问题时能够做出明智的决策。

2. 协议纠纷的可能原因合伙企业的协议纠纷多种多样，常见的原因包括但不限于以下几点：2.1 权益分配不均当合伙人对于利润分配不满意或出现争议时，很容易产生协议纠纷。

例如，某一合伙人认为自己付出的努力较多，应该获得更大的份额；或者某一合伙人未按照协议约定履行义务，导致其他合伙人减少了收益。

2.2 决策权分歧合伙企业中的重大决策通常需要通过合伙人会议进行讨论和表决。

当合伙人对于重要决策意见不一致时，容易产生协议纠纷。

例如，在扩大经营规模、投资新项目或解散企业等事项上各方意见分歧。

2.3 违反协议条款当一方合伙人违反协议约定时，比如未按时支付资金或未履行其他义务，可能引发其他合伙人抱怨并导致协议纠纷。

此外，如果协议中存在模糊或含糊不清的条款，也可能会给争端解决带来困难。

3. 协议纠纷解决方式当出现协议纠纷时，及时采取适当的解决方式是关键。

以下是几种常用的解决方式：3.1 协商解决作为最基本也是最常见的方式，双方可以尝试通过协商解决争端。

在协商过程中，建议通过积极沟通、充分表达各自诉求，并寻找双赢解决方案。

为了保证协商的效果和公平性，在这一过程中有必要制定明确的规则或采用中立第三方担任调解人。

3.2 仲裁程序如果协商无法达成一致或无法公正解决争端，则可转向仲裁程序。

仲裁是一种非诉讼形式，通过由专门机构组织的公正第三方仲裁员进行裁决来解决争端。

仲裁程序通常比诉讼程序简单、快速且成本较低，并且裁决结果具有强制性。

3.3 诉讼程序如果仲裁不能解决争端或一方坚持要求进行诉讼，则可以通过司法程序解决。

第十一章能量要领之阳早格格创做第十一章问案图示桁架各杆的资料相共，截里里积相等.试供正在F 力效率下，桁架的变形能.估计图示各杆的应变能.传动轴受力情况如图所示.轴的直径为40mm ，资料为45钢，E = 210GPa ，G = 80GPa.由扭转引起的应变能： 由蜿蜒引起的应变能：估计图示梁的应变能，并证明是可谦脚叠加本理及其本果.而没有谦脚叠加本理，果为应变能取内力的闭系没有是线性的.借帮于附录E ，供跨度中面（睹课本下册p40例12-4）11.6 图示刚刚架的各杆的EI 皆相等，试供截里A 、B 的位移战截里C 的转角.(a)A 面：正在A 面加一个背下的单位力.M (x 1)=0, M (x 2)=Fx 2, M (x 3)=FbC 面：正在C 加一个顺时针的力奇矩为１的单位力奇(b) A 面：正在A面加一个背下的单位力B 面：正在B 面加一个背左的单位力图示桁架各杆的资料相共，截里里积相等C 处的火仄位移战笔直位移.CF BAR火仄位移：(122) 3.828Fl FlEA EA +=-=-.笔直位移：Fl EA ∆=-.2，E 索 = 177GPa.F = 20kN ，(a)假设横梁ABCD 为刚刚体，供C 面的笔直位移.(2)若没有把ABCD 假设为刚刚体，且已知其抗直刚刚度为EI 2，试再供C 面的笔直位移.(1)42110.87.891033F EA -⎛⎫∆=⨯=⨯ ⎪⎝⎭m.(2)20.44047.89102Fx dx EI -∆=⨯+⎰4447.8910 1.48109.3710---=⨯+⨯=⨯m.11.9 等截里直杆BC 的轴线为四分之三的圆周.若AB 杆可视为刚刚性杆，试供正在F 力效率下，截里B 的火仄位移及笔直位移.火仄位移：M ()=FR cos, ()sin M R θθ=33320sin cos 2FR FRd EI EI πθθθ∆==⎰.D CFAB60 ° 60 ° 800 400400RFO B BF ORA F笔直位移：()(1cos )M R θθ=--33.36FR EI =.11.10 图示圆弧形小直率杆，仄衡半径为R .力F笔直于圆环中线地圆的仄里.试供二个F 力效率面的相对于线位移.M ()=FR sin, ()sin M R θθ= T ()=FR (1-cos), ()(1cos )T R θθ=-333pFR FR EI GI ππ=+.11.11图示圆弧形小直率杆，仄衡半径为R .正在横截里A 取B 处受一对于集结力F 效率.力F 正在圆环中线地圆的仄里内.试供二个F 力效率面的相对于线位移. M ()=FR sin,()sin M R θθ=32320sin FR FRd EI EI πθπθ∆==⎰.11.12图示轴线为火仄里内四分之一圆周的直杆，正在自由端B 效率笔直荷载F ，设EI 战GI P 为已知，试供正在F 力效率下端里B 的笔直位移.F O O Rθ B F AM ()=FR sin, ()sin M R θθ= T ()=FR (1-cos), ()(1cos )T R θθ=- 33(38)44pFR FR EI GI ππ-=+.。

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。

( × ) 1.2 力只作用在杆件截面的形心处。

( × ) 1.3 杆件某截面上的力是该截面上应力的代数和。

( × ) 1.4 确定截面力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。

( ∨ ) 1.5 根据各向同性假设，可认为材料的弹性常数在各方向都相同。

( ∨ ) 1.6 根据均匀性假设，可认为构件的弹性常数在各点处都相同。

( ∨ ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。

( ∨ ) 1.8 同一截面上各点的正应力σ必定大小相等，方向相同。

( × ) 1.9 同一截面上各点的切应力τ必相互平行。

( × ) 1.10 应变分为正应变ε和切应变γ。

( ∨ ) 1.11 应变为无量纲量。

( ∨ ) 1.12 若物体各部分均无变形，则物体各点的应变均为零。

( ∨ ) 1.13 若物体各点的应变均为零，则物体无位移。

( × ) 1.14 平衡状态弹性体的任意部分的力都与外力保持平衡。

( ∨ ) 1.15 题1.15图所示结构中，AD 杆发生的变形为弯曲与压缩的组合变形。

( ∨ )1.16 题1.16图所示结构中，AB 杆将发生弯曲与压缩的组合变形。

( × )二、填空题1.1 材料力学主要研究 受力后发生的以及由此产生1.2 拉伸或压缩的受力特征是 ，变形特征是 。

1.3 剪切的受力特征是 ，变形特征B题1.15图题1.16图外力的合力作用线通过杆轴线 杆件 沿杆轴线伸长或缩短 受一对等值，反向，作用线距离很近的力的作用 沿剪切面发生相对错动是 。

1.4 扭转的受力特征是 ，变形特征是 。

1.5 弯曲的受力特征是 ，变形特征是 。

1.6 组合受力与变形是指 。

1.7 构件的承载能力包括 ， 和 三个方面。

第一章习题答案一、解释下列名词1、弹性比功：又称为弹性比能、应变比能，表示金属材料吸收弹性变形功的能力。

2、滞弹性：在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象。

3、循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力，称为金属的循环韧性。

4、包申格效应：先加载致少量塑变，卸载，然后在再次加载时，出现σe升高或降低的现象。

5、解理刻面：大致以晶粒大小为单位的解理面称为解理刻面。

6、塑性、脆性和韧性：塑性是指材料在断裂前发生不可逆永久（塑性）变形的能力。

韧性：指材料断裂前吸收塑性变形功和断裂功的能力，或指材料抵抗裂纹扩展的能力7、解理台阶：高度不同的相互平行的解理平面之间出现的台阶叫解理台阶；8、河流花样：当一些小的台阶汇聚为在的台阶时，其表现为河流状花样。

9、解理面：晶体在外力作用下严格沿着一定晶体学平面破裂，这些平面称为解理面。

10、穿晶断裂和沿晶断裂：沿晶断裂：裂纹沿晶界扩展，一定是脆断，且较为严重，为最低级。

穿晶断裂裂纹穿过晶内，可以是韧性断裂，也可能是脆性断裂。

11、韧脆转变：指金属材料的脆性和韧性是金属材料在不同条件下表现的力学行为或力学状态，在一定条件下，它们是可以互相转化的，这样的转化称为韧脆转变。

二、说明下列力学指标的意义１、Ｅ（Ｇ）：Ｅ（Ｇ）分别为拉伸杨氏模量和切变模量，统称为弹性模量，表示产生100%弹性变形所需的应力。

２、σr、σ0.2、σs: σr :表示规定残余伸长应力，试样卸除拉伸力后，其标距部分的残余伸长达到规定的原始标距百分比时的应力。

σ0.2：表示规定残余伸长率为0.2%时的应力。

σs：表征材料的屈服点。

３、σb：韧性金属试样在拉断过程中最大试验力所对应的应力称为抗拉强度。

４、n:应变硬化指数，它反映了金属材料抵抗继续塑性变形的能力，是表征金属材料应变硬化行为的性能指标。

５、δ、δgt、ψ：δ是断后伸长率，它表征试样拉断后标距的伸长与原始标距的百分比。

第11章典型习题解析1.用卡氏第二定理求图12.3所示刚架A 截面的位移和B 截面的转角。

略去剪力Q 和轴力N 的影响，E Ⅰ为已知.解：（1）A 截面的位移AB 段弯矩：M(x)=-Px （0≤x ≤l ） ∂M(x) /∂P=-x在A 处虚加一水平力向右的力Q,之后，再令其为0.那么,BC 段弯矩：M(y)=-2P l - Q l +(P+Q)y∂M(y) /∂P=-2l +y ∂M(y) /∂ Q=-l +yA 截面的竖直位移:Y A ==∂∂∑⎰EI P Mdx ML 0 ()()()()⎰⎰+-+-+--L LEIdy y L Py PL EI dx x Px 00222 =EIPL 223A 截面的水平位移: X A =EI Q M M L ∂∂∑⎰0dx=()()EI dy y L Qy Py QL PL L 200+-++--⎰ 积分，令Q=0得 ()()EIPL EI dy y L Py PL XA L 1252230=+-+-=⎰(2)B 截面的转角在B 处虚加一力偶M B,AB 段弯矩：M(x)=-Px （0≤x<l ）BC 段弯矩：M(y)=-2P l -B M +Py （0<y<l ）∂M(x) /∂MB=0 ∂M(y) /∂MB =-1 ∑⎰∂∂=L B B EI dx M M M 0θ =()()⎰-+--L B EI dxPy M PL 0212 EIPL 432= 2.用卡氏第二定理求图示的A 截面的位移和B 截面的转角。

略去剪力Q 和轴力N 的影响，E Ⅰ为已知。

解：（1）A 截面的位移在A 点虚加一向下的力F ，支反力2qL F P Y B ++= （L 为AB 和AD 的长度） P X qL P Y C C -=--=,2AB 段弯矩： M1=0∂ M1 /∂F=0AD 段弯矩：M2(x)=2qL P F qx 2++⋅1（）x-2∂M2(x) /∂F=xCD 段弯矩：M3(y)=PyaⅠⅠ2ⅠC DA 截面的竖直位移:∑⎰∂∂=L A EIdx F M M Y 0=⎰⋅⎥⎦⎤⎢⎣⎡-⋅⎪⎭⎫ ⎝⎛++L EI xdx qx x F qL P 02222 积分，令F=0得34A PL qL Y 6EI 24EI =+求A 截面的水平位移时， 在A 处虚加一水平力向右的力Q, 再令其为0.那么, 支反力B qL Y P Q 2=++ （L 为AB 和AD 的长度）C C qL Y P Q X P Q 2=-+=-+（）+，（） AB 段弯矩： M1=0∂ M1 /∂Q=0AD 段弯矩：M2(x)=(P+Q)x ⋅∂M2(x) /∂Q=xCD 段弯矩：M3(y)=（P+Q ）y∂M3(y) /∂Q=yA 截面的水平位移∑⎰∂∂=L A EI dx Q M M X 0=()⎰⋅+L EIdx x Q P 022=()⎰⋅+L EI ydy y Q P 0积分，令Q=0得 EIPL X A 23= (2) B 截面的转角在B 处虚加一顺时针的力偶M B, 积分，并令其为零。