函数基本性质的综合应用优秀课件

• 当 > 时， − < ，则
• − ＝ −

− ＝ − ＝ − ()．
• 综上，对 ∈ (−∞，) ∪ (，＋∞)，
• ∴ ()为奇函数．
都有 − ＝ − ()．
奇偶性判定
• 【解析】 (4) =
−
−
• 定义域为 −， 关于原点对称
• ③一个奇函数，一个偶函数的积是 奇函数 ．
函数的奇偶性
• 判断函数的奇偶性
• 1、首先分析函数的定义域，在分析时，不要把函数化简，而要根据
原来的结构去求解定义域，如果定义域不关于原点对称，则一定是非
奇非偶函数．
• 2、如果满足定义域对称，则计算(−)，看与()是否有相等或互为
相反数的关系.
−
−−
+
++
−+
• 即
= 恒成立，
• 则2(＋)2＋2＝0对任意的实数恒成立．
• ∴ ＝＝0.
函数的单调性

+
•
(2)∵ =
∈ 是奇函数, 只需研究(, ＋∞)上()的单调区间即可．
•
任取， ∈ (，＋∞)，且 < ，则
应值，故函数取得最值时，一定有相应的x的值．
抽象函数的单调性
• 函数()对任意的、 ∈ ，都有 ＋ ＝ ＋ − ，并且当
> 时，() > .
• (1)求证：()是上的增函数；
• (2)若()＝，解不等式( − − ) < .
抽象函数的单调性
• ∴ ()＝， ∴原不等式可化为( − − ) < ()，
• ∵ ()是上的增函数，

x
[a,b]时g(x)=f(x)且g(x)的值域为[
1 b
,1 a
]？
若存在，求出a、b的值；若不存在，说明理由.
典例分析
引例 已知定义在[1,m]上的函数
f(x)=
1 2
x2
-x+
3 2
的值域也是[1,m]，
则实数m的值为. 3
典例分析
例3 二次函数f(x)= log3
x2
ax x
b
,
x (0, ),是否存在实数a,b，使f a(x-1)-x+3的 图象经过点（5，-4），求证：f(x)在 其定义域上仅有一个零点.
典例分析
例2 已知定义在R上的函数y=f(x)满足
f(x)+f(-x)=0,且x 0时，f(x)=2x-x2.
(1)求x<0时，函数f(x)的解析式；
(2)是否存在这样的正实数a、b，使得当
(2)当且仅当x [4,m](m>4)时,f(x-t) x 恒成立，试求t、ｍ的值.
方法提炼
1.理解函数的概念，掌握函数的图象和 性质是解决函数综合问题的基础，也是 历年高考的重点、热点和难点。
2.解决函数的综合问题,要认真分析,把 握问题的主线,把问题化归为基本问题来 解决.
3.注意等价转化,数形结合等思想的运用.
同时满足下列两个条件: ① f(x)在
（０，１］上单调递减,在[1,+)上
单调递增: ② 最小值为1.若存在,
求出a、b的值；若不存在，说明理由.
典例分析
例4 二次函数f(x)=ax2 +bx(a 0) 满足条件: ① 对任意x R,均有f(4-x)=f(2-x); ② 函数f(x)的图象与直线y=x相切. (1)求f(x)的解析式；

解 设提高x个2元，则将有10x辆电瓶车空出，且租金 总收人为
y=(20+2x)(300-10x) =-20x2+600x-200x+6000 =-20(x2-20x+100-100）十6000 =-20(x-10)2+8000.(x∈N且x≤30)
调动思维，探究新知 在活初动中2，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
2=a(0-6)2+5，
巩固练习，提升素养 在活初动中3，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
调动思维，探究新知 在活初动中2，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
解 如果x∈[0,180]，则 f(x)=5x；如果x∈(180,260]，
按照题意有
f(x)=5×180+7(x-180)=7x-360.
因此
f
x
7
x
5x , x 0 360 , x
2. 北京市自2014年5月1日起，居民用水实行阶梯水 价制度、其中年用水量不超过180m3的部分，综合用水 单价为5元/m3；超过180m3但不超过 260m3的部分，综合用水单价为7元/m3． 如果北京市一居民年用水量为xm3，其要 缴纳的水费为f(x)元。假设0≤x≤260， 试写出f(x)的解析式，并作出f(x)的图象．
由此得到，当x=10时，ymax=8000，即每辆电瓶车 的租金为
20+10×2=40 元时，毎天租金的总收人最高，为8000元.
ห้องสมุดไป่ตู้
巩固练习，提升素养 在活初动中3，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？

4 f(x)是定义在(-∞,-5],[5,+∞)上的奇函数,且 f(x)在
[5,+∞)上单调递减,试判断 f(x)在(-∞,-5]上的单调性, 并用定义给予证明.
【解析】f(x)在(-∞,-5]上单调递减,任取 x1<x2≤-5,则x1>-x2≥5,因 f(x)是奇函数且在[5,+∞)上单调递减,所以 f(x1)<f(-x2)⇒-f(x1)<-f(x2)⇒f(x1)>f(x2),即 f(x)在(-∞,-5]上 是单调减函数.
结论恒成立的是 ① . ①f(x)+ ������(������) 是偶函数; ②f(x)- ������(������) 是奇函数; ③ ������(������) +g(x)是偶函数; ④ ������(������) -g(x)是奇函数.
【解析】由 f(x)是偶函数,g(x)是奇函数,得 ������(������) 和 ������(������) 都是偶 函数,所以 f(x)+ ������(������) 与 f(x)- ������(������) 都是偶函数, ������(������) +g(x)与 ������(������) -g(x)的奇偶性不能确定.
问题1
函数单调性的证明或判断方法的归纳: 作差 → 变形 →定号; (1)用定义(点差法); (2)直接运用已知函数(如: 一次函数 、 二次函数 、反比例函数等)的单调性; (3)如果f(x)在区间D上是增(减)函数,那么f(x) 在D的任一非空子区间上也是增(减)函数; (4)图象法:根据图象的上升或下降的趋势判断函 数的单调性; (5)奇函数在对称的单调区间内有 相同 的单调 相反 的单调性. 性,偶函数在对称的单调区间内具有

3
(log1 0.5)－y，则实数x，y的关系是( )
3
A．x－y>0
B．x－y<0
C．x＋y>0
D．x＋y<0
主干回顾 ·夯基础 考点技法 ·全突破 学科素能 ·重培养
专题强化突破
数学（理用） 在日常生活中，随处都可以看到浪费粮食的现象。也许你并未意识到自己在浪费，也许你认为浪费这一点点算不了什么
专题强化突破
数学（理用） 在日常生活中，随处都可以看到浪费粮食的现象。也许你并未意识到自己在浪费，也许你认为浪费这一点点算不了什么
第二章 函数与基本初等函数
解析：选 C 由 f(t)＝f(1－t)得 f(1＋t)＝f(－t)＝－f(t)， 所以 f(2＋t)＝－f(1＋t)＝f(t)，所以 f(x)的周期为 2. 又 f(1)＝f(1－1)＝f(0)＝0， 所以 f(3)＋f－32＝f(1)＋f12＝0－122＝－14.故选 C.
5 ． 图 象 的 三 种 变 换 ： _平__移__变__换____ 、 __伸__缩__变__换___ 和 _对__称__变__换__．
6．函数的零点即为对应方程的__解__，也是函数图象与x 轴交点的__横__坐__标___．
主干回顾 ·夯基础 考点技法 ·全突破 学科素能 ·重培养
专题强化突破
数学（理用） 在日常生活中，随处都可以看到浪费粮食的现象。也许你并未意识到自己在浪费，也许你认为浪费这一点点算不了什么
第二章 函数与基本初等函数
1．(2014·烟台诊断性测试)已知幂函数 y＝f(x)的图象过点
12， 22，则 log2 f(2)＝________.
解析：12 设 f(x)＝xα，则 22＝12α， 故 α＝12，f(2)＝212 ，

时,f(x)=2x2-x,则 f(1)等于( )
(A)-3 (B)-1 (C)1 (D)3 (2)设函数 f(x)=x(ex+ae-x)(x∈R)是偶函数,则实数 a 的值
为
.
(3)已知函数 y=f(x)是 R 上的偶函数,且在(-∞,0]上是减
函数,若 f(a)≥f(2),3;1=2-x 得 x= 1 . 2
由图象可以看出,
当 x= 1 时,f(x)取到最小值 3 .
2
2
答案:(1) 1 +2 1 + 1 (2)1 (3) 3
a a2
2
反思归纳 (1)求函数值域与最值的常用方法:
①先确定函数的单调性,再由单调性求值域或最值.
②图象法:先作出函数在给定区间上的图象,再观察其最高、最低 点,求出最值. ③配方法:对于二次函数或可化为二次函数形式的函数,可用配方 法求解. ④换元法:对较复杂的函数可通过换元法转化为熟悉的函数,再用 相应的方法求值域或最值. ⑤基本不等式法:先对解析式变形,使之具备“一正二定三相等” 的条件后,再用基本不等式求出最值. ⑥导数法:先求导,然后求在给定区间上的极值,最后结合端点值,
2
4
4
(D) 1 2
(2)(2013 年高考天津卷)已知函数 f(x)是定义在 R 上的偶函数,且在区间[0,+∞)上单调递增.若
实数 a 满足 f(log2a)+f( log 1 a)≤2f(1),则 a 的
2
取值范围是( )
(A)[1,2] (B)(0, 1 ](C)[ 1 ,2](D)(0,2]
3.函数 f(x)= 1 的最大值是( D )
1 x 1 x
(A) 4 5

栏目 导引
第三章 函数的概念与性质
由函数单调性求参数范围的类型及处理方法 (1)由函数解析式求参数
栏目 导引
第三章 函数的概念与性质
(2)利用抽象函数单调性求范围 ①依据：定义在[m，n]上的单调递增(减)函数中函数值与自变 量的关系 f(a)<f(b)⇔am<≤b（a≤a>nb，），
m≤b≤n. ②方法：依据函数单调性去掉符号“f”，转化为不等式问题求解． [提醒] 单调区间是 D≠在区间 D 上单调． (1)单调区间是 D：指单调区间的最大范围是 D. (2)在区间 D 上单调：指区间 D 是单调区间的子集．
栏目 导引
第三章 函数的概念与性质
＝（x1－x2）x1（x2x1x2－4）. 因为 0＜x1＜x2＜2， 所以 x1－x2＜0，0＜x1x2＜4，x1x2－4＜0， 所以 f(x1)－f(x2)＞0，即 f(x1)＞f(x2)． 所以函数 f(x)＝x＋4x在(0，2)上单调递减．
栏目 导引
第三章 函数的概念与性质
栏目 导引
第三章 函数的概念与性质
(2)如果∀x1，x2∈D，当 x1＜x2 时，都有__f_(x_1_)_＞__f(_x_2_) ___，那么 就称函数 f(x)在区间 D 上单调递减(如图②) 特别地，当函数 f(x)在它的定义域上_单__调__递__减__时，我们就称它 是减函数．
栏目 导引
栏目 导引
第三章 函数的概念与性质
2．已知函数 f(x)＝2x－＋x1，证明：函数 f(x)在(－1，＋∞)上为减 函数． 证明：∀x1，x2∈(－1，＋∞)， 且 x1＜x2， 则 f(x1)－f(x2)＝x21－＋x11－x22－＋x12
栏目 导引
第三章 函数的概念与性质

答案 [－2，＋∞)
►单调性的两个易错点：单调性；单调区间.
（2）函数的单调递增(减)区间有多个时，不能用并集表示， 可以用逗号或“和”。
例如 函数 f(x)＝x＋1x的单调递增区间为________.
解析 由f(x)图象易知递增区间为(－∞，－1]，[1，＋∞). 答案 (－∞，－1]，[1，＋∞)
变式训练：
已知奇函数f (x)的定义域为- 2,2，且在区间 - 2,0上递减，则满足f (1 m) f (1 m2) 0的 实数m的取值范围是-1,1
题型五、函数的周期性解题方略
1.有关函数周期性的常用结论 (1)若 f(x＋a)＝f(x－a)，则函数的周期为 2|a|； (2)若 f(x＋a)＝－f(x)，则函数的周期为 2|a|； (3)若 f(x＋a)＝f（1x），则函数的周期为 2|a|； (4)若 f(x＋a)＝－f（1x），则函数的周期为 2|a|.
叫做f(x)的最小正周期.
题型归纳
题型一 判断函数的单调性 判断函数的单调性或求单调区间的方法 (1)利用已知函数的单调性. (2)定义法：先求定义域，再利用单调性定义.
(3) 图 象 法 ： 如 果 f(x) 是 以 图 象 形 式 给 出 的 ， 或 者 f(x)的图象易作出，可由图象的直观性写出它的单
域为[a－1，2a]，则a＝________，b＝________.
解析 由定义域关于原点对称得 a－1＋2a＝0，解得 a＝13，即
f(x)＝13x2＋bx＋b＋1，又 f(x)为偶函数，由 f(－x)＝f(x)得 b＝0.
答案
1 3
0
（2）若函数 f(x)为奇函数且在原点有意义，则 f(0)＝0
[点评] 解题(1)的关键是会判断复合函数的单调性；解题(2) 的关键是利用奇偶性和单调性的性质画出草图.

−

1
即函数f（x）＝x＋ 为奇函数．

函数的基本性质
例1 判断下列函数的奇偶性：
（3）f（x）＝0；
（2）f（x）＝ ；
解：（1）函数f（x）的定义域为R．
∀x∈R，都有－x∈R，且f（－x）＝0＝-f(x)＝f（x），
函数f（x）既是奇函数，又是偶函数．
1
（2）函数f（x）＝x＋ 的定义域I为[0，＋∞）．
(1)若函数f(x)在区间[a，b]上是增(减)函数，则f(x)在区间
[a，b]上的最小(大)值是f(a)，最大(小)值是f(b)．
(2)若函数f(x)在区间[a，b]上是增(减)函数，在区间[b，c]
上是减(增)函数，则f(x)在区间[a，c]上的最大(小)值是f(b)，
最小(大)值是f(a)与f(c)中较小(大)的一个．
当 > 0时,(1 ) − (2 )<0，即(1 ) < (2 )
所以函数() = + 在R上单调递增，即函数() = + 是增函数。
当 < 0时,(1 ) − (2 )>0，即(1 ) > (2 )
所以函数() = + 在R上单调递减，即函数() = + 是减函数。
1
（2）f（x）＝x＋

；
解：（1）函数f（x）＝x4的定义域为R．
∀x∈R，都有－x∈R，且f（－x）＝（－x）4＝x4＝f（x），
函数f（x）＝x4为偶函数．
1
（2）函数f（x）＝x＋ 的定义域I为（－∞，0）∪（0，＋∞）．

1
1
∀x∈I，都有－x∈I，且f（－x）＝－x＋ ＝－（x＋ ）＝－f（x），

②两个偶函数的和函数、积函数是偶函数
③一个奇函数，一个偶函数和积函数是奇函数 4、若奇函数f(x)在x=0处有定义，则f(0)=0
5、奇函数图象关于原点对称，偶函数图象关于y轴对称
（三）奇偶性式子的变形 f ( x) f ( x) f ( x) f ( x) 0 f ( x) 1( f ( x) 0) f ( x)
5、f ( x) a x a x (a 0, 且a 1)在定义域上是奇函数 6、f ( x y ) f ( x) f ( y )(a 0, 且a 1)在定义域上是奇函数
周期性
（1）定义 设函数y f ( x), x D如果存在非零常数T ,使得对任何x D都有f ( x T ) f ( x)， 则称函数y f ( x)为周期函数 T 为的一个周期，所有周期中最小的正数，称为最小正周期，简称周期。
变式：设函数f ( x)对任意实数满足f (2 x) f (2 x)，f (7 x) f (7－x)且f (0) 0, 判断函数f ( x)图象在区间上 －30， 30 与x轴至少有多少个交点.
解：由题设知函数f ( x)图象关于直线x 2和x 7对称，又由函数的性质得 是以10为周期的函数.在一个周期区间 0， 10 内 f (0) 0, f (4) f (2 2) f (2 2) f (0) 0且f ( x)不能恒为零, 故图象与x轴至少有2个交点 而区间 30,30 上有6个周期，故在闭区间－30， 30 上f ( x)图象与x轴至少有13个交点.
C. f ( x) x cos x D . f ( x) x( x
例3．已知函数f ( x)

2

∴f(x)－g(x)＝－2x＋x2，
②
(①＋②)÷2，得f(x)＝x2；
(①－②)÷2，得g(x)＝2x.
二、利用函数的奇偶性与单调性比较大小
例3 设偶函数f(x)的定义域为R，当x∈[0，＋∞)时，f(x)是增函数，则f(－2)，f(π)，
f(－3)的大小关系是
√A.f(π)>f(－3)>f(－2)
反思
感悟 利用函数的奇偶性与单调性比较大小 (1)自变量在同一单调区间上，直接利用函数的单调性比较大小； (2)自变量不在同一单调区间上，需利用函数的奇偶性把自变量转化到同 一单调区间上，然后利用单调性比较大小.
跟踪训练3 (1)已知偶函数f(x)在[0，＋∞)上单调递减，则f(1)和f(－10)的大小关系为
12345
4.奇函数f(x)在区间[0，＋∞)上的图象如图,则函数f(x)的增区间为_(－__∞__，__－__1_]_，__[_1_，__＋__∞__) . 解析 奇函数的图象关于原点对称，可知函数f(x)的增区间为(－∞，－1]，[1，＋∞).
12345
5.已知偶函数f(x)在[0，＋∞)上单调递减，f(2)＝0.若f(x－1)>0，则x的取值范围是 __(－__1_,_3_)_.
知识点二 奇偶性与单调性
若函数f(x)为奇函数，则f(x)在关于原点对称的两个区间[a，b]和[－b，－a]上具有 相同的单调性；若函数f(x)为偶函数，则f(x)在关于原点对称的两个区间[a，b]和 [－b，－a]上具有相反的单调性.
预习小测 自我检验
YU XI XIAO CE ZI WO JIAN YAN
1.若f(x)的定义域为R，且f(x)为奇函数，则f(0)＝___0_____. 2. 若 f(x) 为 R 上 的 奇 函 数 ， 且 在 [0 ， ＋ ∞) 上 单 调 递 减 ， 则 f( － 1)____>____f(1).( 填 “>”“＝”或“<”)

3.3 函数的性质 ——单调性
情境导入 探索新知
例题辨析 巩固练习 归纳总结 布置作业
下图是某市某天气温（℃）是时间(时)的函数图像，
记这个函数为 = ()．
由图可知：
在给定区间[4，14]上，对于图像上的
任意两点1 1 , 1 ，2 2 , 2 ，当1 < 2
时，都有1 < 2 ，即，f(x1)＜f(x2)．
讨论函数() = 2 + 1在(−∞， + ∞）上的单调性．
解 任取1 , 2 ∈ (−∞， + ∞）且1 < 2 ，
因为 1 − 2 = 21 + 1 － 22 + 1 =21 − 22
= 2 1 －2 ，
由1 − 2 < 0，所以 1 − 2 < 0,即
1.书面作业：完成课后习题和学习与训练；
2.查漏补缺：根据个人情况对课题学习复习与回顾;
3.拓展作业：阅读教材扩展延伸内容.
再见
3.3 函数的性质 ——单调性
例1
情境导入 探索新知
例题辨析 巩固练习 归纳总结 布置作业
根据函数在R上的图像，如图所示，写出其单调区间：
解 （1）由图（1）所示函数图像可知，函数 = ()的定义域为R，增区间为
(−∞， 0]，减区间为[0， + ∞)．
（2）由函数图像（2）可知，函数 = () 的定义域为 (−∞， 0) ∪ （0, +∞) ，
3.3 函数的性质 ——单调性
情境导入 探索新知
例题辨析 巩固练习 归纳总结 布置作业
1．填空题（填“增”或“减”）：
（1）函数 = + 1 在（－，+）上是_________函数；

x2时取等号)
凹函数 :
f
( x1
x2 2
)
1( 2
f
(x1)
f
(x2 ))(仅当x1
x2时取等号)
例3.已知定义域为[1,1]的函数f ( x)为奇函数,
当x [0,1]时, f ( x) 2x 2 x, 求f ( x)的最大值与 最小值
变式1、若f（x）是R上的减函数，且f（x）的图象经过点A （0，3）和B（3，－1），则不等式|f（x+1）－1|＜2的解集 是__________________
• 午餐：既要补充上午的能量消耗，又要为下午 的消耗储备能量。如蛋白质、脂肪及一定 量的蔬菜。
• 晚餐：要做到吃得适量、吃得好。保证足够的 热量和适量的蛋白质、脂肪及一定量的蔬 菜。
• 学以致用中学生每日吃食物的合适量 （营养食谱）
• 主食：（米、面、杂粮）400—500克 肉类：（包括鱼、虾）50—75克 蛋类：（1—2个）50—100克 豆制品：50—100克 新鲜蔬菜：400—500克 植物油：10克 食盐：4—8克 除以上食物外酌情增加下列食物： 牛奶：150—200克 水果：400—500克 芝麻、花生、大蒜不多于50克 甜食（糕点、糖果）不多于15克
• 1.下列元素在人体内最终代谢产物错误的是 （B）
•
A. 碳→碳酸
B. 氮→硝酸
•
C. 硫→硫酸
D. 磷→磷酸
• 2.下列食物属碱性食物的是（B ）
• A.面包 B.海带 C.大米 D. 鸡蛋
1、膳食结构？ 2、要求：种类齐全，数量充足，比例适当且
与人体的需要保持平衡。
3、平衡膳食宝塔？
1. 平衡膳食要求各种营养素搭配合理，在 可能的情况下，要吃得品种多些、杂些、

变1式 :若函 f(x)数 ax b,上述结 ? 果 y 如何
yf(x)
变式 2:若函f数 (x)图象如右,图所示
上述结果 ? 如何
x
点评：凹凸型两种函数图象规律
O
凸 函 数 : f ( x 1 2 x 2 ) 1 2 ( f ( x 1 ) f ( x 2 ) ) ( 仅 当 x 1 x 2 时 取 等 号 )
研究函数时，常考虑函数哪些问题？
1、函数三要素： 定义域、值域、对应法则
2、函数图象： 作图、图象特征（对称性、最高或最低点、拐点、
凹凸等） 3、函数的奇偶性、单调性、最值、有界性 4、常用思想方法：
数形结合法、化归法、恒等变换、分类讨论等
例 1 . 已 知 函 数 f ( x ) = a x 3 + b x - 2 , 且 f ( - 2 ) = 1 , 则 f ( 2 ) = _ _ _ _ _ _ _
4.已知x 不 2a等 x1式 0对 x(2,4)恒成 , 立 则实 a的数 取值 __范 __围 __是 ____
2.已知 f(x 函 )a数 x2a1在区 [1,1]上 间函数 值有正 ,则 也 实 a的 有 数 取 负值 __范 __围 _ 是 3.已 知 定 R上 义的 在偶 f(x函 )满数 足 :对 任 意 x[0, )(x1 x2),有f(xx22) xf1(x1)0,则 f(3),f(2),f(1)的 大 小_关 __系 __是 ______
例 5 .已 知 f(x) 函 2x2 数 8x4a 对 任 x [ 意 2 ,3 ] 的 恒 0 有 f(x)4,求 0 a 实 的数 取 值 范 围
变 .已 式知 f(x) 函 x2 数 a x 4 对任 x (0 意 ,1 ] 的 恒f(x 有 )0 ,求a 实 的数 取 值 范 围

2、组合函数的性质应用： 1 的图像大致 1函数f x ln x 1

lg x 的图像大致是 2 函数y x

3、单调、奇偶性、对称性的综合应用 例3、设f x 是R上的奇函数，当0 x 1时，f x x, 则f x _______ 2x , x0 练习 、设奇函数f x 1 , 则g 2 __ g x , x 0 1 1 2、设函数f x f x 并且f x 有三个零点，则 2 2 所有零点和=_______ 3、定义在R上的奇函数f x f x , 且x 0,2时，f x log 2 x 1 , 请研究函数在 8, 8的性质
4、函数性质的综合应用： 1 x 例已知2 256且 log 2 x , 求函数f x log 2 log 2 2 的最大和最小值
x 2
x 2
练习1、已知函数y=4x 32 x 3的值域为1, 7 ，试确 定x的范围
函数的基本性质
函数的性质的综合应用
1、函数性质的综合应用：单调性奇偶性的应用 例1、若函数f x k 1 a x a x a 0且a 1 在R上既 是奇函数，又是减函数，则g x log a x k 的图像是
ቤተ መጻሕፍቲ ባይዱ
4x 1 例2、函数f x x 的图像 2 A关于原点对称B关于直线y=x对称C关于x轴对称D关于y轴对称 2 练习2、函数f x lg 1的图像 x 1 A关于原点对称B关于直线y=x对称C关于x轴对称D关于y轴对称

函数有定义域、对应关系和值域三要素，为什么判断两个函数是不是同一个函数， 只看定义域和对应关系？
提示：由函数的定义域和对应关系可以求出函数的值域，所以判断两个函数是不 是同一个函数，只看定义域和对应关系即可．
1．区间[1，＋∞)与集合{x|x≥1} 表达的意思一致吗？
2．若两个函数的定义域与值域都相同，则这两个函数是同一个函数吗？ 3．函数 f(x)＝x2－x 与 g(t)＝t2－t 是同一个函数吗？ 提示：1.一致；2.不是；3.是．
20.因为 g(x)＝x＋1 2 ，所以 g(a)＋g(0)＝a＋1 2 ＋0＋1 2 ＝a＋1 2 ＋12 (a≠－2).g(f(2))＝g(10)＝
1 10＋2
＝112
.
(2)g(f(x))＝f（x）1 ＋2 ＝2x2＋12＋2 ＝2x21＋4 .
【备选例题】 已知函数 f(x)＝x＋x1 ， (1)求 f(x)的定义域； (2)求 f(－1)，f(2)的值；
（x－1）2 ＝x1－－1x，，xx≥＜11，， 当 x＜1 时，y＝ （x－1）2 与 y＝x－1 对应关系不同，所以 y ＝ （x－1）2 与 y＝x－1 不是同一个函数，故 D 不符合题意．
判断同一个函数的三个步骤和两个注意点 (1)判断函数是否为同一个函数的三个步骤．
(2)两个注意点． ①在化简解析式时，必须是等价变形； ②与用哪个字母表示无关． 微提醒：不能将函数的解析式变形后求定义域．
2．函数 f(x)＝ 1－x2 ＋2x1－1 的定义域为(
)
A．[－1，1]
B．－1，12 ∪21，1
C．－12，12
D．12，1
ቤተ መጻሕፍቲ ባይዱ
【解析】选 B.要使函数有意义，则需 1－x2≥0 且 2x－1≠0，

函数的基本性质1. 函数的定义函数是一种特殊的关系，它将一个或多个输入值映射到唯一的输出值。

数学上，函数被表示为f(x)，其中x是函数的输入值，f(x)是对应的输出值。

函数可以用图像、映射关系、表格或公式来表示。

每个输入值对应唯一的输出值。

2. 函数的图像函数的图像是函数在坐标系中的图形表示。

在二维坐标系中，函数的图像通常是一条曲线。

函数的图像描述了函数的性质，包括函数的增减性、奇偶性、最值等。

通过观察函数的图像，我们可以得到很多关于函数的信息。

3. 函数的定义域和值域函数的定义域是指函数所有可能输入值的集合。

函数的值域是指函数所有可能输出值的集合。

函数的定义域可以是实数集、整数集、有限集或者其他数学对象的集合，具体根据函数的性质而定。

函数的值域取决于定义域和函数本身的性质。

例如，一个一元线性函数的值域是实数集，而一个常值函数的值域只有一个值。

4. 函数的性质4.1. 奇偶性一个函数被称为奇函数，如果对于定义域内的每个x，都有f(-x) = -f(x)。

换句话说，奇函数的图像关于原点对称。

一个函数被称为偶函数，如果对于定义域内的每个x，都有f(-x) = f(x)。

换句话说，偶函数的图像关于y轴对称。

奇偶性是函数的基本性质之一，在分析函数的图像时常常用到。

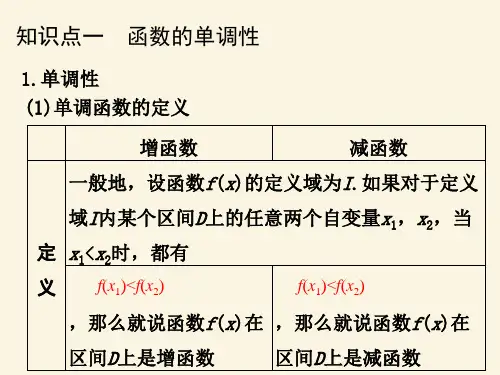
4.2. 单调性一个函数被称为单调递增，如果对于定义域内的任意两个不同的x和y，都有x < y时，f(x) < f(y)。

一个函数被称为单调递减，如果对于定义域内的任意两个不同的x和y，都有x < y时，f(x) > f(y)。

4.3. 最值函数的最大值是定义域内的最大输出值，函数的最小值是定义域内的最小输出值。

4.4. 周期性一个函数被称为周期函数，如果存在一个正数T，使得对于所有的x，有f(x+T) = f(x)。

这个正数T被称为函数的周期。

周期函数的图像在一个周期内是重复的，我们可以通过观察一个周期内的图像来推断函数的性质。