2019-2020年高中数学 第二章 算法初步 2.3 循环结构教学案 北师大版必修3

2019-2020学年高中数学 第二章 算法初步 2.3 几种基本语句2.3.2 循环语句教案 北师大版必修3 本节教材分析一、三维目标1、知识与技能(1)理解、掌握循环语句；(2)能运用循环语句表达解决具体问题的过程；(3)培养学生逻辑思维能力与表达能力，进一步体会算法思想．2、过程与方法提出问题——自主学习——讨论结果．二、教学重点：循环语句的表示方法、结构和用法三、教学难点：循环语句的写法．四、教学建议通过前面的学习，学生学会了输入语句、输出语句、赋值语句和条件语句的基本用法，本节将介绍循环语句的用法． 程序中的循环语句与程序框图中的循环结构存在一一对应关系，这种对应关系对于学生理解循环语句的结构，进一步理解算法中的循环结构都是很有帮助的．我们可以给出循环语句的一般格式，让学生自己画出相应的程序框图，也可以给出程序框图，让学生写出算法语句，提高学生的应用能力． 新课导入设计导入一作为老师，我经常用Excel 来算每一次考试全班学生的总分、平均分，Excel 很神奇，它能在不到一秒钟的时间内就算出了全班学生的平均分．大家能不能帮我解释一下，Excel 是怎么实现这些功能的呢？学好本节我相信对大家解决这个问题有很大的帮助． 导入二一位同学不小心违反了学校纪律，班主任令其写检查，他写完后交给班主任，班主任看后说：“认识不深刻，拿回去重写，直到认识深刻为止”．这位同学一想，这不是一个循环结构吗？可惜我还没学循环语句，不然可以写一个算法语句输入计算机了．同学们，今天我们开始学习循环语句．导入三在上一节，我们学习了For 语句，它是用来解决循环次数一定时的循环结构的算法描述的，但我们在学习循环结构时，我们还见到了很多循环条件未知的循环结构，这样的循环结构该怎么用算法语句描述呢?【教学过程】 一、问题情境1．问题1：设计计算135799⨯⨯⨯⨯⨯的一个算法，并画出流程图．二、学生活动解决问题1的算法是：对于以上算法过程，我们可以用循环语句来实现．S1 S ←1S2 I ←3S3 S ←S ×IS4 I ←I+2S5 若I ≤99，则返回S3S6 输出S流程图：三、建构数学1．循环语句：循环语句一般有种：For 语句、Do Loop 语句．（1）“For 语句”是在循环次数已知时使用的循环， 其一般形式为：例如：问题1中算法可用For 语句表示为：说明：①上面 “For”和“Next ”之间缩进的步骤称为循环体；②如果省略“Step 2”，默认的“步长”为1，即循环时，I 的值每次增加1（步长也可以为负，例如，以上“For 循环”第1行可写成：For I = 99 To 1 Step -2）； ③“For 循环”是直到型循环结构，即先执行后判断．（2）“Do Loop 语句” 是在循环次数未知时使用的循环，其一般形式为：例如：问题1中的算法可“While 循环”语句表示为：说明：①上面“Do ”和“Loop While”之间缩进的步骤称为循环体；②“While 循环”是当型循环结构，其特点是“前测试”，即先判断，后执行.若初始条件不成立，则一次也不执行循环体中的内容；③任何一种需要重复处理的问题都可以用这种前测试循环来实现．四、数学运用1．例题：例1．编写程序，计算自然数1+2+3+……+99+100的和。

§2.2.3循环结构一、课程标准：通过模仿、操作、探索，经历通过设计程序框图表达解决问题的过程.在具体问题的解决过程中，理解程序框图的三种基本逻辑结构：顺序、条件、循环.二、教学目标：1.进一步理解程序框图的概念；2.掌握运用程序框图表达循环结构的算法；3.培养学生逻辑思维能力与表达能力.三、教学重点：运用程序框图表达循环结构的算法。

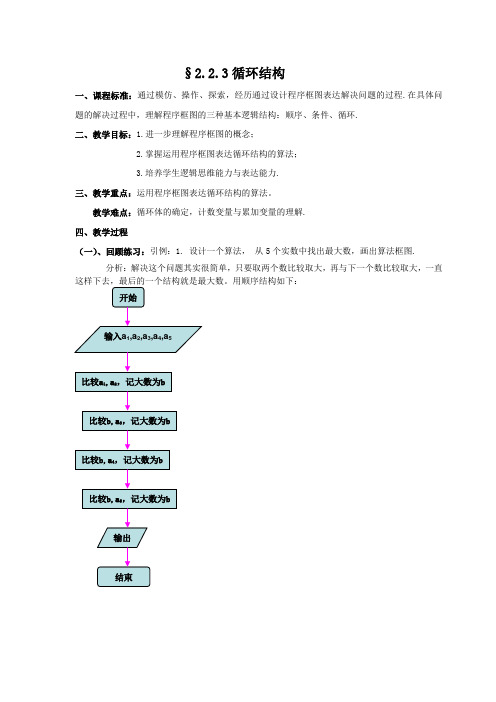
教学难点：循环体的确定，计数变量与累加变量的理解.四、教学过程（一）、回顾练习：引例：1. 设计一个算法，从5个实数中找出最大数，画出算法框图.分析：解决这个问题其实很简单，只要取两个数比较取大，再与下一个数比较取大，一直这样下去，最后的一个结构就是最大数。

用顺序结构如下：2.设计一个算法，求100个实数中的最大数，画出算法框图.能用上述方法吗？在本题中如果我们仍然用顺序结构和选择结构来画流程图，就显得比较繁琐，为了使得算法简洁我们今天学习循环往复的逻辑结构――循环结构。

（二）、新课例1 （见课本P93 例7）归纳：循环结构：在一些算法中，也经常会出现从某处开始，按照一定条件，反复执行某一处理步骤的情况，这种结构称为循环结构..计数变量：在循环结构中，通常都有一个起到循环计数作用的变量，这个变量的取值一般都含在执行或终止循环体的条件中. 例2 （ 见课本P94 例8）解：（1）变量y是循环变量，控制着循环的开始和结束.（2）虚线所框部分，其功能是判断年份y是否是闰年，并输出结果.（3）算法的处理功能是：判断2000～2500（包括2500）年中，哪些年份是闰年，哪些年份不是闰年，并输出结果.例3 （见课本P94 例9）例9 设计一个算法，求100个实数中的最大数，画出算法框图.分析：点评：需要反复进行的相同操作，如果按照顺序结构来描述，算法显的十分烦琐，不利于阅读，如果采取循环结构来描述，算法就显得简洁，清楚。

循环结构是一种简化算法叙述的结构。

练习1：画出100321⨯⨯⨯⨯ 的程序框图. 练习2；见课件课时训练小结：画循环结构程序框图前：①确定循环变量和初始条件；②确定算法中反复执行的部分，即循环体；③确定循环的转向位置；④确定循环的终止条件. （四）、课堂小结1. 理解循环结构的逻辑，主要用在反复做某项工作的问题中；2. 画循环结构程序框图前：①确定循环变量和初始条件；②确定算法中反复执行的部分，即循环体；③确定循环的转向位置；④确定循环的终止条件。

<<循环结构>>教学设计一、教学目标1．知识与技能目标①理解循环结构，能识别和理解简单的框图的功能。

②能运用循环结构设计程序框图解决简单的问题。

2．过程与方法目标通过模仿、操作、探索，学习设计程序框图表达，解决问题的过程，发展有条理的思考与表达的能力，提高逻辑思维能力。

3．情感、态度与价值观目标通过本节的自主性学习，让学生感受和体会算法思想在解决具体问题中的意义，增强学生的创新能力和应用数学.二、教学重点与难点重点：理解循环结构，能识别和画出简单的循环结构框图。

难点：循环结构中循环条件和循环体的确定。

三、教学过程设计（一）【创设情境】引列：试求自然数1+2+3+……+99+100的和。

显然大家都能准确地口算出它的答案：5050。

而能不能将这项计算工作交给计算机来完成呢？你能写出它的一个算法，并用框图表示你的算法吗？【设计意图】这是一个累加问题，解决问题的方法不是惟一的，当然程序的设计也是有多种的，只是程序简单与复杂的问题。

此环节旨在提出递推求和的方法，复习顺序结构，导入新课。

目的是提升学生的求知欲、探索欲，使学生保持良好、积极的情感体验。

（二）【探究新知】1．循序渐进，理解知识①将“递推求和”转化为“循环求和”的方法和途径通常，我们按照下列过程计算的值。

第1步，0+1=1第2步，1+2=3第3步，3+3=6即21324312,3,4(2,3,,100)i i S S S S S S S S i i -=+=+=+=+=用递推公式表示为：111(2,3,100)ii S i S S i -=⎧=⎨=+⎩ 即第i 步的结果＝第（i －1）步的结果＋i 。

为了方便，有效地表示上述过程，我们用一个累加变量S 来表示每一步的计算结果，即把i S +的结果仍记为S ,从而把第i 步表示为i S S +=, 其中S 的初始值为0, 依次取1,2,……,100.由于i 同时记录了循环的次数,所以也称为计数变量.② 对赋值语句“1i i =+”、“ i S S +=”含义的解释赋值语句, 用来表明赋给某一个变量一个具体的确定值的语句。

3．2 循环语句整体设计教学分析教科书通过实例介绍了循环语句，For语句和Do Loop语句的区别是For语句适用于预先知道循环次数的循环结构，而Do Loop语句适用于预先不知道循环次数的循环结构．值得注意的是尽可能借助于信息技术，上机实习，以便学习更为准确的算法大体语句．三维目标1．掌握循环语句及其用法，提高解决问题的能力．2．通过学习循环语句，进一步体会算法的思想．重点难点教学重点：循环语句及其应用．教学难点：设计循环语句．课时安排1课时教学过程导入新课思路1(情境导入)．一名同窗不小心违背了学校纪律，班主任令其写检查，他写完后交给班主任，班主任看后说：“熟悉不深刻，拿归去重写，直到熟悉深刻为止．”这位同窗一想，这不是一个循环结构吗？可惜我还没学循环语句，不然可以写一个算法语句输入计算机了．同窗们，今天咱们开始学习循环语句．思路2(直接导入).2006年年末，我国互联网上大规模暴发“熊猫烧香”病毒及其变种，该病毒通过量种方式进行传播，并将感染的所有程序文件改成熊猫举着三根香的样子，同时该病毒还具有盗取用户游戏账号等功能．该病毒传播速度快，危害范围广，全国有上百万个人用户、网吧及企业局域网用户蒙受感染和破坏．经查，“熊猫烧香”病毒的制作者为湖北省武汉市人李俊，据李俊交代，其于2006年10月16日编写了“熊猫烧香”病毒并在网上普遍传播，而且还以自己出售和由他人代卖的方式，在网络上将该病毒销售给120余人，非法获利10万余元．经病毒购买者进一步传播，致使该病毒的各类变种在网上大面积传播，对互联网用户计算机安全造成了严重破坏．其实电脑病毒就是循环语句，你知道循环语句有几种吗？教师点出课题．推动新课新知探究提出问题阅读教科书指出两种循环语句的格式、各自适用范围和区别.讨论结果：语句(1)格式：For 循环变量＝初始值To 终值循环体Next(2)适用于预先知道循环次数的循环结构．2．Do Loop语句(1)格式：Do循环体Loop While 条件为真(2)适用于预先不知道循环次数的循环结构．3．两种循环语句的区别是For语句先从循环变量的初始值开始执行一次循环体后，直到循环变量取到其终值则结束循环，适用于预先知道循环次数的循环结构；而Do Loop语句则是先判断条件，当条件为真时，执行循环体，不然结束循环，适用于预先不知道循环次数的循环结构．应用示例思路1例1 设计算法，输出菲波那契数列的前50项，利用For语句描述该算法．f1＝0f2＝1输出”菲波那契数列为”，f1，f2For i＝3 To 50f3＝f1＋f2输出f3f1＝f2f2＝f3Next变式训练请阅读下列用For语句写出的算法，说明该算法的处置功能．S＝0T＝1For i＝1 To 20S＝S＋iT＝T iNext输出S输出T分析：由For语句的形式，咱们知道i是循环变量，初始值为1，终止值为20，循环体为：S＝S＋i；T＝T i．解：算法的算法框图如图1.图1因此，这个算法实际上处置的是求和S＝1＋2＋3＋…＋20及求积T＝1×2×3×…×20这两件事情.例2 二分法算法求方程近似解，算法框图如图2所示．用Do Loop语句描述这个算法．图2解：用语句描述为：输入ε；a ＝0；b ＝1；DoIf f ⎝ ⎛⎭⎪⎫a ＋b 2＝0 Then 跳出循环ElseIf f (a )·f ⎝ ⎛⎭⎪⎫a ＋b 2＜0 Then b ＝a ＋b 2Elsea ＝a ＋b 2End IfEnd IfLoop While b －a ≥ε输出a ＋b 2. 点评：在Do Loop 语句中，每一次重复后，都需要查验While 后的条件是不是被知足，一旦不知足条件，循环停止．思路2例1 下列程序执行后输出的结果是__________．S ＝1For i ＝9 To 11S ＝S iNext输出S分析：该程序的运行进程是：S＝1 9＝9，S＝9 10＝90，S＝90 11＝990.答案：990点评：按照循环语句讨论其执行结果时，通常按照循环语句所表达的意义，具体执行程序，明确程序的功能，就可以够取得其程序结果；已知循环次数用For循环，无法预知循环次数时用Do Loop循环.变式训练1．下列程序：A＝1DoA＝A＋1Loop While A≤100输出A程序运行的结果是( )．A．99 B．100 C．101 D．102答案：C2．下列程序：B＝1For A＝1 To 5B＝A B；Next输出B该程序的功能是__________．答案：计算1×2×3×4×5的值例2 编写程序计算12＋22＋32＋…＋1002的值．分析：由于重复做加法运算，所以用循环语句来实现．算法框图如图3所示．图3解：程序1(Do Loop循环语句)：i＝1sum＝0Dosum＝sum＋i^ 2i＝i＋1Loop While i≤100输出sum程序2(For循环语句)：sum＝0For i＝1 to 100sum＝sum＋i^ 2i＝i＋1Next输出sum点评：若是事前不知道循环的次数时，通常常利用Do Loop循环语句来实现．对于重复做一个动作时，一般用循环语句来实现.变式训练编写程序，求知足1＋3＋5＋…＋n＞500的最小自然数n.分析：结束循环的条件即和大于500，可以用累加的方式，一个数一个数地加到累加器中，每加一个数就把累加器的值与500比较，直到大于500为止，用Do Loop循环．注意：最后输出的是i的值，此时i的值不是知足条件的最小．．自然数.解：用Do Loop循环结构的算法框图，如图4所示．图4程序如下：i＝1sum＝0Dosum＝sum＋ii＝i＋2Loop While sum≤500i＝i－2输出i知能训练1．循环语句对应的大体逻辑结构是( )．A．模块结构B．顺序结构C．选择结构D．循环结构答案：D2．以下程序：x＝－1Dox＝x xLoop While x＜10输出xA．输出结果是1B．能执行一次C．能执行10次D．是“死循环”，有语法错误分析：从循环语句的格式看，这个循环语句是Do Loop循环语句，那么当知足条件x＞10时，终止循环体，可是第一次执行循环体后x＝1，由于x＝1＜10成立，则再次执行循环体后，x＝1，这样无穷循环下去，是一个“死循环”，有语法错误，循环终止的条件永远不能知足．答案：D3．若是程序运行后输出的结果是720，则在横线处应填入的正整数是______．t＝10S＝1DoS＝S* tt＝t－1Loop While t＞______输出S答案：7拓展提升某班50人参加数学单元测试，统计出所得分数在80分或80分以上的人数，画出算法框图，编写程序．解：算法框图如图5所示．图5程序如下：t＝0For n＝1 To 50输入mIf m≥80t＝t＋1End IfNext输出t课堂小结这节课学习了利用大体语句描述算法，和自然语言相较，大体语句描述的算法显得直观、清楚、明了，它的另一个长处是比较接近程序语言，便于编写程序，上机实现．作业习题2－3 A组6，B组 1.设计感想本节的导入符合学生心理要求，能够激发学生的学习兴趣．算法像一个故事，循环语句就是故事的高潮，它以前面的内容为基础，是前面内容的总结和发展．本节选用了大量的出色例题为故事高潮的到来作好了铺垫，出色的点评把本节推向了高潮，所以本节教案值得期待．备课资料备选习题1．设计一个计算1×3×5×7×…×99的算法，并编写算法程序．解：算法如下：1．S ＝1.2．i ＝3.3．S ＝S ×i.4．i ＝i ＋2.5．若是i≤99，那么转到第3步．6．输出S .程序如下：(“Do Loop 型”循环语句)S ＝1i ＝3DoS ＝S *ii ＝i ＋2Loop While i≤99输出S2．已知S ＝1＋12＋13＋ (1)，输入n 的值，输出S 的值．画出算法框图，并编写程序． 解：算法框图如图6所示．图6程序如下：输入ni ＝1sum ＝0Dosum ＝sum ＋1/ii ＝i ＋1Loop While i≤n输出sum。

高中数学第二章算法初步2.2.3 循环结构教案北师大版必修3编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第二章算法初步2.2.3 循环结构教案北师大版必修3）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第二章算法初步2.2.3 循环结构教案北师大版必修3的全部内容。

2。

3 循环结构错误!教学分析教科书通过实例介绍了循环结构．在教学过程中，教师应注意通过实例来分析循环结构，以加深学生的感性认识．三维目标掌握循环结构及其相应的算法框图，提高学生分析问题和解决问题的能力．重点难点教学重点：理解循环结构,会设计循环结构．教学难点:设计循环结构．课时安排1课时错误!导入新课思路1（情境导入)．我们都想生活在一个优美的环境中,希望看到的是碧水蓝天，大家知道工厂的污水是怎样处理的吗？污水进入处理装置后进行第一次处理，如果达不到排放标准，则需要再进入处理装置进行处理，直到达到排放标准．污水处理装置是一个循环系统，对于处理需要反复操作的事情有很大的优势．我们数学中有很多问题需要反复操作,今天我们学习能够反复操作的逻辑结构——循环结构．思路2(直接导入）．前面我们学习了顺序结构，顺序结构像一条没有分支的河流，奔流到海不复回;上一节我们学习了选择结构,选择结构像有分支的河流最后归入大海．事实上,很多水系是循环往复的,今天我们开始学习循环往复的逻辑结构-—循环结构．推进新课错误!错误!1．请大家举出一些常见的需要反复计算的例子．2．什么是循环结构、循环体？3．试用算法框图表示循环结构．讨论结果：1．例如用二分法求方程的近似解、数列求和等．2．在一些算法中，经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是循环结构．反复执行的步骤称为循环体．3．在一些算法中要求重复执行同一操作的结构称为循环结构，即从算法某处开始,按照一定条件重复执行某一处理的过程．重复执行的处理步骤称为循环体．循环结构,如图1所示，它的功能是先执行重复执行的A框，然后判断给定的条件P是否成立，如果P仍然不成立，则返回来继续执行A框，再判断条件P是否成立．继续重复操作，直到某一次给定的判断条件P成立时为止,此时不再返回来执行A框，离开循环结构．继续执行下面的框图．图1错误!思路1例1 设计算法，输出1 000以内能被3和5整除的所有正整数，画出算法框图．分析:这个问题很简单，凡是能被3和5整除的正整数都是15的倍数，由于1 000＝15×66＋10，因此1 000以内一共有66个这样的正整数．解：引入变量a表示待输出的数，则a＝15n（n＝1,2,3，…,66）．n从1变到66，反复输出a，就能输出1 000以内的所有能被3和5整除的正整数．算法框图如图2所示．图2点评：像这样的算法结构称为循环结构,其中反复执行的第②部分称为循环体．变量n控制着循环的开始和结束，称为循环变量，第①部分就是赋予循环变量初始值，预示循环开始．第③部分判断是否继续执行循环体，称为循环的终止条件。

循环结构一、教学内容分析《循环结构》是北师大版必修3第二章第三节的内容，它与顺序结构，选接结构是算法的三种基本逻辑结构，特别是循环结构，是整章的重点和难点，它的优点在于能够让计算机快速的重复计算。

二、学生学情分析学生已经掌握了算法的思想以及框图的基本含义，还有顺序结构，大部分学生对算法感兴趣，这就大大的提升了学生的学习兴趣，但是学生的自主探索能力还有待提高。

三、教学目标1知识与技能（1）理解循环结构的概念，把握循环结构的三个要素。

（2）体会循环结构在有关重复计算的算法设计中的重要作用，能识别和理解循环结构的框图以及功能。

（3）掌握三种算法结构的区别与联系。

2过程与方法通过模仿，探索，操作，学习设计程序框图的表达，解决问题，提高逻辑思维能力。

3情感态度与价值观通过启发，自主探究，让学生感受体会算法思想在解决实际问题中的三、教学重难点重点：循环结构的概念及构成要素。

难点：循环结构三要素的确定以及循环执行时变量的变化规律。

四、教学方式教师启发与学生探究相结合。

五、教学手段多媒体辅助教学。

六、教学过程1情景引入日本取得2020奥运会主办权的投票过程：对遴选出的五个城市进行投票表决的操作程序：首先进行第一轮投票，如果有一个城市得票超过一半，那么这个城市取得主办权；如果没有一个城市得票超过一半，那么将其中得票最少的城市淘汰，然后重复上述过程，直到选出一个城市为止。

（请学生思考并回答奥运会主办权投票过程的算法）1、投票；2、计票：如果有一个城市得票超过一半，那么这个城市取得主办权，进入3；否则淘汰得票数最少的城市，转入1；3、宣布主办城市。

奥运会主办权投票表决程序框图：设计意图：通过大家熟知的奥运会举办城市选取的具体事例，让学生明确整个选取的步骤，用框图的形式表达来引入课题。

其实这种程序的设计有多种，区别在于复杂与简单。

这此环节的目的是提升学生的求知欲，兴趣，使学生保持良好的学习氛围。

2概念探究例1如何画出1+2+3+……+100的框图？（这是一个数累加的过程，我们都知道它的结果是5050，但是能否设计程序让计算机快速的把它算出来呢？）通常，我们按照下列过程计算1+2+3+…+100的值第1步，0+1=1第2步，1+2=3第3步，3+3=6……第100步，4950+100=5050也就是21324312,3,4(2,3,,100)i i S S S S S S S S i i -=+=+=+=+= 即第i 步的结果＝第（i －1）步的结果＋i 。

2.3 循环结构整体设计教学分析教材通过实例介绍了循环结构.在教学过程中,教师应注意通过实例来分析循环结构,以加深学生的感性认识.三维目标掌握循环结构及其相应的流程图,提高学生分析问题和解决问题的能力.重点难点教学重点：理解循环结构,会设计循环结构.教学难点：设计循环结构.课时安排1课时教学过程导入新课思路1（情境导入）.我们都想生活在一个优美的环境中，希望看到的是碧水蓝天，大家知道工厂的污水是怎样处理的吗？污水进入处理装置后进行第一次处理，如果达不到排放标准，则需要再进入处理装置进行处理，直到达到排放标准.污水处理装置是一个循环系统，对于处理需要反复操作的事情有很大的优势.我们数学中有很多问题需要反复操作，今天我们学习能够反复操作的逻辑结构——循环结构.思路2（直接导入）.前面我们学习了顺序结构，顺序结构像一条没有分支的河流，奔流到海不复回；上一节我们学习了选择结构，选择结构像有分支的河流最后归入大海.事实上,很多水系是循环往复的，今天我们开始学习循环往复的逻辑结构——循环结构.推进新课新知探究提出问题（1）请大家举出一些常见的需要反复计算的例子.（2）什么是循环结构、循环体？（3）试用流程图表示循环结构.讨论结果：（1）例如用二分法求方程的近似解、数列求和等.（2）在一些算法中，经常会出现从某处开始，按照一定的条件反复执行某些步骤的情况，这就是循环结构.反复执行的步骤称为循环体.（3）在一些算法中要求重复执行同一操作的结构称为循环结构,即从算法某处开始，按照一定条件重复执行某一处理的过程.重复执行的处理步骤称为循环体.循环结构，如下图所示，它的功能是先执行重复执行的A框，然后判断给定的条件P是否成立，如果P仍然不成立，则返回来继续执行A框，再判断条件P是否成立.继续重复操作，直到某一次给定的判断条件P成立时为止，此时不再返回来执行A框，离开循环结构.继续执行下面的框图.图1应用示例思路1例1 设计算法,输出1 000以内能被3和5整除的所有正整数,画出算法流程图.这个问题很简单,凡是能被3和5整除的正整数都是15的倍数,由于1 000=15×66+10,因此1 000以内一共有66个这样的正整数.解：引入变量a表示待输出的数,则a=15n (n=1,2,3,…,66).n从1变到66,反复输出a,就能输出1 000以内的所有能被3和5整除的正整数.算法流程图如图2所示.图2点评：像这样的算法结构称为循环结构,其中反复执行的第②部分称为循环体.变量n控制着循环的开始和结束,称为循环变量,第①部分就是赋予循环变量初始值,预示循环开始.第③部分判断是否继续执行循环体,称为循环的终止条件.变式训练请用流程图表示前面讲过的“判断整数n(n>2)是否为质数”的算法.解：算法流程图如下：图3例2 阅读下图中所示的流程图,回答下列问题：(1)变量y在这个算法中的作用是什么?(2)这个算法的循环体是哪一部分,功能是什么?(3)这个算法的处理功能是什么?图4解：(1)变量y 是循环变量,控制着循环的开始和结束;(2)流程图中的第②部分是循环体,其功能是判断年份y 是否是闰年,并输出结果;(3)由前面的分析,我们知道,这个算法的处理功能是：判断2000—2500年中,哪些年份是闰年,哪些年份不是闰年,并输出结果.点评：需要反复进行相同的操作,如果按照顺序结构来描述,算法显得十分烦琐,不利于阅读,如果采取循环结构来描述,算法就显得简洁、清楚.循环结构是一种简化算法叙述的结构. 变式训练观察下面的流程图,指出该算法解决的问题.图5解：这是一个累加求和问题,共99项相加,该算法是求100991431321211⨯++⨯+⨯+⨯ 的值.思路2例1 设计一个计算1+2+……+100的值的算法，并画出流程图.算法分析：通常，我们按照下列过程计算1+2+……+100的值.第1步，0+1=1.第2步，1+2=3.第3步，3+3=6.第4步，6+4=10.……第100步，4 950+100=5 050.显然，这个过程中包含重复操作的步骤，可以用循环结构表示.分析上述计算过程，可以发现每一步都可以表示为第（i-1）步的结果+i=第i 步的结果.为了方便、有效地表示上述过程，我们用一个累加变量S 来表示第一步的计算结果，即把S+i 的结果仍记为S ，从而把第i 步表示为S=S+i ，其中S 的初始值为0，i 依次取1，2，…，100，由于i 同时记录了循环的次数，所以也称为计数变量.流程图如下：图6点评：这是一个典型的用循环结构解决求和的问题，有典型的代表意义，可把它作为一个范例，仔细体会三种逻辑结构在流程图中的作用，学会画流程图.变式训练已知有一列数1,,43,32,21+n n ，设计流程图实现求该列数前20项的和. 分析：该列数中每一项的分母是分子数加1，单独观察分子，恰好是1，2，3，4，…，n ，因此可用循环结构实现，设计数器i ，用i=i+1实现分子，设累加器S ，用S=S+1+i i ，可实现累加，注意i 只能加到20.解：流程图如下：图7例2 某厂2005年的年生产总值为200万元，技术革新后预计以后每年的年生产总值都比上一年增长5%，设计一个流程图，输出预计年生产总值超过300万元的最早年份.算法分析：先写出解决本例的算法步骤：1.输入2005年的年生产总值.2.计算下一年的年生产总值.3.判断所得的结果是否大于300，若是，则输出该年的年份；否则，返回第2步.4.算法结束.由于“第2步”是重复操作的步骤，所以本例可以用循环结构来实现.我们按照“确定循环”“初始化变量”“设定循环控制条件”的顺序来构造循环结构.（1）确定循环体：设a为某年的年生产总值，t为年生产总值的年增长量，n为年份，则循环体为t=0.05a,a=a+t,n=n+1.（2）初始化变量：若将2005年的年生产总值看成计算的起始点，则n的初始值为2005，a 的初始值为200.（3）设定循环控制条件：当“年生产总值超过300万元”时终止循环，所以可通过判断“a>300”是否成立来控制循环体.流程图如下：图8变式训练1.设计流程图实现1+3+5+7+…+131的算法.分析：由于需加的数较多，所以要引入循环结构来实现累加.观察所加的数是一组有规律的数（每相邻两数相差2），那么可考虑在循环过程中，设一个变量i，用i=i+2来实现这些有规律的数，设一个累加器sum，用来实现数的累加，在执行时，每循环一次，就产生一个需加的数，然后加到累加器sum中.解：算法如下：1.赋初值i=1，sum=0.2.sum=sum+i，i=i+2.3.如果i≤131，则反复执行第2步；否则，执行下一步.4.输出sum.5.结束.流程图如下图.图9点评：（1）设计流程图要分步进行，把一个大的流程图分割成几个小的部分，按照三个基本结构即顺序、条件、循环结构来局部安排，然后把流程图进行整合.（2）流程图画完后，要进行验证，按设计的流程分析是否能实现所求的数的累加，分析条件是否加到131就结束循环，所以我们要注意初始值的设置、循环条件的确定以及循环体内语句的先后顺序，三者要有机地结合起来.最关键的是循环条件，它决定循环次数，可以想一想，为什么条件不是“i<131”或“i=131”，如果是“i<131”，那么会少执行一次循环，131就加不上了.2.高中某班一共有40名学生，设计算法流程图，统计班级数学成绩良好(分数>80)和优秀(分数>90)的人数.分析：用循环结构实现40个成绩的输入，每循环一次就输入一个成绩s，然后对s的值进行判断.设两个计数器m,n，如果s>90，则m=m+1，如果80<s≤90，则n=n+1.设计数器i，用来控制40个成绩的输入，注意循环条件的确定.解：流程图如下图：知能训练由相应的流程图如图11，补充完整一个计算1+2+3+…+100的值的算法.图111.设i的值为____________.2.设sum的值为____________.3.如果i≤100执行第____________步,否则，转去执行第____________步.4.计算sum+i并将结果代替____________.5.计算____________并将结果代替i.6.转去执行第3步.7.输出sum的值并结束算法.分析：流程图各图框的内容（语言和符号）要与算法步骤相对应，在流程图中算法执行的顺序应按箭头方向进行.解：1.设i的值为1.2.设sum的值为0.3.如果i≤100，执行第四步,否则，转去执行第7步.4.计算sum+i并将结果代替sum.5.计算i+1并将结果代替i.6.转去执行第3步.7.输出sum的值并结束算法.拓展提升设计一个算法，求1+2+4+…+249的值，并画出流程图.解：算法步骤：1.sum=0.2.i=0.3.sum=sum+2i.4.i=i+1.5.判断i是否大于49，若成立，则输出sum，结束.否则，返回第3步重新执行.流程图如图12.点评：（1）如果算法问题里涉及的运算进行了许多次重复的操作，且先后参与运算的数之间有相同的规律，就可引入变量循环参与运算（我们称之为循环变量），应用于循环结构.在循环结构中，要注意根据条件设计合理的计数变量、累加和累乘变量及其个数等，特别要求条件的表述要恰当、精确.（2）累加变量的初始值一般取成0，而累乘变量的初始值一般取成1.课堂小结（1）熟练掌握循环结构的特点及功能.（2）能用循环结构画出求和等实际问题的流程图，进一步理解学习算法的意义.作业习题2—2 A组 8、9.设计感想本节的引入抓住了本节的特点，利用计算机进行循环往复运算，解决累加、累乘等问题.循环结构是逻辑结构中的难点，它一定包含一个选择结构，它能解决很多有趣的问题.本节选用了大量精彩的例题，对我们系统掌握流程图有很大的帮助.。

第3课时循环结构[核心必知]1．循环结构的概念在算法中，从某处开始，按照一定的条件反复执行某些步骤的结构称为循环结构，用算法框图如下图．反复执行的部分称为循环体，控制着循环的开始和结束的变量，称为循环变量，决定是否继续执行循环体的判断条件，称为循环的终止条件．2．循环结构的设计过程设计循环结构之前需要确定的三件事：(1)确定循环变量和初始值；(2)确定算法中反复执行的部分，即循环体；(3)确定循环的终止条件．循环结构的算法框图的基本模式，如下图．[问题思考]1．循环结构中一定含有选择结构吗？提示：在循环结构中需要判断是否继续循环，故循环结构中一定含有选择结构．2．循环结构中判断框中条件是唯一的吗？提示：不是，在具体的算法框图设计时，判断框中的条件可以不同，但不同的表示应该有共同的确定的结果．3．算法框图的基本结构有哪些？提示：顺序结构、选择结构和循环结构.讲一讲1.利用循环结构写出12＋23＋…＋100101的算法并画出相应的算法框图．[尝试解答] 算法如下： 1．S ＝0； 2．i ＝1； 3．S ＝S ＋ii ＋1；4．i ＝i ＋1；5．如果i 不大于100，转第3步，否那么输出S . 相应框图如以下图表示：1．如果算法问题中涉及到的运算进行了多次重复，且参与运算的数前后有规律可循，就可以引入变量以参与循环结构．2．在不同的循环结构中，应注意判断条件的差别，及计数变量和累加(乘)变量的初始值与运算框先后关系的对应性．练一练1．利用循环结构写出1×2×3×…×100的算法．并画出相应的框图． 解：算法步骤如下：1．S＝1；2．i＝1；3．S＝S×i；4．i＝i＋1；5．判断i是否大于100，假设成立，那么输出S，结束算法；否那么返回第3步重新执行．算法框图如下图：讲一讲2.1×3×5×…×n>1000.问：如何寻找满足条件的n的最小正整数值？请设计算法框图．[尝试解答] 算法框图如以下图所示：解决该类问题一般分以下几个步骤：(1)根据题目条件写出算法并画出相应的框图；(2)依据框图确定循环结束时，循环变量的取值；(3)得出结论．练一练2．看下面的问题：1＋2＋3＋…＋( )＞10 000，这个问题的答案虽然不唯一，但我们只要确定出满足条件的最小正整数n0，括号内填写的数字只要大于或等于n0即可．画出寻找满足条件的最小正整数n0的算法的算法框图．解：1.S＝0；2．n＝0；3．n＝n＋1；4．S＝S＋n；5．如果S＞10 000，那么输出n，否那么执行6；6．回到3，重新执行4,5.框图如右图：讲一讲3.某高中男子田径队的50 m赛跑成绩(单位：s)如下：6.3,6.6,7.1,6.8,7.1,7.4,6.9,7.4,7.5,7.6,7.8, 6.4, 6.5,6.4,6.5,6.7,7.0,6.9,6.4,7.1,7.0,7.2.设计一个算法，从这些成绩中搜索出成绩小于6.8 s的队员，并画出算法框图．[尝试解答] 此男子田径队有22人，要解决该问题必须先对运动员进行编号．设第i个运动员编号为N i，成绩为G i，设计的算法如下：1．i＝1.2．输入N i，G i.3．如果G i＜6.8，那么输出N i，G i，并执行4；否那么直接执行4.4．i＝i＋1.5．如果i≤22，那么返回2；否那么，算法结束．该算法的框图如下图．解决此类问题的关键是读懂题目，建立合适的模型，注意循环结构与选择结构的灵活运用．练一练3．2000年底我国人口总数约为13亿，现在我国人口平均年增长率为1%，写出计算多少年后我国的人口总数将达到或超过18亿的算法框图．解：[解题高手][易错题]阅读如下图的算法框图，假设输出S的值为－7，那么判断框内可填写( )A．i＜3 B．i＜4C．i＜5 D．i＜6[错解]i＝1，S＝2；S＝2－1＝1，i＝1＋2＝3；S＝1－3＝－2，i＝3＋2＝5；S＝－2－5＝－7.由题意可知，S＝－7.故应填“i＜5〞．选C.[错因] 循环终止的条件写错，没有将循环进行彻底，计算完S值后，忽略了i值的计算，假设填“i＜5〞，那么输出S值为－2.[正解]i＝1，S＝2；S＝2－1＝1，i＝1＋2＝3；S＝1－3＝－2，i＝3＋2＝5；S＝－2－5＝－7，i＝5＋2＝7.假设终止循环后输出s值为－7，那么判断框内应填“i＜6〞．[答案] D1．以下说法不．正确的选项是( ) A ．顺序结构是由假设干个依次执行的处理步骤组成的，每一个算法都离不开顺序结构 B ．循环结构是在一些算法中从某处开始按照一定的条件，反复执行某些处理步骤，故循环结构一定包含选择结构C ．循环结构不一定包含选择结构D ．用算法框图表示的算法更形象、直观，容易理解 解析：选C 显然循环结构一定包含选择结构．2．用二分法求方程x 2－2＝0的近似解的算法中要用到的算法结构是( ) A ．顺序结构 B ．选择结构C ．循环结构 D ．以上都用解析：选D 任何一个算法都有顺序结构，循环结构一定包含选择结构，二分法用到循环结构． 3．(某某高考)执行两次如下图的算法框图，假设第一次输入的a 的值为－1.2，第二次输入的a 的值为1.2，那么第一次、第二次输出的a 的值分别为( )A ．0.2,0.2B ．0.2,0.8C ．0.8,0.2D ．0.8,0.8解析：选C 两次运行结果如下：第一次：－1.2→－1.2＋1→－0.2＋1→0.8； 第二次：1.2→1.2－1→0.2.4．如下图，该框图是计算12＋14＋16＋…＋120的值的一个算法框图，其中判断框内应填入的条件是________．解析：要实现算法，算法框图中最后一次执行循环体时，i 的值应为10，当条件i ＝11＞10时就会终止循环，所以条件为i ≤10.答案：i ≤105．(某某高考)假设某程序框图如下图，那么该程序运行后输出的值是________．解析：运行程序后，i ＝1，T ＝1；i ＝2，T ＝12；i ＝3，T ＝16；i ＝4，T ＝124；i ＝5，T ＝1120；i ＝6>5，循环结束．那么输出的值为1120. 答案：11206．给出以下10个数：5,9,80,43,95,73,28,17,60,36，要求把大于40的数找出来并输出，试画出解决该问题的算法框图．解：一、选择题1．下面的框图中是循环结构的是( )A．①②B．②③C．③④D．②④解析：选C①是顺序结构，②是选择结构，③④是循环结构．2．(某某高考)阅读下边的程序框图，运行相应的程序，那么输出S的值为( )A．8 B．18C．26 D．80解析：选C程序执行情况为S＝31－30＝2，n＝2；S＝2＋32－31＝8，n＝3；S＝8＋33－32＝26，n＝4≥4，跳出循环．故输出26.3．(高考)执行如下图的程序框图，输出的S值为( )A．2 B．4 C．8 D．16解析：选C框图的功能为计算S＝1·20·21·22的值，计算结果为8. 4．图中所示的是一个算法的框图，那么其表达式为( )A.11＋2＋3＋…＋99B.11＋2＋3＋…＋100C.199D.1100解析：选 A依题意当i≤99时，S＝1＋2＋…＋99，当i＝100时，S＝11＋2＋3＋…＋99.5．(某某高考)阅读如下图的算法框图，运行相应的算法．假设输入x的值为1, 那么输出S的值为( )A．64 B．73 C．512 D．585解析：选B 第1次循环，S ＝1，不满足判断框内的条件，x ＝2；第2次循环，S ＝9，不满足判断框内的条件，x ＝4；第3次循环，S ＝73，满足判断框内的条件，跳出循环，输出S ＝73.二、填空题6．阅读如下图的框图，假设输入m ＝4，n ＝3，那么输出a ＝________，i ＝________.解析：由算法框图可知，当a ＝m ×i ＝4×i 能被n ＝3整除时输出a 和i 并结束程序．显然，当i ＝3时，a 可以被3整除，故i ＝3，此时a ＝4×3＝12.答案：12 37．(某某高考)以下图是某算法的程序框图，那么程序运行后输出的结果是________．解析：此框图依次执行如下循环：第一次：T ＝0，k ＝1，sin π2>sin 0成立，a ＝1，T ＝T ＋a ＝1，k ＝2,2<6，继续循环； 第二次：sin π>sin π2不成立，a ＝0，T ＝T ＋a ＝1，k ＝3，3<6，继续循环； 第三次：sin 3π2>sin π不成立，a ＝0，T ＝T ＋a ＝1，k ＝4,4<6，继续循环； 第四次：sin 2π>sin 3π2成立，a ＝1，T ＝T ＋a ＝2，k ＝5，5<6，继续循环； 第五次：sin 5π2>sin 2π成立，a ＝1，T ＝T ＋a ＝3，k ＝6，跳出循环，输出的结果是3. 答案：38．假设算法框图所给的程序运行的结果为S ＝90，那么判断框中应填入的关于k 的判断条件是________．解析：由算法框图可知其作用是计算S＝1×10×9×…，当运行结果为S＝90时，应有S＝1×10×9，∴当k＝8时应符合条件且k＞8不符合条件，∴条件应为k≤8或k<9.答案：k≤8或k<9三、解答题9．设计求1＋4＋7＋10＋…＋40的一个算法，并画出相应的算法框图．解：算法：1．令S＝0，i＝1.2．S＝S＋i.3．i＝i＋3.4．假设i≤40，返回第2步；重新执行第2、3、4步；假设i>40，执行第5步．5．输出S的值．算法框图如下图：法一：法二：10．以下是某次考试中某班15名同学的数学成绩：72,91,58,63,84,88,90,55,61,73,64,77,82,94,60.要求将80分以上的同学的平均分求出来，画出算法框图．解：算法框图如下所示：。

《循环结构》教学设计1、教材及学情分析（1）教材地位：本节是北师版必修三第二章第二节第三课时内容，本节所在章节“算法”是高中数学课程中新内容,而循环结构是算法这一部分的重点和难点,它的重要性就是能使计算机以极快的速度进行重复计算。

同时，本节在教材中起着承上启下的作用：一方面它与顺序结构、选择结构是算法的三种基本逻辑结构，可以表示任何一个算法；另一方面，把算法转化为框图，为后面算法语句打下基础。

（2）学生状况分析：学生在学习本课以前，已经学习了算法的概念、顺序结构、选择结构及简单的赋值问题，顺序结构和选择结构学生比较容易理解，而在循环结构中更多的涉及了变量和对变量的处理，正是这些内容使得循环结构的理解和使用变得困难，为了分散难点，教材在讲循环结构之前已利用一个课时来分析变量和赋值，但在这节课中这些依然是学生的难点，因此，在教学中通过对实例的分析，学生逐步经历循环结构设计的全过程（确定循环变量、循环体和循环终止的条件），学会有条理的思考问题，正确表达循环结构，并尝试整理成程序框图。

根据以上对教材和学生的分析，考虑到学生已有的认知规律，学生应达到以下三个教学目标。

2、教学目标（1）知识与技能：学生理解循环结构概念；学生把握循环三要素：循环变量赋初值、循环体、循环的终止条件；并能运用循环结构设计简单的算法框图。

（2）过程与方法：通过模仿、操作、探究，学习设计循环结构程序框图，体会算法思想(程序化思想)，发展有条理的思考与表达能力，提高逻辑思维能力，增强识图用图的能力。

（3）情感、态度与价值观：通过本节课的学习，学生感受和体会算法思想在解决具体问题中的意义，增强学生的创新能力、应用数学能力以及程序化的思想意识。

3、教学重难点（1）重难点的制定：重点：理解循环结构，能识别和画出简单的循环结构框图难点：循环结构中的循环变量、循环体和循环终止条件的确定（2）重难点的突破：本课的重点主要是理解循环结构，能识别和画出简单的循环结构框图。