苏科版九年级数学上册初三练习

一、选择题（每题3分，共30分）1. 下列各数中，绝对值最小的是（）A. -3B. -2C. 0D. 12. 已知a、b是方程x² - 5x + 6 = 0的两根，则a + b的值是（）A. 5B. -6C. 1D. 23. 如果平行四边形ABCD的对角线AC和BD相交于点O，且OA = 3cm，OB = 4cm，那么平行四边形ABCD的面积是（）A. 6cm²B. 12cm²C. 15cm²D. 24cm²4. 下列函数中，是反比例函数的是（）A. y = 2x + 1B. y = x²C. y = 1/xD. y = 35. 在△ABC中，∠A = 60°，∠B = 45°，则∠C的度数是（）A. 75°B. 90°C. 105°D. 120°6. 已知x² - 2x - 3 = 0，那么x² - 4x + 4的值是（）A. 1B. 3C. 5D. 77. 在直角坐标系中，点A（2，3）关于y轴的对称点是（）A.（-2，3）B.（2，-3）C.（-2，-3）D.（2，3）8. 下列各数中，有理数是（）A. √2B. πC. 0.1010010001...D. 2/39. 如果x = -2是方程2x + 5 = 0的解，那么x - 3的值是（）A. -1B. 1C. 3D. -510. 下列图形中，不是轴对称图形的是（）A. 正方形B. 等腰三角形C. 长方形D. 平行四边形二、填空题（每题3分，共30分）11. 2的平方根是__________。

12. 如果sinθ = 1/2，那么cosθ的值是__________。

13. 在△ABC中，如果a = 3，b = 4，c = 5，那么△ABC是__________三角形。

14. 函数y = 2x - 1的图象是一条__________。

苏科版九年级数学上册全册同步练习题（共56套带答案）第3章数据的集中趋势和离散程度 [测试范围：3.1～3.3 时间：40分钟分值：100分] 一、选择题(每小题4分，共32分) 1．一组数据1，3，4，2，2的众数是( ) A．1 B．2 C．3 D．4 2．一组数据7，8，10，12，13的平均数是( ) A．7 B．9 C．10 D．12 3．一组数据3，3，5，6，7，8的中位数是( ) A．3 B．5 C．5.5 D．6 4．一次数学检测中，有5名学生的成绩(单位：分)分别是86，89，78，93，90.则这5名学生成绩的平均数和中位数分别是( ) A．87.2分，89分 B．89分，89分 C．87.2分，78分 D．90分，93分 5．学习全等三角形时，数学兴趣小组设计并组织了“生活中的全等”的比赛，全班同学的比赛结果统计如下表：得分(分) 60 70 80 90 100 人数 7 12 10 8 3 则得分的众数和中位数分别是( ) A．70分，70分 B．80分，80分 C．70分，80分 D．80分，70分 6．如图4－G－1是根据某班40名同学一周的体育锻炼情况绘制的条形统计图．那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( ) 图4－G－1 A．16小时，10.5小时 B．8小时，9小时 C．16小时，8.5小时 D．8小时，8.5小时 7．某公司欲招聘一名公关人员，对甲、乙、丙、丁四名候选人进行了面试和笔试，他们的成绩如下表所示：候选人甲乙丙丁测试成绩 (百分制) 面试 86 92 90 83 笔试90 83 83 92 如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权，根据四人各自的平均成绩，公司将录取( ) A．甲 B．乙 C．丙 D．丁 8．数据x1，x2，x3，x4，x5的平均数是x，则数据x1＋3，x2＋3.5，x3＋2.5，x4＋2，x5＋4的平均数为( ) A．x＋2 B．x＋2.5 C．x＋3 D．x＋3.5 二、填空题(每小题4分，共24分) 9．在演唱比赛中，5位评委给一位歌手的打分如下：8.2分，8.3分，7.8分，7.7分，8.0分，则这位歌手的平均得分是________分． 10．如图4－G－2是根据某地某段时间的每天最低气温绘成的折线图，那么这段时间最低气温的平均数是________．图4－G－2 11．某班学生综合实践作物栽培操作能力评估成绩的统计结果如下表：成绩/分 3 4 5 6 7 8 9 10 人数 1 12 2 8 9 15 12 则这组成绩的众数为________． 12. 某校在进行“阳光体育活动”中，统计了7名原来偏胖的学生的情况，他们的体重分别降低的千克数为5，9，3，10，6，8，5，则这组数据的中位数是________．13．一个样本为1，3，2，2，a，b，c，已知这个样本的众数为3，平均数为2，则这组数据的中位数为________． 14．某校抽样调查了七年级学生每天的体育锻炼时间，整理数据后制成了如下所示的频数分布表，这个样本的中位数在第________组．组别时间(时) 频数第1组0≤t＜0.5 12 第2组0.5≤t＜1 24 第3组1≤t＜1.5 18 第4组1.5≤t＜2 10 第5组2≤t＜2.5 6 三、解答题(共44分) 15．(8分)已知一组数据：3，a，4，5，b，c，6.(1)若这组数据是按由小到大的顺序排列的，则中位数是________；(2)若该组数据的平均数是12，求a＋b＋c的值．16．(10分)一销售某品牌冰箱的公司有营销人员14人，销售部为制定营销人员月销售冰箱定额(单位：台)，统计了14人某月的销售量如下表：每人销售量(台) 20 17 13 8 5 4 人数 1 1 2 5 3 2 (1)这14名营销人员该月销售冰箱的平均数、众数和中位数分别是多少？ (2)你认为销售部经理给这14名营销人员定出每月销售冰箱的定额为多少台才比较合适？并说明理由．17．(12分)九(3)班A，B，C三名同学的知识测试、实践能力、成长记录三项成绩(单位：分)如下表所示．测试项目测试成绩 A B C 知识测试 90 88 90 实践能力 82 84 87 成长记录 95 95 90 (1)如果根据三项测试的平均成绩评价他们的综合成绩，那么谁的成绩最好？ (2)如果把他们的知识测试、实践能力、成长记录三项成绩按5∶3∶2的比例计入综合成绩，那么谁的成绩最好？18．(14分)为增强学生的身体素质，教育行政部门规定学生每天户外活动的平均时间不少于1小时，为了解学生参加户外活动的情况，对部分学生参加户外活动的时间进行抽样调查，并将调查结果绘制成如图4－G－3中两幅不完整的统计图，请你根据图中提供的信息解答下列问题： (1)在这次调查中共调查了多少名学生？ (2)求户外活动时间为0.5小时的人数，并补全条形统计图； (3)求表示户外活动时间为2小时的扇形圆心角的度数； (4)本次调查中学生参加户外活动的平均时间是否符合要求？户外活动时间的众数和中位数各是多少？图4－G－3详解详析 1．B 2.C 3．C [解析] 这组数据已经从小到大排列了，中间的两个数是5和6，故中位数是(5＋6)÷2＝5.5. 4．A 5．C [解析] 全班有40人，取得70分的人数最多，故众数是70分；把这40人的得分按大小顺序排列后知，第20个与第21个得分都是80分，故中位数是80分． 6．B [解析] 众数是一组数据中出现次数最多的数，所以该班40名同学一周参加体育锻炼时间的众数是8小时；将这组数据按从小到大的顺序排列后，第20个和第21个数都是9，故该班40名同学一周参加体育锻炼时间的中位数是9小时． 7．B [解析] 因为甲的平均成绩为86×0.6＋90×0.4＝51.6＋36＝87.6(分)；乙的平均成绩为92×0.6＋83×0.4＝55.2＋33.2＝88.4(分)；丙的平均成绩为90×0.6＋83×0.4＝54＋33.2＝87.2(分)；丁的平均成绩为83×0.6＋92×0.4＝49.8＋36.8＝86.6(分)．所以乙的平均成绩最高．故选B. 8． C 9．8.0 [解析] 根据题意，得(8.2＋8.3＋7.8＋7.7＋8.0)÷5＝8.0(分)． 10．4 ℃ 11．9分 12．6 13．2 14． 2 [解析] 中位数应是第35个和第36个数的平均数，第35个数和第36个数都在第2组．15．解：(1)5 (2)由题意可知17(3＋a＋4＋5＋b＋c＋6)＝12，所以a＋b＋c＝66. 16．解：(1)平均数为20×1＋17×1＋13×2＋8×5＋5×3＋4×214＝9(台)， 8台出现了5次，出现的次数最多，所以众数为8台， 14个数据按从小到大的顺序排列后，第7个，第8个数都是8，所以中位数是(8＋8)÷2＝8(台)． (2)每月销售冰箱的定额为8台才比较合适．因为8台既是众数，又是中位数，是大部分人能够完成的台数．若定为9台，则只有少量人才能完成，打击了大部分职工的积极性． 17．解：(1)xA＝13(90＋82＋95)＝89(分)； xB ＝13(88＋84＋95)＝89(分)； xC＝13(90＋87＋90)＝89(分)．可见，三名同学的成绩一样． (2)xA＝90×50%＋82×30%＋95×20%＝88.6(分)； xB＝88×50%＋84×30%＋95×20%＝88.2(分)； xC＝90×50%＋87×30%＋90×20%＝89.1(分)．可见，C同学的成绩最好． 18．解：(1)共调查了32÷40%＝80(名)学生． (2)户外活动时间为0.5小时的人数为80×20%＝16(名)．补全条形统计图如下． (3)表示户外活动时间为2小时的扇形圆心角的度数为1280×360°＝54°. (4)本次调查中学生参加户外活动的平均时间为16×0.5＋32×1＋20×1.5＋12×280＝1.175(时)．∵1.175＞1，∴平均活动时间符合要求．户外活动时间的众数和中位数均为1小时．第2章对称图形――圆 [测试范围：2.1～2.3 时间：40分钟分值：100分] 一、选择题(每小题3分，共24分) 1．已知⊙O的半径为8，点P与点O的距离为6 2，则( ) A．点P在⊙O的内部 B．点P在⊙O的外部 C．点P在⊙O上 D．以上选项都不对 2．下列说法中正确的个数为( ) ①直径不是弦；②三点确定一个圆；③圆是轴对称图形，任何一条直径所在的直线都是它的对称轴；④相等的圆心角所对的弧相等，所对的弦也相等． A．1 B．2 C．3 D．4 3．如图2－G－1，在半径为13 cm的圆形铁片上切下一块高为8 cm的弓形铁片，则弦AB的长为( ) A．10 cm B．16 cm C．24 cm D．26 cm 图2－G－1 图2－G－24．如图2－G－2，在Rt△ABC中，∠ACB＝90°，∠A＝26°，以点C 为圆心，BC长为半径的圆分别交AB，AC于点D，E，则BD�嗟亩仁�为( ) A．26° B．64° C．52° D．128° 图2－G－3 5．如图2－G－3，已知⊙O的半径为10，弦AB＝12，M是AB上任意一点，则线段OM的长可能是( ) A．5 B．7 C．9 D．11 6．一个点到一个圆上的点的最短距离是3 cm，最长距离是6 cm，则这个圆的半径是( ) A．4.5 cm B．1.5 cm C．4.5 cm或1.5 cm D．9 cm或3 cm 7．如图2－G－4所示，一圆弧过方格的格点A，B，C，试在方格中建立平面直角坐标系，使点A的坐标为(－2，4)，点C的坐标为(0，4)，则该圆弧所在圆的圆心坐标是( ) A．(－1，2) B．(1，－1) C．(－1，1) D．(2，1) 图2－G－4 图2－G－5 8．如图2－G－5，在⊙O中，弦AB∥CD，直径MN⊥AB且分别交AB，CD于点E，F，下列4个结论：①AE＝BE；②CF＝DF；③AC�啵�BD�啵虎�MF ＝EF.其中正确的有( ) A．1个 B．2个 C．3个 D．4个二、填空题(每小题4分，共24分) 9．圆是轴对称图形，它的对称轴是______________． 10．在平面内，⊙O的半径为3 cm，点P到圆心O的距离为7 cm，则点P与⊙O的位置关系是________． 11．如图2－G－6，⊙O的半径为5，点A，B在⊙O上，∠AOB＝60°，则弦AB 的长为________．图2－G－6 图2－G－712．如图2－G－7，在半径为5的⊙O中，AB，CD是互相垂直的两条弦，垂足为P，且AB＝CD＝8，则OP的长为________． 13．如图2－G－8，矩形ABCD与⊙O交于点A，B，F，E，DE＝1 cm，EF＝3 cm，则AB＝________ cm. 图2－G－8 图2－G－914．已知：如图2－G－9，A是半圆上的一个三等分点，B是AN�嗟闹械悖�P是MN上一动点，⊙O的半径为1，则AP＋BP的最小值是________．三、解答题(共52分) 15．(12分)如图2－G－10，AB，CD为⊙O的直径，点E，F在直径CD上，且CE＝DF. 求证：AF＝BE. 图2－G－1016．(12分)如图2－G－11，AB是⊙O的直径，AC�啵�CD�啵�∠COD＝60°. (1)△AOC是等边三角形吗？请说明理由； (2)求证：OC∥BD. 图2－G－1117．(14分)如图2－G－12，已知AB是⊙O的直径，AB＝10，弦CD与AB相交于点N，∠ANC＝30°，ON∶AN＝2∶3，OM⊥CD，垂足为M.(1)求OM的长； (2)求弦CD的长．图2－G－1218．(14分)把球放在长方体纸盒内，球的一部分露出盒外，其截面如图2－G－13所示．圆O与纸盒交于E，F，G三点，已知EF＝CD＝16 cm. (1)利用直尺和圆规作出圆心O； (2)求出球的半径．图2－G－13详解详析 1．B [解析] ∵82＝64，6 22＝72，且64<72，∴8<6 2，∴点P与点O的距离大于⊙O的半径，∴点P在⊙O的外部．故选B. 2．A [解析] ③正确，这是根据圆的轴对称的性质来判断的．①错误，直径是过圆心的弦；②错误，不在同一条直线上的三点才能确定一个圆；④错误，相等的圆心角所对的弧不一定相等，所对的弦也不一定相等，缺少“在同圆或等圆中”这一条件．正确的只有③.故选A. 3．C 4．C [解析] ∵∠ACB＝90°，∠A＝26°，∴∠B＝64°.∵CB＝CD，∴∠CDB＝∠B＝64°，∴∠BCD＝180°－64°－64°＝52°，∴BD�嗟亩仁�为52°.故选C. 5．C [解析] 连接OA.过点O作ON⊥AB，垂足为N.∵ON⊥AB，AB＝12，∴AN＝BN＝6.在Rt△OAN 中，ON＝OA2－AN2＝102－62＝8，∴8≤OM≤10.故选C. 6． C [解析] 根据题意，画出图形如图所示．设圆的半径为r cm，分两种情况来考虑： (1)如图①，若点P在圆内，则PA＋PB＝2r，∴3＋6＝2r，解得r＝4.5，即圆的半径为4.5 cm； (2)如图②，若点P在圆外，则PA－PB＝2r，∴6－3＝2r，解得r＝1.5，即圆的半径为1.5 cm. 故此圆的半径为4.5 cm或1.5 cm.故选C. 7．C [解析] 连接AB，AC，利用网格图的特征，作出AB，AC的垂直平分线，其交点即为圆心，则可得它的坐标为(－1，1)．故选C. 8． C 9．过圆心的任意一条直线[解析] 圆是轴对称图形，它的对称轴是过圆心的任意一条直线． 10．点P在⊙O外[解析] ∵⊙O的半径为3 cm，点P到圆心O的距离为7 cm，∴d＞r，∴点P与⊙O的位置关系是点P在⊙O外． 11．5 [解析] ∵⊙O的半径为5，∴OA＝OB＝5. 又∵∠O＝60°，∴∠A＝∠B＝60°，∴△ABO是边长为5的等边三角形，∴AB＝5. 12．3 2 [解析] 如图，过点O分别作OM⊥AB于点M，ON⊥CD于点N，连接OB，OD. ∵AB＝CD＝8，∴BM＝DN＝4. 又∵OB＝OD＝5，∴OM＝ON＝52－42＝3. ∵AB⊥CD，∴∠DPB＝90°. ∵OM⊥AB，ON⊥CD，∴∠OMP＝∠ONP＝90°，∴四边形MONP是矩形．又∵OM＝ON，∴矩形MONP是正方形，∴PM＝OM＝3，∴OP＝3 2. 13．5 [解析] 由图形的轴对称性易知CF＝DE. ∵DE＝1 cm，∴CF＝1 cm. ∵EF＝3 cm，∴DC＝5 cm，∴AB＝5 cm. 14.2 [解析] 利用对称法，作点A或点B关于MN的对称点是解决问题的关键．如图，作点A关于MN的对称点A′，连接A′B，交MN于点P，则此时PA＋PB的值最小，连接OA，OA′. ∵点A与点A′关于MN对称，点A是半圆上的一个三等分点，∴∠A′ON＝∠AON＝60°，PA＝PA′，∴PA＋PB＝PA′＋PB＝A′B. 连接OB. ∵B是AN�嗟闹械悖�∴∠BON＝30°，∴∠A′OB＝90°，∴在Rt△A′OB中，A′B＝OA′＋OB2＝2，∴PA＋PB的最小值为2. 15．证明：∵AB，CD为⊙O的直径，∴OA＝OB，OC＝OD. ∵CE＝DF，∴OE＝OF. 在△AOF和△BOE 中，OA＝OB，∠AOF＝∠BOE，OF＝OE，∴△AOF≌△BOE(SAS)，∴AF ＝BE. 16．解：(1)△AOC是等边三角形．理由：∵AC�啵�CD�啵�∴∠AOC＝∠COD＝60°. ∵OA＝OC，∴△AOC是等边三角形． (2)证明：∵∠AOC＝∠COD＝60°，∴∠BOD＝60°. ∵OB＝OD，∴△OBD 是等边三角形，∴∠OBD＝60°，∴∠OBD＝∠AOC，∴OC∥BD. 17．解：(1)∵AB＝10，∴OA＝5. ∵ON∶AN＝2∶3，∴ON＝2. ∵∠ANC＝30°，∴∠ONM＝30°，∴在Rt△OMN中，OM＝12ON＝1. (2)如图，连接OC. 在Rt△COM中，由勾股定理，得CM2＝CO2－OM2＝25－1＝24，∴CM＝2 6. 又∵OM⊥CD，∴CD＝2CM＝4 6. 18．解：(1)如图①所示，点O即为所求． (2)如图②，过点O作OM⊥EF于点M，连接OF，延长MO，则MO与BC的交点为G. 设球的半径为r cm，则OF＝r cm，OM＝(16－r)cm，MF＝12EF＝8 cm. 在Rt△OFM中，由勾股定理，得OF2＝OM2＋MF2，即r2＝(16－r)2＋82，解得r＝10. 即球的半径为10 cm.。

初中数学试卷桑水出品初三数学阶段性练习一选择题1．关于x的方程x2﹣4=0的根是（）A．2 B．﹣2 C．2，﹣2 D．2，2．下列说法中正确的是（）A．弦是直径 B．弧是半圆 C．半圆是圆中最长的弧 D．直径是圆中最长的弦3．某地区周一至周六每天的平均气温为：2，-1，3，5，6，5，（单位℃）则这组数据的极差是（）℃A．7 B．6 C．5 D．04．在⊙O中，弦AB等于圆的半径，则它所对应的圆心角的度数为（）A．30° B．60° C．75° D．120°5．在如图所示的正方形纸片上做随机扎针实验，则针头扎在阴影区域内的概率为( )A．14B．13C．12D．356．三角形的内心是三角形的（）A．三条高的交点 B．三条角平分线的交点C．三条中线的交点 D．三条边的垂直平分线的交点7、如图，AB、AC是⊙O的两条弦，∠A＝25°，过点C的切线与OB的延长线交于点D，则∠D的度数（）A．25° B．30° C．40° D．50°第9题第10题第5题(第6题图)OAB8某县2014年的GDP 是250亿元，要使2016年的GDP 达到360亿元，求这两年该县GDP 年平均增长率.设年平均增长率为x ，可列方程……………………………( ) A 250（1+2x ）2=360 B 250（1+2x ）=360 C 250（1+x ）(1+2x) =360 D 250（1+x ）2=3609如图，梯形ABCD 中，AB∥DC，AB⊥BC，AB=2cm ，CD=4cm ，以BC 上一点O 为圆心的圆经过A 、D 两点，且∠AOD=90°，则圆心O 到弦AD 的距离是（ ）A ．6B ．10C ．32D ．5210、如图，圆中有四条弦，每一条弦都将圆分割成面积比为1:3的两个部分，若这些弦的交点恰是一个正方形的顶点，那么这个正方形的外接圆的面积与图中阴影部分面积的比值为……………………………………………………………………………………（ ） A . 2 π B . π C . 2-π D . 2π二 填空题11 一元二次方程01522=--x x 的两根为1x ，2x ，则=+21x x 。

初三数学综合练习1 2015.1 班级 姓名一、填空题（本大题共10小题，每小题3分，共30分）１.在3.14、2-、327、π、0.2020020002……这六个数中，无理数有 （ ） A ．1个 B ．2个 C ．3个 D ．4个 2．下面是一位同学做的四道题：①()b a ab 33=；②1-=+--ba ba ；③326a a a =÷； ④222)(b a b a +=+ 其中做对了几道题 ( ) A ．0 B ．1 C ．2 D ．33.无锡市轨道交通1号线一期工程批复总投资8.123亿元，工程于2009年6月全面开工建设，工期为5年，到2014年通车试运营. 8.123亿元用科学记数法表示为 ( )A.1010238.1⨯元B.910238.1⨯元C.8108.123⨯元D.7108.123⨯元4．用6个球（除颜色外没有区别）设计满足以下条件的游戏：摸到白球、红球、黄球的概率分别为１２、１３、１６．则应准备的白球，红球，黄球的个数分别为 ( )A ．3，2，1B ． 1，2，3C ． 3，1，2 D.无法确定 5. 实数a 、b 在数轴上的位置如图所示，且a ＞b ，则化简2a a b -+的结果为( ) A ．2a ＋b B ．－2a ＋b C ．bD ．2a －b6. 下列各式，能用平方差公式计算的是 （ ） A ．()()22x y x y +- B ．()()2x y x y +-Ｃ．()()22x y y x +- D ．()()-22x y x y -7. 结果为2a 的式子是 （ ） Ａ．63a a ÷Ｂ．42a a -•Ｃ．12()a -Ｄ．42a a -8. 在截面为半圆形的水槽内装有一些水，如图.水面宽AB 为6分米，如果再注入一些水后，水面AB 上升1分米，水面宽变为8分米，则该水槽截面直径为 （ ）A ．5分米B ．6分米C ．8分米D ．10分米（第8题） （第9题）9.二次函数2y ax bx =+的图象如图，若一元二次方程20ax bx m ++=有实数根，则m 的取值范围是 （ ）A.m 3≥-B. m 3≤-C. m 3≤D. m 3≥ 10. 下面是按一定规律排列的一列数：第1个数：12–（1+–12）；第2个数：13–（1+–12）[1+(–1)23][1+(–1)34]；第3个数：14–（1+–12）[1+(–1)23][1+(–1)34][1+(–1)45][1+(–1)56]；……第n 个数：1n +1–（1+–12）[1+(–1)23][1+(–1)34]…[1+(–1)2n -12 n ]．那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是 （ ） A ．第10个数 B ．第11个数 C ．第12个数 D ．第13个数二、选择题（本大题共11小题，每空2分，共30分） 11.3-2的倒数 ，64 的平方根 ,12．当x 时，代数式x －３x －５有意义．当a= 时,分式a 2-1a 2-2a-3 的值为零.13．因式分解：=+-8822a a ；322x x x +-= 14．2a 2,3,a m n m n a -===则 ；若43xy =，则y x y=+ ． 15．若单项式12-m xy 与233n x y --和仍是单项式，则m n +的值是 16．若代数式3x 3＋5y 2＋4的值是15，则代数式6x 3＋10y 2－12的值是 17．若圆锥的底面半径为3cm ，母线长为4cm ，则这个圆锥的全面积为 cm 2． 18. 已知二次函数c bx ax y ++=2中，函数y 与自变量x 的部分对应值如下表：x… 1- 0 1 2 34 …[来y…1052125…若1()A m y ，，2(6)B m y -，两点都在该函数的图象上，当m ＝ 时，1y ＝2y ．19.已知0|1||2|=-+-a ab ，则+ab 1()()111++b a ()()221+++b a +…+()()201420141++b a ＝ ．20．已知点A （0，－4），B （8，0）和C （a ，a ）,若过点C 的圆的圆心是线段ＡＢ的中点，则这个圆的半径的最小值等于 . 21.如图，在平面直角坐标系中，O 为原点，点A （-2，0），点B （0，2），点E ，点F 分别为OA ，OB 的中点.若正方形OEDF 绕点O 顺时针旋转，得正方形OE ’D ’F ’，直线AE'与直线BF'相交于点P ， 则点P 的横坐标的最大值为 . 三、解答题（本题共8题，共70分） 22. （本题满分8分）计算： 0112+32(π6)2----+. ()()()2323132-+--．23．（本题满分10分）（1）先化简，再求值：222()()()b a b a b a b ++---其中3a =-，12b =.(2)先化简，再求值：222441112a a a a a a -+++•---，其中21a =+．24.（本题满分10分）某校组织了一次经典诵读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：甲7 8 9 7 10 10 9 10 10 10乙10 8 7 9 8 10 10 9 10中9 （1）甲队成绩的中位数是分，乙队成绩的众数是分；（2）计算乙队的平均成绩和方差；（3）已知甲队成绩的方差是1.4分2，则成绩较为整齐的是队.25.（本题满分6分）如图，正方形网格中的每个小的边长都是1，每个小正方形的顶点叫做格点。

九年级数学练习（4）1．在实数π、13、2、sin30°,无理数的个数为( ) A.1 B.2 C.3 D.42．若二次函数y=ax 2+bx+c 的x 与y 的部分对应值如下表：x -7 -6 -5 -4 -3 -2 y-27-13-3353则当x =1时，y 的值为 ( ) A.5 B.-3 C.-13 D.-273．已知线段AB ＝7cm ．现以点A 为圆心，2cm 为半径画⊙A ；再以点B 为圆心，3cm 为半径画⊙B ，则⊙A 和⊙B 的位置关系是( ) A ．内含 B ．相交 C ．外切 D ．外离4．如图，在四边形ABCD 中，E 、F 分别是AB 、AD 的中点，若EF=2，BC=5，CD=3，则tanC 等于 A.43 B.34 C.53 D. 54（第4题） （第7题）5．关于x 的方程2210x kx k ++-=的根的情况描述正确的是（ ）A . k 为任何实数，方程都没有实数根B . k 为任何实数，方程都有两个不相等的实数根C . k 为任何实数，方程都有两个相等的实数根D. 根据 k 的取值不同，方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 6．已知AC ⊥BC 于C ，BC =a ，CA =b ，AB =c ，下列选项中⊙O 的半径为ba ab+的是（ ）7．如图，⊙O 的半径为2，点O 到直线l 的距离为3，点P 是直线l 上的一个动点，PB 切⊙O 于点B ，则PB 的最小值是（ ）A .13 B .5 C . 3 D .28．若x 1,x 2(x 1 ＜x 2)是方程(x -a )(x-b ) = 1(a < b)的两个根，则实数x 1, x 2 ,a, b 的大小关系为 ( ) A ．x 1＜x 2＜a ＜b B ．x 1＜a ＜x 2＜b C ．x 1＜a ＜b ＜x 2 D ．a ＜x 1＜b ＜x 2（第10题）xy AC BA第17题 第15题图9．已知二次函数的图象(0≤x ≤3)如图所示．关于该函数在所给自变量取值范围内，下列说法正确的是( ) A ．有最小值0，有最大值3 B ．有最小值－1，有最大值0 C ．有最小值－1，有最大值3 D ．有最小值－1，无最大值 10．如图，抛物线y = x 2 + 1与双曲线y = k x 的交点A 的横坐标是1，则关于x 的不等式 kx+ x 2 + 1 < 0的解集是 ( )A ．x > 1B ．x < −1C ．0 < x < 1D ．−1 < x < 011．已知a b 、为有理数，m n 、分别表示57的整数部分和小数部分，且21amn bn +=，则2a b += 。

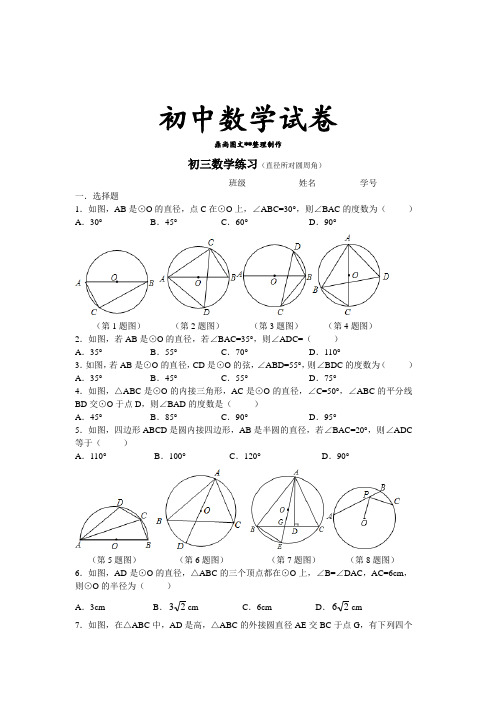
初中数学试卷鼎尚图文**整理制作初三数学练习（直径所对圆周角）班级____________姓名__________学号__________ 一．选择题1．如图，AB是⊙O的直径，点C在⊙O上，∠ABC=30°，则∠BAC的度数为（）A．30°B．45°C．60°D．90°（第1题图）（第2题图）（第3题图）（第4题图）2．如图，若AB是⊙O的直径，若∠BAC=35°，则∠ADC=（）A．35°B．55°C．70°D．110°3．如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=55°，则∠BDC的度数为（）A．35°B．45°C．55°D．75°4．如图，△ABC是⊙O的内接三角形，AC是⊙O的直径，∠C=50°，∠ABC的平分线BD交⊙O于点D，则∠BAD的度数是（）A．45°B．85°C．90°D．95°5．如图，四边形ABCD是圆内接四边形，AB是半圆的直径，若∠BAC=20°，则∠ADC 等于（）A．110°B．100°C．120°D．90°（第5题图）（第6题图）（第7题图）（第8题图）6．如图，AD是⊙O的直径，△ABC的三个顶点都在⊙O上，∠B=∠DAC，AC=6cm，则⊙O的半径为（）A．3cm B．23cm C．6cm D．26cm7．如图，在△ABC中，AD是高，△ABC的外接圆直径AE交BC于点G，有下列四个OE DC B A 结论：①AD 2=BD•CD ；②BE 2=EG•AE ；③AE•AD=AB•AC ；④AG•EG=BG•CG ．其正确个数（ ）A ．1个B ．2个C ．3个D ．4个8．如图，点P 为弦AB 上一点，连接OP ，过点P 作PC ⊥OP ，PC 交⊙O 于点C ，若AP=4，PB=2，则PC 的长是（ ）A ．2B ．2C ．22D ．39．如图所示，AB 是⊙O 的直径，AD=DE ，AE 与BD 相交于点C ，则图中与∠BCE 相等的角有（ ）A ．2个B ．3个C ．4个D ．5个二．填空题10．如图，点A 、D 在⊙O 上，BC 是直径，∠D=35°，则∠OAC=________.（第10题图） （第11题图） （第12题图） （第13题图）11．如图，AB 是半圆的直径，D 是⌒ AC 的中点，∠B=40°，则∠A=______. 12．如图，AB 是⊙O 的直径，若AB=4cm ，则∠B=_______，AC=_______.13．如图，AB 是⊙O 的直径，AB=AC ，∠C=70°，则∠A=________，OD 与AC 的关系是_________.14．如图，△ABC 的顶点在⊙O 上，∠BAC=120°，AB=AC ，BD 为⊙O 的直径，AD=6，则AC=_______.（第14题图） （第15题图） （第16题图） （第17题图） 15．在如图，已知EF 是⊙O 的直径，把∠A 为60°的直角三角板ABC 的一条直角边BC 放在直线EF 上，斜边AB 与⊙O 交于点P ，点B 与点O 重合，将三角板ABC 沿OE 方向平移，使得点B 与点E 重合为止．设∠POF=x°，则x 的取值范围是_________________.16．如图，AB 为⊙O 的直径，AC 交⊙O 于点E ，BC 交⊙O 于点D ，CD=BD ，∠C=70°现给出以下四个结论：①∠A=45°；②AC=AB ；③弧AE=弧BE ； ④2CE•AB=BC 2，其中正确结论的序号为___________.17．已知，如图，⊙C 过原点，并与坐标轴分别交于点A 、D ，∠OBA=30°，点D 的坐标为（0，3）,则A 点坐标为_________；C 点坐标为__________.18．如图，量角器的直径与直角三角形ABC 的斜边AB 重合，其中D B ECA量角器0刻度线的端点N 与点A 重合，射线CP 从CA 处出发沿顺时针方向以每秒2度的速度旋转，CP 与量角器的半圆弧交于点E ，第35秒时，点E 在量角器上对应的度数是___________秒19．在⊙O 中，已知⊙O 的直径AB=2，弦AC 长为3，弦AD 长为2，则∠DAC 的度数为________________.三．解答题 20．如图，⊙O 的直径AB 为10cm ，弦AC 为6cm ，∠ACB 的平分线交⊙O 于点D ，求BC 、AD 、BD 的长.21．如图△ADC 的外接圆直径AB 交CD 于点E ，已知∠C=65°，∠D=47°，求∠CEB 的度数.22．如图，已知BE 是△ABC 外接圆⊙O 的直径，CD 是△ABC 的高.（1）求证：CD BE BC AC ⋅=⋅；（2）已知CD=6，AD=3，BD=8，求⊙O 直径BE 的长.23．如图，在⊙O 上，弦AB=AC ，延长CA 到点D ，使AD=AC ，连接DB 并延长交⊙O 于点E ，连接CE.试说明CE 是⊙O 的直径.24．如图，AB 是⊙O 的直径，AE 为弦，C 为⌒ AE 的中点，CD ⊥ABP N M D C BAO 于点D ，交AE 于点F ，BC 交AE 于点G.求证：AF=GF25．如图，△ABC 内接于⊙O ，弦AB 的垂直平分线OD 与AB 、BC 分别相交于点M 、N ，与AC 的延长线相交于点P ，与⊙O 相交于点D.求证：（1）CN NB PN ON ⋅=⋅ （2）OP ON OB ⋅=226．如图，已知⊙O 的内接等边三角形ABC 的边长为32，P 是⌒ AC 上一动点，AP 的延长线交BC 的延长线于点D.（1）求⊙O 的半径R 的长；（2）求证：AD AP AB ⋅=2（3）P 在⌒ AC 上什么位置时，PB=PD ？并求出此时PB 的值.27．已知△ABC 中，AB=AC ，以AB 为直径的圆O 交BC 于D ，交AC 于E ，（1）如图①，若AB=6，CD=2，求CE 的长；（2）如图②，当∠A 为锐角时，使判断∠BAC 与∠CBE 的关系，并证明你的结论；（3）若②中的边AB 不动，边AC 绕点A 按逆时针旋转，当∠BAC 为钝角时，如图③，CA 的延长线与圆O 相交于E ．请问：∠BAC 与∠CBE 的关系是否与（2）中你得出的关系相同？若相同，请加以证明，若不同，请说明理由．。

初三上册数学练习题苏教版[正文]一、选择题1. 下列各数是有理数的是（）A. 3.14B. □2C. √7D. 0.12. 若x = 3，那么2x² + 3x等于（）A. 21B. 33C. 24D. 153. 已知集合A = {1, 2, 3, 4}，B = {2, 4, 6}，则A - B的结果是（）A. {1, 2, 3}B. {1, 3, 4}C. {1, 3}D. {3, 4}4. 下列各图形中，一定不是平行四边形的是（）A. □B. △C. ◇D. ▱二、填空题1. 将100解析为素因数的积为（）。

2. 整式的乘法运算性质是（）。

3. 下列各数中，是无理数的是（）。

三、解答题1. 在一个数字游戏中，小明比小红多5个点，小丽比小红少4个点，小强比小丽多2个点，已知小红得了15分，求出小强得了多少分。

2. 一种化肥中，氮、磷、钾的百分含量分别是5%，10%，15%。

现需要用这种化肥在某块地里施肥，若需要施肥300kg，求出需要的氮、磷、钾的质量分别是多少。

三、证明题证明根号2是无理数。

【思路提示】：设根号2是一个有理数，即可以表示为a/b，其中a与b互质且b ≠ 0。

根据有理数的性质，可以将根号2的平方化简为整数形式（a²/b²），求得a² = 2b²。

因此，a²为偶数，可设a = 2c（其中c为整数），代入可得4c²= 2b²，进一步化简得到2c²= b²。

由此得出，b也为偶数。

然而，a和b均为偶数与原设相违背，所以假设有理数的假设不成立，根号2是无理数。

四、应用题某种商品原价为200元，商场举办促销活动，打折力度为8折，同时又可使用满减券，满300元减50元。

小明购买了该商品，并使用了满减券。

请你计算小明最终需要支付多少钱。

【解题步骤】：1. 计算商品打折后的价格：200元 × 8折 = 160元。

初中数学试卷初三 一 元 二 次 方 程 自 测 题姓名一、选择题：（20分）1．下列方程中，关于x 的一元二次方程是 （ ）22222113(1)2(1) 200 21A x x B C ax bx c D x x x y x+=++-=++=+=-．． ．． 2、要使代数式22231x x x ---的值等于0，则x 等于 （ ） A 、1 B 、-1 C 、3 D 、3或-13、已知关于x 的方程（a 2-1）x 2+（1-a ）x+a-2=0，下列结论正确的是 （ ）A 、 当a ≠±1时，原方程是一元二次方程。

B 、当a ≠1时，原方程是一元二次方程。

C 、当a ≠-1时，原方程是一元二次方程。

D 、原方程是一元二次方程。

4、某饮料厂今年一月份的产量是500吨，三月份上升到720吨，设平均每月增长的百分率是x ，根据题意可得方程 （ ）A 、500（1+2x ）=720B 、B 、500+500（1+x ）+500（1+x ）2=720C 、720（1+x ）2=500D 、D 、500（1+x ）2=7205、下列一元二次方程中,有实数根是 ( )A.x 2-x+1=0B.x 2-2x+3=0；C.x 2+x-1=0D.x 2+4=06、关于x 的一元二次方程02=++m nx x 两根中只有一个根等于0，则下列条件正确的是（ ）A 、0,0==n mB 、0,0≠=n mC 、0,0=≠n mD 、0,0≠≠n m7、如图，已知矩形ABCD ∽矩形ECDF ，且AB=BE ，那么BC 与AB 的比值是 （ ） A、12+ B、12 C、12 D、128、已知关于x 的方程221(3)04x m x m --+= 有两个不相等的实根，（ ）那么m 的最大整数是 A ．2 B ．－1 C ．0 D ．l9、关于x 的一元二次方程x 2＋kx －1=0的根的情况是 （ ）A 、有两个不相等的同号实数根B 、有两个不相等的异号实数C 、有两个相等的实数根D 、没有实数根10、关于x 的一元二次方程（m-2）x 2+（2m-1）x+m 2-4=0的一个根是0，则 m 的值是（ ）A 、2 B 、-2 C 、2或-2 D 、12二、填空题：（32分）11、关于x 的方程（m-1）x 2+（m+1）x+3m-1=0，当m_________时,是一元一次方程;当m_________时,是一元二次方程12、已知关于x 的一元二次方程x 2+kx+k=0的一个根是–2，那么k=_ ___。

G F ECBD A苏科版九年级上册数学练习题(1)1．下面4个算式中，正确的是 （ ）A ．23+32=56B ． 8÷2=2C ．2(6)-= -6D ．53×56=562．计算29328+-的结果是 （ ） A ． 22-B ． 22C ． 2D ．223 3．等式b a b a -=2成立的条件是 ( ) A ．a ＜0，b ＞0B ．a ≤0，b ≥0C ．a ＜0，b ≥0D ．a ，b 为异号的实数4．已知⊙O 中，2AB CD =，则下列结论正确的是（ ）A ．AB < 2CD B ．AB = 2CDC ．AB > 2CD D ．AB ≤2CD 5．如图，△ABC 和△ADE 都是等腰三角形，AB=AC ，AD=AE ，∠BAC =∠DAE ， 四边形ACDE 是平行四边形，连结CE 交AD 于点F ，连结BD 交 CE 于 点G ，连结BE . 下列结论中：① CE =BD ； ② △ADC 是等腰三角形； ③∠CGD+∠D AE=180°； ④ CD ·AE =EF ·CG ．一定正确的结论有( ) A ．1个B ．2个C ．3个D ．4个6．⊙O 的半径为2，点P 在⊙O 外一点，OP 的长为3，那么以P 为圆心，且与⊙O•相切的圆的半径一定是（ ）A ．1或5B ．1C ．5D ．1或47．如图，在□ABCD 中，E 是BC 的中点，且∠AEC =∠DCE ，则下列结论不正确．．．的是（ ） A ．2AFD EFB S S =△△ B ．12BF DF =C ．四边形AECD 是等腰梯形 D ．AEB ADC ∠=∠8．将矩形纸片ABCD 按如图所示的方式折叠，得到菱形AECF ．若AB ＝3，则BC 的长 为 （ ） A ．1 B ．2 C ． 2 D ．39．当a ≥023a = ；当m <32(3)m -；10．方程(1)x x x -=的解是 ．AC B （第7题） EFABCFEOABD（第8题）11．若关于x 的方程250x x k -+=的一个根是0，则另一个根是 ．12．质检部门对甲、乙两工厂生产的同样产品抽样调查，计算出甲厂的样本方差为0.99，乙厂的样本方差为1.02，那么，由此可以推断出生产此类产品，质量比较稳定的是 厂． 13．等腰ABC △两边的长分别是一元二次方程2560x x -+=的两个解，则这个等腰三角形的周长是 ．14．在直角梯形ABCD 中，AD ∥BC ，AB ⊥AD ，AB=103，AD 、BC 的长是方程x 2-20x+75=0的两根，那么，以点D 为圆心，AD 为半径的圆与以点C 为圆心，BC 为半径的圆的位置关系是____________．15．如图，已知P 是正方形ABCD 对角线BD 上一点，且BP = BC ，则∠ACP 度数是 ．16．如图，矩形ABCD 中，AB ＝2，BC ＝3，对角线AC 的垂直平分线分别交AD ，BC 于点E 、F ，连接CE ，则CE 的长________.17. 如图，菱形ABCD 的两条对角线分别长6和8，点P 是对角线AC 上的一个动点，点M 、N 分别是边AB 、BC 的中点，则PM +PN 的最小值是_____________．18．如图，正方形纸片ABCD 的边长为1，M 、N 分别是AD 、BC 边上的点，将纸片的 一角沿过点B 的直线折叠，使A 落在MN 上，落点记为A ′，折痕交AD 于点E,若M 、N 分别是AD 、BC 边的中点，则A ′N=.第18题图 19．计算下列两题：（1）()()()2123527527---+ (2) (2－313)× 6 ÷2第19题图 FADOE BC第15题图BCDAP第17题图D ABCPMN 第16题图20．解方程：（1）2220x x --=．（用配方法） （2）2410x x +-=．21. 已知x ＝3，求xx x x x x x 244244222-+---+-的值22.如图，PA 和PB 分别与⊙O 相切于A ，B 两点，作直径AC ，并延长交PB 于点D ．连结OP ，CB ．（1）求证：OP ∥CB ；（2）若PA ＝12，DB ：DC ＝2：1，求⊙O 的半径．第22题图23. 如图，AB 是⊙O 的直径，AE 平分∠BAF 交⊙O 于E ，过E 点作直线与AF 垂直交AF 延长线于D 点，且交AB 于C 点．求证：CD 与⊙O 相切于点E ．第23题图24．古希腊数学家丢番图（公元250年前后）在《算术》中就提到了一元二次方程的问题，不过当时古希腊人还没有寻求到它的求根公式，只能用图解等方法来求解。

初中数学试卷初三数学练习(圆的对称性2)班级____________姓名__________学号__________ 一．选择题1．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，AB=20，CD=16，则线段OE的长为为（）A．4 B．6 C．8 D．10（第1题图） （第2题图） （第3题图） （第5题图） 2．如图，已知⊙O 的直径AB ⊥弦CD 于点E ，下列结论中一定正确的是（ ） A.AE=OE B.CE=DE C.OE=21CE D.∠AOC=60° 3．如图，⊙O 过点B ，C ，圆心O 在等腰直角△ABC 的内部，∠BAC=90°，OA=1，BC=6，则⊙O 的半径为（ ）A ．10B ．32C ．23D ．134．已知AB 、CD 为⊙O 中非直径的两条弦，且AB=CD=8，AB ⊥CD 于点E ，⊙O 的半径为5，那么OE 的长等于（ ）A ．2B ．23C ．4D ．225．如图，P 是半径为5的⊙O 内一点，且OP=3，在过点P 的所有⊙O 的弦中，弦长为整数的弦有（ ）A ．2条B ．3条C ．4条D ．5条6．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=16，则球的半径为（）A．8 B．9 C．10 D．12（第6题图） （第7题图） （第8题图） 7．如图所示，在圆O 内有折线OABC ，其中OA=8，AB=12，∠A=∠B=60°，则BC 的长为（ ） A ．19 B ．16 C ．18 D ．208．如图，梯形ABCD 中，AB ∥DC ，AB ⊥BC ，AB=2cm ，CD=4cm ，以BC 上一点O 为圆心的圆经过A 、D 两点，且∠AOD=90°，则圆心O 的弦AD 的距离是（ ） A ．6 B ．10 C ．32 D ．52二．填空题9．已知⊙O 的半径为5，弦AB 的弦心距为3，则AB 的长是__________.10．D 是半径为5cm 的⊙O 内一点，且OD=3cm ，则经过点D 的所有弦中最短弦AB=________. 11．已知⊙O 的弦AB 为10cm ，所对圆心角为120°，则圆心O 到弦AB 的距离为_______. 12．如图，已知⊙O 的半径为5，弦AB 的长为8，点P 是弦AB 上的一动点，则OP 的取值范围为________.（第12题图）（第13题图）（第14题图）（第15题图）13．如图，在⊙O中，弦AB=AC=5cm，BC=8cm，则⊙O的半径等于________.14．如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为（4，2），点A的坐标为（2，0），则点B的坐标为________.15．如图，AB、AC都是圆O的弦，OM⊥AB，ON⊥AC，垂足分别为M、N，如果MN=3，那么BC=_______. 16．圆的半径为13cm，弦AB∥CD，AB=24cm，CD=10cm，则两弦AB、CD的距离是_________.2cm，OC=1cm，则17．已知⊙O中，AB为弦，半径OD所在直线垂直于AB于点C，若AB=3CD的长是__________.二．解答题18．如图，⊙O的半径为5，P是⊙O外的一点，PO=8，∠OPA=30°.求AB的长.19．如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB，OE⊥AC，垂足分别为D、E.试判断四边形ADOE的形状，并说明理由.20．已知：如图，⊙O的直径AB与弦CD相交于点E，AE=1cm，BE=5cm，∠DEB=60°.求CD 的长.OB D EA 21．如图，⊙O 的半径r =10cm ，弦AB=12cm ，D 是⌒ AB 的中点，OD 与AB 相交于点E.求弦BD 的长.22．如图，A 、B 、C 为⊙O 上三点，D 、E 分别是⌒ AB 、⌒ AC 的中点，连接DE 分别交AB 、AC 于点M 、N求证：AM=AN23．如图1，MN 是⊙O 的直径，弦AB 、CD 相交于MN 上的一点，∠APM=∠CPM. （1）试判断AB 、CD 的大小关系，并说明理由.（2）若焦点P 在⊙O 的外部，如图2，上述结论是否成立？若成立，请证明；若不成立，请说明理由.24．如图，在半径为2的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点（不与A、B 重合），OD⊥BC，OE⊥AC，垂足分别为D、E.（1）当BC=1时，求线段OD的长；（2）在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由；（3）设BD=x，△DOE的面积为y，求y与x的函数关系式，并写出它的自变量取值范围.。