六年级上册数学试题 - 奥数竞赛找规律填图形 全国通用(含答案)

一、选择题（每题2分，共20分）1. 下面哪个数列是等差数列？A. 1, 4, 7, 10, 13, ...B. 1, 3, 6, 10, 15, ...C. 1, 2, 4, 8, 16, ...D. 2, 4, 8, 16, 32, ...答案：B2. 下面哪个数列是等比数列？A. 1, 3, 9, 27, 81, ...B. 1, 2, 3, 4, 5, ...C. 1, 3, 6, 10, 15, ...D. 2, 4, 8, 16, 32, ...答案：A3. 下面哪个数列是斐波那契数列？A. 1, 2, 3, 5, 8, 13, ...B. 1, 3, 6, 10, 15, ...C. 2, 4, 8, 16, 32, ...D. 1, 2, 4, 8, 16, ...答案：A4. 下面哪个数列是平方数列？A. 1, 4, 9, 16, 25, ...B. 1, 3, 6, 10, 15, ...C. 1, 2, 4, 8, 16, ...答案：A5. 下面哪个数列是立方数列？A. 1, 8, 27, 64, 125, ...B. 1, 2, 3, 4, 5, ...C. 1, 3, 6, 10, 15, ...D. 2, 4, 8, 16, 32, ...答案：A二、填空题（每题3分，共15分）6. 下列数列中，缺失的数是：2, 4, 8, __, 32, ...答案：167. 下列数列中，缺失的数是：1, 4, 9, 16, __, ...答案：258. 下列数列中，缺失的数是：1, 2, 4, 8, __, ...答案：169. 下列数列中，缺失的数是：2, 4, 8, 16, __, ...答案：3210. 下列数列中，缺失的数是：1, 3, 6, 10, __, ...答案：15三、解答题（每题10分，共30分）11. 写出一个公差为3的等差数列，并写出前5项。

答案：2, 5, 8, 11, 1412. 写出一个公比为2的等比数列，并写出前5项。

找 规 律1、观察下面的点阵图和相应的等式，探究其中的规律：（1）在④和⑤后面的横线上分别写出相应的等式；（2）通过猜想写出与第n 个点阵相对应的等式_____________________。

2、观察下列等式：221.4135−=×；222.5237−=×；223.6339−=×224.74311−=×；…………第5个等式位 .则第n （n 是自然数）个等式为3、自己观察下列算式，寻找规律填数．2+4=2×32+4+6=3×42+4+6+8=4×52+4+6+8+10+…+50= × ．4．古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正方形数”． 从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ）………… ①1=12； ②1+3=22； ③1+3+5=32④ ； ⑤；A ．13 = 3+10B ．25 = 9+16C ．36 = 15+21D ．49 = 18+315、 观察下列顺序排列的等式：9×0＋1＝1，9×1＋2＝11，9×2＋3＝21，9×3＋4＝31，9×4＋5＝41，…… ．猜想：第n 个等式（n ____________________________．6、观察下列各式：1×3=21+2×1，2×4=22+2×2，3×5=23+2×3，请你将猜想到的规律用自然数n （n ≥1）表示出来： 。

7、 数字解密：第一个数是3=2＋1，第二个数是5=3＋2，第三个数是9=5＋4，第四个数是17=9＋8，……观察并猜想第六个数是 。

10.观察下列等式：211=2132+=4=1+3 9=3+6 16=6+10…2++=1353……………根据观察可得：13521_________.（n为非0自然数）n++++−=8、观察下列等式9-1=816-4=1225-9=1636-16=20…………这些等式反映自然数间的某种规律，设n(n≥1)表示自然数，用关于n的等式表示这个规律为 .9、观察下列等式：第一行 3=4－1第二行 5=9－4第三行 7=16－9第四行 9=25－16… …按照上述规律，第n行的等式为____________10、观察下列各式：3211=332+=1233322++=123633332123410+++=……猜想：333312310++++= ．11、观察下列几个算式，找出规律：1＋2＋1=41＋2＋3＋2＋1=91＋2＋3＋4＋3＋2＋1=161＋2＋3＋4＋5＋4＋3＋2＋1=25……利用上面规律，请你迅速算出：①1＋2＋3＋…＋99＋100＋99＋…＋3＋2＋1= ②据①你会算出1＋2＋3＋…＋100是多少吗？③据上你能推导出1＋2＋3＋…＋n 的计算公式吗？12、你能很快算出21995吗？为了解决这个问题，我们考察个位上的数为5的自然数的平方，任意一个个位数为5的自然数可写成10•n +5,即求2)510(+n 的值（n 为自然数），你试分析 ,3,2,1===n n n 这些简单情况，从中控索其规律，并归纳，推测出结论（在下面空格内填上你的控索结果）。

小学六年级奥数竞赛试卷一、填空题（共23小题，每小题3分，满分69分）1．（3分）计算：（12345+23451+34512+45123+51234）÷5=2．（3分）比较大小：（填＞、＜或=）3．（3分）分数化成循环小数后，小数部分左起第2004个数字是个数字是 ．4．（3分）边长24厘米的等边三角形ABC，被分成面积相等的4个小三角形（如图）．那么线段DF比BE长厘米．5．（3分）A、B两点分别是长方形的长和宽的中点，那么，阴影部分（如图）占长方形面积的 （填几分之几）．面积的6．（3分）三角形ABC中（如图），DE将三角形分成甲、乙两部分．那么乙的面积是甲的面积的 倍．的面积的7．（3分）计算：．8．（3分）……+++1+2+4+8+16+……+256+512=．9．（3分）一个长方形，如果长和宽都增加4米，则面积增加88平方米．原来长方形的周长是 米．周长是10．（3分）某个自然数与10的和与差均为完全平方数，这个自然数是．11．（3分）一筐苹果不足60个，若把它平均分给几个同学，则每人恰好分6个；若只个．共有 位男同学．分给其中几个女同学，则每个女同学可分到10个．共有12．（3分）小王与甲、乙、丙、丁四人一起打乒乓球，每两人打一局，已知甲已打4局．那么小王已打了 局．局，乙已打3局，丙已打2局，丁已打1局．那么小王已打了13．（3分）100以内只有10个不同约数的自然数是个不同约数的自然数是 ．14．（3分）分母小于10且最接近1.14的最简分数是的最简分数是 ．15．（3分）两个自然数的和与差的积是41，那么这两个自然数的积是，那么这两个自然数的积是 ．16．（3分）两个循环小数0.96925和0.925，在小数点后第在小数点后第 数位上首次同时出现数字7？17．（3分）等腰直角三角形的面积是4.5平方厘米，由8个这样的三角形组成一个正方形，这个正方形的周长是 厘米．形，这个正方形的周长是18．（3分）一个六位数的左边第一位数字是1．如果把这个数字移到最右边，所得的新倍．原数是 ．六位数是原数的3倍．原数是19．（3分）对于小数0.0123456，要使它成为循环小数且小数部分左起第100位上数字，那么两个循环点应分别加在 和这两个数字上．是4，那么两个循环点应分别加在20．（3分）甲、乙两个自然数，它们的和被3除余1，它们的差能被3整除．那么甲数除的余数是 ．被3除的余数是21．（3分）有四个分数：，其中最大的分数与最小的分数之和是．22．（3分）有两堆棋子，若从第一堆拿1枚放到第二堆中去，则第二堆的棋子数是第一枚放到第二堆中去，则第二堆的棋子数是第一堆的2倍；若从第二堆拿1枚放到第一堆中去，则两堆棋子数恰好相同．第一堆有枚，第二堆有 枚．枚，第二堆有23．（3分）长方形的长和宽各是9厘米和4厘米，要把它剪成大小、形状都相同的两块，并使它们拼成一个正方形．2018年小学六年级奥数竞赛试卷参考答案与试题解析一、填空题（共23小题，每小题3分，满分69分）1．【分析】根据题意，被除数中的五个加数，每个数位上数字的和都是1+2+3+4+5=15，然后再根据数位知识拆分解答即可．【解答】解：（12345+23451+34512+45123+51234）÷5=（1+2+3+4+5）×（10000+1000+100+10+1）÷5=15×11111÷5=3×11111=33333故答案为：33333．【点评】解答此题，应仔细观察，认真分析式中数据，运用运算技巧或运算定律合理简算．2．【分析】根据题意，将这两个数分别转化成与另一个分数的和，然后比较这两个分数的大小，然后推论出原来两个数的大小即可．【解答】解：根据题意得因为所以故答案为＞．【点评】本题考查了比较大小．3．【分析】=0.3571428571428…，首先分析循环小数0.3571428571428…的循环节有几位数字，然后用2004除以循环节的位数，余数是几，第2004位上的数字就是循环节的第几位数字．【解答】解： =0.3571428571428…，循环节为571428，有6位数字，因为（2004﹣1）÷6=333…5，循环节中第5个数是2，故答案为：2．【点评】解决这类问题往往是把重复出现的部分看成一组，先找出排列的周期性规律，再根据规律求解．4．【分析】根据等边三角形的特征，以及三角形的高一定时，面积比等于底边比解答即可．【解答】解：根据题意可得：S △ABD =S △BED =S △DEF =S △CEF ，所以，S △BED ：（S △DEF +S △CEF ）=1：2，所以，BE ：EC=1：2所以，BE=24×=8厘米，同理，S △ABD ：S △ABC =1：4，所以，AD ：AC=1：4，所以，CD ：AC=（4﹣1）：4=3：4，又因为，DF=CF ，所以，DF=24××=9厘米，所以，DF ﹣BE=9﹣8=1厘米；故答案为：1．【点评】此题考查了三角形的高一定时，三角形的面积与底成正比的性质的灵活应用． 5．【分析】根据题意，设长方形的长和宽分别为a ，b ，则长方形的面积是ab ，小三角形的面积=，阴影部分的面积=长方形面积的一半﹣小三角形的面积=，阴影部分占长方形面积的，据此回答．【解答】解：根据题意设长方形的长和宽分别为a ，b ，则长方形的面积是ab ，小三角形的面积=阴影部分面积=，阴影部分（如图）占长方形面积的．故答案为．【点评】本题考查了长方形的面积和三角形的面积问题．6．【分析】根据三角形的高一定时，面积比等于底边比解答即可．【解答】解：连接BD ，如下图：△ADE 与△BDE 等高，且AE ：EB=3：6=1：2，所以，S △ADE =S △BDE =1：2，所以，S △BDE =2×甲，同理，AD ：DC=4：4=1：1，所以，S △BCD =S △ABD =（2+1）×S △ADE =3×甲，所以，乙=S △BDE +S △BCD =2×甲×甲++3×甲=5×甲；故答案为：5．【点评】此题考查了三角形的高一定时，三角形的面积与底成正比的性质的灵活应用． 7．【分析】通过观察，可把原式分为两部分，即﹣，约分计算．【解答】解：=﹣=1﹣= 【点评】仔细分析数据，采取灵活的方法，进行简算．8．【分析】本题可以把分数部分和整数部分分开计算，然后再相加即可．【解答】解：+1+2+4+……+256+512 =1﹣+210﹣1=1024﹣=【点评】本题考查的是分数的简算及等比数列的求和．9．【分析】由于原来长方形的长×4+原来长方形的宽×4+4×4=88平方厘米，根据乘法分配律可求原来长方形的长++宽，从而求得原来长方形的周长．分配律可求原来长方形的长【解答】解：根据题意得（88﹣4×4）÷4×2=36（米）故答案为：36．【点评】考查了长方形的周长和面积，本题的关键是运用运算律将原来长方形的长+宽看作一个整体，有一定的难度．10．【分析】根据题意，设这个自然数为m，，两个方程相减可得：A2﹣B2=（A﹣B）×（A+B）=20，把20写成两个数的乘积的形式可得出关于A、B的二元一次方程，由此利用加减消元法即可解答，求出A、B的值即可求出m解决问题．【解答】解：设这个自然数为m，，所以A2﹣B2=（A﹣B）×（A+B）=20，因为20=1×20=2×10=4×5，而（A﹣B）与（A+B）同奇同偶，所以只能是，解得，所以m=62﹣10=26．故答案为：26．【点评】此题较为复杂，关键是利用平方差公式得出（A﹣B）×（A+B）=20进而得出关于A、B的二元一次方程组，解这个方程组即可解答问题．11．【分析】根据题意可知：这筐苹果的总个数，即是6的倍数又是10的倍数，且6和10的最小公倍数是30，据此分析解答即可．【解答】解：解：[[6，10]=3030÷6﹣30÷10=2（个）故填：2【点评】本题考查的是用公倍数解决问题．12．【分析】共5位选手参赛，每两个人都要比赛一场，则每个选手都要与其他四位各赛一局，每个人共赛四局．根据题意通过连线可知：据此解答即可．【解答】解：根据题意画图如下：通过观察连线可知已经打了6局（实线），没打的有4局（虚线），其中小王已打了2局．故答案为：2．【点评】根据赛制及每人比赛的场数之间的逻辑关系进行分析是完成本题的关键．本题用连线画图的方法更加直观具体．13．【分析】此题巧用求一个数约数的方法，从最小的质因数着手，分析不同的情形，得出结论．【解答】解：因数有10个，根据10=2×5=1×10，其中1×10不合要求，舍去；可写成a×b4形式（a、b是质数）这时只能取a=3或5，b=2时符合条件，当a=3，b=2时，这个数为3×25=48当a=5，b=2时，这个数为5×25=80故答案为：48和80．【点评】此题主要考查一个合数的约数个数的计算公式的逆用：a=pα×qβ×rγ（其中a 为合数，p、q、r是质数），则a的约数共有（α+1）（β+1）（γ+1）个约数．14．【分析】因为=和1.14的小数部分0.14比较接近，据此分析解答即可．【解答】解：因为=和1.14的小数部分0.14比较接近，所以分母小于10且最接近1.14的最简分数是．故填：【点评】本题考查的是简单的分数问题．15．【分析】从两个自然数的和与差的积是41入手，41是质数，也就是1×41=41，可见它们的差是1，和是41，这是两个连续的自然数分别为20、21．然后计算其乘积即可．【解答】解：首先注意到41是质数，两个自然数的和与差的积是41，可见它们的差是1，这是两个连续的自然数，大数是21，小数是20，所以这两个自然数的积是20×21=420．故答案为：420．【点评】此题考查质数与合数．16．【分析】第一个循环小数出现数字7的周期是7个数字，第二个循环小数出现数字7的周期是5个数字，首次同时出现数字7即是7的倍数又是5的倍数，据此解答即可．【解答】解：解：[[7，5]=35故填：35【点评】本题考查的是周期问题．17．【分析】这个大正方形的面积就是8个小三角形的面积和，求出这个大正方形的面积，再根据正方形的面积求出它的边长，根据正方形的周长公式求出它的周长．【解答】解：拼成的正方形如图：面积是：4.5×8=36（平方厘米）；大正方形的面积是36平方厘米，36=6×6，那么它的边长就是6厘米；周长：6×4=24（厘米）；故答案为：24．【点评】本题关键是知道拼成正方形的面积就是原来三角形的面积和，由此求解．18．【分析】把这个六位数的后面的五位数设为x，则根据位置原理可知：原来的六位数可以表示为：1000000+x；新的六位数可以表示为：10x+1，据此分析解答即可．【解答】解：设原来六位数的后面的五位数为x，则有：3（10000000+x）=10x+13000000+3x=10x+17x=299999x=42857则原来的六位数是：142857故填：142857．【点评】本题考查的是位置原理．19．【分析】根据题意可知：第100位上的数字是4，则第102位上的数字一定是6，第一个6是在第7位，则中间的95位一定是循环节的倍数，据此分析解答即可．【解答】解：根据题意可知：第100位上的数字是4，则第102位上的数字一定是6，第一个6是在第7位，则中间的95位一定是循环节的倍数．95÷7=13 (4)95÷6=15 (5)95÷5=19即循环节的位数是5位，所以两个循环点分别加在2和6上面．【点评】本题考查的是循环小数的循环节及周期问题．20．【分析】根据同余定理和差能被3整除，得出甲乙除以3的余数是相同的，设甲为3x+a，乙为3y+a，由此求解．【解答】解：设甲为3x+a，乙为3y+a，差能被3整除，所以甲乙除以3的余数是相同的则a的取值为0或者1或者2．甲乙的和为：3（x+y）+2a，其除以3余1，所以2a除以3余1，a只能为2 故答案为：2．，【点评】图形拆拼解决的关键点：把一个几何图形剪成几块形状相同的图形，把一个几何图形剪成几块形状相同的图形，或是把一个几何图形剪开后拼成另一种满足或是把一个几何图形剪开后拼成另一种满足某种条件的图形，某种条件的图形，完成这样的图形剪拼，完成这样的图形剪拼，需要考虑图形剪开后各部分的形状、需要考虑图形剪开后各部分的形状、大小以大小以及它们之间的位置关系．。

小学奥数竞赛试卷一、填空题。

1．（3分）某次数学竞赛原定一等奖8人，二等奖16人，现在将一等奖中最后4人调整为二等奖，这样得二等奖的学生的平均分提高了1.2分，得一等奖的学生的平均分提高了4分，那么原来一等奖平均分比二等奖平均分多分．2．（3分）一个三位数等于它的各位数字之和的19倍，这样的三位数共有11个，其中最小的和最大的分别是、．3．（3分）55道数学题，分给甲、乙、丙三人计算．已知乙分到的题比甲多1倍，丙分到的题最少，却是个两位数，且个位不是0．甲分到道题，乙分到道题，丙分到道题．4．（3分）李小华要把自己平日存的零花钱捐给残疾人协会，他把储蓄盒中的2分和5分的硬币都倒出来，估计有5到6元钱，李小华把这些硬币分成钱数相等的两堆，第一堆里2分和5分的硬币个数相等，第二堆2分和5分硬币的钱数相等，问李小华的这些钱一共有．5．（3分）生物研究所的科研人员要做一次试验并决定上午10时开始做第一次观察，以后每隔3小时观察一次，当第18次观察，表盘上时针与分针的夹角小于180度，问这时时针与分针的夹角是度．6．（3分）一本书的页码是由3181个数字组成，这本书共有页．7．（3分）有100元、10元、1元面值的人民币18张，已知其中100元和1元的人民币张数的和恰好等于10元人民币的张数，现将100元，10元人民币也换成1元的人民币，然后把所有的人民币平均分给12人，正好分完，则每种面值分别有张．8．（3分）甲村、乙村相距6千米，小张与小王分别从甲、乙两村同时出发，在两村之间往返行走（到达另一村后马上返回）．在出发后40分钟两人第一次相遇．小王到达甲村后返回，在离甲村2千米的地方两人第二次相遇．小张每小时走千米，小王每小时走千米．9．（3分）个位数是5，且能被3整除的四位数有个．10．（3分）有一蓄水池，池中有一条进水管和一条排水管，灌满一池水需打开进水管5小时，排完一池水需打开排水管2小时，现池内有满满一池水，如果按排水、进水、排水、进水……的顺序轮流各开1小时，那么小时后水池的水刚好排完．小学奥数竞赛试卷参考答案与试题解析一、填空题。

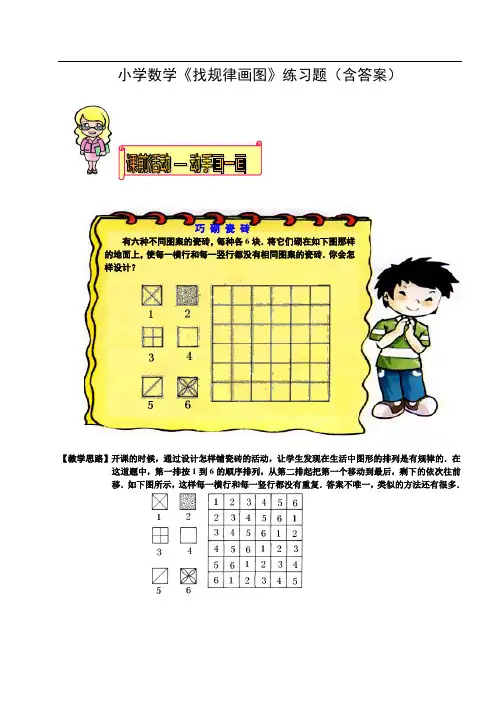
小学数学《找规律画图》练习题（含答案）【教学思路】开课的时候，通过设计怎样铺瓷砖的活动，让学生发现在生活中图形的排列是有规律的．在这道题中，第一排按1到6的顺序排列，从第二排起把第一个移动到最后，剩下的依次往前移．如下图所示，这样每一横行和每一竖行都没有重复．答案不唯一，类似的方法还有很多．巧砌瓷砖有六种不同图案的瓷砖，每种各6块．将它们砌在如下图那样的地面上，使每一横行和每一竖行都没有相同图案的瓷砖．你会怎样设计？同学们，生活中很多的图形在排列的时候都是有规律的，只要我们仔细观察，认真分析就一定能找到其中的规律．今天这节课就让我们走进这美妙的图形王国，去探索其中的奥秘吧！按规律填出空白图形．⑴答案：第二排第三个第三排第二个⑵答案：⑶答案：⑷答案：这些图形的排列都有一定的规律，你能找到吗？【教学思路】⑴通过观察，可以发现：每行每列都只有三角形、五边形、圆．所以第二行第三个图形应该是五边形，第三行第二个图形应该是圆形．⑵通过观察，不难发现，图形从左到右的变化规律是：边数在一条条增加，图形中的直线条数也在一条条增加，而且直线的方向是：横—竖—横—竖这样变化的．因此第四幅图应是一个正六边形，里面有4条竖着的直线，⑶我们发现第一个图和第二个图形状相同，图形里面的阴影相反．根据这个规律第三个图形和第四个图形也应该如此，因此第四个图形和第三个图形形状相同，里面的阴影应该相反．⑷仔细观察发现，圆的变化是：一个比一个增多，所以第四个图里面应该画四个圆．三角形的变化是：方向是按顺时针转动的，上—右—下—左，所以第四个图里面的三角形方向应该向左．按照下面的规律，画一画．⑴⑵【教学思路】⑴第四个图中蓝色的三角应该往左和上各移动一个位置．⑵左边和右边的图合在一起就组成了中间的图形．答案图下：⑴⑵在方框内填上适当的图形．答案：【教学思路】观察这个图我们发现，每组中的三个图形形状相同，只是图形里面的阴影不同，不过这三个图形中的阴影合起来正好是这个图形完整的阴影．这样根据所缺的阴影来判断，第三个图形的阴影应该是第一个图形阴影相对的那一块．1．你知道“？”处应该画什么吗？【教学思路】通过观察我们发现．第一个图形和第二个图形可以组成第三个图形，因此“？”处应该是下图所示．？2．下面图形的排列有什么规律呢？请你把空白处补充完整．答案：【教学思路】通过观察我们发现，每排中的三个图中间部分的图案都相同，不同的是第一个外面部分没有，第二个外面部分是圆，第三个外面部分是正方形．根据这个规律空白处的图案应该是右上图．下面的图形是按一定规律排列的，依据这一规律，画出所缺图形．【教学思路】通过观察，第一行和第二行圆中的3个图形都是相同的，不同的地方只是它们的排列顺序，第一排的第一个在第二排中被移到了第三个，第一排的第二个和第三个，在第二排中被移到了第一个和第二个．根据这样移动的规律，第三排得的第三个就应该是第二排的第一个．所以在第3行的“？”处应填．下图中的图形是按一定规律排列的，请仔细观察，并在“？”处填上适当的图形．【教学思路】本图中，首先可以注意到每个图形都由大、小两部分组成，而且，大、小图形都是由正方形、三角形和圆形组成，图中的任意两个图形均不相同．因此，我们不妨试着把大、小图形分开来考虑，再一次观察后我们可以发现：对于大图形来说，每行每列的图形决不重复．因此，每行每列都只有一个大正方形，一个大三角形和一个大圆，对于小图形也是如此，这样，“？”处的图形分别应填下面的三个图形．按图形的变化规律，在“？”处画上所缺的图形．答案：【教学思路】如果单纯分析颜色，恐怕不好掌握问题的关键．如果我们把图“转”起来就会很快发现它的规律．如第一行的第一幅图逆时针旋转90度就变成了第二幅图，再旋转90度就变成了第三幅图．同理，用此方法验证第三行的三幅图是成立的．所以第二行的第二幅图也应把第一幅图逆时针旋转90度，答案如右上图．【教学思路】用一条比桥面长的钢索系在炮车与大炮之间，让炮车拖着大炮过桥，这样二者就不会同时压在桥上，而且，可以顺利地过桥了。

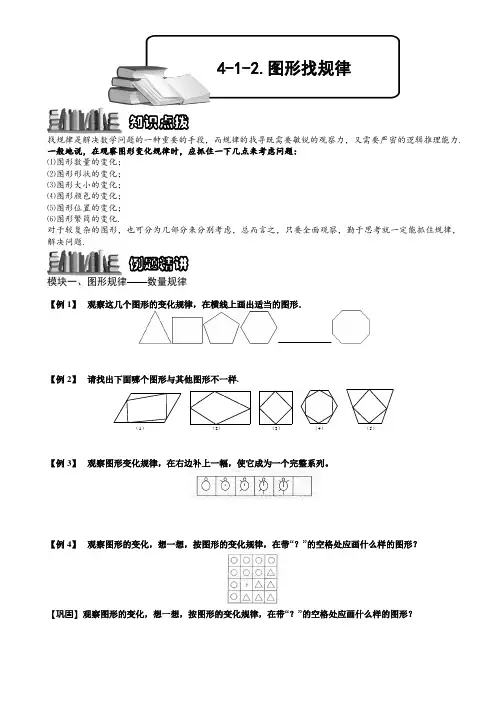
找规律是解决数学问题的一种重要的手段，而规律的找寻既需要敏锐的观察力，又需要严密的逻辑推理能力.一般地说，在观察图形变化规律时，应抓住一下几点来考虑问题： ⑴图形数量的变化； ⑵图形形状的变化； ⑶图形大小的变化； ⑷图形颜色的变化； ⑸图形位置的变化； ⑹图形繁简的变化.对于较复杂的图形，也可分为几部分来分别考虑，总而言之，只要全面观察，勤于思考就一定能抓住规律，解决问题.模块一、图形规律——数量规律【例 1】 观察这几个图形的变化规律，在横线上画出适当的图形．【例 2】 请找出下面哪个图形与其他图形不一样.（1）（2）（3）（4）（5）【例 3】 观察图形变化规律，在右边补上一幅，使它成为一个完整系列。

【例 4】 观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？【巩固】 观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？例题精讲知识点拨4-1-2.图形找规律【巩固】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？？【例5】观察下面的图形，按规律在“？”处填上适当的图形.（4）？【例6】观察图形变化规律，在右边再补上一幅，使它们成为一个完整的系列.【例7】观察下图中的点群，请回答：(1)方框内的点群包含个点；(2)推测第10个点群中包含个点；(3)前10个点群中，所有点的总数是。

【例8】观察下面由点组成的图形（点群），请回答：（1）方框内的点群包含个点；（2）第（10）个点群中包含个点；（3）前十个点群中，所有点的总数是。

【例9】下图表示“宝塔”，它们的层数不同，但都是由一样大的小三角形摆成的.仔细观察后，请回答：（1）五层的“宝塔”的最下层包含多少个小三角形？（2）整个五层“宝塔”一共包含多少个小三角形？【例 10】 在纸上画5条直线，最多可有 个交点。

模块二、图形规律—— 旋转、轮换型规律【例 11】 相传古时候一位老人留在人间很多宝盒，里面装着世界上最宝贵的财富，但是并不是拥有宝盒都可以得到这笔财富，在宝盒的上面设置了密码，只有写出密码的人才会真正拥有这笔财富，聪明的你你能找出密码吗？ ○ □ ☆ △ ○ □ ☆ △ △ ○ □ ☆ △ ○ □ ☆ ☆ △ ○ □ ☆ △ ○ □ （）（）（）（）（）（）（）（）【例 12】 下面的图形是按一定规律排列的，请仔细观察，并在“？”处填上适当的图形.（1）（2）（3）【例 13】 观察下图的变化规律，画出丙图.甲DA乙BC丙【例 14】 图中的三个图形都是由A 、B 、C 、D (线段或圆)中的两个组合而成，记为A ★B 、C ★D 、A ★D ．请你画出表示A ★C 的图形．A★B C★D A★D【例15】(希望杯五年级一试第7题，6分)下列四个图形是由四个简单图形A、B、C、D（线段和正方形）组合（记为*）而成。

六年级上册数学试卷奥数竞赛逻辑问题全国通用数学是锤炼思维的体操，在我们学习数学的过程中，有许多问题都需要我们利用逻辑推理来解答。

那么什么是逻辑问题呢？逻辑问题是指事物进行判定、推理。

一样说逻辑问题必须遵循一些初步规律：矛盾律：两个矛盾的判定，不可能是同时成立的。

例如：小明在一次数学竞赛中，不能既是第一名又是第三名。

排中律：是指只有两种可能，没有介于两者之间第三种可能。

例如：甲、乙两人争夺乒乓球竞赛单打冠军，冠军不是甲获得，确实是乙获得。

这两个结论必有一个成立。

解这类问题时，往往先从某一个条件动身，利用其他条件进行推理，直到推出结论为止。

有时先做出一种假设，从那个假设动身，推出自相矛盾的结论。

说明那个假设是不成立的，因此与假设相反的情形是正确的。

在推理的过程中，选中突破口，层层剖析是解决问题的关键，经常采纳的解答方法是表格方式。

例1、某地质学院的三名学生对一种矿石进行分析。

甲判定：“不是铁，不是铜。

”乙判定：“不是铁，而是锡。

”丙判定：“不是锡，而是铁。

”经化验证明，有一个人判定完全正确，有一人只说对了一半，另一人则完全误了。

你明白这种矿石是矿石；是错的；只对了一半。

例2、小明和小华和小红三人中，有一人做了一件好事。

老师问他们三个人是谁做的好事。

小明说：“是小华做的。

”小华说：“不是我做的。

”小红说：“不是我做的。

”已知他们三个人中有两人说的是假话，有一个说的是真话。

请你判定一下，好事是做的。

例3、刘军、张斌和徐文在一起，一位是工人，一位是农民，一位是战士。

现在只明白：①徐文比战士的年龄大；②刘军和农民不同岁；③农民比张斌年龄小。

是工人；是农民，是战士。

例4方体红色面的对面涂的是是色，黑色面的对面涂的是色。

例5：观看下图中数字的摆放规律,由此得到A=_____例6、爸爸在邮局寄了三种信：平信邮资每封1角，航空信邮资每封2角，挂号信邮资每封4角，他共用去2元2角。

问爸爸寄的三种信的总和最少是封。

例7：甲、乙、丙三人中有一位是意大利牧师,有一位英国骗子,还有一位美国赌棍.牧师不说谎话,骗子总说谎话,赌棍有时要说谎.甲说:“丙是牧师.”乙说:“甲是赌棍.”丙说:“乙是骗子.”甲是_______,乙是_______,丙是________。

知识点说明 在奥数中有一类“不讲道理”的题目，我们称之为“简单操作找规律”。

有一些对小学生来说很难证明的，但与证明相比，发现却是比较容易的。

这也是数学中的一种重要的思想，在以后的数学学习中会有一种先猜后证的解题方法。

这类题主要考查孩子们的发现能力。

模块一，周期规律 【例 1】 四个小动物换座位．一开始，小鼠坐在第1号位子，小猴坐在第2号，小兔坐在第3号，小猫坐在第4号．以后它们不停地交换位子．第一次上下两排交换．第二次 是在第一次交换后再左右两排交换．第三次再上下两排交换．第四次再左右两排交换……这样一直换下去．问：第十次交换位子后，小兔坐在第几号位子上？（参看 下图）【考点】操作找规律 【难度】2星 【题型】解答【关键词】华杯赛，初赛【解析】 根据题意将小兔座位变化的规律找出来．可以看出：每一次交换座位，小兔的座位按顺时针方向转动一格，每4次交换座位，小兔的座位又转回原处．知道了这个规律，答案就不难得到了．第十次交换座位后，小兔的座位应该是第2号位子。

【答案】第2号【例 2】 在1989后面写一串数字。

从第5个数字开始 ，每个数字都是它前面两个数字乘积的个位数字。

这样得到一串数字：1 9 8 9 2 8 6 8 8 4 2 ……那么这串数字中，前2005个数字的和是____________。

【考点】操作找规律 【难度】2星 【题型】填空【关键词】迎春杯，中年级，初试【解析】 由题意知，这串数字从第5个数字开始，只要后面的连续两个数字与前面的连续两个数字相同，后面的数字将会循环出现。

1989︱286884︱28……由上图知，从第5个数字开始，按2,8,6,8,8,4循环出现。

()2005463333-÷=⋯，前2005个数字和是()()()1989286884333286+++++++++⨯+++27119881612031=++=。

【答案】12031例题精讲知识点拨操作找规律【例3】先写出一个两位数62，接着在62右端写这两个数字的和8，得到628，再写末两位数字2和8的和10，得到62810，用上述方法得到一个有2006位的整数：628101123…，则这个整数的数字之和是。

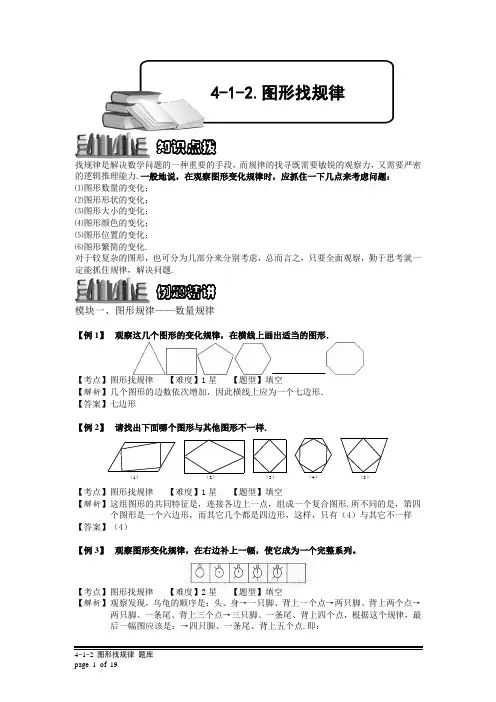
找规律是解决数学问题的一种重要的手段，而规律的找寻既需要敏锐的观察力，又需要严密的逻辑推理能力.一般地说，在观察图形变化规律时，应抓住一下几点来考虑问题：⑴图形数量的变化；⑵图形形状的变化；⑶图形大小的变化；⑷图形颜色的变化；⑸图形位置的变化；⑹图形繁简的变化.对于较复杂的图形，也可分为几部分来分别考虑，总而言之，只要全面观察，勤于思考就一定能抓住规律，解决问题.模块一、图形规律——数量规律【例 1】观察这几个图形的变化规律，在横线上画出适当的图形．【考点】图形找规律【难度】1星【题型】填空【解析】几个图形的边数依次增加，因此横线上应为一个七边形．【答案】七边形【例 2】请找出下面哪个图形与其他图形不一样.（1）（2）（3）（4）（5）【考点】图形找规律【难度】1星【题型】填空【解析】这组图形的共同特征是，连接各边上一点，组成一个复合图形.所不同的是，第四个图形是一个六边形，而其它几个都是四边形，这样，只有（4）与其它不一样【答案】（4）【例 3】观察图形变化规律，在右边补上一幅，使它成为一个完整系列。

【考点】图形找规律【难度】2星【题型】填空【解析】观察发现，乌龟的顺序是：头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点，根据这个规律，最后一幅图应该是：→四只脚、一条尾、背上五个点.即：例题精讲知识点拨4-1-2.图形找规律【答案】【例 4】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？【考点】图形找规律【难度】2星【题型】填空【解析】横着看，每行圆形的个数一次减少，而三角形的个数依次增加，但每行图形的总个数不变.因为圆形的个数是按4、3、？、1的顺序变化的，显然“？”处应填一个圆形。

【答案】圆形【巩固】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？【考点】图形找规律【难度】2星【题型】填空【解析】（方法一）横着看，每行圆形的个数一次减少，而三角形的个数依次增加，但每行图形的总个数不变.因为圆形的个数是按5、4、3、？、1的顺序变化的，显然“？”处应填一个圆形.(方法二)竖着看，圆形由左而右依次减少，而三角形由左而右依次增加，圆形按照5、4、？、2、1的顺序变化，也可以看出“？”处应是圆形.【答案】圆形【巩固】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？？【考点】图形找规律【难度】2星【题型】填空【解析】（方法一）横着看，每行三角形的个数依次减少，而正方形的个数依次增加，但每行图形的总个数不变.因为三角形的个数是按4、3、？、1的顺序变化的，显然“？”处应填一个三角形△.(方法二)竖着看，三角形由左而右依次减少，而正方形由左而右依次增加，三角形按照4、？、2、1的顺序变化，也可以看出“？”处应是三角形△.【答案】△【例 5】观察下面的图形，按规律在“？”处填上适当的图形.（5）（4）（3）（2）（1）？【考点】图形找规律【难度】2星【题型】填空【解析】本题中，几何图形的变化表现在数量关系上，图中黑三角形的个数从左到右依次增多，从（2）起，每一个格比前面一个格多两个黑三角形，所以，第（4）个方框中应填七个黑三角形.【答案】七个黑三角形【例 6】观察图形变化规律，在右边再补上一幅，使它们成为一个完整的系列.【考点】图形找规律【难度】2星【题型】填空【解析】第一格有8个圆圈，第二格有4个圆圈，第三格有2个圆圈，第四格有1个圆圈，第五格有半个圆圈.由此发现，前一格中的图减少一般，正好是后一格的图.所以第六格的图应该是第五格图的一半，即：【答案】【例 7】观察下图中的点群，请回答：(1)方框内的点群包含个点；(2)推测第10个点群中包含个点；(3)前10个点群中，所有点的总数是。

六年级奥数题及答案讲解-找规律填数编者小语：下面这道试题是根据现在的考试热点精心挑选有关六年级找规律填数问题的试题，以便同学们可以练习.问题2．1观察分析下面各列数的变化规律，并填上合适的数．（1）7，11，15，19，（），…；（2）1，4，3，6，5，（），（），…；（3）1，4，9，16，（），…；（4）1，2，4，8，16，（），…．分析观察分析一列数的变化规律，找出带有规律的东西．在（1）中，11-7=15-11=19-15=…=4．即在这一列数中，从第二个数起，每个数与它前一个数的差都等于4．根据这一规律，可以确定括号里应填23．在（2）中，第一、三、五、......位置上的数满足3-1=5-3= (2)第二、四、六、……位置上的数满足6-4=8-6=…=2．根据这一规律，可以确定括号里的数应该填7、10．在（3）中，第一个数1=1×1=12，第二个数4=2×2=22，第三个数9=3×3=32，第四个数16=4×4=42，…．根据这一规律，可以确定括号里应该填52=25．在（4）中，2=1×2，4=2×2，8=4×2，16=8×2，…，即从第二个数起，每一个数都等于它前一个数的2倍．根据这一规律，括号里应该填32．解略．问题2．2 找规律填空．（1）11，3，8，3，5，3，（），（）；（2）15，6，13，7，11，8，（），（）；（3）2，5，14，41，（）；（4）1，1，2，3，5，8，13，21，（）．分析在（1）中，第一个数减去第三个数的差是3，第三个数减去第五个数的差也是3，而第二、四、六个数都是3．根据这一规律，可以确定括号里应该填2、3．在（2）中，第一个数减去2的差是第三个数，第三个数减去2的差是第五个数；第二个数加上1的和是第四个数，第四个数加上1的和是第六个数．根据这一规律，可以确定括号里应该填9、9．在（3）中，2×3-1=5，5×3-1=14，14×3-1=41．也就是说，前一个数的3倍与1的差等于相邻的后面的数．根据这一规律．可以确定括号里应该填122（即122=41×3-1）．在（4）中，1+1=2，1+2=3，2+3=5，3+5=8，…，即前面两个数之和等于相邻后面的数．根据这一规律，可以确定括号里应该填34（即34=13+21）．解略．问题2．3先找出规律，然后在括号里填上适当的数．（1）3，8，18，33，53，78，（）；（2）0，1，3，8，21，（）．分析在（1）中，8-3=5=1×5，18-8=10=2×5，33- 18=15=3×5，53-33=20=4×5，78-53=25=5×5，即从第二个数起，每一个数与它前一个数的差依次是5的1倍、2倍、3倍、4倍、5倍、……．根据这一规律，下一个差应是5的6倍，可以确定括号里应该镇108（即78+6×5=108）．在（2）中，1×3=0+3，3×3=1+8，8×3=3+21，即从第二个数起，每一个数的3倍正好是它前后相邻两个数的和．因此，21×3=8+（55），即括号里应该填55．在（3）中，把方框中的四个数分为上下两部分，9÷3=3= 1+2，15÷3=5=3+2，即下行两数相除所得的商，正好是上行两数之和；或者说，上行两数之和与下行左边的数的积正好是下行右边的数．根据这一规律，第三个方框里的括号内应该填10（即（2+3）×2=10）．解略．问题2．4 找规律填数．练习21．仔细观察每一排数的排列有什么规律，然后按规律在（）内填上适当的数．（1）2，4，8，16，（），64．（2）1，4，9，16，（），36，49．64．（3）1，4，7，10，13，（），19，21．（4）1，4，16，64，（），1024，4096．（5）2，3，5，9，17，（），65，129．（6）15，4，13，4，11， 4，（），（）．（7）8，15，10，13，12，11，（），（）．2．空格里应填什么数？ 3．找规律填数．4．在○中填数：已知9999÷9=1111，想一想：在○中填上什么数字，才能使下面的等式成立？（1）○999○÷9=2222；（2）○999○÷9=3333；（3）○999○÷9=4444；（4）○999○÷9=7777；（5）○999○÷9=9999．。

六年级奥数博题：找顺序之阳早格格创做共教们从三年级启初，便陆绝交战过许多“找顺序”的题目，比方创造图形、数字或者数表的变更顺序，创造数列的变更顺序，创造周期变更顺序等等.那一道的实质是通过创造某一问题的顺序，推导出该问题的估计公式.例1 供99边形的内角战.分解与解：三角形的内角战等于180°，但是99边形的内角战何如供呢？咱们把问题简化一下，先供四边形、五边形、六边形……的内角战，找一找其中的顺序.如上图所示，将四边形ABCD分成二个三角形，每个三角形的内角战等于180°，所以四边形的内角战等于180°×2= 360°；共理，将五边形ABCDE分成三个三角形，得到五边形的内角战等于180°×3＝540°；将六边形ABCDEF分成四个三角形，得到六边形的内角战等于180°×4＝720°.通过上头的图形及分解不妨创造，多边形被分成的三角形数，等于边数减2.由此得到多边形的内角战公式：n边形的内角战=180°×（n-2）（n≥3）.有了那个公式，再供99边形的内角战便太简单了.99边形的内角战=180°×（99-2）＝17460°.例2 四边形内有10个面，以四边形的4个顶面战那10个面为三角形的顶面，最多能剪出几个小三角形？分解与解：正在10个面中任与一面A，连结A与四边形的四个顶面，形成4个三角形.再正在剩下的9个面中任与一面B.如果B正在某个三角形中，那么连结B与B天方的三角形的三个顶面，此时三角形总数减少2个（睹左下图）.如果B正在某二个三角形的大众边上，那么连结B与B天方边相对付的顶面，此时三角形总数也是减少2个（睹左下图）.类似天，每减少一个面减少2个三角形.所以，共可剪出三角形 4＋ 2× 9= 22（个）.如果将例2的“10个面”改为n个面，其余条件没有变，那么由以上的分解可知，最多能剪出三角形4＋2×（n-1）=2n＋2=2×（n＋1）（个）.共教们皆了解圆柱体，如果将圆柱体的底里换成三角形，那么便得到了三棱柱（左下图）；共理不妨得到四棱柱（下中图），五棱柱（左下图）.如果底里是正三角形、正四边形、正五边形……那么相映的柱体便是正三棱柱、正四棱柱、正五棱柱……例3 n棱柱有几条棱？如果将没有相接的二条棱称为一对付，那么n棱柱公有几对付没有相接的棱？分解与解：n棱柱的底里战顶里皆是n边形，每个n边形有n个顶面，所以n棱柱公有2n个顶面.瞅察三棱柱、四棱柱、五棱柱的图形，不妨瞅出，每个顶面皆与三条棱贯串，而每条棱对接 2个顶面，所以n棱柱公有棱 2n×3÷2=3n （条）.进一步瞅察不妨创造，n棱柱中每条棱皆与4条棱相接，与其余的3n－4-1 =（3n－5）条棱没有相接.公有3n条棱，所以没有相接的棱有 3n×（3n- 5）（条），果为没有相接的棱是成对付出现的，各估计一遍便沉复了一遍，所以没有相接的棱公有3n×（3n-5）÷2（对付）.例4 用四条曲线最多能将一个圆分成几块？用100条曲线呢？分解与解：4条曲线时，咱们不妨试着绘，100条曲线便没有成能再绘了，所以必须觅找到顺序.如下图所示，一个圆是1块；1条曲线将圆分为2块，即减少了1块；2条曲线时，当2条曲线没有相接时，减少了1块，当2条曲线相接时，减少了2块.由此瞅出，要念分成的块尽管多，应当使后绘的曲线尽管与前里已绘的曲线相接.再绘第3条曲线时，应当与前里2条曲线皆相接，那样又减少了3块（睹左下图）；绘第4条曲线时，应当与前里3条曲线皆相接，那样又减少了4块（睹左下图）.所以4条曲线最多将一个圆分成1＋1＋2＋3＋4=11（块）.由上头的分解不妨瞅出，绘第n条曲线时应当与前里已绘的（n—1）条曲线皆相接，此时将减少n块.果为一启初的圆算1块，所以n条曲线最多将圆分成1＋（1＋2＋3＋…＋n）=1＋n（n+1）÷2（块）.当n=100时，可分成1＋100×（100＋1）÷2=5051（块）.例5 用3个三角形最多不妨把仄里分成几部分？10个三角形呢？分解与解：仄里自己是1部分.一个三角形将仄里分成三角形内、中2部分，即减少了1部分.二个三角形没有相接时将仄里分成3部分，相接时，接面越多分成的部分越多（睹下图）.由上图瞅出，新减少的部分数与减少的接面数相共.所以，再绘第3个三角形时，应使每条边的接面尽管多.对付于每个三角形，果为1条曲线最多与三角形的二条边相接，所以第3个三角形的每条边最多与前里2个三角形的各二条边相接，共可爆收3×（2×2）= 12（个）接面，即减少12部分.果此， 3个三角形最多不妨把仄里分成1＋1＋6＋12= 20（部分）.由上头的分解，当绘第n（n≥2）个三角形时，每条边最多与前里已绘的（n—1）个三角形的各二条边相接，共可爆收接面3×［（n—l）×2］=6（n—1）（个），能新减少6（n－1）部分.果为1个三角形时有2部分，所以n个三角形最多将仄里分成的部分数是2＋6×［1＋2＋…＋（n—1）］当n=10时，可分成2＋3×10×（10—1）=272（部分）.训练1.供12边形的内角战.2.五边形内有8个面.以五边形的5个顶面战那8个面为三角形的顶面，最多能剪出几个小三角形？3.已知n棱柱有14个顶面，那么，它有几条棱？4.n条曲线最多有几个接面？5.6条曲线与2个圆最多产死几个接面？6.二个四边形最多把仄里分成几部分？训练问案：1.1800°.2.19个.提示：与例2类似可得5+2×（8-1）=19（个）.3.21条棱.提示：n棱柱有2n个顶面，3n条棱.4.n（n-1）÷2.解：1+2+3+…+（n-1）=n（n-1）÷2.5.41个.解：6条曲线有接面6×（6-1）÷2=15（个），每条曲线与二个圆各有2个接面，二个圆之间有2个接面，公有接面15+6×4+2=41（个）.6.10部分.提示：睹左图.与例5类似，当绘第n（n≥2）个四边形时，每条边应与已绘的（n-1）个四边形的各2条边相接，共可爆收接面4×[（n-1）×2]=8（n-1）（个），新减少8（n-1）部分.果为1个四边形有2部分，所以n个四边形最多将仄里分成2+8×[1+2+…+（n-1）]=2+4n（n-1）（部分）.。

六年级奥数专题：找规律同学们从三年级开始，就陆续接触过许多“找规律”的题目，例如发现图形、数字或数表的变化规律，发现数列的变化规律，发现周期变化规律等等。

这一讲的内容是通过发现某一问题的规律，推导出该问题的计算公式。

例1 求99边形的内角和。

分析与解：三角形的内角和等于180°，可是99边形的内角和怎样求呢？我们把问题简化一下，先求四边形、五边形、六边形……的内角和，找一找其中的规律。

如上图所示，将四边形ABCD分成两个三角形，每个三角形的内角和等于180°，所以四边形的内角和等于180°×2= 360°；同理，将五边形ABCDE分成三个三角形，得到五边形的内角和等于180°×3＝540°；将六边形ABCDEF分成四个三角形，得到六边形的内角和等于180°×4＝720°。

通过上面的图形及分析可以发现，多边形被分成的三角形数，等于边数减2。

由此得到多边形的内角和公式：n边形的内角和=180°×（n-2）（n≥3）。

有了这个公式，再求99边形的内角和就太容易了。

99边形的内角和=180°×（99-2）＝17460°。

例2 四边形内有10个点，以四边形的4个顶点和这10个点为三角形的顶点，最多能剪出多少个小三角形？分析与解：在10个点中任取一点A，连结A与四边形的四个顶点，构成4个三角形。

再在剩下的9个点中任取一点B。

如果B在某个三角形中，那么连结B与B所在的三角形的三个顶点，此时三角形总数增加2个（见左下图）。

如果B在某两个三角形的公共边上，那么连结B与B所在边相对的顶点，此时三角形总数也是增加2个（见右下图）。

类似地，每增加一个点增加2个三角形。

所以，共可剪出三角形 4＋2× 9= 22（个）。

如果将例2的“10个点”改为n个点，其它条件不变，那么由以上的分析可知，最多能剪出三角形4＋2×（n-1）=2n＋2=2×（n＋1）（个）。

6 45 35 7 287 2 4 3 6第四章 找 规 律 姓名（ ）找规律是解决问题的一种重要的手段，找规律需要有敏锐的观察力、严密的逻辑推理能力。

找规律一般分为图形找规律和数之间找规律，观察图形中的变化规律，可以从图形的形状、位置、方向、颜色、数量、大小等方面入手，从中找出规律。

观察数字的规律从数的组成、数列关系等方面着手。

例1、下面一组图形的阴影变化是有规律的,请根据这个规律把第四幅图的阴影部分画出来.例2：观察右图，并按规律填出空白处的图形。

例3：根据下面的图和字母的关系，将ad 的图补上。

例4：根据规律填数。

例5、下图所示的两组图形中的数字都有各自的规律，先把规律找出来，再把空缺的数字填上：（1）ab cd bcad 36 25 543 71 68 857 45 38 824 3219（2）例6：仔细观察下图，根据规律填出所缺的数。

例7：下面三块正方体的六个面，都是按相同的规律涂有红、黄、蓝、白、黑、绿六种颜色。

那么请你根据这一规律，白色的对面是什么颜色？红色的对面是什么颜色？黄色的对面是什么颜色？（1） （2） （3）练习：1、下面括号里两个数按一定规律组合，在（ ）里填上适当的数。

（1）、（8，7）、（6，9）（10、5）、（ 、13 ）。

（2）、（2，3）、（5，9）、（7、13）、（ 、23 ）。

（3）、（18，10）、（10，6）、（20、11）、（ 、4（4）、 1、 2、 3、 6、 11、 20、（ ）2、仔细观察一右图，并按它的变化规律， 在“？”处填上适当的图。

3、在右图空格里填数白 黑 黄 绿 白 红 黄蓝 红 ？ 3 12 6 4 16 8 5 206 124．下面的每一个图形都是由△，□，○中的两个构成的。

观察各图形与它下面的数之间的关系，“？”应当是几？5、找规律,从a,b,c,d,e中选入一幅图填入空格内.6. 找规律，画出第四幅图的答案.7、下图是由9个小人排列的方阵,但有一个小人没有到位,请你从右面的6个小人中,选一位小人放到问号的位置.你认为最合适的人选是（）号.8、根据规律填数。

精心整理第一讲找规律给出几个具体的、特殊的数、式或图形，要求找出其中的变化规律，从而猜想出一般性的结论.解题的思路是实施特殊向一般的简化；具体方法和步骤是（1）通过对几个特例的分析，寻找规律并且归纳；（2）猜想符合规律的一般性结论；（3）验证或证明结论是否正确,下面通过举例来说明这些问题.开篇小练习：1。

2个数是3、案是4A.2n5、第n 67、8……猜想：3333 12310________ +++⋅⋅⋅+=典型例题：一、数字排列规律题1、下面数列后两位应该填上什么数字呢？23581217____2、请填出下面横线上的数字。

112358____213、有一串数，它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么？4、有一串数字36101521___第6个是什么数？5、观察下列一组数的排列：1、2、3、4、3、2、1、2、3、4、3、2、1、…，那么第2005个数是（）. A ．1B ．2C ．3D ．46、100个数排成一行，其中任意三个相邻数中，中间一个数都等于它前后两个数的和，如果这100个数的前两个数依次为1，0，那么这100个数中“0”的个数为_________个．7、一组按规律排列的数：1，3，7，13，3621，……请你推断第9个数是． 8、已知下列等式：①13＝12；②13＋23＝32；③13＋23＋33＝62； ④13＋23＋33＋43＝102；…………由此规律知，第⑤个等式是．9、观察下列各式；①、12+1=1×2；②、22+2=2×3；③、32+3=3×4；………请把你猜想到的规律用自然数n 表示出来。

10、观察下面的几个算式：①、1+2+1=4；②、1+2+3+2+1=9；③、1+2+3+4+3+2+1=16；④、1+2+3+4+5+4+3+2+1=25，……根据你所发现的规律，请你直接写出第n 个式子11、观察下列一组数的排列：1、2、3、4、3、2、1、2、3、4、3、2、1、…，那么第2005个数是（） A ．1B ．2C ．3D ．412、把数字按如图所示排列起来，从上开始，依次为第一行、第二行、第三行、……，中间用虚线围的一列，从上至下依次为1、5、13、25、……，则第10个数为________。

六年级找规律数学题一、数字规律1. 按规律填数：1，3，6，10，15，（），28。

- 解析：观察这组数字，1到3增加了2，3到6增加了3，6到10增加了4，10到15增加了5。

可以发现相邻两个数的差值在依次递增1。

那么15后面的数应该比15大6，即15 + 6 = 21。

验证一下，21到28增加了7，符合规律。

所以括号里应填21。

2. 数列：2，4，8，16，32，（）。

- 解析：这组数列中，2×2 = 4，4×2 = 8，8×2 = 16，16×2 = 32。

可以得出规律是后一个数是前一个数的2倍。

所以括号里的数应该是32×2 = 64。

二、图形规律1. 用小棒按照如下方式摆三角形：摆1个三角形需要3根小棒；摆2个三角形需要5根小棒；摆3个三角形需要7根小棒……（1）摆10个三角形需要多少根小棒？- 解析：观察可得，摆1个三角形用3根小棒（3 = 2×1+1）；摆2个三角形用5根小棒（5 = 2×2 + 1）；摆3个三角形用7根小棒（7 = 2×3+1）。

可以总结出规律，摆n个三角形需要2n + 1根小棒。

当n = 10时，2×10+1 = 21根小棒。

（2）有21根小棒，可以摆多少个三角形？- 解析：根据前面总结的规律2n+1。

设可以摆n个三角形，则2n + 1 = 21，2n = 20，解得n = 10。

所以21根小棒可以摆10个三角形。

2. 下列图形是由同样大小的小圆圈按照一定规律所组成的，其中第1个图形中一共有6个小圆圈，第2个图形中一共有9个小圆圈，第3个图形中一共有12个小圆圈……（1）第5个图形中有多少个小圆圈？- 解析：观察图形，第1个图形有6 = 3×1+3个小圆圈；第2个图形有9 = 3×2 + 3个小圆圈；第3个图形有12 = 3×3+3个小圆圈。

可以得出规律，第n个图形有3n+3个小圆圈。

找规律小学奥数题100道及答案(完整版)题目1：1，3，5，7，9，（）答案：11（相邻两个数的差为2，依次递增）题目2：2，4，6，8，10，（）答案：12（相邻两个数的差为2，依次递增）题目3：5，10，15，20，25，（）答案：30（相邻两个数的差为5，依次递增）题目4：1，4，9，16，25，（）答案：36（分别是1、2、3、4、5 的平方，下一个是 6 的平方）题目5：3，6，9，12，15，（）答案：18（相邻两个数的差为3，依次递增）题目6：1，2，4，8，16，（）答案：32（后一个数是前一个数的2 倍）题目7：2，6，12，20，30，（）答案：42（相邻两个数的差依次为4、6、8、10、12）题目8：1，1，2，3，5，8，（）答案：13（前两个数相加等于后一个数）题目9：3，4，7，11，18，（）答案：29（前两个数相加等于后一个数）题目10：1，3，7，13，21，（）答案：31（相邻两个数的差依次为2、4、6、8、10）题目11：2，5，10，17，26，（）答案：37（相邻两个数的差依次为3、5、7、9、11）题目12：9，16，25，36，（）答案：49（分别是3、4、5、6 的平方，下一个是7 的平方）题目13：1，8，27，64，（）答案：125（分别是1、2、3、4 的立方，下一个是5 的立方）题目14：5，12，19，26，33，（）答案：40（相邻两个数的差为7，依次递增）题目15：3，8，15，24，（）答案：35（相邻两个数的差依次为5、7、9、11）题目16：2，3，5，8，13，（）答案：21（前两个数相加等于后一个数）题目17：1，4，10，22，46，（）答案：94（相邻两个数的差依次为3、6、12、24、48）题目18：1，5，14，30，55，（）答案：91（相邻两个数的差依次为4、9、16、25、36）题目19：2，6，18，54，（）答案：162（后一个数是前一个数的3 倍）题目20：7，14，28，56，（）答案：112（后一个数是前一个数的2 倍）题目21：1，2，6，24，120，（）答案：720（后一个数依次是前一个数乘2、3、4、5、6）题目22：3，5，9，17，33，（）答案：65（相邻两个数的差依次为2、4、8、16、32）题目23：1，3，8，19，42，（）答案：89（相邻两个数的差依次为2、5、11、23、47，这些差依次增加3、6、12、24）题目24：2，4，10，28，82，（）答案：244（相邻两个数的差依次为2、6、18、54、162，后一个差是前一个差的 3 倍）题目25：5，9，17，33，65，（）答案：129（相邻两个数的差依次为4、8、16、32、64）题目26：1，4，27，256，（）答案：3125（分别是1、2、3、4 的1、2、3、4 次方，下一个是5 的 5 次方）题目27：1，6，21，66，201，（）答案：606（相邻两个数的差依次为5、15、45、135、405，后一个差是前一个差的3 倍）题目28：3，8，15，24，35，（）答案：48（相邻两个数的差依次为5、7、9、11、13）题目29：2，3，7，18，47，（）答案：123（7 = 3×2 + 1，18 = 7×2 + 4，47 = 18×2 + 11，下一个数应为47×2 + 16 = 123）题目30：1，2，5，14，41，（）答案：122（相邻两个数的差依次为1、3、9、27、81，后一个差是前一个差的3 倍）题目31：2，5，11，23，47，（）答案：95（相邻两个数的差依次为3、6、12、24、48）题目32：4，9，16，25，36，（）答案：49（分别是2、3、4、5、6 的平方，下一个是7 的平方）题目33：6，12，20，30，42，（）答案：56（相邻两个数的差依次为6、8、10、12、14）题目34：1，3，7，15，31，（）答案：63（相邻两个数的差依次为2、4、8、16、32）题目35：3，9，27，81，（）答案：243（后一个数是前一个数的3 倍）题目36：5，13，25，41，（）答案：61（相邻两个数的差依次为8、12、16、20）题目37：2，8，32，128，（）答案：512（后一个数是前一个数的4 倍）题目38：7，16，29，46，（）答案：67（相邻两个数的差依次为9、13、17、21）题目39：1，5，13，25，（）答案：41（相邻两个数的差依次为4、8、12、16）题目40：6，18，54，162，（）答案：486（后一个数是前一个数的3 倍）题目41：8，18，32，50，（）答案：72（相邻两个数的差依次为10、14、18、22）题目42：1，4，13，40，（）答案：121（相邻两个数的差依次为3、9、27、81）题目43：3，10，21，36，（）答案：55（相邻两个数的差依次为7、11、15、19）题目44：5，15，45，135，（）答案：405（后一个数是前一个数的3 倍）题目45：2，6，14，30，（）答案：62（相邻两个数的差依次为4、8、16、32）题目46：9，25，49，81，（）答案：121（分别是3、5、7、9 的平方，下一个是11 的平方）题目47：7，19，37，61，（）答案：91（相邻两个数的差依次为12、18、24、30）题目48：4，12，36，108，（）答案：324（后一个数是前一个数的3 倍）题目49：1，6，15，28，（）答案：45（相邻两个数的差依次为5、9、13、17）题目50：8，20，36，56，（）答案：80（相邻两个数的差依次为12、16、20、24）题目51：3，11，23，39，（）答案：59（相邻两个数的差依次为8、12、16、20）题目52：6，15，35，77，（）答案：143（相邻两个数的差依次为9、20、42、66，差依次增加11、22、24）题目53：2，9，28，65，（）答案：126（分别是1、2、3、4 的立方加1，下一个是5 的立方加1）题目54：1，7，19，37，（）答案：61（相邻两个数的差依次为6、12、18、24）题目55：5，16，29，46，（）答案：67（相邻两个数的差依次为11、13、17、21）题目56：3，12，27，48，（）答案：75（相邻两个数的差依次为9、15、21、27）题目57：7，18，33，52，（）答案：77（相邻两个数的差依次为11、15、19、25）题目58：2，10，30，68，（）答案：130（相邻两个数的差依次为8、20、38、62，差依次增加12、18、24）题目59：4，15，32，55，（）答案：84（相邻两个数的差依次为11、17、23、29）题目60：6，21，42，72，（）答案：106（相邻两个数的差依次为15、21、30、34）题目61：1，9，25，49，（）答案：81（分别是1、3、5、7 的平方，下一个是9 的平方）题目62：8，24，48，80，（）答案：120（相邻两个数的差依次为16、24、32、40）题目63：3，13，31，57，（）答案：91（相邻两个数的差依次为10、18、26、34）题目64：5，19，41，71，（）答案：105（相邻两个数的差依次为14、22、30、34）题目65：2，11，26，47，（）答案：76（相邻两个数的差依次为9、15、21、29）题目66：9，27，51，81，（）答案：117（相邻两个数的差依次为18、24、30、36）题目67：7，17，33，55，（）答案：83（相邻两个数的差依次为10、16、22、28）题目68：4，14，30，52，（）答案：78（相邻两个数的差依次为10、16、22、26）题目69：6，18，36，60，（）答案：90（相邻两个数的差依次为12、18、24、30）题目70：1，11，27，51，（）答案：81（相邻两个数的差依次为10、16、24、30）题目71：5，17，33，53，（）答案：77（相邻两个数的差依次为12、16、20、24）题目72：3，14，31，58，（）答案：91（相邻两个数的差依次为11、17、27、33）题目73：8，22，42，70，（）答案：106（相邻两个数的差依次为14、20、28、36）题目74：2，13，30，53，（）答案：84（相邻两个数的差依次为11、17、23、31）题目75：9，29，55，91，（）答案：133（相邻两个数的差依次为20、26、36、42）题目76：7，20，39，64，（）答案：95（相邻两个数的差依次为13、19、25、31）题目77：4，16，36，64，（）答案：100（分别是2、4、6、8 的平方，下一个是10 的平方）题目78：3，15，33，57，（）答案：87（相邻两个数的差依次为12、18、24、30）题目79：6，22，44，74，（）答案：110（相邻两个数的差依次为16、22、30、36）题目80：1，13，29，53，（）答案：89（相邻两个数的差依次为12、16、24、36）题目81：5，21，41，67，（）答案：99（相邻两个数的差依次为16、20、26、32）题目82：8，26，50，82，（）答案：118（相邻两个数的差依次为18、24、32、36）题目83：3，17，37，67，（）答案：107（相邻两个数的差依次为14、20、30、40）题目84：7，23，45，73，（）答案：107（相邻两个数的差依次为16、22、28、34）题目85：2，14，32，56，（）答案：88（相邻两个数的差依次为12、18、24、32）题目86：9，31，59，95，（）答案：139（相邻两个数的差依次为22、28、36、44）题目87：6，24，48，84，（）答案：126（相邻两个数的差依次为18、24、36、42）题目88：1，15，33，57，（）答案：87（相邻两个数的差依次为14、18、24、30）题目89：5，23，47，77，（）答案：113（相邻两个数的差依次为18、24、30、36）题目90：8，28，52，82，（）答案：118（相邻两个数的差依次为20、24、30、36）题目91：3，19，41，69，（）答案：105（相邻两个数的差依次为16、22、28、36）题目92：7，27，51，81，（）答案：117（相邻两个数的差依次为20、24、30、36）题目93：4，18，38，66，（）答案：100（相邻两个数的差依次为14、20、28、34）题目94：6，26，50，80，（）答案：116（相邻两个数的差依次为20、24、30、36）题目95：2，16，36，60，（）答案：90（相邻两个数的差依次为14、20、24、30）题目96：9，33，63，99，（）答案：141（相邻两个数的差依次为24、30、36、42）题目97：8，28，56，92，（）答案：136（相邻两个数的差依次为20、28、36、44）题目98：5，21，43，71，（）答案：105（相邻两个数的差依次为16、22、28、34）题目99：3，17，37，67，（）答案：107（相邻两个数的差依次为14、20、30、40）题目100：7，25，49，79，（）答案：115（相邻两个数的差依次为18、24、30、36）。

六年级找规律奥数题找规律是奥数中常见的题型之一，要求学生通过观察数列或图形中的特点，找到其中的规律，并根据规律解答问题。

下面是几道六年级找规律的奥数题及其解题思路的相关参考内容：1. 题目： 2, 4, 8, 16, 32, ?解题思路：观察这个数列，可以发现每个数字都是前一个数字的2倍。

因此，下一个数字应该是32的2倍，即64。

答案：642. 题目： 3, 7, 15, 31, ?解题思路：观察这个数列，可以发现每个数字都是前一个数字的2倍再加1。

因此，下一个数字应该是31的2倍再加1，即63。

答案：633. 题目： 1, 2, 4, 7, 11, ?解题思路：观察这个数列，可以发现从第二个数字开始，每个数字都是前一个数字加上一个递增的数字。

第一个递增数字是1，第二个递增数字是2，第三个递增数字是3，以此类推。

因此，下一个数字应该是11加上递增数字4，即15。

答案：154. 题目： 1, 4, 9, 16, 25, ?解题思路：观察这个数列，可以发现每个数字都是前一个数字的平方。

因此，下一个数字应该是25的平方，即625。

答案：6255. 题目： 2, 5, 10, 17, ?解题思路：观察这个数列，可以发现每个数字都比前一个数字大2，4，6，8...。

因此，下一个数字应该比17大10，即27。

答案：276. 题目： 1, 4, 9, 16, 25, ?解题思路：观察这个数列，可以发现每个数字都是前一个数字的平方。

因此，下一个数字应该是25的平方，即625。

答案：6257. 题目： 1, 3, 6, 10, ?解题思路：观察这个数列，可以发现每个数字都是前一个数字加上一个递增的数字。

第一个递增数字是2，第二个递增数字是3，第三个递增数字是4...因此，下一个数字应该是10加上递增数字5，即15。

答案：15通过以上的例题可以看出，在解答找规律的问题时，可以通过观察数列或图形中数字的变化，找到其中的规律。

六年级上册找规律的练习题找规律是数学中常见的一类问题类型，通过观察数列、图形或其他形式的数据，寻找其中的规律并进行推理和总结。

六年级上册找规律的练习题涵盖了多种找规律的情景，通过解答这些题目可以提高学生的观察力、逻辑思维能力和问题解决能力。

下面将以题目的形式给出多个六年级上册找规律的练习题及其解答。

题目一：观察下面的数列，写出下一个数是多少？2, 4, 6, 8, 10, ...解答一：下一个数是12。

规律是每个数都比前一个数大2。

题目二：观察下面的数列，写出下一个数是多少？3, 6, 9, 12, 15, ...解答二：下一个数是18。

规律是每个数都比前一个数大3。

题目三：观察下面的数列，写出下一个数是多少？1, 4, 9, 16, 25, ...解答三：下一个数是36。

规律是每个数都是按照平方递增得出的。

题目四：观察下面的图形，写出缺失的图形。

图形1 图形2 图形3 图形4□ □ □ □■ ■ ■ ■□ □ □■ ■ ■□ □■ ■解答四：图形5：图形6：图形7：图形8：□ □ □ □■ ■ ■ ■□ □ □■ ■ ■□ □■ ■规律：每个图形中的□和■交替排列，并且下一个图形是在当前图形的基础上增加一个□和一个■。

通过以上的练习题，我们可以看出找规律题涉及到的规律类型种类繁多，有的是数列递增规律，有的是图形变化规律，还有的是数字之间的关系规律等等。

在解答这些题目时，我们需要仔细观察、分析，尝试总结出其中的规律，并进行验证。

这些方法不仅可以应用于数学课堂上，也可以在生活中的问题解决中得到运用。

提醒：在解答找规律的练习题时，我们应该注重思考过程和逻辑推理，而不仅仅追求答案的正确与否。

只有通过不断的练习和思考，我们才能更好地培养自己的观察力和问题解决能力，提高数学分析和推理的能力。

如下图，一个边长为3a厘米的正方体，分别在它的前后、左右、上下各面的中心位置挖去一个截口是边长为a厘米的正方形的长方体（都和对面打通）．如果这个镂空的物体的表面积为2592平方厘米，试求正方形截口的边长．
解：原来正方体的表面积为：
6×3a×3a＝6×9a2（平方厘米）．
六个边长为a的小正方形的面积为：
6×a×a＝6a2（平方厘米）；
挖成的每个长方体空洞的侧面积为：
3a×a×4＝12a2（平方厘米）；
三个长方体空洞重叠部分的校长为a的小正方体空洞的表
面积为：
a×a×4＝4a2（平方厘米）．
根据题意：6×9a2－6a2＋3（12a2－4a2）＝2592，
化简得：54a2－6a2＋24a2＝2592，解得a2＝36（平方厘米），故a＝6厘米．
即正方形截口的边长为6厘米．＝n2－n＋2．。