齿轮侧隙计算表

Jnmin—最小法向侧隙（μm）；
Ts1、Ts2—分别为小齿轮、大齿轮的齿厚公差（μm）；
Ta—齿轮副的中心距公差（μm）；
αn’—齿轮压力角（0）。
≤10
＞10-25
＞25-60
＞60
喷油润滑
10
20
30
30-50
油池润滑
5-10
2.齿轮副最大法向侧隙值的计算
计算齿轮副的最大法向侧隙时，主要考虑齿轮的加工精度。其计算公式如下
Jnmax=Jmin+【（Ts12+Ts22）Xcos2αn+（TaX2Xsinαn）】（1/2）
式中 Jnmax—最大法向侧隙（μm）；
式中Jnmin—最小法向侧隙（μm）；
a—齿轮副中心距（μm）；
α1
△t1、△t2—分别为齿轮、箱体温度与标准温度（200C）之差（0C）；
αn’—齿轮副法向啮合角（0）；
δ—润滑状况系数（检附表）；
mn—齿轮模数。
δ表值
润滑方式
齿轮节圆圆周速度v（m/s）
齿轮副侧隙探讨
一、由最小侧隙推导大小齿轮齿厚上偏差：
二、齿轮副最大侧隙计算
齿轮副最小和最大法向侧隙值计算
2010-04-28 12:16
1.齿轮副最小法向侧隙值的计算
计算齿轮副的最小法向侧隙时，主要考虑齿轮副的热变形和润滑状况的工作条件。其计算公式如下：
Jnmin=2a·（α1△t1-α2△t2）sinαn’+δmn

1 2.1 2.4 2.5 2.4 2.5 2.6 3 3.4 2.6 2.8 3 3.2 3.8 4.5 3 3.2 3.4 3.6 4.2 5 3.8 4 4 4.2 4.8 5.5 4.5 4.8 5 5.3 5.5 6.5
2 2.6 3 3.4 3 3.2 3.6 4 4.8 3.4 3.8 4 4.5 5.3 6.5 4.2 4.5 4.8 5 6 7 5.3 5.5 6 6.5 7 8 6.5 7 7.5 7.5 8.5 9.5
1 65 95
2 65 95
3 65 95
偏差代号 C
齿厚偏差数值(mm) 偏差数值
备注 0.014 +1fpt
偏差数值 为自动运 算结果，
D E F G H J K L M N P R S
0 -0.028 -0.056 -0.084 -0.112 -0.14 -0.168 -0.224 -0.28 -0.35 -0.448 -0.56 -0.7
0 -2fpt -4fpt -6fpt -8fpt -10fpt -12fpt -16fpt -20fpt -25fpt -32fpt -40fpt -50fpt
偏差数值 为自动运 算结果， 勿轻易修 改
中 精度等级 数值(自动运算结果勿修改) 备注：数据来源 IT4/2 1 0.004 IT4/2 2 0.004 3 0.0095 IT6/2
z
k个周节累计公差时候k值
4
最小侧隙（μ m）
140
齿厚上偏差ESS(mm) 齿厚公差TS(mm)
-0.056 0.084
非常规部 分，一般 可以不 写，公法 线下偏差 问题仔细 看备注红 字部分
注意非常规部分，最小侧隙与齿厚上偏差齿厚公差组合输入因为相互关 联，公法线计算数据将分开 中间运算量,勿修改 COSβ 中心距（mm） 分度圆直径（mm） 1 74 40

计算齿轮侧隙范文齿轮侧隙是指两个相互啮合的齿轮的齿槽之间的距离。

齿轮侧隙的大小对齿轮的传动精度和使用寿命有着重要的影响。

本文将介绍齿轮侧隙的计算方法以及其在实际应用中的重要性。

一、齿轮侧隙的计算方法齿轮侧隙的计算方法通常有以下几种：1.几何计算法：根据齿槽的几何形状参数来计算侧隙大小。

具体计算方法如下：-首先，计算出齿槽高度h，齿宽b和齿槽角度α等几何参数；-然后，根据几何关系，计算侧隙大小：侧隙大小= h / tan(α/2)2.弹性变形法：考虑到齿轮在工作过程中会发生弹性变形，弹性侧隙需要通过试验和实际测量来确定。

3.标准侧隙法：根据国家标准对齿轮侧隙进行规定，在设计和制造过程中直接按照标准来确定。

二、齿轮侧隙的重要性齿轮侧隙的大小对齿轮传动的精度和性能有着重要的影响，主要体现在以下几个方面：1.传动精度：齿轮侧隙会引起齿轮传动的回程误差，降低传动的精度。

过大的侧隙会导致剧烈的齿根载荷变化，从而影响传动的稳定性和精度。

2.噪声和振动：齿轮侧隙会引起啮合时的冲击和振动，产生噪声。

过大的侧隙会增加齿轮的冲击载荷，导致噪声和振动增加。

3.使用寿命：过大的齿轮侧隙会导致齿端载荷集中，加速齿面疲劳破坏的发生，从而降低齿轮的使用寿命。

三、齿轮侧隙的影响因素齿轮侧隙的大小受到多个因素的影响，主要包括以下几个方面：1.齿轮尺寸和材料：齿轮的几何尺寸和材料的选择会直接影响齿轮侧隙的大小。

一般来说，齿轮尺寸越大，侧隙越大；而齿轮材料的弹性模量越大，侧隙越小。

2.加工精度：齿轮的加工精度对齿轮侧隙有很大影响。

加工精度低会导致齿槽尺寸不准确，从而影响侧隙的准确计算。

3.齿轮啮合方式：齿轮的啮合方式也会对侧隙产生一定的影响。

相对于直齿齿轮，斜齿轮和蜗杆齿轮等特殊形式的齿轮传动通常需要更小的侧隙。

四、总结齿轮侧隙的计算方法涉及到几何计算法、弹性变形法和标准侧隙法等。

齿轮侧隙的大小对齿轮的传动精度、噪声和振动以及使用寿命有着重要的影响。

的加 工 余 量 保 持 一 致"
其次!要控制转速及进给 量!粗镗一次加工余量在
图 $! 刀 头 安 装 示 意 图 ## 为镗削量$
*""%&&!精镗加工余量在""(&&"在粗镗加工中保持主
轴转速 在 $%>%&,-!在 精 镗 中 应 保 持 主 轴 转 速 在 .%>%&,-!
&" 结语
通过上述方法表明’设计合理的夹具能很顺利地利 用卧式车床进行镗深孔加工!并且远比加工费用高的镗 床更易于装夹且加工精度也得到了保证!对于薄壁细长 套等零件来讲!使用此方法效果明显!实践的结果也令 人满意"目前此类零件在我单位已不是加工难题!只需 利用车床夹具就能高效地组织生产!前景非常乐观!此 方法也适合于类似零件的生产加工"
刀 头 #见 图 $$ 时 要 注
切削液经刀杆再输送到工件内孔!从而使刀具和工件同时进
意一 次 安 装 ( 个 刀 头!
行冷却!防止了热变形!还能保证切屑从深孔中排出!使加
采用 正 反 刀 同 时 加 工!
工精度和表面粗糙度都得到了相应的改善"
两个刀头轴向间距保持
在 %!*""&& 范 围 内! 前后刀头径向尺寸所去
工!!艺 !"#$%&’("
齿轮副侧隙计算方法
第四石油机械厂材料工艺研究所! !湖北荆州!!"!#$$" !胡!顺
!" 齿轮副侧隙说明 齿轮传动的正常工作及其良好的润滑条件!都需 要一定的侧隙来保证!以避免因工作温度的变化而使 啮合的齿轮之间的侧隙过小!导致两齿轮卡住"所以 在齿轮设计时!要规定最小极限侧隙" 齿 轮 副 法 向 最 小 极 限 侧 隙 /-&,-! 计 算 时 需 考 虑 两 个部分! 这里用/-8和/-9表示" #"$/-8是 保 证 正 常 润 滑 而 必 须 考 虑 的 齿 轮 副 侧 隙 #见 表 "$! 可 由 润 滑 方 式 和 齿 轮 工 作 的 线 速 度 确 定 "

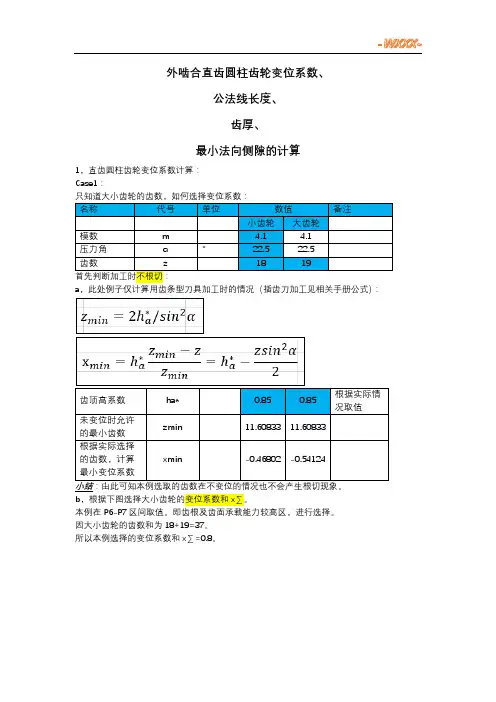
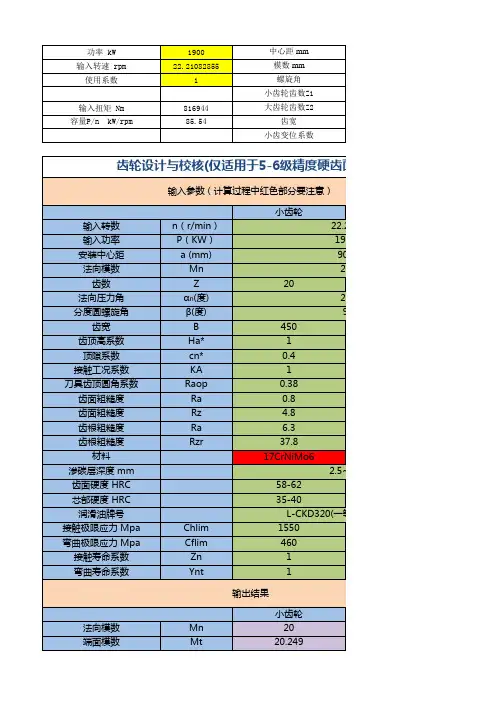
外啮合直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算1，直齿圆柱齿轮变位系数计算：Case1：a，此处例子仅计算用齿条型刀具加工时的情况（插齿刀加工见相关手册公式）：小结：由此可知本例选取的齿数在不变位的情况也不会产生根切现象。

b，根据下图选择大小齿轮的变位系数和x∑。

本例在P6-P7区间取值。

即齿根及齿面承载能力较高区，进行选择。

因大小齿轮的齿数和为18+19=37。

所以本例选择的变位系数和x∑=0.8。

本例我们的两个齿轮在工作时属于减速运动，所以按减速运动的变位系数分配线图，进行2个齿轮的变位系数的选择。

先按(z1+z1)/2=18.5，作为横坐标，做一条垂线（图中蓝色的线），再按x∑/2=0.4，作为纵坐标，做一条水平线（图中橙色的线），接着沿着L线的趋势，穿过上面2条线的交点做一条射线（图中红色的线）最后按大小齿轮的齿数做相应的垂线（图中紫色的线），即得到需要的各自变位系数。

最后我们选择的变位系数即为：小齿轮x1=0.42，大齿轮x2=0.38。

【基本保障其和与之前x ∑一致，即可】。

c，验算变位后的齿顶厚度：注：一般要求齿顶厚Sa≥0.25m；对于表面淬火的齿轮要求Sa≥0.4m下表中的da的计算见后面的计算表格中的计算公式（因为当齿轮变位后，齿顶圆的计算和未变位齿轮的计算稍有差别-涉及到变位系数和中心距变位系数。

）。

分度圆直径db mm 73.8 77.9齿轮的齿顶圆直径da mm 83.027 86.799齿轮的齿顶压力角αa °27.27 26.17中间值invα0.0215 0.0215中间值invαa 0.0587 0.0347齿顶厚Sα 5.77 7.47判断值0.25m 1.025 1.025判断值0.4m 1.64 1.64小结：计算发现变位后的齿轮齿顶厚满足设计需求。

根据上面确定的变位系数，计算齿轮的中心距变位系数和节圆直径、齿根圆直径、齿顶圆直径。

圆棒跨距上 偏差Ems
Ess
-66.0 μm
Esi
-176.0 μm
Ess*cosα n0.72Fr*sin αn
计算结果： Esi*cosα n+0.72Fr*s inαn 计算结果：
-75.80997 μm -151.5956 μm
Ewms/(sin αMt*cosβ b) 计算结果 Ewms/(sin αMt*cosβ b)*cos(π /2z)
★齿厚及 公法线偏 差计算
最小法向极 限侧隙
jbnmin
jnmin=1000* a(α1*Δ
t1-α2*Δ
t2)*2*sin
αn+δ
*mn*1000
齿轮法向模数mn
齿轮法向压力角αn
中心距a 齿轮材料的线膨胀系数 α1 箱体材料的线膨胀系数 α2 齿轮温升Δt1(相对20 度) 箱体温升Δt2(相对20 度)
＞60
喷油润滑 0.01
0.02
0.03 0.03～0.05
油池润滑
0.005～0.01
表10-5 第I公差组精度等级 br
5
6
7
8
9
IT8 1.26IT8 IT9 1.26IT9 IT10
齿厚公差
齿圈径向跳动公差
径向切深公差
齿厚下偏差
齿距极限偏差Fpt 齿厚上偏差/Fpt 齿厚下偏差/Fpt
Ts=2*tanα n*(Fr^2+br ^2)^0.5 Fr
-180.9787
偶数齿
本表不属 于国家标 准,仅供 注:1 参考.
2 αMt1= 25 3 螺旋角β 8.1094
见标准齿轮 参数计算
4
βb= 0.132949

2
13.09189306 76.90810694 33.11061008 33.11061008 4.71238898 0.16 0.37 4.71238898 -0.16 -0.37
xt1查表23.4-9 x1=0.39(1-1/u²)或查表23.4-10
xt2=-xt1 x2=-x1
hf=h-ha c=h-h′ θ f=arctan(பைடு நூலகம்f/Re) δ δ
s2=p/2-(ha1-ha2)tanα /cosβ m-xt1m
Smn1=(0.5πcosβm+2x1tanα+xt1)mm ψmn=Smn*cosδ*cos²βm/(mmZ) Kψ mn=1-ψ mn²/6 S′mn=SmnKψmn h′am1=ha1-0.5b*tanθf2+0.25Smn1ψmn1 查表23.4-11 N0=（θ
f1+θf2）sinβm/20
Smn2=πmmcosβm-Smn1
h′am2=ha2-0.5b*tanθf1+0.25Smn2ψmn2
1.472078944 0.525395815 9.262878463 9.262878463
设定值 传动比 4.3 齿顶高系数 顶隙系数 0.85 0.188
da1=d1+2ha1*cosδ
da2=d2+2ha2*cosδ
21 锥点至轮冠距离 22 理论弧齿厚 23 侧隙 24 中点螺旋角 25 齿宽系数 26 中点模数 27 中点法向模数 28 中点法向齿厚 29 中点法向齿厚半角 30 中点齿厚角系数 31 中点分度圆弦齿厚 32 中点分度圆弦齿高 33 刀盘直径 34 刀号
表5.4-1 序号 1 齿数 2 大端模数 3 齿宽 4 工作齿高 5 齿高 6 压力角 7 轴交角 8 分度圆直径 9 分锥角 10 锥距 11 周节 12 切向变位系数 13 径向变位系数 14 齿顶高 15 齿根高 16 顶隙 17 齿根角 18 顶锥角 19 根锥角 20 顶圆直径 δ δ

齿厚上偏差
中心距极限偏差
fpb1
fpb2
Fβ 计算结果：
Ess=((jnmin+Jn)/ (2cosα n)+fa*tan αn) fa 计算结果：
18 μm 20 μm 21 μm 40.6 μm
31.5 -56.4 μm
大齿轮
编制:
打印日 期：
2021/4/4
表10-4
润滑方式
≤10
圆周速度v(m/s) ＞10～25 ＞25～60
润滑状况系数δ
计算结果：
齿轮编号:
3 20 110 mm
钢为
1.15E-05 11.5*10-6
铸铁为
1.05E-05 10.5*10-6 25 10
0.01 查表10-4 43.7 μm
侧隙减小量
jbn
Jn=(Fpb1^2+ Fpb2^2+2.10 4*Fβ ^2)^0.5
小齿轮基节极限偏差 大齿轮基节极限偏差 齿向公差
-180.9787
偶数齿
本表不属 于国家标 准,仅供 注:1 参考.
2 αMt1= 25 3 螺旋角β 8.1094
见标准齿轮 参数计算
4
βb= 0.132949
5 齿数z= 20
大,小齿轮 分别计算
计算结果 -180.4208
奇数齿
圆棒跨距上 偏差Ems
Ess
-66.0 μm
Esi
-176.0 μm
Ess*cosα n0.72Fr*sin αn
计算结果： Esi*cosα n+0.72Fr*s inαn 计算结果：
-75.80997 μm -151.5956 μm
Ewms/(sin αMt*cosβ b) 计算结果 Ewms/(sin αMt*cosβ b)*cos(π /2z)

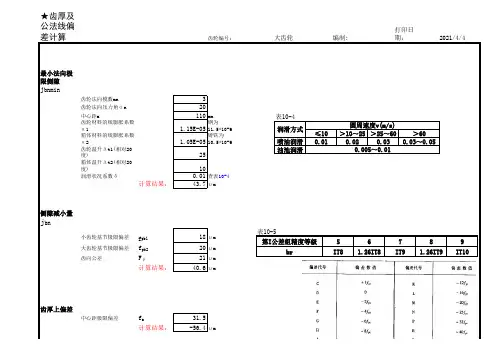
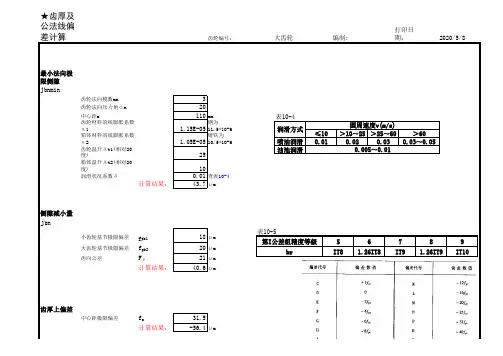
★齿厚及公法线偏差计算齿轮编号:编制:打印日期：最小法向极限侧隙j bnmin j nmin =1000*a(α1*Δt1-α2*Δt2)*2*sin αn+δ*m n *1000齿轮法向模数mn 3齿轮法向压力角αn 20 中心距a 110mm 齿轮材料的线膨胀系数α1 1.15E-05钢为11.5*10-6箱体材料的线膨胀系数α2 1.05E-05铸铁为10.5*10-6齿轮温升Δt1(相对20度)25箱体温升Δt2(相对20度)10润滑状况系数δ0.01查表10-4计算结果：43.7μm 侧隙减小量j bnJn=(F pb 1^2+F pb 2^2+2.104*F β^2)^0.5小齿轮基节极限偏差f pb118μm 大齿轮基节极限偏差f pb220μm 齿向公差F β21μm 计算结果：40.6μm 齿厚上偏差Ess=-((j nmin +J n )/(2cos αn)+fa*tan αn)中心距极限偏差f a 31.5计算结果：-56.4μm 齿厚公差Ts=2*tan αn*(Fr^2+br^2)^0.5齿圈径向跳动公差Fr 56径向切深公差br 145根据分度圆直径从表10-5查取计算计算结果：113.1μm 齿厚下偏差Esi=Ess-Ts 齿距极限偏差Fpt22.0μm 齿厚上偏差/Fpt-2.6-3按齿厚极限偏差表取整齿厚下偏差/Fpt-7.7-8按齿厚极限偏差表取整计算结果：-169.5μm 齿厚上偏差取值:Ess -66.0μm 注:1本表不属于国家标准,仅供参考.齿厚下偏差取值:Esi -176.0μm 2αMt1=25见标准齿轮参数计算3螺旋角β=8.1094公法线平均长度上偏差EwmsEss*cos αn-0.72Fr*sin αn 4βb=0.132949计算结果：-75.80997μm 5齿数z=20大,小齿轮分别计算公法线平均长度下偏差Ewmi Esi*cos αn+0.72Fr*sinαn 计算结果：-151.5956μm 2016/12/20大齿轮表10-4≤10＞10～25＞25～60＞60喷油润滑0.010.020.030.03～0.05油池润滑圆周速度v(m/s)润滑方式0.005～0.01表10-5第I 公差组精度等级56789br IT8 1.26IT8IT9 1.26IT9IT10。

0.47
0.135045625 1
0.027163502 0.035457701
1 1.000880289
900
1.293426574 1.293426574
1.05 0.895121983 1.258990703 1.272792206 5222285.098 0.814271435 1.017060626 1.017060626 1.017060626 1.028136959
9 1 0.925
承受单向脉动负荷
1
0.7 0.9 0.8 1 1 0.910884442 0.85
接触应力基本值
σho
计算接触应力
σh
齿根弯曲应力基本值
σfo
计算弯曲应力
σf
接触安全系数
SH
弯曲安全系数
SF
1951.597452 2239.368791 1186.687513 1520.855224
无干涉刀具最大齿顶圆角 基节极限偏差 齿形公差 螺旋线公差
切向力 输入齿轮节圆线速度
传动比 负载分配系数 单位齿宽柔度 单对齿刚度理论值
啮合刚度 基本齿廓系数 齿形平均直径
诱导质量 主动齿轮临界转数
临界转数比
齿距偏差对Kv影响系数 齿形误差对Kv影响系数 周期性变化对Kv影响系数 扭转共振对Kv影响系数
20 20 1 0.4 9 右 角度变位 0.3975
6 0.054 0.027 0.017 0.028 0.044 900
68
-0.233 -0.387
3 158.849 -0.229 -0.375
Jn
0.36--0.669
Da
460.236
d

±
it7 it8 it9
表5-39 斜齿轮装配后的接触斑点（摘自gb/z18620.4—2002）
齿轮副的侧隙是在齿轮装配后自然形成的，侧隙的大小主要取决于齿厚和中心距。

在最小的中心距条件下，通过改变齿厚偏差来获得大小不同的齿侧间隙。

表5-40为中、大模数齿轮最小侧隙的推荐值。

表5-40 对于中、大模数齿轮最小侧隙j bnm in的推荐值（摘自gb/z18620.2—2002）（mm）
3.齿厚偏差与公差
公称齿厚是指齿厚的理论值，两个具有公称齿厚sn的齿轮在公称中心距下啮合是无侧隙的。

为了得到合理的齿侧间隙，通过将轮齿齿厚减薄一定的数值，在装配后侧隙就会自然形成。

4.公法线长度偏差ebn
公法线长度偏差为公法线实际长度与公称长度之差。

公法线长度是在基圆柱切平面(公法线平面)上跨k个齿，在接触到一个齿的右齿面和另一个齿的左齿面的两个平行平面之间测得的距离。

对于大模数的齿轮，生产中通常测量齿厚控制侧隙；齿轮齿厚的变化必然会引起公法线长度的变化，在中、小模数齿轮的批量生产中，常采用测量公法线长度的方法来控制齿侧间隙。

齿轮副侧隙计算方法
一、齿轮副侧隙的作用
1.几何方法：
几何方法是根据齿轮的几何关系进行计算的，一般适用于标准齿轮。

(1)根据模数计算：
(2)根据齿数计算：
(3)根据齿距计算：
齿轮副的侧隙还可以根据齿轮的齿距p计算。

一般情况下，侧隙可以
按照齿距的0.25%~0.5%进行计算。

几何方法计算简单，适用范围广，但是不考虑具体的工作条件和工艺
因素，因此在一些特殊情况下需要使用经验方法。

2.经验方法：
经验方法是通过实际的生产经验总结出来的侧隙计算方法，一般适用
于非标准齿轮和特殊工况。

(1)按照工作条件计算：
根据具体的工作条件和要求，经验方法可以计算出合适的齿轮副侧隙。

例如，在高速传动时，为了考虑温度膨胀和防止齿轮过热，可以取较大的
侧隙。

(2)按照工艺因素计算：
根据特定的工艺要求和制造工艺能力，经验方法可以计算出合适的齿轮副侧隙。

例如，在高精度要求的齿轮副中，为了考虑加工精度和装配误差，可以取较小的侧隙。

综上所述，齿轮副侧隙的计算方法主要包括几何方法和经验方法。

几何方法适用于标准齿轮，计算简单，但不考虑具体工艺和工作条件。

经验方法适用于非标准齿轮和特殊工况，根据实际经验计算侧隙。

选择合适的计算方法需要根据具体情况和要求进行综合考虑。

齿轮侧隙计算方法
齿轮侧隙是指齿轮啮合时齿面之间的间隙。

侧隙对于齿轮传动的运行非常重要，正确的侧隙设计可以确保齿轮的正常工作和寿命。

下面介绍几种常见的齿轮侧隙计算方法。

1.按标准齿形公式计算：
2.经验公式：
对于切削齿轮或精密齿轮，可以使用经验公式来估计齿侧间隙。

经验公式的计算依赖于齿轮的模数、齿数、压力角等参数，这些参数一般需要事先根据设计需求确定。

经验公式通常通过实际经验和试验数据得出，可以根据具体情况作适当调整。

3.正反弧线计算法：
正反弧线计算法是确定齿侧间隙的一种常用方法。

该方法将齿轮齿面分为正面弧线和背面弧线两部分，通过计算正反弧线间的距离来确定齿侧间隙。

正反弧线计算法的优点是计算相对简便，适用于各种不同类型的齿轮。

4.有限元分析方法：
有限元分析方法是一种基于计算机模拟的方法，通过建立齿轮的三维模型，应用有限元分析软件对齿轮的应力和位移进行数值计算，从而得到齿侧间隙。

这种方法适用于复杂形状的齿轮和特殊工况下的齿轮，可以提供更加精确和准确的结果。

需要注意的是，齿轮侧隙的计算方法并非固定不变的，具体的计算方法会受到齿轮的类型、制造工艺、传动需求等多种因素的影响。

因此，在
实际应用中，需要根据具体情况选择合适的计算方法，并结合实际验收和调试来确定最终的齿侧间隙。

总之，齿轮侧隙是齿轮传动系统中一个重要的参数，合理的齿侧间隙设计可以提高齿轮传动的效率、耐久性和运行稳定性。

通过选择适当的计算方法和合理的参数，可以确保齿轮传动的正常工作并延长寿命。

套改jb179-83标准保证齿轮侧隙的计算
jb179-83标准的出发点是提高齿轮的可靠性和使用寿命。

它是一种可以指导齿轮传动性能设计、装配、检测的标准。

它指定了齿轮采用JIS Z 2201-1990-02参考设计的基础，并开展了更全面的技术方面的优化与细化。

例如，它给出乔哈格法齿轮传动系统的公差值，包括相对靠接公差和侧隙公差。

JB179-83标准对于齿轮侧隙不仅有具体的计算方法，同时也有具体的计算实例，可以更好地帮助设计人员确定最优的侧隙值。

计算齿轮侧隙，最关键的是确定齿轮表面处的内外压力系数，这主要取决于加工工艺、圆柱度误差、锥度误差和轮面基于圆度误差的两端的孔的大小。

根据内外压力系数的数值，可以利用JIS Z 2201-1990-02给出的公式计算出齿轮侧隙。

总之，采用JB179-83标准可以计算出满足技术要求，以保证齿轮传动性能及其可靠性和使用寿命的最佳侧隙大小。

在传动性能设计及装配中，齿轮侧隙的工程师应该有必要采用gJB179-83标准来计算出齿轮的最优侧隙值，以保证齿轮侧隙的合理化。

齿轮侧隙计算范文齿轮的侧隙计算是机械设计中非常重要的一项工作。

准确的计算可以保证齿轮的稳定性和传动精度。

本文将介绍齿轮侧隙的计算方法，并通过实例进行说明。

1.齿轮侧隙的定义和作用：齿轮侧隙是指齿轮齿槽底部与啮合齿槽底部之间的距离。

它的作用是使齿轮啮合时的高点接触，从而减小摩擦损耗和齿轮噪声。

2.齿轮侧隙的计算方法：（1）根据齿轮的模数和压力角，可以确定齿槽的基圆直径d。

（2）侧隙计算的第一步是确定齿顶高h_t。

齿顶高是指齿槽的顶部到基圆直径的距离。

可以通过齿顶高系数kh与齿高h的乘积来确定，即h_t=kh*h。

（3）接下来，确定齿距元素。

齿距元素由齿槽深度hf和齿顶高h_t 之和组成，即m = hf + h_t。

（4）侧隙计算的最后一步是通过计算公式确定齿轮侧隙j，即j = m * (1 - sf * cos(α))，其中sf是齿根附加系数，α是压力角。

3.齿轮侧隙计算实例：现假设有一个齿轮的模数m为2mm，齿数为20，压力角α为20°，齿高系数kh为1.25，齿根附加系数sf为0.157（1）确定基圆直径d：d = m * z = 2 * 20 = 40mm。

（2）确定齿顶高h_t：h_t = kh * h = 1.25 * m = 1.25 * 2 = 2.5mm。

（3）确定齿距元素m：m = hf + h_t = 2m + 2.5mm = 2 * 2 + 2.5 = 6.5mm。

（4）确定齿轮侧隙j：j = m * (1 - sf * cos(α)) = 6.5 * (1 - 0.157 * cos(20°)) ≈ 6.5 * 0.848 ≈ 5.514mm。

所以，该齿轮的侧隙为约5.514mm。

4.齿轮侧隙计算的注意事项：（1）在实际设计中，也可以根据需求对齿轮侧隙进行调整，以满足特定的工作要求。

（2）齿轮侧隙的计算方法可以根据具体情况进行调整和改进，以满足实际需求。

齿轮、齿轮副误差及侧隙的定义和代号（GB11365-89）名称代号定义名称代号定义切向综合误差切向综合公差F iF i被测齿轮与理想精确的测量齿轮按规定的安装位置单面啮合时，被测齿轮一转内，实际转角与理论转角之差的总幅度值。

以齿宽中点分度圆弧长计周期误差周期误差的公差f2kf2k被测齿轮与理想精确的测量齿轮按规定的安装位置单面啮合时，被测齿轮一转内，二次（包括二次）以上各次谐波的总幅度值一齿切向综合误差一齿切向综合公差f if i被测齿轮与理想精确的测量齿轮按规定的安装位置音面啮合时，被测齿轮一齿距角内，实际转角与理论转角之差的最大幅度值以齿宽中点分度圆弧长计齿距累积误差齿距累积公差FpFp在中点分度圆上，任意两个同侧齿面间的实际弧长与公称弧长之差的最大绝对值K个齿距累积误差K个齿距累积公差FpFp在中点分度圆上，K个齿距的实际弧长与公称弧长之差的最大绝对值。

K为2到小于z/2的整数轴交角综合误差轴交角综合公差F iF i被测齿轮与理想精确的测量齿轮在分锥顶点生命的条件下双面啮合时，被测齿轮一转内，齿轮副轴交角的最在变动时。

以齿宽中点处线值计齿圈跳动齿圈跳动公差FrFr齿轮一转范围内，测头在齿槽内与齿面中部双面接触时，沿分锥法向相对齿轮轴线的最大变动量一齿轴交角综合误差f i被测齿轮与一齿轴交角综合公差f i理想精确的测量齿轮在分锥顶点生命的条件下双面啮合时，被测齿轮一齿距角内，齿轮副轴交角的最大变动时。

以齿宽中点处线值计齿距偏差齿距极限偏差上偏差下偏差fpt+fpt-fpt在中点分度圆上，实际齿距与公称齿距之差齿形相对误差齿形相对误差的公差fcfc齿轮绕工艺轴线放置时，各轮齿实际齿面相对于基准实际齿面传递运动的转角之差。

以齿宽中点处线值计齿轮副一齿轴交角综合误差齿轮副一齿轴交角综合公差f i cf i c齿轮副在分角顶点生命条件下双面啮合时，在一齿距角内，轴交角的最大变动量。

在整周期内取值，以齿宽中点处线值计齿厚偏差齿厚极限偏差上偏差下偏差EsEsSEsiTs齿宽中点法向弦齿厚的实际值与公称值之差齿轮副周期误差齿轮副周期误差的公差f zkcf zkc齿轮副按规定的安装位置单面啮合时，在大轮一转范围内，二次（包括二次）以上各次谐波的总幅度值齿轮副切向综合误差齿轮副切向综合公差F icF ic齿轮副按规定的安装位置单面啮合时，在一齿距角内，一个齿轮相对的实际转角与理论转角之差的最大值。

齿轮副圆周侧隙齿轮副是一种常见的传动装置，它由两个或多个啮合齿轮组成。

在实际应用中，齿轮副的运转要求齿轮之间有一定的侧隙。

本文将重点探讨齿轮副圆周侧隙的作用以及如何合理设置。

一、圆周侧隙的作用齿轮副圆周侧隙指的是齿轮与齿轮之间的空隙，一般是指齿向方向的侧面间隙。

它具有以下几个作用：1. 承载能力：圆周侧隙可以为齿轮副提供一定的弹性，使得齿轮的载荷能够得到有效的分配和传递。

在高速运动和高载荷情况下，圆周侧隙可以减小齿轮之间的接触应力，提高传动的可靠性和使用寿命。

2. 自动修正：由于齿轮制造和安装的误差，齿轮副很难做到完全精确的啮合。

合适的圆周侧隙可以为齿轮副提供一定的自动修正能力，使得齿轮在运动过程中能够自动调整位置，从而减小噪声和振动。

3. 温度变化：齿轮副在工作过程中会产生一定的摩擦热量，导致温度的升高。

适当设置圆周侧隙可以使齿轮副在温度变化时有足够的空间进行热胀冷缩，从而避免因温度变化引起的不良影响。

二、圆周侧隙的设计原则在设计齿轮副圆周侧隙时，需要考虑下列原则：1. 全面啮合：圆周侧隙应该能够满足齿轮的全面啮合。

即在齿轮轮齿接触线上的每个齿面都可以与对应齿轮的齿面进行正常啮合，确保传动效果的稳定和可靠。

2. 合理设置：圆周侧隙的大小应根据具体的传动要求来确定。

一般来说，过大的侧隙会增加齿面的相对移动，导致效率下降；而过小的侧隙则容易导致齿轮副过紧，增大运动和噪声。

3. 加工和安装误差考虑：齿轮的加工和安装会带来一定的误差。

在设计圆周侧隙时，需要充分考虑这些误差，并合理设置侧隙的上下限，以保证传动的正常运行。

三、圆周侧隙的计算方法在实际应用中，可以通过以下方法来计算齿轮副的圆周侧隙：1. 标准数值法：根据齿轮副的模数、压力角和精度等级，可以查阅相关的标准手册或规范，找到适用的圆周侧隙数值。

2. 经验公式法：根据实际经验，结合传动的类型和工作条件，可以使用经验公式来计算圆周侧隙。

这种方法比较简便，但精度相对较低。