《微积分》课后答案第4章(复旦大学版)

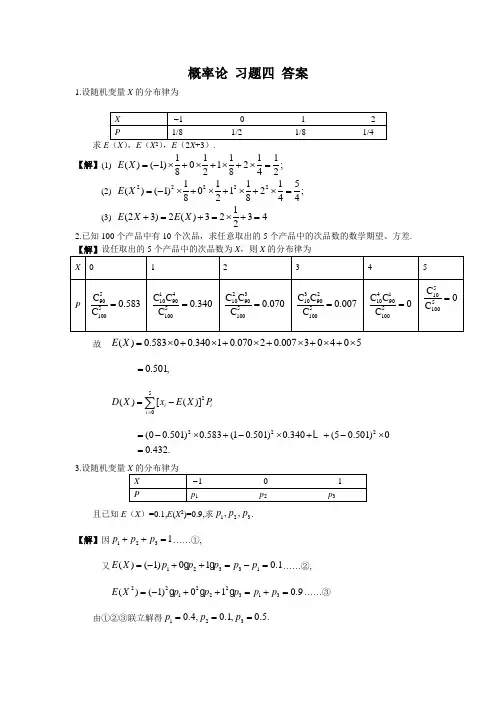
概率论 习题四 答案1.设随机变量X 的分布律为求E （X ），E （X ），E （2X +3）. 【解】(1) 11111()(1)012;82842E X =-⨯+⨯+⨯+⨯= (2) 2222211115()(1)012;82844E X =-⨯+⨯+⨯+⨯=(3) 1(23)2()32342E X E X +=+=⨯+=2.已知100个产品中有10个次品，求任意取出的5个产品中的次品数的数学期望、方差.故 ()0.58300.34010.07020.0073E X =⨯+⨯+⨯+⨯+⨯+⨯0.501,= 52()[()]iii D X x E X P ==-∑222(00.501)0.583(10.501)0.340(50.501)00.432.=-⨯+-⨯++-⨯=3.设随机变量且已知E （X ）=0.1,E (X 2)=0.9,求123,,p p p . 【解】因1231p p p ++=……①,又12331()(1)010.1E X p p p p p =-++=-=……②,222212313()(1)010.9E X p p p p p =-++=+=……由①②③联立解得1230.4,0.1,0.5.p p p ===4.袋中有N 只球，其中的白球数X 为一随机变量，已知E （X ）=n ，问从袋中任取1球为白球的概率是多少？【解】记A ={从袋中任取1球为白球}，则(){|}{}Nk P A P A X k P X k ===∑全概率公式1{}{}1().NNk k k P X k kP X k N Nn E X N N========∑∑5.设随机变量X 的概率密度为f （x ）=⎪⎩⎪⎨⎧≤≤-<≤.,0,21,2,10,其他x x x x求E （X ），D （X ）. 【解】12201()()d d (2)d E X xf x x x x x x x +∞-∞==+-⎰⎰⎰21332011 1.33x x x ⎡⎤⎡⎤=+-=⎢⎥⎢⎥⎣⎦⎣⎦122232017()()d d (2)d 6E X x f x x x x x x x +∞-∞==+-=⎰⎰⎰ 故 221()()[()].6D XE X E X =-=6.设随机变量X ，Y ，Z 相互独立，且E （X ）=5，E （Y ）=11，E （Z ）=8，求下列随机变量的数学期望.（1） U =2X +3Y +1； （2） V =YZ -4X .【解】(1) [](231)2()3()1E U E X Y E X E Y =++=++ 25311144.=⨯+⨯+=(2) [][4][]4()E V E YZ X E YZ E X =-=- ,()()4()Y Z E Y E Z E X -因独立1184568.=⨯-⨯= 7.设随机变量X ，Y 相互独立，且E （X ）=E （Y ）=3，D （X ）=12，D （Y ）=16，求E （3X -2Y ），D （2X -3Y ）. 【解】(1) (32)3()2()3323 3.E X Y E X E Y -=-=⨯-⨯=(2) 22(23)2()(3)412916192.D X Y D X DY -=+-=⨯+⨯=8.设随机变量（X ，Y ）的概率密度为f （x ，y ）=⎩⎨⎧<<<<.,0,0,10,其他x y x k试确定常数k ，并求E （XY ）. 【解】因11(,)d d d d 1,2xf x y x y x k y k +∞+∞-∞-∞===⎰⎰⎰⎰故k =2 1()(,)d d d 2d 0.25xE XY xyf x y x y x x y y +∞+∞-∞-∞===⎰⎰⎰⎰.9.设X ，Y 是相互独立的随机变量，其概率密度分别为2,01,()0,;X x x f x ≤≤⎧=⎨⎩其它 (5)e ,5,()0,.y Y y f y --⎧>=⎨⎩其它 求()E XY .【解】方法一：先求X 与Y 的均值 12()2d ,3E X x x x==⎰5(5)5()e d5e d e d 51 6.z y y zzE Y y y z zz +∞+∞+∞=-----=+=+=⎰⎰⎰令 由X 与Y 的独立性，得2()()()6 4.3E XY E X E Y ==⨯= 方法二：利用随机变量函数的均值公式.因X 与Y 独立，故联合密度为(5)2e ,01,5,(,)()()0,,y X Y x x y f x y f x f y --⎧≤≤>==⎨⎩其他于是11(5)2(5)552()2e d d 2d e d 6 4.3y y E XY xy x x y x xy y +∞+∞----===⨯=⎰⎰⎰⎰10.设随机变量X ，Y 的概率密度分别为()X f x =⎩⎨⎧≤>-;0,0,0,22x x x e ()Y f y =⎩⎨⎧≤>-.0,0,0,44y y y e 求（1） ()E X Y +;（2） 2(23)E X Y -.【解】22-200()()d 2e d [e ]e d x x xX E X xf x x x x x x +∞+∞+∞--+∞-∞===-+⎰⎰⎰201e d .2x x +∞-==⎰401()()d 4e d y .4yY E Y y f y y y +∞+∞--∞===⎰⎰22242021()()d 4e d .48y Y E Y y f y y y y +∞+∞--∞====⎰⎰从而(1) 113()()().244E X Y E X E Y +=+=+= (2)22115(23)2()3()23288E X Y E X E Y -=-=⨯-⨯=11.设随机变量X 的概率密度为f （x ）=⎪⎩⎪⎨⎧<≥-.0,0,0,22x x cx x ke求（1） 系数c ;（2）()E X ;（3） ()D X . 【解】(1) 由222()d e d 12k x c f x x cx x k+∞+∞--∞===⎰⎰得22c k =. (2) 2220()()d()2e d k x E X xf x x x k x x +∞+∞--∞==⎰⎰222202e d k x k x x +∞-==⎰(3) 22222221()()d()2e .k x E X x f x x x k x dx k +∞+∞--∞===⎰⎰故2222214π()()[()].24D X E X E X k k k ⎛-=-=-= ⎝⎭12.袋中有12个零件，其中9个合格品，3个废品.安装机器时，从袋中一个一个地取出（取出后不放回），设在取出合格品之前已取出的废品数为随机变量X ，求()E X 和()D X . 【解】设随机变量X 表示在取得合格品以前已取出的废品数，则X 的可能取值为0，1，2，3.为求其分布律，下面求取这些可能值的概率，易知9{0}0.750,12P X === 39{1}0.204,1211P X ==⨯= 329{2}0.041,121110P X ==⨯⨯= 3219{3}0.005.1211109P X ==⨯⨯⨯=由此可得()00.75010.20420.04130.0050.301.E X =⨯+⨯+⨯+⨯=22222222()075010.20420.04130.0050.413()()[()]0.413(0.301)0.322.E X D X E X E X =⨯+⨯+⨯+⨯==-=-=13.一工厂生产某种设备的寿命X （以年计）服从指数分布，概率密度为41e ,0,()40,0.xx f x x -⎧>⎪=⎨⎪≤⎩为确保消费者的利益，工厂规定出售的设备若在一年内损坏可以调换.若售出一台设备，工厂获利100元，而调换一台则损失200元，试求工厂出售一台设备赢利的数学期望. 【解】厂方出售一台设备净盈利Y 只有两个值：100元和 -200元/41/411{100}{1}e d e4x P Y P X x +∞--==≥==⎰1/4{200}{1}1e.P Y P X -=-=<=- 故1/41/41/4()100e (200)(1e )300e 20033.64E Y ---=⨯+-⨯-=-= (元). 14.设12,,,n X X X 是相互独立的随机变量，且有2(),(),1,2,,i i E X D X i n μσ===,记 11n i i X X n ==∑，2211()1n i i S X X n ==--∑. （1） 验证)(X E =μ，)(X D =n2σ；（2） 验证22211()1ni i S X nX n ==--∑；（3） 验证22()E S σ=.【证】(1) 1111111()()().n nn i i i i i i E X E X E X E X nu u n n n n ===⎛⎫===== ⎪⎝⎭∑∑∑22111111()()n nni i i ii i i D X D X D X X DXn nn ===⎛⎫== ⎪⎝⎭∑∑∑之间相互独立2221.n n nσσ==(2) 因为222221111()(2)2nnnniii ii i i i i XX X X X X X nX X X ====-=+-=+-∑∑∑∑2222112nnii i i X nX X nX X nX ===+-=-∑∑故22211()1ni i S X nX n ==--∑.(3) 因为2(),()i i E X u D X σ==,故2222()()().i i i E X D X EX u σ=+=+同理因为 2(),()E X u D X nσ==,故222()E X u nσ=+.从而222221111()()[()()]11n ni i i i E S E X nX E X nE X n n ==⎡⎤=-=-⎢⎥--⎣⎦∑∑221222221[()()]11().1ni i E X nE X n n u n u n n σσσ==--⎡⎤⎛⎫=+-+=⎢⎥⎪-⎝⎭⎣⎦∑15.对随机变量X 和Y ，已知()2D X =，()3D Y =，(,)1Cov X Y =-,计算：(321,43)Cov X Y X Y -++-【解】Cov(321,43)3()10ov(,)8()X Y X Y D X C X Y D Y -++-=+- 3210(1)8328=⨯+⨯--⨯=-(因常数与任一随机变量独立，故(,3)(,3)0Cov X Cov Y ==,其余类似). 16.设二维随机变量(,)X Y 的概率密度为221,1,(,)π0,.x y f x y ⎧+≤⎪=⎨⎪⎩其它 试验证X 和Y 是不相关的，但X 和Y 不是相互独立的. 【解】设22{(,)|1}D x y x y =+≤.2211()(,)d d d d πx y E X xf x y x y x x y +∞+∞-∞-∞+≤==⎰⎰⎰⎰ 2π1001=cos d d 0.πr r r θθ=⎰⎰ 同理E (Y )=0. （注意到积分区域的对称性和被积函数是奇函数可以直接得到0） 而 Cov(,)[()][()](,)d d X Y x E x y E Y f x y x y +∞+∞-∞-∞=--⎰⎰222π1200111d d sin cos d d 0ππx y xy x y r r r θθθ+≤===⎰⎰⎰⎰, 由此得0XY ρ=,故X 与Y 不相关.下面讨论独立性，当1x ≤时，()X f x =当 1y ≤时，()Y f y =. 显然 ()()(,)X Y f x f y f x y ≠ ,故X 和Y 不是相互独立的. 17.设随机变量(,)X Y 的分布律为验证X 和Y 是不相关的，但X 和Y 不是相互独立的.【解】联合分布表中含有零元素，X 与Y 显然不独立，由联合分布律易求得X ，Y 及XY 的分布律，其分布律如下表：由期望定义易得()E X =()E Y =()E XY =0.从而()E XY =()E X ()E Y ,再由相关系数性质知xy ρ=0, 即X 与Y 的相关系数为0，从而X 和Y 是不相关的. 又331{1}{1}{1,1}888P X P Y P X Y =-=-=⨯≠==-=- 从而X 与Y 不是相互独立的.18.设二维随机变量（X ，Y ）在以（0，0），（0，1），（1，0）为顶点的三角形区域上服从均匀分布，求(,)Cov X Y ，xy ρ. 【解】如图，S D =12，故（X ，Y ）的概率密度为题18图2,(,),(,)0,x y D f x y ∈⎧=⎨⎩其他.()(,)d d D E X xf x y x y =⎰⎰11001d 2d 3x x x y -==⎰⎰22()(,)d d DE X x f x y x y =⎰⎰112001d 2d 6x x x y -==⎰⎰从而222111()()[()].6318D XE X E X ⎛⎫=-=-= ⎪⎝⎭同理11(),().318E Y D Y == 而 1101()(,)d d 2d d d 2d .12xDDE XY xyf x y x y xy x y x xy y -====⎰⎰⎰⎰⎰⎰所以1111Cov(,)()()()123336X Y E XY E X E Y =-=-⨯=-. 从而112)()XY D Y ρ-===-19.设（X ，Y ）的概率密度为f （x ，y ）=1ππsin(),0,0,2220.x y x y ,⎧+≤≤≤≤⎪⎨⎪⎩其他求协方差(,)Cov X Y 和相关系数xy ρ. 【解】π/2π/21π()(,)d d d sin()d .24E X xf x y x y x xx y y +∞+∞-∞-∞==+=⎰⎰⎰⎰ππ2222201ππ()d sin()d 2.282E X x x x y y =+=+-⎰⎰从而222ππ()()[()] 2.162D XE X E X =-=+-同理 2πππ(),() 2.4162E Y D Y ==+- 又 π/2π/2π()d sin()d d 1,2E XY x xy x y x y =+=-⎰⎰故 2ππππ4C o v (,)()()()1.2444X Y E X Y E X E Y -⎛⎫⎛⎫=-=--⨯=- ⎪ ⎪⎝⎭⎝⎭222222π4(π4)π8π164.πππ8π32π8π32)()2162XY D Y ρ-⎛⎫- ⎪--+⎝⎭===-=-+-+-+-20.已知二维随机变量（X ，Y ）的协方差矩阵为⎥⎦⎤⎢⎣⎡4111，试求Z 1=X -2Y 和Z 2=2X -Y 的相关系数.【解】由已知条件得：D (X )=1,D (Y )=4,Cov(X ,Y )=1.从而12()(2)()4()4Cov(,)1444113,()(2)4()()4Cov(,)414414,D Z D X Y D X D Y X Y D Z D X Y D X D Y X Y =-=+-=+⨯-⨯==-=+-=⨯+-⨯=12Cov(,)Cov(2,2)Z Z X Y X Y =--2Cov(,)4Cov(,)Cov(,)2Cov(,)2()5Cov(,)2()215124 5.X X Y X X Y Y Y D X X YD Y =--+=-+=⨯-⨯+⨯=故122)()Z Z D Z ρ===21.对于两个随机变量V ，W ，若E （V 2），E （W 2）存在，证明：［E （VW ）］2≤E （V 2）E （W 2）.这一不等式称为柯西—许瓦兹（Cauchy -Schwarz ）不等式. 【证】考虑实变量t 的二次函数2222()[()]()2()()g t E V tW E V tE VW t E W =+=++因为对于一切t ，有2()0V tW +≥，所以 ()0g t ≥，从而二次方程 ()0g t =或者没有实根，或者只有重根，故其判别式Δ≤0， 即 222[2()]4()()0E VW E W E V ∆=-≤故 222[()]()()E VW E V E W ≤22.假设一设备开机后无故障工作的时间X 服从参数λ=1/5的指数分布.设备定时开机，出现故障时自动关机，而在无故障的情况下工作2小时便关机.试求该设备每次开机无故障工作的时间Y 的分布函数()F y .【解】由题设可知：设备开机后无故障工作的时间1()5XE ，其概率密度为 151,0()50,0x e x f x x -⎧>⎪=⎨⎪≤⎩根据题意 {}min ,2Y X =，所以Y 的分布函数为 {}{}()min ,2F y P X y =≤当0y <时，{}{}{}()min ,20F y P X y P X y =≤=≤=； 当02y ≤<时，{}{}{}115501()min ,215x y yF y P X y P X y e dx e --=≤=≤==-⎰； 当2y ≥时，{}{}()min ,21F y P X y =≤=；于是Y 的分布函数为：150,0,()1,02,1,2y y F y e y y -<⎧⎪⎪=-≤<⎨⎪≥⎪⎩。

第三章习题3-11．设s =12gt ２，求2d d t s t =．解：22221214()(2)2lim lim 22t t t g g ds s t s dt t t t →→=-⨯-==--21lim (2)22t g t g →=+=2．设f (x )=1x，求f '(x 0)(x 0≠0)．解：1211()()()f x x x x--'''===00201()(0)f x x x '=-≠3．试求过点（3，8）且与曲线2y x =相切的直线方程。

解：设切点为00(,)x y ，则切线的斜率为002x x y x ='=，切线方程为0002()y y x x x -=-。

由已知直线过点(3,8),得00082(3)y x x -=-(1)又点00(,)x y 在曲线2y x =上，故200y x =(2)由(1),(2)式可解得002,4x y ==或004,16x y ==，故所求直线方程为44(2)y x -=-或168(4)y x -=-。

也即440x y --=或8160x y --=。

4．下列各题中均假定f ′(x 0)存在，按照导数定义观察下列极限，指出A 表示什么：(1)0limx ∆→00()()f x x f x x-∆-∆=A ;(2)f (x 0)=0,0limx x →0()f x x x-＝A ；(3)0limh →00()()f x h f x h h+--=A ．解：(1)0000000()()[()]()limlim ()x x f x x f x f x x f x f x xx →-→--+--'=-=-- 0()A f x '∴=-(2)000000()()()limlim ()x x x x f x f x f x f x x x x x →→-'=-=--- 0()A f x '∴=-(3)000()()limh f x h f x h h→+-- 00000[()()][()()]lim h f x h f x f x h f x h→+----=000000()()[()]()lim lim h h f x h f x f x h f x h h →-→+-+--=+-000()()2()f x f x f x '''=+=02()A f x '∴=5．求下列函数的导数：(1)y；(2)y；(3)y2．解：(1)12y x==11221()2y x x -''∴===(2)23y x-=225133322()33y x x x ----''∴==-=-=(3)2152362y x x xx-==15661()6y x x -''∴===6．讨论函数y在x =0点处的连续性和可导性．解：00(0)x f →==000()(0)0lim lim 0x x x f x f x x →→→--===∞-∴函数y =在0x =点处连续但不可导。

数学分析复旦答案【篇一：复旦《数学分析》答案第四章1、2节】题 4.1 微分和导数⒈半径为1cm的铁球表面要镀一层厚度为0.01cm的铜，试用求微分的方法算出每只球需要用铜多少克？（铜的密度为8.9g/cm3。

）解球体积v?43?r3，每只球镀铜所需要铜的质量为2m???v?4??r?r?1.12g。

?0⒉用定义证明，函数y点之外都是可微的。

证当x?0时，?y?微。

当x?0时，?y???3x2在它的整个定义域中，除了x这一?x2是?x的低阶无穷小，所以y?x2在x?0不可?x?x?o(?x),所以y?x2在x?0是可微的。

习题 4.2 导数的意义和性质1．设f?(x0)存在，求下列各式的值：⑴⑵⑶lim?x?0f(x0??x)?f(x0) ?x；limx?x0f(x)?f(x0)x?x0；。

f(x0?(??x))?f(x0) (??x)??f(x0)。

limh?0f(x0?h)?f(x0?h) h解 (1)lim⑵⑶f(x0??x)?f(x0) ?xf(x)?f(x0)x?x0?x?0??lim?x?0x?x0lim?limf(x0?(x?x0))?f(x0) x?x0x?x0?0?f(x0)。

limf(x0?h)?f(x0?h) hf(x0?h)?f(x0)hh?0f(x0?h)?f(x0)hh?0?limh?0?lim?2f(x0)。

2．⑴用定义求抛物线y?2x2?3x?1的导函数；⑵求该抛物线上过点(?1,?2)处的切线方程；⑶求该抛物线上过点(?2,1)处的法线方程；⑷问该抛物线上是否有(a,b)，过该点的切线与抛物线顶点与焦点的连线平行？解 (1)因为?y?x?2(x??x)?3(x??x)?1?(2x?3x?1)?xf(x)?lim?y?x?4x?3。

22?4x?3?2?x，所以?x?0(2)由于(3)由于f(?1)??1，切线方程为y??1?[x?(?1)]?(?2)??x?3。

f(?2)??5，法线方程为y??1?5[x?(?2)]?1?x?75。

微积分上册 一元函数微积分与无穷级数第2章 极限与连续2.1 数列的极限1.对于数列n x ,若a x k →2(∞→k ),a x k →+12(∞→k ),证明:a x n → (∞→n )． 证. 0>∀ε, a x k →2 (∞→k ), Z K ∈∃∴1, 只要122K k >, 就有ε<-a x k 2; 又因a x k →+12(∞→k ), Z K ∈∃∴2, 只要12122+>+K k , 就有ε<-+a x k 12. 取{}12,2m ax 21+=K K N , 只要N n >, 就有ε<-a x n , 因此有a x n → (∞→n ). 2．若a x n n =∞→lim ，证明||||lim a x n n =∞→，并举反例说明反之不一定成立.证明： a x n n =∞→lim ，由定义有：N ∃>∀,0ε，当N n >时恒有ε<-||a x n又 ε<-≤-||||||a x a x n n对上述同样的ε和N ，当N n >时，都有ε<-||||a x n 成立 ∴ ||||lim a x n n =∞→反之,不一定成立.如取 ,2,1,)1(=-=n x nn显然 1||lim =∞→n n x ，但n n x ∞→lim 不存在.2.2 函数的极限1. 用极限定义证明:函数()x f 当0x x →时极限存在的充要条件是左、右极限各自存在且相等．证: 必要性. 若()A x f x x =→0lim , 0>∀ε, 0>∃δ, 当δ<-<00x x 时, 就有()ε<-A x f . 因而, 当δ<-<00x x 时, 有()ε<-A x f , 所以()A x f x x =+→0lim ; 同时当δ<-<x x 00时, 有()ε<-A x f , 所以()A x f x x =-→0lim .充分性. 若()A x f x x =+→0lim ,()A x f x x =-→0lim . 0>∀ε, 01>∃δ, 当100δ<-<x x 时, 就有()ε<-A x f , 也02>∃δ, 当200δ<-<x x 时, 有()ε<-A x f . 取{}21,m in δδδ=,则当δ<-<00x x 时, 就有()ε<-A x f . 所以()A x f x x =→0lim .2．写出下列极限的精确定义：（1）A x f x x =+→)(lim 0，（2）A x f x =-∞→)(lim ，（3）+∞=+→)(lim 0x f x x ，（4）-∞=+∞→)(lim x f x ，（5）A x f x =+∞→)(lim ．解：（1）设R x U f →)(:0是一个函数，如果存在一个常数R A ∈，满足关系：0,0>∃>∀δε，使得当δ<-<00x x 时，恒有ε<-|)(|A x f ，则称A 是)(x f 当+→0x x 时的极限，记作A x f x x =+→)(lim 0或 )()(0+→=x x A x f . （2）设R f D f →)(:是一函数，其中0,),,()(>>--∞⊃αααR f D .若存在常数R A ∈，满足关系：0)(,0>∈∃>∀R X ε，使得当X x -<时，恒有ε<-|)(|A x f 成立，则称A 是)(x f 当-∞→x 时的极限，记作：A x f x =-∞→)(lim 或 A x f =)()(-∞→x .（3）设R x U f →)(:0是任一函数，若0>∀M ，0>∃δ，使得当δ<-<00x x 时，恒有M x f >)(，则称当+→0x x 时)(x f 的极限为正无穷大，记作+∞=+→)(lim 0x f x x 或 +∞=)(x f )(0+→x x . （4）设R f D f →)(:是一函数，其中R f D ∈>+∞⊃ααα,0),,()(，若存在常数R A ∈，满足关系：0>∀M ，0)(>∈∃R X ，使得当X x >时，恒有M x f -<)(则称当+∞→x 时)(x f 的极限为负无穷大，记作：-∞=+∞→)(lim x f x 或 -∞=)(x f )(+∞→x .（5）设R f D f →)(:是一函数，其中R f D ∈>+∞⊃ααα,0),,()(，若存在常数R A ∈，满足关系：0,0>∃>∀X ε，使得当X x >时，恒有ε<-|)(|A x f 成立，则称A是)(x f 当+∞→x 时的极限，记作：A x f x =+∞→)(lim 或 A x f =)()(+∞→x .2.3 极限的运算法则1.求∑=∞→+⋯++Nn N n 1211lim． 解. ()()⎪⎭⎫ ⎝⎛+-=+=+=+⋯++111212211211n n n n n n n⎪⎭⎫ ⎝⎛+-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+⋯++∑=1112111312121122111N N N n Nn 21112lim 211lim1=⎪⎭⎫ ⎝⎛+-=+⋯++∴∞→=∞→∑N nN Nn N 2．求xe e xxx 1arctan11lim110-+→． 解. +∞=+→x x e 10lim , 0lim 10=-→xx e,,21arctan lim 11lim 1arctan11lim 0110110π=-+=-++++→--→→x ee x e e x xxx xxx ,21arctan lim 11lim 1arctan11lim 0110110π=-+=-+---→→→x e e x e e x x xx x x x 21arctan 11lim 110π=-+∴→x e e x xx3．设)(lim 1x f x →存在，)(lim 2)(12x f x x x f x →+=，求)(x f . 解：设 )(lim 1x f x →=A ，则A x x x f ⋅+=2)(2再求极限：A A A x x x f x x =+=⋅+=→→21)2(lim )(lim 211⇒ 1-=A∴ x x xA x x f 22)(22-=+=.4．确定a ,b ,c ，使 0)1(3)1()1(lim 2221=-+-+-+-→x x c x b x a x 成立.解：依题意,所给函数极限存在且 0)1(lim 21=-→x x∴ 0]3)1()1([lim 221=+-+-+-→x c x b x a x ⇒ 2=c∴ 上式左边=])32)(1(11[lim ))1(321(lim 21221++-+--+=-+-+-+→→x x x x b a x x x b a x x])32)(1(1)32([lim 221++---+++=→x x x x b a x同理有 0]1)32([lim 21=--++→x x b x ⇒ 21=b ∴ 163)23)(1(8)1(3lim )32)(1(1)32(21lim221221=++---=++---++-=→→x x x x x x xx a x x 故 2,21,163===c b a 为所求.2.4 极限存在准则1. 设1x =10，n n x x +=+61，( ,2,1=n )．试证数列{n x }的极限存在，并求此极限． 证: 由101=x , 4612=+=x x , 知21x x >. 假设1+>k k x x , 则有21166+++=+>+=k k k k x x x x . 由数学归纳法知, 对一切正整数n , 有1+>n n x x ,即数列{n x }单调减少. 又显然, () ,2,10=>n x n , 即{n x }有界. 故n n x ∞→lim 存在.令a x n n =∞→lim , 对n n x x +=+61两边取极限得a a +=6, 从而有062=--a a ,,3=∴a 或2-=a , 但0,0≥∴>a x n , 故3lim =∞→n n x2．证明数列 nn n x x x x ++=<<+3)1(3,3011收敛，并求其极限．证明：利用准则II ，单调有界必有极限来证明.∴301<<x ，由递推公式33312131213213)1(30111112=++<++=++=++=<x x x x x x∴ 302<<x 同理可证：30<<n x 有界又 03)3)(3(333)1(311112111112>++-=+-=-++=-x x x x x x x x x x∴ 12x x > 同理 23x x > ，… ，1->n n x x ∴数列 }{n x 单调递增，由准则II n n x ∞→lim 存在，设为A ，由递推公式有：AA A ++=3)1(3 ⇒ 3±=A （舍去负数）∴ 3lim =∞→n n x .3．设}{n x 为一单调增加的数列，若它有一个子列收敛于a ，证明a x n n =∞→lim .证明：设}{k n x 为}{n x 的一子列，则}{k n x 也为一单调增加的数列，且a x k k n n =∞→lim对于1=ε，N ∃，当N n >时有1||<-a x k n 从而||1||||||||a a a x a a x x k k k n n n +<+-≤+-=取|}|1|,|,|,max {|1a x x M N n n += ，对一切k n 都有 M x k n ≤|| 有界.由子列有界，且原数列}{n x 又为一单调增加的数列，所以，对一切n 有M x n ≤||有界，由准则II ，数列}{n x 极限存在且a x n n =∞→lim .2.5 两个重要极限1. 求]cos 1[cos lim n n n -++∞→．解： 原式 =21sin 21sin2lim nn n n n -+++-+∞→⎪⎪⎭⎫⎝⎛++=-+=-+-+-+++-=+∞→n n n n n n nn nn nn n 1110212121sin21sin2lim 2. 求)1sin(lim 2++∞→n n π．解. 原式=()()n nn n n nn n -+-=-+++∞→+∞→1sin 1lim )1sin(lim 22ππππ()()()()0111sin 1lim 222=-+⋅-+-+-=+∞→n nn n nnnn πππ3. 求x x xx )1cos 1(sinlim +∞→． 解. 原式=()[]()e t t t tttt tt xt =⎥⎦⎤⎢⎣⎡+=+=→→=22sin 2sin 10212012sin 1lim cos sin lim 令4. 设 ⎩⎨⎧+-=32)cos 1(2)(x x x x f 00≥<x x 求 20)(lim x x f x →. 解： 1lim )(lim 232020=+=++→→x x x x x f x x ，1)cos 1(2lim )(lim 2020=-=--→→x x x x f x x ∴ 1)(lim2=→xx f x .2.6 函数的连续性1. 研究函数()[]x x x g -=的连续性，并指出间断点类型. 解. n x =，Z n ∈ (整数集)为第一类 (跳跃) 间断点.2. 证明方程)0(03>=++p q px x 有且只有一个实根.证. 令()()()0,0,3>∞+<∞-++=f f q px x x f , 由零点定理, 至少存在一点ξ使得()0=ξf , 其唯一性, 易由()x f 的严格单调性可得.3．设⎪⎩⎪⎨⎧≤<-+>=-01),1ln(0 ,)(11x x x e x f x ，求)(x f 的间断点，并说明间断点的所属类型. 解. )(x f 在()()()+∞-,1,1,0,0,1内连续, ∞=-→+111lim x x e,0lim 111=-→-x x e, ()00=f , 因此,1=x 是)(x f 的第二类无穷间断点; (),lim lim 1110--→→==++e ex f x x x()()01ln lim lim 00=+=--→→x x f x x , 因此0=x 是)(x f 的第一类跳跃间断点.4．讨论nx nxn e e x x x f ++=∞→1lim )(2的连续性．解. ⎪⎩⎪⎨⎧<=>=++=∞→0,0,00,1lim)(22x x x x x e e x x x f nxnxn , 因此)(x f 在()()+∞∞-,0,0,内连续, 又()()00lim 0==→f x f x , ()x f ∴在()+∞∞-,上连续.5.设函数),()(+∞-∞在x f 内连续，且0)(lim=∞→xx f x ，证明至少存在一点ξ，使得0)(=+ξξf .证：令x x f x F +=)()(，则01]1)([lim )(lim>=+=∞→∞→x x f x x F x x ，从而0)(>xx F .由极限保号性定理可得，存在01>x 使0)(1>x F ；存在02<x 使0)(2<x F .)(x F 在],[12x x 上满足零点定理的条件，所以至少存在一点ξ使得0)(=ξF ，即0)(=+ξξf .6．讨论函数nnx x x x f 2211lim )(+-=∞→的连续性，若有间断点，判别其类型.解： ⎪⎩⎪⎨⎧-=101)(x f 1||1||1||>=<x x x ，显然 1±=x 是第一类跳跃间断点，除此之外均为连续区间.7．证明：方程)0,0(sin >>+=b a b x a x 至少有一个正根，且不超过b a +. 证明：设b x a x x f --=sin )(，考虑区间],0[b a +0)0(<-=b f ，0))sin(1()(≥+-=+b a a b a f ，当0))sin(1()(=+-=+b a a b a f 时，b a x +=是方程的根；当0))sin(1()(>+-=+b a a b a f 时，由零点定理，至少),0(b a +∈∃ξ使0)(=ξf ，即 0sin =--b a ξξ成立,故原方程至少有一个正根且不超过b a +.2.7 无穷小与无穷大、无穷小的比较1. 当0→x 时，下面等式成立吗？(1))()(32x o x o x =⋅；(2))()(2x o xx o =；(3) )()(2x o x o =． 解. （1）()()()002232→→=⋅x xx o x x o x , ()()()032→=⋅∴x x o x o x （2） ()()()0)(,00)()(2222→=∴→→=x x o x x o x x x o xxx o（3） ()2xx o不一定趋于零, )()(2x o x o =∴不一定成立(当0→x 时) 2. 当∞→x 时，若)11(12+=++x o c bx ax ，则求常数c b a ,,．解. 因为当∞→x 时，若)11(12+=++x o c bx ax , 所以01lim 111lim 22=+++=++++∞→+∞→c bx ax x x c bx ax x x , 故c b a ,,0≠任意.3．写出0→x 时，无穷小量3x x +的等价无穷小量.解： 11lim 1lim lim303630=+=+=+→→→x xx xxx x x x∴ 当0→x ，3x x +～6x第3章 导数与微分3.1 导数概念1. 设函数)(x f 在0x 处可导，求下列极限值． (1)hh x f h x f h )3()2(lim000--+→；(2)000)()(lim 0x x x xf x f x x x --→．解.（1） 原式()()()000000533)3(22)2(lim x f h x f h x f h x f h x f h '=⎥⎦⎤⎢⎣⎡⋅---+⋅-+=→（2） 原式()[]()()()()00000000)(limx f x f x x x x x x f x f x f x x x -'=----=→2．设函数R f →+∞),0(:在1=x 处可导，且),0(,+∞∈∀y x 有)()()(y xf x yf xy f += 试证：函数f 在),0(+∞内可导，且)1()()(f xx f x f '+='． 解：令1==y x ，由()()()y xf x yf xy f +=有()()121f f =得()01=f ．()+∞∈∀,0x ，()()()()()()()()()()xx f f x x f xx f x x f x x f x f x x x x xf x x f x x x f x x f x x f x f x x x x +'=+∆-⎪⎭⎫⎝⎛∆+=∆-⎪⎭⎫ ⎝⎛∆++⎪⎭⎫ ⎝⎛∆+=∆-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∆+=∆-∆+='→∆→∆→∆→∆111lim 11lim 1lim lim 0000 故()x f 在()+∞,0内处处可导，且()()()xx f f x f +'='1． 3.设()f x 在(,)-∞+∞内有意义，且(0)0f =，(0)1f '=， 又121221()()()()()f x x f x x f x x ϕϕ+=+，其中22()cos xx x x e ϕ-=+, 求()f x '．解： ()()()()()()()()x x f x x f x x f x x f x x f x f x x ∆-∆+∆=∆-∆+='→∆→∆ϕϕ00lim lim()()()()()()()()()001lim 0lim 00ϕϕϕϕ'+'=∆-∆+∆-∆=→∆→∆x f x f xx x f x x f x f x x ()x e x x x 22cos -+==ϕ4.设函数0)(=x x f 在处可导，且21arctan lim )(0=-→x f x e x，求)0(f '.解：由已知，必有0]1[lim )(0=-→x f x e，从而0)(lim 0=→x f x ，而0)(=x x f 在连续，故0)0(=f .于是)0(1)0()(1lim )(lim 1arctan lim200)(0f xf x f x f x e x x x x f x '=-==-=→→→. 故21)0(='f .5.设)(x f 具有二阶导数，)(,sin )()2(lim )(2x dF t xx f t x f t x F t 求⎥⎦⎤⎢⎣⎡-+=∞→.解： 令t h 1=，则)(2 sin )()2(lim)(0x f x hhxh x f h x f x F t '=⋅-+=→.从而)(2)(2)(x f x x f x F ''+'='，dx x f x x f dx x F x dF )]()([2)()(''+'='=.6．设f 是对任意实数y x ,满足方程 22)()()(xy y x y f x f x f +++= 的函数，又假设1)(lim=→xx f x ,求：（1）)0(f ；（2）)0(f '； （3）)(x f '. 解：（1）依题意 R y x ∈∀,，等式 22)()()(xy y x y f x f y x f +++=+ 成立令0==y x 有 )0(2)0(f f = ⇒ 0)0(=f（2）又 1)(lim=→x x f x ，即 )0(10)0()(lim 0f x f x f x '==--→，∴ 1)0(='f（3）xx f x x f x f x ∆-∆+='→∆)()(lim )(0x x f x x x x x f x f x ∆-∆⋅+∆⋅+∆+=→∆)()()()(lim 220 x x x x x x f x ∆∆⋅+∆⋅+∆=→∆220)()(lim ])([lim 20x x x xx f x ∆⋅++∆∆=→∆ ]1)0(22x x f +=+'=∴ 21)(x x f +='.7．设曲线)(x f y =在原点与x y sin =相切，试求极限 )2(lim 21nf nn ∞→. 解：依题意有 1)0()0(='='f y 且0)0(=f∴ 222)0()2(lim )2(lim 2121=⋅-⋅=⋅∞→∞→n nf n f n nf n n n .8．设函数)(x f 在0=x 处可导且0)0(,0)0(='≠f f ，证明1])0()1([lim =∞→nn f n f .证：n n n n f f n f f n f ])0()0()1(1[lim ])0()1([lim -+=∞→∞→.=10)0(11)0()01(lim )0()0()1(lim ===⋅-+-∞→∞→e ee f nf n f f f n f n n n .1．计算函数baxax xb ab y )()()(= （0,0>>b a ）的导数．解. a xb bx a b a x xb a b a a x b a x a b x b x b a a x x b a b a b y )(1)()()()(ln )(121⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛+='-- ⎥⎦⎤⎢⎣⎡+-=x b x a a b a x x b a b b a x ln )()()( 2.引入中间变量,1)(2x x u +=计算1111ln 411arctan 21222-+++++=x x x y 的导数dx dy ．解. 引入,1)(2x x u += 得11ln 41arctan 21-++=u u u y ,于是dxdudu dy dx dy ⋅=, 又 ()()4242422111111111141121x x x u u u u du dy +-=+-=-=⎪⎭⎫ ⎝⎛--+++=,21xx dx du +=, 则()22242121121xx x x x x x dx dy ++-=+⋅⎪⎭⎫⎝⎛+-= 3.设y y x +=2，232)(x x u +=，求dudy． 解. dudxdx dy du dy ⋅= , 又()()1223,12212++=+=x x x dx du y dy dx ,得121+=y dx dy , ()x x x du dx ++=21232, 则得()()xx x y du dy +++=2121232 4．已知 2arctan )(),2323(x x f x x f y ='+-=，求=x dx dy ．解：22)23(12)2323arctan()2323()2323(+⋅+-='+-⋅+-'='x x x x x x x f y π43)23(12)2323arctan(02200=+⋅+-='=∴===x x x x x x y dxdy .1. 计算下列各函数的n 阶导数. (1) 6512-+=x x y ; (2) x e y xcos =． 解 （1）⎪⎭⎫⎝⎛+--=611171x x y ，()()()()()()⎥⎦⎤⎢⎣⎡+---=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛-=∴++1161117!1611171n n nn n n x x n x x y （2） ()⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡-=-='4cos 2sin 21cos 212sin cos πx e x x e x x e y x x x()⎪⎭⎫ ⎝⎛⋅+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+=''42cos 24sin 4cos 22πππx ex x e y xx由此推得 ()()⎪⎭⎫ ⎝⎛⋅+=4cos 2πn x eyxnn2. 设x x y 2sin 2=, 求()50y ．解 ()()()()()()()()()()"+'+=248250249150250502sin 2sin 2sin x x C x x C x x y⎪⎭⎫ ⎝⎛⋅+⋅⨯+⎪⎭⎫ ⎝⎛⋅+⋅+⎪⎭⎫ ⎝⎛⋅+=2482sin 2249502492sin 2502502sin 24950250πππx x x x xx x x x x 2sin 212252cos 2502sin 24950250⋅+⋅+-= ()[]x x x x 2cos 1002sin 212252249+-=3. 试从y dy dx '=1, 0≠'y , 其中y 三阶可导, 导出()322y y dy x d '''-=, ()()52333y y y y dy x d '''''-''= 解 y dy dx '=1 ，()()322211y y y y y dy dx y dx d dyx d '''-='⋅'-''=⋅⎪⎪⎭⎫ ⎝⎛'=∴ ()()()()()()52623333313y y y y y y y y y y y dy dx y y dx d dy x d '''''-''='⋅'''⋅'⋅''+''''-=⋅⎪⎪⎭⎫ ⎝⎛'''-=∴ 4. 设()x f 满足()()0 312≠=⎪⎭⎫⎝⎛+x xx f x f , 求()()()()x f x f x f n ,,'．解 以x 1代x ，原方程为()x x f x f 321==⎪⎭⎫ ⎝⎛，由()()⎪⎪⎩⎪⎪⎨⎧=+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+x x f x f x x f x f 321 312，消去⎪⎭⎫⎝⎛x f 1，求得()x x x f 12-=，且得()212xx f +='，()()()()2!111≥-=++n x n x f n n n . 5．设()arcsin f x x =，试证明()f x 满足 （1）2(1)()()0x f x xf x '''--= （2） ,1,0,0)()()12()()1()(2)1()2(2==-+--++n x f n x xf n x f x n n n（3）求()(0)n f解 （1）()211x x f -='，()()()22221112211xx xx x x x f --=-⋅--=''， ()()()012='-''-∴x f x x f x ，（2）上式两边对x 求n 阶导数得()()[]()()[]()()()()()()()()()()()()()()()[]x f n x xf x f n n x f x n x f x x f x x f x n n n n n nn⋅⋅+-⋅-⋅---+-='-''-=+++1221211021222即 ()()()()()()()()01212122=-+--++x f nx xf n x f xn n n 。

第一章 函数极限与连续一、填空题1、已知x x f cos 1)2(sin +=，则=)(cos x f 。

2、=-+→∞)1()34(lim22x x x x 。

3、0→x 时，x x sin tan -是x 的 阶无穷小。

4、01sin lim 0=→xx kx 成立的k 为 。

5、=-∞→x e xx arctan lim 。

6、⎩⎨⎧≤+>+=0,0,1)(x b x x e x f x 在0=x 处连续，则=b 。

7、=+→xx x 6)13ln(lim 0 。

8、设)(x f 的定义域是]1,0[，则)(ln x f 的定义域是__________。

9、函数)2ln(1++=x y 的反函数为_________。

10、设a 是非零常数，则________)(lim =-+∞→xx ax a x 。

11、已知当0→x 时，1)1(312-+ax 与1cos -x 是等价无穷小，则常数________=a 。

12、函数xxx f +=13arcsin )(的定义域是__________。

13、lim ____________x →+∞=。

14、设8)2(lim =-+∞→xx ax a x ，则=a ________。

15、)2)(1(lim n n n n n -++++∞→=____________。

二、选择题1、设)(),(x g x f 是],[l l -上的偶函数，)(x h 是],[l l -上的奇函数，则 中所给的函数必为奇函数。

（Ａ）)()(x g x f +；（Ｂ）)()(x h x f +；（C ）)]()()[(x h x g x f +；（D ）)()()(x h x g x f 。

2、xxx +-=11)(α，31)(x x -=β，则当1→x 时有 。

（Ａ）α是比β高阶的无穷小； （Ｂ）α是比β低阶的无穷小； （C ）α与β是同阶无穷小； （D ）βα~。

习题 4-11.验证函数f (x )=lnsin x 在[π5π,66]上满足罗尔定理的条件，并求出相应的ξ，使f ′(ξ)=0.　解: 显然()ln sin f x x =在5π,66x ⎡⎤⎢⎥⎣⎦上连续,在π5π,66⎛⎫⎪⎝⎭内可导,且π5π()()ln 266f f ==-,满足罗尓定理的条件. 令cos ()cot 0sin x f x x x '===,则π2x = 即存在ππ5π(,)66ξα=∈,使()0f ξ'=成立.2. 下列函数在指定区间上是否满足罗尔定理的三个条件?有没有满足定理结论中的ξ ?　[][][]2(1)()1,;(2)(),;1,10,21sin ,0π(3)()0,π1,0e x f x f x x x x f x x =-=--<≤⎧=⎨=⎩解: (1) 2()1e x f x =-在[]1,1-上连续,在()1,1-内可导,且(1)1,(1)1,e e f f -=-=-即 (1)(1)f f -=() f x ∴在[]1,1-上满足罗尓定理的三个条件. 令 2()20ex f x x '==得 0x =,即存在0(1,1)ξ=∈-,使()0f ξ'=.(2) 101()1112x x f x x x x -≤<⎧==-⎨-≤≤⎩显然()f x 在(0,1),(1,2)内连续,又1111(10)lim ()lim(1)0,(10)lim ()lim(1)0,(10)(10)(1)0,即x x x x f f x x f f x x f f f --++→→→→-==-=+==-=-=+==所以()f x 在1x =处连续,而且22(00)lim ()lim (1)1(0),(20)lim ()lim (1)1(2),x x x x f f x x f f f x x f ++--→→→→+==-==-==-==即()f x 在0x =处右连续,在2x =处左连续,所以()f x 在[]0,2 上连续.又w ww .t tl ea rn .n et1111()(1)1(1)lim lim 1,11()(1)1(1)lim lim 111x x x x f x f xf x x f x f xf x x --++-→→+→→--'===-----'===--(1)(1)() f f f x -+''∴≠∴在1x =处不可导,从而()f x 在(0,2)内不可导. 又 (0)(2)1f f == 又由 101()112x f x x -<<⎧'=⎨<<⎩知 ()0f x '≠ 综上所述,函数()f x 满足罗尓定理的条件(1),(3)不满足条件(2),没有满足定理结论的ξ. (3) 由0(00)lim sin 0(0)1x f x f +→+==≠=知()f x 在0x =不右连续, () f x ∴在[]0,π上不连续, 显然()f x 在()0,π上可导,又(0)1,(π)0f f ==,即(0)(π)f f ≠,且()cos (0,π) f x x x '=∈,取π(0,π)2ξ=∈,有π()cos cos 02f ξξ'===. 综上所述,函数()f x 满足罗尓定理的条件(2),不满足条件(1),(3),有满足定理结论的ξ,ξ=π2.3. 不用求出函数()(1)(2)(3)f x x x x =---的导数，说明方程()0f x '=有几个实根，并指出它们所在的区间.解: 显然()f x 在[]1,2上连续,在()1,2内可导,且(1)(2)0f f ==,由罗尓定理知,在()1,2内至少存在一点1ξ,使1()0f ξ'=,即()0f x '=在()1,2内至少有一个实根.同理　()0f x '=在()2,3内也至少有一个实根2ξ.又()0f x '=是二次方程,最多有两个实根,故()0f x '=有两个实根,分别在区间()1,2和()2,3内.4. 验证拉格朗日中值定理对函数3()2f x x x =+在区间［0，1］上的正确性.解: 显然3()2f x x x =+在［0，1］上连续,在()0,1内可导,满足拉格朗日中值定理的条件.若令2(1)(0)()32310f f f x x -'=+==-　则3x =±,取3ξ=,即存在w ww .t tl ea rn .n et(0,1)3ξ=∈,使得(1)(0)()10f f f ξ-=-成立. 从而拉格朗日中值定理对函数3()2f x x x =+在［0，1］上成立.5. 已知函数f (x )在［a ,b ］上连续，在(a ,b )内可导，且f (a )=f (b )=0,试证：在(a ,b )内至少存在一点ξ，使得 f (ξ)+f ′(ξ) = 0，ξ(∈a ,b ). 证: 令()()e xF x f x =,则()()()e e xxF x f x f x ''=+由e x在(),-∞+∞上连续,可导,()f x 在[],a b 上连续,在(),a b 内可导,知()F x 在[],a b 上连续,在(),a b 内可导,而且()()0,()()0,()()e e 即abF a f a F b f b F a F b =====,由罗尓定理至少存在一点(,)a b ξ∈使()0F ξ'=.即 ()()0e e f f ξξξξ'+= 而0e ξ≠ 故 ()()0f f ξξ'+=即在(),a b 内至少存在一点ξ,使得()()0f f ξξ'+=.6.若方程10110n n n a x a x a x --+++= 有一个正根x 0,证明方程12011(1)0n n n a nx a n x a ---+-++=必有一个小于0x 的正根.证: 令1011()…nn n f x a x a xa x --=+++,显然()f x 在[]00,x 连续,在()00,x 内可导,且(0)0f =,依题意知0()0f x =.即有0(0)()f f x =.由罗尓定理,至少存在一点0(0,)x ξ∈,使得()0f ξ'=成立,即12011(1)0…n n n a n a n a ξξ---+-++=成立,这就说明ξ是方程12011(1)0n n n a nx a n x a ---+-++= 的一个小于0x 的正根. 7. 设f (a ) = f (c ) = f (b ),且a ＜c ＜b , f ″(x )在［a ,b ］上存在，证明在(a ,b )内至少存在一点ξ，使f ″(ξ) = 0.证: 显然()f x 分别在[],a c 和[],c b 上满足罗尓定理的条件,从而至少存在1(,)a c ξ∈,2(,)c b ξ∈,使得12()()0f f ξξ''==.w ww .t tl ea rn .n et又由题意知()f x '在[]12,ξξ上满足罗尓定理的条件,从而至少存在一点12(,)(,)a b ξξξ∈⊂,使得()0f ξ''=.即在(,)a b 内至少存在一点ξ,使()0f ξ''=. 习题4-2　1.利用洛必达法则求下列极限：　(1) sin 3limtan 5x x x π→; (2) 0e 1lim (e 1)x x x x x →---; (3)lim m m n n x a x a x a →--； (4) 20()lim x xx a x a x →+-,(a ＞0)； (5) 0ln lim cot x xx +→； (6) 0lim sin ln x x x +→;(7) 1ln(1)lim arccot x x x →+∞+; (8) 0e 1lim(e 1x x x x →--;(9) 10lim(1sin )xx x →+; (10) 2lim (arctan )πx x x →+∞(11) csc 03e lim(2x x x x →-+ ; (12) 2120lim e x x x →;(13) lim )x x →+∞-; (14) 1101lim (1)e xxx x →⎡⎤+⎢⎥⎣⎦.解:222000011sin 33cos33(1)limlim lim cos3cos 5tan 55sec 5533(1)(1)5511(2)limlim lim (1)111lim 22(3)lim lim limπππe e e e e e e e e x x x x x xx x x x x xx x x x m m m n n n x a x a x a x x x x x x x x x x x x a mx x a nx →→→→→→→--→→→==⋅=⋅-⋅-=----==--+++==+-==-.m n m n m m x a n n --= 2002220()ln ln()()(4)lim lim 21()()()ln ln()()lim2x xxxx x x x x x x a x a a a x a x a a x x xa x a x a x a a a x a x a x a x →→→⎡⎤+-++⎢⎥+-+⎣⎦=⎡⎤++++-++⎢⎥+++⎣⎦=w ww .t tl ea rn .n et[]2000221()ln ln 012 aa a a aa a a a ++-⋅+==2200000000001ln sin 2sin cos (5)lim lim lim lim cot csc 12sin 0cos 001ln sin (6)lim sin ln lim lim lim tan csc csc cot sin lim lim tan 100 x x x x x x x x x x x x x x x x x x x x x x x xx x x xxx x ++++++++++→→→→→→→→→→==-=--=-⋅====-⋅-=-⋅=-⨯=222221111ln(1111(7)limlim lim lim 111cot 11arc x x x x xx x x x x x x x x →+∞→+∞→+∞→+∞-++++====+-++ 20002200001(1)(8)lim()lim lim 1(1)21443limlim 12022e e e e e e e e e e e e e e e e e e e x x x x x x x x x x x x xxxx x x x x x x x x x x xx x →→→→→-----==-------====+-++00022cos 11ln(1sin )cos 1sin ln(1sin )lim limlim 11sin 12112ln(arctan )arctan 1limlim 112ln(arctan )(9)lim(1sin )lim 2(10)lim (arctan )lim πππee =eee ee eeπx x x x x xx xx x xxxxx x x x x x x x xxx x x x →→→→+∞→+∞++++→→⋅⋅+-→+∞→+∞+========2221lim12lim(1)arctan (1)arctan πeeex x x x x xx→+∞→+∞--+-+===020033lnln322csc ln lim csc 2sin sin 0002(2)(3)33(2)limlim 1(3)(2)cos cos 3(11)lim()lim lim 21e e e e e e e e eee ee exxxx x x x x x x x x e e ex x x x xxxxx x x x x x x x xxx →→→---+++→→→+-+--⋅----+--+-===+====2222111122000221()(12)lim lim lim lim 11()e e ee x xx x x x x x x x x x→→→→'⋅====∞'w ww .t tl ea rn .n et202211ln(1)1ln(1)1limlim lim 0(13)lim )lim1111lim31(14)lim (1) ee ee x x x x x x x x xx xxx x x x x →→→+∞→+∞+-+-→=++===⎡⎤===+⎢⎥⎣⎦00111211lim2(1)2eex x xx →→-+--+==2.设　21lim 1x x mx nx →++-=5,求常数m ,n 的值.解: 1lim(1)0, x x →-= 而21lim 51x x mx nx →++=-21lim()0 x x mx n →∴++=　且21()lim5(1)x x mx n x →'++='- 即 10m n ++= 且 1lim(2)5x x m →+=即 1m n +=- 且 25m +=于是得 3,4m n ==-. 3.验证极限sin lim x x xx→∞+存在，但不能由洛必达法则得出.　解: sin 1limlim(1sin )1x x x x x x x→∞→∞+=+=,极限存在,但若用洛必达法则,有sin lim lim(1cos )x x x xx x→∞→∞+=+因lim cos x x →∞不存在,所以不能用洛必达法则得出.4.设f (x )二阶可导，求2()2()()limh f x h f x f x h h →+-+-.解: 这是型未定式,利用洛必达法则有 [][]200000()2()()()()limlim2()()()()1lim 21()()1()()11lim lim ()()2222().h h h h h f x h f x f x h f x h f x h h hf x h f x f x h f x hf x h f x f x h f x f x f x h h f x →→→→→''+-+-+--=''''-+---=''''+---''''=+=+-''= w ww .t tl ea rn .n et5.设f (x )具有二阶连续导数，且f (0) = 0,试证g (x ) = (),0'(0),0f x x x f x ⎧≠⎪⎨⎪=⎩可导，且导函数连续. 证: 当0x ≠时,2()()()()()f x xf x f x g x x x '-''==当0x =时,由200000()(0)()(0)()(0)lim lim lim 00()(0)1()(0)1lim lim (0)2202x x x x x f x f g x g f x xf x x x x f x f f x f f x x →→→→→'-'--==--''''--''===- 即 1(0)(0)2g f '''=所以 2()(),0()1(0),02xf x f x x xg x f x '-⎧≠⎪⎪'=⎨⎪''=⎪⎩由(),()f x f x '的连续性知()g x '在0x ≠处连续,又20000()()()()()lim ()limlim 211lim ()(0)(0)22x x x x xf x f x f x xf x f x g x x xf x fg →→→→'''''-+-'=='''''===　故()g x '在0x =处连续,所以()g x '在(),-∞+∞内处处连续.综上所述,(),0()(0),0f x xg x x f x ⎧≠⎪=⎨⎪'=⎩可导,且导函数连续. 习题4-31.求函数f (x ) =e x x 的n 阶马克劳林公式.解:()()(1),()(1)(2),()()ٛ… x x x x x x k x f x e xe e x f x e x e e x f x e k x '=+=+''=++=+=+w ww .t tl ea rn .n et()()(0)1(0),(1,2,3,)!!(1)!k k f k fk k k k k ∴====- 又 (0)0f =321(1)()(01)2!(1)!(1)!n x n x x e n x f x x x x n n θθθ+++∴=+++++<<-+ 2.当01x =-时，求函数f (x ) = 1x的n 阶泰勒公式. 解:()()[]23()2341()1()112212!3!!()(1),()(1),()(1),,()(1)!(1)(1)!(1)(1)!1,(0,1,2,)!!(1)()(1)1(1)111(1)ٛ … n n n n n n n n n n n n f x f x f x f x x x x x n f n f n n n n x f x x x x x θ-++++''''''=-=-=-=-∴-=-⋅=----==-=+∴=-+-⎡⎤+++++++⎣⎦-++(01)θ<<3.按(4)x -的乘幂展开多项式432()53 4.f x x x x x =-+-+　解: 函数432()534f x x x x x =-+-+,根据泰勒公式按(4)x -的幂的展开式是2(4)34(4)()(4)(4)(4)(4)2!(4)(4)(4)(4)3!4! f f x f f x x f f x x '''=+-+-'''+-+- 而[][][]432324244(4)(4)454434456,(4)21,41523(4)137,123022!2(4)111,24303!3!(4)12414!4!x x x f f x x x f x x f x f ====-⨯+-⨯+=-'==-+-''==-+'''==-=⨯=所以,234()5621(4)37(4)11((4)(4)f x x x x x =-+-+-+-+-.4.利用泰勒公式求下列极限:　w ww .t tl ea rn .n et(1) 30sin limx x x x →-; (2) 21lim ln(1)x x x x →+∞⎡⎤-+⎢⎥⎣⎦. 解: (1) 利用泰勒公式,有34sin ()3!x x x o x =-+所以 343300430()sin 3!lim lim 1()1lim()66x x x x o x x x x x o x x→→→--==-= (2) 利用泰勒公式,有221111ln(1(2o x x x x+=-+,所以222222221111lim lim ln(1(())21()1111lim lim .(1222x x x x x x x x o x x x x o x x o x x →+∞→+∞→+∞→+∞⎡⎤⎡⎤=-+--+⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢⎥⎡⎤==-=-⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦习题4-4　1. 求下面函数的单调区间与极值：　(1)32()26187f x x x x =---； (2)()ln f x x x =-； (3)23()1(2)f x x =--； (4)()(4)f x x x =-. 解: (1) 2()612186(1)(3),f x x x x x '=--=+-令()0f x '=得驻点121,3,x x =-=-在()(),,13,-∞-+∞上,()0f x '>,在()1,3-上()0f x '< ∴ ()f x 在(,1],[3,)-∞-+∞上单调增加,在[]1,3-上单调减少.当 1x =-时, ()f x 有极大值,极大值为(1)3f -=, 当 3x =时,　()f x 有极小值,极小值为(3)61f =-.w ww .t tl ea rn .n et(2) 11()1x f x x x-'=-=,令()0f x '=得驻点1x = 在()0,1上,()0f x '<;在()1,+∞上,()0f x '> ∴ ()f x 在(0,1]上单调递减;在[1,)+∞上单调递增. 当1x =时,()f x 有极小值,极小值为(1)1f =.(3) ()()0f x f x ''=≠ 但当2x =时,()f x '不存在, 在(,2)-∞上,()0f x '>;在(2,)+∞上,()0f x '<,∴ ()f x 在(,2]-∞上单调递增;在[2,)+∞上单调递减.当2x =时, ()f x 有极大值,极大值为(2)1f =.(4) 2240()40x xx f x x xx ⎧-≥=⎨-+<⎩ ,则 240()240x x f x x x ->⎧'=⎨-+<⎩且当 0x =时,()f x '不存在,又令()0f x '=得2x =在(,0),(2,)-∞+∞上,()0f x '>,在(0,2)上()0f x '<∴ ()f x 在(,0],[2,)-∞+∞上单调递增;在[0,2]上单调递减;当0x =时,()f x 有极大值,极大值为(0)0f =; 当2x =时, ()f x 有极小值,极小值为(2)4f =-. 2. 试证方程sin x = x 只有一个根.证: 显然0x =是方程sin x x =得一个根(亦可将()sin f x x x =-运用零点定理).令()sin f x x x =-,则()cos 10f x x '=-≤,而()0f x '=的点不是单调区间的分界点,故()f x 在(,)-∞+∞内单调下降,所以()f x 在(,)-∞+∞内只有一个零点,即方程sin x x =只有0x =一个根.　3. 已知()([0,))f x C ∈+∞，若f (0) = 0, f ′(x )在[0,)+∞内存在且单调增加，证明()f x x在［0,＋∞)内也单调增加.　解: 0 x ∀>,由题意知()f x 在[]0,x 上满足拉格朗日中值定理的条件,利用拉格朗日中值定理得,(0,) x ξ∃∈,使w ww .t tl ea rn .n et()(0)()f x f xf ξ'-=, 因 ()f x '在[0,)+∞单调增加,且(0)0f =,所以()()()f x xf xf x ξ''=≤ 即 ()()0xf x f x '-≥令 ()()(0) f x F x x x=>,则 2()()()0xf x f x F x x '-'=≥ 所以()F x 单调递增,即 ()f x x在(0,)+∞内单调增加.4. 证明下列不等式：　(1) 1+12xx ＞0； (2)2ln(1)(0)2 x x x x x -<+<>.证: (1) 令1()12f x x =+,则1()(12f x '=, 当 0x >时1,()0f x '<>即()f x 单调递增,从而 ()(0)0f x f >=,故112x +>. (2) 令 2()ln(1)2x f x x x =+-+,则 21()111x f x x x x '=-+=++ 当 0x >时,有()0f x '>,即()f x 单调递增,从而()(0)0f x f >= ,即2ln(1)2x x x +>-又令 ()ln(1)g x x x =-+,则1()111xg x x x'=-=++ 当 0x >时,()0g x '>,即 ()g x 单调递增,从而()(0)0g x g >=,即ln(1)x x >+.综上所述,当0x >时有2ln(1)2x x x x -<+<.　5. 试问a 为何值时，f (x ) = a sin x +13sin ３x 在x =3π处取得极值?是极大值还是极小值?并求出此极值.　解: ()cos cos3f x a x x '=+w ww .t tl rn et若3πx =为极值点,则cos cos 03ππa +=,所以2a =.又()2sin 3sin 3,()03πf x x x f ''''=--=<故函数在3πx =处取得极大值,极大值为(3πf =.习题4 - 51. 某个体户以每条10元的价格购进一批牛仔裤，设此批牛仔裤的需求函数为402Q P =-,问该个体户应将销售价定为多少时，才能获得最大利润? 解: 利润2()10260400L P PQ Q P P =-=-+-,()460L P P '=-+,令 ()0L P '=得 P =15所以应将销售价定为每条15元,才能获得最大利润.2.设 f (x ) = cx α (c ＞0,0＜α＜1)为一生产函数，其中c 为效率因子，x 为投入量，产品的价格P 与原料价格Q 均为常量，问：投入量为多少时可使利润最大? 解: 依题意,总利润()()()L x Pf x Q x P cx Qx α=-=⋅-则 1()L x Pc xQ αα-'=-令 ()0L x '=得 11Q x Pc αα-⎛⎫=⎪⎝⎭所以,投入量为11Q Pc αα-⎛⎫⎪⎝⎭时利润最大.3. 某产品的成本函数为23()156C Q Q Q Q =-+，(1) 生产数量为多少时，可使平均成本最小?(2) 求出边际成本，并验证边际成本等于平均成本时平均成本最小. 解: (1) 2()()156C Q C Q Q Q Q==-+ 令 260()Q C Q '=-=⎡⎤⎣⎦得Q =3 故 生产数量3Q =时,可使平均成本最小. (2) 2()15123MC C Q Q Q '==-+当 3Q =时,15123396MC =-⨯+⨯= 2()156336C Q =-⨯+=w ww .t tl ea rn .n et即边际成本等于平均成本时平均成本最小. 4. 已知某厂生产Q 件产品的成本为C ＝25000＋2000Q ＋1402Q （元). 问：(1) 要使平均成本最小，应生产多少件产品?(2) 若产品以每件5000元售出，要使利润最大，应生产多少件产品? 解: (1) 平均成本 250001()200040C Q Q Q =++ 边际成本1()200020C Q Q '=+. 当()()C Q C Q '=时,平均成本最小,由()()C Q C Q '=即2500011200020004020Q Q Q ++=+ 得1000Q =(负值不合题意已舍去).所以要使平均成本最小,应生产1000件产品. (2)221()5000()500025000200040130002500040L Q Q C Q Q Q Q Q Q =-=---=-+-令 1()3000020L Q Q '=-+=, 得60000Q =(件) 所以应生产60000件产品.5. 某厂全年消耗(需求)某种钢材5170吨，每次订购费用为5700元，每吨钢材单价为2400元，每吨钢材一年的库存维护费用为钢材单价的13.2%，求： (1) 最优订购批量； (2) 最优批次； (3) 最优进货周期； (4) 最小总费用.解: 由题意 215170,5700,1,240013.2%316.8 R C T C ====⨯= 则(1)最优订购批量*431.325q === (2)最优批次 5170*12*431.325R n q ==≈(次) w ww .t tl ea rn .n et(3)最优进货周期 36530.452*12T t n ===(天) (4)最小总费用*136643.9E ==≈(元)6. 用一块半径为R 的圆形铁皮，剪去一圆心角为α的扇形后，做成一个漏斗形容器，问α为何值时，容器的容积最大?解: 设漏斗的底面半径为r ,高为h ,为了计算方便令2ϕπα=-,则2,,2ππR r R r h ϕϕ==== 漏斗的容积2322123(83)πππV hr V ϕϕ==<<'=-令 0V '=得10ϕ=(舍之),2ϕ=,34222237),40,9πππV V ϕϕϕ''=-+-⎫''=-<⎪⎭故当ϕ=时漏斗得容积最大.由2πϕα=-得2π2ππ3α=-=-, 所以,当2ππ3α=-时,容积最大. 7. 工厂生产出的酒可即刻卖出，售价为k ；也可窖藏一个时期后再以较高的价格卖出.设售价V 为时间t 的函数V = k ，(k ＞0)为常数.若贮存成本为零，年利率为r ，则应何时将酒售出方获得最大利润(按连续复利计算). 解: ()e rtrtA t k k -=⋅=令()0rt r A t k ⎫'-==⎪⎭得214t r = 所以,应窖藏214r 时以后售出可获得最大利润. 8. 若火车每小时所耗燃料费用与火车速度的三次方成正比，已知速度为20km/h ，每小时的w w.t tl ea rn .n et燃料费用40元，其他费用每小时200元，求最经济的行驶速度. 解: 设火车每小时所耗燃料费为Q ,则 3Q kv = (k 为比例常数) 依题意得 34020k =⋅, 解得 1200k =, 又设火车行驶()km s 后,所耗费用为, 32200(200)()s E kv kv s v v=+⋅=+ 令 2200()0100v E s v'=-=, 得27.14v =≈ (km/h), 所以,最经济得行驶速度为27.14 km/h.习题 4-61. 讨论下列函数的凸性，并求曲线的拐点：(1) y =2x －3x ； (2) y = ln(1+2x )；(3) y = x e x； (4) y = 4(1)x +＋e x；(5) y =2(3)x x +； (6) y=arctan e x. 解: (1)223,126,0.3令 得 y x x y x y x '=-''''=-==当13x <时,0y ''>; 当13x >时,0y ''<,且12()327f = 所以,曲线23y x x =-在1(,3-∞内是下凸的,在1(,)3+∞内是上凸的,点12(,)327是曲线的拐点.(2) 222222222(1)222(1),1(1)(1)x x x x x y y x x x +-⋅--'''===+++, 令0y ''=得,121,1x x =-=,这两点将定义域(,)-∞+∞分成三个部分区间,列表考察各部分区间上二阶导数得符号.x (,1)-∞-1-(1,1)-1(1,)+∞y' -0 + 0 -y上凸ln 2 下凸ln 2上凸所以,曲线2ln(1)y x =+在(,1)-∞-及(1,)+∞内是上凸的,在(1,1)-内是下凸的,点w ww .t tl ea rn .n et(1,ln 2)±是曲线的拐点.(3) 324(1),12(1)0x xy x e y x e '''=++=++> 所以,曲线在定义域(,)-∞+∞内处处下凸,没有拐点.(4) 343212,(3)(3)x x y y x x --'''==++,令 0y ''=得6x = 当 6x <时,0y ''<,当6x >时,0y ''>;又2(6)27f =,函数的定义域为(,3)(3,)-∞--+∞ ;所以曲线在(,3),(3,6)-∞--内上凸,在(6,)+∞内下凸,点2(6,)27是拐点. (6)arctan 2arctan arctan arctan 2222221112(12)(1)(1)(1)x x x x y e x x x e y e e x x x '=⋅+-''=⋅-⋅=+++令 0y ''= 得 12x =当 12x <时,0y ''>,当12x >时,0y ''<,且 1arctan 21(2e f =,所以曲线在1(,)2-∞内向下凸,在1(,)2+∞内向上凸,点1arctan 21(,)2e 是拐点.2. 利用函数的凸性证明下列不等式：(1)e e 2x y+＞2e x y+， x ≠y ; (2) x ln x +y ln y ＞(x +y )ln2x y+,x ＞0,y ＞0,x ≠y .证: (1) 令()e x f x =,则()e x f x '=,()0e xf x ''=>,所以函数()f x 的曲线在定义域(,)-∞+∞内是严格下凸的,由曲线下凸的定义有: ()(),()()22x y f x f y x y f x y ++∀≠<≠ 即 22e e ex y x y ++< 即 2()2e e e x yx yx y ++>≠.w ww .t tl ea rn .n et(2) 令()ln f x x x =,则1()1ln ,()f x x f x x'''=+=当 0x >时,恒有()0f x >,所以()f x 的曲线在(0,)+∞内是严格下凸的,由曲线下凸的定义有, 0,0,,x y x y ∀>>≠有()()()22f x f y x y f ++>即ln ln ()ln222x x y x y x y+++> 即 ln ln ()ln 2x yx x y y x y ++>+.3. 当a ，b 为何值时，点(1，3)为曲线y =a 3x +b 2x 的拐点. 解: 因为32y ax bx =+是二阶可导的,所以在拐点处0y ''=,而 232,62y ax bx y ax b '''=+=+ 所以 620a b +=又拐点(1,3)应是曲线上的点,所以3a b +=解方程6203a b a b +=⎧⎨+=⎩ 得 39,22a b =-=所以当39,22a b =-=时,点(1,3)为曲线32y ax bx =+的拐点. 4. 求下列曲线的渐近线：(1) y = ln x ; (2)y =22x -; (3) y = 23x x -； (4) y = 221x x -.解: (1) 0lim lim ln x x y x ++→→==-∞,所以ln y x =有垂直渐近线 0x =. 又 lim x y →+∞=+∞,但1ln lim limlim 01x x x y xx y x x→+∞→+∞→+∞====,lim (0)x y x →+∞-⋅=∞, 所以不存在水平或斜渐近线.(2) 220x x -=,所以有水平渐近线0y =,又22lim 0x x x y x -→∞→∞== ,所以没有斜渐近线,w ww .t tl ea rn .n et又函数22x y -=没有间断点,因而也没有垂直渐近线.(3) 221limlim 0331x x xxx x →∞→∞==--,所以有水平渐近线0y =,又函数23x y x ==-有两个间断点x x ==,且22,,33x x x x x x=∞=∞--所以有两条垂直渐近线x =x =又 21lim lim 3x x y x x →∞→∞==∞-,所以没有斜渐近线.(4) 2lim lim 21x x x y x →∞→∞==∞- ,所以没有水平渐近线,又 函数221x y x =-有间断点12x =,且212lim 21x x x →=∞-,所以有垂直渐近线12x =.又 1limlim 212x x y x x x →∞→∞==- 2111lim()lim()lim 22122(21)4x x x x x y x x x x →∞→∞→∞-=-==--所以有斜渐近线1124y x =+. 5.作出下列函数的图形：(1) f (x ) =21xx+； (2) ()2arctan f x x x =- (3) ()2,(0,)e xf x x x -=∈+∞. 解: (1) (i) 定义域为(,)-∞+∞.()()f x f x -=- ,故曲线关于原点对称.(ii) 21lim limlim012x x x x y x x→∞→∞→∞===+ ,故曲线有渐近线0y =. (iii) 222222121,(1)(1)x x x x y x x +-⋅-'==++22223322423232(1)(1)2(1)222442(3)(1)(1)(1)x x x x x x x x x x x y x x x -+--⋅+⋅---+-''===+++, w ww .t tl ea rn .n et令0y '=即210x -=得驻点1x =±,又使0y ''=的点为0,x =.作图如下:图4-1(2) (i) 定义域为(,)-∞+∞.又 ()arctan y x x x y -=-+=-,故为奇函数.(ii) 2arctan lim ,limlim (1)1,x x x y xy x x→±∞→±∞→±∞=∞=-=πlim ()lim (2arctan )(2)()π2x x y x x →±∞→±∞-=-=-±= 所以有渐近线πy x = .(iii) 222211,11x y x x -'=-=++2222222(1)(1)24,(1)(1)x x x x xy x x +--⋅''==++令 0y '=得驻点1x =±,又使0y ''=的点为0x =. 列表如下:w ww .t tl e a rn .e图4-2(3) (i) 定义域为(,)-∞+∞,且()((,))f x C ∈-∞+∞. (ii) ()2(1),()2(2),e e xxf x x f x x --'''=-=-由()0f x '=得1x =,由()0f x ''=得2x =,把定义域分为三个区间 (,1),(1,2),(2,);-∞+∞(iv) lim ()0x f x →+∞=,故曲线()y f x =有渐近线0y =,lim ()x f x →+∞=-∞.(v) 补充点(0,0)并连点绘图,如图所示:图4-3w wl ea rn .n et。