【推荐】初三下学期锐角三角函数知识点总结及经典例题
- 格式:pdf
- 大小:231.36 KB
- 文档页数:7
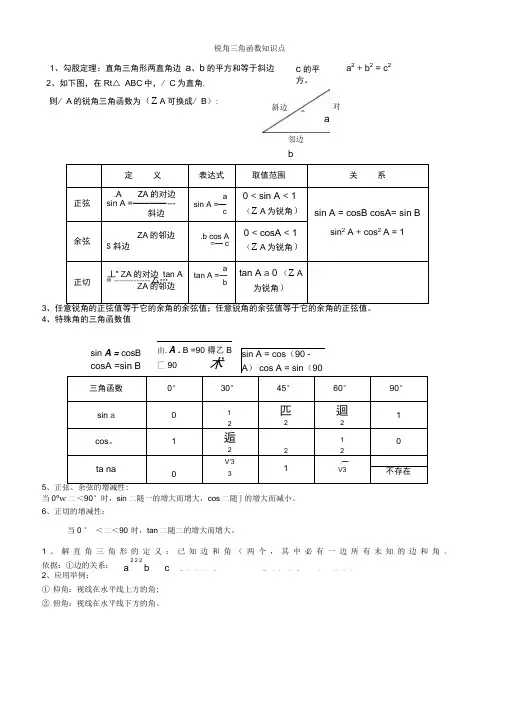
2、如下图,在Rt△ ABC中,/ C为直角,定义表达式取值范围关系正弦.A ZA的对边sin A =————---斜边asin A =—c0 < sin A < 1(Z A为锐角)sin A = cosB cosA= sin Bsin2 A + cos2 A = 1余弦ZA的邻边S斜边.b cos A=—c0 < cosA < 1(Z A为锐角)正切丄“ Z A的对边tan A= ------------- 厶…,Z A的邻边atan A =—btan A a 0 (Z A为锐角)34、特殊角的三角函数值三角函数0°30°45°60°90°sin a012匹2迴21cos。
1逅2212ta naV'31.—03V3不存在5当0°w二<90°时,sin二随一的增大而增大,cos二随J的增大而减小。
6、正切的增减性:当0 ° <二<90°时,tan二随二的增大而增大。
1、解直角三角形的定义:已知边和角(两个,其中必有一边所有未知的边和角。
依据:①边的关系:2 2 2a b c;②角的关系:A+B=90°;③边角关系:三角函数的定义。
2、应用举例:①仰角:视线在水平线上方的角;②俯角:视线在水平线下方的角。
锐角三角函数知识点1、勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方。
a2+ b2 = c2则/ A的锐角三角函数为(Z A可换成/ B):sin A = cosB cosA =sin B 由.A .B =90 得乙B匚90 术sin A = cos(90 -A) cos A = sin(90斜边a邻边b对5、如图,在厶 ABC 中,/ ACB=90 , CD! AB 于 D,若AC二 5 6 , AB =5,则 tan / ACD 的值为()③ 坡面的铅直高度 h 和水平宽度I 的比叫做坡度(坡比)。
![最新初三年级锐角三角函数知识点总结、典型例题、练习[精选]](https://uimg.taocdn.com/78ed1ec4ec3a87c24128c427.webp)
最新初三年级锐角三角函数知识点总结、典型例题、练习[精选]锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方. 222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值.4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小. 6、正切的增减性:当0°<α<90°时,tan α随α的增大而增大,7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角. 依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))90cos(sin A A -︒=)90sin(cos A A -︒=BA cos sin =BA sin cos =A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba c8、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即hil=.坡度一般写成1:m的形式,如1:5i=等.把坡面与水平面的夹角记作α(叫做坡角),那么tanhilα==.3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角.如图3,OA、OB、OC、OD的方向角分别是:45°、135°、225°.4、指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角.如图4,OA、OB、OC、OD的方向角分别是:北偏东45°(东北方向) , 南偏东45°(东南方向), 南偏西45°(西南方向), 北偏西45°(西北方向).类型一:直角三角形求值例1.已知Rt△ABC中,,12,43tan,90==︒=∠BCAC求AC、AB和cos B.例2.已知:如图,⊙O的半径OA=16cm,OC⊥AB于C点,⋅=∠43sin AOC求:AB及OC的长.:i h l=hlα例3.已知A∠是锐角,178sin=A,求Acos,Atan的值对应训练:1.在Rt△ABC中,∠ C=90°,若BC=1,AB=5,则tan A的值为A.55B.255C.12D.22.在△ABC中,∠C=90°,sin A=53,那么tan A的值等于().A.35B.45C.34D.43类型二. 利用角度转化求值:例1.已知:如图,Rt△ABC中,∠C=90°.D是AC边上一点,DE⊥AB于E点.DE∶AE=1∶2.求:sin B、cos B、tan B.例2.如图,直径为10的⊙A经过点(05)C,和点(00)O,,与x轴的正半轴交于点D,B是y 轴右侧圆弧上一点,则cos∠OBC的值为()A.12B.32C.35D.45对应训练:3.如图,O⊙是ABC△的外接圆,AD是O⊙的直径,若O⊙的半径为32,2AC=,则sin B的值是()DCBAOyx第8题图A.23B.32C.34D.434. 如图4,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处.已知8AB=,10BC=,AB=8,则tan EFC∠的值为 ( )A.34B.43C.35D.45A DECBF类型三. 化斜三角形为直角三角形例1 如图,在△ABC中,∠A=30°,∠B=45°,AC=23,求AB的长.例2.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.求:sin∠ABC的值.对应训练1.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC 的周长.(结果保留根号)2.已知:如图,△ABC中,AB=9,BC=6,△ABC的面积等于9,求sin B.3. △ABC中,∠A=60°,AB=6 cm,AC=4 cm,则△ABC的面积是A.23 cm2B.43 cm2C.63 cm2D.12 cm2类型四:利用网格构造直角三角形例1 如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为()A.12B.55C.1010D.255对应训练:1.如图,△ABC的顶点都在方格纸的格点上,则sin A =_______.2.正方形网格中,AOB∠如图放置,则tan AOB∠的值是()A.55B.2 55C.12D. 2类型五:取特殊角三角函数的值1).计算:︒-︒+︒60tan45sin230cos2.2)计算:︒-︒+︒30cos245sin60tan2.3)计算:3-1+(2π-1)0-33tan30°-tan45°4).计算:30tan2345sin60cos221⎪⎪⎭⎫⎝⎛︒-︒+︒+.5).计算:tan45sin301cos60︒+︒-︒;CBAABO类型六:解直角三角形的实际应用例1.如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C 处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是()A.200米B.200米C.220米D.100()米例2.已知:如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离m 23=DE,求点B到地面的垂直距离BC.例3如图,一风力发电装置竖立在小山顶上,小山的高BD=30m.从水平面上一点C测得风力发电装置的顶端A的仰角∠DCA=60°,测得山顶B的仰角∠DCB=30°,求风力发电装置的高AB的长.对应训练:1..如图,小聪用一块有一个锐角为30︒的直角三角板测量树高,已知小聪和树都与地面垂直,且相距33米,小聪身高AB为1.7米,求这棵树的高度.2.如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为()ABCDEA . 10米B . 10米C . 20米D .米类型七:三角函数与圆:例1. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与x 轴的正半轴交于点D ,B 是y轴右侧圆弧上一点,则cos∠OBC 的值为( ) A .12 B .32 C .35D .45例2. 已知:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接AC 与⊙O 交于点D, (1) 求证:∠AOD=2∠C (2) 若AD=8,tanC=34,求⊙O 的半径.对应训练:1.如图,DE 是⊙O 的直径,CE 与⊙O 相切,E 为切点.连接CD 交⊙O 于点B,在EC 上取一个点F,使EF=BF.(1)求证:BF 是⊙O 的切线; (2)若54C cos , DE =9,求BF 的长.DB OACD C B A Oyx第8题图CFDOBECB A作业: 1.已知21sin =A ,则锐角A 的度数是( ) A .75︒B .60︒C .45︒D .30︒ 2.在Rt△ABC 中,∠ C =90°,若BC =1,AB =5,则tan A 的值为( )A .55 B .255 C .12D .2 3.在△ABC 中,∠C =90°,sin A=53,那么tan A 的值等于( ).A .35B . 45C . 34D . 434. 若sin α=32,则锐角α= . 5.将∠α放置在正方形网格纸中,位置如图所示,则tan α的值是A .21B .2C .25D .5526.如图,AB 为⊙O 的弦,半径OC ⊥AB 于点D ,若OB 长为10,3cos 5BOD ∠=, 则AB 的长是A . 20 B. 16 C. 12 D. 87.在Rt△ABC 中,∠C=90°,如果cosA=54,那么tanA 的值是( ) A .53 B .35 C .43 D .348. 如图,在△ABC 中,∠ACB =∠ADC= 90°,若sin A =35,则cos∠BCD 的值为 .9.计算:︒-︒+︒60tan 45sin 230cos 210.计算︒+︒-︒-︒45tan 30tan 345cos 260sin 2.αDCBA11.计算:22sin 604cos 30+sin 45tan 60-⋅oooo.12.已知在Rt△ABC 中,∠C=90°,a=64,b=212.解这个直角三角形13. 已知:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接AC 与⊙O 交于点D, (3) 求证:∠AOD=2∠C (4) 若AD=8,tanC=34,求⊙O 的半径.14.如图,某同学在楼房的A 处测得荷塘的一端 B 处的俯角为30︒,荷塘另一端D 处C 、B 在 同一条直线上,已知32AC =米,16CD =米, 求荷塘宽BD 为多少米?(结果保留根号)15.如图,一艘海轮位于灯塔P 的南偏东45°方向,距离灯塔100海里的A 处,它计划沿正北方向航行,去往位于灯塔P 的北偏东30°方向上的B 处.(1)B 处距离灯塔P 有多远?(2)圆形暗礁区域的圆心位于PB 的延长线上,距离灯塔200海里的O 处.已知圆形暗礁区域的半径为50海里,进入圆形暗礁区域就有触礁的危险.请判断若海轮到达B 处是否有触礁的危险,并说明理由.DBOAC。
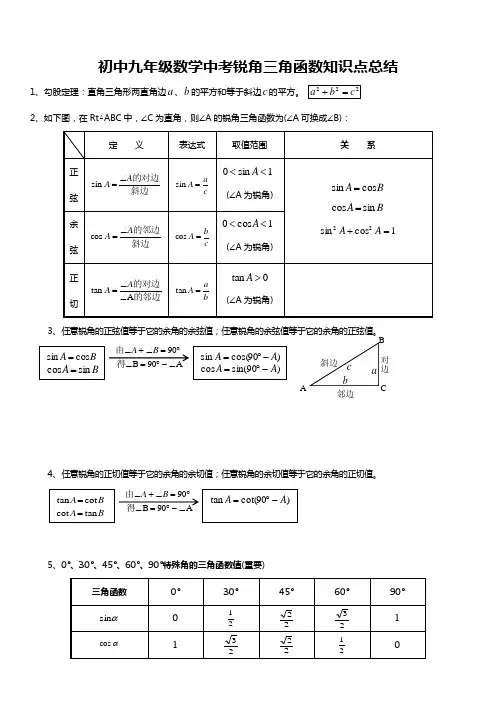
初中九年级数学中考锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)A 90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边 CA 90B 90∠-︒=∠︒=∠+∠得由B A6、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、余切的增减性:当0°<α<90°时,tan α随α的增大而增大,8、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)9、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即hi l=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。

锐角三角函数:知识点一:锐角三角函数的定义:一、锐角三角函数定义:在Rt△ABC 中,∠C=900, ∠A、∠B、∠C 的对边分别为a、b、c,则∠A 的正弦可表示为:sinA= ,∠A 的余弦可表示为cosA=∠A 的正切:tanA= ,它们弦称为∠A 的锐角三角函数【特别提醒:1、sinA、∠cosA、tanA 表示的是一个整体,是两条线段的比,没有,这些比值只与有关,与直角三角形的无关2、取值范围<sinA< cosA< tanA> 】例1.如图所示,在Rt△ABC 中,∠C=90°.①sin A =(②cos A =()=,对对)=,对对第 1 题图sin B =(cos B =()=;对对)=;对对③tan A =( )=,∠A对对对例2. 锐角三角函数求值:tan B =∠B对对对=.( )在Rt△ABC 中,∠C=90°,若a=9,b=12,则c=,sin A=,cos A=,tan A=,sin B=,cos B=,tan B=.例3.已知:如图,Rt△TNM 中,∠TMN=90°,MR⊥TN 于R 点,TN=4,MN=3.求:sin∠TMR、cos∠TMR、tan∠TMR.典型例题:类型一:直角三角形求值5 1. 已知 Rt △ABC 中, ∠C = 90︒, tan A = 3, BC = 12, 4求AC 、AB 和 cos B .2. 已知:如图,⊙O 的半径 OA =16cm ,OC ⊥AB 于 C 点, sin ∠AOC = 3⋅4求:AB 及 OC 的长.3. 已知:⊙O 中,OC ⊥AB 于 C 点,AB =16cm , sin ∠AOC = 3⋅5(1) 求⊙O 的半径 OA 的长及弦心距 OC ; (2) 求 cos ∠AOC 及 tan ∠AOC .4. 已知∠A 是锐角, sin A = 8 17,求cos A , tan A 的值对应训练:(西城北)3.在 Rt △ABC 中,∠ C =90°,若 BC =1,AB = ,则 tan A 的值为A.55B. 2 55C.12D .2(房ft )5.在△ABC 中,∠C =90°,sin A= 3,那么 tan A 的值等于().5A. 3 5B. 4 5C. 3 4D.4 3类型二. 利用角度转化求值:1. 已知:如图,Rt △ABC 中,∠C =90°.D 是 AC 边上一点,DE ⊥AB 于 E 点.DE ∶AE =1∶2.求:sin B 、cos B 、tan B .32.如图,直径为10的⊙A 经过点C(0对5) 和点O(0对0) ,与x 轴的正半轴交于点D,B 是y 轴右侧圆弧上一点,则cos∠OBC 的值为()1 3A.B.2 2C.3D.45 5yCAO D xB图 8图图3.(2009·孝感中考)如图,角的顶点为O,它的一边在x 轴的正半轴上,另一边OA 上有一点P(3,4),则sin=.4.(2009·庆阳中考)如图,菱形ABCD 的边长为10cm,DE⊥AB,sin A =,则这个菱形5 的面积= cm2.5.(2009·齐齐哈尔中考)如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,若⊙O 的3半径为2,AC = 2 ,则sin B 的值是()2 3 3 4A.B.C.D.3 24 3F2 3 6. 如图 4,沿 AE 折叠矩形纸片 ABCD ,使点 D 落在 BC 边的点 F 处.已知 AB = 8 , BC = 10 ,AB=8,则 tan ∠EFC 的值为 ( )ADE 3 4 34 BCA.B.C.D.43557. 如图 6,在等腰直角三角形∆ABC 中, ∠C = 90︒ , AC = 6 , D 为 AC 上一点,若tan ∠DBA = 15,则 AD 的长为()A.B . 2C.1 D . 28. 如图 6,在 Rt △ABC 中,∠C =90°,AC =8,∠A 的平分线 AD = 1633求 ∠B 的度数及边 BC 、AB 的长.ACDB图 6类型三. 化斜三角形为直角三角形例 1 (2012•安徽)如图,在△ABC 中,∠A=30°,∠B=45°,AC=2 ,求 AB 的长.例 2.已知:如图,△ABC 中,AC =12cm ,AB =16cm , sin A = 1⋅3(1)求 AB 边上的高 CD ; (2)求△ABC 的面积 S ; (3)求 tan B .23 33例3.已知:如图,在△ABC 中,∠BAC=120°,AB=10,AC=5.求:sin∠ABC 的值.对应训练1.(2012•重庆)如图,在Rt△ABC 中,∠BAC=90°,点D 在BC 边上,且△ABD 是等边三角形.若AB=2,求△ABC 的周长.(结果保留根号)2.已知:如图,△ABC 中,AB=9,BC=6,△ABC 的面积等于9,求sin B.3.ABC 中,∠A=60°,AB=6 cm,AC=4 cm,则△ABC 的面积是A.2 cm2B.4 cm2C.6 cm2D.12 cm2类型四:利用网格构造直角三角形例1 (2012•内江)如图所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为()1 5A.B.2 5C.1010D.2 55对应练习:1.如图,△ABC 的顶点都在方格纸的格点上,则sin A = .CA B2.如图,A、B、C 三点在正方形网络线的交点处,若将∆ABC 绕着点A 逆时针旋转得到∆AC' B',则tan B' 的值为1 1 1A. B. C.4 3 2D. 13.正方形网格中,∠AOB 如图放置,则tan∠AOB 的值是()A.52B.51C. D. 22特殊角的三角函数值锐角30°45°60°sincostan当时,正弦和正切值随着角度的增大而余弦值随着角度的增大而例1.求下列各式的值.(昌平)1).计算:2 cos 30︒+ 2 sin 45︒- tan 60︒.(朝阳)2)计算:tan 60︒+ sin2 45︒- 2 cos 30︒.(2009·黄石中考)计算:3-1+(2π-1)0-3tan30°-tan45°3AO B33(石景ft)4.计算:⎛+ 2 cos 60︒+ sin 45︒-⎝⎫0tan 30︒⎪.2 ⎭tan 45︒+ sin 30︒ (通县)5.计算:;1- cos 60︒例2.求适合下列条件的锐角.(1)cos=12 (2)tan=3(3) s in 2=22(4) 6 cos(- 16 ) = 3(5)已知为锐角,且tan(+300)=,求tan的值(6)在∆ABC 中,若cos A -+(sin B -2)2= 0 ,∠A,∠B 都是锐角,求∠C 的度数.2例3. 三角函数的增减性1.已知∠A 为锐角,且sin A < 1,那么∠A 的取值范围是2A. 0°< A < 30°B. 30°< A <60°C. 60°< A < 90°D. 30°< A < 90°2.已知A 为锐角,且cos A < sin 300,则()A. 0°< A < 60°B. 30°< A < 60°C. 60°< A < 90°D. 30°< A < 90°例4. 三角函数在几何中的应用1.已知:如图,在菱形ABCD 中,DE⊥AB 于E,BE=16cm,sin A =12⋅ 13123123求此菱形的周长.2. 已知:如图,Rt △ABC 中,∠C =90°, AC = BC=于 D 点,求:(1) ∠BAD ;(2) sin ∠BAD 、cos ∠BAD 和 tan ∠BAD .,作∠DAC =30°,AD 交 CB3. 已知:如图△ABC 中,D 为 BC 中点,且∠BAD =90°, tan ∠B =CAD 、tan ∠CAD .1 ,求:sin ∠CAD 、cos ∠34. 如图,在 Rt △ABC 中,∠C=90°, sin B = 3,点 D 在 BC 边上,DC= AC = 6,求 tan ∠BAD5的值.ABDC5.(本小题5 分)如图,△ABC 中,∠A=30°, tan B =2C, AC = 4 .求 AB 的长.AB解直角三角形:3 333 1.在解直角三角形的过程中,一般要用的主要关系如下(如图所示):在 Rt △ABC 中,∠C =90°,AC =b ,BC =a ,AB =c ,①三边之间的等量关系: . ②两锐角之间的关系: .③边与角之间的关系:sin A = cos B =; cos A = sin B = ; tan A =1 =tan B1;tan A= tan B =.④直角三角形中成比例的线段(如图所示). 在 Rt △ABC 中,∠C =90°,CD ⊥AB 于 D . CD 2= ;AC 2= ; BC 2= ;AC ·BC = .类型一例 1.在 Rt △ABC 中,∠C =90°.(1)已知:a =35, c = 35 ,求∠A 、∠B ,b ;(2)已知: a = 2 , b = 2 ,求∠A 、∠B ,c ;(3)已知: sin A =2 , c = 6 ,求 a 、b ;3(4)已知: tan B = 3, b = 9, 2求 a 、c ;(5)已知:∠A =60°,△ABC 的面积 S = 12 3, 求 a 、b 、c 及∠B .2例2.已知:如图,△ABC 中,∠A=30°,∠B=60°,AC=10cm.求AB 及BC 的长.例3.已知:如图,Rt△ABC 中,∠D=90°,∠B=45°,∠ACD=60°.BC=10cm.求AD 的长.例4.已知:如图,△ABC 中,∠A=30°,∠B=135°,AC=10cm.求AB 及BC 的长.类型二:解直角三角形的实际应用仰角与俯角:例1.(2012•福州)如图,从热气球C 处测得地面A、B 两点的俯角分别是30°、45°,如果此时热气球C 处的高度CD 为100 米,点A、D、B 在同一直线上,则AB 两点的距离是()A.200 米B.200 米C.220 米D.100()米例2.已知:如图,在两面墙之间有一个底端在A 点的梯子,当它靠在一侧墙上时,梯子的顶端在B 点;当它靠在另一侧墙上时,梯子的顶端在D 点.已知∠BAC=60°,∠DAE=45 °.点D 到地面的垂直距离DE 3 2m ,求点 B 到地面的垂直距离BC.例3(昌平)19.如图,一风力发电装置竖立在小ft顶上,小ft的高BD=30m.从水平面上一点C 测得风力发电装置的顶端A 的仰角∠DCA=60°,测得ft顶B 的仰角∠DCB=30°,求风力发电装置的高AB 的长.ADB E例4 .如图,小聪用一块有一个锐角为30 的直角三角板测量树C高,已知小聪和树都与地面垂直,且相距3AB 为1.7 米,求这棵树的高度.米,小聪身高例5.已知:如图,河旁有一座小ft,从ft顶A 处测得河对岸点C 的俯角为30°,测得岸边点D 的俯角为45°,又知河宽CD 为50m.现需从ft顶A 到河对岸点C 拉一条笔直的缆绳AC,求ft的高度及缆绳AC 的长(答案可带根号).例5.(2012•泰安)如图,为测量某物体AB 的高度,在D 点测得A 点的仰角为30°,朝物体AB 方向前进20 米,到达点C,再次测得点A 的仰角为60°,则物体AB 的高度为()C.20 米D.米例6.(2012•益阳)超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A 处,离益阳大道的距离(AC)为30 米.这时,一辆小轿车由西向东匀速行驶,测得此车从B 处行驶到C 处所用的时间为8 秒,∠BAC=75°.(1)求B、C 两点的距离;(2)请判断此车是否超过了益阳大道60 千米/小时的限制速度?(计算时距离精确到1 米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732,≈1.732,60 千米/小时≈16.7 米/秒)3A.10 米B.10 米33 3 3类型四. 坡度与坡角例.(2012•广安)如图,某水库堤坝横断面迎水坡 AB 的坡比是 1: ,堤坝高 BC=50m ,则应水坡面 AB 的长度是( ) A .100mB .100 mC .150mD .50 m类型五. 方位角1. 已知:如图,一艘货轮向正北方向航行,在点 A 处测得灯塔 M 在北偏西 30°,货轮以每小时 20 海里的速度航行,1 小时后到达 B 处,测得灯塔 M 在北偏西 45°,问该货轮 继续向北航行时,与灯塔 M 之间的最短距离是多少?(精确到 0.1 海里,1.732 )2.(2012•恩施州)新闻链接,据[侨报网讯]外国炮艇在南海追袭中国渔船被中国渔政逼退2012 年 5 月 18 日,某国 3 艘炮艇追袭 5 条中国渔船.刚刚完成黄岩岛护渔任务的“中国渔政 310” 船人船未歇立即追往北纬 11 度 22 分、东经 110 度 45 分附近海域护渔,保护 100 多名中国 渔民免受财产损失和人身伤害.某国炮艇发现中国目前最先进的渔政船正在疾速驰救中国渔船,立即掉头离去.(见图 1)324解决问题如图 2,已知“中国渔政 310”船(A )接到陆地指挥中心(B )命令时,渔船(C )位于陆地指挥中心正南方向,位于“中国渔政 310”船西南方向,“中国渔政 310”船位于陆地指挥中心南偏东 60°方向,AB=海里,“中国渔政 310”船最大航速 20 海里/时.根据以上信息,请你求出“中国渔政 310”船赶往出事地点需要多少时间.综合题:三角函数与四边形:(西城二模)1.如图,四边形 ABCD 中,∠BAD=135°,∠BCD=90°,AB=BC=2,6tan ∠BDC= 3.(1) 求 BD 的长; (2) 求 AD 的长.(2011 东一)18.如图,在平行四边形 ABCD 中,过点 A 分别作 AE ⊥BC 于点 E ,AF ⊥CD 于点 F .(1) 求证: ∠BAE =∠DAF ;(2) 若 AE =4,AF =,s in ∠BAE = 53 ,求 CF 的长.5三角函数与圆:1. 如图,直径为 10 的⊙A 经过点C (0对5) 和点O (0对0) ,与 x 轴的正半轴交于点 D ,B 是 y轴右侧圆弧上一点,则 cos ∠OBC 的值为()1 3 A.B .22C .3D . 45 5yC AOD xB图 8图图5 DO4(延庆)19. 已知:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接 AC 与⊙O 交于点 D, (1) 求证:∠AOD=2∠CC4 (2) 若 AD=8,tanC= ,求⊙O 的半径。

锐角三角函数:类型一:直角三角形求值1.已知Rt △ABC 中,,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B .2.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,⋅=∠43sin AOC 求:AB 及OC 的长.3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,⋅=∠53sin AOC(1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC . 4.已知A ∠是锐角,178sin =A ,求A cos ,A tan 的值类型二. 利用角度转化求值:1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点.DE ∶AE =1∶2.求:sin B 、cos B 、tan B .2. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =,AB=8,则tan EFC ∠的值为 ( )A.34 B.43C.35D.45A D ECB F3. 如图6,在等腰直角三角形ABC ∆中,90C ∠=︒,6AC =,D 为AC 上一点,若1tan5DBA∠=,则AD的长为( )A.2 B.2C.1 D.224. 如图6,在Rt△ABC中,∠C=90°,AC=8,∠A的平分线AD=3316求∠B的度数及边BC、AB的长.DABC图6类型三. 化斜三角形为直角三角形例1 (2012•安徽)如图,在△ABC中,∠A=30°,∠B=45°,AC=23,求AB的长.例2.已知:如图,△ABC中,AC=12cm,AB=16cm,⋅=31sin A(1)求AB边上的高CD;(2)求△ABC的面积S;(3)求tan B.例3.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.求:sin∠ABC的值.对应训练1.(2012•重庆)如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)2.已知:如图,△ABC 中,AB =9,BC =6,△ABC 的面积等于9,求sin B .类型四:利用网格构造直角三角形例1 (2012•内江)如图所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为( ) A .12 B .55 C .1010 D .255对应练习:1.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_______.特殊角的三角函数值例1.求下列各式的值..计算:︒-︒+︒60tan 45sin 230cos 2.︒-︒+︒30cos 245sin 60tan 2=. 计算:3-1+(2π-1)0-33tan30°-tan45°= 030tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+= 计算:tan 45sin 301cos 60︒+︒-︒=在ABC ∆中,若0)22(sin 21cos 2=-+-B A ,B A ∠∠,都是锐角,求C ∠的度数.例3. 三角函数的增减性1.已知∠A 为锐角,且sin A <21,那么∠A 的取值范围是 A. 0°< A < 30° B. 30°< A <60° C. 60°< A < 90° D. 30°< A < 90° 2. 已知A 为锐角,且030sin cos <A ,则 ( )CBAA. 0°< A < 60°B. 30°< A < 60°C. 60°< A < 90°D. 30°< A < 90° 例4. 三角函数在几何中的应用1.已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.2.已知:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求:(1)∠BAD ;(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD .3. 已知:如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD .解直角三角形:类型二:解直角三角形的实际应用 仰角与俯角:例1.已知:如图,河旁有一座小山,从山顶A 处测得河对岸点C 的俯角为30°,测得岸边点D 的俯角为45°,又知河宽CD 为50m .现需从山顶A 到河对岸点C 拉一条笔直的缆绳AC ,求山的高度及缆绳AC 的长(答案可带根号).例2.(2012•益阳)超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A 处,离益阳大道的距离(AC )为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B 处行驶到C 处所用的时间为8秒,∠BAC=75°.(1)求B 、C 两点的距离;(2)请判断此车是否超过了益阳大道60千米/小时的限制速度?(计算时距离精确到1米,参考数据:sin75°≈0.9659,cos 75°≈0.2588,tan75°≈3.732,3≈1.732,60千米/小时≈16.7米/秒)类型四. 坡度与坡角例.(2012•广安)如图,某水库堤坝横断面迎水坡AB 的坡比是1:3,堤坝高BC=50m ,则应水坡面AB 的长度是( )A .100mB .1003mC .150mD .503m类型五. 方位角1.已知:如图,一艘货轮向正北方向航行,在点A 处测得灯塔M 在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B 处,测得灯塔M 在北偏西45°,问该货轮继续向北航行时,与灯塔M 之间的最短距离是多少?(精确到0.1海里,732.13≈)综合:1已知,如图,在△ADC 中,90ADC ∠=︒,以DC 为直径作半圆O ,交边AC 于点F ,点B 在CD 的延长线上,连接BF ,交AD 于点E ,2BED C ∠=∠. (1)求证:BF 是O 的切线;(2)若BF FC =,3AE =O 的半径.D O ACF E2.(6分)如图,在△ABC 中,点O 在AB 上,以O 为圆心的圆经过A ,C 两点,交AB 于点D ,已知2∠A +∠B =90 . (1)求证:BC 是⊙O 的切线; (2)若OA =6,BC =8,求BD 的长.3. 已知:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接AC 与⊙O 交于点D,(1) 求证:∠AOD=2∠C(2) 若AD=8,tanC=34,求⊙O 的半径。

初中三角函数知识点总结及典型习题含答案)初三下学期锐角三角函数知识点总结及典型题1.勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方,即a^2+b^2=c^2.2.在直角三角形ABC中,若∠C为直角,则∠A的三角函数为:正弦函数sinA=对边a/斜边c,取值范围为[0,1]。
余弦函数cosA=邻边b/斜边c,取值范围为[0,1]。
正切函数tanA=对边a/邻边b,取值范围为R(实数集)。
3.任意锐角的正弦值等于其余角的余弦值,余弦值等于其余角的正弦值,即sinA=cosB,cosA=sinB,其中A+B=90°。
4.特殊角的三角函数值:30°:sin30°=1/2,cos30°=√3/2,tan30°=1/√3.45°:sin45°=cos45°=√2/2,tan45°=1.60°:sin60°=√3/2,cos60°=1/2,tan60°=√3.6.正弦、余弦的增减性:当0°≤A≤90°时,XXX随A的增大而增大,cosA随A的增大而减小。
7.正切的增减性:当0°<A<90°时,XXX随A的增大而增大。
8.解直角三角形的方法:已知边和角(其中必有一边)→求所有未知的边和角。
依据:①边的关系:a^2+b^2=c^2;②角的关系:A+B=90°;③三角函数的定义。
9.应用举例:仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
坡度:坡面的铅直高度h和水平宽度l的比,用i=h/l表示。
方位角:从某点的指北方向按顺时针转到目标方向的水平角。
方向角:指北或指南方向线与目标方向线所成的小于90°的水平角。
例1:在直角三角形ABC中,已知∠C=90°,sinA=3/5,求XXX的值。
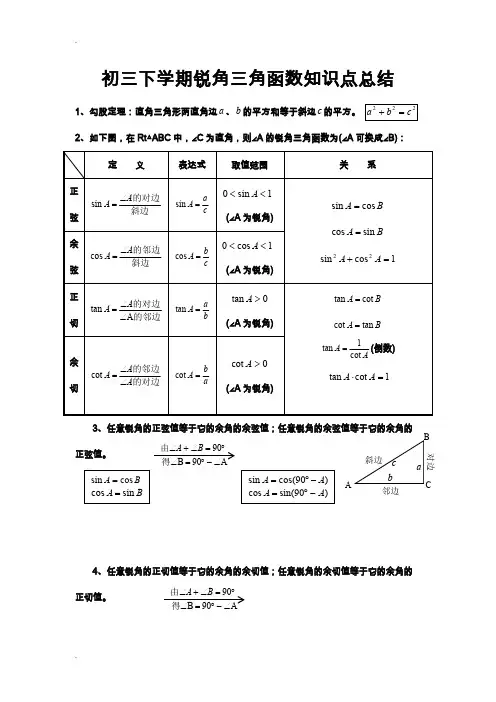

c ,则有: s in A = a = cos B , cos A = = sin B , tan A = ,这就是锐角三角函数所以 cos B = sin(90 - B) = sin A = .在 Rt△BCD 中, cos B = ,所以 = ., cos A = , =(sin 2A 、cos 2A 分别表示 sin A 、cos A 2 2锐角三角函数我们知道,在 Rt△ABC 中,∠C =90°,∠A 、∠B 、∠C 的对边分别为 a 、b 、b ac c b的定义.根据锐角三角函数的定义,再结合直角三角形的性质,我们可以探索出锐角三角函数之间的三个特殊关系.一、余角关系由上面的定义我们已得到 sin A =cos B ,cos A =sin B ,而在直角三角形中,∠A+∠B =90°,即∠B =90°-∠A .因此有:sin A =cos (90°-A ),cos A =sin (90°-A ).应用这些关系式,可以很轻松地进行三角函数之间的转换.例1 如图,在 Rt△ABC 中,∠C =90°,CD ⊥AB 于 D ,已知 sin A ==2,求 BC 的长.解:由于∠A +∠B =90°,12BD 2 1BC BC 2所以 BC =4.二、平方关系a b 由定义知 sin A = c c1 2 ,BD所以 sin 2 A + cos 2 A = a 2 b 2 a 2 + b 2+ c c c 2的平方).又由勾股定理,知 a 2+b 2=c 2,所以 sin 2A +cos 2A = c 2 c 2=1.应用此关系式我们可以进行有关锐角三角函数平方的计算.例 2 计算:sin256°+sin245°+sin234°.=⎪⎪ + 1 = 由定义中 sin A = a, cos A = ,得 = c = ⨯ = = tan A .所以原式 = = =- .5 12 5 12所以 sin B = = .应选(B).5解:由余角关系知 sin56°=cos(90°-56°)=cos34°.所以原式=sin245°+(sin234°+cos234°)⎛ 2 ⎫2 ⎝ 2 ⎭3 2 .三、相除关系b c casin A a c a cos A b c b bc利用这个关系式可以使一些化简求值运算过程变得简单.例 3 已知 α 为锐角,tan α =2,求 3sin α + cos α 4cos α - 5sin α的值.解:因为 tan α = sin α cos α= 2 ,所以 sin α =2cos α ,6cos α + cos α 6 + 1 74cos α - 10cos α 4 - 10 6求三角函数值的方法较多,且方法灵活.是中考中常见的题型.我们可以根据已知条件结合图形选用灵活的求解方法.四、设参数法例 4 如图 △1,在 ABC 中,∠C =90°,如果 t a n A =(A)(B) (C) (D)13 13 12 55 12 ,那么 sin B 等于( )分析:本题主要考查锐角三角函数的定义及直角三角形的有关性质.因为 tan A = a 5 =b 12,所以可设 a =5k ,b =12k (k >0),根据勾股定理得 c =13k ,图 1b 12c 13五、等线段代换法例 5如图 2,小明将一张矩形的纸片 ABC D 沿 C E 折叠,B 点恰好落在 A D 边上,设此点为 F ,若 BA :BC =4:,则 c os∠DCF 的值是______.分析:根据折叠的性质可知 E △B C ≌ EF C ,所以 C F=CB ,又 C D=AB ,AB :BC =4:5, 所以 C D :C F=4:5,图 2=.113911,即=,所以C E=,在Rt△A E C中,tan∠CA E==3=.所以tanα=.C3445所以DB==,所以tanα=,选(A).在Rt D△C F中,c os∠D C F=DC4 CF5六、等角代换法例6如图3,C D是平面镜,光线从A点出发经C D上点E反射后照射到B点,若入射角为α(入射角等于反射角),AC⊥C D,B D⊥C D,垂足分别为C、D,且AC=3,B D=6,C D=11,则tanα的值为()B(A)(B)(C)(D)311119A分析:根据已知条件可得∠α=∠CA E,所以只需求出tan∠CA E.α根据条件可知△A C E∽B DE,所以AC CE3CE=BD ED611-CEC E图3D11311CE11AC39119七、等比代换法例7如图4,在Rt△ABC中,ACB=90,D⊥AB于点D,BC=3,AC=4,设BC D=α,tanα的值为()(A)(B)(C)(D)435分析:由三角形函数的定义知tanα=DB DC,由Rt△C D△B∽Rt ACB,BC33DC AC44图4( :锐角三角函数测试1.比较大小:sin41°________sin42°. 2.比较大小:cot30°_________cot22°. 3.比较大小:sin25°___________cos25°. 4.比较大小:tan52°___________cot52°. 5.比较大小:tan48°____________cot41°. 6.比较大小:sin36°____________cos55°.7、下列命题①sin α 表示角α 与符号 sin 的乘积;② 在△ABC 中,若∠C=90°,则 c=α sinA 成立;③任何锐角的正弦和余弦值都是介于 0 和 1 之间实数.其正确的为()A 、②③B.①②③C.②D. ③8、若 △R t ABC 的各边都扩大 4 倍得到 △R t A ′B ′C ′,那么锐角 A 和锐角 A ′正切值的关系为()A.tanA ′=4tanA B.4tanA ′=tanAC.tanA ′=tanAD.不确定.9(新疆中考题) 1)如图(1)、 2),锐角的正弦值和余弦值都随着锐角的确定而确定, 变化而变化.试探索随着锐角度数的增大.它的正弦值和余弦值变化的规律.(2)根据你探索到的规律,试比较 18°,34°,50°,62°,88°,这些锐角的正弦值的 大小和余弦值的大小。
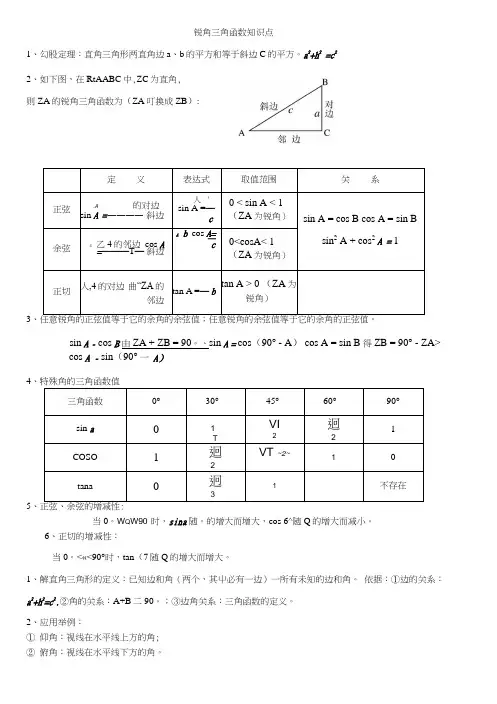
锐角三角函数知识点1、勾股定理:直角三角形两直角边a、b的平方和等于斜边C的平方。
a2+h2 =c22、如下图,在RtAABC中,ZC为直角,则ZA的锐角三角函数为(ZA叮换成ZB):定义表达式取值范围关系正弦.A 的对边sin A =————斜边人asin A =—c0 < sin A < 1(ZA为锐角)sin A = cos B cos A = sin Bsin2 A + cos2A = 1余弦4乙4的邻边cos A=———T—斜边A b cos A=—c0<cosA< 1(ZA为锐角)正切人,4的对边曲“ZA的邻边tan A =—btan A > 0 (ZA为锐角)3sin A - cos B由ZA + ZB = 90。
、sin A = cos(90° - A) cos A = sin B 得ZB = 90° - ZA>cos A - sin(90°一A)4三角函数0°30°45°60°90°sin a01T VI2迴21COSO1迴2VT ~2~10tana0迥31不存在5、正弦、余弦的增减性:当0。
W Q W90°时,sina随。
的增大而增大,cos 6^随Q的增大而减小。
6、正切的增减性:当0。
<«<90°时,tan(7随Q的增大而增大。
1、解直角三角形的定义:已知边和角(两个,其屮必有一边)一所有未知的边和角。
依据:①边的关系:a2+h2=c2.②角的关系:A+B二90。
;③边角关系:三角函数的定义。
2、应用举例:①仰角:视线在水平线上方的角;②俯角:视线在水平线下方的角。
③ 坡面的铅直高度h 和水平宽度I 的比叫做坡度(坡比)o 用字母:表示,,=h即 7。
坡度一般写成1:加的形式,如,=1:5等。
把坡面与水平面 ・h ,i = — = tana的夹角记作Q (叫做坡角),那么 I 。
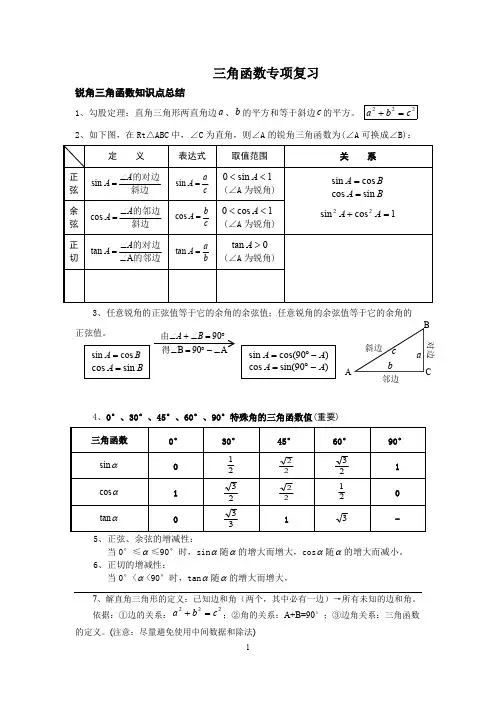
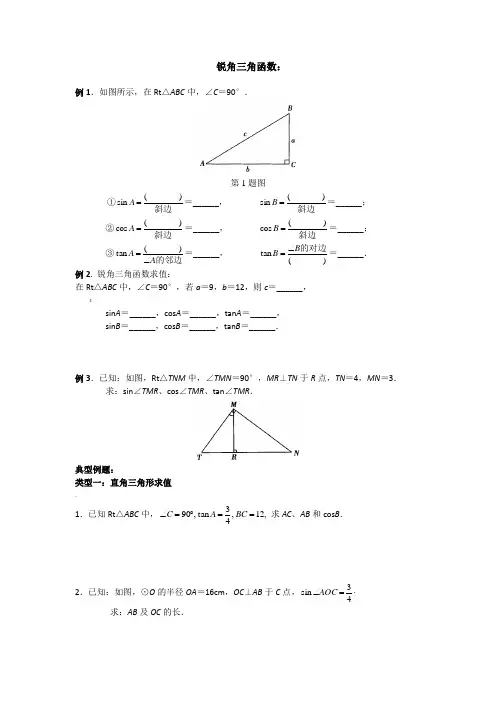
锐角三角函数:例1.如图所示,在Rt △ABC 中,∠C =90°.第1题图①斜边)(sin =A =______, 斜边)(sin =B =______; ②斜边)(cos =A =______,斜边)(cos =B =______;③的邻边A A ∠=)(tan =______,)(tan 的对边B B ∠==______.例2. 锐角三角函数求值:在Rt △ABC 中,∠C =90°,若a =9,b =12,则c =______,$sin A =______,cos A =______,tan A =______, sin B =______,cos B =______,tan B =______.例3.已知:如图,Rt △TNM 中,∠TMN =90°,MR ⊥TN 于R 点,TN =4,MN =3.求:sin ∠TMR 、cos ∠TMR 、tan ∠TMR .典型例题:类型一:直角三角形求值 。
1.已知Rt △ABC 中,,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B .2.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,⋅=∠43sin AOC 求:AB 及OC 的长.3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,⋅=∠53sin AOC(1)求⊙O 的半径OA 的长及弦心距OC ;(2)求cos ∠AOC 及tan ∠AOC .4. 已知A ∠是锐角,178sin =A ,求A cos ,A tan 的值对应训练:3.在Rt △ABC 中,∠ C =90°,若BC =1,AB =5,则tan A 的值为,A .5 B .25 C .12D .2 5.在△ABC 中,∠C =90°,sin A=53,那么tan A 的值等于( ).A .35B . 45C . 34D . 43类型二. 利用角度转化求值:1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点.DE ∶AE =1∶2.求:sin B 、cos B 、tan B .2. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与x 轴的正半轴交于点D ,B 是y 轴右侧圆弧上一点,则cos ∠OBC 的值为( )A.12B.32C.35D.453.如图,角α的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则sinα=.4.如图,菱形ABCD的边长为10cm,DE⊥AB,3sin5A=,则这个菱形的面积= cm2.>5.如图,O⊙是ABC△的外接圆,AD是O⊙的直径,若O⊙的半径为32,2AC=,则sin B的值是()A.23B.32C.34D.436. 如图4,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处.已知8AB=,10BC=,AB=8,则tan EFC∠的值为( )A.34B.43C.35D.45A DECBF7. 如图6,在等腰直角三角形ABC∆中,90C∠=︒,6AC=,D为AC上一点,若DCBAOyx第8题图1tan5DBA∠=,则AD的长为()A.2B.2C.1D.228. 如图6,在Rt△ABC中,∠C=90°,AC=8,∠A的平分线AD=3316求∠B的度数及边BC、AB的长.^DABC图6类型三. 化斜三角形为直角三角形例1 如图,在△ABC中,∠A=30°,∠B=45°,AC=23,求AB的长.例2.已知:如图,△ABC中,AC=12cm,AB=16cm,⋅=31sin A【(1)求AB边上的高CD;(2)求△ABC的面积S;(3)求tan B.例3.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.求:sin∠ABC的值.对应训练1.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号).2.已知:如图,△ABC中,AB=9,BC=6,△ABC的面积等于9,求sin B.3. ABC中,∠A=60°,AB=6 cm,AC=4 cm,则△ABC的面积是3cm23cm23cm2cm2类型四:利用网格构造直角三角形例1 如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为()A.12B.55C.1010D.255@对应练习:1.如图,△ABC的顶点都在方格纸的格点上,则sin A =_______.2.如图,A、B、C三点在正方形网络线的交点处,若将ABC∆绕着点A逆时针旋转得到''BAC∆,则'tan B的值为CBAA.41 B. 31 C.21D. 1$3.正方形网格中,AOB ∠如图放置,则tan AOB ∠的值是( )A . 5 5 B. 2 5 5 C.12 D. 2~特殊角的三角函数值.当 时,正弦和正切值随着角度的增大而 余弦值随着角度的增大而例1.求下列各式的值.(1).计算:︒-︒+︒60tan 45sin 230cos 2.2)计算:︒-︒+︒30cos 245sin 60tan 2.计算:3-1+(2π-1)0-33tan30°-tan45°锐角 sin cos tanABO4.计算:30tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+.5.计算:tan 45sin 301cos 60︒+︒-︒;例2.求适合下列条件的锐角.(1)21cos =α(2)33tan =α !(3)222sin =α(4)33)16cos(6=- α(5)已知为锐角,且3)30tan(0=+α,求αtan 的值*(6)在ABC ∆中,若0)22(sin 21cos 2=-+-B A ,B A ∠∠,都是锐角,求C ∠的度数.例3. 三角函数的增减性 1.已知∠A 为锐角,且sin A <21,那么∠A 的取值范围是 A. 0°< A < 30° B. 30°< A <60° C. 60°< A < 90° D. 30°< A < 90° 2. 已知A 为锐角,且030sin cos <A ,则 ( )A. 0°< A < 60°B. 30°< A < 60°C. 60°< A < 90°D. 30°< A < 90°例4. 三角函数在几何中的应用1.已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.2.已知:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求:(1)∠BAD ;(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD .,3. 已知:如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD .4. 如图,在Rt △ABC 中,∠C=90°,53sin =B ,点D 在BC 边上,DC= AC = 6,求tan ∠BAD 的值.·5.如图,△ABC 中,∠A=30°,3tan B =,43AC =.求AB 的长.DCBAACB解直角三角形:1.在解直角三角形的过程中,一般要用的主要关系如下(如图所示): 在Rt △ABC 中,∠C =90°,AC =b ,BC =a ,AB =c ,①三边之间的等量关系:________________________________. {②两锐角之间的关系:__________________________________.③边与角之间的关系:==B A cos sin ______;==B A sin cos _______;==BA tan 1tan _____;==B A tan tan 1______.④直角三角形中成比例的线段(如图所示).在Rt △ABC 中,∠C =90°,CD ⊥AB 于D .CD 2=_________;AC 2=_________; BC 2=_________;AC ·BC =_________.类型一 @例1.在Rt △ABC 中,∠C =90°.(1)已知:a =35,235=c ,求∠A 、∠B ,b ;(2)已知:32=a ,2=b ,求∠A 、∠B ,c ;(3)已知:32sin =A ,6=c ,求a 、b ; [(4)已知:,9,23tan ==b B 求a 、c ;(5)已知:∠A =60°,△ABC 的面积,312=S 求a 、b 、c 及∠B .…例2.已知:如图,△ABC 中,∠A =30°,∠B =60°,AC =10cm .求AB 及BC 的长.例3.已知:如图,Rt △ABC 中,∠D =90°,∠B =45°,∠ACD =60°.BC =10cm .求AD 的长.例4.已知:如图,△ABC 中,∠A =30°,∠B =135°,AC =10cm .求AB 及BC 的长.*类型二:解直角三角形的实际应用 仰角与俯角: 例1.(2012•福州)如图,从热气球C 处测得地面A 、B 两点的俯角分别是30°、45°,如果此时热气球C 处的高度CD 为100米,点A 、D 、B 在同一直线上,则AB 两点的距离是( )A . 200米B . 200米C . )220米D . 100()米例2.已知:如图,在两面墙之间有一个底端在A 点的梯子,当它靠在一侧墙上时,梯子的顶端在B 点;当它靠在另一侧墙上时,梯子的顶端在D 点.已知∠BAC =60°,∠DAE =45°.点D 到地面的垂直距离m 23=DE ,求点B 到地面的垂直距离BC .例3如图,一风力发电装置竖立在小山顶上,小山的高BD =30m . 从水平面上一点C 测得风力发电装置的顶端A 的仰角∠DCA =60°, 测得山顶B 的仰角∠DCB =30°,求风力发电装置的高AB 的长.!例4 .如图,小聪用一块有一个锐角为30 的直角三角板测量树高,已知小聪和树都与地面垂直,且相距33米,小聪身高AB 为米,求这棵树的高度.例5.已知:如图,河旁有一座小山,从山顶A 处测得河对岸点C 的俯角为30°,测得岸边点D 的俯角为45°,又知河宽CD 为50m .现需从山顶A 到河对岸点C 拉一条笔直的缆绳AC ,求山的高度及缆绳AC的长(答案可带根号).…例5.(2012•泰安)如图,为测量某物体AB 的高度,在D 点测得A 点的仰角为30°,朝物体AB 方向前进20米,到达点C ,再次测得点A 的仰角为60°,则物体AB 的高度为( )A . 10米B . 10米C . 20米D . ~A BCD E米例6.(2012•益阳)超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A 处,离益阳大道的距离(AC )为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B 处行驶到C 处所用的时间为8秒,∠BAC=75°.(1)求B 、C 两点的距离;(2)请判断此车是否超过了益阳大道60千米/小时的限制速度(计算时距离精确到1米,参考数据:sin75°≈,cos75°≈,tan75°≈,3≈,60千米/小时≈米/秒)…类型四. 坡度与坡角例.如图,某水库堤坝横断面迎水坡AB 的坡比是1:3,堤坝高BC=50m ,则应水坡面AB 的长度是( )A .100mB .1003mC .150mD .503m类型五. 方位角1.已知:如图,一艘货轮向正北方向航行,在点A 处测得灯塔M 在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B 处,测得灯塔M 在北偏西45°,问该货轮继续向北航行时,与灯塔M 之间的最短距离是多少(精确到海里,732.13 )2.新闻链接,据[侨报网讯]外国炮艇在南海追袭中国渔船被中国渔政逼退2012年5月18日,某国3艘炮艇追袭5条中国渔船.刚刚完成黄岩岛护渔任务的“中国渔政310”船人船未歇立即追往北纬11度22分、东经110度45分附近海域护渔,保护100多名中国渔民免受财产损失和人身伤害.某国炮艇发现中国目前最先进的渔政船正在疾速驰救中国渔船,立即掉头离去.(见图1)《解决问题如图2,已知“中国渔政310”船(A)接到陆地指挥中心(B)命令时,渔船(C)位于陆地指挥中心正南方向,位于“中国渔政310”船西南方向,“中国渔政310”船位于陆地指挥中心南偏东60°方向,AB=海里,“中国渔政310”船最大航速20海里/时.根据以上信息,请你求出“中国渔政310”船赶往出事地点需要多少时间.}综合题:三角函数与四边形:1.如图,四边形ABCD 中,∠BAD=135°,∠BCD=90°,AB=BC=2, tan ∠BDC= 63. (1) 求BD 的长; (2) 求AD 的长.…2.如图,在平行四边形ABCD 中,过点A 分别作AE ⊥BC 于点E ,AF ⊥CD 于点F . (1)求证:∠BAE =∠DAF ; (2)若AE =4,AF =245,3sin 5BAE ∠=,求CF 的长.三角函数与圆:1. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与x 轴的正半轴交于点D ,B 是y 轴右侧圆弧上一点,则cos ∠OBC 的值为( ) A .12 B 3 C .35D .45;19. 已知:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接AC 与⊙O 交于点D, (1) 求证:∠AOD=2∠C (2) 若AD=8,tanC=34,求⊙O 的半径。
初三年级锐角三角函数知识点总结、典型例题、练习[精选]锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
6、正切的增减性:当0°<α<90°时,tan α随α的增大而增大,7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法))90cos(sin A A -︒=)90sin(cos A A -︒=BA cos sin =BA sin cos =A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba c8、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
初三下学期锐角三角函数知识点总结及经典例题1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
a 2b2c22、如下图,在 Rt △ABC 中,∠ C 为直角,则∠ A 的锐角三角函数为 ( ∠A 可换成∠ B):定义 表达式取值范围 关 系正A 的对边 asin Asin A弦斜边c余A 的邻边 bcos Acos A弦 斜边c正aA 的对边 tan Atan AA 的邻边b切余bA 的邻边cot Acot AA 的对边a切0 sin A 1( ∠A 为锐角)sin A cosBcos Asin B0 cosA1sin 2A cos 2A 1( ∠A 为锐角)tan A( ∠A 为锐角)tan A cot Bcot Atan Bcot A 0tan A1( 倒数 )cot A( ∠A 为锐tan A cot A 1角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦由 A BB值。
90对 得 B90A 斜边ca 边sin A cos(90 A)bsin A cosBcos Asin(90ACcos A sin BA)邻边三角函数的基本关系: 1 sin2cos21 sin21 cos2,cos21 sin2;2 sintansintan cos ,cossin .costan4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正由 AB 90切值。
得 B 90Atan A cot B tan A cot(90A)cot A tan(90A)cot A tan B5、0°、 30°、 45°、 60°、 90°特殊角的三角函数值 ( 重要 )三角函数0°30°45°60°90°sin01231222cos13210222tan0313不存在3cot不存在313036、正弦、余弦的增减性:当 0°≤≤90°时,sin随的增大而增大,cos随的增大而减小。