操纵与耐波计算
- 格式:docx
- 大小:56.71 KB
- 文档页数:4

船舶操纵运动波浪力计算2.1 不规则波入射力计算模型依据概率统计理论,不规则波的波面可以看作是由一系列具有不同的频率、波数、波幅、传播方向以及随机分布初相位角的规则波叠加而成。
在实际应用中寻求海浪的统计特性,通常采用“波能谱”的概念来描述海浪。
海浪形成的过程是风把能量传递给水的过程。
这一过程大致可分为两个阶段,第一阶段为波浪生长阶段,当风最初作用于海面上时,海面开始出现较小的波,随着时间的增长,风不断地把能量传递给水,波浪越来越大,显然这一阶段海浪是比较复杂,其统计特性随时间不断变化,这一阶段的海浪描述描述相当复杂。
但是,当波浪渐趋稳定时,波的能量达到一定值,其统计特征基本上不随时间变化,为了这一阶段海浪的数学描述,应用波谱密度函数,从大量观察分析结果表明海浪以及船舶在波浪中的运动等均属于狭带谱的正态随机过程,因此基于以下假设:1.波浪为弱平稳的、各态历经的、均值为零的正态(高斯)随机过程。
2.波谱的密度函数为窄带。
3.波峰(最大值)为统计上独立的。
由波的方向性谱密度,不规则波的波面可用下列随机积分表示来描述:⎰⎰-∞+-+=220),(2)],()sin cos (cos[),,(ππςθωθωθωεωθηθξηξςd d S t k t (2-1)其中,),(θωςS 为波谱密度函数,表示了不规则波浪中各种频率波的能量在总能量中所占的份量。
仅考虑波沿主浪向运动的情况,并将式(2-1)转化为随船坐标系下表示为:⎰∞+--=0)(2)]()sin cos (cos[),,(ωωωεωμμςςd S t y x k t y x e (2-2)为了方便计算,将波能谱密度函数进行离散,用求和形式代替上式的积分如下:∑=+--∆=ni i ei i i t y x k S t y x 1])sin cos (cos[)(2),,(εωμμωωςς (2-3)其中,相位角i ε可视为均匀分布在(0,2π)区间内的随机变量。


第一章船舶操纵基础理论通过本章的学习,要求学员概念理解正确,定义描述准确,对船舶操纵性能够正确评估,并具有测定船舶操纵性能的知识。
根据船舶操纵理论,操纵性能包括:1)机动性(旋回性能和变速运动性能)2)稳定性(航向稳定性)第一节船舶操纵运动方程为了定量地描述船舶的操纵运动,我们引入船舶操纵运动方程,用数学方法来讨论船舶的运动问题。
一、船舶操纵运动坐标系1.固定坐标系Ox0y0z0其原点为O,坐标分别为x0,y0,z0,由于我们仅讨论水面上的船舶运动,因此,该坐标系固定于地球表面。
作用于船舶重心的合外力在x0,y0轴上的投影分别为X0和Y0对z0轴的合外力矩为N2. 运动坐标系Gxyz其原点为点G (船舶重心),坐标分别为x ,y ,z ,该坐标系固定于船上。
这主要是为了研究船舶操纵性的方便而建立的坐标系。
x ,y ,两个坐标方向的运动速度分别为u 和v ,所受的外力分别为X 和Y ,对z 轴的转动角速度为r ,z 轴的外力矩为N 。
二、 运动方程的建立根据牛顿关于质心运动的动量定理和动量矩定理,船舶在水面的平面运动可由下列方程描述:y 0⎪⎩⎪⎨⎧===ϕZ og o og o I N y m Y x m X该式一般很难直接解出。
为了方便,将其转化为运动坐标系表示,这样可以使问题大为简化。
经过转换,得:⎪⎩⎪⎨⎧=+=-=r I N ur vm Y vr u m X Z )()( 该方程看似复杂,但各函数和变量都与固定坐标系没有关系,因此,可以使问题大为简化。
三、 水动力和水动力矩的求解对于上述方程中的水动力和水动力矩可表示为:⎪⎩⎪⎨⎧===),,,,,,(),,,,,,(),,,,,,(δδδr v u r v u f N r v ur v u f Y r v u r v u f X N Y X经过台劳级数展开,可得X ,Y ,N 对各自变量的偏导数,称为水动力导数和水动力矩导数,它们可以通过船模试验求得。



船舶操纵性:是指船舶按照驾驶者的意图保持或改变其运动状态的性能,即船舶能保持或改变其航速、航向和位置的能力。
航向稳定性:表示船舶在水平面内的运动受扰动而偏离平衡状态,当扰动完全消除后能保持其原有平衡状态的性能。
回转性:表示船舶在一定舵角作用下作圆弧运动的性能。
转首性:表示船舶应舵转首并迅速进入新的稳定状态的性能. 运动稳定性与机动性制约:小舵角下的航向保持性 、中舵角下的航向机动性 、大舵角下的紧急规避性固定与运动坐标系的关系:漂角:速度V 与OX 轴正方向的夹角β。
舵角:舵与OX 轴之间的夹角δ。
舵速角:重心瞬时速度矢量与O 0X 0轴之间的夹角ψ0。
线性水动力导数意义:船舶作匀速直线运动,在其他参数不变时,改变某一运动参数所引起的作用于船舶的水动力或矩对该参数的变化率。
水动力导数:Xu= Yu= 通常可称对线速度分量u 的导数为线性速度导数.如:Xu 等。
对横向速度分量v 的导数为位置导数,如:Yv 、Nv 等。
对回转角速度r 的导数为旋转导数,如:Nr 、Yr 等。
对各加速度分量和角加速度分量的导数为加速度导数Xu 。
,对舵角δ的导数为控制导数,如:Y δ等。
稳定性:对处于定常运动状态的物体(或系统),若受到极小的外界干扰作用而偏离原定常运动状态;当干扰去除后,经过一定的过渡过程,看是否具有回复到原定常运动状态的能力。
若能回复,则称原运动状态是稳定的。
直线稳定性:船舶受到瞬时扰动以后,重心轨迹最终恢复成为一条直线,但航向发生了变化。
方向稳定性:船舶受到的瞬时扰动消失以后,重心轨迹最终成为原航线平行的另一直线。
位置稳定性:船舶受到瞬时扰动,当扰动消失以后,重心轨迹最终恢复成为与原来航线的延长线。
稳定衡准数:C=-Y V (mx G u 1-N r )+N V (mu 1-Y r );C>0 表示船舶在水平面的运动具有直线稳定性;C<0 则不具有直线稳定性。
影响航向稳定性的因素:(1)为改善其航向稳定性,应使Nr 、Yv 二者的负值增加,从C 的表达式可见,此二者之乘积的正值就越大,显然有利于改善稳定性。

耐波性预报的数值方法随着海洋气象学的发展,耐波性预报成为海洋气象学研究的热点之一,其涵盖的范围广泛,包括海上工程、近岸海域和内陆水域等。
耐波性预报主要用于确定海浪对于结构物的影响,其精度和准确度对于海洋结构物的设计和施工来说至关重要。
本文将介绍一种常用的耐波性预报数值方法:波浪谱法。
波浪谱法是一种通过数学模型预测海浪高度的方法。
它基于统计学原理,将海浪高度看作频率的随机变量,利用矩阵特征值问题将其转化为谱表示,从而通过计算海浪频带的谱成分来预报海浪的高度。
波浪谱法可以分为线性和非线性两种方法。
线性波浪谱法适用于海浪高度比较小的情况,其核心公式为:$S(f) = \frac{4\pi^2}{g^2}f^{-5}e^{-\frac{5}{4}(\frac{f_p}{f})^4}$其中,$S(f)$是波浪谱,$f$是频率,$f_p$是波峰频率,$g$是重力加速度。
该公式基于对于波浪动能的能量守恒假设,即使在一定程度上违反了实际水文情况的非线性效应,但其计算精度较高,在近岸海域和海上工程的预报中得到了广泛应用。
非线性波浪谱法适用于海浪高度较大的情况,其核心公式包括:$S(f) = A(f) \times \delta(f-f_p) + B(f), A(f) =\frac{5}{16}\frac{H_m^2}{f_p^4}\frac{e^{\frac{-5}{4}(\frac{f_p}{f})^4}}{f^5}$其中,$H_m$是波高标准差,$\delta(f-f_p)$是一个峰值函数,$B(f)$是定常波谱。
非线性波浪谱法计算过程较为繁琐,需要考虑多种非线性效应,如波浪不对称性、波浪剧烈变化和能量流失等,但其计算精度更高,能够更准确地预报海浪高度。
波浪谱法还有一种改进方法——时域法。
时域法将波浪谱分解成一系列时间域中的波浪组件,通过求解波浪运动方程确定波浪高度随时间的变化。
时域法计算复杂度较高,但它可以考虑更多的非线性效应和海浪的时变性,能够更准确地预报大浪和风浪耦合下的海浪高度。

操纵性1.船舶操纵性定义及研究内容操纵性:船舶按照驾驶者的意图保持或改变其运动状态的性能。
即船舶能保持或改变航速、航向和位置的性能。
研究内容:航向稳定性、回转性、转首性及跟从性、停船性能。
2.船舶附加质量的含义及与物理质量比例的大致范围附加质量:附加惯性力与船的加速度成比例,其比例系数称为附加质量。
(作不定常运动的船舶,除了船体本身受到与加速度成比例的惯性力外,同时船体作用于周围的水,使之得到加速度,根据作用与反作用原理,水对船体存在反作用力,这个反作用力称为附加惯性力。
)附加质量:m x ≈(0.05~0.15)m m y ≈m z ≈(0.9~1.2)m附加惯性矩Jxx ≈(0.05~0.15)Izz Jyy ≈(1~2)Izz Jzz ≈Iyy I 是质量惯性矩 3.漂角、航向角和水动力中心的含义漂角:船舶重心处的速度矢量→V 与x 轴正方向的交角称为漂角β。
并规定速度矢量转向x 轴顺时针方向为正。
航向角:船首指向的方向和船舶在水面上的真实轨迹之间的夹角。
4动坐标系统速度转换到大地坐标系统公式:φφsin cos 00Y X X += φφsin cos 00X Y Y -= 5、线性水动力导数Yv,Nv,Yr,Nr 的物理意义 水动力的位置导数Yv 是一个较大的负值。
水动力力矩的位置导数Nv 是一个不大的负值。
指的是v 引起的升力系数/力矩系数水动力的旋转导数Yr 的绝对值不是很大,其符号由船型决定,可正可负。
水动力矩的旋转导数Nr 是一个很大的负值 。
指的是r 引起的水动力系数/水动力矩系数6、线/角加速度水动力导数的物理意义及数值大小判断水动力的线加速度导数.VY 是一个相当大的负值。
指的是附加质量水动力矩的线加速度导数.VN 是一个不大的数值,其符号取决于船型。
指的是由V •引起的附加惯性力矩系数水动力的角加速度.rY 是一个较小的值,其符号取决于船型水动力矩的角加速度导数.rN 是一个很大的负值。

操纵性简答题以下选择的作业题目,最具有代表意义,最能反馈作业的实际情况,现分析如下:2,线性操纵运动数学模型中八个水动力导数,说明其含义,并分析数量级大小。
答:略【分析】:此题所有答案都可在课本上面找到,但是要答得完全并非易事。
需要指出的是,大多数同学都答得并不完全,少部分同学的答案显得对本题的解答不够耐心,态度不够端正,这是需要改进的地方。
3,某传经实验表明不具备直线稳定性,试问采取什么措施能使稳定性改善?答:与v Y ,v N ,r Y ,r N 相关.1).|v Y |,|r N |越大,航向稳定性就越好 2).r N ,v N 为正,保证了航向稳定性3).升力面设置在尾部可使r N 负值增大,而使v N 值变化,故尾部设置比首部要好.具体措施:a.增大船长使r N 负值增大.b.增大纵中剖面侧面积使r N ,v Y 负值增大.c.增大纵中剖面尾部面积使v N 增大(增加呆木,安装尾鳍,削去前踵等)【分析】:大体上来讲回答情况较好,但是一些要点并没有完全的答出来,说明对概念的理解还需要更进一步的斟酌,回答得不是很仔细。
4,如何粗略估算回转初期转首时间?答:近似认为,阶跃操舵后,初始阶段船舶的回转是等角加速度运动的,首向角ψ的变化为:222121t C t rp δψ== ,则pC t 1.2δψ=(δδδ.p r z C N I N r =-≈,C p 为初始回转有因次角加速度参数),当pooC t 1,5,10===ψδ 经验表明,pC 1相当于操舵角o15时,首向角ψ改变o 5所需的时间.【分析】:学生普遍做得良好,对定义的理解比较深刻。
5,从受力角度来分析船舶回转过程的横倾情况? (图形见课本P27,请与水滴型潜艇做比较) 答:图一内倾:转舵,0==r v图二外倾:过渡 图三外倾:0==rv (V,r为定值) (图形见课本P27)【分析】:此题解答情况不错,大部分同学都回答得很好。

操纵性绪论操纵性定义:船舶按照驾驶者的意图保持或改变其运动状态的性能,即船舶能保持或改变航速、航向和位置的性能。
操纵性内容:1. 航向稳定性:表示船舶在水平面内的运动受扰动而偏离平衡状态,当扰动完全消除后能保持其原有平衡状态的性能。
2.回转性:表示船舶在一定舵角作用下作圆弧运动的性能。
3.转首性和跟从性:表示船舶应舵转首及迅速进入新的稳定运动状态的性能。
4. 停船性能:船舶对惯性停船和盗车停船的相应性能。
附加质量和附加惯性矩:作不定常运动(操纵和耐波运动)的船舶,除了船体本身受到愈加速度成比例的惯性力外,同时船体作用于周围的水,使之得到加速度。
根据作用力和反作用力,水对船体存在反作用力,这个反作用力称为附加惯性力。
附加惯性力是与船的加速度成比例的,其比例系数称为附加质量。
船舶操纵一、操纵运动方程1.1坐标系一、固定坐标系:固定坐标系是固结在地球表面,不随时间而变化的,如图所示。
首向角ψ:X 0与X 的夹角(由X 0转向X ,顺时针为正)。
二、运动坐标系:运动坐标系是固结在船体上的,随船一起运动的,如图所示。
重心坐标:X OG 、Y OG ; 船速:V 重心G 瞬时速度; 航速角ψ0:X0轴与船速V 夹角(顺时针为正);漂角:β船速与X 轴夹角(顺时针为正); 回转角速度:γ=dψdt;回转曲率:R 右舷为正; 舵角:δ左舷为正。
三、枢心:回转时漂角为零点、横向速度为零的点。
1.2线性运动方程一、坐标转换00cos sin sin cos ψψψψ=-=+G G x u v y u v二、简化方程当重心在原点处:X G =0 运动坐标系一般方程:三、对于给定船型、给定流体中的运动情况船型参数和流体特性为已知条件; 操纵运动为缓变过程,忽略高阶小量; 忽略推进器转速影响;操舵过程短暂,忽略转舵加速度。
则可将给定船型流体中受力情况表示如下:由泰勒展开式,用水动力导数表示如下:四、简化后的操纵运动线性方程式:2()()()ψψψψψψ=--=++=++G G Z G X m u v x Y m v u x N I mx vu 00cos sin ψψ=+G G X mx my 00cos sin ψψ=-G G Y mymx ()()ψψψ=-=+=z X m u v Y m v u NI (,,,,,,)(,,,,,,)(,,,,,,)X X u v r u v r Y Y u v r u v r N N u v r u v r δδδ===v r v r v r v r Y Y v Y r Y v Y r Y N N v N r N v N r N δδδδ=++++=++++11111()()()()()()()()v v G r r G v v z r G r v ur v u u r r v u rm Y v Y v mx Y r mu Y r Y mx N v N v I N r mx u N r N δδδδ+=++∆+∆=+--+-+-=--+-+-=1.3水动力导数一、定义:匀速直线运动时,只改变一个运动参数,其他不变引起的作用于船舶水动力对运动参数的变化率。
漂角:船舶重心处速度与动坐标系中ox轴之间的夹角,速度方向顺时针到ox 轴方向为正。
首向角:船舶纵剖面与固定坐标系OX轴之间的夹角,OX到x轴顺时针为正舵角:舵与动坐标系ox轴之间的夹角,偏向右舷为正航速角:重心瞬时速度与固定坐标系OX轴的夹角,OX顺时针到速度方向为正浪向角:波速与船速之间的夹角。
作用于船体的水动力、力矩将与其本身几何形状有关(L、m、I),与船体运动特性有关(u、v、r、n),也与流体本身特性有关(密度、粘性系数、g)。
对线速度分量u的导数为线性速度导数Xu,对横向速度分量v的导数为位置导数Yv,Nv,对回转角速度r的导数为旋转导数Nr,Yr,对各角速度分量和角加速度分量的导数为加速度导数Xu,Yv,Yr,对舵角的导数为控制导数Y。
直线稳定性:船舶受瞬时扰动后,最终能恢复指向航行状态,但是航向发生了变化;方向稳定性:船舶受瞬时扰动后,新航线为与原航线平行的另一直线;位置稳定性:船舶受瞬时扰动后,最终仍按原航线的延长线航行;具备位置稳定性的必须具备直线和方向稳定性,具备方向稳定性的必定具有直线线运动稳定性。
1. 反横距2. 正横距3.纵距4. 战术直径5. 定常回转直径回转的三个阶段船舶回转过程中,在船上还存在一点,于改点上其横向速度分量为零,称之为枢心点P。
一、转舵阶段二、过渡阶段三、定常回转阶段耦合特性:船舶在水平面内作回转运动时会同时产生横摇、纵摇、升沉等运动,以及由于回转过程中阻力增加引起的速降。
以上所述可理解为回转运动的耦合,其中以回转横倾与速降最为明显。
舵的布置原则1. 为了产生尽可能大的舵力矩,舵应布置在远离船舶重心处:船首尾部。
2. 注意使舵得到突出的尾型的保护。
3. 为了获得桨的尾流来提高舵效,一般布置在桨的后方。
4. 多舵布置时必须注意舵之间的干扰问题。
船舶耐波性:船舶任意时刻的运动可以分解为船舶重心G沿Ox轴的直线运动称为纵荡,以x(t)表示;沿Oy轴的直线运动称为横荡,以y(t)表示;沿Oz轴的直线运动称为垂荡,以z(t)表示;船体绕Gxb轴的转动称为横摇,以θ(t)表示;绕Gyb轴的转动称为纵摇,以ψ(t)表示;绕Gzb轴的转动称为首摇,以φ(t)表示。
1.什么是船舶耐波性?船舶耐波性是指船舶在波浪扰动下,产生各种摇荡运动、抨击、甲板上浪、失速、螺旋桨出水以及波浪弯矩等,仍能维持一定航速在波浪中安全航行的性能。
(P1)2.什么是有效波面?船宽、吃水相对波长是很小时,可近似认为船是水中一质点,它所受的浮力近似垂直于波面。
当船宽和吃水相对波长为有限尺度时,由于船宽范围内波形曲率的变化以及沿船体水下表面所受到的浮力方向与波面法向不一致,使船受到的总浮力有所减小,同时其浮力作用线是垂直于某一次波面,这一次波面称为有效波面。
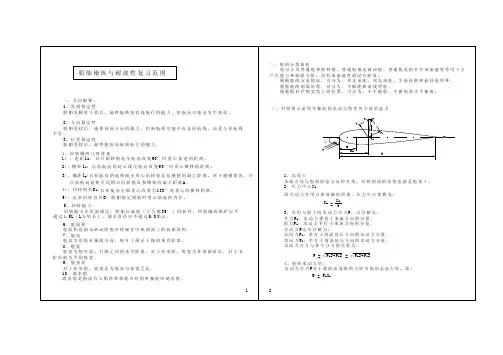
(P17)3.船舶阻尼力(矩)按物理性质大致可分为哪三类?兴波阻尼、旋涡阻尼、摩擦阻尼(P8)4.船在水中可能产生六个自由度的摇荡运动,分别是什么运动?横摇、纵摇、首摇、垂荡(升沉)、横荡和纵荡5.研究船舶耐波性用到的三种坐标系是哪三种,可画图说明?空间固定坐标系:该坐标系用来描述海浪;动坐标系Gxbybzb:随船做摇荡运动,坐标原点取在船的重心G上,坐标轴取作与船的中心惯性主轴相重合,Gxb在船中线面与龙骨线平行,向艏为正;Gzb在船中线面内垂直于Gxb,向上为正;Gyb垂直于船的中线面,向右舷为正。
随船移动的平衡坐标系Oxyz:当船在静水中以航速v航行时,该坐标系随船同速前进,Oxy位于静水面上,Ox正向与航速v同向。
当船在波浪上做摇荡运动时,该坐标系不随船做摇荡,仍保持按船的平均速度和原航向前进。
6.船模实验需要满足的相似律有那几个?几何相似、运动相似、动力相似。
(P136-P137)7.什么是船舶摇荡运动的兴波阻尼?(P9)由于船舶运动使水面产生波浪,消耗船本身的能力所造成的阻尼。
傅汝德认为兴波阻尼与速度一次方成比例。
8.目前采用较广泛的减摇装置有哪些?舭龙骨、减摇水舱、减摇鳍(P168)9.什么是有效波面角?有效波面的切线与水平间线间的夹角,恒小于真实波面角。
(P14 p17)10.什么是史密斯效应?波浪下任一点的压力随深度按指数递减的规律,称为“史密斯效应”。
首向角:船舶纵剖面与OoXo轴的交角。
漂角:重心速度与GX轴正方向夹角。
航速角:重心瞬时速度矢量与OoXo轴夹角。
船舶操纵性是指船舶按照驾驶者的意图保持或改变其运动状态的性能,即船舶能保持或改变其航速、航向和位置的性能。
包括小舵角的航向稳定性、中舵角的航向机动性和大舵角的紧急规避性。
内容如下:1. 航向稳定性:表示船舶在水平面内的运动受扰动而偏离平衡状态,当扰动完全消除后能保持其原有平衡状态的性能。
表示船舶在水平面内的运动受扰动而偏离平衡状态,当扰动完全消除后能保持其原有平衡状态的性能。
2.回转性:表示船舶在一定舵角作用下作圆弧运动的性能。
3.转首性和跟从性:表示船舶应舵转首及迅速进入新的稳定运动状态的性能。
4. 停船性能:船舶对惯性停船和盗车停船的相应性能。
枢心:回转时漂角为零点、横向速度为零的点。
附加惯性力:作不定常运动的船舶,除本身受到与加速度成比例的惯性力外,同时船体作用于周围的水,使之得到加速度,根据作用与反作用力原理,水对船体存在反作用力,这个力称为。
附加质量:附加惯性力是与船的加速度成比例的,其比例系数称为。
水动力导数:位置导数 Yv ,Nv:船体受到一个升力Yv,船体首部和尾部长力方向一致,v都都指向v的负方向,因此合力是一个较大的负值,Yv是一个较大的负值,而水动力矩由于首尾作用相抵消,其绝对值不会很大,因机翼的水动力中心在形成之前,首部作用占优,Nv是一个不大的负值。
加速度导数:Yv点是水动力Y相对于加速度在平衡状态下的变化率,正的加速度的船舶经受一个与加速度相反方向的水反作用力,因此Yv点是一个相当大的负值。
由于船首和船尾对Z轴产生的水动力力矩方向相反,因此水动力矩导数Nv点是一个不大的数值,其符号取决于船型。
旋转导数Yr ,Nr:由于船首和船尾水动力方向相反,因此水动力导数Yr的绝对值不是很大,其符号取决于船型,可正可负。
由于船体回转产生的水动力矩在船首尾有相同的方向,都是阻止船舶回转的,因此水动力矩导数Nr是一个很大的负值。
漂角:船舶重心处速度与动坐标系中ox轴之间的夹角,速度方向顺时针到ox 轴方向为正。
首向角:船舶纵剖面与固定坐标系OX轴之间的夹角,OX到x轴顺时针为正舵角:舵与动坐标系ox轴之间的夹角,偏向右舷为正航速角:重心瞬时速度与固定坐标系OX轴的夹角,OX顺时针到速度方向为正浪向角:波速与船速之间的夹角。
作用于船体的水动力、力矩将与其本身几何形状有关(L、m、I),与船体运动特性有关(u、v、r、n),也与流体本身特性有关(密度、粘性系数、g)。
对线速度分量u的导数为线性速度导数Xu,对横向速度分量v的导数为位置导数Yv,Nv,对回转角速度r的导数为旋转导数Nr,Yr,对各角速度分量和角加速度分量的导数为加速度导数Xu,Yv,Yr,对舵角的导数为控制导数Y。
直线稳定性:船舶受瞬时扰动后,最终能恢复指向航行状态,但是航向发生了变化;方向稳定性:船舶受瞬时扰动后,新航线为与原航线平行的另一直线;位置稳定性:船舶受瞬时扰动后,最终仍按原航线的延长线航行;具备位置稳定性的必须具备直线和方向稳定性,具备方向稳定性的必定具有直线线运动稳定性。
1. 反横距2. 正横距3.纵距4. 战术直径5. 定常回转直径回转的三个阶段船舶回转过程中,在船上还存在一点,于改点上其横向速度分量为零,称之为枢心点P。
一、转舵阶段二、过渡阶段三、定常回转阶段耦合特性:船舶在水平面内作回转运动时会同时产生横摇、纵摇、升沉等运动,以及由于回转过程中阻力增加引起的速降。
以上所述可理解为回转运动的耦合,其中以回转横倾与速降最为明显。
舵的布置原则1. 为了产生尽可能大的舵力矩,舵应布置在远离船舶重心处:船首尾部。
2. 注意使舵得到突出的尾型的保护。
3. 为了获得桨的尾流来提高舵效,一般布置在桨的后方。
4. 多舵布置时必须注意舵之间的干扰问题。
船舶耐波性:船舶任意时刻的运动可以分解为船舶重心G沿Ox轴的直线运动称为纵荡,以x(t)表示;沿Oy轴的直线运动称为横荡,以y(t)表示;沿Oz轴的直线运动称为垂荡,以z(t)表示;船体绕Gxb轴的转动称为横摇,以θ(t)表示;绕Gyb轴的转动称为纵摇,以ψ(t)表示;绕Gzb轴的转动称为首摇,以φ(t)表示。
船舶操纵与避碰9101:3000总吨及以上船舶船长9102:500~3000总吨船舶船长9103:3000总吨及以上船舶大副9104:500~3000总吨船舶大副9105:3000总吨及以上船舶二/三副9106:500~3000总吨船舶二/三副1.11.21.2.2.1 操舵装置的概念与种类:电动操舵装置与液压操舵装置√ √ √ 1.2.2.2 操舵装置——舵角限位器的作用、种类与限制角 √ √ √ 1.2.2.3 SOLAS 公约与我国《钢质船舶入级规范》对操舵装置的要求√ √ √ √ √ √ 1.2.2.4 操舵装置控制系统——随动操舵系统的种类与基本控制原理√ √ √ 1.2.2.5 操舵装置控制系统——应急控制系统的特点与使用要领√ √ √ √ √ √ √ √ 1.2.2.6 自动舵的种类与各自的特点√ √ √ 1.2.2.7 自动舵的操舵转换方式:随动舵、自动舵、应急舵的转换及适用的场合√ √ √ √ √ √ √ √ 1.2.2.8 自动舵调节旋钮的使用 √ √ √ 1.2.2.9 使用自动舵的注意事项 √ √ √ 1.2.2.10 舵设备的作用及其组成√ √ √ 1.2.2.11 舵的种类及特点:分别根据舵叶剖面形状、舵杆轴线位置、舵的支承方式分类、特种舵√ √ √ 1.2.2.12 流线型平衡舵的结构、组成,各组成部分的作用、特点与满足的要求√ √ √ 1.2.2.13 舵力的概念; 影响舵力的因素 √ √ √ √ √ √ 1.2.2.14 舵力转船力矩√ √ √ √ √ √ 1.2.2.15 舵效的概念及其影响因素 √ √ √ √ √ √ 1.2.2.16 舵设备的日常与定期检查保养 √ √ √ 1.2.3 锚设备及其运用1.2.3.1 锚设备的组成及各部分的作用、锚的种类、特点及应用√ √ √ 1.2.3.2 锚链的种类、组成与标记√√√√√√1.2.3.3 锚机的主要技术要求√√√√√√1.2.3.4 锚设备的检查、保养及检验要求√√√1.2.3.5 锚的作用√√√√√√1.2.3.6 锚地选择√√√√√√√√1.2.3.7 锚泊方式、抛起锚作业程序、操纵要领及注意事项√√√√√√√√√1.2.3.8 操纵用锚的抓力及拖锚淌航距离的估算√√√1.2.3.9 单锚泊用锚的抓力的组成、单锚泊用锚的抓力系数√√√√√√√√1.2.3.10 锚泊用锚的出链长度的组成及安全锚泊出链长度的计算√√√√√√√√1.2.3.11 单锚泊船的偏荡、缓解偏荡的方法√√√√√√1.2.3.12 走锚的判断及应急措施√√√√√√√√√1.2.3.13 清解锚链绞缠√√√√√1.2.4 缆的运用1.2.4.1 系船缆的种类和特点√√√1.2.4.2 系缆的名称与作用√√√1.2.4.3 系泊设备的组成与应用√√√1.2.4.4 绞缆机的种类、作用与应用√√√1.2.4.5 缆车及其附属用具的种类与作用√√√1.2.4.6 系泊设备的检查保养和使用注意事项√√√1.2.4.7 靠、离泊时缆绳的应用√√√√√√1.2.4.8 靠、离泊用缆的注意事项√√√√√√1.2.5 拖船的运用1.2.5.1 拖船的种类及其特点√√1.2.5.2 拖船使用方式√√1.2.5.3 协助操船所需拖船功率的估算√√1.32.12.22.3 2.42.53.2 3.33.54.16.16.26.36.46.56.5.3.2 对遇局面构成要件 √ √ √ √ √ √ √ √ √ 6.5.3.3 对遇局面的特点 √ √ √ √ √ √ √ √ √ 6.5.3.4 避让责任与行动√ √ √ √ √ √ √ √ √ 6.5.3.5 危险对驶局面的理解及避让特点 √ √ √ √ √ √ √ √ √ 6.5.4 交叉相遇局面6.5.4.1 适用范围√ √ √ √ √ √ √ √ √ 6.5.4.2 交叉相遇局面的构成要件 √ √ √ √ √ √ √ √ √ 6.5.4.3 交叉相遇局面的特点 √ √ √ √ √ √ √ √ √ 6.5.4.4 避让责任与行动 √ √ √ √ √ √ √ √ √ 6.5.5 让路船的行动6.5.5.1 让路责任的确定 √ √ √ √ √ √ √ √ √ 6.5.5.2 避让原则 √ √ √ √ √ √ √ √ √ 6.5.6 直航船的行动6.5.6.1 直航船的含义√ √ √ √ √ √ √ √ √ 6.5.6.2 保向保速的含义及适用时机√ √ √ √ √ √ √ √ √ 6.5.6.3 可独自采取避让行动的时机及行动的注意事项 √ √ √ √ √ √ √ √ √ 6.5.6.4 应采取最有助于避碰行动的时机及行动的注意事项√ √ √ √ √ √ √ √ √ 6.5.6.5 让路船的责任 √ √ √ √ √ √ √ √ √ 6.5.7 船舶之间的责任6.5.7.1 确定船舶之间责任的原则√ √ √ √ √ √ √ √ √ 6.5.7.2 与其他条款之间的联系以及互见中让路责任的确定√ √ √ √ √ √ √ √ √ 6.5.7.3 机动船与其他船之间的责任 √ √ √ √ √ √ √ √ √ 6.5.7.4 帆船与其他船之间的责任√ √ √ √ √ √ √ √ √ 6.5.7.5 从事捕鱼的船舶与其他船之间的责任 √ √ √ √ √ √ √ √ √ 6.5.7.6 限于吃水的船舶与其他船之间的责任√√√√√√√√√6.66.77.17.28.18.3 8.4。
操纵性简答题以下选择的作业题目,最具有代表意义,最能反馈作业的实际情况,现分析如下:2,线性操纵运动数学模型中八个水动力导数,说明其含义,并分析数量级大小。
答:略【分析】:此题所有答案都可在课本上面找到,但是要答得完全并非易事。
需要指出的是,大多数同学都答得并不完全,少部分同学的答案显得对本题的解答不够耐心,态度不够端正,这是需要改进的地方。
3,某传经实验表明不具备直线稳定性,试问采取什么措施能使稳定性改善?答:与v Y ,v N ,r Y ,r N 相关.1).|v Y |,|r N |越大,航向稳定性就越好 2).r N ,v N 为正,保证了航向稳定性3).升力面设置在尾部可使r N 负值增大,而使v N 值变化,故尾部设置比首部要好.具体措施:a.增大船长使r N 负值增大.b.增大纵中剖面侧面积使r N ,v Y 负值增大.c.增大纵中剖面尾部面积使v N 增大(增加呆木,安装尾鳍,削去前踵等)【分析】:大体上来讲回答情况较好,但是一些要点并没有完全的答出来,说明对概念的理解还需要更进一步的斟酌,回答得不是很仔细。
4,如何粗略估算回转初期转首时间?答:近似认为,阶跃操舵后,初始阶段船舶的回转是等角加速度运动的,首向角ψ的变化为:222121t C t rp δψ== ,则pC t 1.2δψ=(δδδ.p r z C N I N r =-≈,C p 为初始回转有因次角加速度参数),当pooC t 1,5,10===ψδ 经验表明,pC 1相当于操舵角o15时,首向角ψ改变o 5所需的时间.【分析】:学生普遍做得良好,对定义的理解比较深刻。
5,从受力角度来分析船舶回转过程的横倾情况? (图形见课本P27,请与水滴型潜艇做比较) 答:图一内倾:转舵,0==r v图二外倾:过渡 图三外倾:0==rv (V,r为定值) (图形见课本P27)【分析】:此题解答情况不错,大部分同学都回答得很好。
1.某船经实验表明不具备直线稳定性,试问采取什么措施能使稳定性改善?
答:与Yv ,Nv ,Yr ,Nr 相关.
1.|Yr |,|Nr |越大,航向稳定性就越好 2.Nr ,Nv 为正,保证了航向稳定性
3.升力面设置在尾部可使Nr 负值增大.具体措施:a.增大船长使Nr 负值增大.b.增大纵中剖面侧面积使Nr ,Yv 负值增大.c.增大纵中剖面尾部面积使Nv 增大(增加呆木,安装尾鳍,削去前踵等)
2.水滴型潜艇潜入水中重心总比浮心低。
说明其定常回转过程中潜艇的横倾方向。
(假设水动力作用于浮心)
整个过程都是内倾状态。
通过对舵力、船体惯性力和流体惯性力的定性分析,初始状态r=v=0,舵力较大,产生内倾。
过渡阶段舵力逐渐减小,直到定常回转的时候,只有常数v 、r 作用,而舵力较小可忽略,仍为内倾转态。
3.0=δ,受外界干扰8秒后,r 衰减一半,求T?
解:根据一阶操纵运动方程得:δψψ
K T =+ ,当0=+ψψ T ,T
t
e c r -
==*ψ , 当0=t 时,c r r ==0;当8=t 时,02
1r r =,推出08021r e
r T
=-
,即2
1
8
=-T e ,得)(54.11s T =
4.对方程a 22v +a 23ψ
=0,a 32v +a 33ψ
=0,应采取什么办法才能实现ψ稳定。
试写出实现方向稳定性的条件。
解:方程变形:(a 32a 23−a 22a 33)ψ=0 ,若要实现ψ稳定的目的,则ψ=0,
则:a 32a 23
−a 22a 33≠0
5. 求K (回转性指数)、T (应舵指数)过程:
由一阶线性响应方程T r +r =Kδ,因为r
=
dψ
dt ,所以有T
dψ2
dt +
dψ
dt
=Kδ
考虑螺旋桨尾流的不对称性和其他因素,须有一压舵角δr (向左为正)使船保持直航。
当实际舵角为δ,实效舵角为δ+δr 。
在ψ曲线t=0处作切线,后继各峰作平行线得切点O ,e ,e’,e ’’,对应时间为0,te ,te ’,te’’。
①把上述方程两端分别在(0,te ’)和(0,te ’’)区间积分得:
ψe ′=K δdt +Kδr t e ′t e ′0;ψe ′′=K δdt +Kδr t e ′′t e ′′
联立得K 和δr ,K 记作K 68
②在(0,te )积分:ψe =K δdt +Kδr t e t e
,代入已求δr 得K 4
③在(t2,te )(下标为2表示舵角曲线上第二个折点)区间积分得
−T ψ2
−ψe + ψ2−ψe =K δdt +Kδr (t e −t 2)t e
t 2
由于 ψ0
−ψe ,K=K4,代入δr 值可求得T ,记作T 4. ④分别在(t4,te ’)和(t6,te ’’)积分得:
−T ψ4
−ψ0 + ψe ′−ψ4 =K δdt +Kδr (t e ′−t 4)t e ′
t 4
−T ψ6
−ψ0 + ψe ′′−ψ6 =K δdt +Kδr (t e ′′−t 6)t e ′′
t 6
以δr 和K 68代入,分别求的T 6,T 8,且取T 68=(T 6+T 8)/2
⑤K 4,T 4为最初一个峰区的K 、T 指数,K 68和T 68为后两个峰区的K 、T 指数,两者的平均值即为本船指数:即K=(K 4+K 68)/2;T=(T 4+T 68)/2
6、无因次计算
1. m′−Y′v v ′−Y′v v′−Y′r r ′+ m′−Y′r r′=Y′δδ −N ′v v ′−N ′v v′+ I ′zz −N ′r r ′−N r ′r′=N′δδ
2. C =Y v ′N r ′−N v ′ Y r ′−m′ >0
3. r =K δ
,
K =
Y δN v −N δY v
Y v N r +N v mu 1−Y r
=
Y δN v −N δY v
C
4.
R 0
′
=
R 0L
,R 0=
V G r 0=
u 1r 0
→
R 0
′=
u 1′r 0′
5.R 0=V
Kδ
→ K ′
=
1
R 0
′δ
1.某船的排水量为D1=3000t,h=0.8m.横摇周期9s,与其相似的另一艘船排水量D2=4000t,h=0.85,问该船的固有周期T
解:设两船的尺度比为λ,λ3=D1
D2
=3000
4000
,λ5=
I x1
I x2
,因为Tθ=2π I x
Dℎ
由:Tθ1
Tθ2
=I x1
I x2
×D2
D1
×0.85
0.8
得Tθ
2
=9.65s.
万吨级货船,船长L=143.16m,纵摇和垂荡的固有周期T e=Tθ=6.1s,以航速v=17kn=8.74m/s,在三一平均波高ζw/3 =4 m的风浪中迎浪航行判断其临界状态。
解:谐摇周期λ=V∙T e+0.78T e2+V∙T e+0.78T e22−V2∙T e2=145m
其中(波浪对船舶的扰动力周期遭遇周期)T e=
λ
C+V
=
1.25λ+V
λ最大能量=40ζw/3=160m;主成分波区143.16~160m
λ最大有义=60ζw/3=240m;有义成分波区间:110~240m
故船舶在临界区域航行纵摇是最严重的。
1.排水量为10000t,初稳性高h=0.90m的船舶横摇固有周期为14s。
若在重心的上面2m减少1000t重量,问新的横摇周期?(稳心M的位置认为不变,由于重心改变要求绕新的GX轴的转动惯量)
解:重心改变前:
I x=Tθ2
Dℎ=
142
×10000×0.9=44727.98tf∙m∙s2
由静力学知识可知:D−p∆=D×0+P×2
重心改变高度∆=−2
9
m,新的初稳性高h’=1.122m
根据移轴公式,I′x=I x+10000×2
9
2
−1000×2+2
9
2
=40283.6
可求得新的横摇周期Tθ=2π
I′x
D′ℎ′
=12.545s
2.已知船的横摇固有周期T=13s,初稳性高h=1m,无因次阻尼衰减系数μ=0.1.
计算:(1)使船产生共振的波长;
(2)若波浪最大倾角α0=0.534λ−14(弧度),求共振时最大幅值;
(3)若使该船由于载荷分布发生改变(排水量不变),总的质量惯性矩降低了10%,欲使固有周期不变,问初稳性高度改变了多少?在此情况下,假定阻尼距系数2N保持不变,试求共振横摇角度。
解:(1)λ=1.56T2=263.8m
(2)α0=0.534λ−14=0.132rad,
由α0=kζa,ζa=α0
=
λ∙α0
=
263.8×0.132
=5.542m
(3)由Tθ=2π I x
Dℎ
知,总的质量惯性矩降低了10%,且D不变,则欲使固有
周期不变,初稳性高度也降低了10%。
在这种情况下,求共振横摇角度,新的情况下无因次阻尼衰减系数:
μ′=
N
I′x D′h′=
1
0.9×0.9
=0.111
θa=Kθ
a ∙α0=α0
2μ
=0.132
2×0.111
=0.594rad=34.155°。